Linear regression, the ridge regression estimator, and eigenvalue shrinkage

[math] \require{textmacros} \def \bbeta {\bf \beta} \def\fat#1{\mbox{\boldmath$#1$}} \def\reminder#1{\marginpar{\rule[0pt]{1mm}{11pt}}\textbf{#1}} \def\SSigma{\bf \Sigma} \def\ttheta{\bf \theta} \def\aalpha{\bf \alpha} \def\bbeta{\bf \beta} \def\ddelta{\bf \delta} \def\eeta{\bf \eta} \def\llambda{\bf \lambda} \def\ggamma{\bf \gamma} \def\nnu{\bf \nu} \def\vvarepsilon{\bf \varepsilon} \def\mmu{\bf \mu} \def\nnu{\bf \nu} \def\ttau{\bf \tau} \def\SSigma{\bf \Sigma} \def\TTheta{\bf \Theta} \def\XXi{\bf \Xi} \def\PPi{\bf \Pi} \def\GGamma{\bf \Gamma} \def\DDelta{\bf \Delta} \def\ssigma{\bf \sigma} \def\UUpsilon{\bf \Upsilon} \def\PPsi{\bf \Psi} \def\PPhi{\bf \Phi} \def\LLambda{\bf \Lambda} \def\OOmega{\bf \Omega} [/math]

High-throughput techniques measure many characteristics of a single sample simultaneously. The number of characteristics [math]p[/math] measured may easily exceed ten thousand. In most medical studies the number of samples [math]n[/math] involved often falls behind the number of characteristics measured, i.e: [math]p \gt n[/math]. The resulting [math](n \times p)[/math]-dimensional data matrix [math]\mathbf{X}[/math]:

[[math]] \begin{eqnarray*} \mathbf{X} & = & \left( X_{\ast,1} \, | \, \ldots \, | \, X_{\ast,p} \right) \, \, \, = \, \, \, \left( \begin{array}{c} X_{1,\ast} \\ \vdots \\ X_{n,\ast} \end{array} \right) \, \, \, = \, \, \, \left( \begin{array}{ccc} X_{1,1} & \ldots & X_{1,p} \\% \vdots & \ddots & \vdots \\ X_{n,1} & \ldots & X_{n,p} \end{array} \right) \end{eqnarray*} [[/math]]

from such a study contains a larger number of covariates than samples. When [math]p \gt n[/math] the data matrix [math]\mathbf{X}[/math] is said to be high-dimensional, although no formal definition exists.

In this chapter we adopt the traditional statistical notation of the data matrix. An alternative notation would be [math]\mathbf{X}^{\top}[/math] (rather than [math]\mathbf{X}[/math]), which is employed in the field of (statistical) bioinformatics. In [math]\mathbf{X}^{\top}[/math] the columns comprise the samples rather than the covariates. The case for the bioinformatics notation stems from practical arguments. A spreadsheet is designed to have more rows than columns. In case [math]p \gt n[/math] the traditional notation yields a spreadsheet with more columns than rows. When [math]p \gt 10000[/math] the conventional display is impractical. In this chapter we stick to the conventional statistical notation of the data matrix as all mathematical expressions involving [math]\mathbf{X}[/math] are then in line with those of standard textbooks on regression.

The information contained in [math]\mathbf{X}[/math] is often used to explain a particular property of the samples involved. In applications in molecular biology [math]\mathbf{X}[/math] may contain microRNA expression data from which the expression levels of a gene are to be described. When the gene's expression levels are denoted by [math]\mathbf{Y} = (Y_{1}, \ldots, Y_n)^{\top}[/math], the aim is to find the linear relation [math]Y_i = \mathbf{X}_{i, \ast} \bbeta[/math] from the data at hand by means of regression analysis. Regression is however frustrated by the high-dimensionality of [math]\mathbf{X}[/math] (illustrated in Section The ridge regression estimator and at the end of Section Constrained estimation ). These notes discuss how regression may be modified to accommodate the high-dimensionality of [math]\mathbf{X}[/math]. First, linear regression is recaputilated.

Linear regression

Consider an experiment in which [math]p[/math] characteristics of [math]n[/math] samples are measured. The data from this experiment are denoted [math]\mathbf{X}[/math], with [math]\mathbf{X}[/math] as above. The matrix [math]\mathbf{X}[/math] is called the design matrix. Additional information of the samples is available in the form of [math]\mathbf{Y}[/math] (also as above). The variable [math]\mathbf{Y}[/math] is generally referred to as the response variable. The aim of regression analysis is to explain [math]\mathbf{Y}[/math] in terms of [math]\mathbf{X}[/math] through a functional relationship like [math]Y_i = f(\mathbf{X}_{i,\ast})[/math]. When no prior knowledge on the form of [math]f(\cdot)[/math] is available, it is common to assume a linear relationship between [math]\mathbf{X}[/math] and [math]\mathbf{Y}[/math]. This assumption gives rise to the linear regression model:

[[math]] \begin{eqnarray} \label{form.linRegressionModel} Y_{i} & = & \mathbf{X}_{i,\ast} \, \bbeta + \varepsilon_i \, \, \, = \, \, \, \beta_1 \, X_{i,1} + \ldots + \beta_{p} \, X_{i, p} + \varepsilon_i. \end{eqnarray} [[/math]]

In model (\ref{form.linRegressionModel}) [math]\bbeta = (\beta_1, \ldots, \beta_p)^{\top}[/math] is the regression parameter. The parameter [math]\beta_j[/math], [math]j=1, \ldots, p[/math], represents the effect size of covariate [math]j[/math] on the response. That is, for each unit change in covariate [math]j[/math] (while keeping the other covariates fixed) the observed change in the response is equal to [math]\beta_j[/math]. The second summand on the right-hand side of the model, [math]\varepsilon_i[/math], is referred to as the error. It represents the part of the response not explained by the functional part [math]\mathbf{X}_{i,\ast} \, \bbeta[/math] of the model (\ref{form.linRegressionModel}). In contrast to the functional part, which is considered to be systematic (i.e. non-random), the error is assumed to be random. Consequently, [math]Y_{i}[/math] need not be equal [math]Y_{i'}[/math] for [math]i \not= i'[/math], even if [math]\mathbf{X}_{i,\ast}= \mathbf{X}_{i',\ast}[/math]. To complete the formulation of model (\ref{form.linRegressionModel}) we need to specify the probability distribution of [math]\varepsilon_i[/math]. It is assumed that [math]\varepsilon_i \sim \mathcal{N}(0, \sigma^2)[/math] and the [math]\varepsilon_{i}[/math] are independent, i.e.:

[[math]] \begin{eqnarray*} \mbox{Cov}(\varepsilon_{i}, \varepsilon_{i'}) & = & \left\{ \begin{array}{lcc} \sigma^2 & \mbox{if} & i = i', \\ 0 & \mbox{if} & i \not= i'. \end{array} \right. \end{eqnarray*} [[/math]]

The randomness of [math]\varepsilon_i[/math] implies that [math]\mathbf{Y}_i[/math] is also a random variable. In particular, [math]\mathbf{Y}_i[/math] is normally distributed, because [math]\varepsilon_i \sim \mathcal{N}(0, \sigma^2)[/math] and [math]\mathbf{X}_{i,\ast} \, \bbeta[/math] is a non-random scalar. To specify the parameters of the distribution of [math]\mathbf{Y}_i[/math] we need to calculate its first two moments. Its expectation equals:

[[math]] \begin{eqnarray*} \mathbb{E}(Y_i) & = & \mathbb{E}(\mathbf{X}_{i, \ast} \, \bbeta) + \mathbb{E}(\varepsilon_i) \, \, \, = \, \, \, \mathbf{X}_{i, \ast} \, \bbeta, \end{eqnarray*} [[/math]]

while its variance is:

[[math]] \begin{eqnarray*} \mbox{Var}(Y_i) & = & \mathbb{E} \{ [Y_i - \mathbb{E}(Y_i)]^2 \} \qquad \qquad \qquad \qquad \qquad \quad = \, \, \, \mathbb{E} ( Y_i^2 ) - [\mathbb{E}(Y_i)]^2 \\ & = & \mathbb{E} [ ( \mathbf{X}_{i, \ast} \, \bbeta)^2 + 2 \varepsilon_i \mathbf{X}_{i, \ast} \, \bbeta + \varepsilon_i^2 ] - ( \mathbf{X}_{i, \ast} \, \bbeta)^2 \, \, \, = \, \, \, \mathbb{E}(\varepsilon_i^2 ) \\ & = & \mbox{Var}(\varepsilon_i ) \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \, \, = \, \, \, \sigma^2. \end{eqnarray*} [[/math]]

Hence, [math]Y_i \sim \mathcal{N}( \mathbf{X}_{i, \ast} \, \bbeta, \sigma^2)[/math]. This formulation (in terms of the normal distribution) is equivalent to the formulation of model (\ref{form.linRegressionModel}), as both capture the assumptions involved: the linearity of the functional part and the normality of the error.

Model (\ref{form.linRegressionModel}) is often written in a more condensed matrix form:

[[math]] \begin{eqnarray} \mathbf{Y} & = & \mathbf{X} \, \bbeta + \vvarepsilon, \label{form.linRegressionModelinMatrix} \end{eqnarray} [[/math]]

where [math]\vvarepsilon = (\varepsilon_1, \varepsilon_2, \ldots, \varepsilon_n)^{\top}[/math] and distributed as [math]\vvarepsilon \sim \mathcal{N}(\mathbf{0}_{p}, \sigma^2 \mathbf{I}_{nn})[/math]. As above model (\ref{form.linRegressionModelinMatrix}) can be expressed as a multivariate normal distribution: [math]\mathbf{Y} \sim \mathcal{N}(\mathbf{X} \, \bbeta, \sigma^2 \mathbf{I}_{nn})[/math].

Model (\ref{form.linRegressionModelinMatrix}) is a so-called hierarchical model. This terminology emphasizes that [math]\mathbf{X}[/math] and [math]\mathbf{Y}[/math] are not on a par, they play different roles in the model. The former is used to explain the latter. In model (\ref{form.linRegressionModel}) [math]\mathbf{X}[/math] is referred as the explanatory or independent variable, while the variable [math]\mathbf{Y}[/math] is generally referred to as the response or dependent variable.

The covariates, the columns of [math]\mathbf{X}[/math], may themselves be random. To apply the linear model they are temporarily assumed fixed. The linear regression model is then to be interpreted as [math]\mathbf{Y} \, | \, \mathbf{X} \sim \mathcal{N}(\mathbf{X} \, \bbeta, \sigma^2 \mathbf{I}_{nn})[/math]

Example (Methylation of a tumor-suppressor gene)

Consider a study which measures the gene expression levels of a tumor-suppressor genes (TSG) and two methylation markers (MM1 and MM2) on 67 samples. A methylation marker is a gene that promotes methylation. Methylation refers to attachment of a methyl group to a nucleotide of the DNA. In case this attachment takes place in or close by the promotor region of a gene, this complicates the transcription of the gene. Methylation may down-regulate a gene. This mechanism also works in the reverse direction: removal of methyl groups may up-regulate a gene. A tumor-suppressor gene is a gene that halts the progression of the cell towards a cancerous state.

The medical question associated with these data: do the expression levels methylation markers affect the expression levels of the tumor-suppressor gene? To answer this question we may formulate the following linear regression model:

[[math]] \begin{eqnarray*} Y_{i, \texttt{{\tiny tsg}}} & = & \beta_0 + \beta_{\texttt{{\tiny mm1}}} X_{i, \texttt{{\tiny mm1}}} + \beta_{\texttt{{\tiny mm2}}} X_{i, \texttt{{\tiny mm2}}} + \varepsilon_i, \end{eqnarray*} [[/math]]

with [math]i = 1, \ldots, 67[/math] and [math]\varepsilon_i \sim \mathcal{N}(0, \sigma^2)[/math]. The interest focusses on [math]\beta_{\texttt{{\scriptsize mm1}}}[/math] and [math]\beta_{\texttt{{\scriptsize mm2}}}[/math]. A non-zero value of at least one of these two regression parameters indicates that there is a linear association between the expression levels of the tumor-suppressor gene and that of the methylation markers.

Prior knowledge from biology suggests that the [math]\beta_{\texttt{{\scriptsize mm1}}}[/math] and [math]\beta_{\texttt{{\scriptsize mm2}}}[/math] are both non-positive. High expression levels of the methylation markers lead to hyper-methylation, in turn inhibiting the transcription of the tumor-suppressor gene. Vice versa, low expression levels of MM1 and MM2 are (via hypo-methylation) associated with high expression levels of TSG. Hence, a negative concordant effect between MM1 and MM2 (on one side) and TSG (on the other) is expected. Of course, the methylation markers may affect expression levels of other genes that in turn regulate the tumor-suppressor gene. The regression parameters [math]\beta_{\texttt{{\scriptsize mm1}}}[/math] and [math]\beta_{\texttt{{\scriptsize mm2}}}[/math] then reflect the indirect effect of the methylation markers on the expression levels of the tumor suppressor gene.

The linear regression model (\ref{form.linRegressionModel}) involves the unknown parameters: [math]\bbeta[/math] and [math]\sigma^2[/math], which need to be learned from the data. The parameters of the regression model, [math]\bbeta[/math] and [math]\sigma^2[/math] are estimated by means of likelihood maximization. Recall that [math]Y_i \sim \mathcal{N}( \mathbf{X}_{i,\ast} \, \bbeta, \sigma^2)[/math] with corresponding density: [math] f_{Y_i}(y_i) = (2 \, \pi \, \sigma^2)^{-1/2} \, \exp[ - (y_i - \mathbf{X}_{i\ast} \, \bbeta)^2 / 2 \sigma^2 ][/math]. The likelihood thus is:

[[math]] \begin{eqnarray*} L(\mathbf{Y}, \mathbf{X}; \bbeta, \sigma^2) & = & \prod_{i=1}^n (\sqrt{2 \, \pi} \, \sigma)^{-1} \, \exp[ - (Y_i - \mathbf{X}_{i, \ast} \, \bbeta)^2 / 2 \sigma^2 ], \end{eqnarray*} [[/math]]

in which the independence of the observations has been used. Because of the concavity of the logarithm, the maximization of the likelihood coincides with the maximum of the logarithm of the likelihood (called the log-likelihood). Hence, to obtain maximum likelihood (ML) estimates of the parameter it is equivalent to find the maximum of the log-likelihood. The log-likelihood is:

[[math]] \begin{eqnarray*} \mathcal{L}(\mathbf{Y}, \mathbf{X}; \bbeta, \sigma^2) & = & \log[ L(\mathbf{Y}, \mathbf{X}; \bbeta, \sigma^2) ] \, \, \, = \, \, \, % \log \Big[ \prod_{i=1}^n f_{Y_i}(y_i) \Big] -n \, \log(\sqrt{2 \, \pi} \, \sigma) - \tfrac{1}{2} \sigma^{-2} \sum\nolimits_{i=1}^n (y_i - \mathbf{X}_{i, \ast} \, \bbeta)^2. \end{eqnarray*} [[/math]]

After noting that [math]\sum_{i=1}^n (Y_i - \mathbf{X}_{i, \ast} \, \bbeta)^2 = \| \mathbf{Y} - \mathbf{X} \, \bbeta \|^2_2 \, \, \, = \, \, \, (\mathbf{Y} - \mathbf{X} \, \bbeta)^{\top} \, (\mathbf{Y} - \mathbf{X} \, \bbeta)[/math], the log-likelihood can be written as:

[[math]] \begin{eqnarray*} \mathcal{L}(\mathbf{Y}, \mathbf{X}; \bbeta, \sigma^2) & = & -n \, \log(\sqrt{2 \, \pi} \, \sigma) - \tfrac{1}{2} \sigma^{-2} \, \| \mathbf{Y} - \mathbf{X} \, \bbeta \|^2_2. \end{eqnarray*} [[/math]]

In order to find the maximum of the log-likelihood, take its derivate with respect to [math]\bbeta[/math]:

[[math]] \begin{eqnarray*} \frac{\partial }{\partial \, \beta} \mathcal{L}(\mathbf{Y}, \mathbf{X}; \bbeta, \sigma^2) & = & - \tfrac{1}{2} \sigma^{-2} \, \frac{\partial }{\partial \, \beta} \| \mathbf{Y} - \mathbf{X} \, \bbeta \|^2_2 \, \, \, = \, \, \, \tfrac{1}{2} \sigma^{-2} \, \mathbf{X}^{\top} (\mathbf{Y} - \mathbf{X} \, \bbeta). \end{eqnarray*} [[/math]]

Equate this derivative to zero gives the estimating equation for [math]\bbeta[/math]:

[[math]] \begin{eqnarray} \label{form.normalEquation} \mathbf{X}^{\top} \mathbf{X} \, \bbeta & = & \mathbf{X}^{\top} \mathbf{Y}. \end{eqnarray} [[/math]]

Equation (\ref{form.normalEquation}) is called to the normal equation. Pre-multiplication of both sides of the normal equation by [math](\mathbf{X}^{\top} \mathbf{X})^{-1}[/math] now yields the ML estimator of the regression parameter: [math]\hat{\bbeta} = (\mathbf{X}^{\top} \mathbf{X})^{-1} \, \mathbf{X}^{\top} \mathbf{Y}[/math], in which it is assumed that [math](\mathbf{X}^{\top} \mathbf{X})^{-1}[/math] is well-defined.

Along the same lines one obtains the ML estimator of the residual variance. Take the partial derivative of the loglikelihood with respect to [math]\sigma^2[/math]:

[[math]] \begin{eqnarray*} \frac{\partial }{\partial \, \sigma} \mathcal{L}(\mathbf{Y}, \mathbf{X}; \bbeta, \sigma^2) & = & - \sigma^{-1} + \sigma^{-3} \| \mathbf{Y} - \mathbf{X} \, \bbeta \|^2_2. \end{eqnarray*} [[/math]]

Equate the right-hand side to zero and solve for [math]\sigma^2[/math] to find [math]\hat{\sigma}^2 = n^{-1} \| \mathbf{Y} - \mathbf{X} \, \bbeta \|^2_2[/math]. In this expression [math]\bbeta[/math] is unknown and the ML estimate of [math]\bbeta[/math] is plugged-in.

With explicit expressions of the ML estimators at hand, we can study their properties. The expectation of the ML estimator of the regression parameter [math]\bbeta[/math] is:

[[math]] \begin{eqnarray*} \mathbb{E}(\hat{\bbeta}) & = & \mathbb{E}[ (\mathbf{X}^{\top} \mathbf{X})^{-1} \, \mathbf{X}^{\top} \mathbf{Y}] \, \, \, = \, \, \, (\mathbf{X}^{\top} \mathbf{X})^{-1} \, \mathbf{X}^{\top} \mathbb{E}( \mathbf{Y}) \, \, \, = \, \, \, (\mathbf{X}^{\top} \mathbf{X})^{-1} \, \mathbf{X}^{\top} \mathbf{X} \, \bbeta \, \, \, \, \, = \, \, \, \bbeta. \end{eqnarray*} [[/math]]

Hence, the ML estimator of the regression coefficients is unbiased.

The variance of the ML estimator of [math]\bbeta[/math] is:

[[math]] \begin{eqnarray*} \mbox{Var}(\hat{\bbeta}) & = & \mathbb{E} \{ [\hat{\bbeta} - \mathbb{E}(\hat{\bbeta})] [\hat{\bbeta} - \mathbb{E}(\hat{\bbeta})]^{\top} \} \\ & = & \mathbb{E} \{ [(\mathbf{X}^{\top} \mathbf{X})^{-1} \, \mathbf{X}^{\top} \mathbf{Y} - \bbeta] \, [(\mathbf{X}^{\top} \mathbf{X})^{-1} \, \mathbf{X}^{\top} \mathbf{Y} - \bbeta]^{\top} \} \\ & = & (\mathbf{X}^{\top} \mathbf{X})^{-1} \, \mathbf{X}^{\top} \, \mathbb{E} \{ \mathbf{Y} \, \mathbf{Y}^{\top} \} \, \mathbf{X} \, (\mathbf{X}^{\top} \mathbf{X})^{-1} - \bbeta \, \bbeta^{\top} \\ & = & (\mathbf{X}^{\top} \mathbf{X})^{-1} \, \mathbf{X}^{\top} \, \{ \mathbf{X} \, \bbeta \, \bbeta^{\top} \, \mathbf{X}^{\top} + \SSigma \} \, \mathbf{X} \, (\mathbf{X}^{\top} \mathbf{X})^{-1} - \bbeta \, \bbeta^{\top} \\ & = & \bbeta \, \bbeta^{\top} + \sigma^2 \, (\mathbf{X}^{\top} \mathbf{X})^{-1} - \bbeta \, \bbeta^{\top} \\ & = & \sigma^2 \, (\mathbf{X}^{\top} \mathbf{X})^{-1}, \end{eqnarray*} [[/math]]

in which we have used that [math]\mathbb{E} (\mathbf{Y} \mathbf{Y}^{\top}) = \mathbf{X} \, \bbeta \, \bbeta^{\top} \, \mathbf{X}^{\top} + \sigma^2 \, \mathbf{I}_{nn}[/math]. From [math]\mbox{Var}(\hat{\bbeta}) = \sigma^2 \, (\mathbf{X}^{\top} \mathbf{X})^{-1}[/math], one obtains an estimate of the variance of the estimator of the [math]j[/math]-th regression coefficient: [math]\hat{\sigma}^2 (\hat{\beta}_j ) = \hat{\sigma}^2 \sqrt{ [(\mathbf{X}^{\top} \mathbf{X})^{-1}]_{jj} }[/math]. This may be used to construct a confidence interval for the estimates or test the hypothesis [math]H_0: \beta_j = 0[/math]. In the latter [math]\hat{\sigma}^2[/math] should not be the maximum likelihood estimator, as it is biased. It is then to be replaced by the residual sum-of-squares divided by [math]n-p[/math] rather than [math]n[/math].

The prediction of [math]Y_i[/math], denoted [math]\widehat{Y}_i[/math], is the expected value of [math]Y_i[/math] according the linear regression model (with its parameters replaced by their estimates). The prediction of [math]Y_i[/math] thus equals [math]\mathbb{E}(Y_i; \hat{\bbeta}, \hat{\sigma}^2) = \mathbf{X}_{i, \ast} \hat{\bbeta}[/math]. In matrix notation the prediction is:

[[math]] \begin{eqnarray*} \widehat{\mathbf{Y}} & = & \mathbf{X} \, \hat{\bbeta} \, \, \, = \, \, \, \mathbf{X} \, (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{Y} \, \, \, := \, \, \, \mathbf{H} \mathbf{Y}, \end{eqnarray*} [[/math]]

where [math]\mathbf{H}[/math] is the hat matrix, as it ‘puts the hat’ on [math]\mathbf{Y}[/math]. Note that the hat matrix is a projection matrix, i.e. [math]\mathbf{H}^2 = \mathbf{H}[/math] for

[[math]] \begin{eqnarray*} \mathbf{H}^2 & = & \mathbf{X} \, (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{X} \, (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \, \, \, = \, \, \, \mathbf{X} \, (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top}. \end{eqnarray*} [[/math]]

Thus, the prediction [math]\widehat{\mathbf{Y}}[/math] is an orthogonal projection of [math]\mathbf{Y}[/math] onto the space spanned by the columns of [math]\mathbf{X}[/math].

With [math]\widehat{\bbeta}[/math] available, an estimate of the errors [math]\hat{\varepsilon}_i[/math], dubbed the residuals are obtained via:

[[math]] \begin{eqnarray*} \hat{\vvarepsilon} & = & \mathbf{Y} - \widehat{\mathbf{Y}} \, \, \, = \, \, \, \mathbf{Y} - \mathbf{X} \, \hat{\bbeta} \, \, \, = \, \, \, \mathbf{Y} - \mathbf{X} \, (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{Y} \, \, \, = \, \, \, [ \mathbf{I} - \mathbf{X} \, (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} ] \, \mathbf{Y}. \end{eqnarray*} [[/math]]

Thus, the residuals are a projection of [math]\mathbf{Y}[/math] onto the orthogonal complement of the space spanned by the columns of [math]\mathbf{X}[/math]. The residuals are to be used in diagnostics, e.g. checking of the normality assumption by means of a normal probability plot.

For more on the linear regression model confer the monograph of .

The ridge regression estimator

If the design matrix is high-dimensional, the covariates (the columns of [math]\mathbf{X}[/math]) are super-collinear. Recall collinearity in regression analysis refers to the event of two (or multiple) covariates being strongly linearly related. Consequently, the space spanned by super-collinear covariates is then a lower-dimensional subspace of the parameter space. If the design matrix [math]\mathbf{X}[/math], which contains the collinear covariates as columns, is (close to) rank deficient, it is (almost) impossible to separate the contribution of the individual covariates. The uncertainty with respect to the covariate responsible for the variation explained in [math]\mathbf{Y}[/math] is often reflected in the fit of the linear regression model to data by a large error of the estimates of the regression parameters corresponding to the collinear covariates and, consequently, usually accompanied by large values of the estimates.

Example (Collinearity)

The flotillins (the FLOT-1 and FLOT-2 genes) have been observed to regulate the proto-oncogene ERBB2 in vitro . One may wish to corroborate this in vivo. To this end we use gene expression data of a breast cancer study, available as a Bioconductor package: breastCancerVDX. From this study the expression levels of probes interrogating the FLOT-1 and ERBB2 genes are retrieved. For clarity of the illustration the FLOT-2 gene is ignored. After centering, the expression levels of the first ERBB2 probe are regressed on those of the four FLOT-1 probes. The R-code below carries out the data retrieval and analysis.

# load packages
library(Biobase)
library(breastCancerVDX)

# load data into memory
data(vdx)

# ids of genes FLOT1
idFLOT1 <- which(fData(vdx)[,5] == 10211)

# ids of ERBB2
idERBB2 <- which(fData(vdx)[,5] == 2064)

# get expression levels of probes mapping to FLOT genes
X <- t(exprs(vdx)[idFLOT1,])
X <- sweep(X, 2, colMeans(X))

# get expression levels of probes mapping to FLOT genes
Y <- t(exprs(vdx)[idERBB2,])
Y <- sweep(Y, 2, colMeans(Y))

# regression analysis
summary(lm(formula = Y[,1] ~ X[,1] + X[,2] + X[,3] + X[,4]))

# correlation among the covariates
cor(X)

Prior to the regression analysis, we first assess whether there is collinearity among the FLOT-1 probes through evaluation of the correlation matrix. This reveals a strong correlation ([math]\hat{\rho} = 0.91[/math]) between the second and third probe. All other cross-correlations do not exceed the 0.20 (in an absolute sense). Hence, there is collinearity among the columns of the design matrix in the to-be-performed regression analysis.

Coefficients:
           Estimate Std. Error t value Pr(>|t|)
(Intercept)   0.0000     0.0633  0.0000   1.0000
X[, 1]        0.1641     0.0616  2.6637   0.0081 **
X[, 2]        0.3203     0.3773  0.8490   0.3965
X[, 3]        0.0393     0.2974  0.1321   0.8949
X[, 4]        0.1117     0.0773  1.4444   0.1496
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.175 on 339 degrees of freedom
Multiple R-squared:  0.04834,	Adjusted R-squared:  0.03711 
F-statistic: 4.305 on 4 and 339 DF,  p-value: 0.002072

The output of the regression analysis above shows the first probe to be significantly associated to the expression levels of ERBB2. The collinearity of the second and third probe reveals itself in the standard errors of the effect size: for these probes the standard error is much larger than those of the other two probes. This reflects the uncertainty in the estimates. Regression analysis has difficulty to decide to which covariate the explained proportion of variation in the response should be attributed. The large standard error of these effect sizes propagates to the testing as the Wald test statistic is the ratio of the estimated effect size and its standard error. Collinear covariates are thus less likely to pass the significance threshold.

The case of two (or multiple) covariates being perfectly linearly dependent is referred as super-collinearity. The rank of a high-dimensional design matrix is maximally equal to [math]n[/math]: [math]\mbox{rank}(\mathbf{X}) \leq n[/math]. Consequently, the dimension of subspace spanned by the columns of [math]\mathbf{X}[/math] is smaller than or equal to [math]n[/math]. As [math]p \gt n[/math], this implies that columns of [math]\mathbf{X}[/math] are linearly dependent. Put differently, a high-dimensional [math]\mathbf{X}[/math] suffers from super-collinearity.

Example (Super-collinearity)

Consider the design matrix:

[[math]] \begin{eqnarray*} \mathbf{X} & = & \left( \begin{array}{rrr} 1 & -1 & 2 \\ 1 & 0 & 1 \\ 1 & 2 & -1 \\ 1 & 1 & 0 \end{array} \right) \end{eqnarray*} [[/math]]

The columns of [math]\mathbf{X}[/math] are linearly dependent: the first column is the row-wise sum of the other two columns. The rank (more correct, the column rank) of a matrix is the dimension of space spanned by the column vectors. Hence, the rank of [math]\mathbf{X}[/math] is equal to the number of linearly independent columns: [math]\mbox{rank}(\mathbf{X}) = 2[/math].

Super-collinearity of an [math](n \times p)[/math]-dimensional design matrix [math]\mathbf{X}[/math] implies\footnote{If the (column) rank of [math]\mathbf{X}[/math] is smaller than [math]p[/math], there exists a non-trivial [math]\mathbf{v} \in \mathbb{R}^p[/math] such that [math]\mathbf{X} \mathbf{v} = \mathbf{0}_{p}[/math]. Multiplication of this inequality by [math]\mathbf{X}^{\top}[/math] yields [math]\mathbf{X}^{\top} \mathbf{X} \mathbf{v} = \mathbf{0}_{p}[/math]. As [math]\mathbf{v} \not= \mathbf{0}_{p}[/math], this implies that [math]\mathbf{X}^{\top} \mathbf{X}[/math] is not invertible.} that the rank of the [math](p \times p)[/math]-dimensional matrix [math]\mathbf{X}^{\top} \mathbf{X}[/math] is smaller than [math]p[/math], and, consequently, it is singular. A square matrix that does not have an inverse is called singular. A matrix [math]\mathbf{A}[/math] is singular if and only if its determinant is zero: [math]\mbox{det}(\mathbf{A}) = 0[/math].

Example (Singularity)

Consider the matrix [math]\mathbf{A}[/math] given by:

[[math]] \begin{eqnarray*} \mathbf{A} & = & \left( \begin{array}{rr} 1 & 2 \\ 2 & 4 \end{array} \right) \end{eqnarray*} [[/math]]

Clearly, [math]\mbox{det}(\mathbf{A}) = a_{11} a_{22} - a_{12} a_{21} = 1 \times 4 - 2 \times 2 = 0[/math]. Hence, [math]\mathbf{A}[/math] is singular and its inverse is undefined.

As [math]\mbox{det}(\mathbf{A})[/math] is equal to the product of the eigenvalues [math]\nu_j[/math] of [math]\mathbf{A}[/math], the matrix [math]\mathbf{A}[/math] is singular if one (or more) of the eigenvalues of [math]\mathbf{A}[/math] is zero. To see this, consider the spectral decomposition of [math]\mathbf{A}[/math]: [math]\mathbf{A} = \sum_{j=1}^p \nu_j \, \mathbf{v}_j \, \mathbf{v}_j^{\top}[/math], where [math]\mathbf{v}_j[/math] is the eigenvector corresponding to [math]\nu_j[/math]. To obtain the inverse of [math]\mathbf{A}[/math] it requires to take the reciprocal of the eigenvalues: [math]\mathbf{A}^{-1} = \sum_{j=1}^p \nu_j^{-1} \, \mathbf{v}_j \, \mathbf{v}_j^{\top}[/math]. The right-hand side is undefined if [math]\nu_j =0[/math] for any [math]j[/math].

Example (Singularity, continued)

Revisit Example. Matrix [math]\mathbf{A}[/math] has eigenvalues [math]\nu_1 =5[/math] and [math]\nu_2=0[/math]. According to the spectral decomposition, the inverse of [math]\mathbf{A}[/math] is: [math]\mathbf{A}^{-1} = \tfrac{1}{5} \, \mathbf{v}_1 \, \mathbf{v}_1^{\top} + \tfrac{1}{0} \, \mathbf{v}_2 \, \mathbf{v}_2^{\top}[/math]. This expression is undefined as we divide by zero in the second summand on the right-hand side.

In summary, the columns of a high-dimensional design matrix [math]\mathbf{X}[/math] are linearly dependent and this super-collinearity causes [math]\mathbf{X}^{\top} \mathbf{X}[/math] to be singular. Now recall the ML estimator of the parameter of the linear regression model: [math]\hat{\bbeta} = (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{Y}[/math]. This estimator is only well-defined if [math](\mathbf{X}^{\top} \mathbf{X})^{-1}[/math] exits. Hence, when [math]\mathbf{X}[/math] is high-dimensional the regression parameter [math]\bbeta[/math] cannot be estimated.

Above only the practical consequence of high-dimensionality is presented: the expression [math]( \mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{Y}[/math] cannot be evaluated numerically. But the problem arising from the high-dimensionality of the data is more fundamental. To appreciate this, consider the normal equations: [math]\mathbf{X}^{\top} \mathbf{X} \bbeta = \mathbf{X}^{\top} \mathbf{Y}[/math]. The matrix [math]\mathbf{X}^{\top} \mathbf{X}[/math] is of rank [math]n[/math], while [math]\bbeta[/math] is a vector of length [math]p[/math]. Hence, while there are [math]p[/math] unknowns, the system of linear equations from which these are to be solved effectively comprises [math]n[/math] degrees of freedom. If [math]p \gt n[/math], the vector [math]\bbeta[/math] cannot uniquely be determined from this system of equations. To make this more specific let [math]\mathcal{U}[/math] be the [math]n[/math]-dimensional space spanned by the columns of [math]\mathbf{X}[/math] and the [math]p-n[/math]-dimensional space [math]\mathcal{V}[/math] be orthogonal complement of [math]\mathcal{U}[/math], i.e. [math]\mathcal{V} = \mathcal{U}^{\perp}[/math]. Then, [math]\mathbf{X} \mathbf{v} = \mathbf{0}_{p}[/math] for all [math]\mathbf{v} \in \mathcal{V}[/math]. So, [math]\mathcal{V}[/math] is the non-trivial null space of [math]\mathbf{X}[/math]. Consequently, as [math]\mathbf{X}^{\top} \mathbf{X} \mathbf{v} = \mathbf{X}^{\top} \mathbf{0}_{p} = \mathbf{0}_{n}[/math], the solution of the normal equations is:

[[math]] \begin{eqnarray*} \hat{\bbeta} & = & ( \mathbf{X}^{\top} \mathbf{X})^{+} \mathbf{X}^{\top} \mathbf{Y} + \mathbf{v} \qquad \mbox{for all } \mathbf{v} \in \mathcal{V}, \end{eqnarray*} [[/math]]

where [math]\mathbf{A}^{+}[/math] denotes the Moore-Penrose inverse of the matrix [math]\mathbf{A}[/math] (adopting the notation of ). For a square symmetric matrix, the generalized inverse is defined as:

[[math]] \begin{eqnarray*} \mathbf{A}^{+} & = & \sum\nolimits_{j=1}^p \nu_j^{-1} \, I_{\{ \nu_j \not= 0 \} } \, \mathbf{v}_j \, \mathbf{v}_j^{\top}, \end{eqnarray*} [[/math]]

where [math]\mathbf{v}_j[/math] are the eigenvectors of [math]\mathbf{A}[/math] (and are not -- necessarily -- an element of [math]\mathcal{V}[/math]). The solution of the normal equations is thus only determined up to an element from a non-trivial space [math]\mathcal{V}[/math], and there is no unique estimator of the regression parameter. % With this mind, the ridge estimator can then be thought of as altering the normal equations provide a unique solution for [math]\bbeta[/math].

To arrive at a unique regression estimator for studies with rank deficient design matrices, the minimum least squares estimator may be employed.

Definition

The minimum least squares estimator of regression parameter minimizes the sum-of-squares criterion and is of minimum length. Formally, [math]\hat{\bbeta}_{\mbox{{\tiny MLS}}} = \arg \min_{\bbeta \in \mathbb{R}^p} \| \mathbf{Y} - \mathbf{X} \bbeta \|_2^2[/math] such that [math]\| \hat{\bbeta}_{\mbox{{\tiny MLS}}} \|_2^2 \lt \| \bbeta \|_2^2[/math] for all [math]\bbeta[/math] that minimize [math]\| \mathbf{Y} - \mathbf{X} \bbeta \|_2^2[/math].

If [math]\mathbf{X}[/math] is of full rank, the minimum least squares regression estimator coincides with the least squares/maximum likelihood one as the latter is a unique minimizer of the sum-of-squares criterion and, thereby, automatically also the minimizer of minimum length. When [math]\mathbf{X}[/math] is rank deficient, [math]\hat{\bbeta}_{\mbox{{\tiny MLS}}} = (\mathbf{X}^{\top} \mathbf{X})^+ \mathbf{X}^{\top} \mathbf{Y}[/math]. To see this recall from above that [math]\| \mathbf{Y} - \mathbf{X} \bbeta \|_2^2[/math] is minimized by [math](\mathbf{X}^{\top} \mathbf{X})^+ \mathbf{X}^{\top} \mathbf{Y} + \mathbf{v}[/math] for all [math]\mathbf{v} \in V[/math]. The length of these minimizers is:

[[math]] \begin{eqnarray*} \| (\mathbf{X}^{\top} \mathbf{X})^+ \mathbf{X}^{\top} \mathbf{Y} + \mathbf{v} \|_2^2 & = & \| (\mathbf{X}^{\top} \mathbf{X})^+ \mathbf{X}^{\top} \mathbf{Y} \|_2^2 + 2 \mathbf{Y}^{\top} \mathbf{X} (\mathbf{X}^{\top} \mathbf{X})^+ \mathbf{v} + \| \mathbf{v} \|_2^2, \end{eqnarray*} [[/math]]

which, by the orthogonality of [math]V[/math] and the space spanned by the columns of [math]\mathbf{X}[/math], equals [math]\| (\mathbf{X}^{\top} \mathbf{X})^+ \mathbf{X}^{\top} \mathbf{Y} \|_2^2 + \| \mathbf{v} \|_2^2[/math]. Clearly, any nontrivial [math]\mathbf{v}[/math], i.e. [math]\mathbf{v} \not= \mathbf{0}_p[/math], results in [math]\| (\mathbf{X}^{\top} \mathbf{X})^+ \mathbf{X}^{\top} \mathbf{Y} \|_2^2 + \| \mathbf{v} \|_2^2 \gt \| (\mathbf{X}^{\top} \mathbf{X})^+ \mathbf{X}^{\top} \mathbf{Y} \|_2^2[/math] and, thus, [math]\hat{\bbeta}_{\mbox{{\tiny MLS}}} = (\mathbf{X}^{\top} \mathbf{X})^+ \mathbf{X}^{\top} \mathbf{Y}[/math].

An alternative (and related) estimator of the regression parameter [math]\bbeta[/math] that avoids the use of the Moore-Penrose inverse and is able to deal with (super)-collinearity among the columns of the design matrix is the ridge regression estimator proposed by . It essentially comprises of an ad-hoc fix to resolve the (almost) singularity of [math]\mathbf{X}^{\top} \mathbf{X}[/math]. propose to simply replace [math]\mathbf{X}^{\top} \mathbf{X}[/math] by [math]\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp}[/math] with [math]\lambda \in [0, \infty)[/math]. The scalar [math]\lambda[/math] is a tuning parameter, henceforth called the penalty parameter for reasons that will become clear later. The ad-hoc fix solves the singularity as it adds a positive matrix, [math]\lambda \mathbf{I}_{pp}[/math], to a positive semi-definite one, [math]\mathbf{X}^{\top} \mathbf{X}[/math], making the total a positive definite matrix (Lemma 14.2.4 of ), which is invertible.

Example (Super-collinearity, continued)

Recall the super-collinear design matrix [math]\mathbf{X}[/math] of Example. Then, for (say) [math]\lambda = 1[/math]:

[[math]] \begin{eqnarray*} \mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp} & = & \left( \begin{array}{rrr} 5 & 2 & 2 \\ 2 & 7 & -4 \\ 2 & -4 & 7 \end{array} \right). \end{eqnarray*} [[/math]]

The eigenvalues of this matrix are 11, 7, and 1. Hence, [math]\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp}[/math] has no zero eigenvalue and its inverse is well-defined.

With the ad-hoc fix for the singularity of [math]\mathbf{X}^{\top} \mathbf{X}[/math], proceed to define the ridge regression estimator:

[[math]] \begin{eqnarray} \label{form.ridgeRegressionEstimator} \hat{\bbeta}(\lambda) & = & (\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp})^{-1} \mathbf{X}^{\top} \mathbf{Y}, \end{eqnarray} [[/math]]

for [math]\lambda \in [0, \infty)[/math]. Clearly, this is for [math]\lambda[/math] strictly positive (Question discussed the consequences of a negative values of [math]\lambda[/math]) a well-defined estimator, even if [math]\mathbf{X}[/math] is high-dimensional. However, each choice of [math]\lambda[/math] leads to a different ridge regression estimate. The set of all ridge regression estimates [math]\{ \hat{\bbeta}(\lambda) \, : \, \lambda \in [0, \infty) \}[/math] is called the solution or regularization path of the ridge estimator.

Example (Super-collinearity, continued)

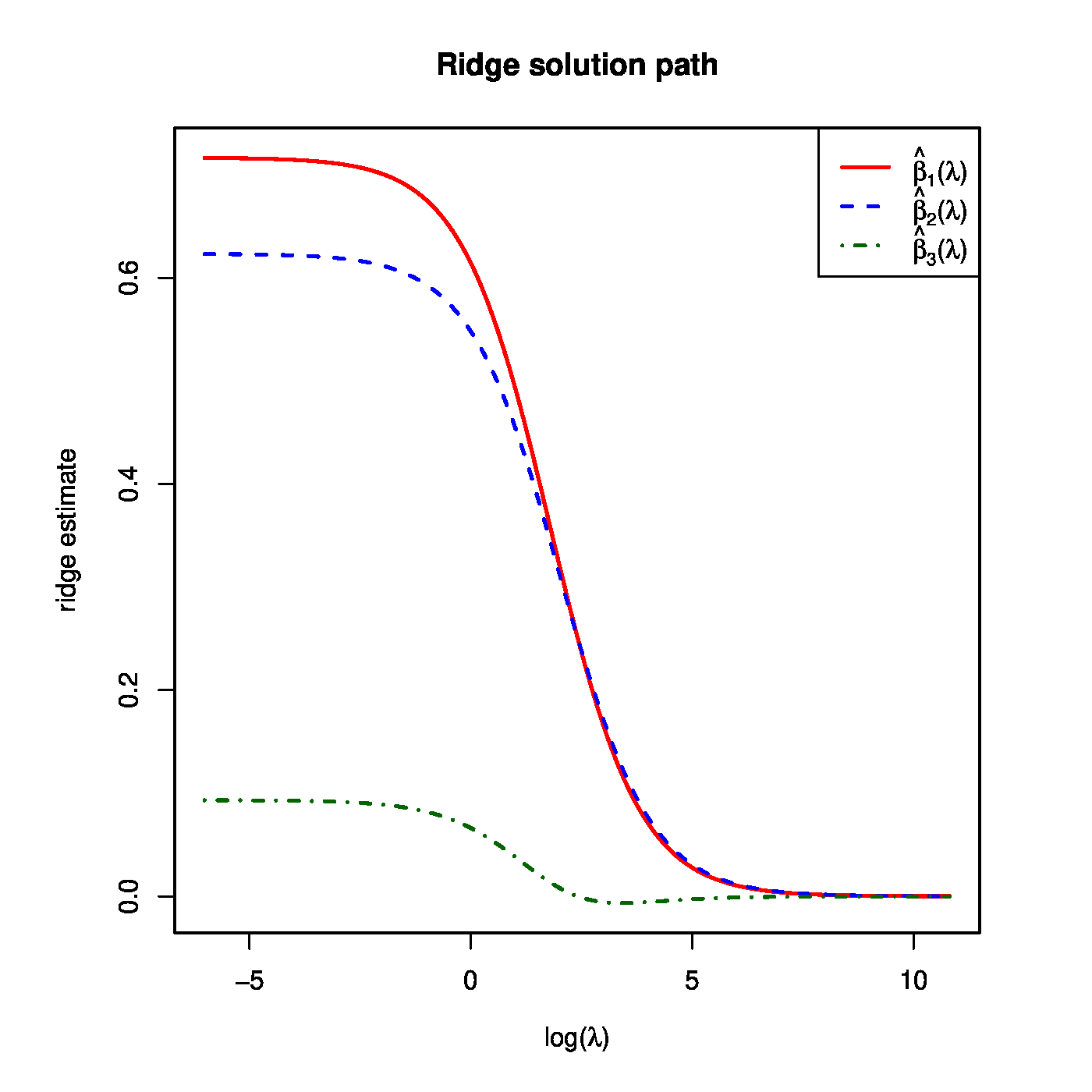
Recall the super-collinear design matrix [math]\mathbf{X}[/math] of Example. Suppose that the corresponding response vector is [math]\mathbf{Y} = (1.3, -0.5, 2.6, 0.9)^{\top}[/math]. The ridge regression estimates for, e.g. [math]\lambda = 1, 2[/math], and [math]10[/math] are then: [math]\hat{\bbeta}(1) = (0.614, 0.548, 0.066)^{\top}[/math], [math]\hat{\bbeta}(2) = (0.537, 0.490, 0.048)^{\top}[/math], and [math]\hat{\bbeta}(10) = (0.269, 0.267, 0.002)^{\top}[/math]. The full solution path of the ridge estimator is shown in the left-hand side panel of Figure.

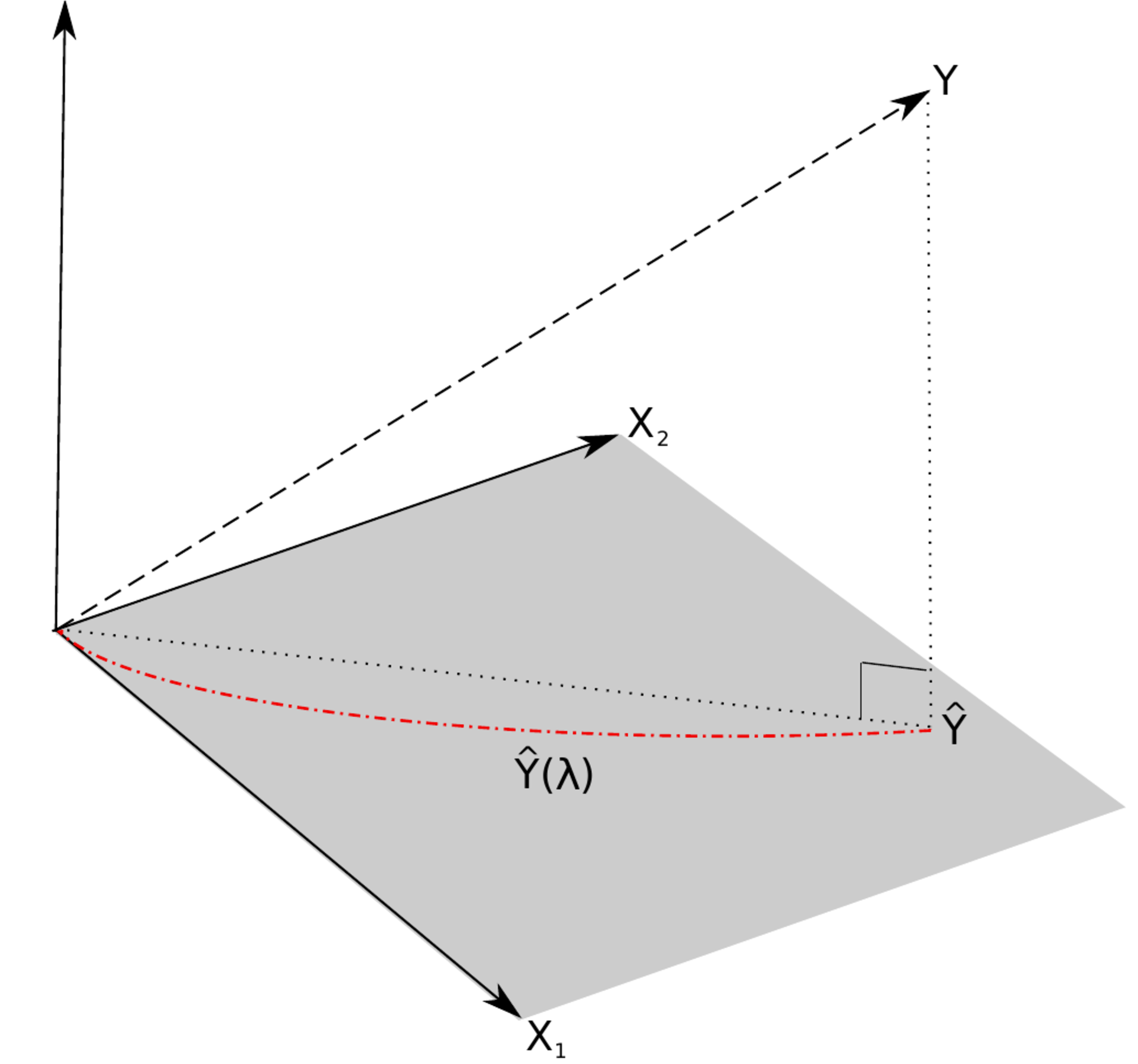
Left panel: the regularization path of the ridge estimator for the data of Example. Right panel: the ‘maximum likelihood fit’ [math]\widehat{Y}[/math] and the ‘ridge fit’ [math]\widehat{Y}(\lambda)[/math] (the dashed-dotted red line) to the observation [math]Y[/math] in the (hyper)plane spanned by the covariates.

Low-dimensionally, when [math]\mathbf{X}^{\top} \mathbf{X}[/math] is of full rank, the ridge regression estimator is linearly related to its maximum likelihood counterpart. To see this define the linear operator [math]\mathbf{W}_{\lambda} = (\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp})^{-1} \mathbf{X}^{\top} \mathbf{X}[/math]. The ridge estimator [math]\hat{\bbeta}(\lambda)[/math] can then be expressed as [math]\mathbf{W}_{\lambda} \hat{\bbeta}[/math] for:

[[math]] \begin{eqnarray*} \mathbf{W}_{\lambda} \hat{\bbeta} & = & \mathbf{W}_{\lambda} (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{Y} \\ & = & ( \mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp} )^{-1} \mathbf{X}^{\top} \mathbf{X} (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{Y} \\ & = & ( \mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp} )^{-1} \mathbf{X}^{\top} \mathbf{Y} \\ & = & \hat{\bbeta}(\lambda). \end{eqnarray*} [[/math]]

The linear operator [math]\mathbf{W}_{\lambda}[/math] thus transforms the maximum likelihood estimator of the regression parameter into its ridge regularized counterpart. High-dimensionally, no such linear relation between the ridge and the minimum least squares regression estimators exists (see Exercise).

With an estimate of the regression parameter [math]\bbeta[/math] available one can define the fit. For the ridge regression estimator the fit is defined analogous to the ML case:

[[math]] \begin{eqnarray*} \widehat{\mathbf{Y}}(\lambda) & = & \mathbf{X} \hat{\bbeta}(\lambda) \, \, \, = \, \, \, \mathbf{X} (\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp})^{-1} \mathbf{X}^{\top} \mathbf{Y} \, \, \, := \, \, \, \mathbf{H}(\lambda) \mathbf{Y}. \end{eqnarray*} [[/math]]

For the ML regression estimator the fit could be understood as a projection of [math]\mathbf{Y}[/math] onto the subspace spanned by the columns of [math]\mathbf{X}[/math]. This is depicted in the right panel of Figure, where [math]\widehat{Y}[/math] is the projection of the observation [math]Y[/math] onto the covariate space. The projected observation [math]\widehat{Y}[/math] is orthogonal to the residual [math]\varepsilon = Y - \widehat{Y}[/math]. This means the fit is the point in the covariate space closest to the observation. Put differently, the covariate space does not contain a point that is better (in some sense) in explaining the observation. Compare this to the ‘ridge fit’ which is plotted as a dashed-dotted red line in the right panel of Figure. The ‘ridge fit’ is a line, parameterized by [math]\{ \lambda : \lambda \in \mathbb{R}_{\geq 0} \}[/math], where each point on this line matches to the corresponding intersection of the regularization path [math]\hat{\bbeta}(\lambda)[/math] and the vertical line [math]x=\lambda[/math]. The ‘ridge fit’ [math]\widehat{Y}(\lambda)[/math] runs from the ML fit [math]\widehat{Y} = \widehat{Y} (0)[/math] to an intercept-only fit in which the covariates do not contribute to the explanation of the observation. From the figure it is obvious that for any [math]\lambda \gt 0[/math] the ‘ridge fit’ [math]\widehat{Y}(\lambda)[/math] is not orthogonal to the observation [math]Y[/math]. In other words, the ‘ridge residuals’ [math]Y - \widehat{Y}(\lambda)[/math] are not orthogonal to the fit [math]\widehat{Y}(\lambda)[/math] (confer Exercise ). Hence, the ad-hoc fix of the ridge regression estimator resolves the non-evaluation of the estimator in the face of super-collinearity but yields a ‘ridge fit’ that is not optimal in explaining the observation. Mathematically, this is due to the fact that the fit [math]\widehat{Y}(\lambda)[/math] corresponding to the ridge regression estimator is not a projection of [math]Y[/math] onto the covariate space (confer Exercise).

Eigenvalue shrinkage

The effect of the ridge penalty is also studied from the perspective of singular values. Let the singular value decomposition of the [math]n \times p[/math]-dimensional design matrix [math]\mathbf{X}[/math] be:

[[math]] \begin{eqnarray*} \mathbf{X} & = & \mathbf{U}_x \mathbf{D}_x \mathbf{V}_x^{\top}. \end{eqnarray*} [[/math]]

In the above [math]\mathbf{D}_x[/math] an [math]n \times p[/math]-dimensional block matrix. Its upper left block is a [math](\mbox{rank}(\mathbf{X}) \times \mbox{rank}(\mathbf{X}))[/math]-dimensional digonal matrix with the singular values on the diagonal. The remaining blocks, zero if [math]p=n[/math] and [math]\mathbf{X}[/math] is of full rank, one if [math]\mbox{rank}(\mathbf{X}) = n[/math] or [math]\mbox{rank}(\mathbf{X}) = p[/math], or three if [math]\mbox{rank}(\mathbf{X}) \lt \min \{ n, p \}[/math], are of appropriate dimensions and comprise zeros only. The matrix [math]\mathbf{U}_x[/math] an [math]n \times n[/math]-dimensional matrix with columns containing the left singular vectors (denoted [math]\mathbf{u}_i[/math]), and [math]\mathbf{V}_x[/math] a [math]p \times p[/math]-dimensional matrix with columns containing the right singular vectors (denoted [math]\mathbf{v}_i[/math]). The columns of [math]\mathbf{U}_x[/math] and [math]\mathbf{V}_x[/math] are orthogonal: [math]\mathbf{U}_x^{\top} \mathbf{U}_x = \mathbf{I}_{nn} = \mathbf{U}_x\mathbf{U}_x^{\top}[/math] and [math]\mathbf{V}_x^{\top} \mathbf{V}_x = \mathbf{I}_{pp} = \mathbf{V}_x\mathbf{V}_x^{\top}[/math].

The maximum likelihood estimator, which is well-defined if [math]n \gt p[/math] and [math]\mbox{rank}(\mathbf{X})=p[/math], can then be rewritten in terms of the SVD-matrices as:

[[math]] \begin{eqnarray*} \hat{\bbeta} & = & (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{Y} \qquad \qquad \qquad \, \, \, \, \, = \, \, \, (\mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{U}_x \mathbf{D}_x \mathbf{V}_x^{\top})^{-1} \mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y} \\ & = & (\mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{D}_x \mathbf{V}_x^{\top})^{-1} \mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y} \, \, \, = \, \, \, \mathbf{V}_x (\mathbf{D}_x^{\top} \mathbf{D}_x)^{-1} \mathbf{V}_x^{\top} \mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y} \\ & = & \mathbf{V}_x (\mathbf{D}_x^{\top} \mathbf{D}_x)^{-1} \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y}. \end{eqnarray*} [[/math]]

The block structure of the design matrix implies that matrix [math](\mathbf{D}_x^{\top} \mathbf{D}_x)^{-1} \mathbf{D}_x[/math] results in an [math]p \times n[/math]-dimensional matrix with the reciprocal of the nonzero singular values on the diagonal of the left [math]p\times p[/math]-dimensional upper left block. Similarly, the ridge regression estimator can be rewritten in terms of the SVD-matrices as:

[[math]] \begin{eqnarray} \nonumber \hat{\bbeta} (\lambda) & = & (\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp})^{-1} \mathbf{X}^{\top} \mathbf{Y} \\ \nonumber & = & (\mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{U}_x \mathbf{D}_x \mathbf{V}_x^{\top} + \lambda \mathbf{I}_{pp})^{-1} \mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y} \\ \nonumber & = & (\mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{D}_x \mathbf{V}_x^{\top} + \lambda \mathbf{V}_x \mathbf{V}_x^{\top})^{-1} \mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y} \\ \nonumber & = & \mathbf{V}_x (\mathbf{D}_x^{\top} \mathbf{D}_x + \lambda \mathbf{I}_{pp})^{-1} \mathbf{V}_x^{\top} \mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y} \\ \label{form:formRidgeSpectral} & = & \mathbf{V}_x (\mathbf{D}_x^{\top} \mathbf{D}_x + \lambda \mathbf{I}_{pp})^{-1} \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y}. \end{eqnarray} [[/math]]

Combining the two results and writing [math](\mathbf{D}_x)_{jj} = d_{x,jj}[/math] for the [math]p[/math] nonzero singular values on the diagonal of the upper block of [math]\mathbf{D}_x[/math] we have: [math] d_{x,jj}^{-1} \geq d_{x,jj} (d_{x,jj}^2 + \lambda)^{-1}[/math] for all [math]\lambda \gt 0[/math]. Thus, the ridge penalty shrinks the singular values.

Return to the problem of the super-collinearity of [math]\mathbf{X}[/math] in the high-dimensional setting ([math]p \gt n[/math]). The super-collinearity implies the singularity of [math]\mathbf{X}^{\top} \mathbf{X}[/math] and prevents the calculation of the OLS estimator of the regression coefficients. However, [math]\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp}[/math] is non-singular, with inverse: [math](\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp})^{-1} = \sum_{j=1}^p (d_{x,jj}^2 + \lambda)^{-1} \mathbf{v}_j \mathbf{v}_j^{\top}[/math] where [math]d_{x,jj} = 0[/math] for [math]j \gt \mbox{rank}(\mathbf{X})[/math]. The right-hand side is well-defined for [math]\lambda \gt 0[/math].

From the ‘spectral formulation’ of the ridge regression estimator (\ref{form:formRidgeSpectral}) the [math]\lambda[/math]-limits can be deduced. The lower [math]\lambda[/math]-limit of the ridge regression estimator [math]\hat{\bbeta}(0_+) = \lim_{\lambda \downarrow 0} \hat{\bbeta}(\lambda)[/math] coincides with the minimum least squares estimator. This is immediate when [math]\mathbf{X}[/math] is of full rank. In the high-dimensional situation, when the dimension [math]p[/math] exceeds the sample size [math]n[/math], it follows from the limit:

[[math]] \begin{eqnarray*} \lim_{\lambda \downarrow 0} \frac{d_{x,jj}}{d_{x,jj}^2 + \lambda} & = & \left\{ \begin{array}{lcl} d_{x,jj}^{-1} & \mbox{if} & d_{x,jj} \not= 0 \\ 0 & \mbox{if} & d_{x,jj} = 0 \end{array} \right. \end{eqnarray*} [[/math]]

Then, [math]\lim_{\lambda \downarrow 0} \hat{\bbeta}(\lambda) = \hat{\bbeta}_{\mbox{{\tiny MLS}}}[/math]. Similarly, the upper [math]\lambda[/math]-limit is evident from the fact that [math]\lim_{\lambda \rightarrow \infty} d_{x,jj} (d_{x,jj}^2 + \lambda)^{-1} = 0[/math], which implies [math]\lim_{\lambda \rightarrow \infty} \hat{\bbeta}(\lambda) = \mathbf{0}_p[/math]. Hence, all regression coefficients are shrunken towards zero as the penalty parameter increases. This also holds for [math]\mathbf{X}[/math] with [math]p \gt n[/math]. Furthermore, this behaviour is not strictly monotone in [math]\lambda[/math]: [math]\lambda_{a} \gt \lambda_b[/math] does not necessarily imply [math]|\hat{\beta}_j (\lambda_a) | \lt |\hat{\beta}_j (\lambda_b) |[/math]. Upon close inspection this can be witnessed from the ridge solution path of [math]\beta_3[/math] in Figure.

Principal components regression

Principal component regression is a close relative to ridge regression that can also be applied in a high-dimensional context. Principal components regression explains the response not by the covariates themselves but by linear combinations of the covariates as defined by the principal components of [math]\mathbf{X}[/math]. Let [math]\mathbf{U}_x \mathbf{D}_x \mathbf{V}_x^{\top}[/math] be the singular value decomposition of [math]\mathbf{X}[/math]. The [math]k_0[/math]-th principal component of [math]\mathbf{X}[/math] is then [math]\mathbf{X} \mathbf{v}_{k_0}[/math], henceforth denoted [math]\mathbf{z}_i[/math]. Let [math]\mathbf{Z}_k[/math] be the matrix of the first [math]k[/math] principal components, i.e. [math]\mathbf{Z}_k = \mathbf{X} \mathbf{V}_{x,k}[/math] where [math]\mathbf{V}_{x,k}[/math] contains the first [math]k[/math] right singular vectors as columns. Principal components regression then amounts to regressing the response [math]\mathbf{Y}[/math] onto [math]\mathbf{Z}_{k}[/math], that is, it fits the model [math]\mathbf{Y} = \mathbf{Z}_k \ggamma + \vvarepsilon[/math]. The least squares estimator of [math]\ggamma[/math] then is (with some abuse of notation):

[[math]] \begin{eqnarray*} \hat{\ggamma} & = & (\mathbf{Z}_k^{\top} \mathbf{Z}_k)^{-1} \mathbf{Z}_k^{\top} \mathbf{Y} \\ & = & (\mathbf{V}_{x,k}^{\top} \mathbf{X}^{\top} \mathbf{X} \mathbf{V}_{x,k})^{-1} \mathbf{V}_k^{\top} \mathbf{X}^{\top} \mathbf{Y} \\ & = & (\mathbf{V}_{x,k}^{\top} \mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{U}_x \mathbf{D}_x \mathbf{V}_x^{\top} \mathbf{V}_{x,k})^{-1} \mathbf{V}_{x,k}^{\top} \mathbf{V}_x \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y} \\ & = & (\mathbf{I}_{kp} \mathbf{D}_x^{\top} \mathbf{D}_x \mathbf{I}_{pk})^{-1} \mathbf{I}_{kp} \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y} \\ & = & (\mathbf{D}_{x,k}^{\top} \mathbf{D}_{x,k})^{-1} \mathbf{D}_{x,k}^{\top} \mathbf{U}_x^{\top} \mathbf{Y} \\ & = & (\mathbf{D}_{x,k}^{\top} \mathbf{D}_{x,k})^{-1} \mathbf{D}_{x,k}^{\top} \mathbf{U}_x^{\top} \mathbf{Y}, \end{eqnarray*} [[/math]]

where [math]\mathbf{D}_{x,k}[/math] is a submatrix of [math]\mathbf{D}_x[/math] formed from [math]\mathbf{D}_x[/math] by removal of the last [math]p-k[/math] columns. Similarly, [math]\mathbf{I}_{kp}[/math] and [math]\mathbf{I}_{pk}[/math] are obtained from [math]\mathbf{I}_{pp}[/math] by removal of the last [math]p-k[/math] rows and columns, respectively. The principal component regression estimator of [math]\bbeta[/math] then is [math]\hat{\bbeta}_{\mbox{{\tiny pcr}}} = \mathbf{V}_{x,k} (\mathbf{D}_{x,k}^{\top} \mathbf{D}_{x,k})^{-1} \mathbf{D}_{x,k}^{\top} \mathbf{U}_x^{\top} \mathbf{Y}[/math]. When [math]k[/math] is set equal to the column rank of [math]\mathbf{X}[/math], and thus to the rank of [math]\mathbf{X}^{\top} \mathbf{X}[/math], the principal component regression estimator [math]\hat{\bbeta}_{\mbox{{\tiny pcr}}} = (\mathbf{X}^{\top} \mathbf{X})^- \mathbf{X}^{\top} \mathbf{Y}[/math], where [math]\mathbf{A}^-[/math] denotes the Moore-Penrose inverse of matrix [math]\mathbf{A}[/math].

The relation between ridge and principal component regression becomes clear when their corresponding estimators are written in terms of the singular value decomposition of [math]\mathbf{X}[/math]:

[[math]] \begin{eqnarray*} \hat{\bbeta}_{\mbox{{\tiny pcr}}} & = & \mathbf{V}_{x,k} (\mathbf{I}_{kp} \mathbf{D}_x^{\top} \mathbf{D}_x \mathbf{I}_{pk})^{-1} \mathbf{I}_{kp} \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y}, \\ \hat{\bbeta} (\lambda) & = & \mathbf{V}_x (\mathbf{D}_x^{\top} \mathbf{D}_x + \lambda \mathbf{I}_{pp})^{-1} \mathbf{D}_x^{\top} \mathbf{U}_x^{\top} \mathbf{Y}. \end{eqnarray*} [[/math]]

Both operate on the singular values of the design matrix. But where principal component regression thresholds the singular values of [math]\mathbf{X}[/math], ridge regression shrinks them (depending on their size). Hence, one applies a discrete map on the singular values while the other a continuous one.

General References

van Wieringen, Wessel N. (2021). "Lecture notes on ridge regression". arXiv:1509.09169 [stat.ME].

References