Gaussian random vectors

We now turn to points that are chosen at random from the whole space according to a Gaussian distribution with mean zero and unit variance. Our first result is the so-called Gaussian Annulus Theorem which states that a point chosen at random will, with high probability, be located in a small annulus around the sphere with radius [math]\sqrt{d}[/math]. On a first sight that might seem surprising as the density function has its largest values around zero and decays if we move away from zero. The results of Chapter Concentration of measure however show that close to the origin there is located only little volume and since for the probability to be in a Borel set [math]A\subseteq\mathbb{R}^d[/math] we ought to integrate the density function over [math]A[/math], the lack of volume around the origin makes this integral small if [math]A[/math] is located in the vicinity of zero. At a certain radius then the concentration of volume compensates the smaller values of the density function. Going beyond this radius, the small values of the density function determine the value of the integral and make it small again.

Before we can start, we need to fill in several facts about Gaussian random vectors, namely that

spherical Gaussian random vectors are precisely those which are independently coordinate-wise Gaussian (Proposition),
a linear combination of normal random variables is Gaussian with mean zero and variance given by the sum of the squares of the coefficients (Proposition).

The reader familiar with the above can skip the proofs and jump directly to Lemma which will be the final preparation for the Gaussian Annulus Theorem.

Proposition

Let [math](\Omega,\Sigma,\P)[/math] be a probability space and [math]X\colon\Omega\rightarrow\mathbb{R}^d[/math] be a random vector with coordinate functions [math]X_1,\dots,X_d[/math]. Then [math]X[/math] is spherically Gaussian distributed with mean zero and variance [math]\sigma \gt 0[/math] if and only if its coordinates are independent and

[[math]] \P[X_i\in A] = {\medfrac{1}{\sqrt{2\pi}\sigma}} \int_A\exp\bigl(-\medfrac{x^2}{2\sigma^2}\bigr)\dd\lambda(x) [[/math]]

holds for every Borel set [math]A\subseteq\mathbb{R}[/math] and every [math]i=1,\dots,d[/math].

Show Proof

Let [math]A=A_1\times\cdots\times A_d\subseteq\mathbb{R}^d[/math] be given with Borel sets [math]A_i\subseteq\mathbb{R}[/math]. By Fubini's Theorem we compute

[[math]] \begin{align*} \P[X\in A] &= {\medfrac{1}{(2\pi\sigma^2)^{d/2}}} \int_A\exp\bigl(-\medfrac{\|x\|^2}{2\sigma^2}\bigr)\dd\lambda^d(x)\\ & = {\medfrac{1}{(2\pi\sigma^2)^{d/2}}} \int_A\exp\bigl(-\medfrac{x_1^2+\cdots+x_d^2}{2\sigma^2}\bigr)\dd\lambda^d(x)\\ & = {\medfrac{1}{(2\pi\sigma^2)^{d/2}}} \int_A\exp\bigl(-\medfrac{x_1^2}{2\sigma^2}\bigr)\cdots\exp\bigl(-\medfrac{x_d^2}{2\sigma^2}\bigr)\dd\lambda^d(x)\\ & = \medfrac{1}{\sqrt{2\pi}\sigma} \int_{A_1}\exp\bigl(-\medfrac{x_1^2}{2\sigma^2}\bigr)\dd\lambda(x_1)\cdots \medfrac{1}{\sqrt{2\pi}\sigma}\int_{A_d}\exp\bigl(-\medfrac{x_d^2}{2\sigma^2}\bigr)\dd\lambda(x_d)\\ \phantom{\int}& = \P[X_1\in A_1]\cdots\P[X_d\in A_d] \end{align*} [[/math]]

where the first equality is true if [math]X\sim\mathcal{N}(0,1)[/math] holds and the last if [math]X_i\sim\mathcal{N}(0,1)[/math] for each [math]i=1,\dots,d[/math]. This computation now shows both implications.

“[math]\Rightarrow[/math]” Let [math]B\subseteq\mathbb{R}[/math] be Borel and let [math]1\leqslant i\leqslant d[/math] be fixed. Then we have [math]\P[X_i\in B] = \P[X\in\mathbb{R}^{i-1}\times{}B\times\mathbb{R}^{d-i}][/math] and reading the computation above from the beginning until line four shows

[[math]] \P[X_i\in B] = \medfrac{1}{\sqrt{2\pi}\sigma} \int_{B}\exp\bigl(-\medfrac{x_i^2}{2\sigma^2}\bigr)\dd\lambda(x_i) [[/math]]

as all the other integrals are equal to one.

“[math]\Leftarrow[/math]” Let [math]A=A_1\times\cdots\times A_d\subseteq\mathbb{R}^d[/math] with bounded and open intervals [math]A_i\subseteq\mathbb{R}[/math] be an open cuboid. Since the [math]X_i[/math]'s are independent, we get [math]\P[X\in A] = \P[X_1\in A_1]\cdots\P[X_d\in A_d][/math]. Reading now our initial computation backwards until the very first equality, we get

[[math]] \P[X\in A]= {\medfrac{1}{(2\pi\sigma^2)^{d/2}}} \int_A\exp\bigl(-\medfrac{\|x\|^2}{2\sigma^2}\bigr)\dd\lambda^d(x) [[/math]]

which extends now to every Borel set in [math]\mathbb{R}^d[/math] as the cuboids are a generator.

■

As mentioned we need also to show that the distribution of the sum of Gaussian random variables is again Gaussian. We start with the case of two summands.

Lemma

Let [math]X,\,Y\colon\Omega\rightarrow\mathbb{R}[/math] be independent real random variables with probability density functions [math]\rho[/math] and [math]\sigma[/math]. Then the random variable [math]X+Y[/math] has a probability density function which is given by the convolution [math]\rho\Conv\sigma\colon\mathbb{R}\rightarrow\mathbb{R}[/math], [math](\rho\Conv\sigma)(s)=\int_{\mathbb{R}}\rho(s-t)\sigma(t)\dd\lambda(t)[/math].

Show Proof

We first show that [math]\varphi\colon\mathbb{R}^2\rightarrow\mathbb{R}[/math], [math]\varphi(x,y):=\rho(x)\sigma(y)[/math] is a probability density function for the random vector [math][\begin{smallmatrix}X\\Y\end{smallmatrix}]\colon\Omega\rightarrow\mathbb{R}^2[/math]. Indeed, for a rectangle [math][a,b]\times[c,d]\subseteq\mathbb{R}^2[/math] with [math]a \lt b[/math] and [math]c \lt d[/math] we compute

[[math]] \begin{align*} \P_{\textstyle[\begin{smallmatrix}X\\Y\end{smallmatrix}]}\bigl([a,b]\times[c,d]\bigr) & = \P\bigl[(X,Y)\in [a,b]\times[c,d]\bigr]\\ & = \P\bigl[X\in [a,b] \text{ and } Y\in[c,d]\bigr]\\ & = \P\bigl[X\in [a,b]\bigr]\cdot\P\bigl[Y\in[c,d]\bigr]\\ & = \int_{[a,b]}\rho\dd\lambda\,\cdot\,\int_{[c,d]}\sigma\dd\lambda\\ & = \int_{[a,b]\times[c,d]}\varphi\dd\lambda^2 \end{align*} [[/math]]

where we used the independence of [math]X[/math] and [math]Y[/math] in the second equality and Tonelli's Theorem in the last. Since the rectangles generate the Borel [math]\sigma[/math]-algebra, we get

[[math]] \begin{equation}\label{EQ-7-0} \P_{\textstyle[\begin{smallmatrix}X\\Y\end{smallmatrix}]}(A) = \int_A\varphi\dd\lambda^2 \end{equation} [[/math]]

for every Borel set [math]A[/math] which establishes the claim. Now we compute for [math]a \lt b[/math]

[[math]] \begin{equation}\label{EQ-7-1} \begin{aligned} \P_{X+Y}\bigl((a,b])\bigr) &= \P\bigl[X+Y\in (a,b)\bigr]= \P\bigl(\bigl\{\omega\in\Omega\:;\:X(\omega)+Y(\omega)\in(a,b)\bigr\}\bigr)\\ & = \P\bigl(\bigl\{\omega\in\Omega\:;\:\bigl[\begin{smallmatrix}X(\omega)\\Y(\omega)\end{smallmatrix}\bigr]\in D \bigr\}\bigr) = \P_{\textstyle[\begin{smallmatrix}X\\Y\end{smallmatrix}]}(D) = \int_D\varphi\dd\lambda^2 \end{aligned} \end{equation} [[/math]]

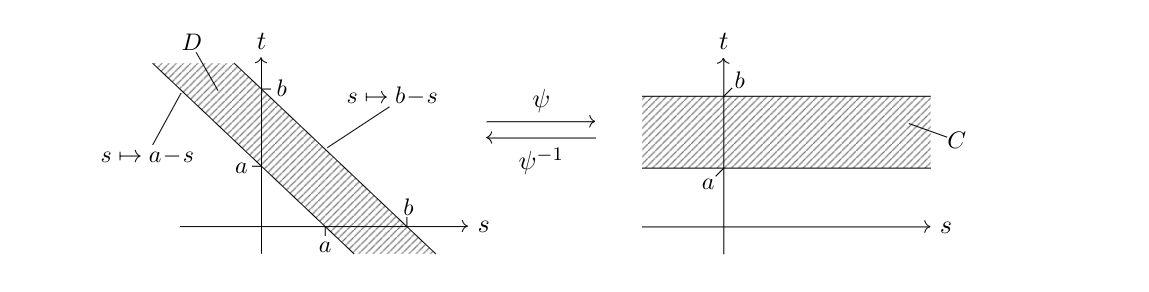
where [math]D = \{(s,t)\in\mathbb{R}^2\:;\:a \lt s+t \lt b\}[/math] is a diagonal strip in the plane as illustrated on the left of following picture and \eqref{EQ-7-0} was used in the last equality. We put [math]C:=\mathbb{R}\times(a,b)[/math] as shown on the right of the following picture and see that [math]\psi\colon C\rightarrow D[/math], [math]\psi(s,t)=(s,t-s)[/math] is a diffeomorphism between open sets and [math]\det(\operatorname{J}_{\psi}(s,t))=1[/math] holds for all [math](s,t)\in C[/math].

We can thus apply the change of variables formula and compute

[[math]] \begin{equation}\label{EQ-7-2} \begin{aligned} \int_D\varphi\dd\lambda^2 & = \int_{F}\varphi\circ\psi\dd\lambda^2\\ & = \int_{(a,b)}\int_{\mathbb{R}}\varphi(s,t-s)\dd\lambda(t)\dd\lambda(s)\\ & = \int_{(a,b)}\int_{\mathbb{R}}\rho(s)\sigma(t-s)\dd\lambda(t)\dd\lambda(s)\\ & = \int_{(a,b)}(\rho\Conv\sigma)(s)\dd\lambda(s) \end{aligned} \end{equation} [[/math]]

where we used Fubini's Theorem in the second equality. Since the open intervals generate the Borel [math]\sigma[/math]--algebra, we conclude from \eqref{EQ-7-1} and \eqref{EQ-7-2} that

[[math]] \P_{X+Y}(A) = \int_{A}\rho\Conv\sigma\dd\lambda [[/math]]

holds for every Borel set as desired.

■

In order to extend the above to more than two summands, we need to establish first that the convolution of density functions is commutative and associative.

Lemma

Let [math]\rho,\,\sigma,\,\tau\colon\mathbb{R}\rightarrow\mathbb{R}[/math] be integrable. Then we have [math]\rho\Conv\sigma=\sigma\Conv\rho[/math] and [math](\rho\Conv\sigma)\Conv\tau=\rho\Conv(\sigma\Conv\tau)[/math].

Show Proof

By substituting [math]u:=s-t[/math] we see that

[[math]] (\rho\Conv\sigma)(s)=\int_{\mathbb{R}}\rho(s-t)\sigma(t)\dd\lambda(t)=\int_{\mathbb{R}}\rho(u)\sigma(s-u)\dd\lambda(u)=(\sigma\Conv\rho)(s) [[/math]]

holds for every [math]s\in\mathbb{R}[/math].

The proof of Lemma shows as a byproduct that the convolution of any two density functions is again a density function and in particular integrable. We thus get

[[math]] \begin{align*} [(\rho\Conv\sigma)\Conv\tau](s)&=\int_{\mathbb{R}}(\rho\Conv\sigma)(u)\tau(s-u)\dd\lambda(u)\\ & = \int_{\mathbb{R}}\int_{\mathbb{R}}\rho(t)\sigma(u-t)\dd\lambda(t)\tau(s-u)\dd\lambda(u)\\ & = \int_{\mathbb{R}}\rho(t)\int_{\mathbb{R}}\sigma(u-t)\tau(s-u)\dd\lambda(u)\dd\lambda(t)\\ & = \int_{\mathbb{R}}\rho(t)\int_{\mathbb{R}}\sigma(s-v-t)\tau(v)\dd\lambda(v)\dd\lambda(t)\\ & = \int_{\mathbb{R}}\rho(t)(\sigma\Conv\tau)(s-t)\dd\lambda(t)\\ &=[\rho\Conv(\sigma\Conv\tau)](s) \end{align*} [[/math]]

where we substituted [math]v:=s-u[/math] in the fourth equality.

■

In view of Lemma we can drop parentheses and simply write [math]\rho_1\Conv\cdots\Conv\rho_n[/math] for the convolution of [math]n[/math] density functions. Employing this, we can now extend Lemma to the sum of more than two random variables.

Proposition

For [math]i=1,\dots,d[/math] let [math]X_i\colon\Omega\rightarrow\mathbb{R}[/math] be independent Gaussian random variables with zero mean and unit variance. Then [math]X:=X_1+\cdots+X_d[/math] is a Gaussian random variable with mean zero and variance [math]d[/math].

Show Proof

Since the sum of measurable functions is measurable, [math]X=X_1+\cdots+X_d[/math] is a random variable. We compute

[[math]] \E(X) = \E(X_1)+\cdots+\E(X_d)=0 \; \text{ and } \; \V(X) = \V(X_1)+\cdots+\V(X_d) = d [[/math]]

where the second equality holds as the [math]X_i[/math] are independent. We now denote by [math]\rho = (2\pi)^{-1/2}\exp(-x/2)[/math] the Gaussian density with mean zero and variance one. Then we need to show that

[[math]] \begin{equation}\label{EQ-GAUSS} (\rho\Conv\cdots\Conv\rho)(x) = \medfrac{1}{\sqrt{2\pi d}}\exp\bigl(-\medfrac{x}{2d}\bigr) \end{equation} [[/math]]

holds where on the left hand side [math]d[/math]--many [math]\rho[/math]'s appear. We will now show \eqref{EQ-GAUSS} for [math]d=2[/math]. The extension to general [math]d[/math] is then immediate by iteration. We compute for arbitrary [math]s\in\mathbb{R}[/math]

[[math]] \begin{equation}\label{CONV-COMP} \begin{aligned} (\rho\Conv\rho)(s) & =\frac{1}{2\pi}\int_{\mathbb{R}}\exp\bigl(-(s-t)^2/2\bigr)\exp\bigl(-t^2/2\bigr)\dd\lambda(t) \\ & = \smallfrac{1}{2\pi}\int_{\mathbb{R}}\exp\bigl(-(t^2-2\,t\,(s/2)+(s/2)^2)-s^2/4\bigr)\dd\lambda(t)\\ & = \smallfrac{1}{2\pi}\exp(-s^2/4)\int_{\mathbb{R}}\exp\bigl(-(t-s/2)^2)\bigr)\dd\lambda(t)\\ & = \smallfrac{1}{2\pi}\exp(-s^2/4)\int_{\mathbb{R}}\exp(-u^2)\dd\lambda(u)\\ & = \smallfrac{1}{2\pi}\exp(-s^2/4)\sqrt{\pi}\\ & = \smallfrac{1}{\sqrt{4\pi}}\exp(-s^2/4) \end{aligned} \end{equation} [[/math]]

where we used the substitution [math]u:=t-s/2[/math].

■

Let us now show what we later really need, namely the case of a linear combination of Gaussian random variables with zero mean and unit variance.

Proposition

For [math]i=1,\dots,d[/math] let [math]X_i\sim\mathcal{N}(0,1)[/math] be independent Gaussian random variables and let [math]\lambda_i\not=0[/math] be real number. Then [math]X:=\lambda_1X_1+\cdots+\lambda_dX_d\sim\mathcal{N}(0,\sigma^2)[/math] with [math]\sigma^2:=\lambda_1^2+\cdots+\lambda_d^2\not=0[/math].

Show Proof

We observe that for [math]\lambda\not=0[/math], [math]X\sim\mathcal{N}(0,1)[/math] and a Borel set [math]A[/math] the following holds

[[math]] \P\bigl[\lambda X\in A\bigr]=\P\bigl[X\in \textfrac{1}{\lambda}A\bigr]=\int_{\frac{1}{\lambda}A}\rho(x)\dd x = \int_{A}\rho(\textfrac{1}{\lambda})\textfrac{1}{\lambda}\dd x [[/math]]

where [math]\rho[/math] is the Gaussian density function. This means that the random variable [math]\lambda X[/math] is given by the density function [math]\rho(\frac{\cdot}{\lambda})\frac{1}{\lambda}[/math]. Subbing in the Gaussian density, the latter becomes

[[math]] \rho(\medfrac{t}{\lambda})\medfrac{1}{\lambda} = \medfrac{1}{\sqrt{2\pi}}\exp\bigl(-(\medfrac{t}{2})^2/2\bigr)\medfrac{1}{\lambda} = \medfrac{1}{\sqrt{2\pi}\lambda}\exp\bigl(-(\medfrac{t^2}{2\lambda^2})\bigr) [[/math]]

for [math]t\in\mathbb{R}[/math], which shows that [math]\lambda X\sim\mathcal{N}(0,\lambda^2)[/math]. We know now that [math]\lambda_iX_i\sim\mathcal{N}(0,\lambda_i^2)[/math] holds for [math]i=1,\dots,d[/math] and need to establish that their sum's density function is given by

[[math]] (\rho_1\Conv\cdots\Conv\rho_d)(x) = (2\pi\sigma^2)^{-1/2}\exp(-x/(2\sigma^2)) [[/math]]

where

[[math]] \rho_i(x)=(2\pi\sigma_i^2)^{-1/2}\exp(-x/(2\sigma_i^2)). [[/math]]

This can be achieved similarly to \eqref{CONV-COMP}. Indeed, let us abbreviate [math]a:=\sigma_1^2[/math] and [math]b:=\sigma_2^2[/math] and [math]c:=a+b[/math], i.e., [math](b+a)/c=1[/math]. Then we get

[[math]] \begin{align*} (\rho_1\Conv{}\rho_2)(s) & =\medfrac{1}{2\pi\sqrt{ab}}\int_{\mathbb{R}}\exp\bigl(-\medfrac{(s-t)^2}{2a}\bigr)\exp\bigl(-\medfrac{t^2}{2b}\bigr)\dd\lambda(t)\\ & =\medfrac{1}{2\pi\sqrt{ab}}\int_{\mathbb{R}}\exp\bigl(-\medfrac{b(s^2-2st+t^2)+at^2}{2ab}\bigr)\dd\lambda(t)\\ & =\medfrac{1}{2\pi\sqrt{ab}}\int_{\mathbb{R}}\exp\bigl(-\medfrac{t^2(b+a)-2stb+bs^2}{2ab}\bigr)\dd\lambda(t)\\ & =\medfrac{1}{2\pi c^2\sqrt{ab/c}}\int_{\mathbb{R}}\exp\bigl(-\medfrac{t^2(b+a)/c-2stb/c+bs^2/c}{2ab/c}\bigr)\dd\lambda(t)\\ & =\medfrac{1}{2\pi c^2\sqrt{ab/c}}\int_{\mathbb{R}}\exp\bigl(-\medfrac{(t-(bs)/c)^2 - (sb/c)^2 +s^2(b/c)}{2ab/c}\bigr)\dd\lambda(t)\\ & =\medfrac{1}{\sqrt{2\pi c}}\exp(- \medfrac{(sb/c)^2 -s^2(b/c)}{2ab/c})\medfrac{1}{\sqrt{2\pi(ab/c)}}\int_{\mathbb{R}}\exp\bigl(-\medfrac{(t-(bs)/c)^2}{2ab/c}\bigr)\dd\lambda(t)\\ & =\medfrac{1}{\sqrt{2\pi c}}\exp(- \medfrac{(sb/c)^2c^2 -s^2(b/c)c^2}{2abc})\\ & =\medfrac{1}{\sqrt{2\pi c}}\exp(- \medfrac{s^2(b^2 -bc)}{2abc})\\ & =\medfrac{1}{\sqrt{2\pi c}}\exp(- \medfrac{s^2}{2c}) \end{align*} [[/math]]

where the integral can be seen to be one by the substitution [math]u:=t-(bs)/c[/math]. Iteration of this completes the proof.

■

We mention that Proposition extends further to the case of a linear combination of arbitrary Gaussian random variables which not necessarily have mean zero or unit variance. The proof then becomes again one step more complicated than the above, as the means [math]\mu_i[/math] appear inside the exponential functions. Since for our purposes below the result as stated above will be sufficient, we leave this last generalization to the reader as Problem.

Our final preparation is the following formula for the integral of the Gaussian function against a polynomial which we will need, in order to estimate moments in the next proof.

Lemma

For [math]k\in\mathbb{N}[/math] the equality

[[math]] \medfrac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}t^{2k}\exp(-t^2/2)\dd t = \medfrac{(2k)!}{2^kk!} [[/math]]

holds.

Show Proof

We first use Lebesgue's Theorem to see that

[[math]] \begin{align*} \medfrac{\operatorname{d}^k}{\dd a^k}\Bigl(\int_{\mathbb{R}}\exp(-at^2)\dd t\Bigr)\Big|_{a=\frac{1}{2}} &= \Bigl(\int_{\mathbb{R}}\medfrac{\operatorname{d}^k}{\dd a^k}\exp(-at^2)\dd t\Bigr)\Big|_{a=\frac{1}{2}}\\ & = \int_{\mathbb{R}}(-t^2)^k\exp(-at^2)\dd t\Big|_{a=\frac{1}{2}}\\ & = (-1)^k\int_{\mathbb{R}}t^{2k}\exp(-t^2/2)\dd t \end{align*} [[/math]]

holds where [math]a \gt 0[/math] and [math]k\in\mathbb{N}[/math] is fixed. On the other hand substituting [math]u:=\sqrt{a}t[/math] leads to

[[math]] \int_{\mathbb{R}}\exp(-at^2)\dd t = \medfrac{1}{\sqrt{a}}\int_{\mathbb{R}}\exp(-u^2)\dd u = \sqrt{\medfrac{\pi}{a}} [[/math]]

now for every [math]a \gt 0[/math]. Combining both equations we obtain

[[math]] \int_{\mathbb{R}}t^{2k}\exp(-t^2/2)\dd t = (-1)^k\medfrac{\operatorname{d}^k}{\dd a^k}\Bigl(\int_{\mathbb{R}}\exp(-at^2)\dd t\Bigr)\Big|_{a=\frac{1}{2}}= (-1)^k\medfrac{\operatorname{d}^k}{\dd a^k}\Bigl(\medfrac{\sqrt{\pi}}{\sqrt{a}}\,\Bigr)\Big|_{a=\frac{1}{2}} [[/math]]

and thus need to compute the derivative on the right hand side. For that purpose we compute

[[math]] \begin{align*} \smallfrac{\operatorname{d}^k}{\dd a^k}(a^{-1/2}) & = (-1/2)\cdot(-1/2-1)\cdots(-1/2-(k-1))\,a^{-1/2-k}\\ & = \smallfrac{(-1)^k}{2^k}(1\cdot 3\cdots(2k-3)\cdot (2k-1))\,a^{-1/2-k}\\ & = \smallfrac{(-1)^k}{2^k}\smallfrac{1\cdot2\cdot 3\cdots(2k-3)\cdot (2k-2)\cdot(2k-1)\cdot(2k)}{2\cdot4\cdots(2k-2)\cdot(2k)}\,a^{-1/2-k}\\ & = \smallfrac{(-1)^k}{2^k}\smallfrac{(2k)!}{2^k k!}\,a^{-1/2-k}. \end{align*} [[/math]]

Putting everything together we arrive at

[[math]] \begin{align*} \smallfrac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}t^{2k}\exp(-t^2/2)\dd t & = \smallfrac{1}{\sqrt{2\pi}}(-1)^k\smallfrac{\operatorname{d}^k}{\dd a^k}\Bigl(\smallfrac{\sqrt{\pi}}{\sqrt{a}}\,\Bigr)\Big|_{a=\frac{1}{2}}\\ & = \smallfrac{(-1)^k}{\sqrt{2}}\smallfrac{(-1)^k}{2^k}\smallfrac{(2k)!}{2^k k!}\,a^{-1/2-k}\Big|_{a=\frac{1}{2}}\\ & = \smallfrac{1}{\sqrt{2}}\,\smallfrac{1}{2^k}\,\smallfrac{(2k)!}{2^k k!}2^{1/2+k} \end{align*} [[/math]]

which after cancelation reduces precisely to the expression on the right hand side in the Lemma.

■

Now we can prove the first main result of this chapter. Notice that the inequality is only non-trivial, i.e., the right hand side strictly less than one, if [math]\epsilon \gt 4\ln2\,(\approx2.8)[/math] holds. This means, although we are using the variable [math]\epsilon[/math] here, the typical intuition that we can let [math]\epsilon\rightarrow0[/math] does not apply.

Theorem

(Gaussian Annulus Theorem) Let [math]x\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then

[[math]] \P\bigl[\big|\|x\|-\sqrt{d}\big|\geqslant\epsilon\bigr]\leqslant 2\exp(-c\epsilon^2). [[/math]]

holds for every [math]0\leqslant\epsilon\leqslant\sqrt{d}[/math] where [math]c=1/16[/math].

Show Proof

Let a random vector [math]X\sim\mathcal{N}(0,1)[/math] be given and let [math]X_1,\dots,X_d[/math] denote its coordinate functions. By Proposition we have [math]X_i\sim\mathcal{N}(0,1)[/math] for every [math]i=1,\dots,d[/math]. We define [math]Y_i:=(X_i^2-1)/2[/math] and see that

[[math]] \begin{equation}\label{EQ-10-1} \begin{aligned} \P\bigl[\big|\|X\|-\sqrt{d}\big|\geqslant\epsilon\bigr] &\leqslant \P\bigl[\big|\|X\|-\sqrt{d}\big|\cdot\bigl(\|X\|+\sqrt{d}\bigr) \gt \epsilon\cdot\sqrt{d}\bigr]\\ &= \P\bigl[\bigl|X_1^2+\cdots+X_d^2-d\bigr| \gt \epsilon\sqrt{d}\bigr]\\ &= \P\bigl[\bigl|(X_1^2-1)+\cdots+(X_d^2-1)\bigr| \gt \epsilon\sqrt{d}\bigr]\\ &= \P\bigl[\bigl|{\textstyle\medfrac{X_1^2-1}{2}}+\cdots+{\textstyle\frac{X_d^2-1}{2}}\bigr| \gt {\textstyle\frac{\epsilon\sqrt{d}}{2}}\bigr]\\ &= \P\bigl[\bigl|Y_1+\cdots+Y_d\bigr| \gt {\textstyle\frac{\epsilon\sqrt{d}}{2}}\bigr] \end{aligned} \end{equation} [[/math]]

where we used [math]\|X\|+\sqrt{d}\geqslant\sqrt{d}[/math] for the inequality. Since we have [math]\E(X_i)=0[/math] and [math]\V(X_i)=1[/math] we get

[[math]] \E(Y_i)=\E\bigl(\medfrac{X_i^2-1}{2}\bigr) = {\textstyle\frac{1}{2}}\bigl(\E(X_i^2)-1\bigr) = 0 [[/math]]

for every [math]i=1,\dots,d[/math]. We now estimate for [math]k\geqslant2[/math] the [math]k[/math]-th moment of [math]Y_i[/math]. For this we firstly note that

[[math]] |X_i^2(\omega)-1|^k\leqslant X_i^{2k}(\omega)+1 [[/math]]

holds for every [math]\omega\in\Omega[/math]. Indeed, if [math]|X_i(\omega)|\leqslant1[/math], then [math]0\leqslant X_i^2(\omega)\leqslant1[/math] and thus [math]|X_i^2(\omega)-1|^k=(1-X_i^2(\omega))^k\leqslant1[/math]. If otherwise [math]|X_i(\omega)| \gt 1[/math], then [math]X_i^2(\omega)-1 \gt 0[/math] and therefore [math]|X_i^2(\omega)-1|^k=(X_i^2(\omega)-1)^k\leqslant X_i^{2k}(\omega)[/math]. We employ the above and estimate

[[math]] \begin{align*} |\E(Y_i^k)| & = \bigl|\E\bigl(\bigl(\medfrac{X_i^2-1}{2}\bigr)^k\bigr)\bigr| = \smallfrac{1}{2^k}\bigl|\E\bigl((X_i^2-1)^k\bigr)\bigr|\\ &\leqslant \smallfrac{1}{2^k}\int_{\Omega}|X_i^2-1|^k\dd\P \leqslant \smallfrac{1}{2^k}\int_{\Omega}X_i^{2k}+1\dd\P = \smallfrac{1}{2^k}\bigl(\E(X_i^{2k})+1\bigr)\\ & = \smallfrac{1}{2^k}\Bigl(\medfrac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}t^{2k}\exp(-t^2/2)\dd t +1\Bigr) = \smallfrac{1}{2^k}\Bigl(\smallfrac{(2k)!}{2^kk!}+1\Bigr)\\ & = \smallfrac{(2k)\cdot(2k-1)\cdot(2k-2)\cdot(2k-3)\cdots5\cdot4\cdot3\cdot2\cdot1}{(2k)^2\cdot(2k-2)^2\cdots(2\cdot3)^2\cdot(2\cdot2)^2\cdot(2\cdot1)^2}k!+\smallfrac{1}{2^k}\\ & = \smallfrac{(2k-1)\cdot(2k-3)\cdots5\cdot3\cdot1}{(2k)\cdot(2k-2)\cdots6\cdot4\cdot2}k!+\smallfrac{1}{2^k}\\ & \leqslant 1\cdot 1\cdots 1\cdot \smallfrac{3}{4}\cdot\smallfrac{1}{2}\cdot k! +\smallfrac{k!}{4\cdot 2}\\ &= \bigl(\smallfrac{3}{4}+\smallfrac{1}{4}\bigr)\smallfrac{k!}{2} \\ &=\smallfrac{k!}{2} \end{align*} [[/math]]

where we used [math]X_i\sim\mathcal{N}(0,1)[/math] to compute [math]\E(X_i^{2k})[/math] and Lemma to evaluate the integral. We thus established that the [math]Y_i[/math] satisfy the assumptions of Theorem and we can thus make use of Bernstein's inequality

[[math]] \P\bigl[|Y_1+\cdots+Y_d|\geqslant a\bigr]\leqslant 2\exp\bigl(-C\min\bigl(\smallfrac{a^2}{d},a\bigr)\bigr) [[/math]]

with [math]a:={\textstyle\frac{\epsilon\sqrt{d}}{2}} \gt 0[/math] to continue our estimate from \eqref{EQ-10-1}. Since [math]\sqrt{d}\geqslant\epsilon[/math] holds, we get

[[math]] \begin{align*} \P\bigl[\big|\|x\|-\sqrt{d}\big|\geqslant\epsilon\bigr]& \leqslant \P\bigl[\bigl|Y_1+\cdots+Y_d\bigr|\geqslant\medfrac{\epsilon\sqrt{d}}{2}\bigr] \\ &\leqslant 2\exp\bigl(-C\min\bigl(\medfrac{(\epsilon\sqrt{d}/2)^2}{d},\medfrac{\epsilon\sqrt{d}}{2}\bigr)\bigr)\\ &\leqslant 2\exp\bigl(-C\min\bigl(\medfrac{\epsilon^2}{4},\medfrac{\epsilon^2}{2}\bigr)\bigr)\\ &= 2\exp\bigl(-C\medfrac{\epsilon^2}{4}\bigr). \end{align*} [[/math]]

Finally, we recall that the constant in Theorem was [math]C=1/4[/math] and thus the exponent equals [math]-c\epsilon^2[/math] with [math]c=1/16[/math].

■

In Chapter The curse of high dimensions we propagated the intuition that a point chosen at random will have norm close to [math]\sqrt{d}[/math] with ‘a high probability.’ More precisely, Figure suggested that the deviation from [math]\sqrt{d}[/math] to be expected will not increase with [math]d[/math]. Theorem allows to quantify this intuition as follows. If we pick, e.g., [math]\epsilon=10[/math] then a random point's norm will satisfy [math]\sqrt{d}-10\leqslant \|x\|\leqslant \sqrt{d}+10[/math] with probability greater or equal to [math]0.99[/math] whenever we are in a space with dimension [math]d\geqslant100[/math].

We note the following byproduct the proof of Theorem which gives a similar estimate but of the square of the norm. Notice that one of our first results in Chapter The curse of high dimensions was the equality [math]\E(\|X\|^2)=d[/math] for any fixed [math]d[/math]---and that we on the other hand proved a statement without the squares, namely [math]\E(\|X\|)\approx\sqrt{d}[/math], asymptotically.

Proposition

Let [math]x\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then

[[math]] \P\bigl[\big|\|x\|^2-d\big|\geqslant\epsilon\bigr]\leqslant 2\exp\bigl(-c\min\bigl(\medfrac{\epsilon^2}{2d},\epsilon\bigr)\bigr). [[/math]]

holds for every [math]\epsilon \gt 0[/math] where [math]c=1/8[/math].

Show Proof

We define the random variables [math]Y_i[/math] as in the proof of Theorem and then proceed using the Bernstein inequality as in the last part of the previous proof. This way we obtain

[[math]] \P\bigl[\bigl|\|X\|^2-d\bigr|\geqslant\epsilon\bigr] = \P\bigl[\bigl|Y_1+\cdots+Y_d\bigr|\geqslant\medfrac{\epsilon}{2}\bigr]\leqslant 2\exp\bigl(-C\min\bigl(\smallfrac{\epsilon^2}{4d},\medfrac{\epsilon}{2}\bigr)\bigr) [[/math]]

which leads to the claimed inequality taking [math]C=1/4[/math] into account.

■

In the next two theorems we divide by [math]\|x\|[/math] and [math]\|y\|[/math] where [math]x[/math] and [math]y[/math] are picked at random. Notice however that [math]x=0[/math] or [math]y=0[/math] occurs only with probability zero. To be completely precise, we could use the conditional probability [math]\P[|\langle{}x/\|x\|,y/\|y\|\rangle{}|\leqslant\epsilon\,|\,x\not=0\text{ and }y\not=0][/math]. We will instead tacitly assume this. Observe that the bound below is non-trivial if [math]\epsilon \gt 2/(\sqrt{d}-7)[/math]. In this result it thus possible to think of [math]\epsilon\rightarrow0[/math], but only if simultaneously [math]d\rightarrow\infty[/math] suitably fast.

Theorem

Let [math]x,y\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then for every [math]\epsilon \gt 0[/math] and for all [math]d\geqslant1[/math] the estimate

[[math]] \P\bigl[\big|\bigl\langle{}\medfrac{x}{\|x\|},\medfrac{y}{\|y\|}\bigr\rangle{}\big|\geqslant\epsilon\bigr]\leqslant \medfrac{2/\epsilon+7}{\sqrt{d}} [[/math]]

holds.

Show Proof

Let [math]y\in\mathbb{R}^d\backslash\{0\}[/math] be fixed and let [math]X\colon\Omega\rightarrow\mathbb{R}^d[/math] be a random vector with [math]X\sim\mathcal{N}(0,1)[/math] whose coordinate functions we denote by [math]X_i[/math] for [math]i=1,\dots d[/math]. We define

[[math]] U_y\colon\Omega\rightarrow\mathbb{R}^d,\;U_y(\omega)=\bigl\langle{}X(\omega),\medfrac{y}{\|y\|}\bigr\rangle{}=\sum_{i=1}^d\medfrac{y_i}{\|y\|}X_i(\omega) [[/math]]

which is itself a random variable which has by Proposition Gaussian distribution with [math]\mu=0[/math] and

[[math]] \sigma^2=\sum_{i=1}^d\medfrac{y_i^2}{\|y\|^2}= \medfrac{1}{\|y\|^2}\sum_{i=1}^d y_i^2 = 1. [[/math]]

This shows that [math]U_y\sim\mathcal{N}(0,1)[/math] is normally distributed. In particular, we have

[[math]] \P\bigl[|U_y|\leqslant \delta\bigr] = \medfrac{1}{\sqrt{2\pi}}\int_{-\delta}^{\delta}\exp(-t^2/2)\dd t [[/math]]

for any [math]\delta \gt 0[/math]. Observe that the right hand side is independent of [math]y[/math]. Therefore, if [math]Y\colon\Omega\rightarrow\mathbb{R}^d[/math] is any other random vector, we can consider the composite random vector [math]U_Y(X)\colon\Omega\rightarrow\mathbb{R}^d[/math] and get for any [math]\delta \gt 0[/math]

[[math]] \begin{align*} \P\bigl[|U_Y(X)|\leqslant \delta\bigr] & = \P\bigl(\{\omega\in\Omega\:;\:(X(\omega),Y(\omega))\in A\}\bigr)= \int_A\rho(x)\rho(y)d(x,y)\\ & = \int_{\mathbb{R}}\rho(x)\int_{A_y}\rho(x)\dd x \dd y = \int_{\mathbb{R}}\rho(x)\P(\{\omega\in\Omega\:;\:X(\omega)\in A_y\}) \dd y \\ & = \int_{\mathbb{R}}\rho(t)\underbrace{\P(\{\omega\in\Omega\:;\:|U_y(X(\omega))|\leqslant\delta\})}_{\text{independent of $y$}} \dd y = 1\cdot\P\bigl[|U_y(X)|\leqslant\delta\bigr] \\ &= \medfrac{1}{\sqrt{2\pi}}\int_{-\delta}^{\delta}\exp(-t^2/2)\dd t \geqslant 1-\medfrac{2}{\sqrt{2\pi}}\int_{\delta}^{\infty}1/t^2\dd t = 1-\medfrac{2}{\sqrt{2\pi}\delta} \end{align*} [[/math]]

where [math]\rho[/math] is the Gaussian density function and [math]A=\{(x,y)\in\mathbb{R}^2\:;\:|U_y(x)|\leqslant\delta\}[/math]. Let now [math]X[/math] and [math]Y\colon\Omega\rightarrow\mathbb{R}^d[/math] both be normally distributed random vectors and let [math]\epsilon \gt 0[/math] be given. We first use the Theorem of Total Probability and drop the second summand. Then we rewrite the first term by using the random variable [math]U_Y(X)[/math] from above and the second term such that the Gaussian Annulus Theorem becomes applicable. We get

[[math]] \begin{align*} \P\bigl[\big|\bigl\langle{}\textfrac{X}{\|X\|},\textfrac{Y}{\|Y\|}\bigr\rangle{}\big|\leqslant\epsilon\bigr] & \geqslant \P\bigl[\big|\bigl\langle{}\textfrac{X}{\|X\|},\textfrac{Y}{\|Y\|}\bigr\rangle{}\big|\leqslant\epsilon\;\big|\;\|X\|\geqslant\textfrac{\sqrt{d}}{2}\bigr]\cdot\P\bigl[\|X\|\geqslant\textfrac{\sqrt{d}}{2}\bigr] \\ &= \P\bigl[\big|\bigl\langle{}X,\textfrac{Y}{\|Y\|}\rangle{}|\leqslant\epsilon\,\|X\|\;\big|\;\|X\|\geqslant\textfrac{\sqrt{d}}{2}\bigr]\cdot\P\bigl[\|X\|\geqslant\textfrac{\sqrt{d}}{2}\bigr] \\ &\geqslant \P\bigl[|U_Y(X)|\leqslant\textfrac{\epsilon\sqrt{d}}{2}\bigr]\cdot\P\bigl[|\|X\|-\sqrt{d}|\geqslant\textfrac{\sqrt{d}}{2}\bigr] \\ &\geqslant \Bigl(1-\medfrac{2}{\sqrt{2\pi}(\epsilon\sqrt{d}/2)}\Bigr)\Bigl(1-2\exp\bigl(-c(\sqrt{d}/2)^2\bigr)\Bigr) \\ &= \Bigl(1-\medfrac{4}{\sqrt{2\pi d}\epsilon}\Bigr)\Bigl(1-2\exp\bigl(-\medfrac{cd}{4}\bigr)\Bigr) \\ &\geqslant 1- \medfrac{4}{\sqrt{2\pi}\epsilon}\medfrac{1}{\sqrt{d}} -2\exp\bigl(-\medfrac{d}{64} \bigr) \end{align*} [[/math]]

since [math]c=1/16[/math]. We see now already that the second summand is the one that goes slower to zero than the third. To get rid of the exponential term we thus only need to find the right constant. We claim that

[[math]] 2\exp\bigl(-\medfrac{x}{64}\bigr)\leqslant \medfrac{7}{\sqrt{x}} [[/math]]

holds for every [math]d\geqslant1[/math]. Indeed, the above is equivalent to [math]f(d):=\frac{49}{4}\exp\bigl(\frac{d}{32}\bigr)-d\geqslant0[/math]. Considering [math]f\colon(0,\infty)\rightarrow\mathbb{R}[/math] we get [math]f'(d)=0[/math] if and only if [math]d=32\ln(\frac{128}{49})[/math] and at this point needs to be the global minimum of [math]f[/math]. Using a calculator one can see that [math]f(32\ln(\frac{128}{49})) \gt 0[/math]. Consequently, we get

[[math]] \P\bigl[\big|\bigl\langle{}\textfrac{X}{\|X\|},\textfrac{Y}{\|Y\|}\bigr\rangle{}\big|\geqslant\epsilon\bigr] \leqslant \medfrac{4}{\sqrt{2\pi}\epsilon}\medfrac{1}{\sqrt{d}} +\medfrac{7}{\sqrt{d}} \leqslant \bigl(\medfrac{2}{\epsilon}+7\bigr) \medfrac{1}{\sqrt{d}} [[/math]]

which concludes the proof.

■

Theorem now also quantifies our intuition that two points chosen at random will have scalar product close to zero and thus will be ‘almost orthogonal’ with ‘a high probability.’ If we pick for instance [math]\epsilon = 0.1[/math] and [math]d\geqslant 100\,000[/math], then by Theorem we get that two points drawn at random will, with probability greater or equal to [math]0.9[/math], have (normalized) scalar product less or equal to [math]0.1[/math]. This corresponds to an angle of [math]90^{\circ}\pm 6^{\circ}[/math].

The proof of the previous result shows also the following.

Corollary

Let [math]X\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math] and [math]0\not=\xi\in\mathbb{R}^d[/math] be fixed. Then we have

[[math]] \P\big[|\langle{}X,\xi\rangle{}|\geqslant\epsilon\bigr]\leqslant \medfrac{4}{\sqrt{2\pi}}\medfrac{\|\xi\|}{\epsilon\sqrt{d}} [[/math]]

for every [math]\epsilon \gt 0[/math].

Show Proof

In the notation of the proof of Theorem we calculate

[[math]] \begin{align*} \P\big[\bigl|\langle{}X,\xi\rangle{}\bigr|\leqslant\epsilon\bigr] & = \P\big[\bigl|\langle{}X,\medfrac{\xi}{\|\xi\|}\rangle{}\bigr|\leqslant\medfrac{\epsilon}{\|\xi\|}\bigr] = \P\big[\bigl|U_{\xi}(X)\bigr|\leqslant\medfrac{\epsilon}{\|\xi\|}\bigr] \geqslant 1-\medfrac{4}{\sqrt{2\pi}}\medfrac{\|\xi\|}{\epsilon\sqrt{d}} \end{align*} [[/math]]

which establishes the result.

■

Since the probability that two random points are exactly orthogonal is obviously zero, we have on the other hand to expect that the probability of being very close to zero is again small. The estimate below is non-trivial if [math]\epsilon \lt 1[/math] and [math]d \gt 16\ln(\frac{2}{1-\epsilon})[/math]. In particular we can now let [math]\epsilon[/math] tend to zero for a fixed [math]d[/math] if we wish so. However, the threshold on the left hand side tends to zero for [math]d\rightarrow\infty[/math] even if we fix [math]0 \lt \epsilon \lt 1[/math] since we divide by [math]\sqrt{d}[/math] inside the square bracket.

Theorem

Let [math]x[/math], [math]y\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then for [math]\epsilon \gt 0[/math] and [math]d\geqslant1[/math] we have

[[math]] \P\bigl[\bigl|\bigl\langle{}\medfrac{x}{\|x\|},\medfrac{y}{\|y\|}\bigr\rangle\bigl|\leqslant\medfrac{\epsilon}{2\sqrt{d}}\,\bigr]\leqslant \epsilon+2\exp(-cd) [[/math]]

where [math]c=1/16[/math].

Show Proof

Let [math]X,Y\colon\Omega\rightarrow\mathbb{R}^d[/math] be random vectors with normal distribution. Let [math]U_Y(X)[/math] be defined as in the proof of Theorem. We compute

[[math]] \begin{align*} \P\bigl[\bigl|\bigl\langle{}\medfrac{X}{\|X\|},\medfrac{Y}{\|Y\|}\bigr\rangle\bigl|\geqslant\medfrac{\epsilon}{2\sqrt{d}}\,\bigr] & = 1-\P\bigl[\bigl|\bigl\langle{}{\textstyle\frac{X}{\|X\|},\frac{Y}{\|Y\|}}\bigr\rangle\bigl| \lt \medfrac{\epsilon}{2\sqrt{d}}\bigr]\\ & = 1-\P\bigl[\medfrac{1}{\|X\|}\cdot\bigl|U_Y(X)\bigl| \lt \medfrac{1}{2\sqrt{d}}\cdot\epsilon\bigr]\\ & \geqslant 1-\P\bigl[\medfrac{1}{\|X\|} \lt \medfrac{1}{2\sqrt{d}} \:\text{ or }\: \bigl|U_Y(X)\bigl| \lt \epsilon\bigr]\\ & \geqslant 1-\Bigl(\P\bigl[\|X\| \gt 2\sqrt{d}\bigr] +\P\bigl[\bigl|U_Y(X)\bigl| \lt \epsilon\bigr]\Bigr)\\ & = \P\bigl[\|X\|\leqslant 2\sqrt{d}\bigr] -\P\bigl[\bigl|U_Y(X)\bigl| \lt \epsilon\bigr]\\ & = \P\bigl[\|X\|-\sqrt{d} \leqslant \sqrt{d}\bigr] -\medfrac{1}{\sqrt{2\pi}}\int_{-\epsilon}^{\epsilon}\exp(-t^2/2)\dd t\\ & \geqslant \P\bigl[\bigl|\|X\|-\sqrt{d}\bigr| \leqslant \sqrt{d}\bigr] -\medfrac{1}{\sqrt{2\pi}}2\epsilon\\ & \geqslant 1-2\exp\Bigl(-\medfrac{1}{16}(\sqrt{d})^2\Bigr) -\sqrt{2/\pi}\,\epsilon\\ & \geqslant 1-2\exp\bigl(\medfrac{d}{16}\bigr) -\epsilon \end{align*} [[/math]]

where we used Theorem and the formula for [math]\P\bigl[|U_Y(X)|\leqslant \delta\bigr][/math] that we established in the proof of Theorem.

■

If we now fix the dimension such that the exponential term is already quite small (e.g., [math]d=100[/math], then [math]2\exp(-cd) \lt 0.01[/math]) and pick, e.g., [math]\epsilon=0.1[/math], then the result shows that the (normalized) scalar product of two random points is less than [math]0.005[/math] only with a probability less than [math]0.11[/math].

Combining the last two results we can think of the scalar products for a fixed high dimension [math]d[/math], with high probability, to be small numbers which are however bounded away from zero.

Our last result in this section quantifies our finding from Chapter The curse of high dimensions that for two points [math]x[/math] and [math]y[/math] drawn at random from a unit Gaussian we have [math]\|x-y\|\approx\sqrt{2d}[/math]. Using [math]\epsilon=18[/math] in (ii) below shows that the values possible for the dimension are [math]d \gt 324[/math]. In this case the estimate is however still trivial. Interesting cases appear only if [math]\epsilon \gt 18[/math] and [math]d[/math] so large that the sum on the right hand side of (ii) stays below one.

Theorem

Let [math]x[/math], [math]y\in\mathbb{R}^d[/math] be drawn at random with respect to a spherical Gaussian distribution with zero mean and unit variance. Then we have the following.

[math]\forall\:\epsilon \gt 18\;\exists\:d_0\in\mathbb{N}\;\forall\:d\geqslant d_0\colon \P\bigl[\bigl|\|x-y\|-\sqrt{2d}\bigr|\geqslant\epsilon\bigr]\leqslant\medfrac{18}{\epsilon}.[/math]
[math]\forall\:\epsilon \gt 18,\,d\geqslant\epsilon^2\colon\P\bigl[\bigl|\|x-y\|-\sqrt{2d}\bigr|\geqslant\epsilon\bigr]\leqslant\medfrac{18}{\epsilon} +\medfrac{8}{\sqrt{d}}.[/math]

Show Proof

We use the same trick as in the beginning of the proof of the Gaussian Annulus Theorem (Theorem) and then use the cosine law to get

[[math]] \begin{align*} \P\bigl[\bigl|\|X-Y\|-\sqrt{2d}\bigr|\geqslant\epsilon\bigr]&\leqslant\P\bigl[\bigl|\|X-Y\|-\sqrt{2d}\bigr|(\|X-Y\|+\sqrt{2d})\geqslant\epsilon\sqrt{2d}\bigr]\\ &=\P\bigl[\bigl|\|X-Y\|^2-2d\bigr|\geqslant\epsilon\sqrt{2d}\bigr]\\ &=1-\P\bigl[\bigl|\|X-Y\|^2-2d\bigr|\leqslant\epsilon\sqrt{2d}\bigr]\\ &=1-\P\bigl[-\epsilon\sqrt{2d}\leqslant\|X\|^2+\|Y\|^2-2\langle{}X,Y\rangle{}-2d\leqslant\epsilon\sqrt{2d}\bigr]\\ & \leqslant1-\P\bigl[\bigr|\|X\|^2-d\bigr|\leqslant\medfrac{\epsilon\sqrt{2d}}{3}\,\bigr]^2\cdot\P\bigl[\bigr|\langle{}X,Y\rangle{}\bigr|\leqslant\medfrac{\epsilon\sqrt{2d}}{6}\,\bigr]=:(\circ) \end{align*} [[/math]]

Now we employ Proposition to obtain

[[math]] \begin{align*} \P\bigl[\bigr|\|X\|^2-d\bigr|\geqslant\medfrac{\epsilon\sqrt{2d}}{3}\,\bigr]&\leqslant2\exp\bigl(-\medfrac{1}{8}\min\bigl(\medfrac{(\epsilon\sqrt{2d}/3)^2}{2d},\medfrac{\epsilon\sqrt{2d}}{3}\bigr)\bigr)\\ & \leqslant 2\exp\bigl(-\medfrac{1}{8}\min\bigl(\medfrac{\epsilon^2}{9},\medfrac{\epsilon^2\sqrt{2}}{3}\bigr)\bigr)\\ & = 2\exp\bigl(-\medfrac{\epsilon^2}{72}\bigr) \end{align*} [[/math]]

where we used [math]\sqrt{d}\geqslant\epsilon[/math] for the second estimate. This leads to

[[math]] \begin{equation}\label{EST-1} P\bigl[\bigr|\|X\|^2-d\bigr|\leqslant\medfrac{\epsilon\sqrt{2d}}{3}\,\bigr]\geqslant1-2\exp\bigl(-\medfrac{\epsilon^2}{72}\bigr) \end{equation} [[/math]]

which will allow us below to estimate the squared term in [math](\circ)[/math]. In order to estimate the non-squared term we use Theorem from which we get with [math]\delta:=\epsilon/(6\sqrt{2d}) \gt 0[/math] the estimate

[[math]] \begin{align*} \medfrac{2/\delta+7}{\sqrt{d}}&\geqslant\P\bigl[\big|\bigl\langle{}X,Y\bigr\rangle{}\big|\geqslant\delta\|X\|\|Y\|\bigr]\\ &\geqslant \P\bigl[\big|\bigl\langle{}X,Y\bigr\rangle{}\big|\geqslant\delta\|X\|\|Y\|\,\big|\,\|X\|,\|Y\|\leqslant\sqrt{2d}\bigr]\cdot \P\bigl[\|X\|,\|Y\|\leqslant\sqrt{2d}\bigr]\\ & \geqslant \P\bigl[\big|\bigl\langle{}X,Y\bigr\rangle{}\big|\geqslant\delta\sqrt{2d}\sqrt{2d}\bigr]\cdot \P\bigl[\|X\|\leqslant\sqrt{2d}\bigr]^2\\ & =\P\bigl[\big|\bigl\langle{}X,Y\bigr\rangle{}\big|\geqslant\delta6\sqrt{2d}\cdot\medfrac{\sqrt{2d}}{6}\bigr]\cdot \P\bigl[\big|\|X\|^2-d\big|\leqslant d\bigr]^2\\ & \geqslant\P\bigl[\big|\bigl\langle{}X,Y\bigr\rangle{}\big|\geqslant\epsilon\medfrac{\sqrt{2d}}{6}\bigr]\cdot \bigl(1-2\exp\bigl(-\medfrac{1}{8}\min(d/2,d)\bigr)\bigr)^2\\ &=\P\bigl[\big|\bigl\langle{}X,Y\bigr\rangle{}\big|\geqslant\medfrac{\epsilon\sqrt{2d}}{6}\bigr]\cdot \bigl(1-2\exp\bigl(-\medfrac{d}{16}\bigr)\bigr)^{2} \end{align*} [[/math]]

where we used Proposition with [math]\epsilon=d[/math] to treat the second factor in the last estimate. Bringing the squared factor in the last expression on the other side and recalling [math]\delta:=\epsilon/(6\sqrt{2d})[/math] leads to

[[math]] \begin{equation}\label{EST-2} \begin{array}{rl} \P\bigl[\bigr|\langle{}X,Y\rangle{}\bigr|\leqslant\medfrac{\epsilon\sqrt{2d}}{6}\,\bigr]&=1-\P\bigl[\bigr|\langle{}X,Y\rangle{}\bigr|\geqslant\medfrac{\epsilon\sqrt{2d}}{6}\,\bigr]\\ &\geqslant 1-\medfrac{2/\delta+7}{\sqrt{d}}\cdot\bigl(1-2\exp\bigl(-\medfrac{d}{16}\bigr)\bigr)^{-2}\\ &\geqslant 1- \bigl(\medfrac{12\sqrt{2}}{\epsilon}+\medfrac{7}{\sqrt{d}} \bigr)\cdot\bigl(1-2\exp\bigl(-\medfrac{d}{16}\bigr)\bigr)^{-2}\\ \end{array} \end{equation} [[/math]]

Now we combine \eqref{EST-1} and \eqref{EST-2} to continue estimating

[[math]] \begin{align*} (\circ) & = 1-\P\bigl[\bigr|\|X\|^2-d\bigr|\leqslant\medfrac{\epsilon\sqrt{2d}}{3}\,\bigr]^2\cdot\P\bigl[\bigr|\langle{}X,Y\rangle{}\bigr|\leqslant\medfrac{\epsilon\sqrt{2d}}{6}\,\bigr]\\ &\leqslant 1-\bigl(1-2\exp\bigl(-\medfrac{\epsilon^2}{72}\bigr)\bigr)^2\cdot\Bigr[1- \bigl(\medfrac{12\sqrt{2}}{\epsilon}+\medfrac{7}{\sqrt{d}} \Bigr)\cdot\bigl(1-2\exp\bigl(-\medfrac{d}{16}\bigr)\bigr)^{-2}\Bigr]\\ & \leqslant 1-\bigl(1-4\exp\bigl(-\medfrac{\epsilon^2}{72}\bigr)\bigr)\cdot\Bigr[1- \frac{\textstyle\frac{12\sqrt{2}}{\epsilon}+\frac{7}{\sqrt{d}}}{\textstyle(1-2\exp(-\frac{d}{16}))^2}\Bigr]\\ & \leqslant 4\exp\bigl(-\medfrac{\epsilon^2}{72}\bigr) + \frac{\textstyle\frac{12\sqrt{2}}{\epsilon}+\frac{7}{\sqrt{d}}}{\textstyle(1-2\exp(-\frac{d}{16}))^2}=:f(\epsilon,d) \end{align*} [[/math]]

where we see that [math]\lim_{d\rightarrow\infty}f(\epsilon,d)=4\exp(-\epsilon^2/72)+12\sqrt{2}/\epsilon[/math] holds. Using a calculator one verifies that [math]4\exp(-\epsilon^2/72) \lt 1/\epsilon[/math] holds for [math]\epsilon \gt 17.5[/math]. From this we get that for suitable large [math]d[/math] and [math]\epsilon \gt 17.5[/math] the estimate

[[math]] f(\epsilon,d)\leqslant\medfrac{1}{\epsilon}+\medfrac{12\sqrt{2}}{\epsilon} \lt \medfrac{18}{\epsilon} [[/math]]

holds which implies (i). For (ii) we continue estimating [math]f(\epsilon,d)[/math]. For [math]\epsilon \gt 17.5[/math], we pick [math]d\geqslant\epsilon^2 \gt 306.25[/math], so [math]d\geqslant307[/math]. For this choice of [math]d[/math] we check with a calculator that [math](1-2\exp(-d/16))^{-2}\leqslant1.0002[/math] which leads to an estimate for the fraction. With this we get

[[math]] \begin{align*} f(\epsilon,d) & = 4\exp\bigl(-\medfrac{\epsilon^2}{72}\bigr) + \frac{\textstyle\frac{12\sqrt{2}}{\epsilon}+\frac{7}{\sqrt{d}}}{\textstyle1-4\exp(-\frac{d}{16})}\leqslant \medfrac{1}{\epsilon}+1.0002\bigl(\medfrac{12\sqrt{2}}{\epsilon} +\medfrac{7}{\sqrt{d}}\bigr)\leqslant\medfrac{18}{\epsilon}+\medfrac{8}{\sqrt{d}} \end{align*} [[/math]]

as desired.

■

Since we do need this later, let us formulate the following probability estimate that we established in the proof above.

Corollary

Let [math]x[/math], [math]y\in\mathbb{R}^d[/math] be drawn at random with respect to the spherical Gaussian distribution with zero mean and unit variance. Then

[[math]] \forall\:\epsilon \gt 18,\,d\geqslant\epsilon^2\colon \P\bigl[\bigl|\|x-y\|^2-2d\bigr|\geqslant\epsilon\sqrt{2d}\bigr]\leqslant \medfrac{18}{\epsilon}+\medfrac{8}{\sqrt{d}} [[/math]]

holds.

General references

Wegner, Sven-Ake (2024). "Lecture Notes on High-Dimensional Data". arXiv:2101.05841 [math.FA].