The Black-Scholes Greeks
\label{sec:greeks} The Greeks a set of letters labeling the quantities of risk associate with small changes in various inputs and model parameters. The Greeks have importance in risk management where hedging and risks are determined by how much/little of the Greeks are exposed on a portfolio. There are 5 main Greeks associated with the Black-Scholes, one of which has already been instrumental in setting up the hedging portfolio, namely the [math]\Delta[/math]. The other Greeks can be equally as important in determining the quality of a hedge.
The Delta Hedge
Recall the derivation of the Black-Scholes PDE of equation eq:BSpde. In particular, recall the hedging allocation in the underlying was the first derivative. This is the Black-Scholes [math]\Delta[/math],
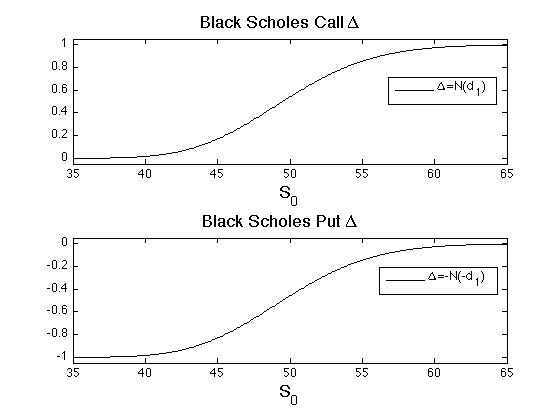
In general, the hedge in the underlying what's referred to when someone talks about being long, short or neutral in [math]\Delta[/math]. With continuos trading the hedging portfolio is a perfect replication because it continuously rebalances to remain [math]\Delta[/math]-neutral. A long position in [math]\Delta [/math] would be when the hedging portfolio holds the underlying in excess of the [math]\Delta[/math] (e.g. a covered call), and a short position in [math]\Delta [/math] would be a hedge with less (e.g. a naked call). For the European call and put options, the Black-Scholes [math]\Delta[/math] is
which are obtained by differentiating the formulas in Proposition and Proposition, respectively. Plots of the [math]\Delta[/math]'s for varying [math]s[/math] are shown in Figure. Notice that all the action in the [math]\Delta[/math]-hedge occurs when the underlying price is near the strike price. Intuitively, a call or put that is far money is efficiently hedged by either holding a share of the underling or simply holding the cash, and the risk is low because there very little probability of the underlying changing dramatically enough to effect your position. Hence, the [math]\Delta[/math]-hedge is like a covered call/put when the derivative is far from the money.
The Theta
The next Greek to discuss is the [math]\Theta[/math], which measures the sensitivity to time. In particular,
The financial interpretation is that [math]\Theta[/math] measures the decay of the time value of the security. Intrinsic value of a security is fairly clear to understand: it is the value of the derivative at today's price of the underlying. However, derivatives have an element of time value on top of the intrinsic value, and in cases where the intrinsic value is zero (e.g. an out-of-the-money option) the derivative's entire cost is its time value. For option contracts, time value quantifies the cost to be paid for having the option to buy/sell, as opposed to taking a position that is long/short the underlying with no option involved. In most cases the time value is positive and decreases with time, hence [math]\Theta \lt 0[/math], but there are contracts (such as far in-the-money put options) that have positive [math]\Theta[/math]. The [math]\Theta[/math]'s for European calls and puts are
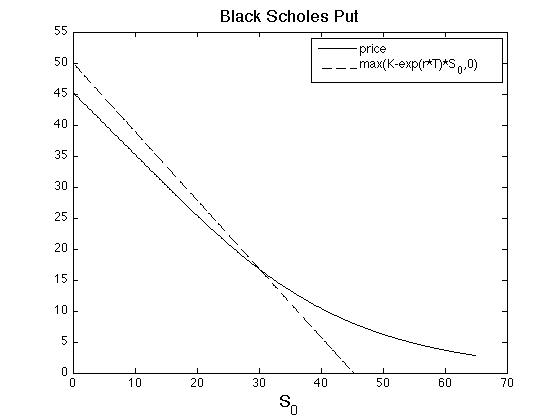
and are shown in Figure. To understand why a far in-the-money put option has positive [math]\Theta[/math], look at Figure and realize that the option price must with rise with time if it is below the intrinsic value.
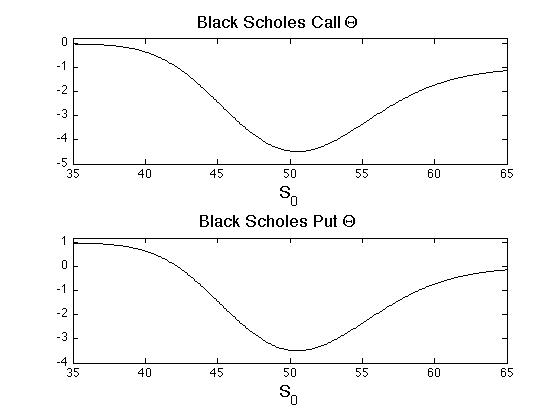
In terms of hedging, a short position in a derivative is said to be short in [math]\Theta[/math], and a long position in the derivative is also long the [math]\Theta[/math]. Hence, a [math]\Delta[/math]-neutral hedge will exposed to [math]\Theta[/math], and a decrease in [math]\Theta[/math] will benefit the short position because it means that the time value of the derivative decreases at a faster rate.
The Gamma
The [math]\Gamma[/math] of a security is the sensitivity of its [math]\Delta[/math]-hedge to changes in the underlying, and there a handful of ways in which the [math]\Gamma[/math] explains hedging and risk management. In a nutshell, the [math]\Gamma[/math] is the higher order sensitivity of the hedging portfolio, and is essentially a convexity term for higher order hedging. Let [math]\Delta t[/math] be the amount of time that goes by in between hedge adjustments. From It\^o's lemma we have the following approximations of the derivative dynamics and a self-financing portfolio:
where [math]\Delta C_t = C_{t+\Delta t}-C_t[/math] and [math]\Delta S_t = S_{t+\Delta t}-S_t[/math], and where [math]\Theta_t,~\Delta_t[/math] and [math]\Gamma_t[/math] are the derivative's Greeks. Subtracting one from the other gets the (approximate) dynamics of a long position in the portfolio and short the derivative,
and so while the [math]\Delta[/math]-hedge replicates perfectly in continuous time, there will be error if this hedge is readjusted in discrete time. However, [math]-\Theta_t -\frac{\sigma^2S_t^2}{2}\Gamma_t \gt 0[/math] corresponds to the premium over the risk-free rate earned by the hedging portfolio. Often times [math]\Gamma \gt 0[/math] and [math]\Theta \lt 0[/math], and so the risk taken by rebalancing a [math]\Delta[/math]-hedge in discrete time is compensated with lower (more negative) [math]\Theta[/math] and lower [math]\Gamma[/math]. For European call and put options, the [math]\Gamma [/math] is
which proportional to the probability density function of [math]\log(S_T/S_t)[/math] and is always positive for long positions. Furthermore, combining the [math]\Gamma[/math] in \eqref{eq:gamma} with equation \eqref{eq:callTheta} we find the premium of equation \eqref{eq:deltaPrem} is
and so the [math]\Delta[/math]-hedge for a European call option earns a premium over the risk-free rate. However, the [math]\Delta[/math]-hedge of the put option has a negative premium
which means the portfolio that longs the put option and shorts the [math]\Delta[/math]-hedge will earn a return over the risk-free rate. If [math]\Delta[/math]-hedging is too risky then the [math]\Gamma[/math] is used in higher order hedging, namely the [math]\Delta[/math]-[math]\Gamma[/math] hedge. The idea is to consider a second derivative security [math]C'(t,s)[/math] with which to hedge. A hedge that is both [math]\Delta[/math]-neutral and [math]\Gamma[/math]-neutral is found by solving the equations
where [math]\alpha_t[/math] is the number of contracts in the underlying, [math]\beta_t[/math] is number of contracts in [math]C'[/math], and [math]\eta_t[/math] is the \$-amount held in the risk-free bank account. This hedge is more expensive and will earn less premium over the risk-free rate,
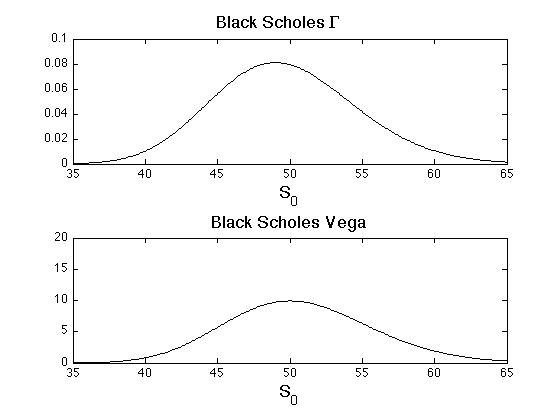
with [math]\frac{\Gamma_t}{\Gamma_t'}\Theta_t'-\Theta_t[/math] being the premium over the risk-free rate. A plot of the Black-Scholes [math]\Gamma[/math] is shown in Figure.
The Vega
The Vega is the Greek to describe sensitivity to [math]\sigma[/math]. Of the 5 main Greeks it is the only one that corresponds to a latent parameter (although some could argue that the risk-free rate is also somewhat latent or abstract). Hence, not only is it important to have a good estimate of [math]\sigma[/math], it is also important to know if your hedging position is sensitive to estimation error. Indeed, volatility is a major question inn derivative pricing, and will be addressed in complete detail in Section. For the Black-Scholes call and puts, the Vega is
which is proportional to the [math]\Gamma[/math] and to the probability density function of [math]\log(S_T/S_t)[/math] (see Figure). There are some portfolios that are particularly sensitive Vega, for instance a straddle consisting of a call and put with the same strike [math]K[/math] if [math]K[/math] is near the money.
The Rho
The [math]\rho[/math] is the sensitivity of to changes in the risk-free rate
Of the 5 main Greeks it widely considered to be the least sensitive. For the Black-Scholes call and put options, the [math]\rho[/math] is
Notice that [math]\rho_{call} \gt 0[/math] because higher interest rates means risky assets should rise in price and hence it will be more likely that you will exercise. Similarly, [math]\rho_{put} \lt 0[/math] because higher interest rates means it is less likely that you will exercise.
Other Greeks
There are also other Greeks of interest in derivatives. Some of the are
- [math]\Lambda[/math], [math]\frac{\partial}{\partial S}C\times \frac{S}{C}[/math], elasticity, or measure of leverage.
- Vanna, [math]\frac{\partial^2}{\partial s\partial \sigma}C[/math], The sensitivity of the [math]\Delta[/math] to changes in volatility.
- Volga, [math]\frac{\partial^2}{\partial \sigma^2}C[/math], used for more elaborate volatility hedging.
General references
Papanicolaou, Andrew (2015). "Introduction to Stochastic Differential Equations (SDEs) for Finance". arXiv:1504.05309 [q-fin.MF].