Static, Simultaneous-Move Finite Games with Multiple Equilibria
An Inference Approach Robust to Bidding Behavior Assumptions
[1] and [2] substantially enlarge the scope of partial identification analysis of structural models by showing how to apply it to learn features of payoff functions in static, simultaneous-move finite games of complete information with multiple equilibria. [3] extend the approach and considerations that follow to games of incomplete information. To start, here I focus on two-player entry games with complete information.[Notes 1]
Let [math](\ey_1,\ey_2,\ex_1,\ex_2)\sim\sP[/math] be observable random variables in [math]\{0,1\}\times\{0,1\}\times\R^d\times\R^d[/math], [math]d \lt \infty[/math]. Suppose that [math](\ey_1,\ey_2)[/math] result from simultaneous move, pure strategy Nash play (PSNE) in a game where the payoffs are [math]\bu_j(\ey_j,\ey_{3-j},\ex_j;\beta_j,\delta_j)\equiv \ey_j(\ex_j\beta_j+\delta_j\ey_{3-j}+\eps_j)[/math], [math]j=1,2[/math] and the strategies are “enter” ([math]\ey_j=1[/math]) or “stay out”([math]\ey_j=0[/math]). Here [math](\ex_1,\ex_2)[/math] are observable payoff shifters, [math](\eps_1,\eps_2)[/math] are payoff shifters observable to the players but not to the econometrician, [math]\delta_1\le 0,\delta_2\le 0[/math] are interaction effect parameters, and [math]\beta_1,\beta_2[/math] are parameter vectors in [math]B\subset\R^d[/math] reflecting the effect of the observable covariates on payoffs. Each player enters the market if and only if entering yields non-negative payoff, so that [math]\ey_j=\one(\ex_j\beta_j+\delta_j\ey_{3-j}+\eps_j\ge 0)[/math]. For simplicity, assume that [math]\eps\equiv(\eps_1,\eps_2)[/math] is independent of [math]\ex\equiv(\ex_1,\ex_2)[/math] and has bivariate Normal distribution with mean vector zero, variances equal to one (a normalization required by the threshold crossing nature of the model), and correlation [math]\rho\in [-1,1][/math]. In the absence of additional information, what can the researcher learn about [math]\theta=[\delta_1\delta_2\beta_1\beta_2\rho][/math]?
From the econometric perspective, this is a generalization of a standard discrete choice model to a bivariate simultaneous response model which yields a stochastic representation of equilibria in a two player, two action game. Generically, for a given value of [math]\theta[/math] and realization of the payoff shifters, the model just laid out admits multiple equilibria (existence of PSNE is guaranteed because the interaction parameters are non-positive). In other words, it yields set valued predictions as depicted in Figure.[Notes 2] Why does this set valued prediction hinder point identification? Intuitively, the challenge can be traced back to the fact that for different values of [math]\theta\in\Theta[/math], one may find different ways to assign the probability mass in [math][-\ex_1\beta_1,-\ex_1\beta_1-\delta_1)\times [-\ex_2\beta_2,-\ex_2\beta_2-\delta_2)[/math] to [math](0,1)[/math] and [math](1,0)[/math], so as to match the observed distribution [math]\sP(\ey_1,\ey_2|\ex_1,\ex_2)[/math]. More formally, for fixed [math]\vartheta\in\Theta[/math] and given [math](\ex,\eps)[/math] and [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math], let
so that in Figure [math]\cE_\vartheta[(1,0),(0,1);\ex][/math] is the gray region, [math]\cE_\vartheta[(0,1);\ex][/math] is the dotted region, etc. Let [math]\sR(y_1,y_2|\ex,\eps)[/math] be a ’'selection mechanism that assigns to each possible outcome of the game [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math] the probability that it is played conditional on observable and unobservable payoff shifters. In order to be admissible, [math]\sR(y_1,y_2|\ex,\eps)[/math] must be such that [math]\sR(y_1,y_2|\ex,\eps)\ge 0[/math] for all [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math], [math]\sum_{(y_1,y_2)\in\{0,1\}\times\{0,1\}}\sR(y_1,y_2|\ex,\eps)=1[/math], and
Let [math]\Phi_r[/math] denote the probability distribution of a bivariate Normal random variable with zero means, unit variances, and correlation [math]r\in[-1,1][/math]. Let [math]\sM(y_1,y_2|\ex)[/math] denote the model predicted probability that the outcome of the game realizes equal to [math](y_1,y_2)[/math]. Then the model yields
Because [math]\sR(\cdot|\ex,\eps)[/math] is left completely unspecified, other than the basic restrictions listed above that render it an admissible selection mechanism, one can find multiple values for [math](\vartheta,\sR(\cdot|\ex,\eps))[/math] such that [math]\sM(y_1,y_2|\ex)=\sP(y_1,y_2|\ex)[/math] for all [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math] [math]\ex[/math]-a.s.
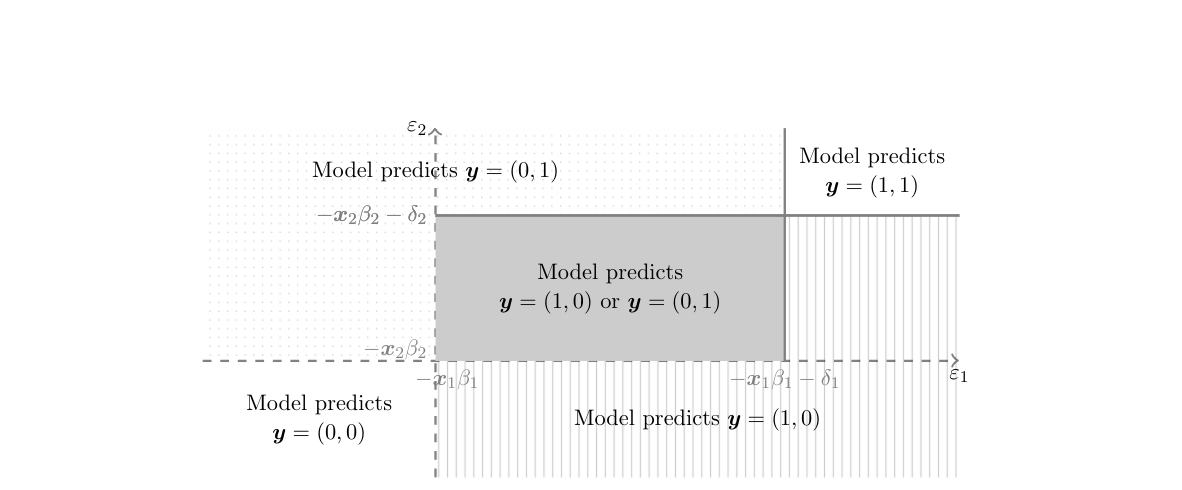
Multiplicity of equilibria implies that the mapping from the model's exogenous variables [math](\ex_1,\ex_2,\eps_1,\eps_2)[/math] to outcomes [math](\ey_1,\ey_2)[/math] is a correspondence rather than a function. This violates the classical “principal assumptions” or “coherency conditions” for simultaneous discrete response models discussed extensively in the econometrics literature (e.g., [4][5][6][7][8]). Such coherency conditions require the existence of a unique reduced form, mapping the model's exogenous variables and parameters to a unique realization of the endogenous variable; hence, they constrain the model to be recursive or triangular in nature. As pointed out by [9], however, the coherency conditions shut down exactly the social interaction effect of interest by requiring, e.g., that [math]\delta_1\delta_2=0[/math], so that at least one player's action has no impact on the other player's payoff.
The desire to learn about interaction effects coupled with the difficulties generated by multiplicity of equilibria prompted the earlier literature to provide at least two different ways to achieve point identification. The first one relies on imposing simplifying assumptions that shift focus to outcome features that are common across equilibria. For example, [10][11][12] and [13] study entry games where the number, though not the identities, of entrants is uniquely predicted by the model in equilibrium. Unfortunately, however, these simplifying assumptions substantially constrain the amount of heterogeneity in player's payoffs that the model allows for. The second approach relies on explicitly modeling a selection mechanism which specifies the equilibrium played in the regions of multiplicity. For example, [9] assume it to be a constant; [14] assume a more flexible, covariate dependent parametrization; and [13] considers two possible selection mechanism specifications, one where the incumbent moves first, and the other where the most profitable player moves first. Unfortunately, however, the chosen selection mechanism can have non-trivial effects on inference, and the data and theory might be silent on which is more appropriate. A nice example of this appears in [13](Table VII). [3] review and extend a number of results on the identification of entry models extensively used in the empirical literature. [15] discusses the observable implications of models with multiple equilibria, and within the analysis of a model with homogeneous preferences shows that partial identification is possible (see [15](p. 1435)). I refer to [16] for a review of the literature on econometric analysis of games with multiple equilibria.
[2] show, on the other hand, that it is possible to partially identify entry models that allow for rich heterogeneity in payoffs and for any possible selection mechanism (even ones that are arbitrarily dependent on the unobservable payoff shifters after conditioning on the observed payoff shifters). In addition, [1] provides sufficient conditions for point identification based on exclusion restrictions and large support assumptions. [17] analyze partial identification of nonparametric models of entry in a two-player model, drawing connections with the program evaluation literature.
Key Insight: An important conceptual contribution of [1] is to clarify the distinction between a model which is incoherent, so that no reduced form exists, and a model which is incomplete, so that multiple reduced forms may exist. Models with multiple equilibria belong to the latter category. Whereas the earlier literature in partial identification had been motivated by measurement problems, e.g., missing or interval data, the work of [1] and [2] is motivated by the fact that economic theory often does not specify how an equilibrium is selected in the regions of the exogenous variables which admit multiple equilibria. This is a conceptually completely distinct identification problem.
[2] propose to use simple and tractable implications of the model to learn features of the structural parameters of interest. Specifically, they point out that the probability of observing any outcome of the game cannot be smaller than the model's implied probability that such outcome is the unique equilibrium of the game, and cannot be larger than the model's implied probability that such outcome is one of the possible equilibria of the game. Looking at Figure this means, for example, that the observed [math]\sP((\ey_1,\ey_2)=(0,1)|\ex_1,\ex_2)[/math] cannot be smaller than the probability that [math](\eps_1,\eps_2)[/math] realizes in the dotted region, and cannot be larger than the probability that it realizes either in the dotted region or in the gray region. Compared to the model predicted distribution in \eqref{eq:games_model:pred}, this means that [math]\sP((\ey_1,\ey_2)=(0,1)|\ex_1,\ex_2)[/math] cannot be smaller than the expression obtained setting, for [math]\eps\in\Eps_\vartheta[(1,0);(0,1);\ex][/math], [math]\sR(0,1|\ex,\eps)=0[/math], and cannot be larger than that obtained with [math]\sR(0,1|\ex,\eps)=1[/math]. Denote by [math]\Phi(A_1,A_2;\rho)[/math] the probability that the bivariate normal with mean vector zero, variances equal to one, and correlation [math]\rho[/math] assigns to the event [math]\{\eps_1\in A_1,\eps_2\in A_2\}[/math]. Then [2] show that any [math]\vartheta=[d_1,d_2,b_1,b_2,r][/math] that is observationally equivalent to the data generating value [math]\theta[/math] satisfies, [math](\ex_1,\ex_2)[/math]-a.s.,
While the approach of [2] is summarized here for a two player entry game, it extends without difficulty to any finite number of players and actions and to solution concepts other than pure strategy Nash equilibrium.
[18] build on the insights of [2] to study what is the identification power of equilibrium in games. To do so, they compare the set-valued model predictions and what can be learned about [math]\theta[/math] when one assumes only level-[math]k[/math] rationality as opposed to Nash play. In static entry games of complete information, they find that the model's predictions when [math]k\ge 2[/math] are similar to those obtained with Nash behavior and allowing for multiple equilibria and mixed strategies. [19] extend the analysis of [18] to the class of supermodular games.
The collections of parameter vectors satisfying (in)equalities \eqref{eq:CT_00}-\eqref{eq:CT_01L} yields the sharp identification region [math]\idr{\theta}[/math] in the case of two player entry games with pure strategy Nash equilibrium as solution concept, as shown by [20](Supplementary Appendix D, Corollary D.4). When there are more than two players or more than two actions (or with different solutions concepts, such as, e.g., mixed strategy Nash equilibrium; correlated equilibrium; or rationality of level [math]k[/math] as in [18]), the characterization in [2] obtained by extending the reasoning just laid out yields an outer region. [20] use elements of random set theory to provide a general and computationally tractable characterization of the identification region that is sharp, regardless of the number of players and actions, or the solution concept adopted. For the case of PSNE with any finite number of players or actions, [21] provide a computationally tractable sharp characterization of the identification region using elements of optimal transportation theory.
Characterization of Sharpness through Random Set Theory
[20] provide a general approach based on random set theory that delivers sharp identification regions on parameters of structural semiparametric models with set valued predictions. Here I summarize it for the case of static, simultaneous move finite games of complete information, first with PSNE as solution concept and then with mixed strategy Nash equilibrium. Then I discuss games of incomplete information.
For a given [math]\vartheta\in\Theta[/math], denote the set of pure strategy Nash equilibria (depicted in Figure) as [math]\eY_\vartheta(\ex,\eps)[/math]. It is easy to show that [math]\eY_\vartheta(\ex,\eps)[/math] is a random closed set as in Definition. Under the assumption in Identification Problem that [math]\ey[/math] results from simultaneous move, pure strategy Nash play, at the true DGP value of [math]\theta\in\Theta[/math], one has
Equation \eqref{eq:y_in_Y_games} exhausts the modeling content of Identification Problem. Theorem can be leveraged to extract its empirical content from the observed distribution [math]\sP(\ey,\ex)[/math]. For a given [math]\vartheta\in\Theta[/math] and [math]K\subset\cY[/math], let [math]\sT_{\eY_{\vartheta}(\ex,\eps)}(K;\Phi_r)[/math] denote the probability of the event [math]\{\eY_\vartheta(\ex,\eps)\cap K\neq \emptyset\}[/math] implied when [math]\eps\sim\Phi_r[/math], [math]\ex[/math]-a.s.
Under the assumptions of Identification Problem, the sharp identification region for [math]\theta[/math] is
To simplify notation, let [math]\eY_\vartheta\equiv \eY_\vartheta(\ex,\eps)[/math]. In order to establish sharpness, it suffices to show that [math]\vartheta\in \idr{\theta}[/math] if and only if one can complete the model with an admissible selection mechanism [math]\sR(y_1,y_2|\ex,\eps)[/math] such that [math]\sR(y_1,y_2|\ex,\eps)\ge 0[/math] for all [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math], [math]\sum_{(y_1,y_2)\in\{0,1\}\times\{0,1\}}\sR(y_1,y_2|\ex,\eps)=1[/math], and satisfying \eqref{eq:games:sel:mec:1}-\eqref{eq:games:sel:mec:2}, so that [math]\sM(y_1,y_2|\ex)=\sP(y_1,y_2|\ex)[/math] for all [math](y_1,y_2)\in\{0,1\}\times\{0,1\}[/math] [math]\ex[/math]-a.s., with [math]\sM(y_1,y_2|\ex)[/math] defined in \eqref{eq:games_model:pred}. Suppose first that [math]\vartheta[/math] is such that a selection mechanism with these properties is available. Then there exists a selection of [math]\eY_\vartheta[/math] which is equal to the prediction selected by the selection mechanism and whose conditional distribution is equal to [math]\sP(\ey|\ex)[/math], [math]\ex[/math]-a.s., and therefore [math]\vartheta \in \idr{\theta}[/math]. Next take [math]\vartheta \in \idr{\theta}[/math]. Then by Theorem, [math]\ey[/math] and [math]\eY_\vartheta[/math] can be realized on the same probability space as random elements [math]\ey'[/math] and [math]\eY'_\vartheta[/math], so that [math]\ey'[/math] and [math]\eY'_\vartheta[/math] have the same distributions, respectively, as [math]\ey[/math] and [math]\eY_\vartheta[/math], and [math]\ey' \in \Sel(\eY'_\vartheta)[/math], where [math]\Sel(\eY'_\vartheta)[/math] is the set of all measurable selections from [math]\eY'_\vartheta[/math], see Definition. One can then complete the model with a selection mechanism that picks [math]\ey'[/math] with probability 1, and the result follows.
The characterization provided in Theorem SIR- for games with multiple PSNE, taken from [20](Supplementary Appendix D), is equivalent to the one in [21]. When [math]J=2[/math] and [math]\cY=\{0,1\}\times\{0,1\}[/math], the inequalities in \eqref{eq:SIR:entry_game} reduce to \eqref{eq:CT_00}-\eqref{eq:CT_01L}. With more players and/or more actions, the inequalities in \eqref{eq:SIR:entry_game} are a superset of those in \eqref{eq:CT_00}-\eqref{eq:CT_01L}, with the latter comprised of the ones in \eqref{eq:SIR:entry_game} for [math]K=\{k\}[/math] and [math]k=\cY\setminus\{k\}[/math], for all [math]k\in\cY[/math]. Hence, the inequalities in \eqref{eq:SIR:entry_game} are more informative. Of course, the computational cost incurred to characterize [math]\idr{\theta}[/math] may grow with the number of inequalities involved. I discuss computational challenges in partial identification in Section.
Key Insight:(Random set theory and partial identification -- continued) In Identification Problem lack of point identification can be traced back to the set valued predictions delivered by the model, which in turn derive from the model incompleteness defined by [1]. As stated in the Introduction, constructing the (random) set of model predictions delivered by the maintained assumptions is an exercise typically carried out in identification analysis, regardless of whether random set theory is applied. Indeed, for the problem studied in this section, [1](Figure 1) put forward the set of admissible outcomes of the game. [20] propose to work directly with this random set to characterize [math]\idr{\theta}[/math]. The fundamental advantage of this approach is that it dispenses with considering the possible selection mechanisms that may complete the model. Selection mechanisms may depend on the model's unobservables even after conditioning on observables and may constitute an infinite dimensional nuisance parameter, which creates great difficulties for the computation of [math]\idr{\theta}[/math] and for inference.
Next, I discuss the case that the outcome of the game results from simultaneous move, mixed strategy Nash play.[Notes 3] When mixed strategies are allowed for, the model predicts multiple mixed strategy Nash equilibria (MSNE). But whereas when only pure strategies are allowed for, if the model is correctly specified, the observed outcome of the game is one of the predicted PSNE, with mixed strategy it is only the result of a random mixing draw from one of the predicted MSNE. Hence, the identification problem is more complex, and in order to obtain a tractable characterization of [math]\theta[/math]'s sharp identification region one needs to use different tools from random set theory.
To keep the treatment simple here I continue to consider the case of two players with two strategies, as in Identification Problem, with mixed strategies allowed for, and refer to [22](Section 3.4) for the general case. Fix [math]\vartheta\in\Theta[/math]. Let [math]\sigma_j:\{0,1\}\to [0,1][/math] denote the probability that player [math]j[/math] enters the market, with [math]1-\sigma_j[/math] the probability that she stays out. With some abuse of notation, let [math]\bu_j(\sigma_j,\sigma_{-j},\ex_j,\eps_j,\vartheta)[/math] denote the expected payoff associated with the mixed strategy profile [math]\sigma=(\sigma_1,\sigma_2)[/math]. For a given realization [math](x,e)[/math] of [math](\ex,\eps)[/math] and a given value of [math]\vartheta\in\Theta[/math], the set of mixed strategy Nash equilibria is
[20] show that [math]\eS_\vartheta\equiv S_\vartheta(\ex,\eps)[/math] is a random closed set in [math][0,1]^2[/math]. Its realizations are illustrated in Panel (a) of Figure as a function of [math](\eps_1,\eps_2)[/math].[Notes 4]
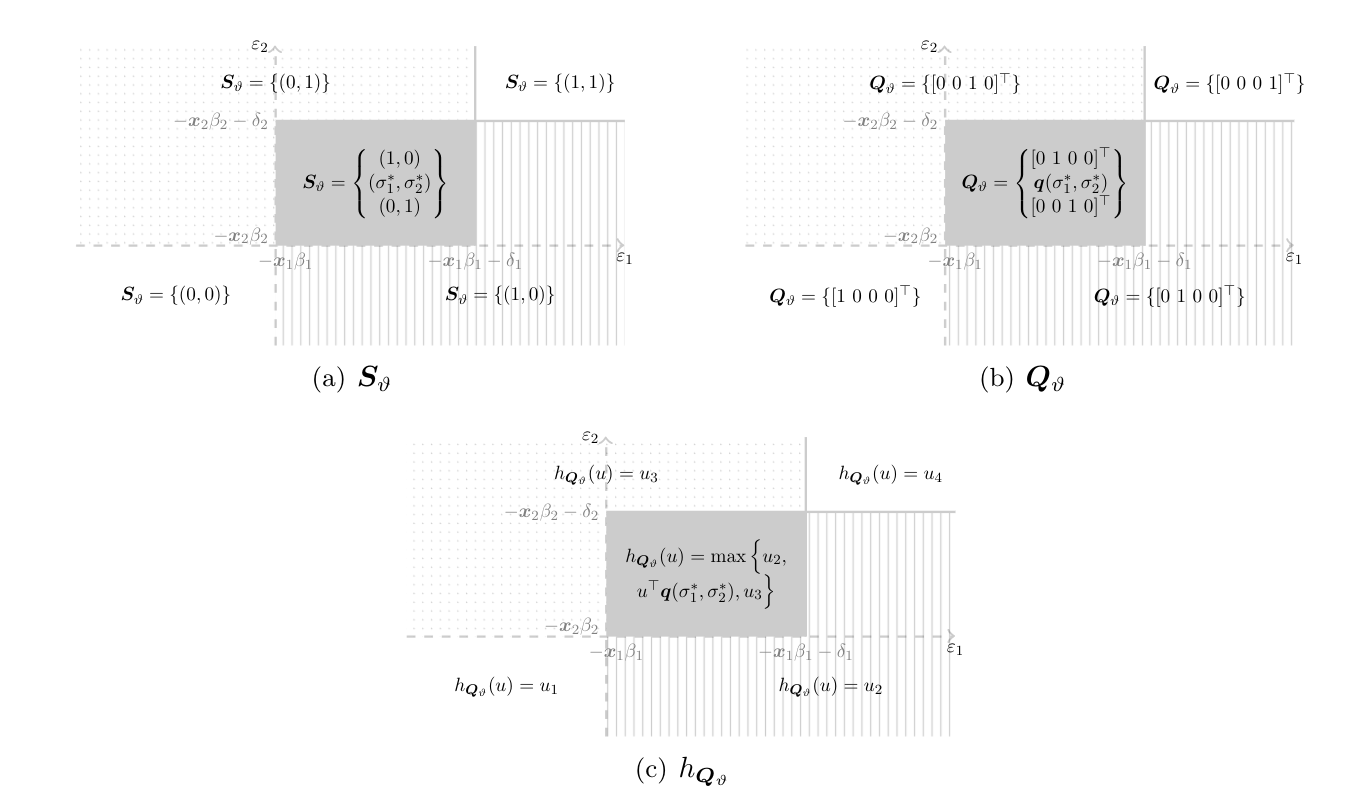
Define the set of possible multinomial distributions over outcomes of the game associated with the selections [math]\sigma[/math] of each possible realization of [math]\eS_{\vartheta}[/math] as
As [math]\eQ_\vartheta[/math] is the image of a continuous map applied to the random compact set [math]\eS_\vartheta[/math], it is a random compact set. Its realizations are plotted in Panel (b) of Figure as a function of [math](\eps_1,\eps_2)[/math].
The multinomial distribution over outcomes of the game determined by a given [math]\sigma\in\eS_\vartheta[/math] is a function of [math]\eps[/math]. To obtain the predicted distribution over outcomes of the game conditional on observed payoff shifters only, one needs to integrate out the unobservable payoff shifters [math]\eps[/math]. Doing so requires care, as it needs to be done for each [math]\eq(\sigma)\in\eQ_\vartheta[/math]. First, observe that all the [math]\eq(\sigma)\in\eQ_\vartheta[/math] are contained in the [math]3[/math] dimensional unit simplex, and are therefore integrable. Next, define the conditional selection expectation (see Definition) of [math]\eQ_\vartheta[/math] as
where [math]\Sel(\eS_\vartheta)[/math] is the set of all measurable selections from [math]\eS_\vartheta[/math], see Definition. By construction, [math]\E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] is the set of probability distributions over action profiles conditional on [math]\ex[/math] which are consistent with the maintained modeling assumptions, i.e., with all the model's implications (including the assumption that [math]\eps\sim\Phi_r[/math]). If the model is correctly specified, there exists at least one vector [math]\theta\in\Theta[/math] such that the observed conditional distribution [math]\cp(\ex)\equiv[\sP(\ey=y^1|\ex),\dots,\sP(\ey=y^4|\ex)]^\top[/math] almost surely belongs to the set [math]\E_{\Phi_\rho}(\eQ_\theta|\ex)[/math]. Indeed, by the definition of [math]\E_{\Phi_\rho}(\eQ_\theta|\ex)[/math], [math]\cp(\ex)\in \E_{\Phi_\rho}(\eQ_\theta|\ex)[/math] almost surely if and only if there exists [math]\eq\in \Sel(\eQ_\theta)[/math] such that [math]\E_{\Phi_\rho}(\eq|\ex)=\cp(\ex)[/math] almost surely, with [math]\Sel(\eQ_\theta)[/math] the set of all measurable selections from [math]\eQ_\theta[/math]. Hence, the collection of parameter vectors [math]\vartheta\in\Theta[/math] that are observationally equivalent to the data generating value [math]\theta[/math] is given by the ones that satisfy [math]\cp(\ex)\in \E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] almost surely. In turn, observing that by Theorem the set [math]\E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] is convex, we have that [math]\cp(\ex)\in \E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] if and only if [math]u^\top \cp(\ex)\leq h_{\E_{\Phi_r}(\eQ_\vartheta|\ex)}(u)[/math] for all [math]u[/math] in the unit ball (see, e.g., [23](Theorem 13.1)), where [math]h_{\E_{\Phi_r}(\eQ_\vartheta|\ex)}(u)[/math] is the support function of [math]\E_{\Phi_r}(\eQ_\vartheta|\ex)[/math], see Definition.
Under the assumptions in Identification Problem, allowing for mixed strategies and with the observed outcomes of the game resulting from mixed strategy Nash play, the sharp identification region for [math]\theta[/math] is
where [math]\mu[/math] is any probability measure on [math]\mathbb{B}^{|\cY|}[/math], and [math]|\cY|=4[/math] in this case.
Show ProofTheorem (equation eq:dom_Aumann:cond) yields \eqref{eq:SIR_sharp_mixed_sup}, because by the arguments given before the theorem, [math]\idr{\theta}=\{\vartheta \in \Theta:\;\cp(\ex)\in \E_{\Phi_r}(\eQ_\vartheta|\ex),\ex\text{-a.s.}\}[/math]. The result in \eqref{eq:SIR_sharp_mixed_int} follows because the integrand in \eqref{eq:SIR_sharp_mixed_int} is continuous in [math]u[/math] and both conditions inside the curly brackets are satisfied if and only if [math]u^\top \cp(\ex)-\E_{\Phi_r}[h_{\eQ_\vartheta}(u)|\ex]\leq 0[/math] [math]\forall u\in \mathbb{B}^{|\cY|}[/math] [math]\ex[/math]-a.s.
For a fixed [math]u\in\mathbb{B}^4[/math], the possible realizations of [math]h_{\eQ_\vartheta}(u)[/math] are plotted in Panel (c) of Figure as a function of [math](\eps_1,\eps_2)[/math]. The expectation of [math]h_{\eQ_\vartheta}(u)[/math] is quite straightforward to compute, whereas calculating the set [math]\E_{\Phi_r}(\eQ_\vartheta|\ex)[/math] is computationally prohibitive in many cases. Hence, the characterization in \eqref{eq:SIR_sharp_mixed_sup} is computationally attractive, because for each [math]\vartheta\in\Theta[/math] it requires to maximize an easy-to-compute superlinear, hence concave, function over a convex set, and check if the resulting objective value vanishes. Several efficient algorithms in convex programming are available to solve this problem, see for example the MatLab software for disciplined convex programming CVX [24]. Nonetheless, [math]\idr{\theta}[/math] itself is not necessarily convex, hence tracing out its boundary is non-trivial. I return to computational challenges in partial identification in Section.\medskip
Key Insight: Random set theory and partial identification -- continued [20] provide a general characterization of sharp identification regions for models with convex moment predictions. These are models that for a given [math]\vartheta\in\Theta[/math] and realization of observable variables, predict a set of values for a vector of variables of interest. This set is not necessarily convex, as exemplified by [math]\eY_\vartheta[/math] and [math]\eQ_\vartheta[/math], which are finite. No restriction is placed on the manner in which, in the DGP, a specific model prediction is selected from this set. When the researcher takes conditional expectations of the resulting elements of this set, the unrestricted process of selection yields a convex set of moments for the model variables (all possible mixtures). This is the model's convex set of moment predictions. If this set were almost surely single valued, the researcher would learn (features of) [math]\theta[/math] by solving moment equality conditions involving the observed variables and predicted ones. The approach reviewed in this section is a set-valued method of moments that extends the singleton-valued one commonly used in econometrics.
I conclude this section discussing the case of static, simultaneous move finite games of incomplete information, using the results in [20](Supplementary Appendix C).[Notes 5] For clarity, I formalize the maintained assumptions.
Impose the same structure on payoffs, entry decision rule, outcome space, parameter space, and observable variables as in Identification Problem. Assume that the observed outcome of the game results from simultaneous move, pure strategy Bayesian Nash play. Both players and the researcher observe [math](\ex_1,\ex_2)[/math]. However, [math]\eps_j[/math] is private information to player [math]j=1,2[/math] and unobservable to the researcher, with [math]\eps_1\independent\eps_2|(\ex_1,\ex_2)[/math]. Assume that players have correct common prior [math]\sF_\gamma[/math] on the distribution of [math](\eps_1,\eps_2)[/math] and the researcher knows this distribution up to [math]\gamma[/math], a finite dimensional parameter vector. Under these assumptions, multiple Bayesian Nash equilibria (BNE) may result.[Notes 6] In the absence of additional information, what can the researcher learn about [math]\theta=[\delta_1\delta_2\beta_1\beta_2\gamma][/math]?
With incomplete information, players' strategies are decision rules that map the support of [math](\eps,\ex)[/math] into [math]\{0,1\}[/math]. The non-negativity condition on expected payoffs that determines each player's decision to enter the market results in equilibrium mappings (decision rules) that are step functions determined by a threshold: [math]y_j(\eps_j) =\one(\eps_j\geq t_j), j=1,2[/math]. As a result, player [math]j[/math]'s beliefs about player [math]3-j[/math]'s probability of entry under the common prior assumption is [math]\int y_{3-j}(\eps_{3-j}) d\sF_\gamma(\eps_{3-j}|\ex) =1-\sF_\gamma(t_{3-j}|\ex)[/math], and therefore player [math]j[/math]'s best response cutoff is
Hence, the set of equilibria can be defined as the set of cutoff rules:
The equilibrium thresholds are functions of [math]\ex[/math] and [math]\theta[/math] only. The set [math]\eT_{\theta}(\ex)[/math] might contain a finite number of equilibria (e.g., if the common prior is the Normal distribution), or a continuum of equilibria. For ease of notation I suppress its dependence on [math]\ex[/math] in what follows. Given the equilibrium decision rules (the selections of the set [math]\eT_\theta[/math]), it is possible to determine their associated action profiles. Because in the simple two-player entry game that I consider actions and outcomes coincide, I denote the set of admissible action profiles by [math]\eY_\theta[/math]:
with [math]\Sel(\eT_\theta)[/math] the set of all measurable selections from [math]\eT_\theta[/math], see Definition. To obtain the predicted set of multinomial distributions for the outcomes of the game, one needs to integrate out [math]\eps[/math] conditional on [math]\ex[/math]. Again this can be done by using the conditional Aumann expectation:
This set is closed and convex. Regardless of whether [math]\eT_\theta[/math] contains a finite number of equilibria or a continuum, [math]\eY_\theta[/math] can take on only a finite number of realizations corresponding to each of the vertices of the three dimensional simplex, because the vectors [math]\ey(\et)[/math] in \eqref{eq:q_incomplete} collect threshold decision rules. This implies that [math]\E_{\sF_\gamma}(\eY_\theta|\ex)[/math] is a closed convex polytope [math]\ex[/math]-a.s., fully characterized by a finite number of supporting hyperplanes. Hence, it is possible to determine whether [math]\vartheta\in\idr{\theta}[/math] using efficient algorithms in linear programming.
Under the assumptions in Identification Problem, the sharp identification region for [math]\theta[/math] is
The result in \eqref{eq:SIR:incomplete_info:1} follows by the same argument as in the proof of Theorem SIR-. Next I show equivalence of the conditions
One can use the same argument as in the proof of Theorem SIR-, to show that the Aumann expectation/support function characterization of the sharp identification region in Theorem SIR- coincides with the characterization based on the capacity functional in Theorem SIR-, when only pure strategies are allowed for. This shows that in this class of models, the capacity functional based characterization is a special case of the Aumann expectation/support function based one. [18] study what is the identification power of equilibrium also in the case of static entry games with incomplete information. They show that in the presence of multiple equilibria, assuming Bayesian Nash behavior yields more informative regions for the parameter vector [math]\theta[/math] than assuming only rational behavior, but at the price of a higher computational cost. [27] propose a procedure to test for the sign of the interaction effects (which here I have assumed to be non-positive) in discrete simultaneous games with incomplete information and (possibly) multiple equilibria. As a by-product of this procedure, they also provide a test for the presence of multiple equilibria in the DGP. The test does not require parametric specifications of players' payoffs, the distributions of their private signals, or the equilibrium selection mechanism. Rather, the test builds on the commonly invoked assumption that players' private signals are independent conditional on observed states. [28] introduces an important class of models with flexible information structure. Each player is assumed to have a vector of payoff shifters unobservable by the researcher composed of elements that are private information to the player, and elements that are known to all players. The results of [20] reported in this section apply to this set-up as well.
General references
Molinari, Francesca (2020). "Microeconometrics with Partial Identification". arXiv:2004.11751 [econ.EM].
Notes
- Completeness of information is motivated by the idea that firms in the industry have settled in a long-run equilibrium, and have detailed knowledge of both their own and their rivals' profit functions.
- This figure is based on Figure 1 in [1].
- The same reasoning given here applies if instead of mixed strategy Nash the solution concept is correlated equilibrium, by replacing the set of MSNE below with the set of correlated equilibria.
- This figure is based on Figure 1 in [2].
- See [3](Section 3) and [4] for a thorough discussion of the literature on identification problems in games of incomplete information with multiple Bayesian Nash equilibria (BNE). [5] explain how to extend the approach proposed by [6] to obtain outer regions on [math]\theta[/math] when no restrictions are imposed on the equilibrium selection mechanism that chooses among the multiple BNE.
- Both the independence assumption and the correct common prior assumption are maintained here to simplify exposition. Both could be relaxed with no conceptual difficulty, though computation of the set of Bayesian Nash equilibria, for example, would become more cumbersome.
References
- 1.0 1.1 1.2 1.3 1.4 1.5 Tamer, E. (2003): “Incomplete Simultaneous Discrete Response Model with Multiple Equilibria” The Review of Economic Studies, 70(1), 147--165.
- 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 Ciliberto, F., and E.Tamer (2009): “Market Structure and Multiple Equilibria in Airline Markets” Econometrica, 77(6), 1791--1828.
- 3.0 3.1 Berry, S.T., and E.Tamer (2006): “Identification in Models of Oligopoly Entry” in Advances in Economics and Econometrics: Theory and Applications, Ninth World Congress, ed. by R.Blundell, W.K. Newey, and T.E. Persson, vol.2 of Econometric Society Monographs, p. 46–85. Cambridge University Press.
- Heckman, J.J. (1978): “Dummy Endogenous Variables in a Simultaneous Equation System” Econometrica, 46(4), 931--959.
- Gourieroux, C., J.J. Laffont, and A.Monfort (1980): “Coherency Conditions in Simultaneous Linear Equation Models with Endogenous Switching Regimes” Econometrica, 48, 675--695.
- Schmidt, P. (1981): “Constraints on the Parameters in Simultaneous Tobit and Probit Models” in Structural Analysis of Discrete Data and Econometric Applications, ed. by C.F. Manski, and D.McFadden, chap.12, pp. 422--434. MIT Press.
- Maddala, G.S. (1983): Limited-Dependent and Qualitative Variables in Econometrics. Cambridge University Press, New York.
- Blundell, R., and J.R. Smith (1994): “Coherency and Estimation in Simultaneous Models with Censored or Qualitative Dependent Variables” Journal of Econometrics, 64, 355--373.
- 9.0 9.1 Bjorn, P.A., and Q.H. Vuong (1984): “Simultaneous Equations Models for Dummy Endogenous Variables: A Game Theoretic Formulation with an Application to Labor Force Participation” CIT working paper SSWP 537, California Institute of Technology, available at http://resolver.caltech.edu/CaltechAUTHORS:20170919-140310752.
- Bresnahan, T.F., and P.C. Reiss (1988): “Do Entry Conditions Vary Across Markets?” Brookings Papers on Economic Activity, pp. 833--871.
- Bresnahan, T.F., and P.C. Reiss (1990): “Entry in Monopoly Markets” The Review of Economic Studies, 57(4), 531--553.
- Bresnahan, T.F., and P.C. Reiss (1991): “Empirical models of discrete games” Journal of Econometrics, 48(1), 57--81.
- 13.0 13.1 13.2 Berry, S.T. (1992): “Estimation of a Model of Entry in the Airline Industry” Econometrica, 60(4), 889--917.
- Bajari, P., H.Hong, and S.P. Ryan (2010): “Identification and estimation of a discrete game of complete information” Econometrica, 78(5), 1529--1568.
- 15.0 15.1 Jovanovic, B. (1989): “Observable Implications of Models with Multiple Equilibria” Econometrica, 57(6), 1431--1437.
- {\noopsort{Paula}}{de Paula}, A. (2013): “Econometric Analysis of Games with Multiple Equilibria” Annual Review of Economics, 5(1), 107--131.
- Kline, B., and E.Tamer (2012): “Bounds for best response functions in binary games” Journal of Econometrics, 166(1), 92 -- 105.
- 18.0 18.1 18.2 18.3 Aradillas-Lopez, A., and E.Tamer (2008): “The Identification Power of Equilibrium in Simple Games” Journal of Business & Economic Statistics, 26(3), 261--283.
- Molinari, F., and A.M. Rosen (2008): “The Identification Power of Equilibrium in Games: The Supermodular Case (Comment on Aradillas-Lopez and Tamer, 2008)” Journal of Business and Economic Statistics, 26(3), 297--302.
- 20.0 20.1 20.2 20.3 20.4 20.5 20.6 20.7 20.8 Beresteanu, A., I.Molchanov, and F.Molinari (2011): “Sharp identification regions in models with convex moment predictions” Econometrica, 79(6), 1785--1821.
- 21.0 21.1 Galichon, A., and M.Henry (2011): “Set Identification in Models with Multiple Equilibria” The Review of Economic Studies, 78(4), 1264--1298.
- Molchanov, I., and F.Molinari (2018): Random Sets in Econometrics. Econometric Society Monograph Series, Cambridge University Press, Cambridge UK.
- Rockafellar, R. (1970): Convex Analysis, Princeton landmarks in mathematics and physics. Princeton University Press.
- Grant, M., and S.Boyd (2010): “{CVX}: Matlab Software for Disciplined Convex Programming, Version 1.21” available at http://cvxr.com/cvx.
- Molchanov, I. (2017): Theory of Random Sets. Springer, London, 2 edn.
- Schneider, R. (1993): Convex Bodies: The Brunn-Minkowski Theory, Encyclopedia of Mathematics and its Applications. Cambridge University Press, 1 edn.
- {\noopsort{Paula}}{de Paula}, A., and X.Tang (2012): “Inference of Signs of Interaction Effects in Simultaneous Games With Incomplete Information” Econometrica, 80(1), 143--172.
- Grieco, P. L.E. (2014): “Discrete games with flexible information structures: an application to local grocery markets” The RAND Journal of Economics, 45(2), 303--340.