The Parabola
The Parabola.
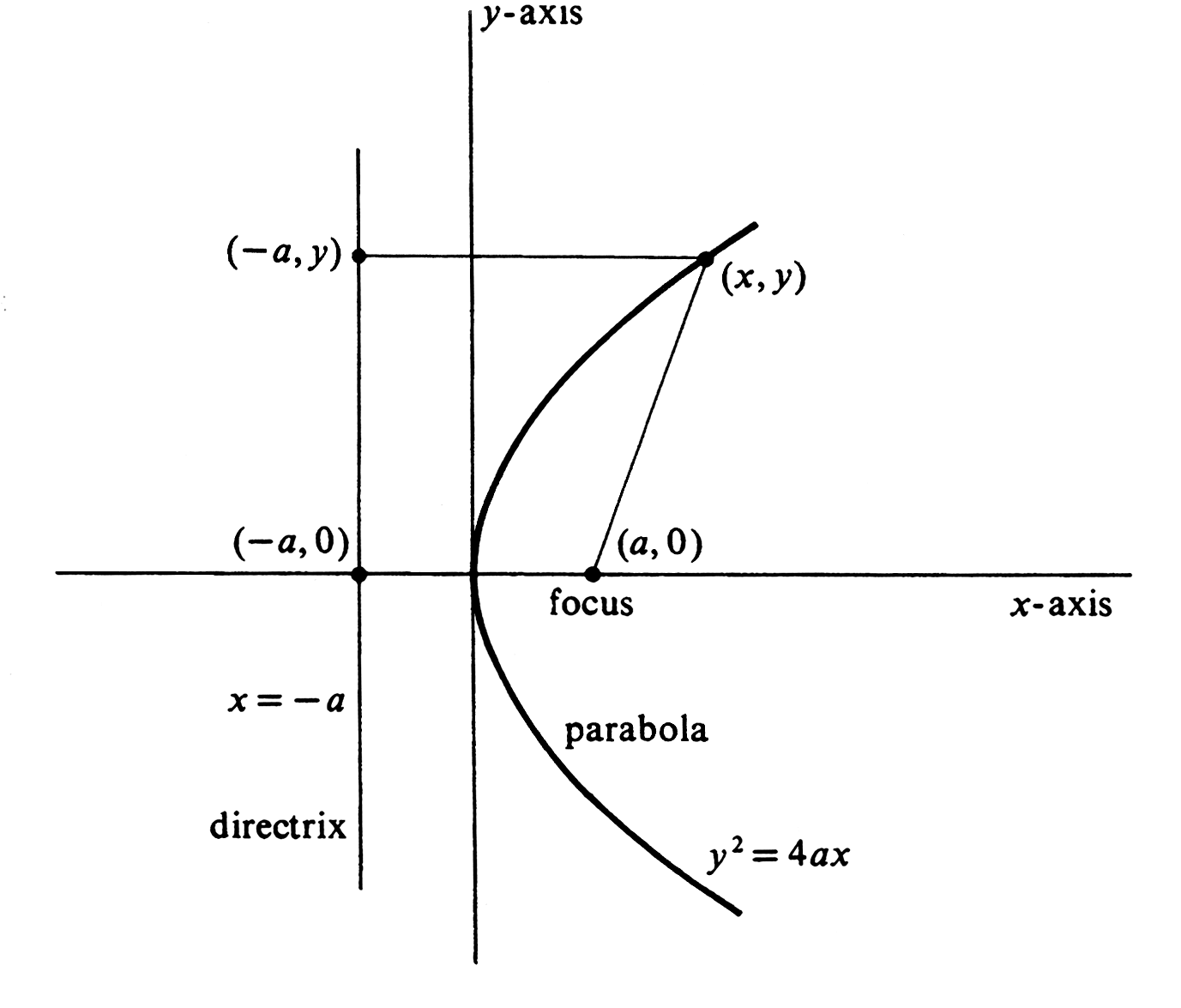
A second conic section, which appears in a great many physical applications, is the parabola. In this section we shall derive its equation and study its properties. By definition, a parabola is the locus of points in a plane equidistant from a given line and a given point not on the line. The line is called the directrix, and the point is called the focus. A simple equation for a parabola is found if a point on the [math]x[/math]-axis is used for the focus and a line perpendicular to the [math]x[/math]-axis and on the opposite side of the origin from the focus is used as the directrix. In Figure, the focus is at [math](a, 0)[/math] and an equation of the directrix is [math]x = -a[/math]. The distance from an arbitrary point [math](x, y)[/math] to the focus [math](a, 0)[/math] is, by the distance formula, [math]\sqrt{(x-a)^2 + (y-0)^2}[/math]. The perpendicular from [math](x, y)[/math] to the directrix intersects that line at [math](-a, y)[/math], and so the distance from the point to the line is [math]\sqrt{(x + a)^2 + (y - y)^2} = | x + a |[/math]. The point [math](x, y)[/math] lies on the parabola if and only if the two distances are equal. Hence an equation of the parabola is
An equivalent equation, which is simpler, is obtained by squaring both sides. We get
or
This equation has been derived in such a way that its graph contains all points and only those points equidistant from the focus and the directrix.
The point on a parabola nearest its directrix is called the vertex. For the parabola defined by [math]y^2 = 4ax[/math], the vertex is the origin, and there are no points on the curve to the left of the vertex. Since [math]|y|[/math] increases indefinitely as [math]x[/math] increases, the graph is not a closed curve but opens to the right. We cannot, of course, draw the entire curve, but the incomplete graph in Figure is sufficient to describe the entire curve for us. Note that the graph is symmetric with respect to the [math]x[/math]-axis. If we had chosen [math](-a, 0)[/math] for the focus and the line [math]x = a[/math] for the directrix, we would have a parabola with equation [math]y^2 = -4ax[/math]. This parabola would also have its vertex at the origin, also be symmetric with respect to the [math]x[/math]-axis, but would open to the left. With a horizontal directrix and the focus on the [math]y[/math]-axis, the equation would be [math]x^2= 4ay[/math] or [math]x^2= - 4ay[/math], opening upward or downward, respectively. Thus the graphs of [math]y^2 = kx[/math] and [math]x^2 = ky[/math] are parabolas with their vertices at the origin. The line through the vertex and the focus is called the axis of the parabola. The graph of [math]y^2 = kx[/math] has the [math]x [/math]-axis for its axis and opens to the right or left, depending on the sign of [math]k[/math]. The graph of [math]x^2 = ky[/math] has the [math]y[/math]-axis for its axis and opens upward or downward, depending on the sign of [math]k[/math]. The absolute value of [math]k[/math] determipes the shape of the parabola. If [math]k = 0[/math], the two equations reduce to [math]y^2= 0[/math] and [math]x^2 = 0[/math], whose graphs are the [math]x[/math]-axis and the [math]y[/math]-axis respectively. Thus a straight line may be regarded as a degenerate parabola. \medskip Example
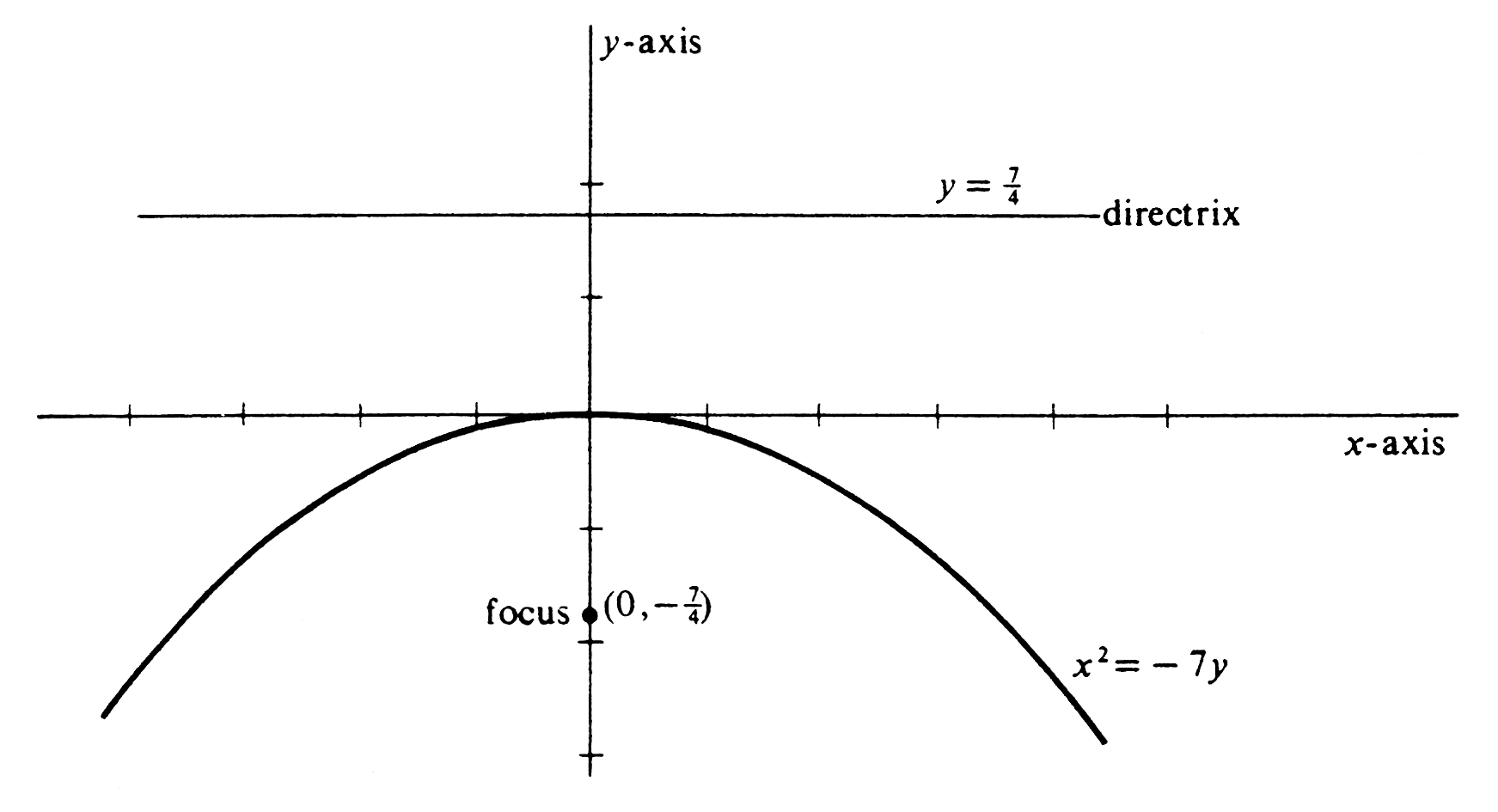
Find the coordinates of the focus and an equation of the directrix of [math]x^2 = - 7y[/math], and sketch its graph. An equivalent form of the equation is [math]x^2 = - 4(\frac{7}{4})y[/math], from which it follows that the focus is [math](0, - \frac{7}{4})[/math], that the directrix is [math]y = \frac{7}{4}[/math], and that the graph opens downward. It is shown in Figure. \medskip
Example
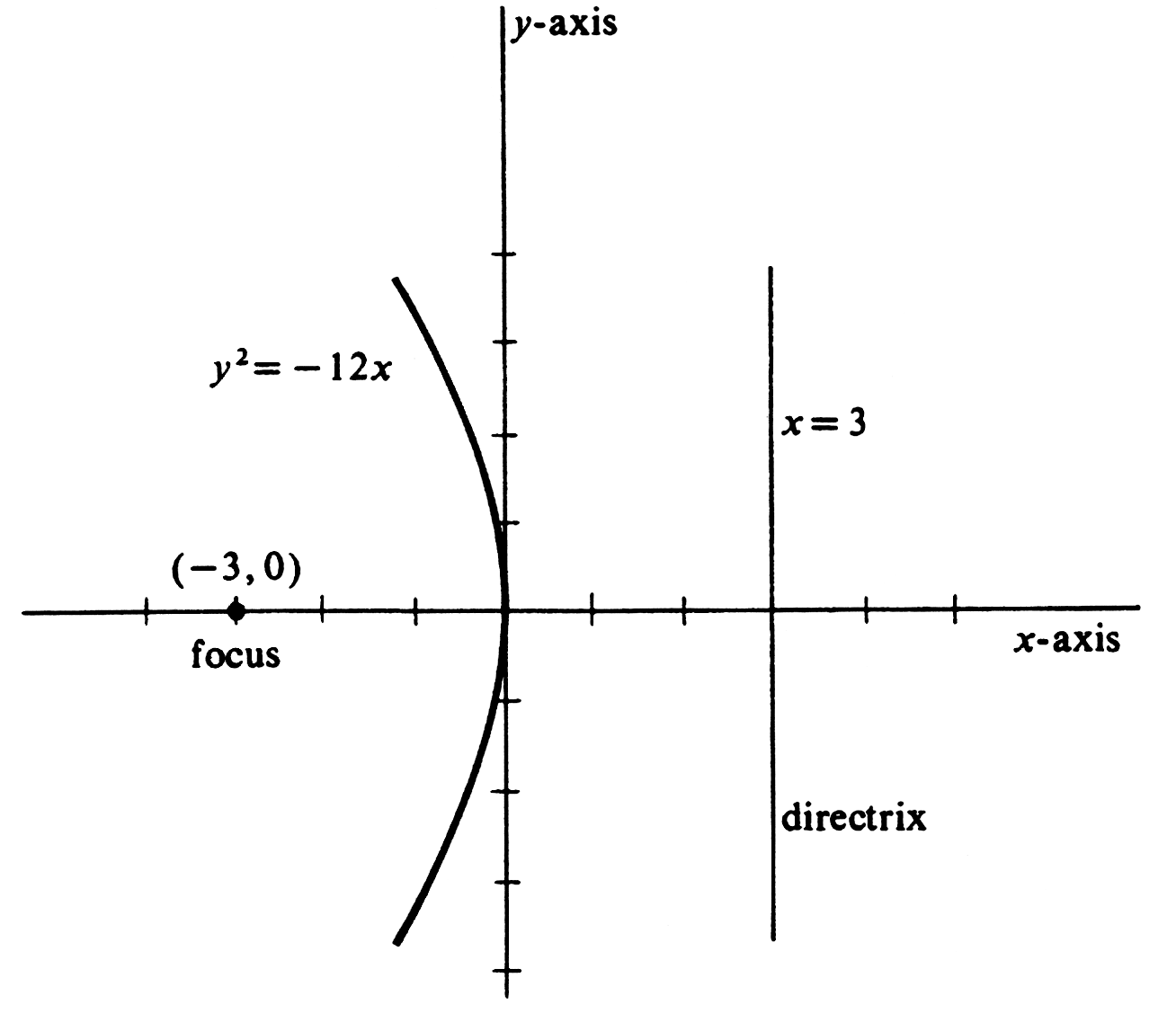
Write an equation of the parabola with focus at [math](-3, 0)[/math] and directrix [math]x = 3[/math]. Sketch its graph. An equation may be found by use of the definition or by use of the formulas, either method giving [math]y^2 = -12x[/math] as the simplest equation. The graph is shown in Figure. \medskip In every case considered so far, the parabola has one of the coordinate axes for its axis and the focus and directrix are equally spaced on opposite sides of the origin. The equations are somewhat more involved if other vertical or horizontal lines are chosen as axes, and even more involved if the parabolas have axes which are not parallel to one of the coordinate axes.
Example
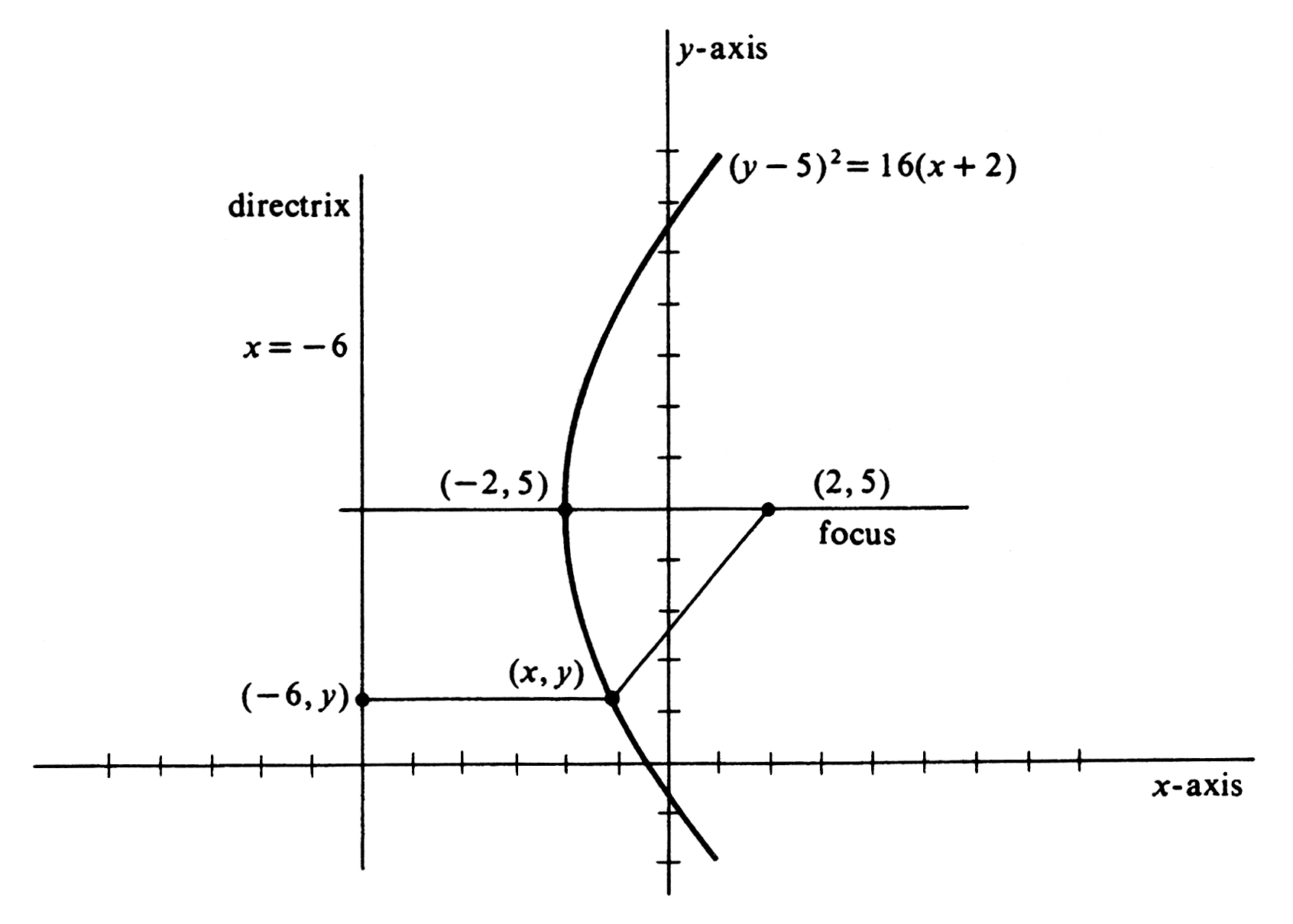
Write an equation of the parabola with focus at (2, 5) and directrix [math]x = - 6[/math]. Sketch the graph (see Figure). From the definition of the parabola,
Note the similarity of this form to the [math]y^2 = 4ax[/math] form. The [math]x[/math]-coordinate of the vertex, which is located halfway along the perpendicular from the focus to the directrix, is equal to [math]-2[/math]. That is, it is found by setting [math]x + 2[/math] equal to zero. Hence the [math]y[/math]-coordinate of the vertex is found by setting [math]y - 5[/math] equal to zero. Thus the vertex is the point [math](-2, 5)[/math]. \medskip
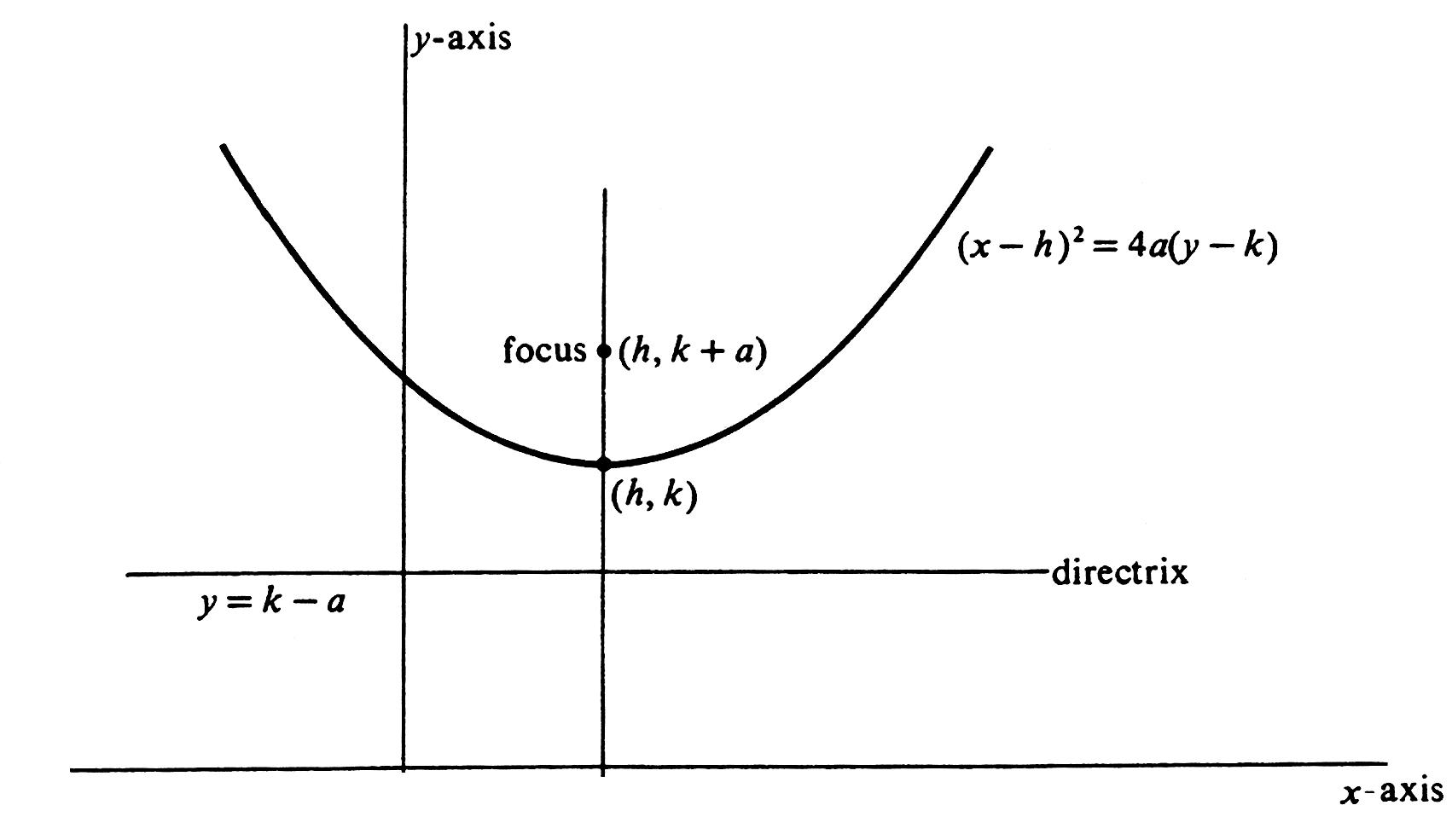
Let us now write a general equation of an arbitrary parabola with a horizontal directrix (see Figure). Consider the perpendicular from the focus to the directrix, and denote the midpoint of this line segment by [math](h, k)[/math]. This is the vertex, the point on the parabola nearest the directrix. Let the focus be the point [math](h, k + a)[/math]. Then the length of the segment is [math]|2a|[/math] and the directrix is the line [math]y = k - a[/math]. By algebra similar to that in Example 3, we go from
to
This parabola will have the same shape and the same orientation (opening upward or downward) as [math]x^2 = 4ay[/math], but will have its vertex at [math](h, k)[/math]. Similarly, [math](y-k)^2 = 4a(x - h)[/math] will have the same shape and the same orientation as [math]y^2 = 4ax[/math], but will have its vertex at [math](h, k)[/math]. \medskip Example
Write an equation of the parabola with focus at [math](-3, 2)[/math] and directrix [math]y = 6[/math]. The midpoint of the segment connecting focus and directrix and perpendicular to the directrix is at [math](-3, 4)[/math] and the segment is of length 4. With directrix above the focus, the parabola opens downward and has the equation
Example
Describe the graph of [math]y^2 + 2x - 3y + 7 = 0[/math]. We first write [math]y^2 - 3y = - 2x - 7[/math] and, completing the square, add [math]\frac{9}{4}[/math] to each side of the equation:
The graph is a parabola with vertex at [math](-\frac{19}{8}, \frac{3}{2})[/math], focus at [math]( -\frac{23}{8}, \frac{3}{2})[/math], and directrix [math]x = -\frac{15}{8}[/math]. It opens to the left and has the same shape and orientation as the graph of [math]y^2 = -2x[/math].
The graph of any function [math]f[/math] defined by an equation [math]f(x) = ax^2 + bx + c[/math], where [math]a \neq 0[/math], is a parabola. The defining equation may be written
or
Hence the graph of the function, which is the graph of the equation [math]y = f(x)[/math], is the graph of [math]y = a \Bigl(x + \frac{b}{2a} \Bigr)^2 + \frac{4ac - b^2}{4a}[/math], or, equivalently, of
Comparing this equation with (1), we see that the graph is a parabola with a vertical axis and its vertex at [math]\Bigl( -\frac{b}{2a}, \frac{4ac - b^2}{4a} \Bigr)[/math].
\end{exercise}
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.