Other Exponential and Logarithm Functions

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

Other Exponential and Logarithm Functions.

If [math]m[/math] and [math]n[/math] are integers and [math]n \gt 0[/math], then

[[math]] 2^{m/n} = \sqrt[n]{2^{m}}. [[/math]]

Hence, for any rational number [math]r[/math], the number [math]2^r[/math] is defined. But what is [math]2^x[/math] if [math]x[/math] is not rational? More generally, how should [math]a^x[/math] be defined for an arbitrary real number [math]x[/math] and a positive number [math]a[/math]? If [math]x[/math] is a rational number and [math]a[/math] is positive, we have shown that [math]\ln a^{x} = x \ln a[/math], and therefore [math]a^{x} = e^{x \ln a}[/math]. However, [math]e^{x \ln a}[/math] is defined for every real number [math]x[/math]. We shall take advantage of this fact, and, if [math]x[/math] is real but not rational, we define [math]a^x[/math] to be [math]e^{x \ln a}[/math]. Consequently, for every real number [math]x[/math], we have

[[math]] a^{x} = e^{x \ln a}, \;\;\; a \gt 0. [[/math]]

This function, so defined, has all the familiar properties of an exponential function:

Theorem

[[math]] \left \{ \begin{array}{l} a^{x} \gt 0, \;\;\; -\infty \lt x \lt \infty,\\ \\ a^{0} = 1,\\ \\ a^{1} = a,\\ \\ a^{x} \cdot a^{y} = a^{x + y},\\ \\ a^{-x} = \frac{1}{a^x},\\ \\ \frac{a^x}{a^y} = a^{x-y}. \end{array} \right. [[/math]]

The proofs follow readily from the properties of the functions [math]\ln[/math] and [math]\exp[/math]. For example,

[[math]] a^{1} = e^{1 \ln a} = e ^{\ln a} = a, [[/math]]

[[math]] a^{x} \cdot a^{y} = e ^{x \ln a} \cdot e ^{y \ln a} = e^{x \ln a + y \ln a} = e^{(x + y)\ln a} = a^{x + y}. [[/math]]

The derivative of [math]a^{x}[/math] is easily computed from its defining equation. Since

[[math]] \frac{d}{dx}a^{x} = \frac{d}{dx} e^{x \ln a} = e^{x \ln a} \frac{d}{dx} (x \ln a) = a^{x} \ln a, [[/math]]

we have the formula

Theorem

[[math]] \frac{d}{dx} a^{x} = a^{x} \ln a. [[/math]]

More generally, if [math]u[/math] is a differentiable function of [math]x[/math], the Chain Rule implies that

[[math]] \begin{equation} \frac{d}{dx} a^{u} = a^{u} \ln a \frac{du}{dx}. \label{eq5.4.1} \end{equation} [[/math]]

Example

Compute the derivative of each of the following functions:

[[math]] (a)\; 2^x, \;\;\;(b)\; 2^{(x^2)}, \;\;\;(c)\; 2^{(2^x)}. [[/math]]

For (a) we get

[[math]] \frac{d}{dx} 2^{x} = 2^{x} \ln 2; [[/math]]

for (b),

[[math]] \begin{eqnarray*} \frac{d}{dx} 2^{(x^2)} &=& 2^{(x^2)} \ln 2 \frac{d}{dx} x^2 = 2^{(x^2)} (\ln 2) (2x) \\ &=& x 2^{x^{2} + 1} \ln 2; \end{eqnarray*} [[/math]]

and for (c),

[[math]] \begin{eqnarray*} \frac{d}{dx} 2^{(2^x)} &=& 2^{(2^{x})} \ln 2 \frac{d}{dx} 2^{x} = 2^{(2^{x})} (\ln 2) 2^{x} \ln 2 \\ &=& 2^{2^{x} +x} (\ln 2)^2. \end{eqnarray*} [[/math]]

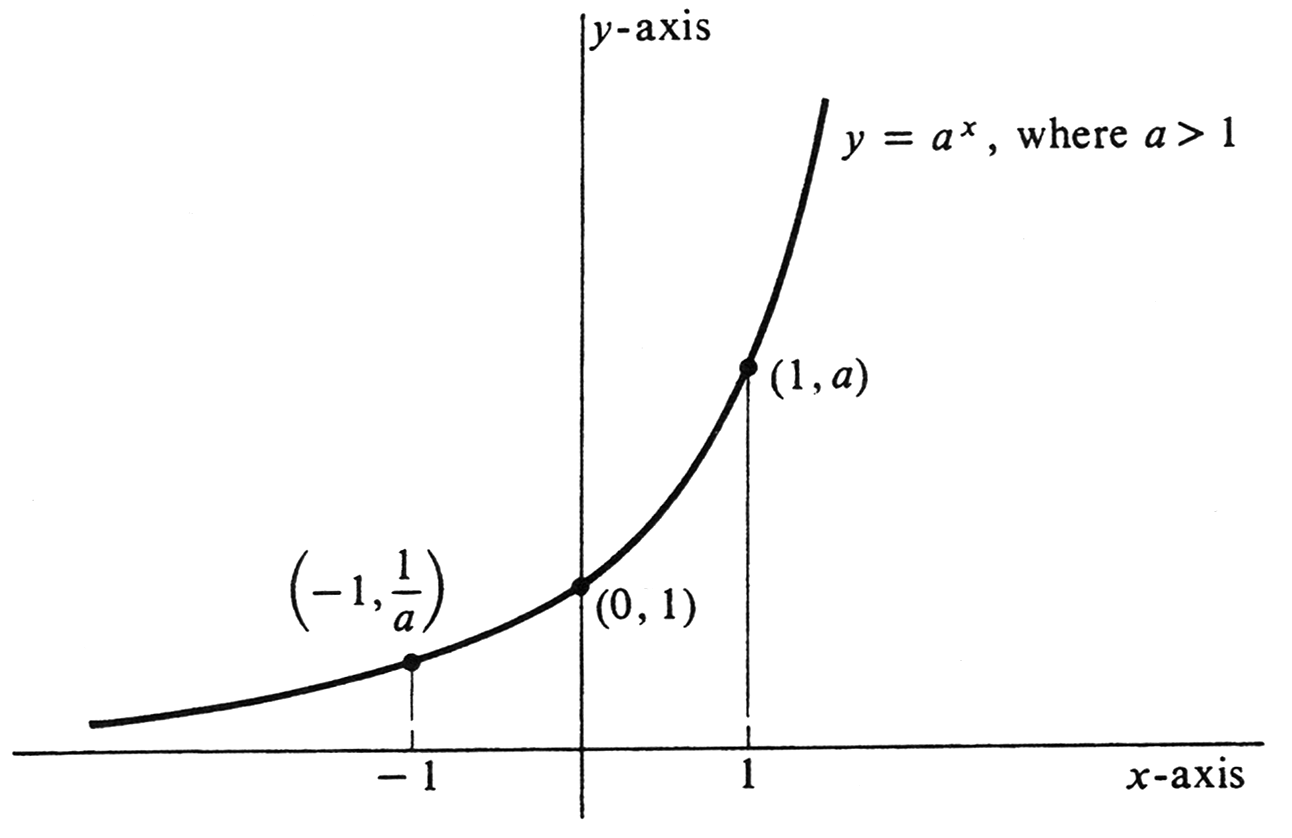
If [math]a = 1[/math], then [math]a^{x} = e^{x \ln 1} = e^{0} = 1[/math] for every real number [math]x[/math]. Hence [math]1^{x}[/math] is the constant function 1. If [math]a \gt 1[/math], then the graph of the function [math]a^{x}[/math] resembles the graph of [math]e^{x}[/math]. The slope of the tangent line to the graph is always positive, for if [math]a \gt 1[/math], then [math]\ln a \gt 0[/math], and, since [math]a^{x} \gt 0[/math], we see that

[[math]] \frac{d}{dx} a^x = a^{x} \ln a \gt 0. [[/math]]

This means that [math]a^x[/math] is a strictly increasing function (see Problem 10 at the end of this section). The second derivative is also always positive, since

[[math]] \frac{d^2}{dx^2} a^x = \frac{d}{dx} (a^{x} \ln a) = a^{x}(\ln a)^2 \gt 0. [[/math]]

Hence the graph is concave upward for all [math]x[/math]. Moreover, there are no extreme points, critical points, or points of inflection. The graph is drawn in Figure. It is relatively flat on the left, passes through [math]\Bigl( -1, -\frac{1}{a} \Bigr)[/math], (0, 1), and [math](1, a)[/math], and goes upward to the right. For greater values of [math]a[/math], the graph is flatter on the left and steeper on the right.

File:Guide c5467 scanfig5 7.png

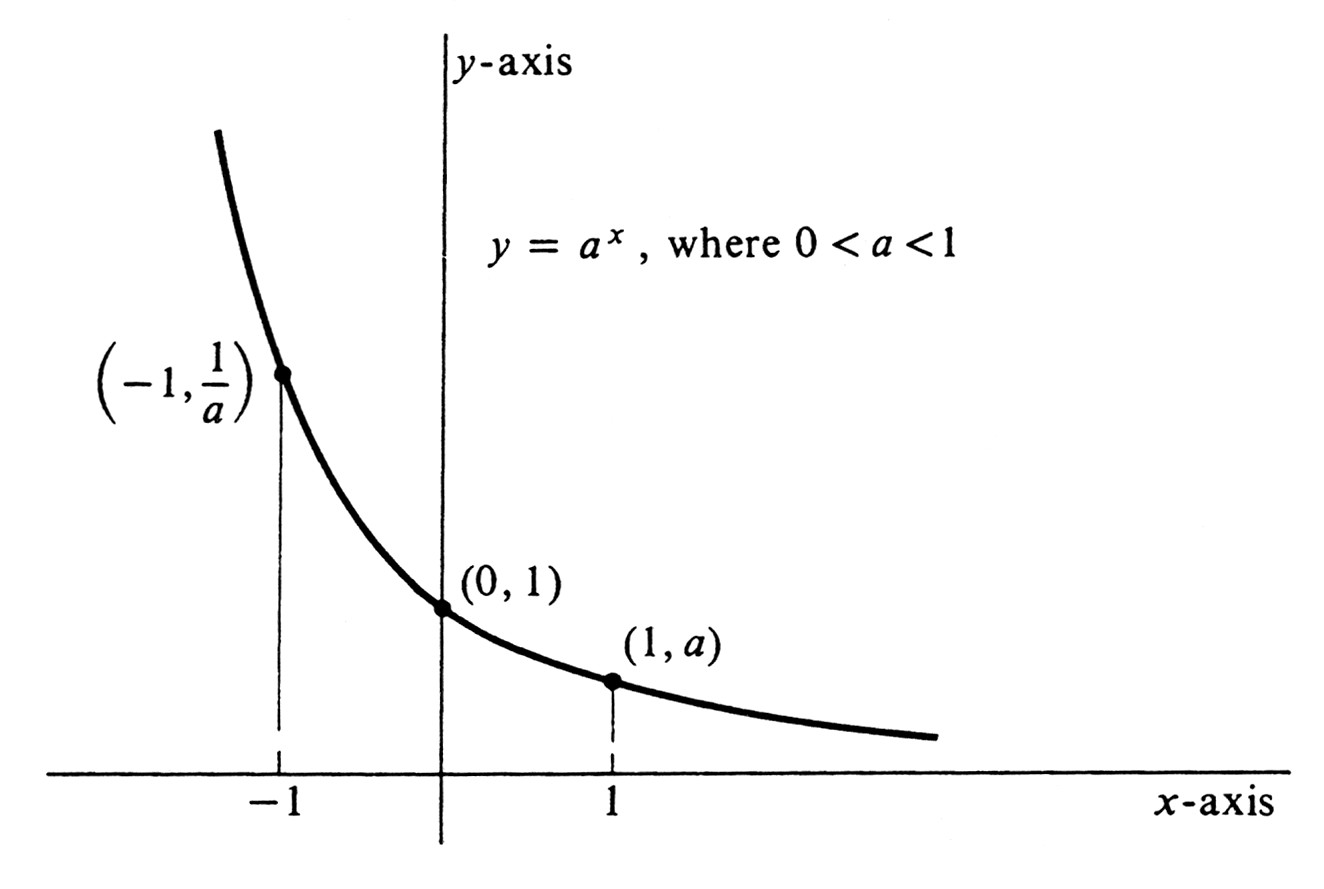
If [math]0 \lt a \lt 1[/math], the function [math]a^x[/math] may be studied by considering it in another form, [math]\Bigl( \frac{1}{a} \Bigr)^{-x}[/math]. Since [math]\frac{1}{a} \gt 1[/math], the graph of the function [math]\Bigl( \frac{1}{a} \Bigr)^{x}[/math] is of the type described in the preceding paragraph, and the graph of [math]a[/math], which is equal to [math]\Bigl( \frac{1}{a} \Bigr)^{-x}[/math] , is the same curve reflected across the [math]y[/math]-axis. It is steep on the left, passes through [math]\Bigl( -1, \frac{1}{a} \Bigr)[/math], (0, 1), and [math](1, a)[/math], and flattens out as it goes to to the right. It is drawn in Figure. Every derivative formula has a corresponding integral formula. Since

[[math]] \frac{d}{dx} \Bigl( \frac{a^x}{ \ln a} \Bigr) = \frac{1}{\ln a} \frac{d}{dx} a^{x} = a^{x}, [[/math]]

the integral formula corresponding to (4.2) is

Theorem

[[math]] \int a^x dx = \frac{a^x}{\ln a} + c. [[/math]]

As always, the Chain Rule provides a generalization. If [math]u[/math] is a differentiable function of [math]x[/math], then

[[math]] \begin{equation} \int a^{u} \frac{du}{dx} dx = \frac{a^u}{\ln a} + c. \label{eq5.4.2} \end{equation} [[/math]]

File:Guide c5467 scanfig5 8.png

Example

Compute each of the following indefinite integrals:

[[math]] (a) \int 3^{y}dy, \;\;\; (b) \int x 10^{x^2 - 7} dx, \;\;\; (c) \int\frac{1}{x}\; (2.31)^{\ln x} dx. [[/math]]

A direct use of (4.3) gives for (a)

[[math]] \int 3^{y} dy = \frac{ 3^y}{\ln 3} + c. [[/math]]

Since [math]\frac{d}{dx}(x^2 - 7) = 2x[/math], integral (b) can be written [math]\frac{1}{2} \int 10^{x^2 - 7} \cdot 2x \cdot dx[/math], which by (2) is equal to [math]\frac{1}{2} \frac{10^{x^2 - 7}}{\ln 10} + c[/math]. Hence

[[math]] \int x 10^{x^2 - 7} dx = \frac{10^{x^{2} - 7}}{2 \ln 10} + c. [[/math]]

For part (c) we note that [math]\frac{d}{dx} \ln x = \frac{1}{x}[/math], and therefore that the integral is of the form in (2). Thus

[[math]] \int (2.31)^{\ln x} \frac{1}{x}dx = \frac{(2.31)^{\ln x}}{\ln 2.31} + c. [[/math]]

It was proved on page 241 that [math]\ln a^r = r \ln a[/math], for every rational number [math]r[/math] and every positive real number [math]a[/math]. We are now in a position to remove the restriction that [math]r[/math] be rational. Let [math]x[/math] be an arbitrary real number. Then [math]a^x = e^{x \ln a}[/math], and so [math]\ln a^x = \ln e^{x \ln a} = \ln \exp(x \ln a)[/math]. Since [math]\ln[/math] and [math]\exp[/math] are inverse functions of each other it follows that [math]\ln \exp(x \ln a) = x \ln a[/math]. We have therefore proved that

Theorem

[math]\ln a^x = x \ln a[/math], for every real number [math]x[/math] and every positive real number [math]a[/math].

Another of the well-known laws of exponents now follows easily:

Theorem

[math](a^x)^y = a^{xy}[/math] for all real numbers [math]x[/math] and [math]y[/math] and every positive real number [math]a[/math].

Show Proof

If we let [math]a^x = b[/math], then [math](a^x)^y = b^y = e^{y \ln b}[/math]. Replacing [math]b[/math] in the last expression, we have

[[math]] (a^x)^y = e^{y \ln a^x}, [[/math]]

and, using (4.4),

[[math]] e^{y \ln a^x} = e^{y(x \ln a)} = e^{xy \ln a}. [[/math]]

Since [math]e^{xy \ln a} = a^{xy}[/math], it follows that [math](a^x)^y = a^{xy}[/math], and the proof is complete.

■

In particular, [math](e^x)^y = e^{xy}[/math] for all real numbers [math]x[/math] and [math]y[/math]. Let [math]a[/math] be any real number, and consider the function [math]f[/math] defined for every positive real number [math]x[/math] by

[[math]] f(x) = x^{a}. [[/math]]

Hitherto in this section we have considered the function [math]a^x[/math]. Now we reverse the roles of constant and variable. One of the basic rules of differentiation proved in Chapter 1 states that, if [math]a[/math] is a rational number, then

[[math]] f'(x) = \frac{d}{dx} x^a = ax^{a - 1}. [[/math]]

We now remove the restriction that [math]a[/math] be rational. Observe first that [math]x^a[/math] is certainly a differentiable function, since it is the composition of differentiable functions:

[[math]] x^a= e^{a \ln x} = \mbox{exp} (a\; \ln x). [[/math]]

Knowing this, we use implicit differentiation to compute its derivative. Let [math]y = x^a[/math]. Then [math]\ln y = \ln x^a = a \ln x[/math], and so

[[math]] \begin{eqnarray*} \frac{d}{dx} \ln y &=& \frac{d}{dx} a \ln x,\\ \frac{1}{y} \frac{dy}{dx} &=& a \frac{1}{x},\\ \frac{dy}{dx} &=& \frac{ay}{x}. \end{eqnarray*} [[/math]]

Since [math]y = x^a[/math], it follows that [math]\frac{ay}{x}=\frac{ax^a}{x}= ax^{a-1}[/math]. Thus we have proved that

Theorem

[[math]] \frac{d}{dx}x^a = ax^{a-1}, \; \mbox{for any real number $a$}. [[/math]]

The technique of taking logarithms and differentiating implicitly, which was used in proving, can also be used to compute the derivative of a positive differentiable function which is raised to a power which is itself a differentiable function. For example, to compute [math]\frac{d}{dx} x^{x}[/math], we let [math]y = x^{x}[/math]. Then

[[math]] \ln y= \ln x^{x}= x \ln x, [[/math]]

and it follows that

[[math]] \begin{eqnarray*} \frac{1}{y} \frac{dy}{dx} &=& \frac{d}{dx} (x \ln x) = x \frac{1}{x} + \ln x = 1 + \ln x, \\ \frac{dy}{dx} &=& y( 1 + \ln x) = x^{x} ( 1 + \ln x), \;\;\;(x \gt 0). \end{eqnarray*} [[/math]]

This technique is known as logarithmic differentiation and is a basic tool for finding derivatives. We can use it to derive a formula for [math]\frac{d}{dx} u^{v}[/math], where [math]u[/math] is a positive differentiable function of [math]x[/math] and [math]v[/math] is any differentiable function of [math]x[/math]. Let [math]y = u^v[/math], and then [math]\ln y = v \ln u[/math]. Hence

[[math]] \begin{eqnarray*} \frac{1}{y} \frac{dy}{dx} &=& \frac{d}{dx} (v \ln u) = v \frac{1}{u} \frac{du}{dx} + \ln u \frac{du}{dx},\\ \frac{dy}{dx} &=& y \Bigl( \frac{v}{u} \frac{du}{ dx} + \ln u \frac{dv}{dx} \Bigr),\\ \frac{dy}{dx} &=& u^{v} \Bigl( \frac{v}{u} \frac{du}{dx} + \ln u \frac{dv}{dx} \Bigr), \end{eqnarray*} [[/math]]

and finally, therefore,

[[math]] \begin{equation} \frac{d}{dx} u^{v} = vu^{v - 1}\frac{du}{dx} + u^{v} \ln u \frac{dv}{dx}. \label{eq5.4.3} \end{equation} [[/math]]

We do not suggest that the reader memorize this formula. It is more important to be able to use the method of logarithmic differentiation. \medskip Example

Find [math]\frac{d}{dx} (x^2 + 1) ^{e^x}[/math]. Letting [math]y = (x^{2} + 1)^{e^x}[/math] and taking natural logarithms, we have

[[math]] \ln y = \ln (x^2 + 1)^{e^x} = e^x \ln (x^2 + 1). [[/math]]

Differentiating, we obtain

[[math]] \begin{eqnarray*} \frac{1}{y} \frac{dy}{dx} &=& e^{x} \frac {1}{x^{2}+1} 2x + e^{x} \ln (x^{2} + 1),\\ \frac{dy}{dx}&=& ye^{x} \Bigl[ \frac{2x}{x^2 + 1} + \ln (x^2 + 1) \Bigr). \end{eqnarray*} [[/math]]

Hence

[[math]] \frac{d}{dx} (x^2 + 1)^{e^x} = e^{x}(x^2 + 1)^{e^{x}} \Bigl[ \frac{2x}{x^2 + 1} + \ln (x^{2} + 1) \Bigr]. [[/math]]

The function [math]a^x[/math] is strictly monotonic if [math]a[/math] is positive and not equal to 1, increasing if [math]a \gt 1[/math] and decreasing if [math]0 \lt a \lt 1[/math]. Moreover, it has a nonzero derivative at every [math]x[/math]. It follows by Theorem (3.4), page 261, that [math]a^x[/math] has a differentiable inverse function. Even as the inverse function of [math]e^x[/math] is the natural logarithm, we call the inverse function of [math]a^x[/math] the logarithm to the base [math]a[/math]. Hence

[[math]] y = \mbox{log}_{a}x \;\;\; \mbox{if and only if} \;x = a^{y}. [[/math]]

We emphasize that [math]a[/math] must be a positive number different from 1 and that [math]\log_{a}x[/math] is defined only for positive values of [math]x[/math]. The so-called common logarithm, usually denoted by simply log and encountered in the usual tables of logarithms, is the logarithm to the base 10. Thus [math]\log 100 = \log_{10} 100 = 2[/math], since [math]10^2 = 100[/math]. The logarithm to the base a has the same algebraic properties as the natural logarithm:

Theorem

[[math]] \left \{ \begin{array}{l} \mbox{log}_{a} 1 = 0, \\ \\ \mbox{log}_{a} a = 1,\\ \\ \mbox{log}_{a} pq = \mbox{log}_{a}p + \log_{a}q,\\ \\ \mbox{log}_{a}\frac{p}{q} = \log_{a}p - log_{a}q,\\ \\ \mbox{log}_{a}p', = b \log_{a}p. \end{array} \right. [[/math]]

The above properties hold for every positive real number [math]a[/math] different from 1, for all positive real numbers [math]p[/math] and [math]q[/math], and for every real number [math]b[/math]. Each one may be proved by considering the corresponding exponential function. Note that since [math]a^x[/math] and [math]\log_{a}x[/math] are inverse functions of each other,

[[math]] \left \{ \begin{array}{ll} \log_{a}a^x = x,\;\;\; &\mbox{for all real}\; x, \\ a^{\log_{a} x} = x,\;\;\; &\mbox{for all positive real}\; x. \end{array} \right. [[/math]]

For example, if we let [math]x = \log_{a}p[/math] and [math]y = \log_{a}q[/math], then we have [math]p = a^{x}[/math] and [math]q = a^{y}[/math], and so

[[math]] \begin{eqnarray*} \log_{a}pq &=& \log_{a}(a^{x} a^{y}) = \log_{a}a^{x + y} = x + y\\ &=& \log_{a}p + \log_{a}q. \end{eqnarray*} [[/math]]

The other properties are proved in the same way. To compute the derivative of [math]\log_{a}x[/math], we let [math]y = \log_{a}x[/math]. The equivalent exponential equation is [math]x = a^y[/math], from which it follows that [math]\ln x = \ln a^y = y \ln a[/math]. By implicit differentiation, therefore,

[[math]] \begin{eqnarray*} \frac{d}{dx}(y \ln a) &=& \frac{d}{dx} \ln x,\\ \ln a \frac{dy}{dx} &=& \frac{1}{x}. \end{eqnarray*} [[/math]]

Solving for [math]\frac{dy}{dx}[/math], which equals [math]\frac{d}{dx} \log_{a}x[/math], we obtain

Theorem

[[math]] \frac{d}{dx} \log_{a}x = \frac{1}{\ln a} \frac{1}{x}. [[/math]]

\end{exercise}

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.