Revision as of 11:42, 5 May 2023 by Admin (Created page with "A device contains two components. The device fails if either component fails. The joint density function of the lifetimes of the components, measured in hours, is <math>f(s,t)...")
May 05'23
Exercise
A device contains two components. The device fails if either component fails. The joint density function of the lifetimes of the components, measured in hours, is [math]f(s,t)[/math], where [math]0 \lt s \lt 1[/math] and [math]0 \lt t \lt 1 [/math].
Determine which of the following represents the probability that the device fails during the first half hour of operation.
- [math]\int_{0}^{0.5}\int_{0}^{0.5}f(s,t)\,ds\,dt[/math]
- [math]\int_0^1\int_0^{0.5}f(s,t)\,ds\,dt[/math]
- [math]\int_{0.5}^1\int_{0.5}^1f(s,t)\,ds\,dt[/math]
- [math]\int_{0}^{0.5}\int_{0}^1f(s,t)\,ds\,dt + \int_{0}^1\int_{0}^{0.5}f(s,t)\,ds\,dt[/math]
- [math]\int_{0}^{0.5}\int_{0.5}^1f(s,t)\,ds\,dt + \int_{0}^1\int_0^{0.5}f(s,t)\,ds\,dt[/math]
May 05'23
Solution: E
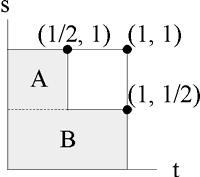
The domain of s and t is pictured below.
Note that the shaded region is the portion of the domain of s and t over which the device fails sometime during the first half hour. Therefore,
[[math]]
\operatorname{P}\left[ (S \leq \frac{1}{2}) \cup \left( T \leq \frac{1}{2}\right)\right] = \int_{0}^{0.5}\int_{0.5}^1f(s,t)\,ds\,dt + \int_{0}^1\int_0^{0.5}f(s,t)\,ds\,dt
[[/math]]
(where the first integral covers A and the second integral covers B).