Revision as of 16:28, 5 May 2023 by Admin (Created page with "A company is reviewing tornado damage claims under a farm insurance policy. Let <math>X</math> be the portion of a claim representing damage to the house and let <math>Y</math...")
May 05'23
Exercise
A company is reviewing tornado damage claims under a farm insurance policy. Let [math]X[/math] be the portion of a claim representing damage to the house and let [math]Y[/math] be the portion of the same claim representing damage to the rest of the property. The joint density function of [math]X[/math] and [math]Y[/math] is
[[math]]
f(x,y) = \begin{cases}
6 [1 − ( x + y ) ], \,\, x \gt 0, y \gt 0, x+y \lt 1 \\
0, \, \textrm{Otherwise.}
\end{cases}
[[/math]]
Calculate the probability that the portion of a claim representing damage to the house is less than 0.2.
- 0.360
- 0.480
- 0.488
- 0.512
- 0.520
May 05'23
Solution: C
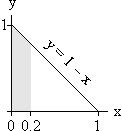
The domain of X and Y is pictured below. The shaded region is the portion of the domain over which X < 0.2 .
Now observe
[[math]]
\begin{align*}
\operatorname{P}[ X \lt 0.2 ] &= \int_0^{0.2} \int_0^{1-x} 6[1-(x+y)] dy dx \\
&= 6 \int_0^{0.2} [y - xy - \frac{1}{2} y^2]_0^{1-x} dx \\
&= 6 \int_0^{0.2} [1 - x - x(1-x) - \frac{1}{2}(1-x)^2 ]dx \\
&= 6 \int_0^{0.2} [(1-x)^2 - \frac{1}{2}(1-x)^2 ]dx \\
&= 6 \int_0^{0.2} \frac{1}{2}(1-x)^2 \, dx \\
&= -(1-x)^3 \Big |_0^{0.2} \\
&= -(0.8)^3 + 1\\
&=0.488.
\end{align*}
[[/math]]