Let [math]X[/math] and [math]Y[/math] be continuous random variables with joint density function

[[math]] f(x,y) = \begin{cases} 15y, \,\, x^2 \leq y \leq x \\ 0, \, \textrm{Otherwise.} \end{cases} [[/math]]

Let [math]g[/math] be the marginal density function of [math]Y[/math]. Determine which of the following represents [math]g[/math].

• [[math]]g(y) = \begin{cases} 15y, \, 0 \lt y \lt 1 \\ 0, \, \textrm{Otherwise.} \end{cases}[[/math]]
• [[math]]g(y) = \begin{cases} \frac{15y^2}{2}, \, x^2 \lt y \lt x \\ 0, \, \textrm{Otherwise.} \end{cases}[[/math]]
• [[math]]g(y) = \begin{cases} \frac{15y^2}{2}, \, 0 \lt y \lt 1 \\ 0, \, \textrm{Otherwise.} \end{cases}[[/math]]
• [[math]]g(y) = \begin{cases} 15y^{3/2}(1-y^{1/2}), \, x^2 \lt y \lt x \\ 0, \, \textrm{Otherwise.} \end{cases}[[/math]]
• [[math]]g(y) = \begin{cases} 15y^{3/2}(1-y^{1/2}), \, 0 \lt y \lt 1\\ 0, \, \textrm{Otherwise.} \end{cases}[[/math]]

Copyright 2023. The Society of Actuaries, Schaumburg, Illinois. Reproduced with permission.

Solution: E

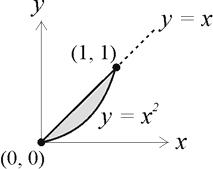
The shaded portion of the graph below shows the region over which f(x, y) is nonzero:

We can infer from the graph that the marginal density function of [math]Y[/math] is given by

[[math]] g(y) = \int_y^{\sqrt{y}} 15y dx = 15 xy \Big |_y^{\sqrt{y}} = 15y( \sqrt{y} - y ) = 15 y^{3/2}(1-y^{1/2}), \, 0 \lt y \lt 1 [[/math]]

or more precisely,

[[math]] g(y) = \begin{cases} 15y^{3/2}(1-y)^{1/2}, \quad 0 \lt y \lt 1 \\ 0, \quad \textrm{otherwise } \end{cases} [[/math]]

Copyright 2023. The Society of Actuaries, Schaumburg, Illinois. Reproduced with permission.