Exercise
A family buys two policies from the same insurance company. Losses under the two policies are independent and have continuous uniform distributions on the interval from 0 to 10. One policy has a deductible of 1 and the other has a deductible of 2. The family experiences exactly one loss under each policy.
Calculate the probability that the total benefit paid to the family does not exceed 5.
- 0.13
- 0.25
- 0.30
- 0.32
- 0.42
Solution: C
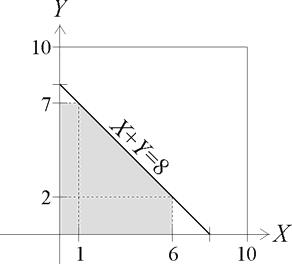
Define X and Y to be loss amounts covered by the policies having deductibles of 1 and 2, respectively. The shaded portion of the graph below shows the region over which the total benefit paid to the family does not exceed 5:
We can also infer from the graph that the uniform random variables [math]X[/math] and [math]Y[/math] have joint density function
We could integrate f over the shaded region in order to determine the desired probability. However, since X and Y are uniform random variables, it is simpler to determine the portion of the 10 x 10 square that is shaded in the graph above. That is, [math]\operatorname{P} ( \textrm{Total Benefit Paid Does not Exceed 5})[/math]