Revision as of 23:46, 15 May 2023 by Admin
May 14'23
Exercise
May 14'23
Key: E
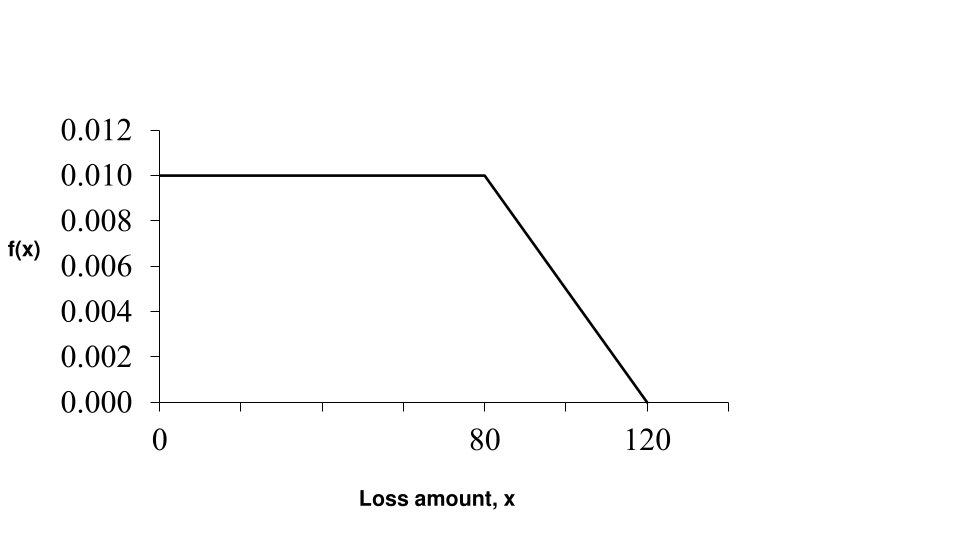
[[math]]
f(x) = \begin{cases}
=0.01, \quad 0 \leq x \leq 80 \\
=0.01-0.00025(x-80)=0.03-0.00025 x, \quad 80 \lt x \leq 120 \\
\end{cases}
[[/math]]
[[math]]\begin{aligned}
\operatorname{E}(x) &=\int_{0}^{80} 0.01 x d x+\int_{80}^{120}\left(0.03 x-0.00025 x^{2}\right) d x \\
& =\left.\frac{0.01 x^{2}}{2}\right|_{0} ^{80}+\left.\frac{0.03 x^{2}}{2}\right|_{80} ^{120}-\left.\frac{0.00025 x^{3}}{3}\right|_{80} ^{120} \\
& =32+120-101.33=50.66667 \\
\end{aligned}
[[/math]]
[[math]]
\begin{aligned}
\operatorname{E}(X-20)_{+} &=\operatorname{E}(X)-\int_{0}^{20} x f(x) d x-20\left[1-\int_{0}^{20} f(x) d x\right] \\
&=50.6667-\left.\frac{0.01 x^{2}}{2}\right|_{0} ^{20}-20\left(1-\left.0.01 x\right|_{0} ^{20}\right) \\
& =50.6667-2-20(0.8) \\
&=32.6667
\end{aligned}[[/math]]
Loss Elimination Ratio
[[math]]=1-\frac{32.6667}{50.6667}=0.3553[[/math]]