Classical Probability distributions

[math] \newcommand{\R}{\mathbb{R}} \newcommand{\A}{\mathcal{A}} \newcommand{\B}{\mathcal{B}} \newcommand{\N}{\mathbb{N}} \newcommand{\C}{\mathbb{C}} \newcommand{\Rbar}{\overline{\mathbb{R}}} \newcommand{\Bbar}{\overline{\mathcal{B}}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\E}{\mathbb{E}} \newcommand{\p}{\mathbb{P}} \newcommand{\one}{\mathds{1}} \newcommand{\0}{\mathcal{O}} \newcommand{\mat}{\textnormal{Mat}} \newcommand{\sign}{\textnormal{sign}} \newcommand{\CP}{\mathcal{P}} \newcommand{\CT}{\mathcal{T}} \newcommand{\CY}{\mathcal{Y}} \newcommand{\F}{\mathcal{F}} \newcommand{\mathds}{\mathbb}[/math]

Let [math](\Omega,\A,\p)[/math] denote a probability space and let [math]X:(\Omega,\A,\p)\to(E,\mathcal{E})[/math] be a r.v. taking values in some measureable space [math](E,\mathcal{E})[/math].

Discrete distributions

The uniform distribution

Let [math]\vert E\vert \lt \infty[/math]. A r.v. [math]X[/math] with values in [math]E[/math] is said to be uniform on [math]E[/math] if [math]\forall x\in E[/math]

[[math]] \p[X=x]=\frac{1}{\vert E\vert}. [[/math]]

The Bernoulli distribution with parameter [math]p\in[0,1][/math]

This is a r.v. [math]X[/math] with values in [math]\{0,1\}[/math] such that

[[math]] \p[X=1]=p,\p[X=0]=1-p. [[/math]]

The r.v. [math]X[/math] can be interpreted as the outcome of a coin toss. The expectation of [math]X[/math] is then given by

[[math]] \E[X]=0\cdot\p[X=0]+1\cdot\p[X=1]. [[/math]]

The Binomial distribution [math]\B(n,p)[/math], [math]n\in \N[/math], [math]n\geq 1[/math], [math]p\in[0,1][/math]

This is the distribution of a r.v. [math]X[/math] taking its values in [math]\{0,1,...,n\}[/math] such that

[[math]] \p[X=k]=\binom{n}{k}p^k(1-p)^{n-k}. [[/math]]

Histogram of a binomial distributed r.v.

The r.v. [math]X[/math] is interpreted as the number of heads of the [math]n[/math] tosses of the previous case. One has to check that its a probability distribution:

[[math]] \sum_{k=0}^n\p[X=k]=\sum_{k=0}^n\binom{n}{k}p^k(1-p)^{n-k}=(p+(1-p))^n=1. [[/math]]

The expected value for the binomial distribution is given by

[[math]] \begin{align*} \E[X]=\sum_{k=0}^nk\p[X=k]&=\sum_{k=0}^nk\binom{n}{k}p^k(1-p)^{n-k}=np\sum_{k=0}^nk\frac{(n-1)!}{(n-k)!k!}p^{k-1}(1-p)^{(n-1)-(k-1)}\\ &=np\sum_{k=1}^n\frac{(n-1)!}{(n-k)!(k-1)!}p^{k-1}(1-p)^{(n-1)-(k-1)}\\ &=np\sum_{k=1}^n\binom{n-1}{k-1}p^{k-1}(1-p)^{(n-k)-(k-1)}\\ &=np\sum_{l=0}^{n-1}\binom{n-1}{l}p^l(1-p)^{(n-1)-l},(l:=k-1)\\ &=np\sum_{l=0}^m\binom{m}{l}p^l(1-p)^{m-l},(m:=n-1)=np(p+(1-p))^m=np \end{align*} [[/math]]

The Geometric distribution with parameter [math]p\in[0,1][/math]

This is a r.v. [math]X[/math] with values in [math]\N[/math] such that

[[math]] \p[X=k]=(1-p)p^k. [[/math]]

The r.v. [math]X[/math] can be interpreted as the number of heads obtained before tail shows for the first time. It is also a probability distribution, since

[[math]] \sum_{k=0}^\infty\p[X=k]=\sum_{k=0}^\infty(1-p)p^k=(1-p)\sum_{k=0}^\infty p^k=\frac{1-p}{1-p}=1. [[/math]]

The Poisson distribution with parameter [math]\lambda \gt 0[/math]

This is a r.v. [math]X[/math] with values in [math]\N[/math] such that

[[math]] \p[X=k]=e^{-\lambda}\frac{\lambda^k}{k!},k\in\N. [[/math]]

Histogram of a poisson distributed r.v.

The Poisson distribution is very important, both from the point of view of applications and from the theoretical point of view. Intuitively it describes the number of rare events that have occurred during a long period. If [math]X_n\sim \B(n,p_n)[/math] and if [math]np_n\xrightarrow{n\to\infty}\lambda \gt 0[/math], i.e. [math]p_n\sim \frac{\lambda}{n}[/math] for [math]n\geq 1[/math], then for every [math]k\in\N[/math]

[[math]] \p[X_n=k]\xrightarrow{n\to\infty} e^{-\lambda}\frac{\lambda^k}{k!}. [[/math]]

The expected value is then given by

[[math]] \E[X]=\sum_{k=0}^\infty k\frac{\lambda^k}{k!}e^{-\lambda}=\lambda e^{-\lambda}\sum_{k=1}^\infty\frac{\lambda^{k-1}}{(k-1)!}=\lambda e^{-\lambda}\sum_{j=0}\frac{\lambda^j}{j!}=\lambda. [[/math]]

Absolutely continuous distributions

Let now [math]E\subset\R[/math]. The question here is about the densities [math]P(x)[/math] of a certain distributed r.v. in the continuous case.

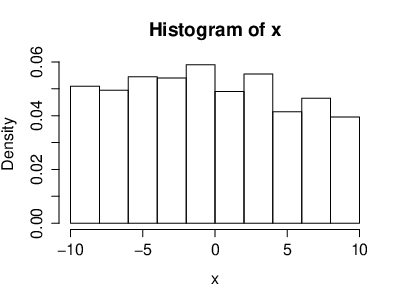
The uniform distribution on [math][a,b][/math]

The density of a continuous, uniformly distributed r.v. [math]X[/math] is given by

[[math]] P(x)=\frac{1}{b-a}\one_{[a,b]}(x). [[/math]]

Histogram of a uniformly distributed r.v.

We want to check that it is a probability density. We have to check that [math]\int_\R P(x)dx=1[/math], so we have

[[math]] \int_{-\infty}^\infty P(x)dx=\int_{-\infty}^\infty \frac{1}{b-a}\one_{[a,b]}(x)dx=\frac{1}{b-a}\int_{-\infty}^\infty\one_{[a,b]}(x)dx=\frac{1}{b-a}(b-a)=1. [[/math]]

Hence it's a probability density. If [math]X[/math] is uniform on [math][a,b][/math], then [math]\vert X\vert\leq \vert a\vert +\vert b\vert \lt \infty[/math] a.s. and [math]\E[\vert a\vert +\vert b\vert ]=\vert a\vert +\vert b\vert \lt \infty\Longrightarrow \E[X] \lt \infty[/math]. The expectation is given by

[[math]] \E[X]=\int_{-\infty}^{\infty}xP(x)dx=\int_{-\infty}^\infty\frac{1}{b-a}\one_{[a,b]}(x)dx=\frac{1}{b-a}\int_a^bxdx=\frac{1}{b-a}\frac{1}{2}(b^2-a^2)=\frac{a+b}{2}. [[/math]]

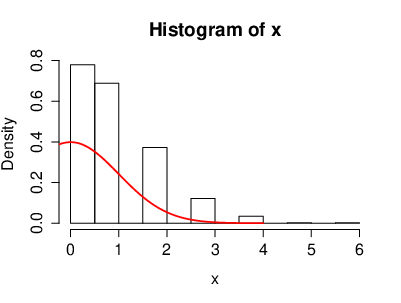
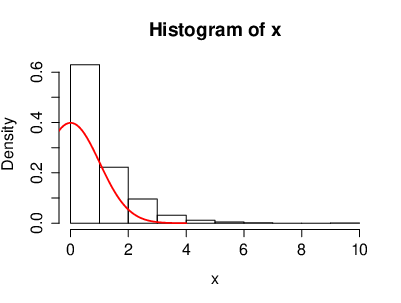
The Exponential distribution with parameter [math]\lambda \gt 0[/math]

The density is given by

[[math]] P(x)=\lambda e^{-\lambda x}\one_{\R^+}(x), [[/math]]

with [math]X\geq 0[/math] a.s. The expectation is given by

[[math]] \E[X]=\int_{-\infty}^\infty xP(x)dx=\int_{0}^\infty x\lambda e^{-\lambda x}dx=\lambda\int_0^\infty xe^{-\lambda x}dx. [[/math]]

With [math]u=\lambda x[/math] we get [math]dx=\frac{du}{\lambda}[/math] and hence

[[math]] \lambda\int_0^\infty \frac{u}{\lambda}e^{-u}\frac{du}{\lambda}=\frac{1}{\lambda}\int_0^\infty ue^{-u}du=\frac{1}{\lambda}. [[/math]]

If [math]a,b \gt 0[/math], then

[[math]] \p[X \gt a+b]=\int_{a+b}^\infty \lambda e^{-\lambda x}dx=\lambda\left[-\frac{1}{\lambda}e^{-\lambda x}\right]_{a+b}^\infty=e^{-\lambda(a+b)}=e^{-\lambda a}e^{-\lambda b}=\p[X \gt a]\p[X \gt b]. [[/math]]

Histogram of an exponentially distributed r.v.

Note that

[[math]] \p[X \lt 0]=\E[\one_{\{X \lt 0\}}]=\int_{-\infty}^\infty\one_{\{x \lt 0\}}P(x)dx=\int_{-\infty}^\infty\one_{\{x \lt 0\}}\lambda e^{-\lambda x}\one_{\{x\geq 0\}}dx=0 [[/math]]

and also that

[[math]] \p[X=x]=\int_{-\infty}^{\infty} \one_{\{y=x\}}P(y)dy=0. [[/math]]

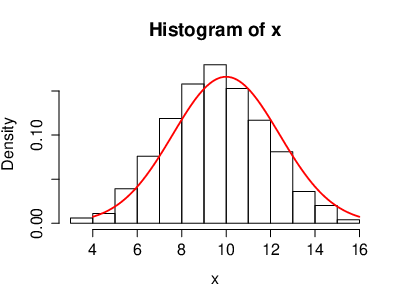
The Gaussian distribution [math]\mathcal{N}(m,\sigma^2)[/math], [math]m\in\R[/math], [math]\sigma \gt 0[/math]

The density is given by

[[math]] P(x)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-m)^2}{2\sigma^2}\right). [[/math]]

This is the most important distribution in probability theory. We have to check that [math]P(x)[/math] is a probability density, i.e.

[[math]] \int_{-\infty}^\infty\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-m)^2}{2\sigma^2}\right) dx=1. [[/math]]

Histogram of a Gaussian distributed r.v.

We set [math]u=x-m[/math] and hence [math]du=dx[/math]. So we get

[[math]] \int_{-\infty}^{\infty}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{u^2}{2\sigma^2}}du. [[/math]]

Now we set [math]t=\frac{u}{\sigma}[/math] and hence [math]du=\sigma dt[/math]. So now we get

[[math]] \int_{-\infty}^\infty \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{t^2}{2}}\sigma dt=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-\frac{t^2}{2}}dt=\frac{\sqrt{2\pi}}{\sqrt{2\pi}}=1. [[/math]]

We have used the fact that [math]\int_{-\infty}^{\infty}e^{-\frac{x^2}{2}}dx=\sqrt{2\pi}[/math], by change of coordinates from cartesian coordinates to polar coordinates. Consider [math]\mathcal{N}(0,1)[/math] with density [math]P(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}[/math]. It is called the standard Gaussian distribution ([math]m=0[/math], [math]\sigma=1[/math]). We note that if [math]X[/math] is distributed according to [math]\mathcal{N}(m,\sigma^2)[/math], then

[[math]] \E[X]=m,\text{and}\E[(X-m)^2]=\sigma^2. [[/math]]

Indeed we have

[[math]] \E[\vert X\vert]=\int_{-\infty}^{\infty}\vert x\vert\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-m)^2}{2\sigma^2}\right)dx \lt \infty [[/math]]

and therefore

[[math]] \E[X]=\int_{-\infty}^\infty x\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-m)^2}{2\sigma^2}\right)dx. [[/math]]

We set [math]u=x-m[/math] and hence [math]du=dx[/math]. So we get

[[math]] \int_{-\infty}^{\infty}\frac{(u+m)}{\sigma\sqrt{2\pi}}e^{-\frac{u^2}{2\sigma^2}}du=\underbrace{\int_{-\infty}^\infty\frac{u}{\sigma\sqrt{2\pi}}e^{-\frac{u^2}{2\sigma^2}}du}_{=0}+\underbrace{m\int_{-\infty}^\infty \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{u^2}{2\sigma^2}}du}_{=m}. [[/math]]

Therefore we get [math]\E[X]=m[/math]. One can show similarly that [math]\E[(X-m)^2]=\sigma^2[/math].

The distribution function

Let [math]X:\Omega\to\R[/math] be a real valued r.v. The distribution function of [math]X[/math] is the function

[[math]] F_X:\R\to[0,1],t\mapsto F_X(t):=\p[X\leq t]=\p_X[(-\infty,t)]. [[/math]]

We claim that [math]F_X[/math] is increasing and right continuous. Meaning that

[[math]] \lim_{t\to-\infty}F_X(t)=0,\lim_{t\to \infty}F_X(t)=1 [[/math]]

We can thus write

[[math]] \p[a\leq X\leq b]=F_X(b)-\underbrace{F_X(a^-)}_{\lim_{t\to a\atop t \lt a}F_X(t)}\text{and thus}\p[a \lt X \lt b]=F(b^-)-F_X(a), [[/math]]

Moreover, for a single value we get

[[math]] \p[X=a]=F_X(a)-F_X(a^-), [[/math]]

which is called the jump of the function [math]F_X[/math]. If [math]X[/math] and [math]Y[/math] are two r.v.'s, such that [math]F_X(t)=F_Y(t)[/math], then [math]\p_X=\p_Y[/math] (this is a consequence of the monotone class theorem). If [math]F[/math] is an increasing and right continuous function, then the set

[[math]] A=\{a\in\R\mid F(a)\not=F(a^-)\} [[/math]]

is at most countable. If [math]\p_X[/math] is absolutely continuous, then

[[math]] \p_X[\{ a\}]=\p[X=a]=0, [[/math]]

which implies that for all [math]a\in\R[/math] we have [math]F_X(a)=F_X(a^-)[/math] and hence [math]F_X[/math] is continuous. An alternative point of view is to say that, if [math]P(x)[/math] is the density of of [math]\p_X[/math], then

[[math]] F_X(x)=\p_X[(-\infty,t]]=\int_\R\one_{(-\infty,t]}(x)P(x)dx=\int_{-\infty}^tP(x)dx, [[/math]]

is a continuous function of [math]t[/math].

[math]\sigma[/math]-Algebras generated by a Random Variable

Let [math](\Omega,\A,\p)[/math] be a probability space. Let [math]X[/math] be a r.v. taking values in [math](E,\mathcal{E})[/math], i.e. [math]X:(\Omega,\A,\p)\to(E,\mathcal{E})[/math]. The [math]\sigma[/math]-Algebra generated by [math]X[/math], denoted by [math]\sigma(X)[/math], is by definition the smallest [math]\sigma[/math]-Algebra, which makes [math]X[/math] measurable. So we have

[[math]] \sigma(X)=\{A=X^{-1}(B)\mid B\in\mathcal{E}\}. [[/math]]

One can of course extend this definition to the case of a family of r.v.'s [math]X_i[/math] for [math]i\in I[/math], taking values in [math](E_i,\mathcal{E}_i)[/math]. In this case we have

[[math]] \sigma((X_i)_{i\in I})=\sigma(\{X_i^{-1}(B)\mid B_i\in\mathcal{E}_i,i\in I\}). [[/math]]

Proposition

Let [math](\Omega,\A,\p)[/math] be a probability space. Let [math]X[/math] be a r.v. with values in a measure space [math](E,\mathcal{E})[/math] and let [math]Y[/math] be a real valued r.v. Then the following are equivalent.

• [math]Y[/math] is [math]\sigma(X)[/math]-measurable.
• There exists a measurable map [math]f:(E,\mathcal{E})\to(\R,\B(\R))[/math], such that
  [[math]] Y=f(X). [[/math]]

Show Proof

So we have the following cases

[[math]] X:(\Omega,\A,\p)\longrightarrow(E,\mathcal{E}),X:(\Omega,\sigma(X),\p)\longrightarrow (E,\mathcal{E}),Y:(\Omega,\A,\p)\longrightarrow (\R,\B(\R)) [[/math]]

• [math](2)\Longrightarrow (1)[/math]: This follows from the fact that the composition of two measurable maps is measurable.
• [math](1)\Longrightarrow(2)[/math]: Assume that [math]Y[/math] is [math]\sigma(X)[/math]-measurable. Assume first [math]Y[/math] is simple, i.e.
  [[math]] Y=\sum_{i=1}^n\lambda_i\one_{A_i}(x),\forall i\{1,...,n\},\lambda_i\in\R,A_i\in\sigma(X). [[/math]]
  Now by definition of [math]\sigma(X)[/math], there is a [math]\B_i\in\mathcal{E}[/math], such that [math]A_i\in X_i^{-1}(B_i)[/math], [math]\forall i\in\{1,...,n\}[/math]. So it follows that
  [[math]] Y=\sum_{i=1}^n\lambda_i\one_{A_i}=\sum_{i=1}^n\lambda_i\one_{B_i}\circ X=f\circ X, [[/math]]
  where [math]f=\sum_{i=1}^n\lambda_i\one_{B_i}[/math] is [math]\mathcal{E}[/math]-measurable. More generally, if [math]Y[/math] is [math]\mathcal{E}[/math]-measurable, there exists a seqence [math](Y_n)[/math] of simple functions such that [math]Y_n[/math] is [math]\sigma(X)[/math]-measurable and [math]Y_n\xrightarrow{n\to\infty} Y[/math]. The above implies [math]Y_n=f_n(X)[/math] when [math]f_n:E\to\R[/math] is a measurable map. For [math]x\in E[/math], set
  [[math]] f(x)=\begin{cases}\lim_{n\to\infty}f_n(x),&\text{if the limit exists}\\ 0,&\text{otherwise}\end{cases} [[/math]]
  Then [math]f[/math] is measurable. Moreover for all [math]\omega \in\Omega[/math] we get
  [[math]] X(\omega)\in\left\{x\mid \lim_{n\to\infty}f_n(x)\text{exists}\right\}, [[/math]]
  since [math]\lim_{n\to\infty}f_n(X(\omega))=\lim_{n\to\infty}Y_n(\omega)=Y(\omega)[/math] and [math]f(X(\omega))=\lim_{n\to\infty}f_n(X(\omega))[/math]. Hence [math]Y=f(X)[/math].

■

General references

Moshayedi, Nima (2020). "Lectures on Probability Theory". arXiv:2010.16280 [math.PR].