$L^2(\Omega,\F,\p)$ as a Hilbert space and orthogonal projections
In this section we will always work on a probability space [math](\Omega,\F,\p)[/math]. Consider the space [math]L^2(\Omega,\F,\p)[/math], which is given by
More precisely, consists only of equivalence classes, i.e. [math]X[/math] and [math]Y[/math] are identified if [math]X=Y[/math] a.s. We also know that we have a norm on this space given by
Recall that on [math]\mathcal{L}^2(\Omega,\F,\p)[/math] this would only be a semi-norm rather than a norm.
We can also define an inner product on [math]L^2(\Omega,\F,\p)[/math] by
One can easily check that this satisfies the conditions of an inner product. It remains to show that [math]\vert\langle X,Y\rangle\vert \lt \infty[/math]. By Cauchy-Schwarz we get
and since we assume that the second moment of our r.v.'s exists, this is finite. Moreover one can see that
Now we know that [math]L^2(\p)[/math] is a Banach space and therefore a complete, normed vector space, i.e. every Cauchy sequence has a limit inside the space with respect to the norm. Since we have also an inner product on [math]L^2(\p)[/math], it is also a Hilbert space. We shall recall what a Hilbert space is.
An inner product space [math](\mathcal{H},\langle\cdot,\cdot\rangle)[/math] is called a Hilbert space, if it is complete and the norm is derived from the inner product. If it is not complete it is called a pre-Hilbert space.
It is in fact important that we have noted [math]L^2(\Omega,\F,\p)[/math], for instance if [math]\mathcal{G}[/math] is a [math]\sigma[/math]-Algebra and [math]\mathcal{G}\subset\F[/math], then [math]L^2(\Omega,\mathcal{G},\p)\subset L^2(\Omega,\F,\p)[/math]. When we have several [math]\sigma[/math]-Algebras, we write explicitly the dependence of them, by noting for instance [math]L^2(\Omega,\mathcal{G},\p),L^2(\Omega,\F,\p)[/math], etc.
Example
Take [math]\mathcal{H}=\R^n[/math]. This is indeed a Hilbert space with the euclidean inner product, i.e. if [math]X,Y\in\R^n[/math] then
Be aware that this is an example of a finite dimensional Hilbert space, but [math]L^2(\p)[/math] is a infinite dimensional Hilbert space. Another example would be [math]\mathcal{H}=l^2(\N)[/math] the space of square summable sequences a subspace of [math]l^\infty(\N)[/math] which is the space of convergent sequences, i.e.
This is also an example of an infinite dimensional Hilbert space. It is clearly related to the [math]L^p(\mu)[/math] spaces, where we use the counting measure. The theory of Hilbert spaces is discussed in more detail in a course on functional analysis.
We want to give here more, maybe a bit harder, examples of Hilbert spaces used in functional analysis.
- Sobolev spaces: Sobolev spaces, denoted by [math]H^s[/math] or [math]W^{s,2}[/math], are Hilbert spaces. These are a special kind of a function space in which differentiation may be performed, but that support the structure of an inner product. Because differentiation is permitted, Sobolev spaces are a convenient setting for the theory of partial differential equations. They also form the basis of the theory of direct methods in the calculus of variations. For [math]s[/math] a nonnegative integer and [math]\Omega\subset\R^n[/math], the Sobolev space [math]H^s(\Omega)[/math] contains [math]L^2[/math]-functions whose weak derivatives of order up to [math]s[/math] are also in [math]L^2[/math]. The inner product in [math]H^s(\Omega)[/math] is
[[math]] \langle f,g\rangle_{H^s(\Omega)}=\int_\Omega f(x)\bar g(x)d\mu(x)+\int_\Omega Df(x)\cdot D\bar g(x)d\mu(x)+...+\int_\Omega D^sf(x)\cdot D^s\bar g(x)d\mu(x), [[/math]]where the dot indicates the dot product in the euclidean space of partial derivatives of each order. Slobber spaces can also be defined when [math]s[/math] is not an integer.
- Hardy spaces: The Hardy spaces are function spaces, arising in complex analysis and harmonic analysis, whose elements are certain holomorphic functions in a complex domain. Let [math]U[/math] denote the unit disc in the complex plane. Then the Hardy space [math]\mathcal{H}^2(U)[/math] is defined as the space of holomorphic functions [math]f[/math] on [math]U[/math] such that the means
[[math]] M_r(f)=\frac{1}{2\pi}\int_0^{2\pi}\vert f(re^{i\theta})\vert^2d\theta [[/math]]remains bounded for [math]r \lt 1[/math]. The norm on this Hardy space is defined by[[math]] \|f\|_{\mathcal{H}^2(U)}=\lim_{r\to 1}\sqrt{M_r(f)}. [[/math]]Hardy spaces in the disc are related to Fourier series. A function [math]f[/math] is in [math]\mathcal{H}^2(U)[/math] if and only if [math]f(z)=\sum_{n=0}^\infty a_nz^n[/math], where [math]\sum_{n=0}^\infty\vert a_n\vert^2 \lt \infty[/math]. Thus [math]\mathcal{H}^2(U)[/math] consists of those functions that are [math]L^2[/math] on the circle and whose negative frequency Fourier coefficients vanish.
- Bergman spaces: The Bergman spaces are another family of Hilbert spaces of holomorphic functions. Let [math]D[/math] be a bounded open set in the complex plane (or a higher-dimensional complex space) and let [math]L^{2,h}(D)[/math] be the space of holomorphic functions [math]f[/math] in [math]D[/math] that are also in [math]L^2(D)[/math] in the sense that
[[math]] \|f\|^2=\int_D\vert f(z)\vert^2 d\mu(z) \lt \infty, [[/math]]where the integral is taken with respect to the Lebesgue measure in [math]D[/math]. Clearly [math]L^{2,h}(D)[/math] is a subspace of [math]L^2(D)[/math]; in fact, it is a closed subspace and so a Hilbert space in its own right. This is a consequence of the estimate, valid on compact subsets [math]K[/math] of [math]D[/math], that[[math]] \sup_{z\in K}\vert f(z)\vert\leq C_K\|f\|_2, [[/math]]which in turn follows from Cauchy's integral formula. Thus convergence of a sequence of holomorphic functions in [math]L^2(D)[/math] implies also compact convergence and so the function is also holomorphic. Another consequence of this inequality is that the linear functional that evaluates a function [math]f[/math] at a point of [math]D[/math] is actually continuous on [math]L^{2,h}(D)[/math]. The Riesz representation theorem (see notes on measure and integral) implies that the evaluation functional can be represented as an element of [math]L^{2,h}(D)[/math]. Thus, for every [math]z\in D[/math], there is a function [math]\eta_z\in L^{2,h}(D)[/math] such that[[math]] f(z)=\int_Df(\zeta)\overline{\eta_z(\zeta)}d\mu(\zeta) [[/math]]for all [math]f\in L^{2,h}(D)[/math]. The integrand [math]K(\zeta,z)=\overline{\eta_z(\zeta)}[/math] is known as the Bergman kernel of [math]D[/math]. This integral kernel satisfies a reproducing property[[math]] f(z)=\int_D f(\zeta) K(\zeta,z)d\mu(\zeta). [[/math]]A Bergman space is an example of a reproducing kernel Hilbert space, which is a Hilbert space of functions along with a kernel [math]K(\zeta,z)[/math] that verifies a reproducing property analogous to this one. The Hardy space [math]\mathcal{H}^2(D)[/math] also admits a reproducing kernel, known as the [math]Szeg\ddot{o}[/math] kernel. Reproducing kernels are common in other areas of mathematics as well. For instance, in harmonic analysis the Poisson kernel is a reproducing kernel for the Hilbert space of square integrable harmonic functions in the unit ball. That the latter is a Hilbert space at all is a consequence of the mean value theorem for harmonic functions.
The notion of Hilbert spaces allow us to do basic geometry on them. Even if our space is an infinite dimensional vector space, we can still make sense of geometrical meanings, for example orthogonality, only by using the inner product on the space.
Two elements [math]X,Y[/math] in a Hilbert space [math](\mathcal{H},\langle\cdot,\cdot\rangle)[/math] are said to be orthogonal if
For a real valued Hilbert space [math]\mathcal{H}[/math] we get the following identity. For every [math]X,Y\in\mathcal{H}[/math]
Let [math](X_n)_{n\geq1}[/math] and [math](Y_n)_{n\geq 1}[/math] be two converging sequences in a Hilbert space [math]\mathcal{H}[/math] such that [math]X_n\xrightarrow{n\to\infty}X[/math] and [math]Y_n\xrightarrow{n\to\infty}Y[/math]. Then
We can look at the difference, which is given by
Let [math]\mathcal{H}[/math] be a Hilbert space. For all [math]X,Y\in\mathcal{H}[/math] we get
Exercise[a].
Let [math]\mathcal{H}[/math] be a Hilbert space and let [math]\mathcal{L}\subset\mathcal{H}[/math] be a linear subset. [math]\mathcal{L}[/math] is called closed if for every sequence [math](X_n)_{n\geq1}[/math] in [math]\mathcal{L}[/math] with [math]X_n\xrightarrow{n\to\infty}X[/math] we get that [math]X\in\mathcal{L}[/math].
Let [math]\mathcal{H}[/math] be a Hilbert space and let [math]\Gamma\subset\mathcal{H}[/math] be a subset. Let [math]\Gamma^\perp[/math] denote the set of all elements of [math]\mathcal{H}[/math] which are orthogonal to [math]\Gamma[/math], i.e.
Let [math]\alpha,\beta\in \R[/math] and [math]X,X'\in\Gamma^\perp[/math]. It is clear that for all [math]Y\in\Gamma[/math]
Let [math]\mathcal{H}[/math] be a Hilbert space and let [math]X\in\mathcal{H}[/math]. Moreover let [math]\mathcal{L}\subset\mathcal{H}[/math] be a closed subspace. The distance of [math]X[/math] to [math]\mathcal{L}[/math] is given by
Since [math]\mathcal{L}[/math] is closed, [math]X\in\mathcal{L}[/math] if and only if [math]d(X,\mathcal{L})=0[/math].
Convex sets in uniformly Convex spaces
While the emphasis in this section is on Hilbert spaces, it is useful to isolate a more abstract property which is precisely what is needed for several proofs.
A normed vector space [math](V,\|\cdot\|)[/math] is called uniformly convex if for [math]X,Y\in V[/math]
A Hilbert space [math](\mathcal{H},\langle\cdot,\cdot\rangle)[/math] is uniformly convex.
For [math]X,Y\in \mathcal{H}[/math] with [math]\|X\|,\|Y\|\leq 1[/math] then by parallelogram identity we have
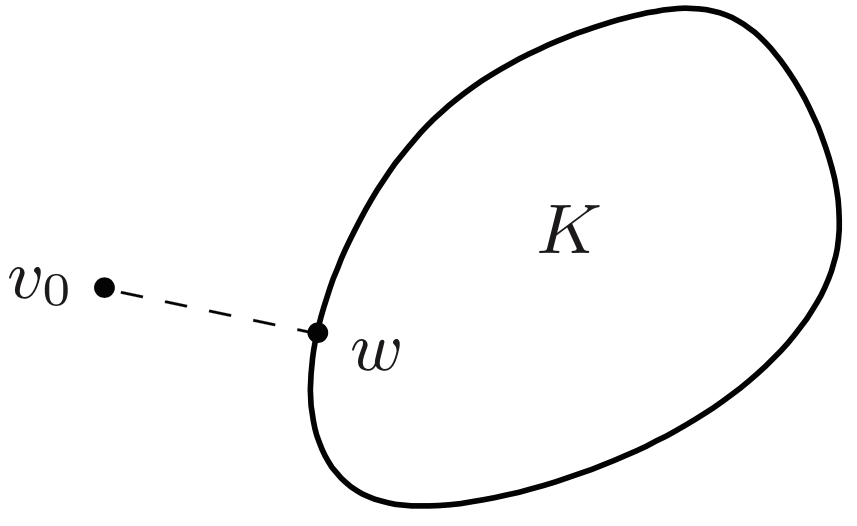
Heuristically, we can think of Definition 1.4 as having the following geometrical meaning. If vectors [math]X[/math] and [math]Y[/math] have norm (length) one, then their mid-point [math]\frac{X+Y}{2}[/math] has much smaller norm unless [math]X[/math] and [math]Y[/math] are very close together. This accords closely with the geometrical intuition from finite-dimensions spaces with euclidean distance. The following theorem, whose conclusion is illustrated in the figure, will have many important consequences for the study of Hilbert spaces.
Let [math](V,\|\cdot\|)[/math] be a Banach space with a uniformly convex norm, let [math]K\subset V[/math] be a closed convex subset and assume that [math]v_0\in V[/math]. Then there exists a unique element [math]w\in K[/math] that is closest to [math]v_0[/math] in the sense that [math]w[/math] is the only element of [math]K[/math] with
By translating both the set [math]K[/math] and the point [math]v_0[/math] by [math]-v_0[/math] we may assume without loss of generality that [math]v_0=0[/math]. We define
Let [math]\mathcal{H}[/math] be a Hilbert space and let [math]\mathcal{L}\subset\mathcal{H}[/math] be a closed subspace. Then [math]\mathcal{L}^\perp[/math] is a closed subspace with
As [math]H\mapsto \langle H,Y\rangle[/math] is a (continuous linear) functional for each [math]Y\in\mathcal{L}[/math], the set [math]\mathcal{L}^\perp[/math] is an intersection of closed subspaces and hence is a closed subspace. Using positivity of the inner product, it is easy to see that [math]\mathcal{L}\cap\mathcal{L}^\perp=\{0\}[/math] and from this the uniqueness of the decomposition
Orthogonal projection
Let again [math]\mathcal{H}[/math] be a Hilbert space. The projection of an element [math]X\in\mathcal{H}[/math] onto a closed subspace [math]\mathcal{L}\subset\mathcal{H}[/math] is the unique point [math]Y\in\mathcal{L}[/math] such that
We denote this projection by
Let [math]\mathcal{H}[/math] be a Hilbert space and let [math]\mathcal{L}\subset\mathcal{H}[/math] be a closed subspace. Then the projection operator [math]\Pi[/math] of [math]\mathcal{H}[/math] onto [math]\mathcal{L}[/math] satisfies
- [math]\Pi^2=\Pi[/math]
- [math]\begin{cases}\Pi X=X,& X\in\mathcal{L}\\ \Pi X=0,& X\in\mathcal{L}^\perp\end{cases}[/math]
- [math](X-\Pi X)\perp \mathcal{L}[/math] for all [math]X\in\mathcal{H}[/math]
[math](i)[/math] is clear. The first statement of [math](ii)[/math] is clear from [math](i)[/math]. For the second statement of [math](ii)[/math], if [math]X\in\mathcal{L}^\perp[/math], then for [math]Y\in\mathcal{L}[/math] we get
Let [math]\mathcal{H}[/math] be a Hilbert space and let [math]\mathcal{L}\subset\mathcal{H}[/math] be a closed subspace. Moreover let [math]\Pi[/math] be the projection operator of [math]\mathcal{H}[/math] onto [math]\mathcal{L}[/math]. Then
This is just a consequence of Corollary
Let [math]\mathcal{H}[/math] be a Hilbert space and let [math]\mathcal{L}\subset\mathcal{H}[/math] be a closed subspace. Moreover let [math]\Pi[/math] be the projection operator of [math]\mathcal{H}[/math] onto [math]\mathcal{L}[/math]. Then
- [math]\langle \Pi X,Y\rangle =\langle X,\Pi Y\rangle[/math] for all [math]X,Y\in\mathcal{H}[/math].
- [math]\Pi(\alpha X+\beta Y)=\alpha\Pi X+\beta \Pi Y[/math] for all [math]\alpha,\beta\in\R[/math] and [math]X,Y\in\mathcal{H}[/math].
For [math](i)[/math], let [math]X,Y\in\mathcal{H}[/math], [math]X=X_1+X_2[/math] with [math]X_1\in\mathcal{L}[/math] and [math]X_2\in\mathcal{L}^\perp[/math] and [math]Y=Y_1+Y_2[/math] with [math]Y_1\in\mathcal{L}[/math] and [math]Y_2\in\mathcal{L}^\perp[/math]. Then we get
General references
Moshayedi, Nima (2020). "Lectures on Probability Theory". arXiv:2010.16280 [math.PR].