Supervised Learning with Neural Networks

[math] \newcommand{\varitem}[1]{\vspace{0.1cm}\hspace*{1cm}\raisebox{0.1cm}{ \tikz[baseline=(SebastianoItem.base),remember picture]{% \node[fill=green!20,inner sep=4pt,font=\sffamily] (SebastianoItem){#1};}\hspace{0.25cm} \vspace*{0.1cm}}} \newcommand{\SebastianoHighlight}{\tikz[overlay,remember picture]{% \fill[red!20] ([yshift=-20pt,xshift=-\pgflinewidth]SebastianoItem.east) -- ++(2pt,-2pt) -- ++(-2pt,-2pt) -- cycle; }} \newcommand{\rz}[1]{\displaystyle\stackrel{#1}{\phantom{.}}} % to raise exponent just a bit \newcommand{\CC}{C\nolinebreak\hspace{-.05em}\raisebox{.4ex}{\tiny\bf +}\nolinebreak\hspace{-.10em}\raisebox{.4ex}{\tiny\bf +}} \newcommand{\bm}[1]{\boldsymbol{#1}} \newcommand{\sectionbreak}{\clearpage} \newcommand\pythonstyle{\lstset{ language=Python, basicstyle=\ttm, otherkeywords={self},  % Add keywords here keywordstyle=\ttb\color{deepblue}, emph={MyClass,__init__},  % Custom highlighting emphstyle=\ttb\color{deepred},  % Custom highlighting style stringstyle=\color{deepgreen}, frame=tb,  % Any extra options here showstringspaces=false  % }} \newcommand\pythoninline[1]{{\pythonstyle\lstinline!#1!}} \DeclareMathOperator{\sign}{sign} \newcommand{\mathds}{\mathbb}[/math]

In the previous chapter, we covered the basics of machine learning using conventional methods such as linear regression and principle component analysis. In the present chapter, we move towards a more complex class of machine learning models: neural networks. Neural networks have been central to the recent vast success of machine learning in many practical applications. The idea for the design of a neural network model is an analogy to how biological organisms process information. Biological brains contain neurons, electrically activated nerve cells, connected by synapses that facilitate information transfer between neurons. The machine learning equivalent of this structure, the so-called artificial neural networks or neural networks in short, is a mathematical function developed with the same principles in mind. It is composed from elementary functions, the neurons, which are organized in layers that are connected to each other. To simplify the notation, a graphical representation of the neurons and network is used, see Fig.fig:NN_carrot. The connections in the graphical representation means that the output from one set of neurons (forming one layer) serves as the input for the next set of neurons (the next layer). This defines a sense of direction in which information is handed over from layer to layer, and thus the architecture is referred to as a feed-forward neural network. In general, an artificial neural network is simply an example of a variational non-linear function that maps some (potentially high-dimensional) input data to a desired output. Neural networks are remarkably powerful and it has been proven that under some mild structure assumptions they can approximate any smooth function arbitrarily well as the number of neurons tends to infinity. A drawback is that neural networks typically depend on a large amount of parameters. In the following, we will learn how to construct these neural networks and find optimal values for the variational parameters. In this chapter, we are going to discuss one option for optimizing neural networks: the so-called supervised learning. A machine learning process is called supervised whenever we use training data comprising input-output pairs, in other words input with known correct answer (the label), to teach the network-required task.

Neural Network. Graphical representation and basic architecture.

Computational neurons

The basic building block of a neural network is the neuron. Let us consider a single neuron which we assume to be connected to [math]k[/math] neurons in the preceding layer, see Fig.fig:NN_act left side. The neuron corresponds to a function [math]f:\mathbb{R}^k\to \mathbb{R}[/math] which is a composition of a linear function [math]q:\mathbb{R}^k\to \mathbb{R}[/math] and a non-linear (so-called activation function) [math]g:\mathbb{R}\to \mathbb{R}[/math]. Specifically,

[[math]] \begin{equation} f(z_1,\ldots,z_k) = g(q(z_1,\ldots,z_k)) \end{equation} [[/math]]

where [math]z_1, z_2, \dots, z_k[/math] are the outputs of the neurons from the preceding layer to which the neuron is connected. The linear function is parametrized as

[[math]] \begin{equation} q(z_1,\ldots,z_k) = \sum_{j=1}^k w_jz_j + b. \end{equation} [[/math]]

Here, the real numbers [math]w_1, w_2, \dots, w_k[/math] are called weights and can be thought of as the “strength” of each respective connection between neurons in the preceding layer and this neuron. The real parameter [math]b[/math] is known as the bias and is simply a constant offset. The weights and biases are the variational parameters we will need to optimize when we train the network. The activation function [math]g[/math] is crucial for the neural network to be able to approximate any smooth function, since so far we merely performed a linear transformation. For this reason, [math]g[/math] has to be nonlinear. In analogy to biological neurons, [math]g[/math] represents the property of the neuron that it “spikes”, i.e., it produces a noticeable output only when the input potential grows beyond a certain threshold value. The most common choices for activation functions, shown in Fig.fig:NN_act, include:

The artificial neuron. Left: schematic of a single neuron and its functional form. Right: examples of the commonly used activation functions: ReLU, sigmoid function and hyperbolic tangent.

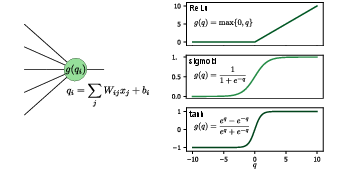
• ReLU: ReLU stands for rectified linear unit and is zero for all numbers smaller than zero, while a linear function for all positive numbers.
• Sigmoid: The sigmoid function, usually taken as the logistic function, is a smoothed version of the step function.
• Hyperbolic tangent: The hyperbolic tangent function has a similar behaviour as sigmoid but has both positive and negative values.
• Softmax: The softmax function is a common activation function for the last layer in a classification problem (see below).

The choice of activation function is part of the neural network architecture and is therefore not changed during training (in contrast to the variational parameters weights and bias, which are adjusted during training). Typically, the same activation function is used for all neurons in a layer, while the activation function may vary from layer to layer. Determining what a good activation function is for a given layer of a neural network is typically a heuristic rather than systematic task. Note that the softmax provides a special case of an activation function as it explicitly depends on the output of the [math]q[/math] functions in the other neurons of the same layer. Let us label by [math]l=1,\ldots,n [/math] the [math]n[/math] neurons in a given layer and by [math]q_l[/math] the output of their respective linear transformation. Then, the softmax is defined as

[[math]] \begin{equation} g_l(q_1,\ldots, q_n)= \frac{e^{-q_{l}}}{\sum_{l'=1}^ne^{-q_{l'}}} \end{equation} [[/math]]

for the output of neuron [math]l[/math]. A useful property of softmax is that

[[math]] \begin{equation} \sum_l g_l(q_1,\ldots, q_n)=1, \end{equation} [[/math]]

so that the layer output can be interpreted as a probability distribution. The softmax function is thus a continuous generalization of the argmax function introduced in the previous chapter.

A simple network structure

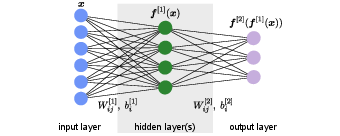
Now that we understand how a single neuron works, we can connect many of them together and create an artificial neural network. The general structure of a simple (feed-forward) neural network is shown in Fig.fig:simple_network. The first and last layers are the input and output layers (blue and violet, respectively, in Fig.fig:simple_network) and are called visible layers as they are directly accessed. All the other layers in between them are neither accessible for input nor providing any direct output, and thus are called hidden layers (green layer in Fig.fig:simple_network).

Simple neural network. Architecture and variational parameters.

Assuming we can feed the input to the network as a vector, we denote the input data with [math]\bm x[/math]. The network then transforms this input into the output [math]\bm{F}(\bm{x})[/math], which in general is also a vector. As a simple and concrete example, we write the complete functional form of a neural network with one hidden layer as shown in Fig.fig:simple_network,

[[math]] \begin{equation} \bm{F}(\bm{x}) = \bm{g}^{[2]}\left( W^{[2]}\bm{g}^{[1]} \left(W^{[1]}\bm{x}+\bm{b}^{[1]}\right)+\bm{b}^{[2]} \right). \label{eq: 2-layer NN} \end{equation} [[/math]]

Here, [math]W^{[n]}[/math] and [math]\bm{b}^{[n]}[/math] are the weight matrix and bias vectors of the [math]n[/math]-th layer. Specifically, [math]W^{[1]}[/math] is the [math]k\times l[/math] weight matrix of the hidden layer with [math]k[/math] and [math]l[/math] the number of neurons in the input and hidden layer, respectively. [math]W_{ij}^{[1]}[/math] is the [math]j[/math]-the entry of the weight vector of the [math]i[/math]-th neuron in the hidden layer, while [math]b_i^{[1]}[/math] is the bias of this neuron. The [math]W_{ij}^{[2]}[/math] and [math]\bm{b}_i^{[2]}[/math] are the respective quantities for the output layer. This network is called fully connected or dense, because each neuron in a given layer takes as input the output from all the neurons in the previous layer, in other words all weights are allowed to be non-zero. Note that for the evaluation of such a network, we first calculate all the neurons' values of the first hidden layer, which feed into the neurons of the second hidden layer and so on until we reach the output layer. This procedure, which is possible only for feed-forward neural networks, is obviously much more efficient than evaluating the nested function of each output neuron independently.

Training

Adjusting all the weights and biases to achieve the task given using data samples [math]\mathcal{D}= \{(\bm{x}_1,\bm{y}_1),\dots, (\bm{x}_m,\bm{y}_m)\}[/math] constitutes the training of the network. In other words, the training is the process that makes the network an approximation to the mathematical function [math]\bm{F}(\bm{x}) = \bm{y}[/math] that we want it to represent. Since each neuron has its own bias and weights, a potentially huge number of variatonial parameters, and we will need to adjust all of them. We have already seen in the previous chapter how one in principle trains a variational function. For the purpose of learning, we introduce a loss function [math]L(W,B)[/math], which characterizes how well the network is doing at predicting the correct output for each input. The loss function now depends, through the neural network, on all the weights and biases that we collectively denote by the vectors [math]W[/math] and [math]B[/math]. The choice of loss function may strongly impact the efficiency of the training and is based on heuristics (as was the case with the choice of activation functions). In the previous chapter, we already encountered one loss function, the mean square error

[[math]] \begin{equation} L(\theta) = \frac{1}{2m}\sum_{i=1}^m||\bm{F}(\bm{x}_i) - \bm{y}_i ||_2^2. \label{eq:MSE} \end{equation} [[/math]]

Here, [math]||\bm{a}||_2=\sqrt{\sum_i a_i^2}[/math] is the [math]L2[/math] norm and thus, this loss function is also referred to as [math]L2[/math] loss. An advantage of the L2 loss is that it is a smooth function of the variational parameters. Another natural loss function is the mean absolute error, which is given by

[[math]] \begin{equation} L(\theta) = \frac{1}{2m}\sum_{i=1}^m||\bm{F}(\bm{x}_i) - \bm{y}_i ||_1, \label{eq:MAE} \end{equation} [[/math]]

where [math]||\bm{a}||_1 = \sum_i |a_i|[/math] denotes the [math]L1[/math] norm. This loss function is thus also called the [math]L1[/math] loss. Note that the [math]L2[/math] norm, given the squares, puts more weight on outliers than the [math]L1[/math] loss. The two loss functions introduced so far are the most common loss functions for networks providing a continuous output. For discrete classification problems, a great choice is the cross-entropy between true label, [math]\bm{y}_i[/math] and the network output, [math]\bm{F}(\bm{x}_i)[/math] defined as

[[math]] \begin{equation} L_{\mathrm{ent}}{}(\theta) =-\sum_{i=1}^m \left[ \bm{y}_i\cdot \ln \left( \bm{F}(\bm{x}_i) \right) + (1- \bm{y}_i)\cdot \ln \left(1- \bm{F}(\bm{x}_i) \right) \right] , \label{eq:cross-entropy} \end{equation} [[/math]]

where the logarithm is taken element-wise. This loss function is also called negative log likelihood. It is here written for outputs that lie between 0 and 1, as is the case when the activation function of the last layer of the network is sigmoid [math]\sigma(z)=1/(1+e^{-z})[/math]. (The cross-entropy is preferably combined with sigmoid activation in the last layer.) Of these loss functions the cross entropy is probably the least intuitive one. We want to understand what it means and gain some intuition about it. The different cost functions actually differ by the speed of the learning process. The learning rate is largely determined by the partial derivatives of the cost function [math]\partial L/\partial \theta[/math]. Slow learning appears when these derivatives become small. Let us consider the toy example of a single neuron with sigmoid activation [math]F(x)=\sigma(wx+b)[/math] and a single input-output pair [math]\{x,y\}=\{1,0\}[/math]. Then the quadratic cost function has derivatives

[[math]] \begin{equation} \frac{\partial L}{\partial w}= \frac{\partial L}{\partial b}=\sigma(w+b)\sigma'(w+b). \end{equation} [[/math]]

We observe that this derivative gets very small for [math]\sigma(w+b)\to 1[/math], because [math]\sigma'[/math] gets very small in that limit. Therefore, a slowdown of learning appears. This slowdown is also observed in more complex neural networks with L2 loss, we considered the simple case here only to be able to say something analytically. Given this observation, we want to see whether the cross entropy can improve the situation. We again compute the derivative of the cost function with respect to the weights for a single term in the sum and a network that is composed of a single sigmoid and a general input-output pair [math]\{x,y\}[/math]

[[math]] \begin{equation} \begin{split} \frac{\partial L_{\mathrm{ent}}}{\partial w} &=-\left( \frac{y}{\sigma(wx+b)}-\frac{1-y}{1-\sigma(wx+b)}\right)\sigma'(wx+b)x \\ &=\frac{\sigma'(wx+b) x}{\sigma(wx+b)[1-\sigma(wx+b)]}[\sigma(wx+b)-y] \\ &=x[\sigma(wx+b)-y], \end{split} \label{eq: cost derivative w} \end{equation} [[/math]]

where in the last step we used that [math]\sigma'(z)=\sigma(z)[1-\sigma(z)][/math]. This is a much better result than what we got for the L2 loss. The learning rate is here directly proportional to the error between data point and prediction [math][\sigma(wx+b)-y][/math]. The mathematical reason for this change is that [math]\sigma'(z)[/math] cancels out due to this specific form of the cross entropy. A similar expression holds true for the derivative with respect to [math]b[/math],

[[math]] \begin{equation} \frac{\partial L_{\mathrm{ent}}}{\partial b} =[\sigma(wx+b)-y]. \label{eq: cost derivative b} \end{equation} [[/math]]

In fact, if we insisted that we want the very intuitive form of Eqs.\eqref{eq: cost derivative w} and\eqref{eq: cost derivative b} for the gradients, we can derive the cost function for the sigmoid activation function to be the cross-entropy. This follows simply because

[[math]] \begin{equation} \frac{\partial L}{\partial b}=\frac{\partial L}{\partial F}F' \end{equation} [[/math]]

and [math]F'=F(1-F)[/math] for the sigmoid activation, which, in comparison to Eq.\eqref{eq: cost derivative b}, yields

[[math]] \begin{equation} \frac{\partial L}{\partial F}=\frac{F-y}{F(1-F)}, \end{equation} [[/math]]

which, when integrated with respect to [math]F[/math], gives exactly the cross-entropy (up to a constant). We can thus, starting from Eqs.\eqref{eq: cost derivative w} and\eqref{eq: cost derivative b}, think of the choice of cost functions as a backward engineering. Following this logic, we can think of other pairs of final layer activations and cost functions that may work well together.

What happens if we change the activation function in the last layer from sigmoid to softmax? For the loss function, we consider just the first term in the cross entropy for the shortness of presentation (for softmax, this form is appropriate, as compared to a sigmoid activation)

[[math]] \begin{equation} L(\theta) =-\sum_{i=1}^m \bm{y}_i\cdot \ln \left( \bm{F}(\bm{x}_i) \right) , \label{eq:cross-entropy 2} \end{equation} [[/math]]

where again the logarithm is taken element-wise. For concreteness, let us look at one-hot encoded classification problem. Then, all [math]\bm{y}_i[/math] labels are vectors with exactly one entry “1”. Let that entry have index [math]n_i[/math] in the vector. The loss function then reads

[[math]] \begin{equation} L(\theta) =-\sum_{i=1}^m \ln \left( F_{n_i}(\bm{x}_i) \right) . \label{eq:cross-entropy 3} \end{equation} [[/math]]

Due to the properties of the softmax, [math] F_{n_i}(\bm{x}_i)[/math] is always [math]\leq 1[/math], so that loss function is minimized, if it approaches 1, the value of the label. For the gradients, we obtain

[[math]] \begin{equation} \begin{split} \frac{\partial L}{\partial b_{j}}=& -\sum_{i=1}^m\frac{1}{F_{n_i}(\bm{x}_i)}\frac{\partial F_{n_i}(\bm{x}_i)}{\partial b_j} \\ =& -\sum_{i=1}^m\frac{1}{F_{n_i}(\bm{x}_i)} \left[ F_{n_i}(\bm{x}_i)\delta_{n_i,j} -F_{n_i}(\bm{x}_i)^2 \right] \\ =& \sum_{i=1}^m \left[ F_{n_i}(\bm{x}_i) -y_{n_i} \right]. \end{split} \end{equation} [[/math]]

We observe that again, the gradient has a similar favorable structure to the previous case, in that it is linearly dependent on the error that the network makes. (The same can be found for the derivatives with respect to the weights.) Once we have defined a loss function, we also already understand how to train the network: we need to minimize [math]L(\theta)[/math] with respect to [math]W[/math] and [math]B[/math]. However, [math]L[/math] is typically a high-dimensional function and may have many nearly degenerate minima. Unlike in the previous chapter, finding the loss function's absolute minimum exactly is typically intractable analytically and may come at prohibitive costs computationally. The practical goal is therefore rather to find a “good” instead than the absolute minimum through training. Having found such “good” values for [math]W,B[/math], the network can then be applied on previously unseen data.

It remains to be explained how to minimize the loss function. Here, we employ an iterative method called gradient descent. Intuitively, the method corresponds to “walking down the hill” in our many parameter landscape until we reach a (local) minimum. For this purpose, we use the (discrete) derivative of the cost function to update all the weights and biases incrementally and search for the minimum of the function via tiny steps on the many-dimensional surface. More specifically, we can update all weights and biases in each step as

[[math]] \begin{align} \theta_\alpha \rightarrow \theta_\alpha - \eta \frac{\partial L(\theta)}{\partial \theta_\alpha}. \end{align} [[/math]]

The variable [math]\eta[/math], also referred to as learning rate, specifies the size of step we use to walk the landscape---if it is too small in the beginning, we might get stuck in a local minimum early on, while for too large [math]\eta[/math] we might never find a minimum. The learning rate is a hyperparameter of the training algorithm. Note that gradient descent is just a discrete many-variable version of the analytical search for extrema which we know from calculus: An extremum is characterized by vanishing derivatives in all directions, which results in convergence in the gradient descent algorithm outlined above.

While the process of optimizing the many variables of the loss function is mathematically straightforward to understand, it presents a significant numerical challenge: For each variational parameter, for instance a weight in the [math]k[/math]-th layer [math]W_{ij}^{[k]}[/math], the partial derivative [math]\partial L/ \partial W_{ij}^{[k]}[/math] has to be computed. And this has to be done each time the network is evaluated for a new dataset during training. Naively, one could assume that the whole network has to be evaluated each time. Luckily there is an algorithm that allows for an efficient and parallel computation of all derivatives -- it is known as backpropagation. The algorithm derives directly from the chain rule of differentiation for nested functions and is based on two observations:

• [(1)] The loss function is a function of the neural network [math]F(\bm{x})[/math], that is [math]L \equiv L(F)[/math].
• [(2)] To determine the derivatives in layer [math]k[/math] only the derivatives of the following layer, given as Jacobi matrix
  [[math]] \begin{equation} D\bm{f}^{[l]}(\bm{z}^{[l-1]}) = \partial \bm{f}^{[l]}/\partial \bm{z}^{[l-1]}, \end{equation} [[/math]]
  with [math]l \gt k[/math] and [math]z^{[l-1]}[/math] the output of the previous layer, as well as
  [[math]] \begin{equation} \frac{\partial \bm{z}^{[k]} }{ \partial \theta_\alpha^{[k]}} = \frac{\partial \bm{g}^{[k]}}{\partial q_i^{[k]}} \frac{{\partial q_i^{[k]}}}{\partial\theta_\alpha} = \begin{cases} \frac{\partial \bm{g}^{[k]}}{\partial q_i^{[k]}} z^{[k-1]}_j&\theta_\alpha=W_{ij} \\ \frac{\partial \bm{g}^{[k]}}{\partial q_i^{[k]}} &\theta_\alpha=b_{i} \end{cases} \end{equation} [[/math]]
  are required. The derivatives [math]\bm{z}^{[l]}[/math] are the same for all parameters.

The calculation of the Jacobi matrix thus has to be performed only once for every update. In contrast to the evaluation of the network itself, which is propagating forward, (output of layer [math]n[/math] is input to layer [math]n+1[/math]), we find that a change in the Output propagates backwards though the network. Hence the name. The full algorithm looks then as follows:

Backpropagation

Input:

Loss function [math]L[/math] that in turn depends on the neural network, which is parametrized by weights and biases, summarized as [math]\theta=\{W,b\}[/math].

Output:

Partial derivatives [math]\partial L / \partial \theta^{[n]}_{\alpha}[/math] with respect to all parameters [math]\theta^{[n]}[/math] of all layers [math]k=1\dots n[/math].

Calculate the derivatives with respect to the parameters of the output layer: [math]\partial L / \partial W^{[n]}_{ij} = (\bm{\nabla} L)^T \frac{\partial \bm{g}^{[n]}}{\partial q_i^{[n]}} z^{[n-1]}_j [/math], [math]\quad\partial L / \partial b^{[n]}_{i} = (\bm{\nabla} L)^T \frac{\partial \bm{g}^{[n]}}{\partial q_i^{[n]}}[/math]

for [math]k=n\dots 1[/math] do

Calculate the Jacobi matrices for layer [math]k[/math]: [math]D\bm{g}^{[k]}=(\partial \bm{g}^{[k]}/\partial \bm{q}^{[k]})[/math] and [math]D\bm{f}^{[k]}=(\partial \bm{f}^{[k]}/\partial \bm{z}^{[k-1]})[/math];

Multiply all following Jacobi matrices to obtain the derivatives of layer [math]k[/math]:

[math]\partial L / \partial \theta^{[k]}_{\alpha} = (\nabla L)^T D\bm{f}^{[n]}\cdots D\bm{f}^{[k+1]}D\bm{g}^{[k]} (\partial \bm{q}^{[k]}/\partial \theta^{[k]}_\alpha)[/math];

end

A remaining question is when to actually perform updates to the network parameters. One possibility would be to perform the above procedure for each training data individually. Another extreme is to use all the training data available and perform the update with an averaged derivative. Not surprisingly, the answer lies somewhere in the middle: Often, we do not present training data to the network one item at the time, but the full training data is divided into co-called batches, a group of training data that is fed into the network together. Chances are the weights and biases can be adjusted better if the network is presented with more information in each training step. However, the price to pay for larger batches is a higher computational cost. Therefore, the batch size can greatly impact the efficiency of training. The random partitioning of the training data into batches is kept for a certain number of iterations, before a new partitioning is chosen. The consecutive iterations carried out with a chosen set of batches constitute a training epoch.

Simple example: MNIST

As we discussed in the introduction, the recognition of hand-written digits [math]0[/math], [math]1[/math], [math]\ldots 9[/math] is the “Drosophila” of machine learning with neural networks. There is a dataset with tens of thousands of examples of hand-written digits, the so-called MNIST data set. Each data sample in the MNIST dataset, a [math]28\times28[/math] grayscale image, comes with a label, which holds the information which digit is stored in the image. The difficulty of learning to recognize the digits is that handwriting styles are incredibly personal and different people will write the digit “4” slightly differently. It would be very challenging to hardcode all the criteria to recognize “4” and not confuse it with, say, a “9”.

We can use a simple neural network as introduced earlier in the chapter to tackle this complex task. We will use a network as shown in Fig.fig:simple_network and given in Eq.\eqref{eq: 2-layer NN} to do just that. The input is the image of the handwritten digit, transformed into a [math]k=28^2[/math] long vector, the hidden layer contains [math]l[/math] neurons and the output layer has [math]p=10[/math] neurons, each corresponding to one digit in the one-hot encoding. The output is then a probability distribution over these 10 neurons that will determine which digit the network identifies. As an exercise, we build a neural network according to these guidelines and train it. How exactly one writes the code depends on the library of choice , but the generic structure will be the following:

Example (MNIST)

• Import the data: The MNIST database is available for download at [3]
• Define the model:
  • Input layer: [math]28^2=784[/math] neurons (the greyscale value of each pixel of the image, normalized to a value in [math][0,1)[/math], is one component of the input vector).
  • Fully connected hidden layer: Here one can experiment, starting from as few as 10 neurons. The use of a sigmoid activation function is recommended, but others can in principle be used.
  • Output layer: Use 10 neurons, one for each digit. The proper activation function for this classification task is, as discussed, a softmax function.
• Choose the loss function: Since we are dealing with a classification task, we use the cross-entropy, Eq.\eqref{eq:cross-entropy}.
• Train and evaluate the model: Follow the standard machine-learning workflow to train and evaluate the model. However, unlike in the regression example of the previous chapter, where we evaluated the model using the mean square error, here we are rather interested in the accuracy of our prediction.

With the training completed, we want to understand how well the final model performs in recognizing handwritten digits. For that, we introduce the accuracy defined by

[[math]] \begin{equation} \text{accuracy} = \frac{\text{correct predictions}}{\text{total predictions}}. \label{eq:accuracy} \end{equation} [[/math]]

If we use 30 hidden neurons, set the learning rate to [math]\eta=0.5[/math] (a mini-batch size of 10 and train for 30 epochs), we obtain an accuracy of 95.49 %. With a quadratic cost we obtain only slightly worse results of 95.42%. For 100 hidden neurons, we obtain 96.82%. That is a considerable improvement over a quadratic cost, where we obtain 96.59%. (Meaning that now about 1 in 14 wrongly classified pictures will now be correctly classified.) Still, these numbers are not even close to state of the art neural network performances. The reason is that we have used the simplest possible all-to-all connected architecture with only one hidden layer. Below, we will introduce more advanced neural network features and show how to increase the performance.

Before doing so, we briefly introduce other important measures used to characterize the performance of specifically binary-classification models in statistics are: precision, specificity and recall. In the language of true (false) positives (negatives) the precision is defined as

[[math]] \begin{equation} \text{precision} = \frac{\text{true positives}}{\text{true positives}+\text{false positives}}. \end{equation} [[/math]]

Recall (also referred to as sensitivity) is defined as

[[math]] \begin{equation} \text{recall} = \frac{\text{true positives}}{\text{true positives}+\text{false negatives}}. \end{equation} [[/math]]

While recall can be interpreted as true positive rate as it represents the ratio between actual positives and outcomes identified as positive, the specificity is an analogous measures for negatives

[[math]] \begin{equation} \text{specificity} = \frac{\text{true negatives}}{\text{true negatives}+\text{false positives}}. \end{equation} [[/math]]

Note, however, that these measures can be misleading, in particular when dealing with very unbalanced data sets.

Regularization

In the previous sections, we have illustrated an artificial neural network that is constructed analogous to neuronal networks in the brain. A model is only given a rough structure a priori, within which they have a huge number of parameters to adjust by learning from the training set. While we already understand that this is an extraordinarily powerful process, this method of learning comes with its own set of challenges. The most prominent of them is the generalization of the rules learned from training data to unseen data.

We have already encountered in the previous chapter how the naive optimization of a linear model reduces the generalization. However, we have also seen how the generalization error can be improved using regularization. Training neural network comes with the same issue and the same solution: we are always showing the algorithm we built the training that is limited in one way or another and we need to make sure that the neural network does not learn particularities of that given training set, but actually extracts a general knowledge.

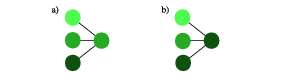
The step zero to avoid over-fitting is to create sufficiently representative and diverse training set. Once this is taken care of, we can take several steps for the regularization of the network. The simplest, but at the same time most powerful option is introducing dropout layers. This regularization is very similar to dropping features that we discussed for linear regression. However, the dropout layer ignores a randomly selected subset of neuron outputs in the network only during training. Which neurons are dropped is chosen at random for each training step. This regularization procedure is illustrated in Fig.fig:dropout. By randomly discarding a certain fraction of neurons we ensure that the network does not get fixed at small particular features of the training set and is better equipped to recognize the more general features. Another way of looking at it is that this procedure corresponds to training a large number of neural networks with different neuron connections in parallel. The fraction of neurons that are ignored in a dropout layer is a hyperparameter that is fixed a priori. Maybe it is counter-intuitive but the best performance is often achieved when this number is sizable, between 20% and 50%. It shows the remarkable resilience of the network against fluctuations.

Dropout layer

As for the linear models, regularization can also be achieved by adding regularization terms [math]R[/math] to the [math]L[/math], [math]L \rightarrow L + R[/math]. Again, the two most common regularization terms are [math]L1[/math]- or Lasso-regularisation, where

[[math]] \begin{equation} R_{L1} = \frac{\lambda}{2} \sum_j |W_j|, \end{equation} [[/math]]

and the sum runs over all weights [math]W_j[/math] of the network, as well as the [math]L2[/math]-regularization, or ridge regression, which we already discussed for linear regression with

[[math]] \begin{equation} R_{L2} = \frac{\lambda}{2} \sum_j W_j^2, \end{equation} [[/math]]

where the sum runs again over all weights [math]W_j[/math] of the network. As for the linear models, [math]L2[/math] regularization shrinks all parameters symmetrically, whereas [math]L1[/math]-regularization usually causes a subset of parameters to vanish. For this reason, the method is also called weight decay. Either way, both [math]L1[/math] and [math]L2[/math] regularizations restrict the expressiveness of the neural network, thus encouraging it to learn generalizable features rather than overfitting specific features of the data set. The weights are commonly initialized with small values and increase during training. This naturally limits the capacity of the network, because for very small weights it effectively acts as a linear model (when one approximates the activation function by a linear function). Only once the weights become bigger, the network explores its nonlinearity. Another regularization technique consists in artificially enlarging the data set. Data is often costly, but we have extra knowledge about what further data might look like and feed this information in the machine learning workflow. For instance, going back to the MNIST example, we may shift or tilt the existing images or apply small transformations to them. By doing that, researchers were able to improve MNIST performance by almost 1 percent . In particular if we know symmetries of the problem from which the data originates (such as time translation invariance, invariance under spatial translations or rotations), effective generation of augmented datasets is possible. Another option is the addition of various forms of noise to data in order to prevent overfitting to the existing noise or in general resilience of the neural network to noise. Finally, for classification problems in particular, data may not be distributed between categories equally. To avoid a bias, it is the desirable to enhance the data in the underrepresented categories.

Convolutional neural networks

The fully-connected simple single-layer architecture for a neural network is in principle universally applicable. However, this architecture is often inefficient and hard to train. In this section, we introduce more advanced neural-network layers and examples of the types of problems for which they are suitable.

Convolutional layers

Convolutional layer in 2D. Here with filter size [math]k=3[/math] and stride [math]s=2[/math]. The filter is first applied to the [math]3\times 3[/math] sub-image in the top left of the input, which yields the first pixel in the feature map. The filter then moves [math]s[/math] neurons to the right, which yields the next pixel and so on. After moving all the way to the right, the filter moves [math]s[/math] pixels down and starts from the left again until reaching the bottom right.

The achieved accuracy in the MNIST example above was not as high as one may have hoped, being much worse than the performance of a human. A main reason was that, using a dense network structure, we discarded all local information contained in the pictures. In other words, connecting every input neuron with every neuron in the next layer, the information whether two neurons are close to each other is lost. This information is, however, not only crucial for pictures, but quite often for input data with an underlying geometric structure or natural notion of ‘distance’ in its correlations. To use this local information, so-called convolutional layers were introduced. The neural networks that contain such layers are called convolutional neural networks (CNNs).

The key idea behind convolutional layers is to identify certain (local) patterns in the data. In the example of the MNIST images, such patterns could be straight and curved lines, or corners. A pattern is then encoded in a kernel or filter in the form of weights, which are again part of the training. The convolutional layer than compares these patterns with a local patch of the input data. Mathematically, identifying the features in the data corresponds to a convolution [math](f * x)(t)=\sum_{\tau}f(\tau)x(t-\tau)[/math] of the kernel [math]f[/math] with the original data [math]x[/math]. For two-dimensional data, such as shown in the example in Fig.fig:conv_2D, we write the discrete convolution explicitly as

[[math]] \begin{equation} q_{i,j} = \sum_{m=1}^{k} \sum_{n=1}^{k} f_{n,m} x_{si-m,sj-n} + b_0, \end{equation} [[/math]]

where [math]f_{n,m}[/math] are the weights of the kernel, which has linear size [math]k[/math], and [math]b_0[/math] is a bias. Finally, [math]s[/math] is called stride and refers to the number of pixels the filter moves per application. The output, [math]q[/math], is called feature map. Note that the dimension of the feature map is [math]n_q\times n_q[/math] with [math]n_q = \lfloor (n_{in} - k)/s + 1 \rfloor [/math] when the input image is of dimensions [math]n_{in} \times n_{in}[/math]: application of a convolutional layer thus reduces the image size, an effect not always intended. To avoid this reduction, the original data can be padded, for example by adding zeros around the border of the data to ensure the feature map has the same dimension as the input data. For typical convolutional networks, one applies a number of filters for each layer in parallel, where each filter is trained to recognize different features. For instance, one filter could start to be sensitive to contours in an image, while another filter recognizes the brightness of a region. Further, while filters in the first layers may be sensitive to local patterns, the ones in the later layers recognize larger structures. This distribution of functionalities between filters happens automatically, it is not preconceived when building the neural network.

Pooling

Pooling layer (a) an average pooling and (b) a max pooling layer (both [math]n=3[/math]).

Another very useful layer, in particular in combination with convolutional layers, is the pooling layer. Each neuron in the pooling layer takes input from [math]n[/math] (neighboring) neurons in the previous layer---in the case of a convolutional network for each feature map individually---and only retains the most significant information. Thus, the pooling layer helps to reduce the spatial dimension of the data. What is considered significant depends on the particular circumstances: Picking the neuron with the maximum input among the [math]n[/math], called max pooling, detects whether a given feature is present in the window. Furthermore, max pooling is useful to avoid dead neurons, in other words neurons that are stuck with a value near 0 irrespective of the input and such a small gradient for its weights and biases that this is unlikely to change with further training. This is a scenario that can often happen especially when using the ReLU activation function. Average pooling, in other words taking the average value of the [math]n[/math] inputs is a straight forward compression. Note that unlike other layers, the pooling layer has just a small set of [math]n[/math] connections with no adjustable weights. The functionality of the pooling layer is shown in Fig.fig:pooling(a) and(b).

An extreme case of pooling is global pooling, where the full input is converted to a single output. Using a max pooling, this would then immediately tell us, whether a given feature is present in the data.

Example: DNA sequencing

With lowering costs and expanding applications, DNA sequencing has become a widespread tool in biological research. Especially the introduction of high-throughput sequencing methods and the related increase of data has required the introduction of data science methods into biology. Sequenced data is extremely complex and thus a great playground for machine learning applications. Here, we consider a simple classification as an example. The primary structure of DNA consists of a linear sequence of basic building blocks called nucleotides. The key component of nucleotides are nitrogen bases: Adenine (A), Guanine (G), Cytosine (C), and Thymine (T). The order of the bases in the linear chains defines the DNA sequence. Which sequences are meaningful is determined by a set of complex specific rules. In other words, there are series of letters A, G, C, and T that correspond to DNA and while many other sequences do not resemble DNA. Trying to distinguish between strings of nitrogen bases that correspond to human DNA and those that don not is a simple example of a classification task that is at the same time not so easy for an untrained human eye.

Comparison of DNA and random sequences.

In Fig.fig:DNAcompare, we show a comparison of five strings of human DNA and five strings of 36 randomly generated letters A, G, C, and T. Without deeper knowledge it is hard to distinguish the two classes and even harder to find the set of empirical rules that quantify their distinction. We can let a neural network have a go and see if it performs any better than us studying these sequences by visual analysis.

Neural network classification of DNA sequences. The two lower panels show loss function and accuracy on the training (evaluation) data in green (orange) as a function of the training step respectively.

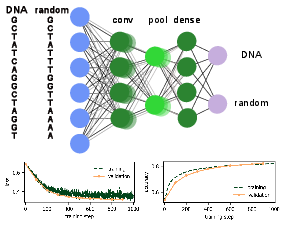
We have all ingredients to build a binary classifier that will be able to distinguish between DNA and non-DNA sequences. First, we download a freely available database of the human genome from [4]. Here, we downloaded a database of encoding genomes that contains [math]100 000[/math] sequences of human DNA (each is 36 letters long). Additionally, we generate [math]100 000[/math] random sequences of letters A, G, C, T. The learning task we are facing now is very similar to the MNIST classification, though in the present case, we only have two classes. Note, however, that we generated random sequences of bases and labeled them as random, even though we might have accidentally created sequences that do correspond to human DNA. This limits the quality of our data set and thus naturally also the final performance of the network. The model we choose here has a standard architecture and can serve as a guiding example for supervised learning with neural networks that will be useful in many other scenarios. In particular, we implement the following architecture:

Example (DNA classification)

• Import the data from [5]
• Define the model:
  • Input layer: The input layer has dimension [math]36\times 4[/math] ([math]36[/math] entries per DNA sequence, [math]4[/math] to encode each of 4 different bases A, G, C, T) Example:[[0,0,1,0], [0,0,1,0], [0,0,0,1]] = ACCT
  • Convolutional layer: Kernel size [math]k= 4[/math], stride [math]s= 1[/math] and number of filters [math]N=64[/math].
  • Pooling layer: max pooling over [math]n=2[/math] neurons, which reduces the output of the previous layer by a factor of 2.
  • Dense layer: 256 neurons with a ReLU activation function.
  • Output layer: 2 neurons (DNA and non-DNA output) with softmax activation function.
• Loss function: Cross-entropy between DNA and non-DNA.

A schematic of the network structure as well as the evolution of the loss and the accuracy measured over the training and validation sets with the number of training steps are shown in Fig.fig:DNA. Comparing the accuracies of the training and validation sets is a standard way to avoid overfitting: On the examples from the training set we can simply check the accuracy during training. When training and validation accuracy reach the same number, this indicates that we are not overfitting on the training set since the validation set is never used to adjust the weights and biases. A decreasing validation accuracy despite an increasing training accuracy, on the other hand, is a clear sign of overfitting. We see that this simple convolutional network is able to achieve around 80% accuracy. By downloading a larger training set, ensuring that only truly random sequences are labeled as such, and by optimizing the hyper-parameters of the network, it is likely that an even higher accuracy can be achieved. We also encourage you to test other architectures: one can try to add more layers (both convolutional and dense), adjust the size of the convolution kernel or stride, add dropout layers, and finally, test whether it is possible to reach higher accuracies without over-fitting on the training set.

Example: advanced MNIST

We can now revisit the MNIST example and approach the classification with the more advanced neural network structures of the previous section. In particular, we use the following architecture

Example (Advanced MNIST)

• Input layer: [math]28^2 = 784[/math] neurons.
• Convolutional layer 1: Kernel size [math]k= 5[/math], stride [math]s= 1[/math] and number of filters [math]N=32[/math] with a ReLU activation function.
• Pooling layer: max pooling over [math]n=2\times 2[/math] neurons.
• Convolutional layer 2: Kernel size [math]k= 5[/math], stride [math]s= 1[/math] and number of filters [math]N=64[/math] with a ReLU activation function.
• Pooling layer: max pooling over [math]n=2\times 2[/math] neurons.
• Dropout: dropout layer for regularization with a 50% dropout probability.
• Dense layer: 1000 neurons with a ReLU activation function.
• Output layer: 10 neurons with softmax activation function.

For the loss function, we again use cross-entropy between the output and the labels. Notice here the repeated structure of convolutional layers and pooling layers. This is a very common structure for deep convolutional networks. With this model, we achieve an accuracy on the MNIST test set of 98.8%, a massive improvement over the simple dense network.

Recurrent neural networks

Recurrent neural network architecture. The input [math]x_t[/math] is fed into the recurrent cell together with the (hidden) memory [math]h_{t-1}[/math] of the previous step to produce the new memory [math]h_t[/math] and the output [math]y_t[/math]. One can understand the recurrent structure via the “unwrapped” depiction of the structure on the right hand side of the figure. The red arrows indicate how gradients are propagated back in time for updating the network parameters.

We have seen in the previous section how the convolutional neural network allows to retain local information through the use of filters. While this context-sensitivity of the CNN is applicable in many situations, where geometric information is important, there are situations we have more than neighborhood relations, namely sequential order. An element is before or after an other, not simply next to it. A common situation, where the order of the input is important, is with time-series data. Examples are measurements of a distant star collected over years or the events recorded in a detector after a collision in a particle collider. The classification task in these examples could be the determination whether the star has an exoplanet, or whether a Higgs boson was observed, respectively. Another example without any temporal structure in the data is the prediction of a protein's functions from its primary amino-acid sequence.

A property that the above examples have in common is that the length of the input data is not necessarily always fixed for all samples. This emphasizes again another weakness of both the dense network and the CNN: The networks only work with fixed-size input and there is no good procedure to decrease or increase the input size. While we can in principle always cut our input to a desired size, of course, this finite window is not guaranteed to contain the relevant information.

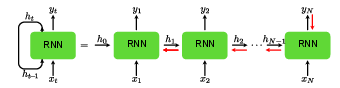
In this final section on supervised learning, we introduce one more neural network architecture that solves both problems discussed above: recurrent neural networks (RNNs). The key idea behind a recurrent neural network is that input is passed to the network one element after another---unlike for other neural networks, where an input 'vector' is given the network all at once---and to recognize context, the network keeps an internal state, or memory, that is fed back to the network together with the next input. Recurrent neural networks were developed in the context of natural language processing(NLP), the field of processing, translating and transforming spoken or written language input, where clearly, both context and order are crucial pieces of information. However, over the last couple of years, RNNs have found applications in many fields in the sciences. The special structure of a RNN is depicted in Fig.fig:RNN. At step [math]t[/math], the input [math]\bm{x}_t[/math] and the (hidden) internal state of the last step [math]\bm{h}_{t-1}[/math] are fed to the network to calculate [math]\bm{h}_t[/math]. The new hidden memory of the RNN is finally connected to the output layer [math]\bm{y}_t[/math]. As shown in Fig.fig:RNN, this is equivalent to having many copies of the input-output architecture, where the hidden layers of the copies are connected to each other. The RNN cell itself can have a very simple structure with a single activation function. Concretely, in each step of a simple RNN we update the hidden state as

[[math]] \begin{equation} \bm{h}_{t} = \tanh(W_{hh} \bm{h}_{t-1} + W_{xh} \bm{x}_{t-1} + \bm{b}_h), \label{eq:rnn first step} \end{equation} [[/math]]

where we used for the nonlinearity the hyperbolic tangent, a common choice, which is applied element-wise. Further, if the input data [math]\bm{x}_t[/math] has dimension [math]n[/math] and the hidden state [math]\bm{h}_t[/math] dimension [math]m[/math], the weight matrices [math]W_{hh}[/math] and [math]W_{ih}[/math] have dimensions [math]m\times m[/math] and [math]m\times n[/math], respectively. Finally, the output at step [math]t[/math] can be calculated using the hidden state [math]\bm{h}_t[/math],

[[math]] \begin{equation} \bm{y}_{t} = W_{ho} \bm{h}_t. \label{eq:rnn output} \end{equation} [[/math]]

A schematic of this implementation is depicted in Fig.fig:lstm(a). Note that in this simplest implementation, the output is only a linear operation on the hidden state. A straight forward extension---necessary in the case of a classification problem---is to add a non-linear element to the output as well, i.e.,

[[math]] \begin{equation} \bm{y}_{t} = \bm{g}(W_{ho}\bm{h}_t + \bm{b}_y) \end{equation} [[/math]]

with [math]\bm{g}(\bm{q})[/math] some activation function, such as a softmax. Note that while in principle an output can be calculated at every step, this is only done after the last input element in a classification task. An interesting property of RNNs is that the weight matrices and biases, the parameters we learn during training, are the same for each input element. This property is called parameter sharing and is in stark contrast to dense networks. In the latter architecture, each input element is connected through its own weight matrix. While it might seem that this property could be detrimental in terms of representability of the network, it can greatly help extracting sequential information: Similar to a filter in a CNN, the network does not need to learn the exact location of some specific sequence that carries the important information, it only learns to recognize this sequence somewhere in the data. Note that the way each input element is processed differently is instead implemented through the hidden memory. Parameter sharing is, however, also the root of a major problem when training a simple RNN. To see this, remember that during training, we update the network parameters using gradient descent. As in the previous sections, we can use backpropagation to achieve this optimization. Even though the unwrapped representation of the RNN in Fig.fig:RNN suggests a single hidden layer, the gradients for the backpropagation have to also propagate back through time. This is depicted in Fig.fig:RNN with the red arrows.

Looking at the backpropagation algorithm in Training, we see that to use data points from [math]N[/math] steps back, we need to multiply [math]N-1[/math] Jacobi matrices [math]D\bm{f}^{[t']}[/math] with [math]t-N \lt t' \leq t[/math]. Using Eq.\eqref{eq:rnn output}, we can write each Jacobi matrix as a product of the derivative of the activation function, [math]\partial_q \tanh(q)[/math], with the weight matrix. If either of these factors is much smaller (much larger) than [math]1[/math], the gradients decrease (grow) exponentially. This is known as the problem of vanishing gradients (exploding gradients) and makes learning long-term dependencies with simple RNNs practically impossible. Note that the problem of exploding gradients can be mitigated by clipping the gradients, in other words scaling them to a fixed size. Furthermore, we can use the ReLU activation function instead of a hyperbolic tangent, as the derivative of the ReLU for [math]q \gt 0[/math] is always 1. However, the problem of the shared weight matrices can not so easily be resolved. In order to learn long-time dependencies, we have to introduce a different architecture. In the following, we will discuss the long short-term memory (LSTM) network. This architecture and its variants are used in most applications of RNNs nowadays.

Long short-term memory

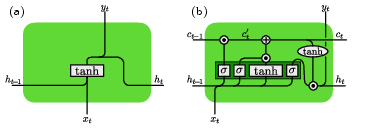
The key idea behind the LSTM is to introduce another state to the RNN, the so-called cell state, which is passed from cell to cell, similar to the hidden state. However, unlike the hidden state, no matrix multiplication takes place, but information is added or removed to the cell state through gates. The LSTM then commonly comprises four gates which correspond to three steps: the forget step, the input and update step, and finally the output step. We will in the following go through all of these steps individually.

Comparison of (a) a simple RNN and (b) a LSTM. The boxes denote neural networks with the respective activation function, while the circles denote element-wise operations. The dark green box indicates that the four individual neural networks can be implemented as one larger one.

Forget step

In this step, specific information of the cell state is forgotten. Specifically, we update the cell state as

[[math]] \begin{equation} \bm{c}'_t = \sigma(W_{hf} \bm{h}_{t-1} + W_{xf} \bm{x}_t + \bm{b}_f)\odot \bm{c}_{t-1}. \label{eq:forget} \end{equation} [[/math]]

where [math]\sigma[/math] is the sigmoid function (applied element-wise) and [math]\odot[/math] denotes element-wise multiplication. Note that this step multiplies each element of the gate state with a number [math]\in(0,1)[/math], in other words elements multiplied with a number close to [math]0[/math] forget their previous memory.

Input and update step

In the next step, we decide what and how much to add to the cell state. For this purpose, we first decide what to add to the state. We first define what we would like to add to the cell,

[[math]] \begin{equation} \bm{g}_t = \tanh(W_{hu}\bm{h}_{t-1} + W_{xu} \bm{x}_t + \bm{b}_u), \label{eq:gate gate} \end{equation} [[/math]]

which due to the hyperbolic tangent, [math]-1 \lt g^\alpha_t \lt 1[/math] for each element. However, we do not necessarily update each element of the cell state, but rather we introduce another gate, which determines whether to actually write to the cell,

[[math]] \begin{equation} \bm{i}_t = \sigma(W_{hi} \bm{h}_{t-1} + W_{xi} \bm{x}_t + \bm{b}_i), \label{eq:input} \end{equation} [[/math]]

again with [math]0 \lt i^\alpha_t \lt 1[/math]. Finally, we update the cell state

[[math]] \begin{equation} \bm{c}_t = \bm{c}'_t + \bm{i}_t \odot \bm{g}_t. \label{eq:update} \end{equation} [[/math]]

Output step

In the final step, we decide how much of the information stored in the cell state should be written to the new hidden state,

[[math]] \begin{equation} \bm{h}_t = \sigma(W_{ho} \bm{h}_{t-1} + W_{xo} \bm{x}_t + \bm{b}_o) \odot \tanh (\bm{c}_t). \label{eq:output step} \end{equation} [[/math]]

The full structure of the LSTM with the four gates and the element-wise operations is schematically shown in Fig.fig:lstm(b). Note that we can concatenate the input [math]\bm{x}_t[/math] and hidden memory [math]\bm{h}_{t-1}[/math] into a vector of size [math]n+m[/math] and write one large weight matrix [math]W[/math] of size [math]4m \times (m+n)[/math]. So far, we have only used the RNN in a supervised setting for classification purposes, where the input is a sequence and the output a single class at the end of the full sequence. A network that performs such a task is thus called a many-to-one RNN. We will see in the next section, that unlike the other network architectures encountered in this section, RNNs can straight-forwardly be used for unsupervised learning, usually as one-to-many RNNs.

General references

Neupert, Titus; Fischer, Mark H; Greplova, Eliska; Choo, Kenny; Denner, M. Michael (2022). "Introduction to Machine Learning for the Sciences". arXiv:2102.04883 [physics.comp-ph].