Stochastic Volatility
Stochastic volatility is another popular way to fit the implied volatility smile. It has the advantage of assuming volatility brings another source of randomness, and this randomness can be hedge if it is also a Brownian motion. Furthermore, calibration of stochastic volatility models does have some robustness to the market's daily changes. However, whereas local volatility models are generally calibrated to fit the implied volatility surface (i.e. to fit options of all maturities), stochastic volatility models have trouble fitting more than one maturity at a time. Consider the following stochastic volatility model,
where [math]W_t[/math] and [math]B_t[/math] are Brownian motions with correlation [math]\rho\in(-1,1)[/math] such that [math]\mathbb E[dW_tdB_t]=\rho dt[/math], [math]\sigma(x) \gt 0[/math] is the volatility function, and [math]X_t[/math] is the volatility process and is usually mean-reverting. An example of a mean-revering process is the square-root process,
The square-root process is used in the Heston model (along with [math]\sigma(x) =\sqrt{x}[/math]), and usually relies on what is known as the Feller condition ([math]\gamma^2\leq 2\bar X\kappa[/math]) so that [math]X_t[/math] never touches zero.
Hedging and Pricing
Assuming that [math]\alpha[/math] and [math]\beta[/math] are ‘well-behaved’ functions, we define the differential operator
the interpretation of [math]\mathcal L[/math] is the following: [math]\frac{\sigma^2(X_t)S_t^2}{2}\frac{\partial^2}{\partial s^2}+\mu S_t \frac{\partial}{\partial s}[/math] are the generator of [math]S_t[/math]; [math]\frac{\beta^2(X_t)}{2}\frac{\partial^2}{\partial x^2}+\alpha(X_t)\frac{\partial}{\partial x}[/math] are the generator of [math]X_t[/math]; [math]\rho\beta(X_t)\sigma(X_t)S_t\frac{\partial^2}{\partial x\partial s}[/math] is the cross-term; and the remaining are the separate stochastic terms. We use when applying bi-variate It\^o Lemma for the process in \eqref{eq:SVM} and \eqref{eq:dX}:\\ For any twice differentiable function [math]f(t,s,x)[/math], the It\^o differential is
The price [math]C(t,s,x)[/math] is the price of claim [math]\psi(s,x)[/math] paid at time [math]T[/math] given [math]S_t=s[/math] and [math]X_t=x[/math]. We hedge with a self-financing portfolio [math]V_t[/math] consisting of risky-asset, the risk-free bank account, and a 2nd derivative [math]C'[/math] that is settled at time [math]T' \gt T[/math]. This method for hedging stochastic volatility is called the Hull-White method.
The self-financing condition is
Now, taking a long position in [math]V_t[/math] and a short position in [math]C(t,S_t,X_t)[/math], we apply the bivariate It\^o lemma of \eqref{eq:2Dito} to get the dynamics of this new portfolio:
We now choose [math]a_t[/math] and [math]b_t[/math] so that the [math]dW_t[/math] and the [math]dB_t[/math] terms vanish, which means that
or
Plugging these solutions into the differential, the [math]\alpha(X_t)\frac{\partial}{\partial x}[/math] terms cancel, the [math]\mu S_t\frac{\partial}{\partial s}[/math] terms cancel, and by the same arbitrage argument as Black-Scholes, it follows that [math]V_t-C(t,S_t,X_t)[/math] must grow at the risk-free rate:
Inserting [math]a_t[/math] and [math]b_t[/math] from equations \eqref{eq:a_t} and \eqref{eq:b_t}, and after some rearranging of terms (and dropping the [math]dt[/math]'s), we get
and dividing both sides by [math]\frac{\partial}{\partial x}C(t,S_t,X_t)[/math], we get
The left-hand side of this equation does not depend on specifics of [math]C'[/math] (e.g. maturity and strikes), and the right-hand side does not depend on specifics of [math]C[/math]. Therefore, there is a function [math]R(t,s,x)[/math] that does not depend on parameters such as strike price and maturity, and it equates the two sides of the expression. We let [math]R[/math] take the form
where
where [math]g[/math] is an arbitrary function. Hence, we arrive at the PDE for the price [math]C(t,s,x)[/math] of a European Derivative with stochastic vol:
Given the stochastic volatility model of equations \eqref{eq:SVM} and \eqref{eq:dX}, the price of a European claim with payoff [math]\psi(S_T)[/math] satisfies
The PDE in \eqref{eq:SVpde} can be solved with Feynman-Kac,
which yields a description of an EMM, [math]\mathbb Q[/math], under which the stochastic volatility model is
where [math]W_t^Q[/math] and [math]B_t^Q[/math] are [math]\mathbb Q[/math]-Brownian motions with the same correlation [math]\rho[/math] as before. The interpretation of [math]\Lambda(t,s,x)[/math] is that it is the market price of volatility risk. One can think of a market as complete when there are as many non-redundant assets as there are sources of randomness. In this sense we have ‘completed’ this market with stochastic volatility by including the derivative [math]C'[/math] among the traded assets. This has allowed us to replicate the European claim and obtain a unique no-arbitrage price that must be the solution to \eqref{eq:SVpde}.\\
Example
where [math]\lambda X_t[/math] is the assumed form of the volatility price of risk. This model can be re-written,
where [math]\tilde\kappa =\kappa-\lambda[/math] and [math]\tilde{\bar X} = \frac{\kappa\bar X}{\kappa-\lambda}[/math]. It is important to have the Feller condition
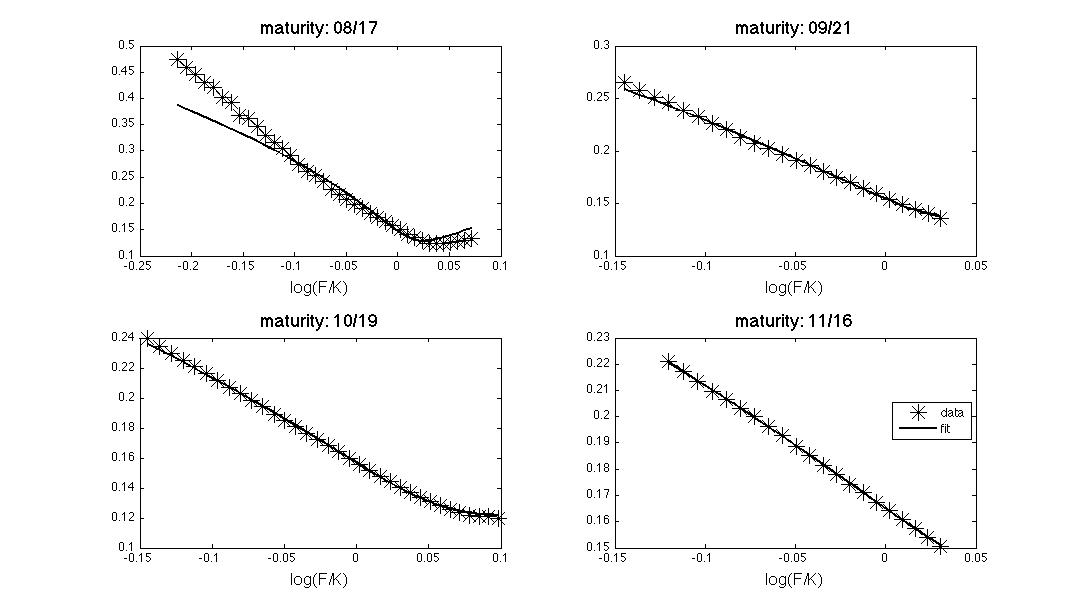
otherwise the PDE requires boundaries for the event [math]X_t = 0[/math]. The process [math]X_t[/math] is degenerate, but it is well-known that the Feller condition is the critical assumption for the application of Feynman-Kac. The fit of the Heston model to the implied volatility of market data is shown in Figure.
Monte Carlo Methods
A slow but often reliable method for pricing derivatives is to approximate the risk-neutral expectation with independent samples. Essentially, sample paths of Brownian motion are obtained using a pseudo-random number generated, the realized derivative payoff is computed for each sample, and then the average of these sample payoffs is an approximation of the true average. For example, let [math]\ell=1,2,\dots,N[/math], let [math]S_T^{(\ell)}[/math] be the index for an independent sample from [math]S_T[/math]'s probability distribution. If [math]\mathbb E^QS_T^2 \lt \infty[/math], then by the law of large numbers we have
For stochastic differential equations, the typical method is to generate samples that are approximately from the same distribution as the price. The basic idea is to use an Euler-Maruyama scheme,
for some small [math]\Delta t \gt 0[/math], with
This scheme is basically the discrete backward Riemann sum from which the It\^o integral was derived (see Chapter). In the limit, the Monte-Carlo average will be with little-o of the true expectation,
The scheme in \eqref{eq:EMscheme} can easily be adapted for a local volatility model, and can also be adapted to stochastic volatility models, but the latter will also need a scheme for generating the volatility process [math]X_t[/math]. Example
with correlation [math]\rho[/math] between [math]W_t^Q[/math] and [math]B_t^Q[/math]. The Euler-Maruyama scheme is
where [math]B_{t+\Delta t}^{(\ell)}-B_t^{(\ell)}[/math] and [math]W_{t+\Delta t}^{(\ell)}-W_t^{(\ell)}[/math] are increments of independent Brownian motions.
Sometimes, there more clever methods of sampling need to be employed. For instance, the Heston model: Example
will allow the volatility process to become negative. An alternative is to consider the Stratonovich-type differential,[Notes 1]
and then use an implicit Euler-Maruyama scheme
which can be solved for [math]\sqrt{\tilde X_{t+\Delta t}}[/math] using the quadratic equation. Notice that a condition for the discriminant to be real is the Feller condition that [math]\gamma^2\leq 2\kappa\bar X[/math].
In general, Monte Carlo methods are good because they can be used to price pretty much any type of derivative instrument, so long as the EMM is given. For instance, it is very easy to price an Asian option with Monte Carlo. Another advantages of Monte Carlo is that there is no need for an explicit solution to any kind of PDE; the methodology for pricing is to simply simulate and average. However, as mentioned above, this can be very slow, and so there is a need (particularly among practitioners) for faster ways to compute prices. Another important topic to remark on is importance sampling, which refers to simulations generated under an equivalent measure for which certain rare events are more common. For instance, suppose one wants to use Monte Carlo to price a call option with extreme strike. It will be a waste of time to generate samples from the EMM's model if the overwhelming majority of them will finish out of the money. Instead, one can sample from another model that has more volatility, so that more samples finish in the money. Then, assign importance weights based on ratio of densities and take the average. See [1] for further reading on Monte Carlo methods in finance.
Fourier Transform Methods
The most acclaimed way to compute a European option price is with the so-called Fourier transform methods. In particular, the class of affine models in [2] have tractable pricing formulae because they have explicit expressions for their Fourier transforms. The essential ingredient to these methods is the characteristic function,
where [math]\mathbb E^Q[/math] now denotes expectation under an EMM. The function [math]\phi_T(u)[/math] is the Fourier transform of the [math]\log S_T[/math]'s distribution function,
where [math]f(s)[/math] is the density function for [math]\log S_T[/math]. The inverse Fourier transform is [math]f(s) = \tfrac{1}{2\pi}\int_{-\infty}^\infty e^{-iu s}\phi_T(u)du[/math], which leads to the cumulative distribution function
The crucial piece of information is the characteristic function, as any European claim can be priced provided there is also a Fourier transform for the payoff function. Let [math]p_T[/math] denote the density function on the risk-neutral distribution of [math]\log(S_T)[/math] and let [math]\widehat\psi[/math] denote the Fourier transform of the payoff function. It is shown in [3] that
where the constant [math]z\in\mathbb R[/math] in the limit of integration is the appropriate strip of regularity for non-smooth payoff functions (see Table). This usage of characteristic functions is far reaching, as the class of L\'evy jump models are defined in terms of their characteristic function, or equivalently with the L\'evy-Khintchine representation (for more on financial models with jumps see [4]).
| asset | [math]\psi(s)[/math] | [math]\widehat\psi(u)[/math] | regularity strip |
|---|---|---|---|
| call | [math](e^s-K)^+[/math] | [math]-\frac{K^{iu+1}}{u^2-iu}[/math] | [math]z \gt 1[/math] |
| put | [math](K-e^s)^+[/math] | [math]-\frac{K^{iu+1}}{u^2-iu}[/math] | [math]z \lt 0[/math] |
| covered call; cash secured put | [math]\min(e^s,K)[/math] | [math]\frac{K^{iu+1}}{u^2-iu}[/math] | [math]0 \lt z \lt 1[/math] |
| cash or nothing call | [math]\indicator{e^s\geq K}[/math] | [math]-\frac{K^{iu}}{iu}[/math] | [math]z \gt 0[/math] |
| cash or nothing put | [math]\indicator{e^s\leq K}[/math] | [math]\frac{K^{iu}}{iu}[/math] | [math]z \lt 0[/math] |
| asset or nothing call | [math]e^s\indicator{e^s\geq K}[/math] | [math]-\frac{K^{iu+1}}{iu+1}[/math] | [math]z \gt 1[/math] |
| asset or nothing put | [math]e^s\indicator{e^s\leq K}[/math] | [math]\frac{K^{iu+1}}{iu+1}[/math] | [math]z \lt 0[/math] |
| Arrow-Debreu | [math]\delta(s-\log(K))[/math] | [math]K^{iu}[/math] | [math]z\in\mathbb R[/math] |
Call-Option Pricing
An important tool is the formula of Gil-Pelaez:
The distribution function [math]F(s)[/math] is given by
First let's prove an identity,
Notice that \eqref{eq:gilPelaezInversion} can be further simplified to have
which is used in pricing a European call option, as the risk-neutral probability of finishing in the money is
where [math]\mathbb Q[/math] denotes probability under the EMM. The ‘delta’ of the option is
but we can define a change of measure,
where [math]s_T=\log S_T[/math]. Then,
and therefore we have the formula
Assuming no dividends, the value of a European call option with strike [math]K[/math], at time [math]t=0[/math], is
The pricing formula of equation \eqref{eq:fourierPrice} is (in one way or another) interpreted as an inverse Fourier transform. Indeed, the method of Carr and Madan [5] shows that \eqref{eq:fourierPrice} can be well-approximated as a fast Fourier transform, which has the advantage of taking less time to compute than numerical integration, but it is also less accurate. Equation \eqref{eq:fourierPrice} has become an important piece of machinery in quantitative finance because it is (or is considered to be) an explicit solution to the pricing equation. In general the pricing formula of \eqref{eq:fourierPrice} applies to just about any situation where the characteristic function is given.
Heston Explicit Formula
Finally, an important application of the Fourier pricing formula in \eqref{eq:fourierPrice} is to the Heston model. The call option formula for the Heston model from equations \eqref{eq:dSheston} and \eqref{eq:dXheston} has a well-known inverse Fourier transform (see [6]) with
which is applied for the Heston model the volatility price of risk absorbed into parameters [math]\kappa[/math] and [math]\bar X[/math]. Warning: Use a well-made Gaussian quadrature function for numerical computation of the integrals for the Heston price; do not attempt to integrate with an evenly-spaced grid.
The Merton Jump Diffusion
Short time-to-maturity options are known to be well fit by the class of models where log-asset prices are L\'evy processes. For instance, the Merton jump diffusion,
where [math]\sigma \gt 0[/math], [math]N_t[/math] is an independent Poisson process with parameter [math]\lambda\in(0,\infty)[/math], [math]J_t[/math] is a sequence of i.i.d. normal random variables with [math]J_{t_i}\sim N(\mu_J,\sigma_J^2)[/math] when [math]N_{t_i}-N_{t_i-} = 1[/math], and [math]\nu = \lambda\left(e^{\mu_J+\frac{\sigma_J^2}{2}}-1\right)[/math] is a compensator to ensure the process is a discounted martingale. The log-price is
For [math]S_0=1[/math], the characteristic function is derived as follows,
This is an example of a characteristic function that is known explicitly. In addition, it is particular example of the general L\'evy-Khintchine representation,
where [math]\eta[/math] is the intensity measure, satisfying [math]\int_{\mathbb R\setminus\{0\}}1\wedge x^2\eta(dx) \lt \infty[/math]. For more on the L\'evy-Khintchine representation, see [4].
General references
Papanicolaou, Andrew (2015). "Introduction to Stochastic Differential Equations (SDEs) for Finance". arXiv:1504.05309 [q-fin.MF].
References
- Glasserman, P. (2004).Monte Carlo Methods in Financial Engineering.Springer.
- Duffie, D., Pan, J., and Singleton, K. (2000).Transform analysis and asset pricing for affine jump-diffusions.Econometrica, 68:1343--1376.
- Lewis, A.L. (2000).Option Valuation under Stochastic Volatility with Mathematica Code.Finance Press.
- 4.0 4.1 Cont., R. and Tankov, P. (2003).Financial modelling with Jump Processes.
- Carr, P., Madan, D., and Smith, R. (1999).Option valuation using the fast Fourier transform.Journal of Computational Finance, 2:61--73.
- Gatheral, J. (2006).The Volatility Surface: A Practitioner's Guide.Wiley.
Notes
- This refers to the Stratonovich-type integral that is the limit of forward Riemann sums, [math]\int f_s\circ dB_s = \lim_N\sum_{n=1}^Nf_{t_n}(B_{t_n}-B_{t_{n-1}})[/math]. For the square-root process, the It\^o lemma on [math]\sqrt{X_t}[/math] is used to show that [math]\gamma\int \sqrt{X_s}dB_s = \gamma\lim_n\sum_n\sqrt{X_{t_{n-1}}}\Delta B_{t_{n-1}} = -\gamma\lim_n\sum_n\left(\sqrt{X_{t_n}}-\sqrt{X_{t_{n-1}}}\right)(B_{t_n}-B_{t_{n-1}}) +\gamma\lim_n\sum_n\sqrt{X_{t_n}}(B_{t_n}-B_{t_{n-1}})=-\frac{\gamma^2}{2}\int ds+\gamma\int \sqrt{X_s}\circ dB_s[/math].