Apr 30'23
Exercise
A company sells two types of life insurance policies (P and Q) and one type of health insurance policy. A survey of potential customers revealed the following:
- No survey participant wanted to purchase both life policies.
- Twice as many survey participants wanted to purchase life policy P as life policy Q.
- 45% of survey participants wanted to purchase the health policy.
- 18% of survey participants wanted to purchase only the health policy.
- The event that a survey participant wanted to purchase the health policy was independent of the event that a survey participant wanted to purchase a life policy.
Calculate the probability that a randomly selected survey participant wanted to purchase exactly one policy.
- 0.51
- 0.60
- 0.69
- 0.73
- 0.78
Apr 30'23
Solution: A
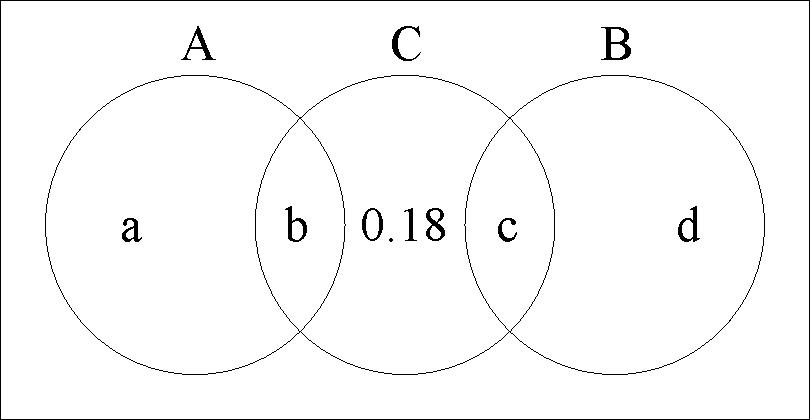
Let A = event that person wants life policy P
B = event that person wants life policy Q
C = event that person wants the health policy
and let a, b, c, d be the probabilities of the regions as shown.
- is reflected by no intersection of A and B
- is reflected by the 0.18 in the diagram
- implies a + b = 2(c + d)
- implies b + c + 0.18 = 0.45 or b + c = 0.27
- implies P([A or B] and C) = P(A or B)P(C) or b + c = (a + b + c + d)(0.45)
So 0.27 = (a + d + 0.27)(0.45) and then a + d = 0.33. The desired probability is a + 0.18 + d = 0.33 + 0.18 = 0.51.