May 07'23
Exercise
Two insurers provide bids on an insurance policy to a large company. The bids must be between 2000 and 2200. The company decides to accept the lower bid if the two bids differ by 20 or more. Otherwise, the company will consider the two bids further. Assume that the two bids are independent and are both uniformly distributed on the interval from 2000 to 2200.
Calculate the probability that the company considers the two bids further.
- 0.10
- 0.19
- 0.20
- 0.41
- 0.60
May 07'23
Solution: B
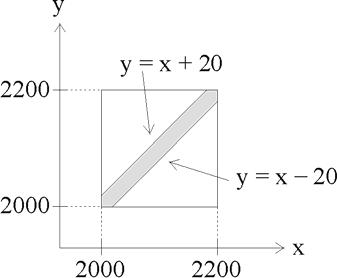
Let X and Y denote the two bids. Then the graph below illustrates the region over which X and Y differ by less than 20:
Based on the graph and the uniform distribution:
[[math]]
\begin{align*}
\operatorname{P}[ |X-Y| \lt 20] &= \frac{\textrm{Shaded Region Area}}{(2200-2000)^2} = \frac{200^2 - 2\frac{1}{2}(180)^2}{200^2} \\
&= 1-\frac{180^2}{200^2} = 1-(0.9)^2 = 0.19.
\end{align*}
[[/math]]