The present value random variable for an insurance policy on [math](x)[/math] is expressed as:

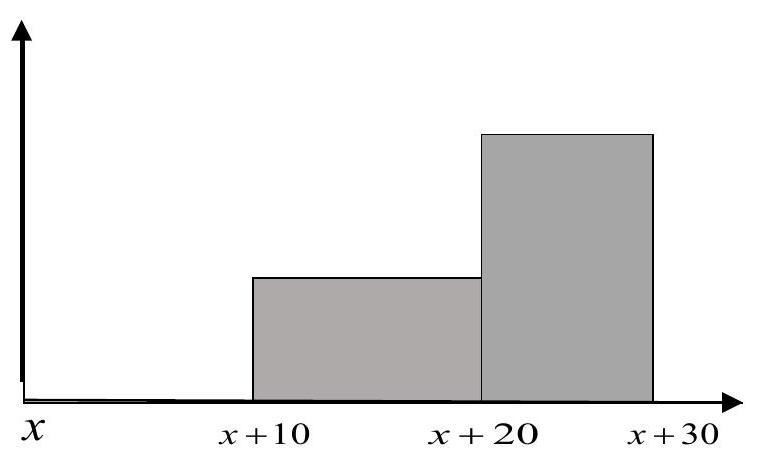
[[math]] Z= \begin{cases}0, & \text { if } T_{x} \leq 10 \\ v^{T_{x}}, & \text { if } 10 \lt T_{x} \leq 20 \\ 2 v^{T_{x}}, & \text { if } 20 \lt T_{x} \leq 30 \\ 0, & \text { thereafter }\end{cases} [[/math]]

Determine which of the following is a correct expression for [math]E[Z][/math].

• [math]{ }_{10 \mid} \bar{A}_{x}+{ }_{20} \bar{A}_{x}-{ }_{30 \mid} \bar{A}_{x}[/math]
• [math]\bar{A}_{x}+{ }_{20} E_{x} \bar{A}_{x+20}-2{ }_{30} E_{x} \bar{A}_{x+30}[/math]
• [math]{ }_{10} E_{x} \bar{A}_{x}+{ }_{20} E_{x} \bar{A}_{x+20}-2{ }_{30} E_{x} \bar{A}_{x+30}[/math]
• [math]{ }_{10} E_{x} \bar{A}_{x+10}+{ }_{20} E_{x} \bar{A}_{x+20}-2{ }_{30} E_{x} \bar{A}_{x+30}[/math]
• [math]{ }_{10} E_{x}\left[\bar{A}_{x+10}+{ }_{10} E_{x+10} \bar{A}_{x+20}-{ }_{10} E_{x+20} \bar{A}_{x+30}\right][/math]

Copyright 2024. The Society of Actuaries, Schaumburg, Illinois. Reproduced with permission.

Answer: D

Drawing the benefit payment pattern:

[math]E[Z]={ }_{10} E_{x} \times \bar{A}_{x+10}+{ }_{20} E_{x} \times \bar{A}_{x+20}-2{ }_{30} E_{x} \times \bar{A}_{x+30}[/math]

Copyright 2024. The Society of Actuaries, Schaumburg, Illinois. Reproduced with permission.