May 05'23
Exercise
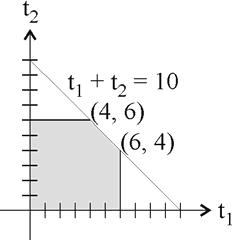
Let [math]T_1[/math] be the time between a car accident and reporting a claim to the insurance company. Let [math]T_2[/math] be the time between the report of the claim and payment of the claim. The joint density function of [math]T_1[/math] and [math]T_2[/math], [math]f(t_1,t_2)[/math], is constant over the region
[[math]]
0 \lt t_1 \lt 6, \,\, 0 \lt t_2 \lt 6, \,\, t_1 + t_2 \lt 10
[[/math]]
and zero otherwise.
Calculate [math]\operatorname{E}(T_1 + T_2)[/math], the expected time between a car accident and payment of the claim.
- 4.9
- 5.0
- 5.7
- 6.0
- 6.7
May 05'23
Solution: C
Let [math]f(t_1 , t_2)[/math] denote the joint density function of [math]T_1[/math] and [math]T_2[/math]. The domain of [math]f[/math] is pictured below:
Now the area of this domain is given by
[[math]]
A = 6^2 - \frac{1}{2}(6-4)^2 = 36-2 = 34.
[[/math]]
Consequently,
[[math]]
f(t_1,t_2) = \begin{cases}
\frac{1}{34}, \quad 0 \lt t_1 \lt 6, 0 \lt t_2 \lt 6, t_1 + t_2 \lt 10 \\
0, \, \textrm{elsewhere}
\end{cases}
[[/math]]
and
[[math]]
\begin{align*}
\operatorname{E}[T_1 + T_2 ] &= \operatorname{E}[T_1 ] + \operatorname{E}[T_2 ] = 2 \operatorname{E}[T_1 ] \quad \textrm{(due to symmetry)} \\
&= 2 \left \{ \int_0^4 t_1 \int_0^6 \frac{1}{34} dt_2 dt_1 + \int_4^6 t_1 \int_0^{10-t_1} \frac{1}{34} dt_2 dt_1\right \} \\
&= 2 \left \{ \int_0^4 t_1 \left [ \frac{t_2}{34} \Big |_0^6 \right ] dt_1 + \int_4^6 t_1 \left [ \frac{t_2}{34} \Big |_0^{10-t_1}\right ] dt_1 \right \} \\
&= 2 \left \{ \int_0^4 \frac{3t_1}{17} dt_1 + \int_4^6 \frac{1}{34} (10t_1 -t_1^2) dt_1 \right \}\\
&= 2 \left \{ \frac{3t_1^2}{34} \Big |_0^4 + \frac{1}{34}(5t_1^2 - \frac{1}{3}t_1^3) \Big |_4^6 \right \}\\
&= 2 \left \{ \frac{24}{17} + \frac{1}{34} \left [ 180-72-80 + \frac{64}{3}\right ]\right \} \\
&= 5.7
\end{align*}
[[/math]]