An auto insurance policy will pay for damage to both the policyholder’s car and the other driver’s car in the event that the policyholder is responsible for an accident. The size of the payment for damage to the policyholder’s car, [math]X[/math], has a marginal density function of 1 for [math] 0 \lt x \lt 1 [/math]. Given [math]X=x[/math], the size of the payment for damage to the other driver’s car, [math]Y[/math], has conditional density of 1 for [math]x \lt y \lt x + 1 [/math].

Given that the policyholder is responsible for an accident, calculate the probability that the payment for damage to the other driver’s car will be greater than 0.5.

• 3/8
• 1/2
• 3/4
• 7/8
• 15/16

Copyright 2023. The Society of Actuaries, Schaumburg, Illinois. Reproduced with permission.

Solution: D

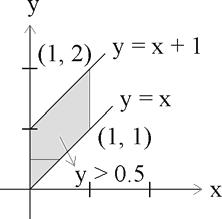
The diagram below illustrates the domain of the joint density [math]f ( x, y )[/math] of [math]X[/math] and [math]Y[/math] .

We are told that the marginal density function of [math]X[/math] is [math]f_X( x ) = 1 , 0 \lt x \lt 1 [/math] while [math]f_{y|x} ( y | x) = 1, \, x \lt y \lt x + 1. [/math] It follows that

[[math]] f(x,y) = f_X(x) f_{y | x}(y | x) = \begin{cases} 1, \, 0 \lt x \lt 1, \, x \lt y \lt x+ 1 \\ 0, \, \textrm{otherwise} \end{cases} [[/math]]

Therefore

[[math]] \begin{align*} \operatorname{P}[ Y \gt 0.5 ] = 1- \operatorname{P}[Y \leq 0.5] &= 1- \int_0^{1/2} \int_x^{1/2} dydx \\ &= 1- \int_0^{1/2} y \Big |_x^{1/2} dx \\ &= 1- \int_0^{1/2} (\frac{1}{2} - x) dx \\ &= 1- [\frac{1}{2}x - \frac{1}{2}x^2] \Big |_0^{1/2} \\ &= 1- \frac{1}{4} + \frac{1}{8} = \frac{7}{8}. \end{align*} [[/math]]

Note since the density is constant over the shaded parallelogram in the figure the solution is also obtained as the ratio of the area of the portion of the parallelogram above y equals 0.5 to the entire shaded area.

Copyright 2023. The Society of Actuaries, Schaumburg, Illinois. Reproduced with permission.