BBot
Jun 01'24
Exercise
[math]
\newcommand{\smallfrac}[2]{\frac{#1}{#2}}
\newcommand{\medfrac}[2]{\frac{#1}{#2}}
\newcommand{\textfrac}[2]{\frac{#1}{#2}}
\newcommand{\tr}{\operatorname{tr}}
\newcommand{\e}{\operatorname{e}}
\newcommand{\B}{\operatorname{B}}
\newcommand{\Bbar}{\overline{\operatorname{B}}}
\newcommand{\pr}{\operatorname{pr}}
\newcommand{\dd}{\operatorname{d}\hspace{-1pt}}
\newcommand{\E}{\operatorname{E}}
\newcommand{\V}{\operatorname{V}}
\newcommand{\Cov}{\operatorname{Cov}}
\newcommand{\Bigsum}[2]{\mathop{\textstyle\sum}_{#1}^{#2}}
\newcommand{\ran}{\operatorname{ran}}
\newcommand{\card}{\#}
\renewcommand{\P}{\operatorname{P}}
\renewcommand{\L}{\operatorname{L}}
\newcommand{\mathds}{\mathbb}[/math]
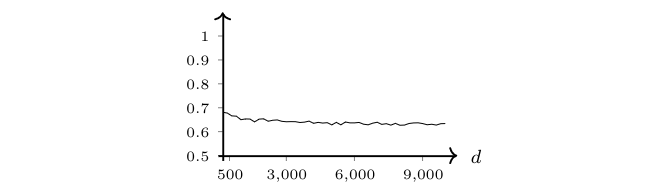
Replicate the results of Figure. More precisely, run the code from Problem for different dimensions [math]d[/math] and different distance functions [math]\Delta=\Delta(d)[/math], e.g., [math]\Delta\equiv c \gt 0[/math], [math]\Delta=2\sqrt{d}[/math], [math]\Delta=d^{0.3}[/math] or [math]\Delta=d^{1/4}[/math]. Plot the rate of correctly classified data points as a function of the dimension. Simulate also the case [math]\Delta=2d^{0.2}[/math] and confirm that this leads to a low correct classification rate which decreases for large dimensions.