May 05'23
Exercise
A device contains two components. The device fails if either component fails. The joint density function of the lifetimes of the components, measured in hours, is [math]f(s,t)[/math], where [math]0 \lt s \lt 1[/math] and [math]0 \lt t \lt 1 [/math].
Determine which of the following represents the probability that the device fails during the first half hour of operation.
- [math]\int_{0}^{0.5}\int_{0}^{0.5}f(s,t)\,ds\,dt[/math]
- [math]\int_0^1\int_0^{0.5}f(s,t)\,ds\,dt[/math]
- [math]\int_{0.5}^1\int_{0.5}^1f(s,t)\,ds\,dt[/math]
- [math]\int_{0}^{0.5}\int_{0}^1f(s,t)\,ds\,dt + \int_{0}^1\int_{0}^{0.5}f(s,t)\,ds\,dt[/math]
- [math]\int_{0}^{0.5}\int_{0.5}^1f(s,t)\,ds\,dt + \int_{0}^1\int_0^{0.5}f(s,t)\,ds\,dt[/math]
May 05'23
Solution: E
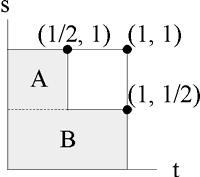
The domain of s and t is pictured below.
Note that the shaded region is the portion of the domain of s and t over which the device fails sometime during the first half hour. Therefore,
[[math]]
\operatorname{P}\left[ (S \leq \frac{1}{2}) \cup \left( T \leq \frac{1}{2}\right)\right] = \int_{0}^{0.5}\int_{0.5}^1f(s,t)\,ds\,dt + \int_{0}^1\int_0^{0.5}f(s,t)\,ds\,dt
[[/math]]
(where the first integral covers A and the second integral covers B).