Alternating Series

[math] \newcommand{\ex}[1]{\item } \newcommand{\sx}{\item} \newcommand{\x}{\sx} \newcommand{\sxlab}[1]{} \newcommand{\xlab}{\sxlab} \newcommand{\prov}[1] {\quad #1} \newcommand{\provx}[1] {\quad \mbox{#1}} \newcommand{\intext}[1]{\quad \mbox{#1} \quad} \newcommand{\R}{\mathrm{\bf R}} \newcommand{\Q}{\mathrm{\bf Q}} \newcommand{\Z}{\mathrm{\bf Z}} \newcommand{\C}{\mathrm{\bf C}} \newcommand{\dt}{\textbf} \newcommand{\goesto}{\rightarrow} \newcommand{\ddxof}[1]{\frac{d #1}{d x}} \newcommand{\ddx}{\frac{d}{dx}} \newcommand{\ddt}{\frac{d}{dt}} \newcommand{\dydx}{\ddxof y} \newcommand{\nxder}[3]{\frac{d^{#1}{#2}}{d{#3}^{#1}}} \newcommand{\deriv}[2]{\frac{d^{#1}{#2}}{dx^{#1}}} \newcommand{\dist}{\mathrm{distance}} \newcommand{\arccot}{\mathrm{arccot\:}} \newcommand{\arccsc}{\mathrm{arccsc\:}} \newcommand{\arcsec}{\mathrm{arcsec\:}} \newcommand{\arctanh}{\mathrm{arctanh\:}} \newcommand{\arcsinh}{\mathrm{arcsinh\:}} \newcommand{\arccosh}{\mathrm{arccosh\:}} \newcommand{\sech}{\mathrm{sech\:}} \newcommand{\csch}{\mathrm{csch\:}} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\mathds}{\mathbb} [/math]

Special among infinite series which contain both positive and negative terms are those whose terms alternate in sign. More precisely, we define the series [math]\sum_{i=m}^\infty a_i[/math] to be \textbf{alternating} if [math]a_{i}a_{i+1} \lt 0[/math] for every integer [math]i \geq m[/math]. It follows from this definition that an alternating series is one which can be written in one of the two forms

[[math]] \sum_{i=1}^\infty (-1)^{i}b_{i}\;\;\; \mbox{or} \;\;\; \sum_{i=m}^\infty (-1)^{i+1}b_{i}, [[/math]]

where [math]b_i \gt 0[/math] for every integer [math]i \geq m[/math]. An example is the alternating harmonic series

[[math]] \sum_{i=1}^\infty (-1)^{i+1} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \cdots . [[/math]]

An alternating series converges under surprisingly weak conditions. The next theorem gives two simple hypotheses whose conjunction is sufficient to imply convergence.

Theorem

The alternuting series [math]\sum_{i=m}^\infty a_i[/math] concerges if:

• [math]|a_{n + 1}| \leq |a_n|, \;\;\; \mathrm{for every integer} n \geq m, \;\mathrm{and}[/math]
• [math]\lim_{n \rightarrow \infty} a_n = 0 \;\mathrm{(or, equivalently,} \; \lim_{n \rightarrow \infty} |a_n| = 0).[/math]

Show Proof

We shall assume for convenience and with no loss of generality that [math]m = 0[/math] and that [math]a_i = (-1)^{i} b_i[/math], with [math]b_i \gt 0[/math] for every integer [math]i \geq 0[/math]. The series is therefore [math]\sum_{i=0}^\infty (-1)^{i} b_i[/math], and the hypotheses (i) and (ii) become

• [math]b_{n + 1} \leq b_n, \;\;\; \mbox{for every integer $n \geq 0$, and}[/math]
• [math]\lim_{n \rightarrow \infty} b_n = 0.[/math]

The proof is completed by showing the convergence of the sequence [math]\{s_n \}[/math] of partial sums, which is defined recursively by the equations

[[math]] \begin{eqnarray*} s_0 &=& (-1)^0 b_0= b_0,\\ s_n &=& s_{n-1} + ( - 1 )^n b_n, \;\;\; n = 1, 2, 3, .... \end{eqnarray*} [[/math]]

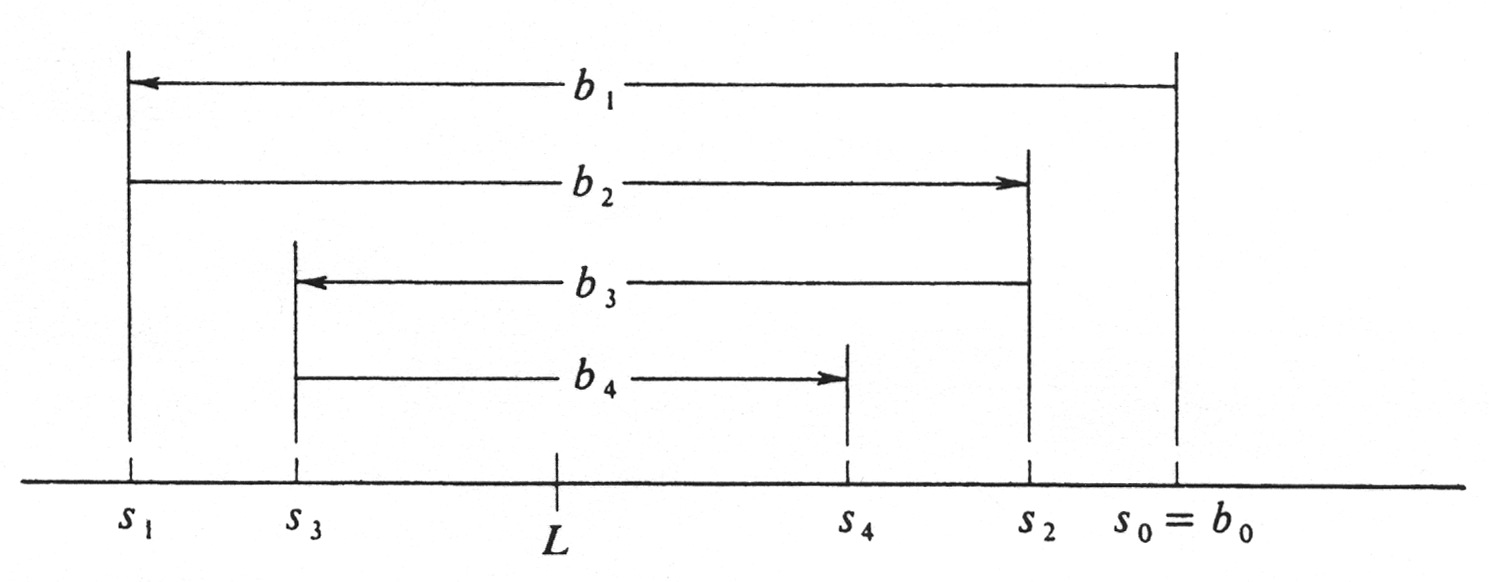
The best proof that [math]\lim_{n \rightarrow \infty} s_n[/math], exists is obtained by an illustration. In Figure 5 we first plot the point [math]s_0 = b_0[/math] and then the point [math]s_1 = s_0 - b_1[/math]. Next we plot [math]s_2 = s_1 + b_2[/math] and observe that, since [math]b_2 \leq b_1[/math], we have [math]s_2 \leq s_0[/math]. After that comes [math]s_3 = s_2 - b_3[/math] and, since [math]b_3 \leq b_2[/math] it follows that [math]s_1 \leq s_3[/math]. Continuing in this way, we see that the odd-numbered points of the sequence [math]\{s_n\}[/math] form an increasing subsequence:

File:Guide c5467 scanfig9 5.png

[[math]] \begin{equation} s_1 \leq s_3 \leq s_5 \leq \cdots \leq s_{2n-1} \leq \cdots, \label{eq9.4.1} \end{equation} [[/math]]

and the even-numbered points form a decreasing subsequence:

[[math]] s_0 \geq s_2 \geq s_4 \geq \cdots \geq s_{2n} \geq \cdots. [[/math]]

Furthermore, every odd-numbered partial sum is less than or equal to every even-numbered one. Thus the increasing sequence (1) is bounded above by any one of the numbers [math]s_{2n}[/math], and it therefore converges [see (1.4), page 479]. That is, there exists a real number [math]L[/math] such that

[[math]] \lim_{n \rightarrow \infty} s_{2n - 1} = L. [[/math]]

For every integer [math]n \geq 1[/math], we have

[[math]] s_{2n} = s_{2n - 1} + b_{2n}, [[/math]]

and, since it follows from (ii') that [math]\lim_{n \rightarrow \infty} b_{2n} = 0[/math], we conclude that

[[math]] \begin{eqnarray*} \lim_{n \rightarrow \infty} s_{2n} &=& \lim_{n \rightarrow \infty} s_{2n - 1} + \lim_{n \rightarrow \infty} s_{2n} \\ &=& L - 0 = L. \end{eqnarray*} [[/math]]

We have shown that both the odd-numbered subsequences [math]\{s_{2n-1} \}[/math] and the even-numbered subsequence [math]\{ s_{2n} \}[/math] converge to the same limit [math]L[/math]. This implies that [math]\lim_{n \rightarrow \infty} s_n = L[/math]. For, given an arbitrary real number [math] \epsilon \gt 0[/math], we have proved that there exist integers [math]N_1[/math], and [math]N_2[/math], such that

[[math]] \begin{eqnarray*} |s_{2n-1} - L| & \lt & \epsilon, \;\;\;\mbox{whenever}\; 2n - 1 \gt N_1, \\ |s_{2n} -L| & \lt & \epsilon, \;\;\;\mbox{whenever}\; 2n \gt N_2. \end{eqnarray*} [[/math]]

Hence, if [math]n[/math] is any integer (odd or even) which is greater than both [math]N_1[/math] and [math]N_2[/math], then [math]|s_n - L| \lt \epsilon[/math]. Thus

[[math]] L = \lim_{n \rightarrow \infty} s_n = \sum_{i=0}^\infty (-1)^{i} b_i, [[/math]]

and the proof is complete.

■

As an application of Theorem (4.1) consider the alternating harmonic series

[[math]] \sum_{ i=1}^\infty (-1)^{i + 1} \frac{1}{i} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots . [[/math]]

The hypotheses of the theorem are obviously satisfied:

• [math]\frac{1}{n + 1} \leq \frac{1}{n}, \;\;\; \mbox{for every integer $n \geq 1$, and}[/math]
• [math]\lim_{n \rightarrow \infty} (-1)^{n+1} \frac{1}{n} = \lim_{n \rightarrow \infty} \frac{1}{n} = 0.[/math]

Hence it follows that the alternating harmonic series is convergent. It is interesting to compare this series with the ordinary harmonic series [math] \sum_{i=1}^\infty \frac{1}{i} = 1 + \frac{1}{2} + \frac{1}{3} +\frac{1}{4} + \cdots [/math], which we have shown to be divergent. We see that the alternating harmonic series is a convergent infinite series [math]\sum_{i=m}^{\infty} a_i[/math] for which the corresponding series of absolute values [math]\sum_{i=m}^{\infty} |a_i|[/math] fail diverges. For practical purposes, the value of a convergent infinite series [math]\sum_{i=m}^{\infty} a_i[/math] is usually approximated by a partial [math]\sum_{i=m}^{\infty} a_i[/math]. The error in the approximation, denoted by [math]E_n[/math], is the absolute value of the difference between the true value of the series and the approximating partial sum; i.e.,

[[math]] E_n = | \sum_{i=m}^{\infty} a_i - \sum_{i=m}^{n} a_i | . [[/math]]

ln general, it is a difficult problem to know how large [math]n[/math] must be chosen to cosure that the error [math]E_n[/math] be less than a given size. However, for those alternating series which satisfy the hypotheses of Theorem (4.1), the problem is an easy one.

Theorem

If the ulternating series [math]\sum_{i=m}^{\infty} a_i[/math] satisfies hypotheses (i) and (ii) of Theorem (4.1), then the error [math]E_n[/math] is less than or equal to the absolute value of the first omitted term. That is,

[[math]] E_n \leq |a_{n+1}|, \;\;\; \mbox{for every integer} \; n \geq m. [[/math]]

Show Proof

We shall use the same notation as in the proof of (4.1). Thus we assume that [math] m = 0[/math] and that [math]a_i = (-1)^{i} b_i[/math] where [math]b_i \gt 0[/math] for every integer [math]i \geq 0[/math]. The value of the series is the number [math]L[/math], and the error [math]E_n[/math] is therefore given by

[[math]] E_n = | \sum_{i=0}^{\infty} a_i - \sum_{i=0}^{n} a_i | = |L - s_n| . [[/math]]

Since [math]|a_{n+1}| = b_{n+1}[/math], the proof is completed by showing that

[[math]] |L - s_n| \leq b_{n+1}, \; \mbox{for every integer}\; n \geq 0. [[/math]]

Geometrically, [math]|L - s_n|[/math] is the distance between the points [math]L[/math] and [math]s_n[/math] and it can be seen immediately from Figure 5 that the preceding inequality is true. To arrive at the conclusion formally, we recall that [math]\{s_{2n-1} \}[/math] is an increasing sequence converging to [math]L[/math], and that [math]\{s_{2n} \}[/math] is a decreasing sequence converging to [math]L[/math]. Thus if [math]n[/math] is odd, then [math]n + 1[/math] is even and

[[math]] s_n \leq L \leq s_{n+1}. [[/math]]

On the other hand, if [math]n[/math] is even, then [math]n + 1[/math] is odd and

[[math]] s_{n +1} \leq L \leq s_n. [[/math]]

In either case, we have [math]|L - s_n| \leq |s_{n+1} - s_n|[/math]. Hence, for every integer [math]n \geq 0[/math],

[[math]] E_n = |L - s_n| \leq |s_{n+1} - s_n| = |a_{n+1}|, [[/math]]

and the proof is complete.

■

General references

Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.