Discrete Conditional Probability
Conditional Probability
In this section we ask and answer the following question. Suppose we assign a distribution function to a sample space and then learn that an event [math]E[/math] has occurred. How should we change the probabilities of the remaining events? We shall call the new probability for an event [math]F[/math] the conditional probability of [math]F[/math] given [math]E[/math] and denote it by [math]P(F|E)[/math].
Example An experiment consists of rolling a die once. Let [math]X[/math] be the outcome. Let [math]F[/math] be the event [math]\{X = 6\}[/math], and let [math]E[/math] be the event [math]\{X \gt 4\}[/math]. We assign the distribution function [math]m(\omega) = 1/6[/math] for [math]\omega = 1, 2, \ldots , 6[/math]. Thus, [math]P(F) = 1/6[/math]. Now suppose that the die is rolled and we are told that the event [math]E[/math] has occurred. This leaves only two possible outcomes: 5 and 6. In the absence of any other information, we would still regard these outcomes to be equally likely, so the probability of [math]F[/math] becomes 1/2, making [math]P(F|E) = 1/2[/math].
Example In the Life Table (see Appendix C), one finds that in a population of 100,00 females, 89.835% can expect to live to age 60, while 57.062% can expect to live to age 80. Given that a woman is 60, what is the probability that she lives to age 80?
This is an example of a conditional probability. In this case, the original sample space
can be thought of as a set of 100,00 females. The events [math]E[/math] and [math]F[/math] are the subsets of the
sample space consisting of all women who live at least 60 years, and at least 80 years,
respectively. We consider [math]E[/math] to be the new sample space, and note that [math]F[/math] is a subset of [math]E[/math].
Thus, the size of [math]E[/math] is 89,35, and the size of [math]F[/math] is 57,62. So, the probability in
question equals [math]57,62/89,35 = .6352[/math]. Thus, a woman who is 60 has a 63.52% chance of
living to age 80.
Example Consider our voting example from Discrete Probability Distributions: three candidates A, B, and C are running for office. We decided that A and B have an equal chance of winning and C is only 1/2 as likely to win as A. Let [math]A[/math] be the event “A wins,” [math]B[/math] that “B wins,” and [math]C[/math] that “C wins.” Hence, we assigned probabilities [math]P(A) = 2/5[/math], [math]P(B) = 2/5[/math], and [math]P(C) = 1/5[/math].
Suppose that before the election is held, [math]A[/math] drops out of the race. As in Example, it would be natural to assign new probabilities to the events [math]B[/math] and [math]C[/math] which are
proportional to the original probabilities. Thus, we would have [math]P(B|~A) = 2/3[/math], and
[math]P(C|~A) = 1/3[/math]. It is important to note that any time we assign probabilities to real-life
events, the resulting distribution is only useful if we take into account all relevant
information. In this example, we may have knowledge that most voters who favor [math]A[/math] will vote
for [math]C[/math] if [math]A[/math] is no longer in the race. This will clearly make the probability that
[math]C[/math] wins greater than the value of 1/3 that was assigned above.
In these examples we assigned a distribution function and then were given new information that determined a new sample space, consisting of the outcomes that are still possible, and caused us to assign a new distribution function to this space. We want to make formal the procedure carried out in these examples. Let [math]\Omega = \{\omega_1,\omega_2,\ldots,\omega_r\}[/math] be the original sample space with distribution function [math]m(\omega_j)[/math] assigned. Suppose we learn that the event [math]E[/math] has occurred. We want to assign a new distribution function [math]m(\omega_j|E)[/math] to [math]\Omega[/math] to reflect this fact. Clearly, if a sample point [math]\omega_j[/math] is not in [math]E[/math], we want [math]m(\omega_j|E) = 0[/math]. Moreover, in the absence of information to the contrary, it is reasonable to assume that the probabilities for [math]\omega_k[/math] in [math]E[/math] should have the same relative magnitudes that they had before we learned that [math]E[/math] had occurred. For this we require that
for all [math]\omega_k[/math] in [math]E[/math], with [math]c[/math] some positive constant. But we must also have
Thus,
(Note that this requires us to assume that [math]P(E) \gt 0[/math].) Thus, we will define
for [math]\omega_k[/math] in [math]E[/math]. We will call this new distribution the conditional distribution given [math]E[/math]. For a general event [math]F[/math], this gives
We call [math]P(F|E)[/math] the conditional probability of [math]F[/math] occurring given that [math]E[/math] occurs, and compute it using the formula
Example Let us return to the example of rolling a die. Recall that [math]F[/math] is the event [math]X = 6[/math], and [math]E[/math] is the event [math]X \gt 4[/math]. Note that [math]E \cap F[/math] is the event [math]F[/math]. So, the above formula gives
in agreement with the calculations performed earlier.
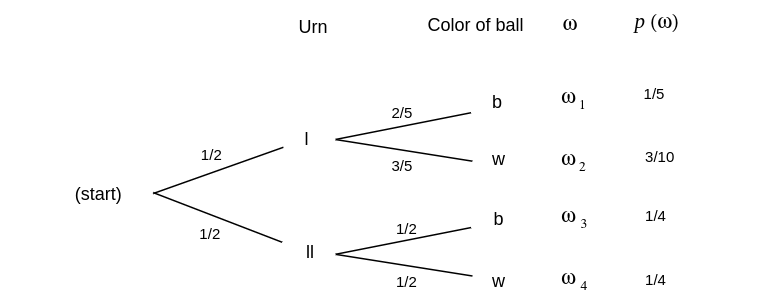
Example We have two urns, I and II. Urn I contains 2 black balls and 3 white balls. Urn II contains 1 black ball and 1 white ball. An urn is drawn at random and a ball is chosen at random from it. We can represent the sample space of this experiment as the paths through a tree as shown in Figure. The probabilities assigned to the paths are also shown.
Let [math]B[/math] be the event “a black ball is drawn,” and [math]I[/math] the event “urn I is
chosen.” Then the branch weight 2/5, which is shown on one branch in the figure, can now be
interpreted as the conditional probability [math]P(B|I)[/math].
Suppose we wish to calculate [math]P(I|B)[/math]. Using the formula, we obtain
Bayes Probabilities
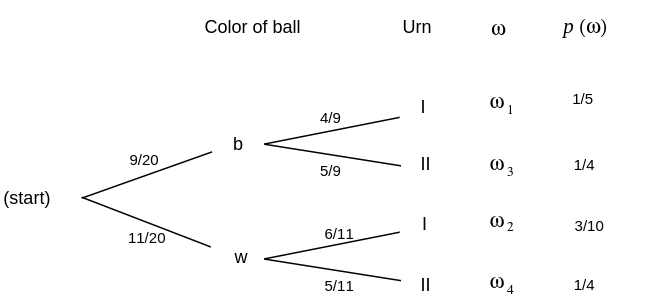
Our original tree measure gave us the probabilities for drawing a ball of a given color, given the urn chosen. We have just calculated the inverse probability that a particular urn was chosen, given the color of the ball. Such an inverse probability is called a Bayes probability and may be obtained by a formula that we shall develop later. Bayes probabilities can also be obtained by simply constructing the tree measure for the two-stage experiment carried out in reverse order. We show this tree in Figure.
The paths through the reverse tree are in one-to-one correspondence with those in the forward tree, since they correspond to individual outcomes of the experiment, and so they are assigned the same probabilities. From the forward tree, we find that the probability of a black ball is
The probabilities for the branches at the second level are found by simple division. For example, if [math]x[/math] is the probability to be assigned to the top branch at the second level, we must have
or [math]x = 4/9[/math]. Thus, [math]P(I|B) = 4/9[/math], in agreement with our previous calculations. The reverse tree then displays all of the inverse, or Bayes, probabilities.
Example We consider now a problem called the Monty Hall problem. This has long been a favorite problem but was revived by a letter from Craig Whitaker to Marilyn vos Savant for consideration in her column in Parade Magazine.[Notes 1] Craig wrote:Suppose you're on Monty Hall's Let's Make a Deal! You are given the choice of
three doors, behind one door is a car, the others, goats. You pick a door, say 1, Monty opens another door, say 3, which has a goat. Monty says to you “Do you want to pick door 2?” Is it to your advantage to switch your choice of doors?
Marilyn gave a solution concluding that you should switch, and if you do, your probability of
winning is 2/3. Several irate readers, some of whom identified themselves as having a PhD in
mathematics, said that this is absurd since after Monty has ruled out one door there are only two
possible doors and they should still each have the same probability 1/2 so there is no advantage to
switching. Marilyn stuck to her solution and encouraged her readers to simulate the game and draw
their own conclusions from this. We also encourage the reader to do this (see Exercise).
Other readers complained that Marilyn had not described the problem completely. In particular, the
way in which certain decisions were made during a play of the game were not specified. This aspect
of the problem will be discussed in Paradoxes. We will assume that the car was put
behind a door by rolling a three-sided die which made all three choices equally likely. Monty
knows where the car is, and always opens a door with a goat behind it. Finally, we assume that if
Monty has a choice of doors (i.e., the contestant has picked the door with the car behind it), he
chooses each door with probability 1/2. Marilyn
clearly expected her readers to assume that the game was played in this manner.
As is the case with most apparent paradoxes, this one can be resolved through careful analysis.
We begin by describing a simpler, related question. We say that a contestant is using
the “stay” strategy if he picks a door, and, if offered a chance to switch to another door,
declines to do so (i.e., he stays with his original choice). Similarly, we say that the
contestant is using the “switch” strategy if he picks a door, and, if offered a chance to switch to
another door, takes the offer. Now suppose that a contestant decides in advance to play the
“stay” strategy. His only action in this case is to pick a door (and decline an invitation to
switch, if one is offered). What is the probability that he wins a car? The same
question can be asked about the “switch” strategy.
Using the “stay” strategy, a contestant will win the car with probability 1/3, since 1/3 of the
time the door he picks will have the car behind it. On the other hand, if a contestant plays
the “switch” strategy, then he will win whenever the door he originally picked does not have
the car behind it, which happens 2/3 of the time.
This very simple analysis, though correct, does not quite solve the problem that Craig posed. Craig
asked for the conditional probability that you win if you switch, given that you have chosen door 1
and that Monty has chosen door 3. To solve this problem, we set up the problem before
getting this information and then compute the conditional probability given this information.
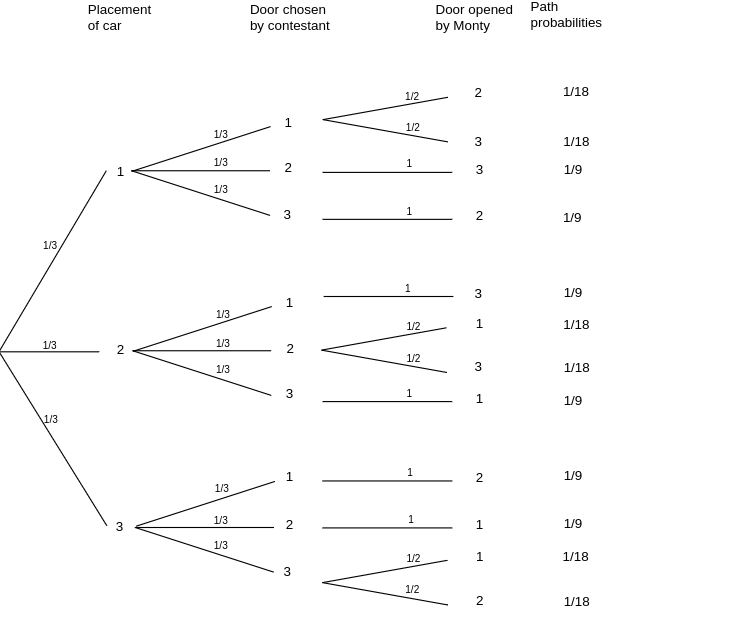
This is a process that takes place in several stages; the car is put behind a door, the contestant
picks a door, and finally Monty opens a door. Thus it is natural to analyze this using a tree
measure. Here we make an additional assumption that if Monty has a choice of doors (i.e., the
contestant has picked the door with the car behind it) then he picks each door with probability
1/2. The assumptions we have made determine the branch probabilities and these in turn determine
the tree measure. The resulting tree and tree measure are shown in Figure. It is tempting to
reduce the tree's size by making certain assumptions such as: “Without loss of generality, we
will assume that the contestant always picks door 1.” We have chosen not to make any such
assumptions, in the interest of clarity.
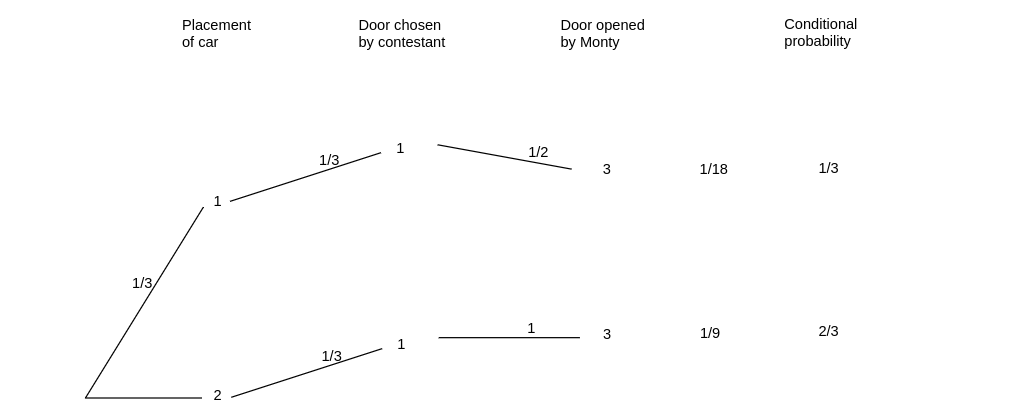
Now the given information, namely that the contestant chose door 1 and Monty chose door 3, means
only two paths through the tree are possible (see Figure).
For one of these paths, the car is behind door 1 and for the other it is behind door 2. The path with the car behind door 2 is twice as likely as the one with the car behind door 1. Thus the conditional probability is 2/3 that the car is behind door 2 and 1/3 that it is behind door 1, so if you switch you have a 2/3 chance of winning the car, as Marilyn claimed.
At this point, the reader may think that the two problems above are the same, since they have the
same answers. Recall that we assumed in the original problem if the contestant
chooses the door with the car, so that Monty has a choice of two doors, he chooses each of them with
probability 1/2. Now suppose instead that in the case that he has a choice, he chooses the door
with the larger number with probability 3/4. In the “switch” vs. “stay” problem, the
probability of winning with the “switch” strategy is still 2/3. However, in
the original problem, if the contestant switches, he wins with probability 4/7. The reader can
check this by noting that the same two paths as before are the only two possible paths in the tree.
The path leading to a win, if the contestant switches, has probability 1/3, while the path which
leads to a loss, if the contestant switches, has probability 1/4.
Independent Events
It often happens that the knowledge that a certain event [math]E[/math] has occurred has no effect on the probability that some other event [math]F[/math] has occurred, that is, that [math]P(F|E) = P(F)[/math]. One would expect that in this case, the equation [math]P(E|F) = P(E)[/math] would also be true. In fact (see Exercise), each equation implies the other. If these equations are true, we might say the [math]F[/math] is independent of [math]E[/math]. For example, you would not expect the knowledge of the outcome of the first toss of a coin to change the probability that you would assign to the possible outcomes of the second toss, that is, you would not expect that the second toss depends on the first. This idea is formalized in the following definition of independent events.
Let [math]E[/math] and [math]F[/math] be two events. We say that they are independent if either 1) both events have positive probability and
As noted above, if both [math]P(E)[/math] and [math]P(F)[/math] are positive, then each of the above equations imply the other, so that to see whether two events are independent, only one of these equations must be checked (see Exercise).
The following theorem provides another way to check for independence.
Two events [math]E[/math] and [math]F[/math] are independent if and only if
If either event has probability 0, then the two events are independent and the above equation is true, so the theorem is true in this case. Thus, we may assume that both events have positive probability in what follows. Assume that [math]E[/math] and [math]F[/math] are independent. Then [math]P(E|F) = P(E)[/math], and so
Assume next that [math]P(E\cap F) = P(E)P(F)[/math]. Then
Example Suppose that we have a coin which comes up heads with probability [math]p[/math], and tails with probability [math]q[/math]. Now suppose that this coin is tossed twice. Using a frequency interpretation of probability, it is reasonable to assign to the outcome [math](H,H)[/math] the probability [math]p^2[/math], to the outcome [math](H, T)[/math] the probability [math]pq[/math], and so on. Let [math]E[/math] be the event that heads turns up on the first toss and [math]F[/math] the event that tails turns up on the second toss. We will now check that with the above probability assignments, these two events are independent, as expected. We have [math]P(E) = p^2 + pq = p[/math], [math]P(F) = pq + q^2 = q[/math]. Finally [math]P(E\cap F) = pq[/math], so [math]P(E\cap F) = P(E)P(F)[/math].
Example It is often, but not always, intuitively clear when two events are independent. In Example, let [math]A[/math] be the event “the first toss is a head” and [math]B[/math] the event “the two outcomes are the same.” Then
Example Finally, let us give an example of two events that are not independent. In Example, let [math]I[/math] be the event “heads on the first toss” and [math]J[/math] the event “two heads turn up.” Then [math]P(I) = 1/2[/math] and [math]P(J) = 1/4[/math]. The event [math]I \cap J[/math] is the event “heads on both tosses” and has probability [math]1/4[/math]. Thus, [math]I[/math] and [math]J[/math] are not independent since [math]P(I)P(J) = 1/8 \ne P(I \cap J)[/math].
We can extend the concept of independence to any finite set of events [math]A_1, A_2, \ldots, A_n[/math].
A set of events [math]\{A_1,\ A_2,\ \ldots,\ A_n\}[/math] is said to be mutually independent if for any subset [math]\{A_i,\ A_j,\ldots,\ A_m\}[/math] of these events we have
Using this terminology, it is a fact that any sequence [math](\mbox S,\mbox S,\mbox F,\mbox F, \mbox S, \ldots,\mbox S)[/math] of possible outcomes of a Bernoulli trials process forms a sequence of mutually independent events.
It is natural to ask: If all pairs of a set of events are independent, is the whole set
mutually independent? The answer is not necessarily, and an example is given in Exercise.
It is important to note that the statement
Joint Distribution Functions and Independence of Random Variables
It is frequently the case that when an experiment is performed, several different quantities concerning the outcomes are investigated. Example Suppose we toss a coin three times. The basic random variable [math]{\bar X}[/math] corresponding to this experiment has eight possible outcomes, which are the ordered triples consisting of H's and T's. We can also define the random variable [math]X_i[/math], for [math]i = 1, 2, 3[/math], to be the outcome of the [math]i[/math]th toss. If the coin is fair, then we should assign the probability 1/8 to each of the eight possible outcomes. Thus, the distribution functions of [math]X_1[/math], [math]X_2[/math], and [math]X_3[/math] are identical; in each case they are defined by [math]m(H) = m(T) = 1/2[/math].
If we have several random variables [math]X_1, X_2, \ldots, X_n[/math] which correspond to a given experiment, then we can consider the joint random variable [math]{\bar X} = (X_1, X_2, \ldots, X_n)[/math] defined by taking an outcome [math]\omega[/math] of the experiment, and writing, as an [math]n[/math]-tuple, the corresponding [math]n[/math] outcomes for the random variables [math]X_1, X_2, \ldots, X_n[/math]. Thus, if the random variable [math]X_i[/math] has, as its set of possible outcomes the set [math]R_i[/math], then the set of possible outcomes of the joint random variable [math]{\bar X}[/math] is the Cartesian product of the [math]R_i[/math]'s, i.e., the set of all [math]n[/math]-tuples of possible outcomes of the [math]X_i[/math]'s.
Example In the coin-tossing example above, let [math]X_i[/math] denote the outcome of the [math]i[/math]th toss. Then the joint random variable [math]{\bar X} = (X_1, X_2, X_3)[/math] has eight possible outcomes.
Suppose that we now define [math]Y_i[/math], for [math]i = 1, 2, 3[/math], as the number of heads which occur in
the first [math]i[/math] tosses. Then [math]Y_i[/math] has [math]\{0, 1, \ldots, i\}[/math] as possible outcomes, so at
first glance, the set of possible outcomes of the joint random variable [math]{\bar Y} = (Y_1,
Y_2, Y_3)[/math] should be the set
We now illustrate the assignment of probabilities to the various outcomes for the joint
random variables [math]{\bar X}[/math] and [math]{\bar Y}[/math]. In the first case, each of the
eight outcomes should be assigned the probability 1/8, since we are assuming that we have a
fair coin. In the second case, since [math]Y_i[/math] has [math]i+1[/math] possible outcomes, the set of possible
outcomes has size 24. Only eight of these 24 outcomes can actually occur, namely the ones
satisfying [math]a_1 \le a_2 \le a_3[/math]. Each of these outcomes corresponds to exactly one of the
outcomes of the random variable [math]{\bar X}[/math], so it is natural to assign probability 1/8
to each of these. We assign probability 0 to the other 16 outcomes. In each case, the
probability function is called a joint distribution function.
We collect the above ideas in a definition.
Let [math]X_1, X_2, \ldots, X_n[/math] be random variables associated with an experiment. Suppose that the sample space (i.e., the set of possible outcomes) of [math]X_i[/math] is the set [math]R_i[/math]. Then the joint random variable [math]{\bar X} = (X_1, X_2, \ldots, X_n)[/math] is defined to be the random variable whose outcomes consist of ordered [math]n[/math]-tuples of outcomes, with the [math]i[/math]th coordinate lying in the set [math]R_i[/math]. The sample space [math]\Omega[/math] of [math]{\bar X}[/math] is the Cartesian product of the [math]R_i[/math]'s:
Example We now consider the assignment of probabilities in the above example. In the case of the random variable [math]{\bar X}[/math], the probability of any outcome [math](a_1, a_2, a_3)[/math] is just the product of the probabilities [math]P(X_i = a_i)[/math], for [math]i = 1, 2, 3[/math]. However, in the case of [math]{\bar Y}[/math], the probability assigned to the outcome [math](1, 1, 0)[/math] is not the product of the probabilities [math]P(Y_1 = 1)[/math], [math]P(Y_2 = 1)[/math], and [math]P(Y_3 = 0)[/math]. The difference between these two situations is that the value of [math]X_i[/math] does not affect the value of [math]X_j[/math], if [math]i \ne j[/math], while the values of [math]Y_i[/math] and [math]Y_j[/math] affect one another. For example, if [math]Y_1 = 1[/math], then [math]Y_2[/math] cannot equal 0. This prompts the next definition.
The random variables [math]X_1[/math], [math]X_2[/math], \ldots, [math]X_n[/math] are mutually independent if
for any choice of [math]r_1, r_2, \ldots, r_n[/math]. Thus, if [math]X_1,~X_2, \ldots,~X_n[/math] are mutually independent, then the joint distribution function of the random variable
Example and do or do not have cancer are reported as shown in Table.
| Not smoke | Smoke | Total | |
| Not cancer | 40 | 10 | 50 |
| Cancer | 7 | 3 | 10 |
| Totals | 47 | 13 | 60 |
Let [math]\Omega[/math] be the sample space consisting of these 60 people. A person is chosen at random from the group. Let [math]C(\omega) = 1[/math] if this person has cancer and 0 if not, and [math]S(\omega) = 1[/math] if this person smokes and 0 if not. Then the joint distribution of [math]\{C,S\}[/math] is given in Table.
| S | ||||
| 0 | 1 | |||
| 0 | 40/60 | 10/60 | ||
| C | ||||
| 1 | 7/60 | 3/60 |
For example [math]P(C = 0, S = 0) = 40/60[/math], [math]P(C = 0, S = 1) = 10/60[/math], and so forth. The distributions of the individual random variables are called marginal distributions. The marginal distributions of [math]C[/math] and [math]S[/math] are:
Independent Trials Processes
The study of random variables proceeds by considering special classes of random variables. One such class that we shall study is the class of independent trials.
A sequence of random variables [math]X_1,X_2, \ldots, X_n[/math] that are mutually independent and that have the same distribution is called a sequence of independent trials or an independent trials process. Independent trials processes arise naturally in the following way. We have a single experiment with sample space [math]R = \{r_1,r_2,\ldots,r_s\}[/math] and a distribution function
We repeat this experiment [math]n[/math] times. To describe this total experiment, we choose as sample space the space
with [math]m(\omega_j) = p_k[/math] when [math]\omega_j = r_k[/math]. Then we let [math]X_j[/math] denote the [math]j[/math]th coordinate of the outcome [math](r_1, r_2, \ldots, r_n)[/math]. The random variables [math]X_1, \ldots, X_n[/math] form an independent trials process.
Example [math]X_i[/math] represent the outcome of the [math]i[/math]th roll, for [math]i = 1, 2, 3[/math]. The common distribution function is
The sample space is [math]R^3 = R \times R \times R[/math] with [math]R = \{1,2,3,4,5,6\}[/math]. If [math]\omega = (1,3,6)[/math], then [math]X_1(\omega) = 1[/math], [math]X_2(\omega) = 3[/math], and [math]X_3(\omega) = 6[/math] indicating that the first roll was a 1, the second was a 3, and the third was a 6. The probability assigned to any sample point is
Example for success on each experiment. Let [math]X_j(\omega) = 1[/math] if the [math]j[/math]th outcome is success and [math]X_j(\omega) = 0[/math] if it is a failure. Then [math]X_1[/math], [math]X_2[/math], \ldots, [math]X_n[/math] is an independent trials process. Each [math]X_j[/math] has the same distribution function
Bayes' Formula
In our examples, we have considered conditional probabilities of the following form: Given the outcome of the second stage of a two-stage experiment, find the probability for an outcome at the first stage. We have remarked that these probabilities are called Bayes probabilities. We return now to the calculation of more general Bayes probabilities. Suppose we have a set of events [math]H_1,[/math] [math]H_2[/math], \ldots, [math]H_m[/math] that are pairwise disjoint and such that the sample space [math]\Omega[/math] satisfies the equation
Although this is a very famous formula, we will rarely use it. If the number of hypotheses is small, a simple tree measure calculation is easily carried out, as we have done in our examples. If the number of hypotheses is large, then we should use a computer.
Bayes probabilities are particularly appropriate for medical diagnosis. A
doctor is anxious to know which of several diseases a patient might have. She
collects evidence in the form of the outcomes of certain tests. From
statistical studies the doctor can find the prior probabilities of the various
diseases before the tests, and the probabilities for specific test outcomes,
given a particular disease. What the doctor wants to know is the posterior
probability for the particular disease, given the outcomes of the tests.
Example A doctor is trying to decide if a patient has one of three diseases [math]d_1[/math], [math]d_2[/math], or [math]d_3[/math]. Two tests are to be carried out, each of which results in a positive [math](+)[/math] or a negative [math](-)[/math] outcome. There are four possible test patterns [math]+{}+[/math], [math]+{}-[/math], [math]-{}+[/math], and [math]-{}-[/math]. National records have indicated that, for 10,00 people having one of these three diseases, the distribution of diseases and test results are as in Table.
| Disease | Number having this disease | The results | |||
| ++ | +- | -+ | -- | ||
| [math] d_{1} [/math] | 3215 | 2110 | 301 | 704 | 100 |
| [math] d_{2} [/math] | 2125 | 396 | 132 | 1187 | 410 |
| [math] d_{3} [/math] | 4660 | 510 | 3568 | 73 | 509 |
| Total | 10000 | ||||
From this data, we can estimate the prior probabilities for each of the diseases and, given a particular disease, the probability of a particular test outcome. For example, the prior probability of disease [math]d_1[/math] may be estimated to be [math]3215/10,00 = .3215[/math]. The probability of the test result [math]+{}-[/math], given disease [math]d_1[/math], may be estimated to be [math]301/3215 = .094[/math].
We can now use Bayes' formula to compute various posterior probabilities. The
computer program Bayes computes these posterior probabilities. The
results for this example are shown in Table.
| [math]d_1[/math] | [math]d_2[/math] | [math]d_3[/math] | |
| ++ | .700 | .131 | .169 |
| -+ | .358 | .604 | .038 |
| -- | .098 | .403 | .499 |
We note from the outcomes that, when the test result is [math]++[/math], the disease [math]d_1[/math] has a significantly higher probability than the other two. When the outcome is [math]+-[/math], this is true for disease [math]d_3[/math]. When the outcome is [math]-+[/math], this is true for disease [math]d_2[/math]. Note that these statements might have been guessed by looking at the data. If the outcome is [math]--[/math], the most probable cause is [math]d_3[/math], but the probability that a patient has [math]d_2[/math] is only slightly smaller. If one looks at the data in this case, one can see that it might be hard to guess which of the two diseases [math]d_2[/math] and [math]d_3[/math] is more likely.
Our final example shows that one has to be careful when the prior probabilities are small.
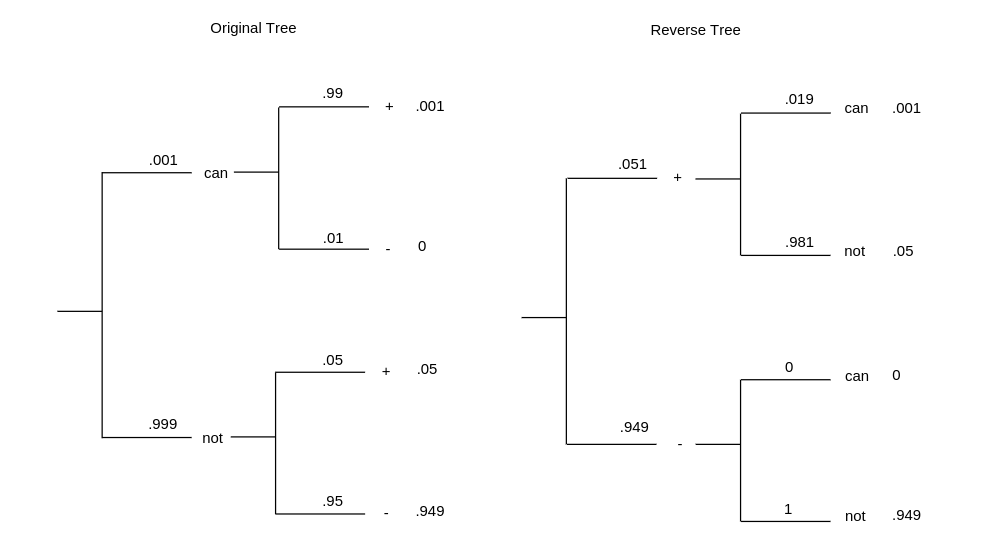
Example A doctor gives a patient a test for a particular cancer. Before the results of the test, the only evidence the doctor has to go on is that 1 woman in 1000 has this cancer. Experience has shown that, in 99 percent of the cases in which cancer is present, the test is positive; and in 95 percent of the cases in which it is not present, it is negative. If the test turns out to be positive, what probability should the doctor assign to the event that cancer is present? An alternative form of this question is to ask for the relative frequencies of false positives and cancers. We are given that [math]\mbox{prior(cancer)} = .001[/math] and [math]\mbox{prior(not\ cancer)} = .999[/math]. We know also that [math]P(+| \mbox{cancer}) = .99[/math], [math]P(-|\mbox{cancer}) = .01[/math], [math]P(+|\mbox{not\ cancer}) = .05[/math], and [math]P(-|\mbox{not\ cancer}) = .95[/math]. Using this data gives the result shown in Figure.
We see now that the probability of cancer given a positive test has only increased from .001 to .019. While this is nearly a twenty-fold increase, the probability that the patient has the cancer is still small. Stated in another way, among the positive results, 98.1 percent are false positives, and 1.9 percent are cancers. When a group of second-year medical students was asked this question, over half of the students incorrectly guessed the probability to be greater than .5.
Historical Remarks
Conditional probability was used long before it was formally defined. Pascal and Fermat considered the problem of points: given that team A has won [math]m[/math] games and team B has won [math]n[/math] games, what is the probability that A will win the series? (See Exercises Exercise--Exercise.) This is clearly a conditional probability problem.
In his book, Huygens gave a number of problems, one of which was:
Three gamblers, A, B and C, take 12 balls of which 4 are white and 8 black. They play with the rules that the drawer is blindfolded, A is to draw first, then B and then C, the winner to be the one who first draws a white ball. What is the ratio of their chances?[Notes 2]
From his answer it is clear that Huygens meant that each ball is replaced after
drawing. However, John Hudde, the mayor of Amsterdam, assumed that he meant to
sample without replacement and corresponded with Huygens about the difference
in their answers. Hacking remarks that “Neither party can understand what the
other is doing.”[Notes 3]
By the time of de Moivre's book, The Doctrine of Chances, these
distinctions were well understood. De Moivre defined independence and
dependence as follows:
Two Events are independent, when they have no connexion one with the other, and that the happening of one neither forwards nor obstructs the happening of the other.
Two Events are dependent, when they are so connected together as that the Probability of either's happening is altered by the happening of the other.[Notes 4]
De Moivre used sampling with and without replacement to illustrate that the probability that two independent events both happen is the product of their probabilities, and for dependent events that:
The Probability of the happening of two Events dependent, is the product of the Probability of the happening of one of them, by the Probability which the other will have of happening, when the first is considered as having happened; and the same Rule will extend to the happening of as many Events as may be assigned.[Notes 5]
The formula that we call Bayes' formula, and the idea of computing the
probability of a hypothesis given evidence, originated in a famous essay of
Thomas Bayes. Bayes was an ordained minister in Tunbridge Wells near London.
His mathematical interests led him to be elected to the Royal Society in 1742,
but none of his results were published within his lifetime. The work upon
which his fame rests, “An Essay Toward Solving a Problem in the Doctrine of
Chances,” was published in 1763, three years after his
death.[Notes 6] Bayes reviewed some of the basic concepts of probability and
then considered a new kind of inverse probability problem requiring the use of
conditional probability.
Bernoulli, in his study of processes that we now call Bernoulli trials, had
proven his famous law of large numbers which we will study in Chapter Law of Large Numbers. This theorem assured the experimenter that if he knew the probability [math]p[/math]
for success, he could predict that the proportion of successes would approach
this value as he increased the number of experiments. Bernoulli himself
realized that in most interesting cases you do not know the value of [math]p[/math] and
saw his theorem as an important step in showing that you could determine [math]p[/math] by
experimentation.
To study this problem further, Bayes started by assuming that the probability
[math]p[/math] for success is itself determined by a random experiment. He assumed in
fact that this experiment was such that this value for [math]p[/math] is equally likely to
be any value between 0 and 1.[Notes 7] Without knowing this value we
carry out
[math]n[/math] experiments and observe [math]m[/math] successes. Bayes proposed the problem of finding
the conditional probability that the unknown probability [math]p[/math] lies between [math]a[/math]
and [math]b[/math]. He obtained the answer:
We shall see in the next section how this result is obtained. Bayes clearly
wanted to show that the conditional distribution function, given the outcomes of
more and more experiments, becomes concentrated around the true value of [math]p[/math].
Thus, Bayes was trying to solve an inverse problem. The computation of
the integrals was too difficult for exact solution except for small values
of [math]j[/math] and [math]n[/math], and so Bayes tried approximate methods. His methods were not
very satisfactory and it has been suggested that this discouraged him from
publishing his results.
However, his paper was the first in a series of important studies carried out
by Laplace, Gauss, and other great mathematicians to solve inverse problems.
They studied this problem in terms of errors in measurements in astronomy. If
an astronomer were to know the true value of a distance and the nature of the
random errors caused by his measuring device he could predict the probabilistic
nature of his measurements. In fact, however, he is presented with the inverse
problem of knowing the nature of the random errors, and the values of the
measurements, and wanting to make inferences about the unknown true value.
As Maistrov remarks, the formula that we have called Bayes' formula does not
appear in his essay. Laplace gave it this name when he studied these inverse
problems.[Notes 8]
The computation of inverse probabilities is fundamental to statistics and has
led to an important branch of statistics called Bayesian analysis, assuring
Bayes eternal fame for his brief essay.
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.
Notes
- Marilyn vos Savant, Ask Marilyn, Parade Magazine, 9 September; 2 December; 17 February 1990, reprinted in Marilyn vos Savant, Ask Marilyn, St. Martins, New York, 1992.
- Quoted in F. N. David, Games, Gods and Gambling (London: Griffin, 1962), p. 119.
- I. Hacking, The Emergence of Probability (Cambridge: Cambridge University Press, 1975), p. 99.
- A. de Moivre, The Doctrine of Chances, 3rd ed. (New York: Chelsea, 1967), p. 6.
- ibid, p. 7.
- T. Bayes, “An Essay Toward Solving a Problem in the Doctrine of Chances,” Phil. Trans. Royal Soc. London, vol. 53 (1763), pp. 370--418.
- Bayes is using continuous probabilities as discussed in Chapter 2 of the complete Grinstead-Snell book.
- L. E. Maistrov, Probability Theory: A Historical Sketch, trans. and ed. Samual Kotz (New York: Academic Press, 1974), p. 100.