The Complex Exponential Function $e^{z}$
Consider the function [math]\varphi[/math] defined by
for every real number [math]x[/math]. This is a complex-valued function of a real variable. The domain of [math]\varphi[/math] is the set [math]R[/math] of all real numbers. For every real number [math]x[/math], we have
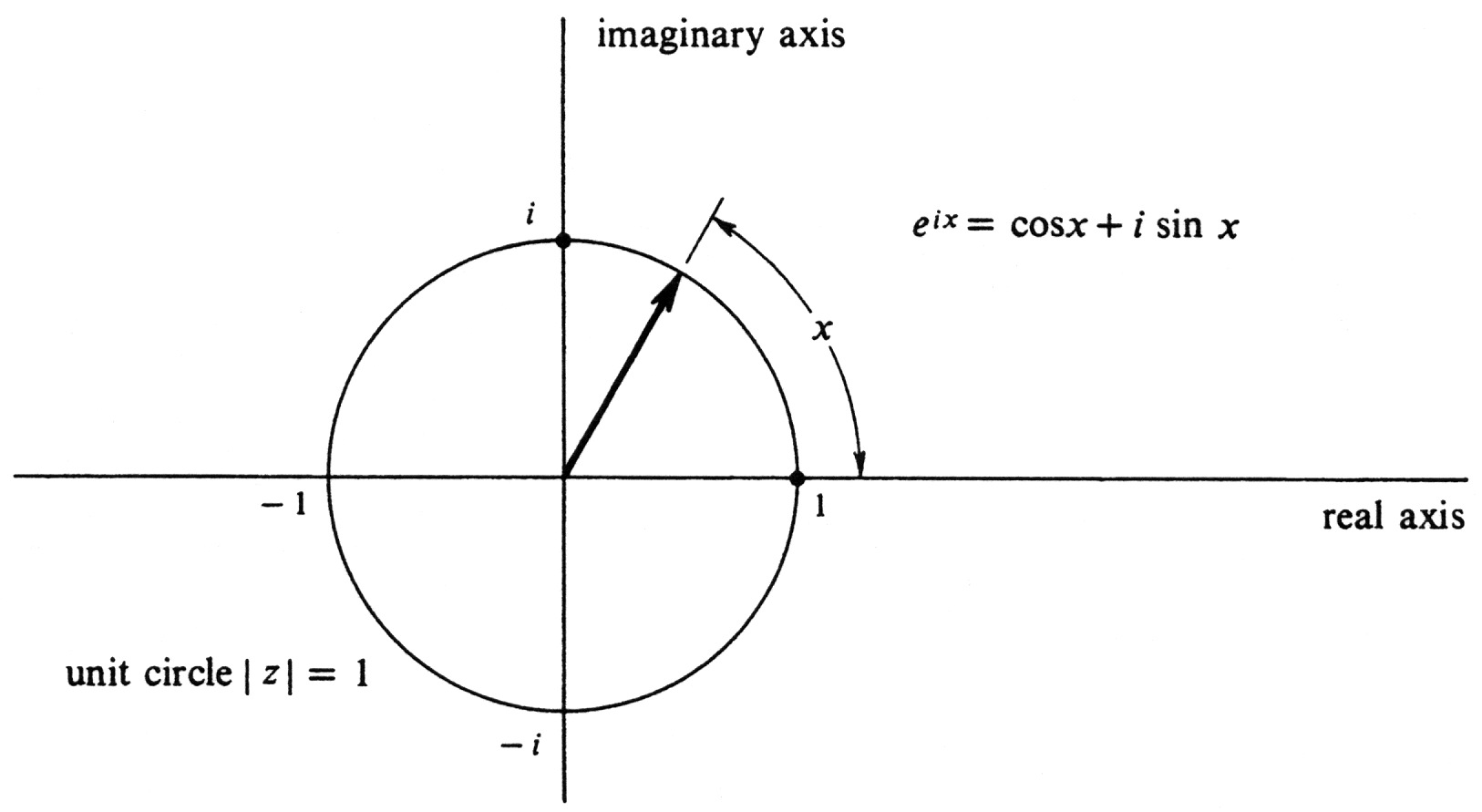
It follows that [math]\varphi (x)[/math] is a point on the unit circle in the complex plane, i.e., the circle with center at the origin and radius 1. Conversely, every point on the unit circle is equal to [math](\cos x, \sin x)[/math], for some real number [math]x[/math], and we know that [math](\cos x, \sin x) = \cos x + i \sin x[/math]. It follows that the range of [math]\varphi[/math] is the unit circle. The function [math]\varphi[/math] has the following properties:
The proofs are completely straightforward. Thus (7.1) follows from the equations
The above four properties of [math]\varphi[/math] are also shared by the real-valued exponential function [math]\exp[/math] [we recall that [math]\exp(x) = e^{x}[/math]]. This fact suggests the possibility of extending the domain and range of [math]\exp[/math] into the complex plane. That is, it suggests that the functions [math]\varphi[/math] and [math]\exp[/math] can be combined to give a complex-valued exponential function of a complex variable which will have the property that when its domain is restricted to the real numbers, it is simply [math]\exp[/math]. We define such a function now. For every complex number [math]z = x + iy[/math], let [math]\mbox{Exp}[/math] be the function defined by
Thus
If [math]z = x + i0[/math], then [math]z = x[/math] and [math]\mbox{Exp}(z) = \exp(x) \varphi (0) = \exp(x)[/math]. Hence the function $\mbox{Exp}$ is an extension of the function $\exp$. It is a routine matter to show that the function [math]\mbox{Exp}[/math] has the exponential properties listed above for [math]\varphi[/math]. Following the practice for the real-valued exponential, we shall write [math]\mbox{Exp}(z)[/math] as [math]e^z[/math]. In this notation therefore, if [math]z = x + iy[/math], the definition reads
The exponential properties are
The proofs simply use the fact that the functions [math]\exp[/math] and [math]e^z[/math] separately have these properties. Thus
If [math]x[/math] is an arbitrary real number, then
Thus we have the equation
Thus if [math]x[/math] is any real number, the complex number [math]e^{ix}[/math] is the ordered pair [math](\cos x, \sin x)[/math]. Hence [math]e^{ix}[/math] is the point on the unit circle obtained by starting at the complex number 1 and measuring along the circle at a distance equal to the absolute value of [math]x[/math], measuring in the counterclockwise direction if [math]x[/math] is positive and in the clockwise direction if it is negative (see Figure 20). In terms of angle, [math]x[/math] is the radian measure of the angle whose initial side is the positive half of the real axis and whose terminal side contains the arrow representing [math]z[/math]. Letting [math]x = \pi[/math] in (7.5), we get [math]e^{i\pi} = \cos \pi + i \sin \pi[/math]. Since [math]\cos \pi = -1[/math] and [math]\sin \pi = 0[/math], it follows that [math]e^{i\pi} = - 1[/math], which is equivalent to the equation
This equation is most famous since it combines in a simple formula the three special numbers [math]\pi[/math], [math]e[/math], and [math]i[/math] with the additive and multiplicative identities 0 and 1. One of the most important features of the complex exponential function is that it provides an alternative way of writing complex numbers. We have
Every complex number [math]z[/math] can be written in the form [math]z = |z| e^{it}[/math], for some real number [math]t[/math]. Furthermore, if [math]z = x + iy[/math] and [math]z \neq 0[/math], then [math]z = |z| e^{it}[/math] if and only if [math]\cos t = \frac{x}{|z|}[/math] and [math]\sin t = \frac{y}{|z|}[/math].
If [math]z = 0[/math], then [math]|z| = 0[/math], and so [math]0 = z = |z|e^{it}[/math], for every real number [math]t[/math]. Next we suppose that [math]z \neq 0[/math]. Then [math]|z| \neq 0[/math], and [math]\frac{z}{|z|}[/math] is defined and lies on the unit circle because
A complex number written as [math]z = |z| e^{it}[/math] is said to be in exponential form. The number [math]|z|[/math] is, of course, the absolute value of [math]z[/math], and the number [math]t[/math] is called the angle, or argument, of [math]z[/math]. The latter is not uniquely determined by [math]z[/math]. Since the trigonometric functions [math]\sin[/math] and [math]\cos[/math] have period [math]2\pi[/math], it follows that
for every integer [math]n[/math]. Consider two complex numbers written in exponential form:
The product and ratio are given by
Hence by formulas (7.2') and (7.3') for the product and ratio of exponentials, we have
That is, two complex numbers are multiplied by multiplying their absolute values and adding their angles. They are divided by dividing their absolute values and subtracting their angles.
Example
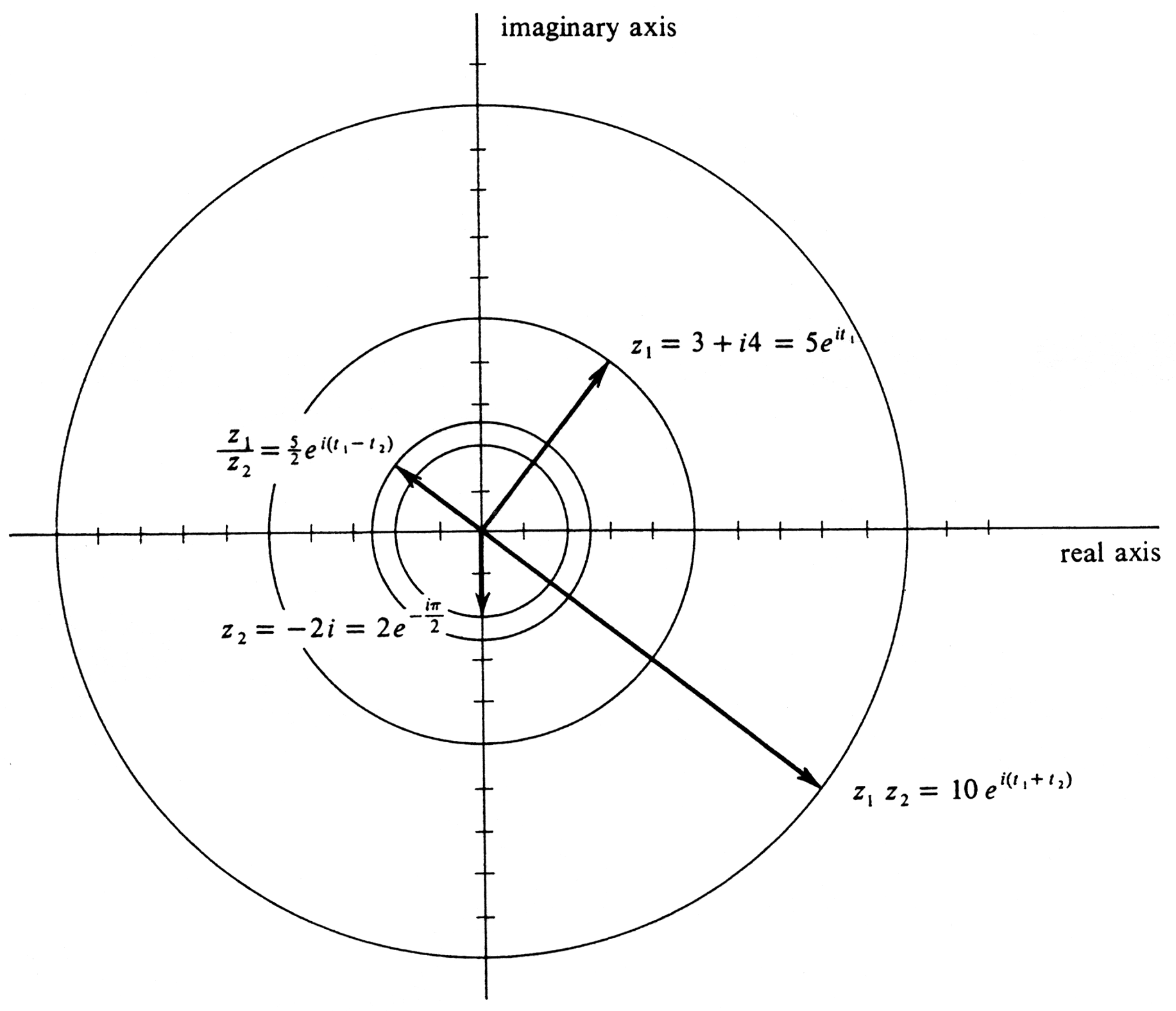
Let [math]z_{1} = 3 + i4[/math] and [math]z_{2} = -2i[/math]. Express [math]z_{1}, z_{2}, z_{1}z_{2}[/math], and [math]\frac{z_{1}}{z_{2}}[/math] in the exponential form [math]|z| e^{it}[/math], and plot the resulting arrows in the complex plane. To begin with,
We next seek a real number [math]t_{1}[/math] such that [math]\cos t_{1} = \frac{3}{5}[/math] and
[math]\sin t_{1} = \frac{4}{5}[/math], and also a number [math]t_{2}[/math] such that [math]\cos t_{2} = 0[/math] and
[math]\sin t_{2} = - 1[/math]. These are given by
Then
Since [math]t_{1} + t_{2} = 0.93 - \frac{\pi}{2} = - 0.64[/math] (approximately) and
[math]t_{1} - t_{2} = 0.93 - \Bigl(-\frac{\pi}{2}\Bigr) = 2.50[/math] (approximately), we obtain
The arrows representing [math]z_{1}, z_{2}, z_{1}z_{2}[/math] and [math]\frac{z_{1}}{z_{2}}[/math] are shown in Figure 21. To locate these numbers geometrically using a ruler and protractor marked off in degrees, we would compute
Of course, we can find the real and imaginary parts of [math]z_{1}z_{2}[/math] and [math]\frac{z_{1}}{z_{2}}[/math] by the computations
If [math]z[/math] is a complex number, then [math]z^n[/math] can be defined inductively, for every nonnegative integer [math]n[/math], by
Another useful property of the complex exponential function is
By induction. If [math]n = 0[/math], then [math](e^z)^n = (e^z)^0[/math]. Since [math]e^z[/math] is a complex number, [math](e^z)^0 = 1[/math], by equation (1). Moreover, in this case, [math]e^{nz} = e^{0z} = 1[/math], by (7.1'). Next suppose that [math]n \gt 0[/math]. By equation (2), we have [math](e^z)^n = e^{z}(e^z)^{n-1}[/math], and by hypothesis of induction [math](e^z)^{n-1} = e^{(n-1)z} = e^{(n - 1)z}[/math]. Hence, by (7.2'),
Let [math]z[/math] be a complex number and [math]n[/math] a positive integer. A complex number [math]w[/math] is said to be an [math]\bf{n}[/math]th root of [math]z[/math] if [math]w^n = z[/math]. We shall now show that
If [math]z \neq 0[/math], then there exist [math]n[/math] distinct [math]n[/math]th roots of [math]z[/math].
Let us write [math]z[/math] in exponential form: [math]z = |z| e^{it}[/math]. By [math]|z|^{1/n}[/math] we mean the positive [math]n[/math]th root of the real number [math]|z|[/math] (which we assume exists and is unique). Consider the complex number
An [math]n[/math]th root of [math]z[/math] is a solution of the complex polynomial equation [math]w^n - z = 0[/math]. It is a well-known theorem of algebra that a polynomial equation of degree [math]n[/math] cannot have more than [math]n[/math] roots. Hence we can strengthen the statement of (7.8) to read that every nonzero complex number [math]z[/math] has precisely [math]n[/math] distinct nth roots.
Example
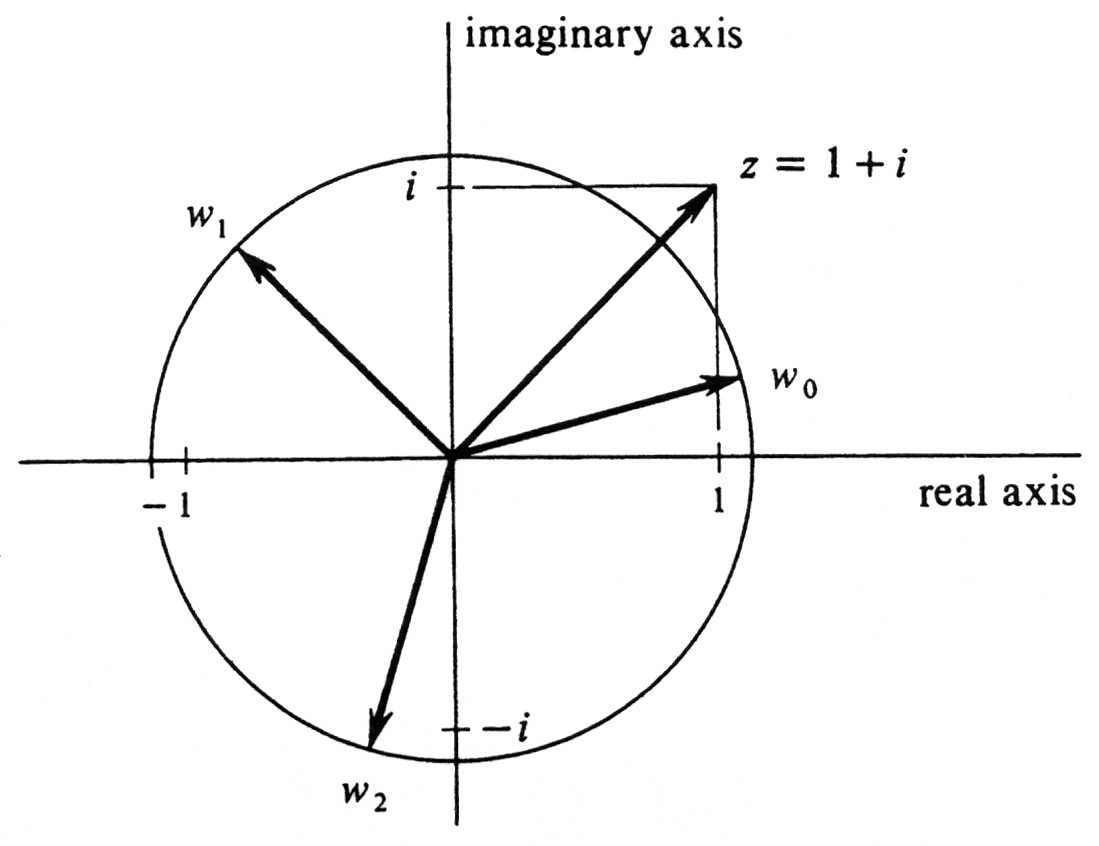
Find the three cube roots of the complex number [math]z = 1 + i[/math], and plot them in the complex plane. Writing [math]z[/math] in exponential form, we have
(see Figure 22). Hence the three cube roots are
Since [math](\sqrt 2)^{1/3} = 2^{1/6} = 1.12[/math] (approximately) and [math]\frac{1}{3} \Bigl(\frac{\pi}{4}\Bigr)[/math] radius = 15 degrees, we see that [math]w_0[/math] is the complex number lying on the circle of radius 1.12 about the origin and making an angle of 15 degrees with the positive [math]x[/math]-axis. The other two roots lie on the same circle and have angles of 15 + 120 degrees and 15 + 240 degrees, respectively. The three roots are thus [math]\sqrt[6]{2} e^{i(\pi/12)}[/math], [math]\sqrt[6]{2} e^{i(3\pi/4)}[/math], and [math]\sqrt[6]{2} e^{i(17 \pi/12)}[/math].
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.