Random projections

Let [math]d, k\geqslant1[/math] with [math]k\leqslant{}d[/math]. In the sequel we identify [math]\mathbb{R}^{k\times d}\cong\L(\mathbb{R}^d,\mathbb{R}^k)[/math] and refer to its elements sometimes as matrices and sometimes as linear maps.

Let us firstly consider a matrix [math]A\in\mathbb{R}^{k\times d}[/math] whose [math]k[/math] rows are orthogonal. Then the map [math]\mathbb{R}^k\rightarrow\mathbb{R}^d[/math], [math]x\mapsto A^Tx[/math] is injective and we can regard [math]\mathbb{R}^k[/math] via [math]A^T[/math] as a subspace of [math]\mathbb{R}^d[/math]. The linear map [math]P\colon\mathbb{R}^d\rightarrow\mathbb{R}^d[/math], [math]Px:=A^TAx[/math] is then idempotent, its range is isomorphic to [math]\mathbb{R}^k\subseteq\mathbb{R}^d[/math] in the aforementioned sense, and thus [math]P[/math] is an orthogonal projection onto [math]\mathbb{R''^k}[/math]. Using the basis extension theorem and the Gram-Schmidt procedure it is easy to see that for every linear subspace [math]V\subseteq \mathbb{R}^d[/math] with [math]\dim V=k[/math] there exists an orthogonal projection and that each such projection can be realized by a matrix [math]A\in\mathbb{R}^{k\times d}[/math] with [math]k[/math] orthogonal rows.

In this chapter our aim is to understand the properties of maps given by matrices that we pick at random. For this let [math](\Omega,\Sigma,\P)[/math] be a probability space.

Definition

A measurable function [math]U\colon\Omega\rightarrow\mathbb{R}^{k\times d}[/math] is called a random matrix.

In order to specify the underlying distribution, we extend Proposition to matrices. We first note that if a matrix

[[math]] U=\begin{bmatrix} u_{11} & u_{12} & \cdots & u_{1d} \\ u_{21} & u_{22} & \cdots & u_{2d} \\ \vdots & & & \vdots \\ u_{k1} & u_{k2} & \cdots & u_{kd} \\ \end{bmatrix} [[/math]]

is given, the map [math]U\colon\mathbb{R}^d\rightarrow\mathbb{R}^k[/math] is given by [math]Ux = \bigl(\langle{}u_1,x\rangle{},\langle{}u_2,x\rangle{},\dots,\langle{}u_k,x\rangle{}\bigr)[/math] for [math]x\in\mathbb{R}^d[/math], if we denote by [math]u_i=(u_{i1},u_{i2},\dots,u_{id})[/math] the [math]i[/math]-th row of [math]U[/math] for [math]i=1,\dots,k[/math]. If [math]U\colon \Omega\rightarrow\mathbb{R}^{k\times d}[/math] is a random matrix, then we denote by [math]u_{ij}\colon\Omega\rightarrow\mathbb{R}[/math] the random variables that arise as the coordinate functions of [math]U[/math] and by [math]u_{i}\colon\Omega\rightarrow\mathbb{R}^d[/math] the random vectors that arise, if we combine the coordinate functions of the [math]i[/math]-th row back into a vector. Employing this notation, we get the following result.

Proposition

Let [math]U\colon\Omega\rightarrow\mathbb{R}^{k\times d}[/math] be a random matrix with entries [math]u_{ij}\colon\Omega\rightarrow\mathbb{R}[/math] and row vectors [math]u_{i}\colon\Omega\rightarrow\mathbb{R}^d[/math]. Then the following are equivalent.

[math]U\sim\mathcal{N}(0,1,\mathbb{R}^{k\times d})[/math].
[math]\forall\:i=1,\dots,k\colon u_i\sim\mathcal{N}(0,1,\mathbb{R}^d)[/math].
[math]\forall\:i=1,\dots,d,\,j=1,\dots,k\colon u_{ij}\sim\mathcal{N}(0,1)[/math].

Show Proof

Since [math]\mathbb{R}^{k\times d}\cong\mathbb{R}^{kd}[/math] holds, we see that a random matrix [math]U\in\mathbb{R}^{k\times d}[/math] can be identified with a real random vector [math]U\colon\Omega\rightarrow\mathbb{R}^{dk}[/math]. In that sense we understand (i). Having done this rearrangement the equivalences follow immediately from Proposition.

■

By Proposition we can write [math]U\sim\mathcal{N}(0,1,\mathbb{R}^{k\times d})[/math] and understand this matrix-wise, row vector-wise or element-wise. If we draw [math]U\in\mathbb{R}^{k\times d}[/math] at random with [math]U\sim\mathcal{N}(0,1,\mathbb{R}^{k\times d})[/math], then by Theorem we have

[[math]] \P\bigl[\bigl|\bigl\langle{}\medfrac{u_i}{\|u_i\|},\medfrac{u_\ell}{\|u_\ell\|}\bigr\rangle{}\bigr|\leqslant\epsilon\bigr]\geqslant \medfrac{2/\epsilon+7}{\sqrt{d}} [[/math]]

for [math]i\not=\ell[/math], which means that the rows are almost orthogonal with high probability for large dimensions [math]d[/math]. We will therefore call a matrix [math]U\sim\mathcal{N}(0,1,\mathbb{R}^{k\times d})[/math] a random projection from [math]\mathbb{R^d}[/math] to [math]\mathbb{R}^k[/math]. Observe however that [math]U[/math] needs in general neither to be orthogonal, nor a projection.

We will study now, how a random projection in the aforementioned sense does distorts length. The bound in the result below is non-trivial for [math]k\epsilon^2 \gt 16\ln2\,(\approx11.1)[/math].

Theorem

(Random Projection Theorem) Let [math]U\in\mathbb{R}^{k\times d}[/math] be a random matrix with [math]U\sim\mathcal{N}(0,1)[/math]. Then for every [math]x\in\mathbb{R}^d\backslash\{0\}[/math] and every [math]0 \lt \epsilon \lt 1[/math] we have

[[math]] \P\bigl[\big|\|Ux\|-\sqrt{k}\|x\|\big|\geqslant\epsilon\sqrt{k}\|x\|\bigr]\leqslant 2\exp(-ck\epsilon^2) [[/math]]

where [math]c=1/16[/math].

Show Proof

Let [math]x\in\mathbb{R}^d\backslash\{0\}[/math] be fixed and let [math]U\colon\Omega\rightarrow\mathbb{R}^{k\times d}[/math] be a random matrix with [math]U\sim\mathcal{N}(0,1)[/math]. We consider

[[math]] U(\cdot)\medfrac{x}{\|x\|}\colon\Omega\rightarrow\mathbb{R}^k [[/math]]

and observe that each of its coordinate functions

[[math]] \pr_i(U(\cdot)\medfrac{x}{\|x\|}) = \bigl\langle{}u_i,\medfrac{x}{\|x\|}\bigr\rangle{} = \Bigsum{j=1}{d}u_{ij}\medfrac{x_j}{\|x\|} [[/math]]

is a linear combination of random variables [math]u_{ij}\sim\mathcal{N}(0,1)[/math] by Proposition whose squared coeffients [math]{\textstyle\frac{x_j^2}{\|x\|^2}}[/math] sum up to one. By Proposition this means [math]U(\cdot){\textstyle\frac{x}{\|x\|}}\sim\mathcal{N}(0,1,\mathbb{R}^k)[/math] and we can deduce

[[math]] \begin{align*} \P\bigl[\bigl|\|Ux\|-\sqrt{k}\|x\|\bigr|\geqslant \epsilon\sqrt{k}\|x\|\bigr] & = \P\bigl[\bigl|\|U\medfrac{x}{\|x\|}\|-\sqrt{k}\bigr|\geqslant \epsilon\sqrt{k}\,\bigr]\\ &\leqslant 2\exp\bigl(-\medfrac{(\epsilon\sqrt{k})^2}{16}\bigr)\\ &=2\exp\bigl(-\medfrac{\epsilon^2 k}{16}\bigr) \end{align*} [[/math]]

where we applied Theorem in the space [math]\mathbb{R}^k[/math] to get the estimate.

■

Notice that we have on both sides of the estimate the expression [math]\epsilon\sqrt{k}[/math]. On the right hand side we need this number to be suitable large to get the probability down, but on the right we would rather have it small in order to get the distortion small. This conundrum we can solve by ‘absorbing’ the factor [math]\sqrt{k}[/math] into the notation. That is, for a random matrix [math]U\sim\mathcal{N}(0,1,\mathbb{R}^{k\times d})[/math] we consider the Johnson-Lindenstrauss projection

[[math]] T_{\scriptscriptstyle U}\colon\mathbb{R}^{d}\rightarrow\mathbb{R}^k,\;T_{\scriptscriptstyle U}x:={\textstyle\frac{1}{\sqrt{k}}}Ux. [[/math]]

Then Theorem reads

[[math]] \P\bigl[\big|\|T_{\scriptscriptstyle U}x\|-\|x\|\big|\geqslant\epsilon\|x\|\bigr]\leqslant 2\exp(-ck\epsilon^2) [[/math]]

and we can think of [math]\epsilon[/math] being small but [math]k[/math] being so large that [math]k\epsilon^2[/math] is large. If we do this, then we get that [math]\big|\|T_{\scriptscriptstyle U}x\|-\|x\|\big| \lt \epsilon\|x\|[/math] holds with high probability. Since this is a multiplicative error estimate, we can further rewrite this as

[[math]] \medfrac{\|T_{\scriptscriptstyle U}x\|}{\|x\|}\approx 1. [[/math]]

If we restrict ourselves to [math]x\in K[/math] with, e.g., a fixed compact set [math]K\subseteq\mathbb{R}^d[/math], then we can even pick [math]k[/math] and [math]\epsilon[/math] accordingly and achieve that [math]\|T_{\scriptscriptstyle U}x\|\approx\|x\|[/math] holds on whole [math]K[/math] with high probability.

The following result will extend the latter to mutual distances within a sets of [math]n[/math] points.

Theorem

(Johnson-Lindenstrauss Lemma) Let [math]0 \lt \epsilon \lt 1[/math] and [math]n\geqslant1[/math] and let [math]k\geqslant\frac{48}{\epsilon^2}\ln n[/math]. Let [math]U\sim\mathcal{N}(0,1,\mathbb{R}^{k\times d})[/math] be a random matrix. Then the Johnson-Lindenstrauss projection [math]T_{\scriptscriptstyle U}[/math] satisfies for any set of [math]n[/math]--many points [math]x_1,\dots,x_n\in\mathbb{R}^d[/math] the estimate

[[math]] \P\bigl[(1-\epsilon)\|x_i-x_j\|\leqslant\|T_{\scriptscriptstyle U}x_i-T_{\scriptscriptstyle U}x_j\|\leqslant (1+\epsilon)\|x_i-x_j\| \text{ for all } i,j\bigr]\geqslant 1-\medfrac{1}{n}. [[/math]]

Show Proof

Firstly, we fix [math]i\not=j[/math], put [math]x:=x_i-x_j[/math] and compute

[[math]] \begin{align*} &\hspace{-35pt}\P\bigl[\|T_{\scriptscriptstyle U}x_i-T_{\scriptscriptstyle U}x_j\|\not\in \bigl((1-\epsilon)\|x_i-x_j\|,(1+\epsilon)\|x_i-x_j\|\bigr)\bigr] \\ \phantom{xxxx}& = \P\bigl[\|T_{\scriptscriptstyle U}x\|\not\in \bigl((1-\epsilon)\|x\|,(1+\epsilon)\|x\|\bigr)\bigr]\\ & =\P\bigl[\bigl|\|T_{\scriptscriptstyle U}x\|-\|x\|\bigr|\geqslant \epsilon\|x\|\bigr]\\ & =\P\bigl[\bigl|\|Ux\|-\sqrt{k}\|x\|\bigr|\geqslant \epsilon\sqrt{k}\|x\|\bigr]\\ &\leqslant 2\exp\bigl(-k\epsilon^2/16\bigr) \end{align*} [[/math]]

where we used Theorem in the last step. Since the inequality [math](1-\epsilon)\|x_i-x_j\|\leqslant\|T_{\scriptscriptstyle U}x_i-T_{\scriptscriptstyle U}x_j\|\leqslant (1+\epsilon)\|x_i-x_j\| [/math] is always true for [math]i=j[/math] and there are [math]{n\choose 2}\leqslant n^2/2[/math] choices for [math]i\not=j[/math], we get

[[math]] \begin{align*} &\P\bigl[\,\forall\:i,j\colon (1-\epsilon)\|x_i-x_j\|\leqslant\|T_{\scriptscriptstyle U}x_i-T_{\scriptscriptstyle U}x_j\|\leqslant (1+\epsilon)\|x_i-x_j\| \bigr]\\ & = 1-\P\bigl[\,\exists\:i\not=j\colon \|T_{\scriptscriptstyle U}x_i-T_{\scriptscriptstyle U}x_j\|\not\in \bigl((1-\epsilon)\|x_i-x_j\|,(1+\epsilon)\|x_i-x_j\|\bigr)\bigr]\\ & \geqslant 1-\frac{n^2}{2}\cdot2\exp\bigl(-k\epsilon^2/16\bigr)\\ & \geqslant 1-n^2\exp\bigl(-\bigl(\medfrac{48}{\epsilon^2}\ln n\bigr)\,\epsilon^2/16\bigr)\\ & \geqslant 1-n^2\exp\bigl(\ln n^{-48/16}\bigr)\bigr)\\ & = 1-n^2 n^{-3}\\ & = 1-\medfrac{1}{n} \end{align*} [[/math]]

where we used the selection of [math]k[/math] for the second last estimate.

■

Similar to our remarks on Theorem, we can derive from Theorem that

[[math]] \medfrac{\|T_{\scriptscriptstyle U}x_i-T_{\scriptscriptstyle U}x_j\|}{\|x_i-x_j\|}\approx 1 [[/math]]

holds for all [math]x_i\not=x_j[/math] with high probability by picking [math]\epsilon[/math] small but [math]k[/math] so large that [math]k\epsilon^2[/math] exceeds [math]48\ln(n)[/math]. We point out here that since the logarithm grows very slowly, making the sample set larger does only require to increase [math]k[/math] a little. If we agree to pick all the families [math]x_1,\dots,x_n[/math] from within a compact set [math]K\subseteq\mathbb{R}^d[/math], then we can again achieve that

[[math]] \|T_{\scriptscriptstyle U}x_i-T_{\scriptscriptstyle U}x_j\|\approx \|x_i-x_j\| [[/math]]

holds with high probability by picking [math]\epsilon[/math] and [math]k[/math] as explained above. From this stems the interpretation that the Johnson-Lindenstrauss Lemma allows to reduce the dimension of a data set while preserving the mutual distances between the data points up to some small error. Notice that the set of points (if it is only [math]n[/math]--many) is arbitrary. In particular the projection map [math]T_{\scriptscriptstyle U}[/math] and its codomain depend only on [math]n[/math] and [math]\epsilon[/math]. That means after agreeing on the number of points we want to project and the error bound we want to achieve, we get the same estimate for all families [math]x_1,\dots,x_n[/math] of [math]n[/math]--many points. Furthermore, the estimate holds indeed for all of the [math]n[/math] points and not only most (one could think of a result saying that if we pick a pair [math](i,j)[/math] then with probability [math]1-1/n[/math] the estimate is true, which would mean that there could be some ‘bad’ pairs whose distance gets distorted by more than [math]\epsilon[/math], but this is not the case!).

The following figure shows the distortion that occurred depending on [math]k[/math] in an experiment compared with the bound provided by the Johnson-Lindenstrauss Lemma, see Problem.

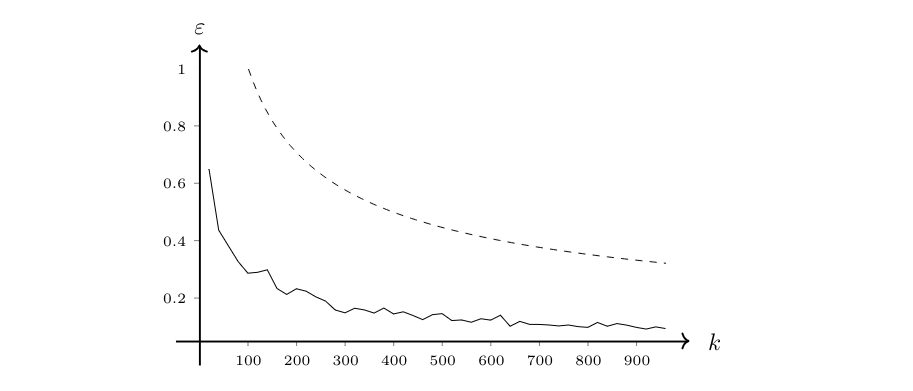
Solid line: Maximal distortion that occurs when [math]n=300[/math] points [math]x\sim\mathcal{N}(0,1,\mathbb{R}^{1000})[/math] are projected to [math]\mathbb{R}^k[/math]. Dashed line: JL-bound [math]\epsilon = (48\ln(n)/k)^{1/2}[/math]

We conclude with the following corollary that describes the length distortion for all points in [math]\mathbb{R}^d[/math] (or in a compact [math]K\subseteq\mathbb{R}^d)[/math]) that we can expect if we apply the Johnson-Lindenstrauss Projection and pick the parameters to treat sets with [math]n[/math]-many points.

Corollary

Under the assumptions of Theorem we have

[[math]] \P\bigl[(1-\epsilon)\|x\|\leqslant\|T_{\scriptscriptstyle U}x\|\leqslant (1+\epsilon)\|x\|\bigr]\geqslant 1-{\textstyle\frac{1}{n}} [[/math]]

for every [math]x\in\mathbb{R}^d[/math].

General references

Wegner, Sven-Ake (2024). "Lecture Notes on High-Dimensional Data". arXiv:2101.05841 [math.FA].