Set Theory and General Probability

Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty. Strictly speaking, a probability of 0 indicates that an event almost never takes place, whereas a probability of 1 indicates than an event almost certainly takes place. This is an important distinction when the sample space is infinite. For example, for the continuous uniform distribution on the real interval [5, 10], there are an infinite number of possible outcomes, and the probability of any given outcome being observed — for instance, exactly 7 — is 0. This means that when we make an observation, it will almost surely not be exactly 7. However, it does not mean that exactly 7 is impossible. Ultimately some specific outcome (with probability 0) will be observed, and one possibility for that specific outcome is exactly 7. The higher the probability of an event, the more likely it is that the event will occur.

These concepts have been given an axiomatic mathematical formalization in probability theory (see probability axioms), which is used widely in such areas of study as mathematics, statistics, finance, gambling, science (in particular physics), artificial intelligence/machine learning, computer science, game theory, and philosophy to, for example, draw inferences about the expected frequency of events. Probability theory is also used to describe the underlying mechanics and regularities of complex systems.

Mathematical treatment

Consider an experiment that can produce a number of results. The collection of all possible results is called the sample space of the experiment. The power set of the sample space is formed by considering all different collections of possible results. For example, rolling a dice can produce six possible results. One collection of possible results gives an odd number on the dice. Thus, the subset {1,3,5} is an element of the power set of the sample space of dice rolls. These collections are called "events." In this case, {1,3,5} is the event that the dice falls on some odd number. If the results that actually occur fall in a given event, the event is said to have occurred.

A probability is a way of assigning every event a value between zero and one, with the requirement that the event made up of all possible results (in our example, the event {1,2,3,4,5,6}) is assigned a value of one. To qualify as a probability, the assignment of values must satisfy the requirement that if you look at a collection of mutually exclusive events (events with no common results, e.g., the events {1,6}, {3}, and {2,4} are all mutually exclusive), the probability that at least one of the events will occur is given by the sum of the probabilities of all the individual events.

The probability of an event [math]A[/math] is written as [math]\operatorname{P}(A)[/math] or [math]\text{Pr}(A)[/math]. This mathematical definition of probability can extend to infinite sample spaces, and even uncountable sample spaces, using the concept of a measure.

The opposite or complement of an event [math]A[/math] is the event [not [math]A[/math]] (that is, the event of [math]A[/math] not occurring), often denoted as [math]\overline{A}, A^C, \neg A[/math], or [math]\sim A[/math]; its probability is given by [math]\operatorname{P}[/math](not [math]A[/math]) = 1 − [math]\operatorname{P}[/math]([math]A[/math]). As an example, the chance of not rolling a six on a six-sided die is 1 – (chance of rolling a six) [math]= 1 - \tfrac{1}{6} = \tfrac{5}{6}[/math].

If two events [math]A[/math] and [math]B[/math] occur on a single performance of an experiment, this is called the intersection of [math]A[/math] and [math]B[/math], denoted as [math]\operatorname{P}(A \cap B)[/math].

Independent events

If two events, [math]A[/math] and [math]B[/math] are independent then the joint probability is

[[math]]\operatorname{P}(A \mbox{ and }B) = \operatorname{P}(A \cap B) = \operatorname{P}(A) \operatorname{P}(B),\,[[/math]]

for example, if two coins are flipped the chance of both being heads is [math]\tfrac{1}{2}\times\tfrac{1}{2} = \tfrac{1}{4}[/math].

Mutually exclusive events

If either event [math]A[/math] or event [math]B[/math] occurs on a single performance of an experiment this is called the union of the events [math]A[/math] and [math]B[/math] denoted as [math]\operatorname{P}(A \cup B)[/math]. If two events are mutually exclusive then the probability of either occurring is

[[math]]\operatorname{P}(A\mbox{ or }B) = \operatorname{P}(A \cup B)= \operatorname{P}(A) + \operatorname{P}(B).[[/math]]

For example, the chance of rolling a 1 or 2 on a six-sided dice is [math]\operatorname{P}(1\mbox{ or }2) = \operatorname{P}(1) + \operatorname{P}(2) = \tfrac{1}{6} + \tfrac{1}{6} = \tfrac{1}{3}.[/math]

Not mutually exclusive events

If the events are not mutually exclusive then

[[math]]\operatorname{P}\left( A \hbox{ or } B\right)=\operatorname{P}\left( A\right)+\operatorname{P}\left( B\right)-\operatorname{P}\left( A \cap B\right).[[/math]]

For example, when drawing a single card at random from a regular deck of cards, the chance of getting a heart or a face card (J,Q,K) (or one that is both) is [math]\tfrac{13}{52} + \tfrac{12}{52} - \tfrac{3}{52} = \tfrac{11}{26}[/math], because of the 52 cards of a deck 13 are hearts, 12 are face cards, and 3 are both: here the possibilities included in the "3 that are both" are included in each of the "13 hearts" and the "12 face cards" but should only be counted once.

Conditional probability

Conditional probability is the probability of some event [math]A[/math], given the occurrence of some other event [math]B[/math]. Conditional probability is written [math]\operatorname{P}(A \mid B)[/math], and is read "the probability of [math]A[/math], given [math]B[/math]". It is defined by

[[math]]\operatorname{P}(A \mid B) = \frac{\operatorname{P}(A \cap B)}{\operatorname{P}(B)}.\,[[/math]]

If [math]\operatorname{P}(B)=0[/math] then [math]\operatorname{P}(A \mid B)[/math] is formally undefined by this expression.

For example, in a bag of 2 red balls and 2 blue balls (4 balls in total), the probability of taking a red ball is [math]1/2[/math]; however, when taking a second ball, the probability of it being either a red ball or a blue ball depends on the ball previously taken, such as, if a red ball was taken, the probability of picking a red ball again would be [math]1/3[/math] since only 1 red and 2 blue balls would have been remaining.

Summary of probabilities

Event	Probability
[math]A[/math]	[math]\operatorname{P}(A)\in[0,1]\,[/math]
not [math]A[/math]	[math]\operatorname{P}(A^c)=1-\operatorname{P}(A)\,[/math]
[math]A[/math] or [math]B[/math]	[math] \operatorname{P}(A\cup B) = \operatorname{P}(A)+\operatorname{P}(B)-\operatorname{P}(A\cap B) [/math]
[math]A[/math] and [math]B[/math]	[math] \operatorname{P}(A\cap B) = \operatorname{P}(A|B)\operatorname{P}(B) = \operatorname{P}(B|A)\operatorname{P}(A) [/math]
[math]A[/math] given [math]B[/math]	[math]\operatorname{P}(A \mid B) = \frac{\operatorname{P}(A \cap B)}{\operatorname{P}(B)} = \frac{\operatorname{P}(B|A)\operatorname{P}(A)}{\operatorname{P}(B)} \,[/math]

Inclusion–exclusion principle

Venn diagram showing the union of sets [math]A[/math] and [math]B[/math] as everything not in white

In combinatorics, a branch of mathematics, the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; symbolically expressed as

[[math]] |A \cup B| = |A| + |B| - |A \cap B| [[/math]]

where [math]A[/math] and [math]B[/math] are two finite sets and [math]|S|[/math] indicates the cardinality of a set [math]S[/math] (which may be considered as the number of elements of the set, if the set is finite). The formula expresses the fact that the sum of the sizes of the two sets may be too large since some elements may be counted twice. The double-counted elements are those in the intersection of the two sets and the count is corrected by subtracting the size of the intersection.

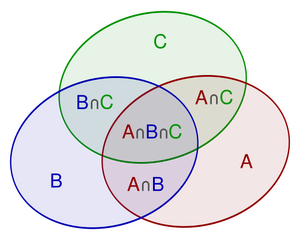
The inclusion-exclusion principle, being a generalization of the two-set case, is perhaps more clearly seen in the case of three sets, which for the sets [math]A,B[/math] and [math]C[/math] is given by

[[math]]|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|[[/math]]

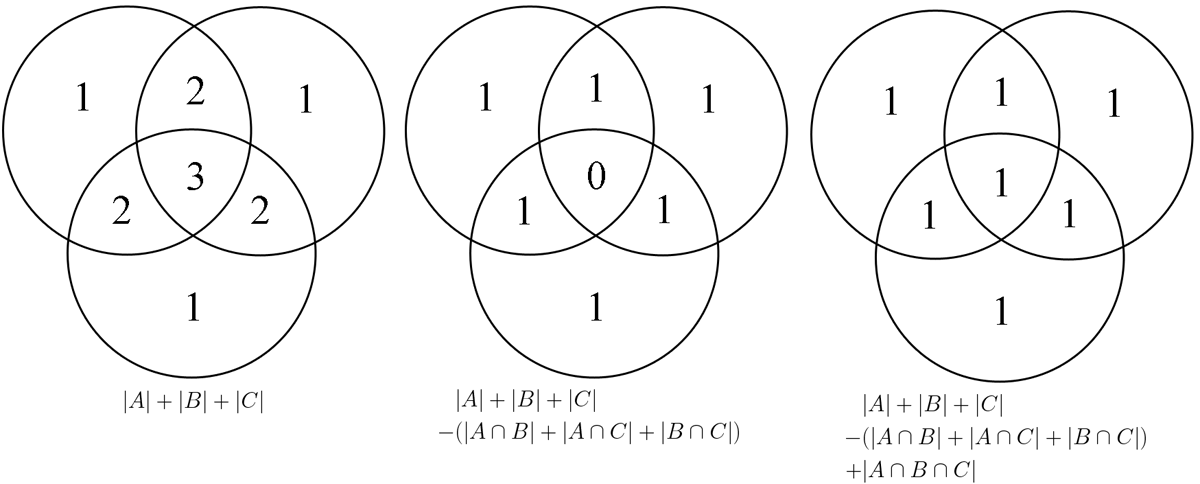
This formula can be verified by counting how many times each region in the Venn diagram figure is included in the right-hand side of the formula. In this case, when removing the contributions of over-counted elements, the number of elements in the mutual intersection of the three sets has been subtracted too often, so must be added back in to get the correct total.

Inclusion–exclusion illustrated by a Venn diagram for three sets

Generalizing the results of these examples gives the principle of inclusion–exclusion. To find the cardinality of the union of [math]n[/math] sets:

1. Include the cardinalities of the sets.
2. Exclude the cardinalities of the pairwise intersections.
3. Include the cardinalities of the triple-wise intersections.
4. Exclude the cardinalities of the quadruple-wise intersections.
5. Include the cardinalities of the quintuple-wise intersections.
6. Continue, until the cardinality of the [math]n[/math]-tuple-wise intersection is included (if [math]n[/math] is odd) or excluded ([math]n[/math] even).

The name comes from the idea that the principle is based on over-generous inclusion, followed by compensating exclusion. This concept is attributed to Abraham de Moivre (1718), although it first appears in a paper of Daniel da Silva (1854) and later in a paper by J. J. Sylvester (1883). Sometimes the principle is referred to as the formula of Da Silva or Sylvester, due to these publications. The principle can be viewed as an example of the sieve method extensively used in number theory and is sometimes referred to as the sieve formula.

As finite probabilities are computed as counts relative to the cardinality of the probability space, the formulas for the principle of inclusion–exclusion remain valid when the cardinalities of the sets are replaced by finite probabilities. More generally, both versions of the principle can be put under the common umbrella of measure theory.

In a very abstract setting, the principle of inclusion–exclusion can be expressed as the calculation of the inverse of a certain matrix. This inverse has a special structure, making the principle an extremely valuable technique in combinatorics and related areas of mathematics. As Gian-Carlo Rota| put it:

"One of the most useful principles of enumeration in discrete probability and combinatorial theory is the celebrated principle of inclusion–exclusion. When skillfully applied, this principle has yielded the solution to many a combinatorial problem."

Formula

In its general formula, the principle of inclusion–exclusion states that for finite sets [math]A_1, \ldots, A_n[/math], one has the identity

[[math]]\left|\bigcup_{i=1}^n A_i\right| = \sum_{i=1}^n |A_i| - \sum_{1 \leqslant i \lt j \leqslant n} |A_i\cap A_j| + \sum_{1 \leqslant i \lt j \lt k \leqslant n} |A_i \cap A_j\cap A_k| - \cdots + (-1)^{n+1} \left|A_1\cap\cdots\cap A_n\right|.[[/math]]

Each term of the inclusion–exclusion formula gradually corrects the count until finally each portion of the Venn diagram is counted exactly once.

This can be compactly written as

[[math]]\left|\bigcup_{i=1}^n A_i\right| = \sum_{k=1}^n (-1)^{k+1} \left( \sum_{1 \leqslant i_1 \lt \cdots \lt i_k \leqslant n} | A_{i_1} \cap \cdots \cap A_{i_k} | \right)[[/math]]

or

[[math]]\left| \bigcup_{i=1}^n A_i\right| = \sum_{\emptyset\neq J\subseteq\{1,\ldots,n\}}(-1)^{|J|+1} \left |\bigcap_{j\in J} A_j\right|.[[/math]]

In words, to count the number of elements in a finite union of finite sets, first sum the cardinalities of the individual sets, then subtract the number of elements that appear in at least two sets, then add back the number of elements that appear in at least three sets, then subtract the number of elements that appear in at least four sets, and so on. This process always ends since there can be no elements that appear in more than the number of sets in the union. (For example, if [math]n = 4,[/math] there can be no elements that appear in more than [math]4[/math] sets; equivalently, there can be no elements that appear in at least [math]5[/math] sets.)

In applications it is common to see the principle expressed in its complementary form. That is, letting [math]S[/math] be a finite universal set containing all of the [math]A_i[/math] and letting [math]\bar{A_i}[/math] denote the complement of [math]A_i[/math] in [math]S[/math], by De Morgan's laws we have

[[math]]\left|\bigcap_{i=1}^n \bar{A_i}\right| = \left|S - \bigcup_{i=1}^n A_i \right| =|S| - \sum_{i=1}^n |A_i| + \sum_{1 \leqslant i \lt j \leqslant n} |A_i\cap A_j| - \cdots + (-1)^n |A_1\cap\cdots\cap A_n|.[[/math]]

As another variant of the statement, let [math]P_1,\ldots,P_n[/math] be a list of properties that elements of a set [math]S[/math] may or may not have, then the principle of inclusion–exclusion provides a way to calculate the number of elements of [math]S[/math] that have none of the properties. Just let [math]A_i[/math] be the subset of elements of [math]S[/math] which have the property [math]P_i[/math] and use the principle in its complementary form. This variant is due to J. J. Sylvester.

Notice that if you take into account only the first [math]m \lt n[/math] sums on the right (in the general form of the principle), then you will get an overestimate if [math]m[/math] is odd and an underestimate if [math]m[/math] is even.

In probability

In probability, for events [math]A_1,\ldots,A_n[/math], the inclusion–exclusion principle becomes for [math]n=2[/math]

[[math]]\operatorname{P}(A_1\cup A_2)=\operatorname{P}(A_1)+\operatorname{P}(A_2)-\operatorname{P}(A_1\cap A_2),[[/math]]

for [math]n=3[/math]

[[math]]\operatorname{P}(A_1\cup A_2\cup A_3)=\operatorname{P}(A_1)+\operatorname{P}(A_2)+\operatorname{P}(A_3)-\operatorname{P}(A_1\cap A_2)-\operatorname{P}(A_1\cap A_3)-\operatorname{P}(A_2\cap A_3)+\operatorname{P}(A_1\cap A_2\cap A_3)[[/math]]

and in general

[[math]]\operatorname{P}\left(\bigcup_{i=1}^n A_i\right)=\sum_{i=1}^n \operatorname{P}(A_i) -\sum_{i \lt j}\operatorname{P}(A_i\cap A_j)+\sum_{i \lt j \lt k}\operatorname{P}(A_i\cap A_j\cap A_k) + \cdots +(-1)^{n-1} \sum_{i \lt...\lt n}\operatorname{P}\left(\bigcap_{i=1}^n A_i\right),[[/math]]

which can be written in closed form as

[[math]]\operatorname{P}\left(\bigcup_{i=1}^n A_i\right)=\sum_{k=1}^n \left((-1)^{k-1}\sum_{I\subseteq\{1,\ldots,n\}\atop |I|=k} \operatorname{P}(A_I)\right),[[/math]]

where the last sum runs over all subsets [math]I[/math] of the indices [math]1, \ldots, n[/math] which contain exactly [math]k[/math] elements, and

[[math]]A_I:=\bigcap_{i\in I} A_i[[/math]]

denotes the intersection of all those [math]A_i[/math] with index in [math]I[/math].

Special case

If, in the probabilistic version of the inclusion–exclusion principle, the probability of the intersection [math]A_I[/math] only depends on the cardinality of [math]I[/math], meaning that for every [math]k[/math] in {[math]1,\ldots,n[/math]} there is an [math]a_k[/math] such that

[[math]]a_k=\operatorname{P}(A_I) \text{ for every } I\subset\{1,\ldots,n\} \text{ with } |I|=k,[[/math]]

then the above formula simplifies to

[[math]]\operatorname{P}\left(\bigcup_{i=1}^n A_i\right) =\sum_{k=1}^n (-1)^{k-1}\binom n k a_k [[/math]]

due to the combinatorial interpretation of the binomial coefficient [math]\binom nk[/math]. For example, if the events [math]A_i[/math] are independent and identically distributed, then [math]\operatorname{P}(A_i) = p[/math] for all [math]i[/math], and we have [math]a_k = p^k[/math], in which case the expression above simplifies to

[[math]]\operatorname{P}\left(\bigcup_{i=1}^n A_i\right) = 1 - (1-p)^n. [[/math]]

(This result can also be derived more simply by considering the intersection of the complements of the events [math]A_i[/math].)

Wikipedia References

• Wikipedia contributors. "Probability". Wikipedia. Wikipedia. Retrieved 28 January 2022.
• Wikipedia contributors. "Inclusion–exclusion principle". Wikipedia. Wikipedia. Retrieved 1 October 2024.

Bibliography

• Kallenberg, O. (2005) Probabilistic Symmetries and Invariance Principles. Springer -Verlag, New York. 510 pp. ISBN 0-387-25115-4
• Kallenberg, O. (2002) Foundations of Modern Probability, 2nd ed. Springer Series in Statistics. 650 pp. ISBN 0-387-95313-2
• Olofsson, Peter (2005) Probability, Statistics, and Stochastic Processes, Wiley-Interscience. 504 pp ISBN 0-471-67969-0.
• Wikipedia contributors. "Probability". Wikipedia. Wikipedia. Retrieved 28 January 2022.