Discrete Choice in Single Agent Random Utility Models

[math] \newcommand{\edis}{\stackrel{d}{=}} \newcommand{\fd}{\stackrel{f.d.}{\rightarrow}} \newcommand{\dom}{\operatorname{dom}} \newcommand{\eig}{\operatorname{eig}} \newcommand{\epi}{\operatorname{epi}} \newcommand{\lev}{\operatorname{lev}} \newcommand{\card}{\operatorname{card}} \newcommand{\comment}{\textcolor{Green}} \newcommand{\B}{\mathbb{B}} \newcommand{\C}{\mathbb{C}} \newcommand{\G}{\mathbb{G}} \newcommand{\M}{\mathbb{M}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\T}{\mathbb{T}} \newcommand{\R}{\mathbb{R}} \newcommand{\E}{\mathbb{E}} \newcommand{\W}{\mathbb{W}} \newcommand{\bU}{\mathfrak{U}} \newcommand{\bu}{\mathfrak{u}} \newcommand{\bI}{\mathfrak{I}} \newcommand{\cA}{\mathcal{A}} \newcommand{\cB}{\mathcal{B}} \newcommand{\cC}{\mathcal{C}} \newcommand{\cD}{\mathcal{D}} \newcommand{\cE}{\mathcal{E}} \newcommand{\cF}{\mathcal{F}} \newcommand{\cG}{\mathcal{G}} \newcommand{\cg}{\mathcal{g}} \newcommand{\cH}{\mathcal{H}} \newcommand{\cI}{\mathcal{I}} \newcommand{\cJ}{\mathcal{J}} \newcommand{\cK}{\mathcal{K}} \newcommand{\cL}{\mathcal{L}} \newcommand{\cM}{\mathcal{M}} \newcommand{\cN}{\mathcal{N}} \newcommand{\cO}{\mathcal{O}} \newcommand{\cP}{\mathcal{P}} \newcommand{\cQ}{\mathcal{Q}} \newcommand{\cR}{\mathcal{R}} \newcommand{\cS}{\mathcal{S}} \newcommand{\cT}{\mathcal{T}} \newcommand{\cU}{\mathcal{U}} \newcommand{\cu}{\mathcal{u}} \newcommand{\cV}{\mathcal{V}} \newcommand{\cW}{\mathcal{W}} \newcommand{\cX}{\mathcal{X}} \newcommand{\cY}{\mathcal{Y}} \newcommand{\cZ}{\mathcal{Z}} \newcommand{\sF}{\mathsf{F}} \newcommand{\sM}{\mathsf{M}} \newcommand{\sG}{\mathsf{G}} \newcommand{\sT}{\mathsf{T}} \newcommand{\sB}{\mathsf{B}} \newcommand{\sC}{\mathsf{C}} \newcommand{\sP}{\mathsf{P}} \newcommand{\sQ}{\mathsf{Q}} \newcommand{\sq}{\mathsf{q}} \newcommand{\sR}{\mathsf{R}} \newcommand{\sS}{\mathsf{S}} \newcommand{\sd}{\mathsf{d}} \newcommand{\cp}{\mathsf{p}} \newcommand{\cc}{\mathsf{c}} \newcommand{\cf}{\mathsf{f}} \newcommand{\eU}{{\boldsymbol{U}}} \newcommand{\eb}{{\boldsymbol{b}}} \newcommand{\ed}{{\boldsymbol{d}}} \newcommand{\eu}{{\boldsymbol{u}}} \newcommand{\ew}{{\boldsymbol{w}}} \newcommand{\ep}{{\boldsymbol{p}}} \newcommand{\eX}{{\boldsymbol{X}}} \newcommand{\ex}{{\boldsymbol{x}}} \newcommand{\eY}{{\boldsymbol{Y}}} \newcommand{\eB}{{\boldsymbol{B}}} \newcommand{\eC}{{\boldsymbol{C}}} \newcommand{\eD}{{\boldsymbol{D}}} \newcommand{\eW}{{\boldsymbol{W}}} \newcommand{\eR}{{\boldsymbol{R}}} \newcommand{\eQ}{{\boldsymbol{Q}}} \newcommand{\eS}{{\boldsymbol{S}}} \newcommand{\eT}{{\boldsymbol{T}}} \newcommand{\eA}{{\boldsymbol{A}}} \newcommand{\eH}{{\boldsymbol{H}}} \newcommand{\ea}{{\boldsymbol{a}}} \newcommand{\ey}{{\boldsymbol{y}}} \newcommand{\eZ}{{\boldsymbol{Z}}} \newcommand{\eG}{{\boldsymbol{G}}} \newcommand{\ez}{{\boldsymbol{z}}} \newcommand{\es}{{\boldsymbol{s}}} \newcommand{\et}{{\boldsymbol{t}}} \newcommand{\ev}{{\boldsymbol{v}}} \newcommand{\ee}{{\boldsymbol{e}}} \newcommand{\eq}{{\boldsymbol{q}}} \newcommand{\bnu}{{\boldsymbol{\nu}}} \newcommand{\barX}{\overline{\eX}} \newcommand{\eps}{\varepsilon} \newcommand{\Eps}{\mathcal{E}} \newcommand{\carrier}{{\mathfrak{X}}} \newcommand{\Ball}{{\mathbb{B}}^{d}} \newcommand{\Sphere}{{\mathbb{S}}^{d-1}} \newcommand{\salg}{\mathfrak{F}} \newcommand{\ssalg}{\mathfrak{B}} \newcommand{\one}{\mathbf{1}} \newcommand{\Prob}[1]{\P\{#1\}} \newcommand{\yL}{\ey_{\mathrm{L}}} \newcommand{\yU}{\ey_{\mathrm{U}}} \newcommand{\yLi}{\ey_{\mathrm{L}i}} \newcommand{\yUi}{\ey_{\mathrm{U}i}} \newcommand{\xL}{\ex_{\mathrm{L}}} \newcommand{\xU}{\ex_{\mathrm{U}}} \newcommand{\vL}{\ev_{\mathrm{L}}} \newcommand{\vU}{\ev_{\mathrm{U}}} \newcommand{\dist}{\mathbf{d}} \newcommand{\rhoH}{\dist_{\mathrm{H}}} \newcommand{\ti}{\to\infty} \newcommand{\comp}[1]{#1^\mathrm{c}} \newcommand{\ThetaI}{\Theta_{\mathrm{I}}} \newcommand{\crit}{q} \newcommand{\CS}{CS_n} \newcommand{\CI}{CI_n} \newcommand{\cv}[1]{\hat{c}_{n,1-\alpha}(#1)} \newcommand{\idr}[1]{\mathcal{H}_\sP[#1]} \newcommand{\outr}[1]{\mathcal{O}_\sP[#1]} \newcommand{\idrn}[1]{\hat{\mathcal{H}}_{\sP_n}[#1]} \newcommand{\outrn}[1]{\mathcal{O}_{\sP_n}[#1]} \newcommand{\email}[1]{\texttt{#1}} \newcommand{\possessivecite}[1]{\citeauthor{#1}'s \citeyear{#1}} \newcommand\xqed[1]{% \leavevmode\unskip\penalty9999 \hbox{}\nobreak\hfill \quad\hbox{#1}} \newcommand\qedex{\xqed{$\triangle$}} \newcommand\independent{\perp\!\!\!\perp} \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\cov}{Cov} \DeclareMathOperator{\var}{Var} \DeclareMathOperator{\Sel}{Sel} \DeclareMathOperator{\Bel}{Bel} \DeclareMathOperator{\cl}{cl} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\essinf}{essinf} \DeclareMathOperator{\esssup}{esssup} \newcommand{\mathds}{\mathbb} \renewcommand{\P}{\mathbb{P}} [/math]

In this section I focus on the literature concerned with learning features of structural econometric models. These are models where economic theory is used to postulate relationships among observable outcomes [math]\ey[/math], observable covariates [math]\ex[/math], and unobservable variables [math]\nu[/math]. For example, economic theory may guide assumptions on economic behavior (e.g., utility maximization) and equilibrium that yield a mapping from [math](\ex,\nu)[/math] to [math]\ey[/math]. The researcher is interested in learning features of these relationships (e.g., utility function, distribution of preferences), and to this end may supplement the data and economic theory with functional form assumptions on the mapping of interest and distributional assumptions on the observable and unobservable variables. The earlier literature on partial identification of features of structural models includes important examples of nonparametric analysis of random utility models and revealed preference extrapolation, e.g. , , , , , , and others.

The earlier literature also addresses semiparametric analysis, where the underlying models are specified up to parameters that are finite dimensional (e.g., preference parameters) and parameters that are infinite dimensional (e.g., distribution functions); important examples include , , , , , , , , , , , , and others. Contrary to the nonparametric bounds results discussed in Section, and especially in the case of semiparametric models, structural partial identification often yields an identification region that is not constructive. Indeed, the boundary of the set is not obtained in closed form as a functional of the distribution of the observable data. Rather, the identification region can often be characterized as a level set of a properly specified criterion function. The recent spark of interest in partial identification of structural microeconometric models was fueled by the work of , and , and . Each of these papers has advanced the literature in fundamental ways, studying conceptually very distinct problems. are concerned with partial identification of the decision process yielding binary outcomes in a semiparametric model, when one of the explanatory variables is interval valued.

Hence, the root cause of the identification problem they study is that the data is incomplete.

and are concerned with identification (and estimation) of simultaneous equation models with dummy endogeneous variables which are representations of two-player entry games with multiple equilibria. are concerned with nonparametric identification and estimation of the distribution of valuations in a model of English auctions under weak assumptions on bidders' behavior. In both cases, the root cause of the identification problem is that the structural model is incomplete. This is because the model makes multiple predictions for the observed outcome variables (respectively: the players' actions; and the bidders' bids), but does not specify how one of them is selected to yield the observed data.

Set-valued predictions for the observable outcome (endogenous variables) are a key feature of partially identified structural models. The goal of this section is to explain how they result in a wide array of theoretical frameworks, and how sharp identification regions can be characterized using a unified approach based on random set theory. Although the work of , and , and has spurred many of the developments discussed in this section, for pedagogical reasons I organize the presentation based on application topic rather than chronologically. The work of and further stimulated a large empirical literature that applies partial identification methods to a wide array of questions of substantive economic importance, to which I return in Section Further Theoretical Advances and Empirical Applications.

Let [math]\cI[/math] denote a population of decision makers and [math]\cY=\{c_1,\dots,c_{|\cY|}\}[/math] a finite universe of potential alternatives (feasible set henceforth). Let [math]\bU[/math] be a family of real valued functions defined over the elements of [math]\cY[/math]. Let [math]\in^* [/math] denote “is chosen from.” Then observed choice is consistent with a ’'random utility model if there exists a function [math]\bu_i[/math] drawn from [math]\bU[/math] according to some probability distribution, such that [math]\P(c \in^* C)=\P(\bu_i(c) \ge \bu_i(b)\forall b \in C)[/math] for all [math]c\in C[/math], all non empty sets [math]C \subset \cY[/math], and all [math]i\in\cI[/math] . See for a textbook presentation of this class of models, and for a review of sufficient conditions for point identification of nonparametric and semiparametric limited dependent variables models. As in the seminal work of , assume that the decision makers and alternatives are characterized by observable and unobservable vectors of real valued attributes. Denote the observable attributes by [math]\ex_i \equiv \{\ex_i^1,(\ex_{ic}^2,c\in\cY)\},i\in\cI[/math]. These include attribute vectors [math]\ex_i^1[/math] that are specific to the decision maker, as well as attribute vectors [math]\ex_{ic}^2[/math] that include components that are specific to the alternative and components that are indexed by both. Denote the unobservable attributes (preferences) by [math]\nu_i\equiv(\zeta_i,\{\epsilon_{ic},c\in\cY\}),i\in\cI[/math]. These are idiosyncratic to the decision maker and similarly may include alternative and decision maker specific terms. Denote [math]\cX,\cV[/math] the supports of [math]\ex,\nu[/math], respectively. In what follows, I label “standard” a random utility model that maintains some form of exogeneity for [math]\ex_i[/math] (e.g., mean or quantile or statistical independence with [math]\nu_i[/math]) and presupposes observation of data that include [math]\{(\eC_i,\ey_i,\ex_i):\ey_i \in^* \eC_i\}, i=1,\dots,n[/math], with [math]\eC_i[/math] the choice set faced by decision maker [math]i[/math] and [math]|\eC_i|\ge 2[/math] (e.g., ). Often it is also assumed that all members of the population face the same choice set, [math]\eC_i=D[/math] for all [math]i\in\cI[/math] and some known [math]D\subseteq\cY[/math], although this requirement is not critical to identification analysis.

Semiparametric Binary Choice Models with Interval Valued Covariates

provide inference methods for nonparametric, semiparametric, and parametric conditional expectation functions when one of the conditioning variables is interval valued. I have discussed their nonparametric and parametric sharp bounds on conditional expectations with interval valued covariates in Identification Problems and, and Theorems SIR- and SIR-, respectively. Here I focus on their analysis of semiparametric binary choice models. Compared to the generic notation set forth at the beginning of Section Discrete Choice in Single Agent Random Utility Models, I let [math]\eC_i=\cY=\{0,1\}[/math] for all [math]i\in\cI[/math], and with some abuse of notation I denote the vector of observed covariates [math](\xL,\xU,\ew)[/math].

Identification Problem (Semiparametric Binary Regression with Interval Covariate Data)

Let [math](\ey,\xL,\xU,\ew)\sim\sP[/math] be observable random variables in [math]\{0,1\}\times\R\times\R\times\R^d[/math], [math]d \lt \infty[/math], and let [math]\ex\in\R[/math] be an unobservable random variable. Let [math]\ey=\one(\ew\theta + \delta\ex +\epsilon \gt 0)[/math]. Assume [math]\delta \gt 0[/math], and further normalize [math]\delta=1[/math] because the threshold-crossing condition is invariant to the scale of the parameters. Here [math]\epsilon[/math] is an unobserved heterogeneity term with continuous distribution conditional on [math](\ew,\ex,\xL,\xU)[/math], [math](\ew,\ex,\xL,\xU)[/math]-a.s., and [math]\theta\in\Theta\subset\R^d[/math] is a parameter vector representing decision makers’ preferences, with compact parameter space [math]\Theta[/math]. Assume that [math]\sR[/math], the joint distribution of [math](\ey,\ex,\xL,\xU,\ew,\epsilon)[/math], is such that [math]\sR(\xL\le\ex\le\xU)=1[/math]; [math] \sR(\epsilon |\ew,\ex,\xL,\xU)=\sR(\epsilon|\ew,\ex)[/math]; and for a specified [math]\alpha \in (0,1)[/math], [math]\sq_{\sR}^\epsilon(\alpha,\ew,\ex)=0[/math] and [math]\sR(\epsilon \le 0|\ew,\ex)=\alpha[/math], [math](\ew,\ex)[/math]-a.s.. In the absence of additional information, what can the researcher learn about [math]\theta[/math]?

Compared to Identification Problem, here one continues to impose [math]\ex\in[\xL,\xU][/math] a.s. The sign restriction on [math]\delta[/math] replaces the monotonicity restriction (M) in Identification Problem, but does not imply it unless the distribution of [math]\epsilon[/math] is independent of [math]\ex[/math] conditional on [math]\ew[/math]. The quantile independence restriction is inspired by . For given [math]\theta\in\Theta[/math], this model yields set valued predictions because [math]\ey=1[/math] can occur whenever [math]\epsilon \gt -\ew\theta-\xU[/math], whereas [math]\ey=0[/math] can occur whenever [math]\epsilon\le -\ew\theta-\xL[/math], and [math]-\ew\theta-\xU \le -\ew\theta-\xL[/math]. Conversely, observation of [math]\ey=1[/math] allows one to conclude that [math]\epsilon\in(-\ew\theta-\xU,+\infty)[/math], whereas observation of [math]\ey=0[/math] allows one to conclude that [math]\epsilon\in(-\infty,-\ew\theta-\xL][/math], and these regions of possible realizations of [math]\epsilon[/math] overlap. In contrast, when [math]\ex[/math] is observed the prediction is unique because the value [math]-\ew\theta-\ex[/math] partitions the space of realizations of [math]\epsilon[/math] in two disjoint sets, one associated with [math]\ey=1[/math] and the other with [math]\ey=0[/math]. Figure depicts the model's set-valued predictions for [math]\ey[/math] given [math](\ew,\xL,\xU)[/math] as a function of [math]\epsilon[/math], and the model's set valued predictions for [math]\epsilon[/math] given [math](\ew,\xL,\xU)[/math] as a function of [math]\ey[/math]. Why does this set-valued prediction hinder point identification? The reason is that the distribution of the observable data relates to the model structure in an incomplete manner. The model predicts [math]\sM(\ey=1|\ew,\xL,\xU)=\int \sR(\ey=1|\ew,\ex,\xL,\xU)d\sR(\ex|\ew,\xL,\xU)=\int \sR(\epsilon \gt -\ew\theta-\ex|\ew,\ex)d\sR(\ex|\ew,\xL,\xU),(\ew,\xL,\xU)[/math]-a.s. Because the distribution [math]\sR(\ex|\ew,\xL,\xU)[/math] is left completely unspecified, one can find multiple values for [math](\theta,\sR(\ex|\ew,\xL,\xU),\sR(\epsilon|\ew,\ex))[/math], satisfying the assumptions in Identification Problem, such that [math]\sM(\ey=1|\ew,\xL,\xU)=\sP(\ey=1|\ew,\xL,\xU),(\ew,\xL,\xU)[/math]-a.s. Nonetheless, in general, not all values of [math]\theta\in\Theta[/math] can be paired with some [math]\sR(\ex|\ew,\xL,\xU)[/math] and [math]\sR(\epsilon|\ew,\ex)[/math] so that they are compatible with [math]\sP(\ey=1|\ew,\xL,\xU),(\ew,\xL,\xU)[/math]-a.s. and with the maintained assumptions. Hence, [math]\theta[/math] can be partially identified using the information in the model and observed data.

Predicted value of [math]\ey[/math] as a function of [math]\epsilon[/math], and admissible values of [math]\epsilon[/math] for each realization of [math]\ey[/math], in Identification Problem, conditional on [math](\ew,\xL,\xU)[/math].

Theorem (Semiparametric Binary Regression with Interval Covariate Data)

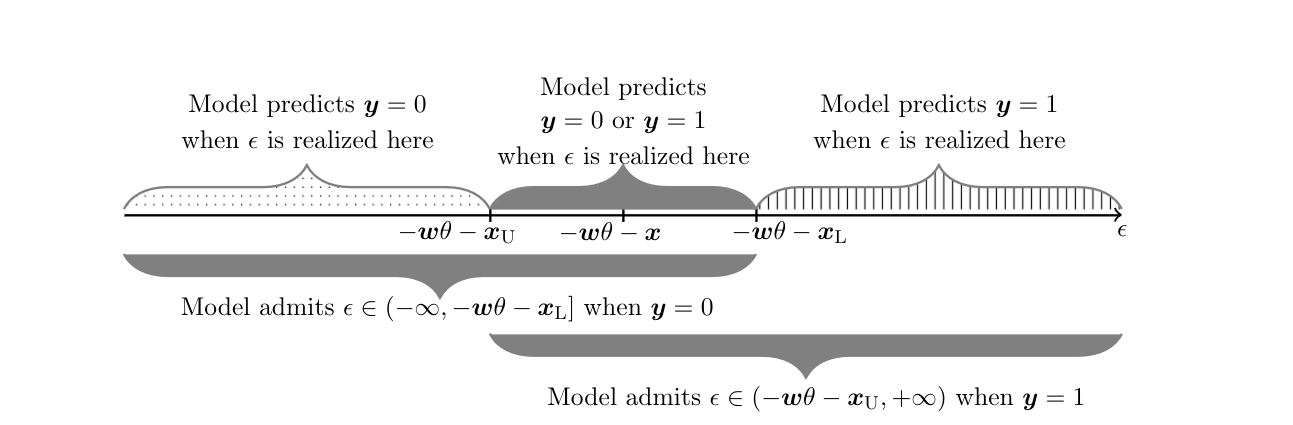
Under the Assumptions of Identification Problem, the sharp identification region for [math]\theta[/math] is

[[math]] \begin{multline} \idr{\theta}=\Big\{\vartheta\in \Theta: \sP\Big((\ew,\xL,\xU):\, \{0\le\ew\vartheta+\xL\cap \sP(\ey=1|\ew,\xL,\xU)\le 1-\alpha\}\\ \cup \{\ew\vartheta+\xU\le 0\cap \sP(\ey=1|\ew,\xL,\xU)\ge 1-\alpha\}\Big) = 0 \Big\}.\label{eq:ThetaI_man:tam02_binary} \end{multline} [[/math]]

Show Proof

For any [math]\vartheta\in\Theta[/math], define the set of possible values for the unobservable associated with the possible realizations of [math](\ey,\ew,\xL,\xU)[/math], illustrated in Figure, as

[[math]] \begin{align} \Eps_\vartheta(\ey,\ew,\xL,\xU) =\left \{ \begin{array}{ll} (-\infty,-\ew\vartheta-\xL] & \textrm{if} &\ey=0,\\ [-\ew\vartheta-\xU,+\infty) & \textrm{if} &\ey=1. \end{array} \right.\label{eq:def_Epsilon:man:tam} \end{align} [[/math]]

Then [math]\Eps_\vartheta(\ey,\ew,\xL,\xU)[/math] is a random closed set as per Definition. To simplify notation, let [math]\Eps_\vartheta(\ey)\equiv\Eps_\vartheta(\ey,\ew,\xL,\xU)[/math] suppressing the dependence on [math](\ew,\xL,\xU)[/math]. Let [math](\Eps_\vartheta(\ey),\ew,\xL,\xU)=\Eps_\vartheta(\ey)\times(\ew,\xL,\xU)=\{(\mathbf{e},\ew,\xL,\xU):\mathbf{e}\in\Eps_\vartheta(\ey)\}[/math]. If the model is correctly specified, for the data generating value [math]\theta[/math], [math](\epsilon,\ew,\xL,\xU) \in (\Eps_\theta(\ey),\ew,\xL,\xU)[/math] a.s. By Theorem and Theorem 2.33 in , this occurs if and only if

[[math]] \begin{align} \sR(\epsilon\in C|\ew,\xL,\xU)&\ge \sP(\Eps_\theta(\ey)\subset C|\ew,\xL,\xU),(\ew,\xL,\xU)\text{-a.s.}\forall C\in\cF,\label{eq:Artstein_on_man:tam} \end{align} [[/math]]

where [math]\cF[/math] here denotes the collection of closed subsets of [math]\R[/math]. We then have that [math]\vartheta[/math] is observationally equivalent to [math]\theta[/math] if and only if \eqref{eq:Artstein_on_man:tam} holds for [math]\Eps_\vartheta(\ey)[/math] as defined in \eqref{eq:def_Epsilon:man:tam}. The condition can be rewritten as

[[math]] \begin{align*} \int \sR(\epsilon\in C|\ew,\ex,\xL,\xU)d\sR(\ex|\ew,\xL,\xU)&\ge \sP(\Eps_\vartheta(\ey)\subset C|\ew,\xL,\xU),(\ew,\xL,\xU)\text{-a.s.}\forall C\in\cF. \end{align*} [[/math]]

The assumption that [math]\sR(\epsilon|\ew,\ex,\xL,\xU)=\sR(\epsilon|\ew,\ex)[/math] yields that the above system of inequalities reduces to

[[math]] \begin{align*} \int \sR(\epsilon\in C|\ew,\ex)d\sR(\ex|\ew,\xL,\xU)&\ge \sP(\Eps_\vartheta(\ey)\subset C|\ew,\xL,\xU),(\ew,\xL,\xU)\text{-a.s.}\forall C\in\cF. \end{align*} [[/math]]

Next, note that given the possible realizations of [math]\Eps_\vartheta(\ey)[/math], the above inequality is trivially satisfied unless [math]C=(-\infty,t][/math] or [math]C=[t,\infty)[/math] for some [math]t\in\R[/math]. Finally, the only restriction on the distribution of [math]\epsilon[/math] is the quantile independence condition, hence it suffices to consider [math]t=0[/math]. To see why this is the case, let for example [math]t \gt 0[/math] and fix a realization [math](w,x_L,x_U)[/math] for [math](\ew,\xL,\xU)[/math]. Then for the inequality not to be trivially satisfied it must be that either [math]w\vartheta+x_L\ge -t[/math] or [math]w\vartheta+x_U\le -t[/math] (both are not possible because [math]w\vartheta+x_L\le w\vartheta+x_U[/math]). If [math]w\vartheta+x_U\le -t[/math], it must be that [math]t\in(0,-w\vartheta-x_U][/math] and [math]-w\vartheta-x_U \gt 0[/math]. Then a distribution [math]\sR[/math] such that [math]\int \sR(\epsilon\in [0,t)|\ew=w,\ex)d\sR(\ex|\ew=w,\xL=x_L,\xU=x_U)=0[/math] is always feasible for [math]t\in(0,-w\vartheta-x_U][/math]. A similar argument holds if [math]w\vartheta+x_L\ge -t[/math]; and also if [math]t \lt 0[/math]. We then have that if the inequalities are satisfied for [math]t=0[/math], they are satisfied also for [math]t\neq 0[/math]. Finally, using the definition of [math]\Eps_\vartheta(\ey)[/math], for [math]t=0[/math] we have

[[math]] \begin{align} 1-\alpha &\ge \sP(\ey=1|\ew,\xL,\xU)\text{for all}(\ew,\xL,\xU)\text{such that } \ew\vartheta+\xU\le 0,\label{eq:key_sharp:man:tam02_1}\\ 1-\alpha & \le \sP(\ey=1|\ew,\xL,\xU)\text{for all}(\ew,\xL,\xU)\text{such that } \ew\vartheta+\xL \ge 0.\label{eq:key_sharp:man:tam02_2} \end{align} [[/math]]

Any given [math]\vartheta\in\Theta[/math], [math]\vartheta\neq\theta[/math], violates the above conditions if and only if [math]\sP\big((\ew,\xL,\xU):\, \{0\le\ew\vartheta+\xL\cap \sP(\ey=1|\ew,\xL,\xU)\le 1-\alpha\}\cup \{\ew\vartheta+\xU\le 0\cap \sP(\ey=1|\ew,\xL,\xU)\ge 1-\alpha\}\big) \gt 0[/math].

■

Key Insight: The analysis in systematically studies what can be learned under increasingly strong sets of assumptions. These include both assumptions that constrain the model from fully nonparametric to semiparametric to parametric, as well as assumptions that constrain the distribution of the observable covariates. For example, provide sufficient conditions on the joint distribution of [math](\ew,\xL,\xU)[/math] that allow for identification of the sign of components of [math]\theta[/math], as well as for point identification of [math]\theta[/math]. The careful analysis of the identifying power of increasingly stronger assumptions is the pillar of the partial identification approach to empirical research proposed by Manski, as illustrated in Section. The work of was the first example of this kind in semiparametric structural models.

Revisiting study of Identification Problem nearly 20 years later yields important insights on the differences between point and partial identification analysis. It is instructive to take as a point of departure the analysis of , which under the additional assumption that [math](\ey,\ew,\ex)[/math] is observed yields

[[math]] \begin{align*} \ew\theta+\ex \gt 0 \Leftrightarrow \sP(\ey=1|\ew,\ex) \gt 1-\alpha. \end{align*} [[/math]]

In this case, [math]\theta[/math] is identified relative to [math]\vartheta\in\Theta[/math] if

[[math]] \begin{align} \sP\left((\ew,\ex):\, \{\ew\theta+\ex\le 0 \lt \ew\vartheta+\ex\} \cup \{\ew\vartheta+\ex\le 0 \lt \ew\theta+\ex\}\right) \gt 0.\label{eq:manski85} \end{align} [[/math]]

extend this reasoning to the case that [math]\ex[/math] is unobserved, but known to satisfy [math]\ex\in [\xL,\xU][/math] a.s. The first part of their analysis, collected in their Proposition 2, characterizes the collection of values that cannot be distinguished from [math]\theta[/math] on the basis of [math]\sP(\ew,\xL,\xU)[/math] alone, through a clear generalization of \eqref{eq:manski85}:

[[math]] \begin{align} \{\vartheta\in \Theta: \sP\left((\ew,\xL,\xU):\, \{\ew\theta+\xU\le 0 \lt \ew\vartheta+\xL\} \cup \{\ew\vartheta+\xU\le 0 \lt \ew\theta+\xL\}\right) = 0\}.\label{eq:region:man:tam02:potential} \end{align} [[/math]]

It is worth emphasizing that the characterization in \eqref{eq:region:man:tam02:potential} depends on [math]\theta[/math], and makes no use of the information in [math]\sP(\ey|\ew,\xL,\xU)[/math]. The Corollary to Proposition 2 yields conditions on [math]\sP(\ew,\xL,\xU)[/math] under which either the sign of components of [math]\theta[/math], or [math]\theta[/math] itself, can be identified, regardless of the distribution of [math]\ey|\ew,\xL,\xU[/math]. provide a second characterization, which presupposes knowledge of [math]\sP(\ey,\ew,\xL,\xU)[/math], yields a set smaller than the one in \eqref{eq:region:man:tam02:potential}, and coincides with the result in Theorem SIR-. use the same notation for the two sets, although the sets are conceptually and mathematically distinct. The result in Theorem SIR- is due to , but the proof provided here is new, as is the use of random set theory in this application.

Key Insight:The preceding discussion allows me to draw a novel connection between the two characterizations in , and the distinction put forward by and in partial identification between potential observational equivalence and observational equivalence. Applying 's definition, parameter vectors [math]\theta[/math] and [math]\vartheta[/math] are potentially observationally equivalent if there exists some distribution of [math]\ey|\ew,\xL,\xU[/math] for which conditions \eqref{eq:key_sharp:man:tam02_1}-\eqref{eq:key_sharp:man:tam02_2} hold. Simple algebra confirms that this yields the region in \eqref{eq:region:man:tam02:potential}. This notion of potential observational equivalence parallels one of the notions used to obtain sufficient conditions for point identification in the semiparametric literature (as in, e.g. ). Both notions, as explained in , make no reference to the conditional distribution of outcomes given covariates delivered by the process being studied. To obtain that parameters [math]\theta[/math] and [math]\vartheta[/math] are observationally equivalent one requires instead that conditions \eqref{eq:key_sharp:man:tam02_1}-\eqref{eq:key_sharp:man:tam02_2} hold for the observed distribution [math]\sP(\ey=1|\ew,\xL,\xU)[/math] (as opposed to “for some distribution” as in the case of potential observational equivalence). This yields the sharp identification region in \eqref{eq:ThetaI_man:tam02_binary}.

studies random ’'expected utility models, where agents choose the alternative that maximizes their expected utility. The core difference with standard models is that does not fully specify the subjective beliefs that agents use to form their expectations, but only a set of such beliefs. shows that the resulting, partially identified, discrete choice model can be formulated similarly to how treat interval valued covariates, and leverages their results to obtain bounds on preference parameters.

consider a different but closely related model to the semiparametric binary response model studied by . They assume that an instrumental variable [math]\ez[/math] is available, that [math]\epsilon[/math] is independent of [math]\ex[/math] conditional on [math](\ew,\ez)[/math], and that [math]Corr(\ez,\epsilon)=0[/math]. They assume that the distribution of [math]\ex[/math] is absolutely continuous with support [math][v_1,v_k][/math], and that [math]\ex[/math] is not a deterministic linear function of [math](\ew,\ez)[/math]. They consider the case that [math]\ex[/math] is unobserved but known to belong to one of the fixed (and known) intervals [math][v_i,v_{i+1})[/math], [math]i=1,\dots,k-1[/math], with [math]\sR[\ex\in[v_i,v_{i+1})|\ew,\ez] \gt 0[/math] almost surely for all [math]i[/math]. Finally, they assume that [math](-\ew\theta-\epsilon)\in [v_1,v_k][/math] with probability one. They do not, however, make quantile independence assumptions. Their point of departure is the fact that under these conditions, if [math]\ex[/math] were observed, one could employ a transformation proposed by for the binary outcome [math]\ey[/math], such that [math]\theta[/math] can be identified through a simple linear moment condition. Specifically, let

[[math]] \begin{align*} \tilde{\ey}=\frac{\ey - \one_{\ex \gt 0}}{f_\ex(\ex|\ew,\ez)}, \end{align*} [[/math]]

where [math]f_\ex(\cdot|\ew,\ez)[/math] is the conditional density function of [math]\ex[/math]. Then, using the assumption that [math]\ez[/math] and [math]\epsilon[/math] are uncorrelated, one has

[[math]] \begin{align} \E_\sP(\ez \tilde{\ey})-\E_\sP(\ez \ew^\top) \theta = 0.\label{eq:sem-bin} \end{align} [[/math]]

With interval valued [math]\ex[/math], denote by [math]\ex^*[/math] the random variable that takes value [math]i\in\{1,\dots,k-1\}[/math] if [math]\ex\in[v_i,v_{i+1})[/math], so that the observed data are draws from the joint distribution of [math](\ey,\ew,\ez,\ex^*)[/math]. They let [math]\delta(\ex^*)=v_{\ex^*+1}-v_{\ex^*}[/math] denote the length of the [math]\ex^*[/math]-th interval, and define the transformed outcome variable:

[[math]] \ey^*=\frac{\delta(\ex^*)}{\sP(\ex^*=i|\ew,\ez)}\ey-v_k. [[/math]]

The assumptions on [math]\ex[/math] yield that, given [math]\ez[/math] and [math]\ew[/math], [math]\epsilon[/math] does not depend on [math]\ex^*[/math]. Moreover, [math]\sP(\ey=1|\ex^*,\ew,\ez)[/math] is non-decreasing in [math]\ex^*[/math] and [math]\sF_\epsilon(\cdot|\ez,\ew,\ex,\ex^*)=\sF_\epsilon(\cdot|\ez,\ew)[/math]. show that the sharp identification region for [math]\theta[/math] is

[[math]] \begin{align} \idr{\theta}=\E_\sP(\ez \ew^\top)^{-1}\E_\sP(\ez \ey^* + \ez \eU),\label{eq:SIR:mag:mau} \end{align} [[/math]]

where [math]\E_\sP(\ez \ey^* + \ez \eU)[/math] is the Aumann (or selection) expectation of the random interval [math]\ez \ey^* + \ez \eU[/math], see Definition, with

[[math]] \begin{align*} \eU=\left[-\sum_{i=1}^{k-1}(r_i(\ew,\ez)-r_{i-1}(\ew,\ez))(v_{i+1}-v_i), \sum_{i=1}^{k-1}(r_{i+1}(\ew,\ez)-r_i(\ew,\ez))(v_{i+1}-v_i) \right]. \end{align*} [[/math]]

In this expression, [math]r_{\ex^*}(\ew,\ez)\equiv\sP(\ey=1|\ex^*,\ew,\ez)[/math] and by convention [math]r_0(\ew,\ez)=0[/math] and [math]r_K(\ew,\ez)=1[/math], see . If [math]r_i(\ew,\ez),i=0,\dots,k[/math], were observed, this characterization would be very similar to the one provided by for Identification Problem, see equation eq:ThetaI_BLP. However, these random functions need to be estimated. While the first-stage estimation of [math]r_i(\ew,\ez),i=0,\dots,k[/math], does not affect the identification arguments, it does complicate inference, see and the discussion in Section.

Endogenous Explanatory Variables

Whereas the standard random utility model presumes some form of exogeneity for [math]\ex[/math], in practice often some explanatory variables are endogenous. This problem has been addressed in the literature to obtain point identification of the model through a combination of several assumptions, including large support conditions, special regressors, control function restrictions, and more (see, e.g., ). analyze the distinct but related problem of identification in a censored regression model with endogeneous explanatory variables, and provide sufficient conditions for point identification. Here I discuss how to carry out identification analysis in the absence of such assumptions when instrumental variables [math]\ez[/math] are available, as proposed by . They consider a more general case than I do here, with utility function that is not parametrically specified and not restricted to be separable in the unobservables. Even in that more general case, the identification analysis follows through similar steps as reported here.

Identification Problem (Discrete Choice with Endogenous Explanatory Variables)

Let [math](\ey,\ex,\ez)\sim\sP[/math] be observable random variables in [math]\cY\times\cX\times\cZ[/math]. Let all members of the population face the same choice set [math]\cY[/math]. Suppose that each alternative has one unobservable attribute [math]\epsilon_c,c\in\cY[/math] and let [math]\nu\equiv(\epsilon_{c_1},\dots,\epsilon_{c_{|\cY|}})[/math]. Let [math]\nu\sim\sQ[/math] and assume that [math]\nu\independent\ez[/math]. Suppose [math]\sQ[/math] belongs to a nonparametric family of distributions [math]\cT[/math], and that the conditional distribution of [math]\nu|\ex,\ez[/math], denoted [math]\sR(\nu|\ex,\ez)[/math], is absolutely continuous with respect to Lebesgue measure with everywhere positive density on its support, [math](\ex,\ez)[/math]-a.s. Suppose utility is separable in unobservables and has a functional form known up to finite dimensional parameter vector [math]\theta\in\Theta\subset\R^m[/math], so that [math]\bu_i(c)=g(\ex_c;\theta)+\epsilon_c[/math], [math](\ex_c,\epsilon_c)[/math]-a.s., for all [math]c\in\cY[/math]. Maintain the normalizations [math]g(\ex_{c_{|\cY|}};\theta)=0[/math] for all [math]\theta\in\Theta[/math] and all [math]\ex\in\cX[/math], and [math]g(x_c^0;\theta)=\bar{g}[/math] for known [math](x_c^0,\bar{g})[/math] for all [math]\theta\in\Theta[/math] and [math]c\in\cY[/math]. Given [math](\ex,\ez,\nu)[/math], suppose [math]\ey[/math] is the utility maximizing choice in [math]\cY[/math]. In the absence of additional information, what can the researcher learn about [math](\theta,\sQ)[/math]?

The key challenge to identification here results because the distribution of [math]\nu[/math] can vary across different values of [math]\ex[/math], both conditional and unconditional on [math]\ez[/math]. Why does this fact hinder point identification? For a given [math]\vartheta\in\Theta[/math] and for any [math]c\in\cY[/math] and [math]x\in\cX[/math], the model yields that [math]c[/math] is optimal, and hence chosen, if and only if [math]\nu[/math] realizes in the set

[[math]] \begin{align} \cE_\vartheta(c,x)=\{e\in\cV:g(x_c;\vartheta)+e_c\ge g(x_d;\vartheta)+e_d\forall d\in\cY\}.\label{eq:che:ros:E} \end{align} [[/math]]

Figure plots the set [math]\cE_\vartheta(\ey,\ex)[/math] in a stylized example with [math]\cY=\{1,2,3\}[/math] and [math]\cX=\{x^1,x^2\}[/math], as a function of [math](\epsilon_1-\epsilon_3,\epsilon_2-\epsilon_3)[/math]. Consider the model implied distribution, denoted [math]\sM[/math] below, of the optimal choice. Then, recalling the restriction [math]\ez\independent\nu[/math], we have

[[math]] \begin{align} \sM(c|\ex\in R_x,\ez;\vartheta)&=\int_{x\in R_x}\sR(\cE_\vartheta(c,\ex)|\ex=x,\ez)d\sP(x|z),\forall R_x\subseteq\cX,\ez\text{-a.s.}\label{eq:che:ros:model:distrib}\\ \sQ(F)&=\int_{x\in\cX}\sR(F|\ex=x,\ez)d\sP(x|z),\forall F\subseteq\cV,\ez\text{-a.s.},\label{eq:che:ros:instrument} \end{align} [[/math]]

Because the joint distribution of [math](\ex,\nu)[/math] conditional on [math]\ez[/math] is left completely unrestricted (other than \eqref{eq:che:ros:instrument}), one can find multiple triplets [math](\vartheta,\sQ,\sR(\nu|\ex,\ez))[/math] satisfying the maintained assumptions and with [math]\sM(c|\ex\in R_x,\ez;\vartheta)=\sP(c|\ex\in R_x,\ez)[/math] for all [math]c\in\cY[/math] and [math]R_x\subseteq\cX[/math], [math]\ez[/math]-a.s.

The set [math]\cE_\vartheta[/math] in equation \eqref{eq:che:ros:E} and the corresponding admissible values for [math](\ey,\ex)[/math] as a function of [math](\epsilon_1-\epsilon_3,\epsilon_2-\epsilon_3)[/math] under the simplifying assumption that [math]\cX=\{x^1,x^2\}[/math] and [math]\cY=\{1,2,3\}[/math]. The admissible values for [math](\ey,\ex)[/math] are [math]\{(c,x^1)\}[/math] in the gray area, and [math]\{(c,x^2)\}[/math] in the area with vertical lines. Because the two areas overlap, the model has set-valued predictions for [math](\ey,\ex)[/math].

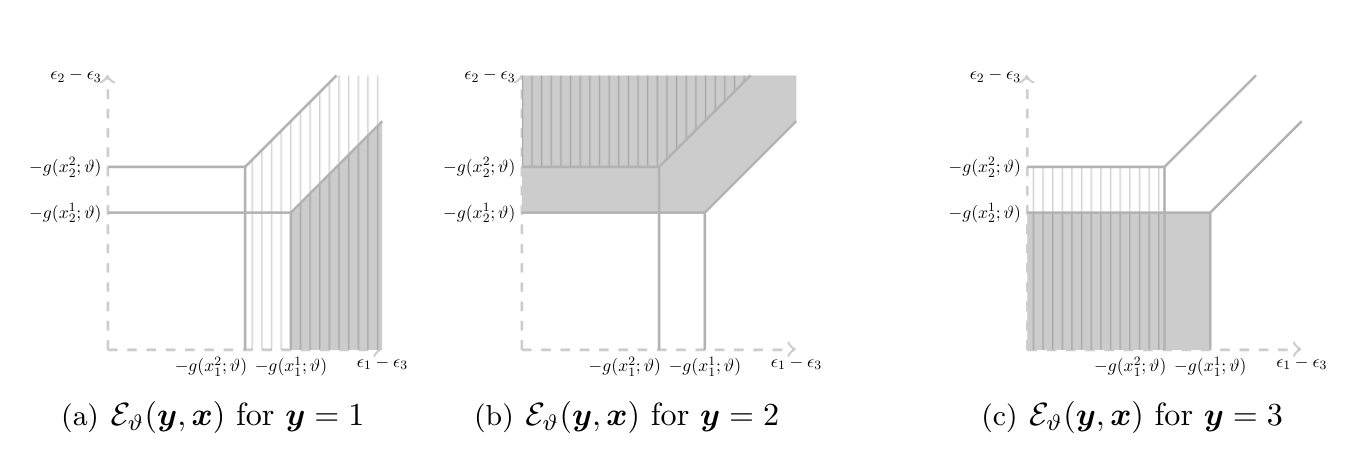
It is instructive to compare \eqref{eq:che:ros:model:distrib}-\eqref{eq:che:ros:instrument} with conditional logit. Under the standard assumptions, [math]\ex\independent\nu[/math] so that no instrumental variables are needed. This yields [math]\sQ(\nu)=\sR(\nu|\ex)[/math] [math]\ex[/math]-a.s., and in addition [math]\sQ[/math] is typically known, with corresponding simplifications in \eqref{eq:che:ros:model:distrib}. The resulting system of equalities can be inverted under standard order and rank conditions to yield point identification of [math]\theta[/math]. Further insights can be gained by looking at Figure. As the value of [math]\ex[/math] changes from [math]x^1[/math] to [math]x^2[/math], the region of values where, say, alternative 1 is optimal changes. When [math]\ex[/math] is exogenous, say independent of [math]\nu[/math], this yields a system of equalities relating [math](\theta,\sQ)[/math] to the observed distribution [math]\sP(\ey,\ex)[/math] which, as stated above, can be inverted to obtain point identification. When [math]\ex[/math] is endogenous, this reasoning breaks down because the conditional distribution [math]\sR(\nu|\ex,\ez)[/math] may change across realizations of [math]\ex[/math]. Figure also offers an instructive way to connect Identification Problem with the identification problem studied in Section Semiparametric Binary Choice Models with Interval Valued Covariates (as well as with those in Sections Static, Simultaneous-Move Finite Games with Multiple Equilibria-Auction Models with Independent Private Values below).

In the latter, the model has set-valued predictions for the outcome variable given realizations of the covariates and unobserved heterogeneity terms, which overlap across realizations of the unobserved heterogeneity terms. In the problem studied here, the model has singleton-valued predictions for the outcome variable of interest [math]\ey[/math] as a function of the observable explanatory variables [math]\ex[/math] and unobservables [math]\nu[/math]. However, for given realization of [math]\nu[/math], the model admits sets of values for the endogenous variables [math](\ey,\ex)[/math], which overlap across realizations of [math]\nu[/math]. Because the model is silent on the joint distribution of [math](\ex,\nu)[/math] (except for requiring that the marginal distribution of [math]\nu[/math] does not depend on [math]\ez[/math]), partial identification results. It is possible to couple the maintained assumptions with the observed data to learn features of [math](\theta,\sQ)[/math]. Because the observed choice [math]\ey[/math] is assumed to maximize utility, for the data generating [math](\theta,\sQ)[/math] the model yields

[[math]] \begin{align} \nu\in \cE_\theta(\ey,\ex)\text{-a.s.},\label{eq:che:ros:e_in_E} \end{align} [[/math]]

with [math]\cE_\theta(\ey,\ex)[/math] a random closed set as per Definition. Equation \eqref{eq:che:ros:e_in_E} exhausts the modeling content of Identification Problem. Theorem (as expressed in equation) can then be leveraged to extract its empirical content from the observed distribution [math]\sP(\ey,\ex,\ez)[/math]. As a preparation for doing so, note that for given [math]F\in\cF[/math] (with [math]\cF[/math] the collection of closed subsets of [math]\cV[/math]) and [math]\vartheta\in\Theta[/math], we have

[[math]] \begin{align*} \sP(\cE_\vartheta(\ey,\ex)\subseteq F|\ez)=\int_{x\in\cX}\sum_{c\in\cY}\one(\cE_\vartheta(c,x)\subseteq F)\sP(\ey=c|\ex=x,\ez)d\sP(x|\ez), \end{align*} [[/math]]

so that this probability can be learned from the observed data.

Discrete Choice with Endogenous Explanatory Variables

Under the assumptions of Identification Problem, the sharp identification region for [math](\theta,\sQ)[/math] is

[[math]] \begin{align} \idr{\theta,\sQ}=\left\{\vartheta\in\Theta,\tilde\sQ\in\cT:\tilde\sQ(F)\ge \sP(\cE_\vartheta(\ey,\ex)\subseteq F|\ez),~\forall F\in\cF,~\ez\text{-a.s.}\right\}.\label{eq:SIR:discrete:choice:endogenous} \end{align} [[/math]]

Show Proof

To simplify notation, I write [math]\cE_\vartheta\equiv\cE_\vartheta(\ey,\ex)[/math]. Let [math](\cE_\vartheta,\ex,\ez)=\{(\mathbf{e},\ex,\ez):\mathbf{e}\in\cE_\vartheta\}[/math]. If the model is correctly specified, [math](\nu,\ex,\ez)\in(\cE_\theta,\ex,\ez)[/math]-a.s. for the data generating value of [math](\theta,\sQ)[/math]. Using Theorem and Theorem 2.33 in , it follows that [math](\vartheta,\tilde\sQ)[/math] is observationally equivalent to [math](\theta,\sQ)[/math] if and only if

[[math]] \begin{align*} \tilde\sQ(F|\ex,\ez)\ge \sP(\cE_\vartheta(\ey,\ex)\subseteq F|\ex,\ez),~\forall F\in\cF,~(\ex,\ez)\text{-a.s.} \end{align*} [[/math]]

As the distribution of [math]\nu[/math] is only restricted so that [math]\nu\independent\ez[/math], one can integrate both sides of the inequality with respect to [math]\ex[/math]. The final result follows because [math]\tilde\sQ[/math] does not depend on [math]\ez[/math].

■

While Theorem SIR- relies on checking inequality \eqref{eq:SIR:discrete:choice:endogenous} for all [math]F\in\cF[/math], the results in and can be used to obtain a smaller collection of sets over which to verify it. In particular, if [math]\ex[/math] has a discrete distribution, it suffices to use a finite collection of sets. For example, in the case depicted in Figure with [math]\cX=\{x^1,x^2\}[/math], show that [math]\idr{\theta,\sQ}[/math] is obtained by checking at most twelve inequalities in \eqref{eq:SIR:discrete:choice:endogenous}. The left hand side of these inequalities is a linear function of six values that the distribution [math]\tilde\sQ[/math] assigns to each of the component regions depicted in Figure (the one where [math]\cE_\vartheta(1,x^1)\cap\cE_\vartheta(1,x^2)[/math] realizes; the one where [math]\cE_\vartheta(1,x^1)\cap\cE_\vartheta(3,x^2)[/math] realizes; etc.) Hence, in this example, [math](\vartheta,\tilde\sQ)\in\idr{\theta,\sQ}[/math] if and only if [math]\tilde\sQ[/math] assigns to these six regions a probability mass such that for [math]\vartheta[/math] the twelve inequalities characterized by hold.

Key Insight: A conceptual contribution of is to show that one can frame models with endogenous explanatory variables as incomplete models. Incompleteness here results from the fact that the model does not specify how the endogenous variables [math]\ex[/math] are determined. One can then think of these as models with set-valued predictions for the endogeneous variables ([math]\ey[/math] and [math]\ex[/math] in this application), even though the outcome of the model ([math]\ey[/math]) is uniquely predicted by the realization of the observed explanatory variables ([math]\ex[/math]) and the unobserved heterogeneity terms ([math]\nu[/math]). Random set theory can again be leveraged to characterize sharp identification regions. discuss related generalized instrumental variables models where random set methods are used to obtain characterizations of sharp identification regions in the presence of endogenous explanatory variables.

Unobserved Heterogeneity in Choice Sets and/or Consideration Sets

Compared to the general framework set forth at the beginning of Section Discrete Choice in Single Agent Random Utility Models, as pointed out in , often the researcher observes [math](\ey_i,\ex_i)[/math] but not [math]\eC_i[/math], [math]i=1,\dots,n[/math]. Even when [math]\eC_i[/math] is observable, the researcher may be unaware of which of its elements the decision maker actually evaluates before selecting one. In what follows, to shorten expressions, I refer to both the measurement problem of unobserved choice sets and the (cognitive) problem of limited consideration as “unobserved heterogeneity in choice sets.”

Learning features of preferences using discrete choice data in the presence of unobserved heterogeneity in choice sets is a formidable task. When a decision maker chooses an alternative, this may be because her choice set equals the feasible set and the chosen alternative is the one yielding the highest utility. Then observed choice reveals preferences. But it can also be that the decision maker has access to/considers only the chosen alternative (e.g., ). Then observed choice is driven entirely by choice set composition, and is silent about preferences. A plethora of scenarios between these extremes is possible, but the researcher does not know which has generated the observed data. This fundamental identification problem calls either for restrictions on the random utility model and consideration set formation process, or for collection of richer data that eliminates unobserved heterogeneity in [math]\eC_i[/math] or allows for enhanced modeling of it (see, e.g., ).

A sizable literature spanning behavioral economics, econometrics, experimental economics, marketing, microeconomics, and psychology, has put forward different models to formalize the complex process that leads to the formation of the set of alternatives that the agent considers or can choose from (see, e.g., ). proposes both a general econometric model where decision makers draw choice sets from an unknown distribution, as well as a specific model of choice set formation, independent from preferences, and studies their implications for the distributional structure of random utility models.

However, assumptions about the choice set formation process are often rooted in a desire to achieve point identification rather than in information contained in the model or observed data. It is then important to ask what can be learned about decision maker’s preferences under minimal assumptions on the choice set formation process. Allowing for unrestricted dependence between choice sets and preferences, while challenging for identification analysis, is especially relevant. Indeed, decision makers' unobserved attributes may determine both their preferences and which items in the feasible set they pay attention to or are available to them (e.g., through unobserved liquidity constraints, unobserved characteristics such as religious preferences in the context of school choice, or behavioral phenomena such as aversion to extremes, salience, etc.). Here I use the framework put forward by to study identification of discrete choice models with unobserved heterogeneity in choice sets and preferences.

Identification Problem (Discrete Choice with Unobserved Heterogeneity in Choice Sets and Preferences)

Let [math](\ey,\ex)\sim \sP[/math] be observable random variables in [math]\cY\times\cX[/math]. Assume that there exists a real valued function [math]g[/math], which for simplicity I posit known up to parameter [math]\delta\in\Delta\subset\R^m[/math] and continuous in its second argument, such that [math]\bu_i(c)=g(\ex_{ic},\nu_i;)[/math], [math](\ex_{ic},\nu_i)[/math]-a.s., for all [math]c\in\cY,i\in\cI[/math], where [math]\ex_{ic}[/math] denotes the vectors of attributes relevant to alternative [math]c[/math], and includes attributes that are alternative invariant and ones that are alternative specific (respectively, [math]\ex_i^1[/math] and [math]\ex_{ic}^2[/math] in the general notation laid out in Section Discrete Choice in Single Agent Random Utility Models). Suppose that [math]\ey=\arg\max_{c\in \eC}g(\ex_c,\nu;\delta)[/math], where ties are assumed to occur with probability zero and [math]\eC[/math] is an unobservable choice set drawn from the subsets of [math]\cY[/math] according to some unknown probability distribution. Suppose [math]\sR(|\eC|\ge\kappa)=1[/math] for some known constant [math]\kappa\ge 2[/math]. Let [math]\sQ[/math] denote the distribution of [math]\nu[/math], and assume that it is known up to a finite dimensional parameter [math]\gamma\in\Gamma\subset\R^k[/math]. For simplicity, assume that [math]\nu\independent\ex[/math]. In the absence of additional information, what can the researcher learn about [math]\theta\equiv[\delta;\gamma][/math]?

Predicted value of [math]\ey[/math] in Identification Problem as a function of [math]\nu[/math] for [math]\kappa=|\cY|-1[/math]. In this case, [math]\eC=\cY\setminus\{c\}[/math] for some [math]c\in\cY[/math], and the model predicts either the first or the second best alternative in [math]\cY[/math].

The model just laid out has set valued predictions for the decision maker's optimal choice, because different alternatives might be optimal depending on which choice set the decision maker draws. Figure, which is based on the analysis in , illustrates the set valued predictions in a stylized example. In the figure [math]\nu[/math] is assumed to be a scalar; [math]\bar{\nu}_{j,m}[/math] denotes the threshold value of [math]\nu[/math] above which [math]c_j[/math] yields higher utility than [math]c_m[/math] and below which [math]c_m[/math] yields higher utility than [math]c_j[/math] (the threshold's dependence on [math](\ex;\delta)[/math] is suppressed for notational convenience). Consider the case that [math]\nu\in[\bar{\nu}_{2,3},\bar{\nu}_{1,2}][/math], so that [math]c_2[/math] is the option yielding the highest utility among all options in [math]\cY[/math]. When [math]\kappa=|\cY|-1[/math], the agent may draw a choice set that does not include one of the alternatives in [math]\cY[/math]. If the excluded alternative is not [math]c_2[/math] (or if [math]\eC[/math] realizes equal to [math]\cY[/math]), the model predicts that the decision maker chooses [math]c_2[/math]. If [math]\eC[/math] realizes equal to [math]\cY\setminus\{c_2\}[/math], the model predicts that the decision maker chooses the second best: [math]c_1[/math] if [math]\nu\in[\bar{\nu}_{1,3},\bar{\nu}_{1,2}][/math], and [math]c_3[/math] if [math]\nu\in[\bar{\nu}_{2,3},\bar{\nu}_{1,3}][/math]. Conversely, observation of [math]\ey=c_1[/math] allows one to conclude that [math]\nu\ge\bar\nu_{1,3}[/math], and [math]\ey=c_2[/math] that [math]\nu\ge\bar\nu_{2,4}[/math], with [math]\bar\nu_{2,4}\le\bar\nu_{1,3}[/math], and these regions of possible realizations of [math]\nu[/math] overlap.

Why does this set valued prediction hinder point identification? The reason is similar to the explanation given for Identification Problem: the distribution of the observable data relates to the model structure in an incomplete manner, because the distribution of the (unobserved) choice sets is left completely unspecified. show that one can find multiple candidate distributions for [math]\eC[/math] and parameter vectors [math]\vartheta[/math], such that together they yield a model implied distribution for [math]\ey|\ex[/math] that matches [math]\sP(\ey|\ex)[/math], [math]\ex[/math]-a.s. propose to work directly with the set of model implied optimal choices given [math](\ex,\nu)[/math] associated with each possible realization of [math]\eC[/math], which is depicted in Figure for a specific example. The key idea is that, according to the model, the observed choice maximizes utility among the alternatives in [math]\eC[/math]. Hence, for the data generating value of [math]\theta[/math], it belongs to the set of model implied optimal choices. With this, the authors are able to characterize [math]\idr{\theta}[/math] through Theorem as the collection of parameter vectors that satisfy a finite number of conditional moment inequalities.

Key Insight: show that working directly with the set of model implied optimal choices given [math](\ex,\nu)[/math] allows one to dispense with considering all possible distributions of choice sets that are allowed for in Identification Problem to complete the model. Such distributions may depend on [math]\nu[/math] even after conditioning on observables and may constitute an infinite dimensional nuisance parameter, which creates great difficulties for the computation of [math]\idr{\theta}[/math] and for inference.

Identification Problem sets up a structure where preferences include idiosyncratic components [math]\nu[/math] that are decision maker specific and can depend on [math]\eC[/math], and where heterogeneity in [math]\eC[/math] can be driven either by a measurement problem, or by the decision maker's limited attention to the options available to her. However, for computational and finite sample inference reasons, it restricts the family of utility functions to be known up to a finite dimensional parameter vector [math]\delta[/math].

A rich literature in decision theory has analyzed a different framework, where the decision maker's choice set is observable to the researcher, but the decision maker does not consider all alternatives in it (for recent contributions see, e.g., ). In this literature, the utility function is left completely unspecified, so that interest focuses on identification of preference orderings of the available options. Unobserved heterogeneity in preferences is assumed away, so that heterogeneous choice is driven by randomness in consideration sets. If the consideration set formation process is left unspecified or is subject only to weak restrictions, point identification of the preference orderings is not possible even if preferences are homogeneous and the researcher observes a representative agent facing multiple distinct choice problems with varying choice sets.

propose a general model for the consideration set formation process where the only restriction is a weak and intuitive monotonicity condition: the probability that any particular consideration set is drawn does not decrease when the number of possible consideration sets decreases. Within this framework, they provide revealed preference theory and testable implications for observable choice probabilities. \begin{IP}[Homogeneous Preference Orderings in Random Attention Models]\label{IP:RAM} Let [math](\ey,\eC)\sim\sP[/math] be a pair of observable random variable and random set in [math]\cY\times\mathfrak{D}[/math], where [math]\mathfrak{D}=\{D:D\subseteq\cY\}\setminus\emptyset[/math]. Let [math]\mu:\mathfrak{D}\times\mathfrak{D}\to[0,1][/math] denote an attention rule such that [math]\mu(A|G)\ge 0[/math] for all [math]A\subseteq G[/math], [math]\mu(A|G)=0[/math] for all [math]A\nsubseteq G[/math], and [math]\sum_{A\subset G}\mu(A|G)=1[/math], [math]A,G\in\mathfrak{D}[/math]. Assume that for any [math]b\in G\setminus A[/math],

[[math]] \begin{align} \label{eq:RAM:monotonicity} \mu(A|G)\le\mu(A|G\setminus\{b\}), \end{align} [[/math]]

and that the decision maker has a strict preference ordering [math]\succ[/math] on [math]\cY[/math]. In the absence of additional information, what can the researcher learn about [math]\succ[/math]? \qedex }} posit that an observed distribution of choice [math]\sP(\ey|\eC)[/math] has a random attention representation, and hence they name it a random attention model, if there exists a preference ordering [math]\succ[/math] over [math]\cY[/math] and a monotonic attention rule [math]\mu[/math] such that

[[math]] \begin{align} \cp(c|G)\equiv\sP(\ey=c|\eC=G)=\sum_{A\subseteq G}\one(c\text{ is }\succ\text{-best in }A)\mu(A|G),\forall c\in G,\forall G\in\mathfrak{D}.\label{eq:RAM} \end{align} [[/math]]

The sharp identification region for the preference ordering, denoted [math]\idr{\succ}[/math] henceforth, is given by the collection of preference orderings for which one can find a monotonic attention rule to pair it with, so that \eqref{eq:RAM} holds. Of course, an observed distribution of choice can be represented by multiple preference orderings and attention rules. The authors, however, show in their Lemma 1 that if for some [math]G\in\mathfrak{D}[/math] with [math]\{b,c\}\in G[/math],

[[math]] \begin{align} \cp(c|G) \gt \cp(c|G\setminus \{b\}),\label{eq:RAM_violation_reg} \end{align} [[/math]]

then [math]c \succ b[/math] for any [math]\succ[/math] for which one can find a monotonic attention rule [math]\mu[/math] such that \eqref{eq:RAM} holds. Because of preference transitivity, one can also learn [math]a\succ b[/math] if in addition to the above condition one has [math]\cp(a|G^\prime) \gt \cp(a|G^\prime\setminus \{c\})[/math] for some [math]c\in G^\prime[/math] and [math]G^\prime\in\mathfrak{D}[/math]. The authors further show in their Theorem 1 that the collection of preference relations associated with all possible instances of \eqref{eq:RAM_violation_reg} for all [math]c\in G[/math] and [math]G\in\mathfrak{D}[/math] yield all information about preferences given the observed choice probabilities. This yields a system of linear inequalities in [math]\cp(c|G)[/math] that fully characterize [math]\idr{\succ}[/math]. Let [math]\vec{\cp}[/math] denote the vector with elements [math][\cp(c|G):c\in G,G\in\mathfrak{D}][/math] and [math]\Pi_\succ[/math] denote a conformable matrix collecting the constraints on [math]\sP(\ey|\eC)[/math] embodied in \eqref{eq:RAM_violation_reg} and its generalizations based on transitive closure. Then

[[math]] \begin{align} \idr{\succ}=\{\succ: \Pi_\succ \vec{\cp}\le 0\}.\label{eq:SIR:RAM} \end{align} [[/math]]

The authors show that for any given preference ordering [math]\succ[/math], the matrix [math]\Pi_\succ[/math] characterizing whether [math]\succ \in \idr{\succ}[/math] through the system of linear inequalities in \eqref{eq:SIR:RAM} is unique, and they provide a simple algorithm to compute it. They also show that mild additional assumptions, such as, for example, that decision makers facing binary choice sets pay attention to both alternatives frequently enough, can substantially increase the informational content of the data (i.e., substantially tighten [math]\idr{\succ}[/math]).

Key Insight: show that learning features of preference orderings in Identification Problem requires the existence in the data of choice problems where the choice probabilities satisfy \eqref{eq:RAM_violation_reg}. The latter is a violation of the principle of “regularity” according to which the probability of choosing an alternative from any set is at least as large as the probability of choosing it from any of its supersets. Regularity is a monotonicity property of choice probabilities, and it is implied by a wide array of models of decision making. The monotonicity of attention rules in \eqref{eq:RAM:monotonicity} can be viewed as regularity of the process that chooses a consideration set from the subsets of the choice set. show that it is implied by various models of limited attention. While the violation required in \eqref{eq:RAM_violation_reg} is weak in that it needs only to occur for some [math]G[/math], it sheds a different light on the severity of the identification problem described at the beginning of this section. Regularity of choice probabilities and (partial) identification of preference orderings can co-exist only under restrictions on the consideration set formation process that are stronger than the regularity of attention rules in \eqref{eq:RAM:monotonicity}.

and provide different sets of sufficient conditions for point identification of models of limited consideration. In both cases, the authors posit specific models of consideration set formation and provide sufficient conditions for point identification under exclusion and large support assumptions. assume that unobserved heterogeneity in preferences and in consideration sets are independent. They exploit violations of Slutsky symmetry that result from inattention, assuming that for each alternative there is an observable characteristic with large support that does not affect the consideration probability of the other options.

provide a thorough analysis of the extent of dependency between consideration and preferences under which semi-nonparametric point identification of the distribution of preferences and consideration attains. They exploit a requirement of standard economic theory --the Spence-Mirrlees single crossing property of utility functions-- coupled with a mild strengthening of the classic conditions for semi-nonparametric identification of discrete choice models with full consideration and identical choice sets (see, e.g., ), assuming that there is at least one decision maker-specific characteristic with large support that affects utility but not consideration.

Prediction of Choice Behavior with Counterfactual Choice Sets

Building on , studies a question related but distinct from those in Identification problem - problem. He is concerned with prediction of choice behavior when decision makers face counterfactual choice sets. frames this question as one of predicting treatment response (see Section Treatment Effects with and without Instrumental Variables). Here the collection of potential treatments is given by [math]\mathfrak{D}[/math], the nonempty subsets of the universe of feasible alternatives [math]\cY[/math], and the response function specifies the alternative chosen by a decision maker when facing choice set [math]G\in\mathfrak{D}[/math]. assumes that the researcher observes realized choice sets and chosen alternatives, [math](\ey,\eC)\sim\sP[/math]. Under the standard assumptions laid out at the beginning of Section Discrete Choice in Single Agent Random Utility Models, specifically if utility functions are (say) linear in [math]\epsilon_{ic}[/math] and the distribution of [math]\epsilon_{ic}[/math] is (say) Type I extreme value or multivariate normal, prediction of choice behavior with counterfactual choice sets is immediate (and point identified). , however, leaves utility functions completely unspecified, and in fact works directly with preference orderings, which he labels decision maker’s types. He places no restriction on the distribution of preference types, except requiring that they are independent of the observed choice sets. shows that under these rather weak assumptions, the distribution of predicted choices from counterfactual choice sets can be partially identified, and characterized as the solution to linear programs.

Specifically, let [math]\ey^*(G)[/math] denote the decision maker's optimal choice when facing choice set [math]G\in\mathfrak{D}[/math]. Assume [math]\ey^*(\cdot)\independent\eC[/math], and let [math]y_k[/math] denote the choice function for a decision maker of type [math]k[/math] --that is, a decision maker with a specific preference ordering labeled [math]k[/math]. One example of such preference ordering might be [math]c_1\succ c_2\succ\dots\succ c_{|\cY|}[/math]. If a decision maker of this type faces, say, choice set [math]G=\{c_2,c_3,c_4\}[/math], then she chooses alternative [math]c_2[/math]. Let [math]K[/math] denote the set of logically possible types, and [math]\theta_k[/math] the probability that a decision maker in the population is of type [math]k[/math]. Suppose that the researcher posits a behavioral model specifying [math]K[/math], [math]\{y_k,k=1,\dots,K\}[/math], and restrictions that constrain [math]\theta[/math] to lie in some specified set of distributions. Let [math]\Theta[/math] denote the values of [math]\vartheta[/math] that satisfy these requirements plus the conditions [math]\vartheta_k\ge 0[/math] for all [math]k\in K[/math] and [math]\sum_{k\in K}\vartheta_k=1[/math]. Then for any [math]c\in\cY[/math] and [math]\vartheta\in\Theta[/math], the model predicts

[[math]] \begin{align*} \sQ(\ey^*(G)=c)=\sum_{k\in K}\one(y_k(G)=c)\vartheta_k. \end{align*} [[/math]]

How can one partially identify this probability based on the observed data? Suppose [math]\eC[/math] is observed to take realizations [math]D_1,\dots,D_m[/math]. Then the data reveal

[[math]] \begin{align*} \sP(\ey(D_j)=d_j)=\sum_{k\in K}\one(y_k(D_j)=d_j)\theta_k\forall d_j\in D_j,j=1,\dots,m.\end{align*} [[/math]]

This yields that the sharp identification region for [math]\theta[/math] is

[[math]] \begin{align*} \idr{\theta}=\{\vartheta\in\Theta:\sP(\ey(D_j)=d_j)=\sum_{k\in K}\one(y_k(D_j)=d_j)\vartheta_k\forall d_j\in D_j,j=1,\dots,m\}. \end{align*} [[/math]]

If the behavioral model is correctly specified, [math]\idr{\theta}[/math] is non-empty. In turn, the sharp identification region for each choice probability is

[[math]] \begin{align*} \idr{\sQ(\ey^*(G)=c)}=\left\{\sum_{k\in K}\one(y_k(G)=c)\vartheta_k:\vartheta\in\idr{\theta}\right\}, \end{align*} [[/math]]

and its extreme points can be obtained by solving linear programs.

provide closely related sharp bounds on features of counterfactual choices in the nonparametric random utility model of demand, where observable choices are repeated cross-sections and one allows for unrestricted, unobserved heterogeneity. Their approach builds on the work of , who test weather agents' behavior is consistent with the Axiom of Revealed Stochastic Preference (SARP) in a random utility model in which the utility function of each consumer over commodity bundles is assumed to satisfy only the basic restriction that “more is better” with no satiation. Because the testing exercise is to be carried out using repeated cross-sections data, the authors maintain the assumption that multiple populations of consumers who face distinct choice sets have the same distribution of preferences. With this structure in place, de facto the task is to test the full implications of rationality without functional form restrictions. ’s approach is based on several novel ideas. As a first step, they leverage an earlier insight of to discretize the data without loss of information, so that they can define a large but finite set of rational preferences types. As a second step, they show that this implies that rationality can be tested by checking whether observed behavior lies in a cone corresponding to positive linear combinations of preference types. While the problem is discrete, its dimension is at first sight prohibitive. Nonetheless, Kitamura and Stoye are able to develop novel computational methods that render the problem tractable. They apply their method to the U.K. Household Expenditure Survey, adapting to their framework results on nonparametric instrumental variable analysis by so that they can handle price endogeneity.

builds on to learn program effects when agents are randomly assigned to control or treatment. The treatment group is provided access to the program, while the control group is not. However, members of the control group may receive access to the program from outside the experiment, leading to noncompliance with the randomly assigned treatment. The researcher wants to learn about the average effect of program access on the decision to participate in the program and on the subsequent outcome. While sufficiently rich data may allow the researcher to learn these effects, is concerned with the identification problem that arises when the researcher only observes the treatment assignment status, the program participation decision, and the outcome, but not the receipt of program access for every agent. formalizes this problem as one where the received treatment is selected from a choice set that depends on the assigned treatment and is unobservable to the researcher, and the agents optimally choose whether to participate in the program by maximizing their utility function over their choice set. Importantly, the utility functions are not subject to parametric restrictions, similarly to . But while assumed independence of choice sets and preference types, allows them to be arbitrarily dependent on each other, as in . approach leverages specific assumptions on random assignment of treatments and on compliance (or lack thereof) of participants to obtain nonparametric bounds on the treatment effects of interest that can be characterized using tractable linear programs.

General references

Molinari, Francesca (2020). "Microeconometrics with Partial Identification". arXiv:2004.11751 [econ.EM].