In this section we shall consider the motion of a particle in the plane during an interval of time. We shall assume that the particle moves without jumping. As a result, if [math]P[/math] is the function which associates to every instant of time in the interval the corresponding position of the particle in the plane, then [math]P[/math] is continuous; i.e., it is a parametrization. The points [math]P(t)[/math] trace out the parametrized curve over which the particle moves.
Velocity is a vector concept which combines two ingredients: the number which measures how fast the particle is moving, and the direction of the motion. If the position of a particle during an interval of time [math]I[/math] is described by a differentiable parametrization [math]P: I \rightarrow R^2[/math], then the velocity of the particle at any time t during the interval will be denoted by [math]v(t)[/math] and defined to be the derived vector of [math]P[/math] at [math]t[/math]. Thus
[[math]]
\begin{equation}
\mbox'''{v'''}(t) = \mbox'''{d'''}P(t)
\label{eq10.5.1}
\end{equation}
[[/math]]
Since the derived vector is a tangent vector, the velocity is also one. Specifically, [math]\mbox'''{v'''}(t)[/math] is a tangent vector at [math]t[/math] to the parametrized curve defined by [math]P[/math]. If we write [math]P(t) = (x(t), y(t))[/math], then it follows from the formula for the derived vector [see (4.1), page 571] that the velocity vector is given by
[[math]]
\begin{equation}
\mbox'''{v'''}(t) = (x'(t), y'(t))_{p(t)}.
\label{eq10.5.2}
\end{equation}
[[/math]]
[[math]]
\begin{equation}
|\mbox'''{v'''}(t)| = \sqrt{x'(t)^2 + y'(t)^2}.
\label{eq10.5.3}
\end{equation}
[[/math]]
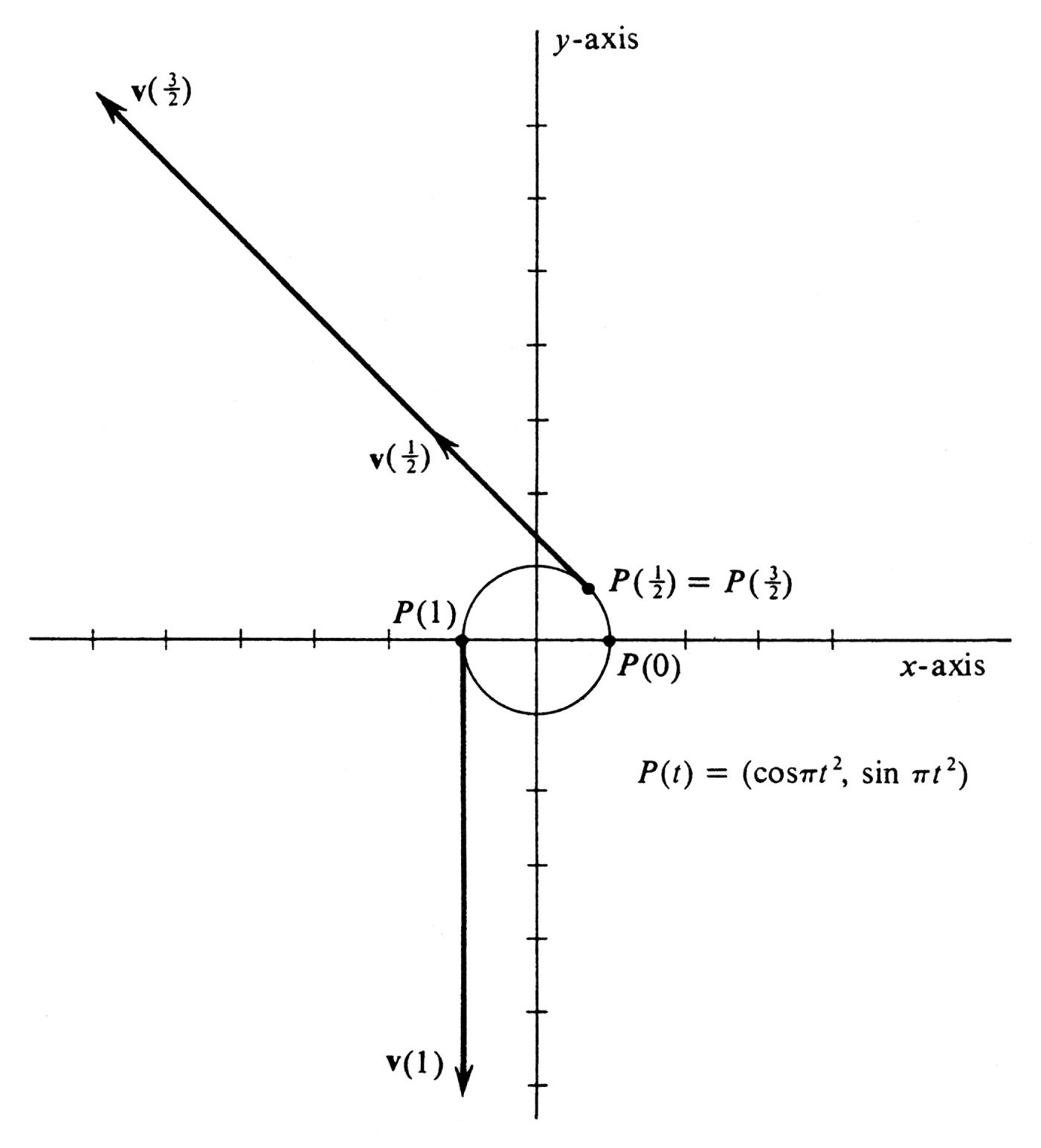
Example
A particle moves in the plane during the time interval [math][0, 2][/math], and its position at any time [math]t[/math] in this interval is given by
[[math]]
P(t) = (x(t), y(t)) = (\cos \pi t^2, \sin \pi t^2).
[[/math]]
Assume that time is measured in seconds and that the unit of distance in the plane is 1 foot.
\smallskip
\item[a]] Identify and draw the curve traced out by the particle, and describe its motion during the interval [math][0, 2][/math].
\item[(b)] Compute the position, velocity, and speed of the particle at [math]t = 0[/math], [math]t = \frac{1}{2}[/math], [math]t = 1[/math], and [math]t = \frac{3}{2}[/math]. Show these four positions, and draw the corresponding velocity vectors in the figure in (a).
\item[(c)] How does the speed of the particle depend on time during the entire interval of motion?
The parametrized curve over which the particle moves is the set of all points [math](x, y)[/math] such that
[[math]]
\left \{ \begin{array}{l}
x = \cos \pi ^2, \\
y = \sin \pi t^2, \;\;\; 0 \leq t \leq 2.
\end{array}
\right .
[[/math]]
Hence the coordinates of every point [math](x, y)[/math] on the curve satisfy
[[math]]
x^2 + y^2 = (\cos \pi t^2)^2 + (\sin \pi t^2)^2 = 1.
[[/math]]
The equation [math]x^2 + y^2 = 1[/math] is the familiar equation of the circle [math]C[/math] with radius 1 and center the origin, and the particle therefore moves on this circle. In accordance with the definition of the functions sine and cosine in Chapter 6, the quantity [math]\pi t^2[/math] is the arc length along [math]C[/math] in the counterclockwise direction from the point (1, 0) to the point [math]P(t) = (x, y)[/math]. As [math]t[/math] increases from 0 to 2, the values of [math]\pi t^2[/math] increase monotonically from 0 to [math]4 \pi[/math], which is twice the circumference of the circle. We conclude that the particle starts from (1, 0) at time [math]t = 0[/math], moves counterclockwise around the circle as time increases, and at [math]t = 2[/math] has gone completely around twice and has come back to its starting position at [math]P(2) = (\cos 4 \pi, \sin 4 \pi) = (1, 0)[/math]. The curve of motion, i.e., the circle [math]C[/math], is shown in Figure 17.
Since [math]P(t) = (\cos \pi t^2, \sin \pi t^2)[/math], the position of the particle at each of the four values of t given in (b) is easily computed:
[[math]]
\begin{eqnarray*}
P(0) &=& (\cos 0, \sin 0) = (1, 0), \\
P(\frac{1}{2}) &=& (\cos \pi \cdot \frac{1}{4}, \sin \pi \cdot \frac{1}{4}) = \Big( \frac{\sqrt 2}{2}, \frac{\sqrt 2}{2} \Big) , \\
P(1) &=& (\cos \pi, \sin \pi) = ( -1, 0),\\
P(\frac{3}{2}) &=& (\cos \pi \cdot \frac{9}{4}, \sin \pi \cdot \frac{9}{4}) = \Big( \frac{\sqrt 2}{2}, \frac{\sqrt 2}{2} \Big) .
\end{eqnarray*}
[[/math]]
The velocity vector is
[[math]]
\begin{eqnarray*}
\mbox'''{v'''}(t) &=& (x'(t),y'(t))_{P(t)}\\
&=& (- 2\pi t \sin \pi t^2, 2\pi t \cos \pi t^2)_{P(t)}.\\
\mbox'''{v'''}(t) &=& 2\pi t (-\sin \pi t^2, cos \pi t^2)_{P(t)} .
\end{eqnarray*}
[[/math]]
Hence
[[math]]
\begin{eqnarray*}
\mbox'''{v'''}(0) &=& \mbox'''{0'''} = (0, 0)_{P(0)},\\
\mbox'''{v'''}(\frac{1}{2}) &=& 2 \pi \frac{1}{2} \Big( -\sin \frac{\pi}{4}, \cos \frac{\pi}{4} \Big)_{P(1/2)} = \frac{\pi \sqrt 2}{2} (- 1, 1)_{P(1/2)},\\
\mbox'''{v'''}(1) &=& 2\pi (-\sin \pi, \cos \pi)_{P(1)} = 2 \pi (0, -1)_{P(1)},\\
\mbox'''{v'''}(\frac{3}{2}) &=& 2\pi \frac{3}{2} \Big( -\sin \frac{\pi 9}{4}, \cos \frac{\pi 9}{4} \Big)_{P(3/2)} = \frac{3 \pi \sqrt 2}{2} (-1, 1)_{P(3/2)} .
\end{eqnarray*}
[[/math]]
The speed is by definition the length of the velocity vector. If [math](b, c)_P[/math] is any vector, and [math]a[/math] any real number, then the length of the scalar product [math]a(b, c)_P[/math], is given by
[[math]]
|a(b, c)_P| = |a| \sqrt{b^2 + c^2} .
[[/math]]
Thus the four speeds are
[[math]]
\begin{eqnarray*}
|\mbox'''{v'''}(0)| &=& 0 \;\mathrm{feet~per~second,} \\
|\mbox'''{v'''}(\frac{1}{2})| &=& \frac{\pi \sqrt 2}{2} \sqrt{(-1)^2 + 1^2} = \pi \;\mathrm{feet~per~second,}\\
|\mbox'''{v'''}(1)| &=& 2 \pi \sqrt{0^2 + (-1)^2} = 2\pi \;\mathrm{feet~per~ second,}\\
|\mbox'''{v'''}(\frac{3}{2})| &=& \frac{3\pi \sqrt 2}{2} \sqrt{(-1 )^2 + 1^2} = 3 \pi \;\mathrm{feet~per~second.}
\end{eqnarray*}
[[/math]]
Since each of the velocity vectors is tangent to the curve at its initial point and since we know their lengths, they can be drawn without difficulty (see Figure 17).
From the preceding computations it appears that the speed of the particle increases as time goes on. By computing the speed [math]|\mbox'''{v'''}(t)|[/math] for an arbitrary [math]t[/math] in the interval [0, 2], we can see that this inference is correct. Using equation (4) we get
[[math]]
|\mbox'''{v'''}(t)| = 2\pi t \sqrt{(-\sin \pi t^2)^2 + (\cos \pi t^2)^2} = 2 \pi t,
[[/math]]
which shows that the speed increases linearly with time over the interval. At [math]t = 0[/math], the particle is at rest, and 2 seconds later, at [math]t = 2[/math], its speed has increased to [math]4 \pi[/math] feet per second.
The motion of a particle along a straight line was studied in Section 3 of Chapter 2 and again in Section 8 of Chapter 4. When the motion is restricted to a straight line, which for convenience we may take to be the [math]x[/math]-axis, then the velocity vector has only one nonzero coordinate, [math]x'(t)[/math]. In this case velocity may be identified with [math]x'(t)[/math], and it is not necessary to consider it as a vector. In our earlier treatments [math]x'(t)[/math] was defined to be the velocity and it was denoted by [math]v(t)[/math]. The distance on the line which the particle moves during the time interval [math][a, b][/math] was defined by the formula
[[math]]
\begin{equation}
distance\Big|_a^b = \int_a^b |v(t)| \;dt
\label{eq10.5.5}
\end{equation}
[[/math]]
(see page 232). We shall show that this definition is consistent with the more sophisticated notions of vector velocity and arc length of parametrized curves, which we are studying in this chapter. Consider a particle in the plane whose position is given by a parametrization [math]P: [a, b] \rightarrow R^2[/math]. By the distance which the particle moves along the curve parametrized by [math]P[/math] during the time interval from [math]t = a[/math] to [math]t = b[/math] we shall mean the arc length [math]L_a^b[/math]. Let
[[math]]
P(t) = (x(t), y(t)), \;\;\;\mathrm{for~every~} t \mathrm{~such~that~} a \leq t \leq b.
[[/math]]
We shall assume that the derivatives [math]x'[/math] and [math]y'[/math] exist and are continuous on [math][a, b][/math]. From Theorem (2.2), page 553, it follows that
[[math]]
L_a^b = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \;dt.
[[/math]]
The speed of the particle at any [math]t[/math] in [math][a, b][/math] is given by
[[math]]
|\mbox'''{v'''}(t)| = \sqrt{x'(t)^2 + y'(t)^2} .
[[/math]]
Hence the distance traveled by the particle along the parametrized curve from $t = a$ to $t = b$ is equal to
[[math]]
L_a^b = \int_a^b |\mbox'''{v'''}(t)| \;dt .
[[/math]]
Formula (5.1) is the generalization of the distance formula (5) from rectilinear to curvilinear motion.
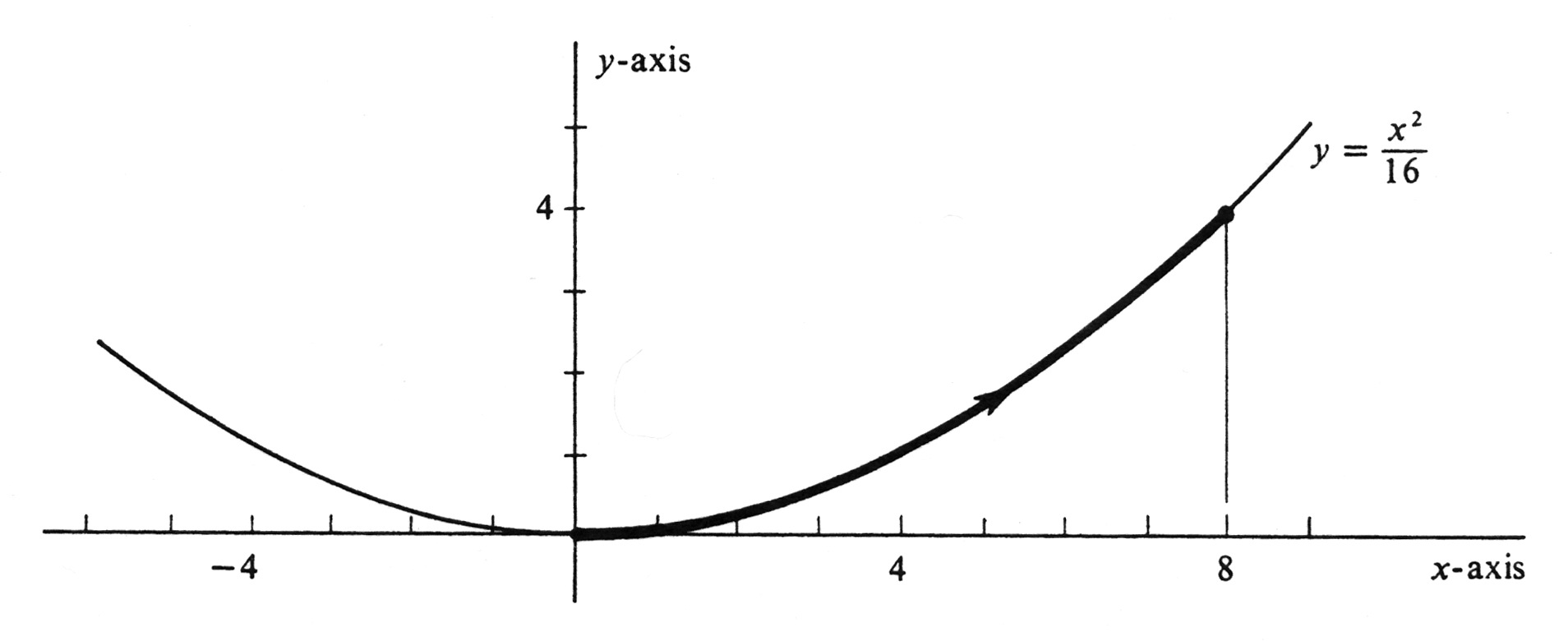
Example
A steel ball is rolling on a plane during an interval from [math]t = 0[/math] to [math]t = 4[/math] seconds. It has an [math]x[/math]-coordinate of velocity which is constant and equal to 2 feet per second. Its [math]y[/math]-coordinate of velocity is [math]\frac{1}{2}t[/math] feet per second, for every [math]t[/math] in the interval. (a) Write a definite integral equal to the distance (in feet) which the ball rolls during the interval from [math]t = 0[/math] to [math]t = 4[/math] seconds. (b) Identify and draw the curve on which the ball rolls.
The coordinates of the velocity vector [math]\mbox'''{v'''}(t)[/math] are [math]x'(t)[/math] and [math]y'(t)[/math]. Hence
[[math]]
\begin{equation}
\left \{ \begin{array}{l}
x'(t) = 2, \\
y'(t) = \frac{1}{2} t, \;\;\; 0 \leq t \leq 4.
\end{array}
\right .
\end{equation}
[[/math]]
It follows at once from (5.1) that the distance which the ball rolls is equal to
[[math]]
\begin{eqnarray*}
L_0^4 &=& \int_0^4 \sqrt{4 + \frac{1}{4} t^2} \;dt \\
&=& \frac{1}{2} \int_0^4 \sqrt{16 + t^2} \;dt.
\end{eqnarray*}
[[/math]]
This answers part (a). Using a table of integrals or integration by trigonometric substitution, one can obtain
[[math]]
\begin{eqnarray*}
\int_0^4 \sqrt{16 + t^2} \;dt &=& 8 \sqrt 2 + 8 \ln (1 + \sqrt 2) \\
&=& 18.3 \;\mathrm{(approximately).}
\end{eqnarray*}
[[/math]]
Hence the distance the ball rolls is half this quantity, approximately 9.2 feet.
A parametrization which defines the position of the ball may be found by integrating the functions [math]x'[/math] and [math]y'[/math]. From equations (6), we get
[[math]]
\left \{ \begin{array}{l}
x(t) = 2t + c_1,\\
y(t) = \frac{t^2}{4} + c_2, \;\;\; 0 \leq t \leq 4.
\end{array}
\right .
[[/math]]
Nothing in the statement of the problem specifies the position of the ball at [math]t = 0[/math], so, for simplicity, we shall choose it to be the origin. This choice is equivalent to setting [math]c_1 = c_2 = 0[/math]. It follows that the parametrized curve in which the ball rolls is the set of all points [math](x, y)[/math] such that
[[math]]
\left \{ \begin{array}{l}
x= 2t, \\
y= \frac{t^2}{4}, \;\;\; 0 \leq t \leq 4.
\end{array}
\right .
[[/math]]
From the first equation, we get [math]t = \frac{x}{2}[/math]. Hence the two equations together with the inequality are equivalent to
[[math]]
y = \frac{x^2}{16}, \;\;\; 0 \leq x \leq 8.
[[/math]]
The graph of this equation is the parabola shown in Figure 18, and the curve over which the ball rolls is that portion of the parabola indicated by the heavy line.
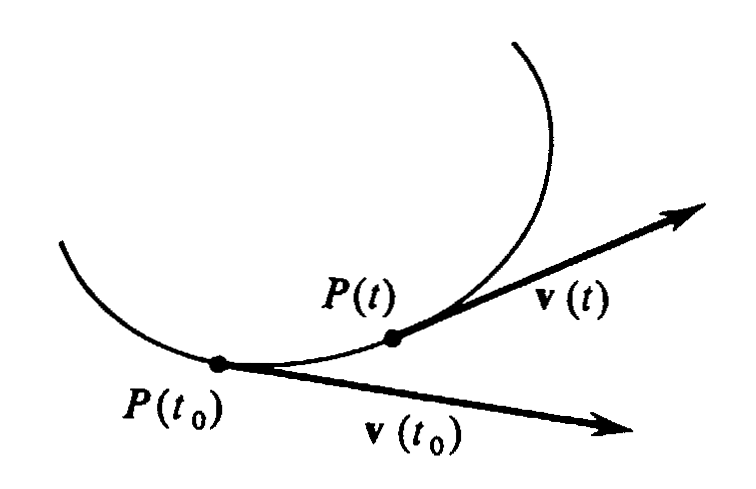
We next consider what is meant by the acceleration of a moving particle. The intuitive idea is that acceleration is the rate of change of the velocity vector. To be more precise: Let the position of the particle during an interval of time [math]I[/math] be given by a differentiable parametrization [math]P: I \rightarrow R[/math], and let [math]t_0[/math] be in [math]I[/math]. If [math]t[/math] is a number in [math]I[/math] distinct from [math]t_0[/math], then the velocity vectors [math]\mbox'''{v'''}(t_0)[/math] and [math]\mbox'''{v'''}(t)[/math] are tangent vectors with initial points [math]P(t_0)[/math] and [math]P(t)[/math], respectively, as
illustrated in Figure 19. In defining the acceleration at [math]t_0[/math], we should like to form the scalar product of [math]\frac{1}{t - t_0}[/math] and the difference [math]\mbox'''{v'''}(t) - \mbox'''{v'''}(t_0)[/math], and to take the limit of this product as [math]t[/math] approaches [math]t_0[/math]. The difficulty is that, since the points [math]P(t)[/math] and [math]P(t_0)[/math] are usually distinct, the difference [math]\mbox'''{v'''}(t) - \mbox'''{v'''}(t_0)[/math] is generally not defined. (Recall that two vectors can be added or subtracted if and only if they have the same initial point.) It is for this reason that, before defining acceleration, we introduce the notion of parallel translation of vectors in [math]R^2[/math].
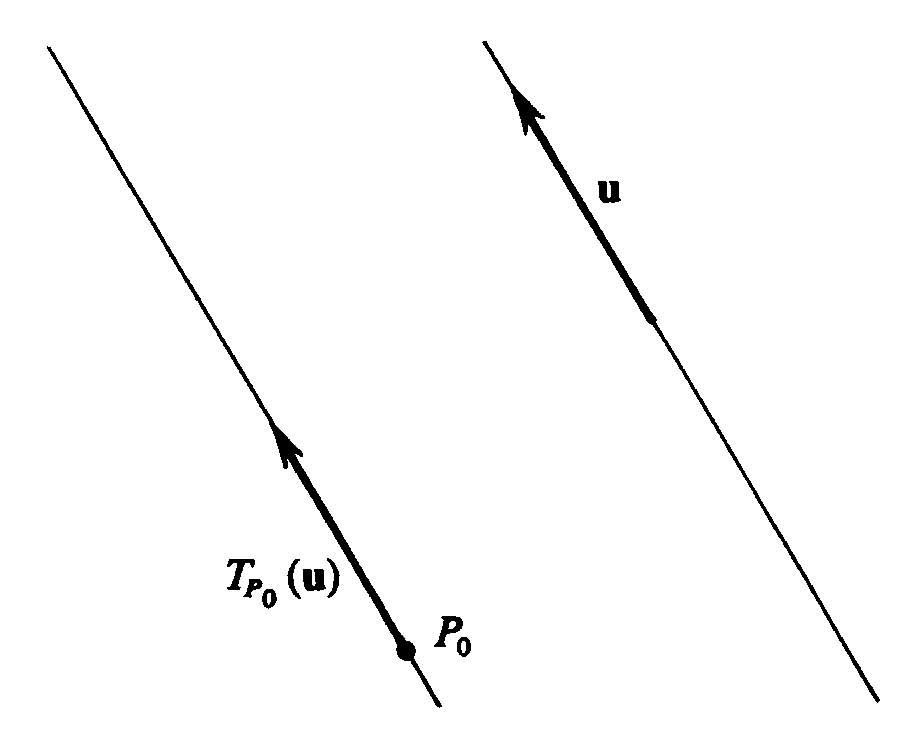
Let [math]P_0[/math] be an arbitrary point in [math]R^2[/math]. We shall define a function [math]T_{P_0}[/math] whose domain is the set [math]\mathcal{V}[/math] of all vectors in [math]R^2[/math] and whose range is the vector space [math]\mathcal{V}_{P_0}[/math] of all vectors with initial point [math]P_0[/math]. The definition is as follows: For every vector [math]\mbox'''{u'''}[/math] in [math]\mathcal{V}[/math], the value [math]T_{P_0}(\mbox'''{u'''})[/math] is the vector with the same coordinates as [math]\mbox'''{u'''}[/math], but with initial point [math]P_0[/math]. Thus
[[math]]
if\; \mbox'''{u'''} = (u_1, u_2)_Q, \;\;\;\mbox{then}\; T_{P_0}(\mbox'''{u'''}) = (u_1, u_2)_{P_0} .
[[/math]]
Geometrically, the vector [math]T_{P_0}(\mbox'''{u'''})[/math] is obtained from [math]\mbox'''{u'''}[/math] by moving the arrow representing the vector [math]\mbox'''{u'''}[/math] parallel to itself until its initial point coincides with [math]P_0[/math]. The process is illustrated in Figure 20, and we call the function [math]T_{P_0}[/math] the operation of parallel translation of vectors to the point [math]P_0[/math].
We can now define the acceleration of a moving particle. As before, let the position be defined by the differentiable parametrization [math]P: I \rightarrow R^2[/math]. We consider [math]t_0[/math] in [math]I[/math], and set [math]P(t_0) = P_0[/math]. Then the acceleration of the particle at [math]t_0[/math] is the vector [math]\mbox'''{a'''}(t_0)[/math] defined by
[[math]]
\begin{equation}
\mbox'''{a'''}(t_0) = \lim_{t \rightarrow t_0} \frac{1}{t - t_0} [T_{P_0}(\mbox'''{v'''}(t) ) - \mbox'''{v'''}(t_0)] .
\label{eq10.5.7}
\end{equation}
[[/math]]
Thus, acceleration, like velocity, is a vector.
We can derive a simple formula for acceleration in terms of the coordinate functions of [math]P[/math]. Let [math]P(t) = (x(t), y(t))[/math], as usual. Then
[[math]]
\begin{eqnarray*}
\mbox'''{v'''}(t_0) &=& (x'(t_0), y'(t_0))_{P(t_0)}, \\
\mbox'''{v'''}(t) &=& (x'(t), y'(t))_{P(t)},
\end{eqnarray*}
[[/math]]
and, if [math]P_0 = P(t_0)[/math], then
[[math]]
T_{P_0} (\mbox'''{v'''}(t)) = (x'(t), y (t))_{P(t_0)} .
[[/math]]
lt follows that
[[math]]
T_{P_0} (\mbox'''{v'''}(t)) - \mbox'''{v'''}(t_0) = (x'(t) - x'(t_0), y'(t) - y'(t_0))_{P(t_0)},
[[/math]]
and thence that
[[math]]
\frac{1}{t - t_0} [T_{P_0} (\mbox'''{v'''}(t)) - \mbox'''{v'''}(t_0)] = \Big( \frac{x'(t) - x'(t_0)}{t - t_0}, \frac{y'(t) - y'(t_0)}{t - t_0} \Big)_{P_(t_0)}.
[[/math]]
Hence
[[math]]
\begin{eqnarray*}
\mbox'''{a'''}(t_0) &=& \lim_{t \rightarrow t_0} \frac{1}{t - t_0} [T_{P_0}(\mbox'''{v'''}(t)) - \mbox'''{v'''}(t_0)] \\
&=& \Big( \lim_{t \rightarrow t_0} \frac{x'(t) - x'(t_0)}{t - t_0},
\lim_{t \rightarrow t_0} \frac{y'(t) - y'(t_0)}{t - t_0} \Big)_{P(t_0)}.
\end{eqnarray*}
[[/math]]
If the two limits which are the coordinates of the preceding vector exist, they are by definition equal to the second derivatives [math]x''(t_0)[/math] and [math]y''(t_0)[/math], respectively. It follows that
If [math]P(t) = (x(t), y(t))[/math], then the acceleration vector [math]\mbox'''{a'''}(t_0)[/math] exists if and only if the second derivatives [math]X,'(t_0)[/math] and [math]y',(t_0)[/math] exist. lf they do exist, then
[[math]]
\mbox'''{a'''}(t_0) = (x''(t_0), y''(t_0))_{P(t_0)}.
[[/math]]
Example
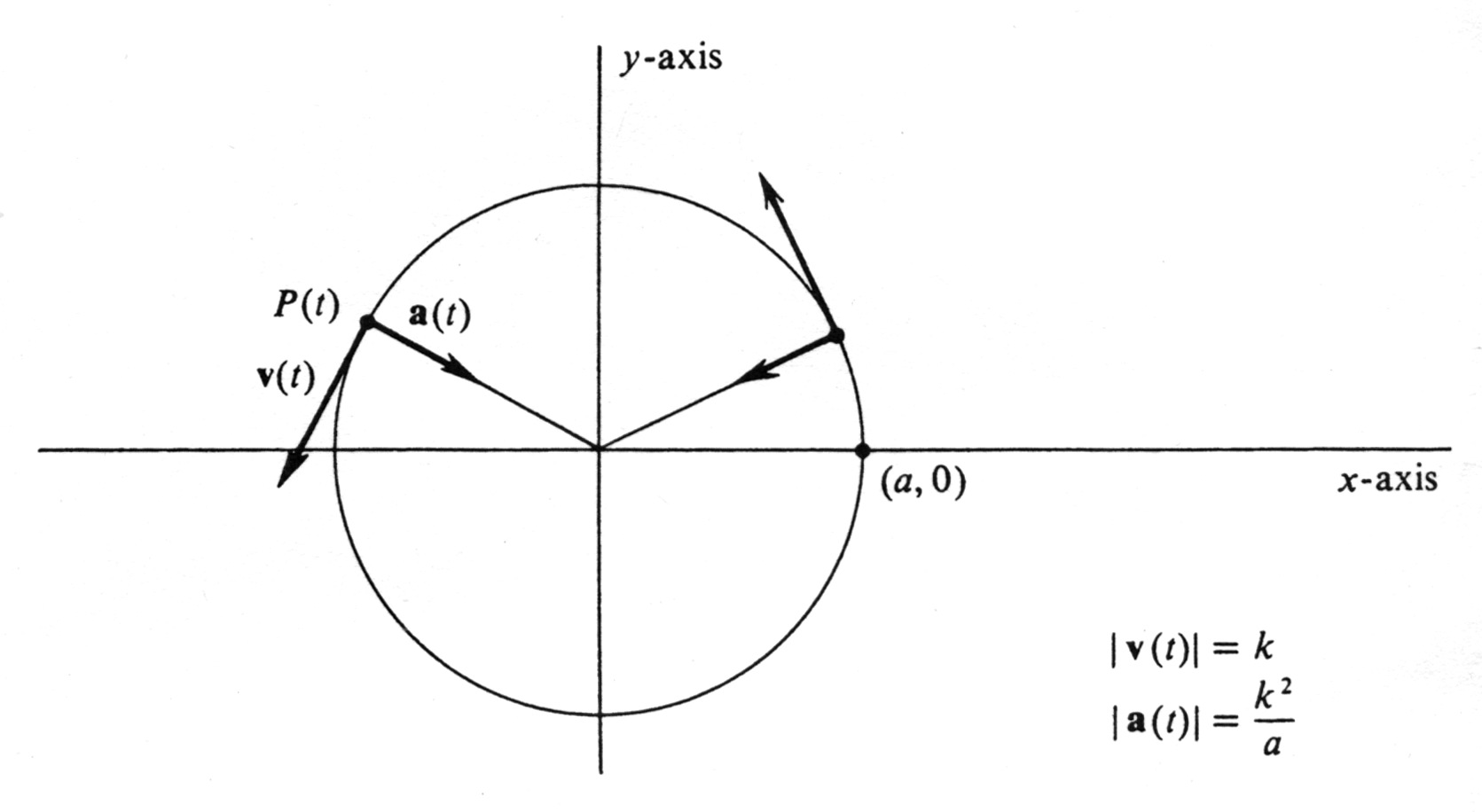
A particle is moving with constant speed [math]k[/math] in a fixed circle of radius [math]a[/math]. Show that, at any time [math]t[/math] during the interval of motion, the acceleration
vector [math]\mbox'''{a'''}(t)[/math] has constant length equal to [math]\frac{k^2}{a}[/math] and always points directly toward the center of the circle (see Figure 21).
We shall take the center of the circle to be the origin in the [math]xy[/math]-plane. The position of the particle can then be defined by a parametrization [math]P(t) = (x(t), y(t)) = (x, y)[/math] for which
[[math]]
\begin{equation}
\left \{ \begin{array}{l}
x = a \cos u, \\
y = a \sin u,
\end{array}
\right .
\label{eq10.5.8}
\end{equation}
[[/math]]
and [math]u[/math] is some function of [math]t[/math] having as domain the interval of time of the motion. To be specific, we shall assume that 0 is in the domain, and that, when [math]t = 0[/math], the particle is at the point [math](a, 0)[/math] on the circle. Hence [math]u = 0[/math] when [math]t = 0[/math]. We shall make the analytic assumption that the second derivative [math]u''(t)[/math] exists, for every [math]t[/math] in the interval, and it follows that [math]x''(t)[/math] and [math]y''(t)[/math] also exist. Differentiating with respect to [math]t[/math] in equations (8), we obtain
[[math]]
\begin{equation}
\left \{ \begin{array}{l}
x' = -au' \sin u, \\
y' = au' \cos u.
\end{array}
\right .
\label{eq10.5.9}
\end{equation}
[[/math]]
Thus the speed of the particle is
[[math]]
|\mbox'''{v'''}(t)| = \sqrt{{x'}^2 + {y'}^2} = \sqrt{a^2{u'}^2(\sin^2 u + \cos^2 u)} = a|u'|,
[[/math]]
which is assumed to be the constant [math]k[/math]. Hence [math]|u'| = \frac{k}{a}[/math]. Since [math]u'[/math] is continuous and has constant positive absolute value, it is either always positive or always negative (depending on whether the particle is moving counter
clockwise or clockwise). We shall assume the former and conclude that [math]u' = \frac{k}{a}[/math]. Integrating, we obtain
[[math]]
u = \frac{k}{a} t + c.
[[/math]]
Since [math]u = 0[/math], when [math]t = 0[/math], it follows that
[[math]]
u = \frac{k}{a} t .
[[/math]]
Substituting this value back into equations (9), we have
[[math]]
\begin{eqnarray*}
x' &=& -a \frac{k}{a} \sin \frac{k}{a} t = -k \sin \frac{k}{a} t,\\
y' &=& a \frac{k}{a} \cos \frac{k}{a} t = k \cos \frac{k}{a} t.
\end{eqnarray*}
[[/math]]
Hence
[[math]]
\begin{eqnarray*}
x'' &=& - \frac{k^2}{a} \cos \frac{k}{a} t = - \frac{k^2}{a} \cos u, \\
y'' &=& - \frac{k^2}{a} \sin \frac{k}{a} t = - \frac{k^2}{a} \sin u,
\end{eqnarray*}
[[/math]]
or, equivalently,
[[math]]
\begin{eqnarray*}
x'' &=& - \frac{k^2}{a^2} a \cos u = - \frac{k^2}{a^2} x,\\
y'' &=& - \frac{k^2}{a^2} a \sin u = - \frac{k^2}{a^2} y.
\end{eqnarray*}
[[/math]]
We know from (5.2) that the acceleration vector is given by
[[math]]
\mbox'''{a'''}(t) = (x'', y'')_{P(t)} .
[[/math]]
Hence
[[math]]
\begin{eqnarray*}
\mbox'''{a'''}(t) &=& \Big( -\frac{k^2}{a^2} x, -\frac{k^2}{a^2} y \Big)_{P(t)} \\
&=& \frac{k^2}{a^2} (-x, -y)_{P(t)}.
\end{eqnarray*}
[[/math]]
Since [math]P(t) = (x,y)[/math], the terminal point of the vector [math](-x,-y)_{P(t)}[/math] is the point (0, 0). Thus the acceleration vector [math]\mbox'''{a'''}(t)[/math] is a positive scalar multiple of the vector with initial point [math]P(t)[/math] and terminal point the origin. This proves that [math]\mbox'''{a'''}(t)[/math] is always pointing directly toward the center of the circle. The length
of the acceleration vector is easily computed from the preceding equation. We get
[[math]]
\begin{eqnarray*}
|\mbox'''{a'''}(t)| &=& \frac{k^2}{a^2} \sqrt{(-x)^2 + (-y^2)}
= \frac{k^2}{a^2} \sqrt{x^2 + y^2} \\
&=& \frac{k^2}{a^2} \cdot a = \frac{k^2}{a} .
\end{eqnarray*}
[[/math]]
This completes the problem. The acceleration in this example is called
centripetal acceleration, and the force acting on the particle necessary to provide this acceleration is the centripetal force. In the case of a planet moving in orbit, the force is the force of gravity.
General references
Doyle, Peter G. (2008). "Crowell and Slesnick's Calculus with Analytic Geometry" (PDF). Retrieved Oct 29, 2024.
