Almost dimension-free convex optimization in non-Euclidean spaces
In the previous chapter we showed that dimension-free oracle complexity is possible when the objective function [math]f[/math] and the constraint set [math]\cX[/math] are well-behaved in the Euclidean norm; e.g. if for all points [math]x \in \cX[/math] and all subgradients [math]g \in \partial f(x)[/math], one has that [math]\|x\|_2[/math] and [math]\|g\|_2[/math] are independent of the ambient dimension [math]n[/math]. If this assumption is not met then the gradient descent techniques of Chapter may lose their dimension-free convergence rates. For instance consider a differentiable convex function [math]f[/math] defined on the Euclidean ball [math]\mB_{2,n}[/math] and such that [math]\|\nabla f(x)\|_{\infty} \leq 1, \forall x \in \mB_{2,n}[/math]. This implies that [math]\|\nabla f(x)\|_{2} \leq \sqrt{n}[/math], and thus projected gradient descent will converge to the minimum of [math]f[/math] on [math]\mB_{2,n}[/math] at a rate [math]\sqrt{n / t}[/math]. In this chapter we describe the method of [1], known as mirror descent, which allows to find the minimum of such functions [math]f[/math] over the [math]\ell_1[/math]-ball (instead of the Euclidean ball) at the much faster rate [math]\sqrt{\log(n) / t}[/math]. This is only one example of the potential of mirror descent. This chapter is devoted to the description of mirror descent and some of its alternatives. The presentation is inspired from [2], [Chapter 11, [3]], [4][5][6].
In order to describe the intuition behind the method let us abstract the situation for a moment and forget that we are doing optimization in finite dimension. We already observed that projected gradient descent works in an arbitrary Hilbert space [math]\mathcal{H}[/math]. Suppose now that we are interested in the more general situation of optimization in some Banach space [math]\mathcal{B}[/math]. In other words the norm that we use to measure the various quantity of interest does not derive from an inner product (think of [math]\mathcal{B} = \ell_1[/math] for example). In that case the gradient descent strategy does not even make sense: indeed the gradients (more formally the Fr\'echet derivative) [math]\nabla f(x)[/math] are elements of the dual space [math]\mathcal{B}^*[/math] and thus one cannot perform the computation [math]x - \eta \nabla f(x)[/math] (it simply does not make sense). We did not have this problem for optimization in a Hilbert space [math]\mathcal{H}[/math] since by Riesz representation theorem [math]\mathcal{H}^*[/math] is isometric to [math]\mathcal{H}[/math]. The great insight of Nemirovski and Yudin is that one can still do a gradient descent by first mapping the point [math]x \in \mathcal{B}[/math] into the dual space [math]\mathcal{B}^*[/math], then performing the gradient update in the dual space, and finally mapping back the resulting point to the primal space [math]\mathcal{B}[/math]. Of course the new point in the primal space might lie outside of the constraint set [math]\mathcal{X} \subset \mathcal{B}[/math] and thus we need a way to project back the point on the constraint set [math]\mathcal{X}[/math]. Both the primal/dual mapping and the projection are based on the concept of a {\em mirror map} which is the key element of the scheme. Mirror maps are defined in Section Mirror maps, and the above scheme is formally described in Section Mirror descent. In the rest of this chapter we fix an arbitrary norm [math]\|\cdot\|[/math] on [math]\R^n[/math], and a compact convex set [math]\cX \subset \R^n[/math]. The dual norm [math]\|\cdot\|_*[/math] is defined as [math]\|g\|_* = \sup_{x \in \mathbb{R}^n : \|x\| \leq 1} g^{\top} x[/math]. We say that a convex function [math]f : \cX \rightarrow \R[/math] is (i) [math]L[/math]-Lipschitz w.r.t. [math]\|\cdot\|[/math] if [math]\forall x \in \cX, g \in \partial f(x), \|g\|_* \leq L[/math], (ii) [math]\beta[/math]-smooth w.r.t. [math]\|\cdot\|[/math] if [math]\|\nabla f(x) - \nabla f(y) \|_* \leq \beta \|x-y\|, \forall x, y \in \cX[/math], and (iii) [math]\alpha[/math]-strongly convex w.r.t. [math]\|\cdot\|[/math] if
We also define the Bregman divergence associated to [math]f[/math] as
The following identity will be useful several times:
Mirror maps
Let [math]\cD \subset \R^n[/math] be a convex open set such that [math]\mathcal{X}[/math] is included in its closure, that is [math]\mathcal{X} \subset \overline{\mathcal{D}}[/math], and [math]\mathcal{X} \cap \mathcal{D} \neq \emptyset[/math]. We say that [math]\Phi : \cD \rightarrow \R[/math] is a mirror map if it safisfies the following properties[Notes 1]:
- [math]\Phi[/math] is strictly convex and differentiable.
- The gradient of [math]\Phi[/math] takes all possible values, that is [math]\nabla \Phi(\cD) = \R^n[/math].
- The gradient of [math]\Phi[/math] diverges on the boundary of [math]\cD[/math], that is
[[math]] \lim_{x \rightarrow \partial \mathcal{D}} \|\nabla \Phi(x)\| = + \infty . [[/math]]
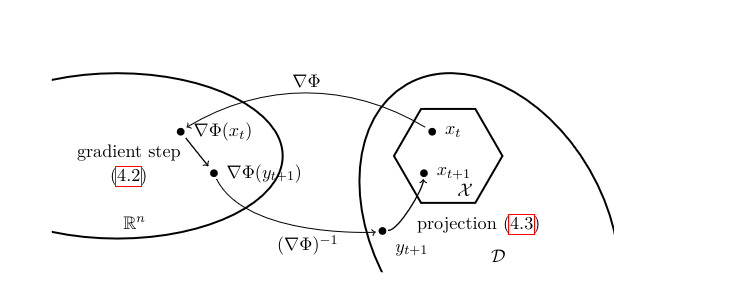
In mirror descent the gradient of the mirror map [math]\Phi[/math] is used to map points from the ‘`primal" to the ``dual" (note that all points lie in [math]\R^n[/math] so the notions of primal and dual spaces only have an intuitive meaning). Precisely a point [math]x \in \mathcal{X} \cap \mathcal{D}[/math] is mapped to [math]\nabla \Phi(x)[/math], from which one takes a gradient step to get to [math]\nabla \Phi(x) - \eta \nabla f(x)[/math]. Property (ii) then allows us to write the resulting point as [math]\nabla \Phi(y) = \nabla \Phi(x) - \eta \nabla f(x)[/math] for some [math]y \in \cD[/math]. The primal point [math]y[/math] may lie outside of the set of constraints [math]\cX[/math], in which case one has to project back onto [math]\cX[/math]. In mirror descent this projection is done via the Bregman divergence associated to [math]\Phi[/math]. Precisely one defines
Property (i) and (iii) ensures the existence and uniqueness of this projection (in particular since [math]x \mapsto D_{\Phi}(x,y)[/math] is locally increasing on the boundary of [math]\mathcal{D}[/math]). The following lemma shows that the Bregman divergence essentially behaves as the Euclidean norm squared in terms of projections (recall Lemma).
Let [math]x \in \cX \cap \cD[/math] and [math]y \in \cD[/math], then
The proof is an immediate corollary of Proposition together with the fact that [math]\nabla_x D_{\Phi}(x,y) = \nabla \Phi(x) - \nabla \Phi(y)[/math].
Mirror descent
We can now describe the mirror descent strategy based on a mirror map [math]\Phi[/math]. Let [math]x_1 \in \argmin_{x \in \mathcal{X} \cap \mathcal{D}} \Phi(x)[/math]. Then for [math]t \geq 1[/math], let [math]y_{t+1} \in \mathcal{D}[/math] such that
and
See Figure for an illustration of this procedure.
Let [math]\Phi[/math] be a mirror map [math]\rho[/math]-strongly convex on [math]\mathcal{X} \cap \mathcal{D}[/math] w.r.t. [math]\|\cdot\|[/math]. Let [math]R^2 = \sup_{x \in \mathcal{X} \cap \mathcal{D}} \Phi(x) - \Phi(x_1)[/math], and [math]f[/math] be convex and [math]L[/math]-Lipschitz w.r.t. [math]\|\cdot\|[/math]. Then mirror descent with [math]\eta = \frac{R}{L} \sqrt{\frac{2 \rho}{t}}[/math] satisfies
Let [math]x \in \mathcal{X} \cap \mathcal{D}[/math]. The claimed bound will be obtained by taking a limit [math]x \rightarrow x^*[/math]. Now by convexity of [math]f[/math], the definition of mirror descent, equation \eqref{eq:useful1}, and Lemma, one has
We observe that one can rewrite mirror descent as follows:
This last expression is often taken as the definition of mirror descent (see [2]). It gives a proximal point of view on mirror descent: the method is trying to minimize the local linearization of the function while not moving too far away from the previous point, with distances measured via the Bregman divergence of the mirror map.
Standard setups for mirror descent
``Ball setup". The simplest version of mirror descent is obtained by taking [math]\Phi(x) = \frac{1}{2} \|x\|^2_2[/math] on [math]\mathcal{D} = \mathbb{R}^n[/math]. The function [math]\Phi[/math] is a mirror map strongly convex w.r.t. [math]\|\cdot\|_2[/math], and furthermore the associated Bregman divergence is given by [math]D_{\Phi}(x,y) = \frac{1}{2} \|x - y\|^2_2[/math]. Thus in that case mirror descent is exactly equivalent to projected subgradient descent, and the rate of convergence obtained in Theorem recovers our earlier result on projected subgradient descent. \newline
``Simplex setup". A more interesting choice of a mirror map is given by the negative entropy
on [math]\mathcal{D} = \mathbb{R}_{++}^n[/math]. In that case the gradient update [math]\nabla \Phi(y_{t+1}) = \nabla \Phi(x_t) - \eta \nabla f(x_t)[/math] can be written equivalently as
The Bregman divergence of this mirror map is given by [math]D_{\Phi}(x,y) = \sum_{i=1}^n x(i) \log \frac{x(i)}{y(i)}[/math] (also known as the Kullback-Leibler divergence). It is easy to verify that the projection with respect to this Bregman divergence on the simplex [math]\Delta_n = \{x \in \mathbb{R}_+^n : \sum_{i=1}^n x(i) = 1\}[/math] amounts to a simple renormalization [math]y \mapsto y / \|y\|_1[/math]. Furthermore it is also easy to verify that [math]\Phi[/math] is [math]1[/math]-strongly convex w.r.t. [math]\|\cdot\|_1[/math] on [math]\Delta_n[/math] (this result is known as Pinsker’s inequality). Note also that for [math]\mathcal{X} = \Delta_n[/math] one has [math]x_1 = (1/n, \dots, 1/n)[/math] and [math]R^2 = \log n[/math]. The above observations imply that when minimizing on the simplex [math]\Delta_n[/math] a function [math]f[/math] with subgradients bounded in [math]\ell_{\infty}[/math]-norm, mirror descent with the negative entropy achieves a rate of convergence of order [math]\sqrt{\frac{\log n}{t}}[/math]. On the other hand the regular subgradient descent achieves only a rate of order [math]\sqrt{\frac{n}{t}}[/math] in this case! \newline
‘`Spectrahedron setup". We consider here functions defined on matrices, and we are interested in minimizing a function [math]f[/math] on the {\em spectrahedron} [math]\mathcal{S}_n[/math] defined as:
In this setting we consider the mirror map on [math]\mathcal{D} = \mathbb{S}_{++}^n[/math] given by the negative von Neumann entropy:
where [math]\lambda_1(X), \dots, \lambda_n(X)[/math] are the eigenvalues of [math]X[/math]. It can be shown that the gradient update [math]\nabla \Phi(Y_{t+1}) = \nabla \Phi(X_t) - \eta \nabla f(X_t)[/math] can be written equivalently as
where the matrix exponential and matrix logarithm are defined as usual. Furthermore the projection on [math]\mathcal{S}_n[/math] is a simple trace renormalization. With highly non-trivial computation one can show that [math]\Phi[/math] is [math]\frac{1}{2}[/math]-strongly convex with respect to the Schatten [math]1[/math]-norm defined as
It is easy to see that for [math]\mathcal{X} = \mathcal{S}_n[/math] one has [math]x_1 = \frac{1}{n} \mI_n[/math] and [math]R^2 = \log n[/math]. In other words the rate of convergence for optimization on the spectrahedron is the same than on the simplex!
Lazy mirror descent, aka Nesterov’s dual averaging
In this section we consider a slightly more efficient version of mirror descent for which we can prove that Theorem still holds true. This alternative algorithm can be advantageous in some situations (such as distributed settings), but the basic mirror descent scheme remains important for extensions considered later in this text (saddle points, stochastic oracles, ...). In lazy mirror descent, also commonly known as Nesterov's dual averaging or simply dual averaging, one replaces \eqref{eq:MD1} by
and also [math]y_1[/math] is such that [math]\nabla \Phi(y_1) = 0[/math]. In other words instead of going back and forth between the primal and the dual, dual averaging simply averages the gradients in the dual, and if asked for a point in the primal it simply maps the current dual point to the primal using the same methodology as mirror descent. In particular using \eqref{eq:MD3} one immediately sees that dual averaging is defined by:
Let [math]\Phi[/math] be a mirror map [math]\rho[/math]-strongly convex on [math]\mathcal{X} \cap \mathcal{D}[/math] w.r.t. [math]\|\cdot\|[/math]. Let [math]R^2 = \sup_{x \in \mathcal{X} \cap \mathcal{D}} \Phi(x) - \Phi(x_1)[/math], and [math]f[/math] be convex and [math]L[/math]-Lipschitz w.r.t. [math]\|\cdot\|[/math]. Then dual averaging with [math]\eta = \frac{R}{L} \sqrt{\frac{\rho}{2 t}}[/math] satisfies
We define [math]\psi_t(x) = \eta \sum_{s=1}^{t} g_s^{\top} x + \Phi(x)[/math], so that [math]x_t \in \argmin_{x \in \mathcal{X} \cap \mathcal{D}} \psi_{t-1}(x)[/math]. Since [math]\Phi[/math] is [math]\rho[/math]-strongly convex one clearly has that [math]\psi_t[/math] is [math]\rho[/math]-strongly convex, and thus
Mirror prox
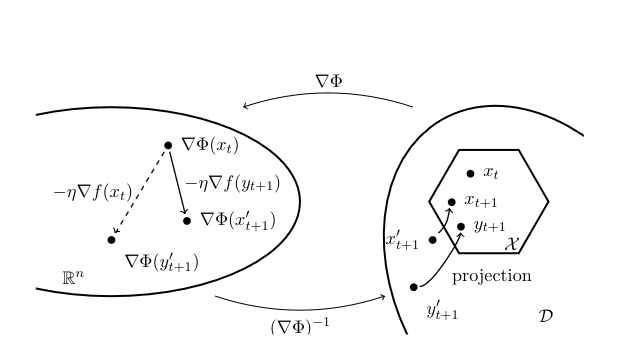
It can be shown that mirror descent accelerates for smooth functions to the rate [math]1/t[/math]. We will prove this result in Chapter (see Theorem). We describe here a variant of mirror descent which also attains the rate [math]1/t[/math] for smooth functions. This method is called mirror prox and it was introduced in [7]. The true power of mirror prox will reveal itself later in the text when we deal with smooth representations of non-smooth functions as well as stochastic oracles[Notes 2]. Mirror prox is described by the following equations:
In words the algorithm first makes a step of mirror descent to go from [math]x_t[/math] to [math]y_{t+1}[/math], and then it makes a similar step to obtain [math]x_{t+1}[/math], starting again from [math]x_t[/math] but this time using the gradient of [math]f[/math] evaluated at [math]y_{t+1}[/math] (instead of [math]x_t[/math]), see Figure for an illustration. The following result justifies the procedure.
Let [math]\Phi[/math] be a mirror map [math]\rho[/math]-strongly convex on [math]\mathcal{X} \cap \mathcal{D}[/math] w.r.t. [math]\|\cdot\|[/math]. Let [math]R^2 = \sup_{x \in \mathcal{X} \cap \mathcal{D}} \Phi(x) - \Phi(x_1)[/math], and [math]f[/math] be convex and [math]\beta[/math]-smooth w.r.t. [math]\|\cdot\|[/math]. Then mirror prox with [math]\eta = \frac{\rho}{\beta}[/math] satisfies
Let [math]x \in \mathcal{X} \cap \mathcal{D}[/math]. We write
The vector field point of view on MD, DA, and MP
In this section we consider a mirror map [math]\Phi[/math] that satisfies the assumptions from Theorem. By inspecting the proof of Theorem one can see that for arbitrary vectors [math]g_1, \dots, g_t \in \R^n[/math] the mirror descent strategy described by \eqref{eq:MD1} or \eqref{eq:MD2} (or alternatively by \eqref{eq:MDproxview}) satisfies for any [math]x \in \cX \cap \cD[/math],
The observation that the sequence of vectors [math](g_s)[/math] does not have to come from the subgradients of a {\em fixed} function [math]f[/math] is the starting point for the theory of online learning, see [6] for more details. In this monograph we will use this observation to generalize mirror descent to saddle point calculations as well as stochastic settings. We note that we could also use dual averaging (defined by \eqref{eq:DA0}) which satisfies
In order to generalize mirror prox we simply replace the gradient [math]\nabla f[/math] by an arbitrary vector field [math]g: \cX \rightarrow \R^n[/math] which yields the following equations:
Under the assumption that the vector field is [math]\beta[/math]-Lipschitz w.r.t. [math]\|\cdot\|[/math], i.e., [math]\|g(x) - g(y)\|_* \leq \beta \|x-y\|[/math] one obtains with [math]\eta = \frac{\rho}{\beta}[/math]
General references
Bubeck, Sébastien (2015). "Convex Optimization: Algorithms and Complexity". arXiv:1405.4980 [math.OC].
References
- A.Nemirovski and D.Yudin.Problem Complexity and Method Efficiency in Optimization.Wiley Interscience, 1983.
- 2.0 2.1 A.Beck and M.Teboulle.Mirror Descent and nonlinear projected subgradient methods for convex optimization.Operations Research Letters, 31 (3): 167--175, 2003.
- N.Cesa-Bianchi and G.Lugosi.Prediction, Learning, and Games.Cambridge University Press, 2006.
- A.Rakhlin.Lecture notes on online learning.2009.
- "E.Hazan.The convex optimization approach to regret minimization.In S.Sra, S.Nowozin, and S.Wright, editors, Optimization for Machine Learning, pages 287--303. MIT press, 2011."
- 6.0 6.1 S.Bubeck.Introduction to online optimization.Lecture Notes, 2011.
- A.Nemirovski.Prox-method with rate of convergence o (1/t) for variational inequalities with lipschitz continuous monotone operators and smooth convex-concave saddle point problems.SIAM Journal on Optimization, 15 (1): 229--251, 2004{\natexlaba}.
Notes
- Assumption (ii) can be relaxed in some cases, see for example [1].
- Basically mirror prox allows for a smooth vector field point of view (see Section The vector field point of view on MD, DA, and MP), while mirror descent does not.