Exotic Options
This section describes some of the better-known facts regarding a few exotic derivatives. The American and the Asian options are considered ‘path-dependent’ because the payoff of the option will vary depending on the history of the price process, whereas exchange options and binary options are not path-dependent because the payoff only depends on the asset price(s) are the terminal time.
Asian Options
Asian option consider the average price of the underlying in the payoff,
These options are path dependent because the path taken by the underlying is considered. The averaging in the Asian option makes it harder to manipulate the payoff by driving the underlying's price up or down when the option is close to maturity.
Delta Hedge. In the Black-Scholes framework, the Asian option is a relatively simple extension of the hedging argument used to derive the Black-Scholes PDE. The trick is to consider an use an integrated field,
and consider the price
Let the underlying's dynamics be
where [math]W_t[/math] is a Brownian motion. From It\^o's lemma we have
On the other hand, we have a self-financing portfolio,
where [math]\alpha_t[/math] is the number of contracts in [math]S_t[/math] and [math](V_t-\alpha_tS_t)[/math] is the \$-amount in the risk-free asset. Comparing the It\^o lemma of the option to the self-financing portfolio, we see that a portfolio that is long [math]V_t [/math] and short the Asian option will be risk-less if we have the [math]\Delta[/math]-hedge
Furthermore, since the portfolio long [math]V_t[/math] and short the option is risk-less, it must be that it earns at the risk-free rate. Hence,
Hence, the price of the Asian option satisfies the following PDE,
Equations \eqref{eq:asianPDE} and \eqref{eq:asianPDEtc} can be solved with a Feynman-Kac formula,
where [math]\mathbb E^Q[/math] is the expected value under the unique EMM [math]\mathbb Q[/math], and the asset price is [math]\frac{dS_t}{S_t} = rdt+\sigma dW_t^Q[/math] under [math]\mathbb Q[/math]. We knew from Chapter that this market was complete, so it shouldn't come as a surprise that we were able to hedge perfectly the Asian option.\\
PDE of Reduced Dimension. A useful formula is the dimension reduction of the Asian option price to a function of just time and one stochastic field. Define a new function
Then let [math]\mathcal F_t[/math] denote the history of prices up time time [math]t[/math], and define the martingale
where [math]X_t \doteq \frac{K-\frac{1}{T}\int_0^tS_udu}{S_t}[/math]. Applying the It\^o lemma to [math]\xi_t[/math], we have
and assuming that [math]\phi(t,x)[/math] is twice differentiable we apply the It\^o lemma to [math]\phi(t,X_t)[/math]:
Then applying It\^o's lemma to [math]M_t[/math], we have
and in order for [math]M_t[/math] to be a martingale the [math]dt[/math] terms must all cancel out. Therefore, we must have
which gives us the PDE of reduced dimension for a new function [math]\tilde \phi(t,x)\doteq e^{-r(T-t)}\phi(t,x)[/math],
The PDE of equations \eqref{eq:reducedPDE} and \eqref{eq:reducedPDEtc} is of reduced dimension and is solvable with a Feynman-Kac formula,
with [math]d\widetilde X_t = -\left(\frac 1T+r\widetilde X_t\right)dt+\sigma\widetilde X_t dW_t[/math]. Finally, the option price is
Equation \eqref{eq:reducedDim} is the pricing formula of reduced dimension.\\
Exchange Options (Margrabe Formula)
Consider two tradable assets, [math]S_t^1[/math] and [math]S_t^2[/math]. An exchange option with strike [math]K[/math] has payoff
which we price price under an EMM. In particular, for [math]K=0[/math] we have
Options like this are found in forex markets and in commodities, the latter of which uses them to hedge risk in the risk between the retail price of a finished good verses the cost of manufacture. In electricity markets, the price of a megawatt hour of electricity needs to be hedged against the price of natural gas in what's called the spark spread; in the soy market the cost of soy meal verses the cost of soy beans is called the crush spread; in the oil market the cost of refined oil products verses the cost of crude oil is called the crack spread. In commodities markets these options are called sometimes called spread options. The Margrabe formula prices spread/exchange options with [math]K=0[/math]. Suppose we have a double Black-Scholes model for the two assets,
where [math]W_t^1[/math] and [math]W_t^2[/math] are independent risk-neutral Brownian motions and [math]\rho\in(-1,1)[/math]. Now we define ratio in \eqref{eq:ratioOption} as
define an exponential martingale
and notice that
Recall the Girsanov Theorem from Chapter and recognize that [math]Z_t[/math] defines a new measure [math]\widetilde{\mathbb P}^Q[/math] under which [math]\widetilde W_t\doteq W_t^2-\sigma_2t[/math] is Brownian motion, and under which [math]W_t^1[/math] remains a Brownian motion independent of [math]\widetilde W_t[/math]. Applying the It\^o lemma to [math]Y_t[/math] we get
and we can now write the option price under the new measure to get the Margrabe Formula:
where [math]N(\cdot)[/math] is the standard normal CDF function and
where [math]\sigma^2 = \sigma_1^2+\sigma_2^2-2\sigma_2\sigma_1\rho[/math]. Essentially, the Margrabe formula is the Black-Scholes call option price with [math]r=0[/math], [math]S_0=s_1[/math], [math]K=s_2[/math], and [math]\sigma^2= \sigma_1^2+\sigma_2^2-2\sigma_2\sigma_1\rho[/math].
American Options and Optimality of Early Exercise
Broadly speaking, options on index funds (such as S\&P 500) are European, whereas options on individual stocks (such as Apple) are American. American options have the same features as their European counterparts, but with the additional option of early exercise. The option of early exercise can be equated with the option to wait and see, as the prices of these options is usually thought of the present value of the payoff when exercised at an optimal time. For this reason the American options are consider path-dependent. Methods for pricing American options are quite involved, as there are no explicit solutions. Instead, pricing is done by working backward from the terminal condition on a binomial tree, or by solving a PDE with a free boundary. Pricing methods are not covered here; these notes focus on some fundamental facts about American options. The first thing to notice is that an American option is worth at least as much as a European. Hence, the prices are such that
In particular, we will that an American put has positive value for the right to early exercise, and so does the American call when the underlying asset pays dividend. \\
American Call Option. Let [math]C_t^A[/math] denote the price of an American call option with strike [math]K[/math] and maturity [math]T[/math]. At any time [math]t\leq T[/math] we obviously must have [math]C_t^A \gt S_t-K[/math], otherwise there is an arbitrage opportunity by buying the option and exercising immediately for a risk-less profit. Therefore, we can write
where [math]C_t^{cont}[/math] is the continuation value of the option at time [math]t[/math]; at time [math]t\leq T[/math] the price is determined by whether or not it is optimal to exercise. Letting [math]C_t^E[/math] denote the price of the European call, it is clear that the long party cannot lose anything by having the option to exercise early (provided they do so at a good time) and so
For an American call option on a non-dividend paying asset, it is never optimal to exercise early. Hence, American and European calls have the same price and
The proof follows from the European Put-Call parity and is simple. Early exercise is clearly not optimal if [math]S_t \lt K[/math]. Now suppose that [math]S_t \gt K[/math]. Letting [math]P^E[/math] denote the price of a European put option, we have
To illustrate this proposition consider the following scenario: Suppose you're long an ITM American call, and you have a strong feeling that the asset price will go down and leave the option OTM. In this case you should not exercise but should short the asset and use the call to cover your short position. For example, suppose the asset is trading at $105, you're long a 3 month American call with [math]K=100[/math], and the risk-free rate is 5%. Now compare the following two strategies:
- Exercise the option and invest the proceeds:
- Pay [math]K=$100[/math]; sell the asset at [math]$105[/math].
- Invest proceeds of $5 in bond.
- In three months have $5.06.
- Short the asset, hold the option, and invest the proceeds:
- Short the asset at $105.
- Invest the proceeds of $105 in bond.
- In three months have $106.32 in the bank; owe no more than $100 to cover your short position.
From these two strategies it is clear that early exercise is sub-optimal, as the latter strategy has at least an edge of \$1.32. Alternatively, one could simply sell the call, which will also be better than exercising early.
The introduction of dividends changes things. In particular, early exercise can be optimal if the present value of the dividends is worth more than the interest earned on the strike and the time value of the option. We see this from the put-call parity
where [math]PV_t(D)[/math] is the present value of dividends received during the life of the option. For European options, dividends can be expressed in terms of a yield, [math]\delta\geq 0[/math], so that [math]PV_t(D) = S_t(1-e^{-\delta(T-t)})[/math] and
It may be optimal to exercise early if [math]C_t^E \lt S_t-K[/math], which is possible in the presence of dividends as we can see in Figure. The intuition for this figure is that [math]P_t^E\rightarrow 0[/math] as [math]S_t\rightarrow\infty[/math], and that [math]C_t^E\sim S_te^{-\delta(T-t)}-Ke^{-r(T-t)} \lt S_t-K[/math] for [math]S_t[/math] big enough. This only proves that the option for early exercise has positive value, therefore implying that early exercise may be optimal at some point; it does not mean that one should exercise their American option right now.
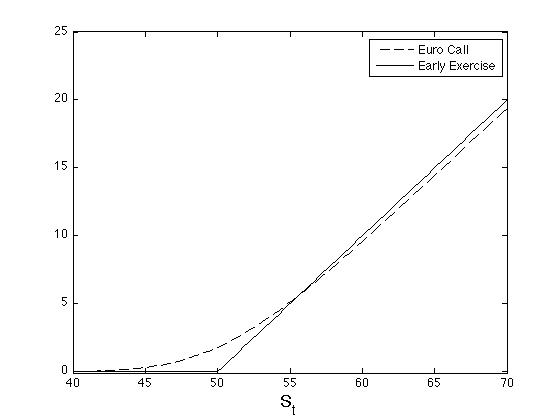
For an American call option on a dividend-paying asset, it may be optimal to exercise early.
Let [math]\delta \gt 0[/math] be the dividend rate and assume [math]r \gt 0[/math]. From the put-call parity,
In practice, dividends are paid at discrete times, and early exercise of an American options should only occur immediately prior to the time of dividend payment. The intuition is similar to the non-dividend case: at non-dividend times it is optimal to wait; time value of strike amount in bank and the right to exercise are more valuable.
American Put Option. Regardless of dividends, early exercise of an American put option may be optimal. To understand why, simply consider a portfolio consisting of an American put with strike [math]K \gt 0[/math] and a single contract in the underlying. If the underlying hits zero, then it is certainly optimal to exercise. In general, early exercise of a put option will be optimal if the price drops low enough to where the time value of the strike amount in the bank account is worth more than the option to wait on selling the asset plus the present value of any dividends that might be recieved.
Early exercise of an American put option may be optimal if [math]r \gt 0[/math].
By contradiction. Suppose it is never optimal to exercise an American put. Then
Proposition is valid regardless of whether or not there are dividends, but the time value of dividends will counterbalance the time value of the cash received from exercise. If [math]r=0[/math], then the European put option is always greater or equal to its intrinsic value, which means
with strict inequality between [math]K-S_t[/math] and [math]P_t^E[/math] if [math]S_t \gt 0[/math]. Hence, if [math]\mathbb P(S_t \gt 0)=1[/math], then [math]\mathbb P(P_t^A=P_t^{cont})=1[/math] and early exercise is never optimal. Joke: Therefore, the Fed should drop interest rates if they are worried about rampant sell-offs by option holders.\\
To summarize, American options have three components beyond their intrinsic value,
- value of option to early exercise (always positive impact on price),
- time value of money (positive for calls, negative for puts),
- dividends (negative for calls, positive for puts).
The value of an American option over the price of a European option is essentially the value of early exercise. While the above results are model-free, the price (and the optimal exercise boundary) will be model-dependent.
Bermuda Options
A Bermuda call option has two exercise times [math]T_1[/math] and [math]T_2[/math] with
At time [math]T_1[/math] the holder of the option has the right to exercise a call with strike [math]K_1[/math], or to continue with the possibility to exercise at time [math]T_2[/math] with exercise [math]K_2[/math]. Hence, the risk-neutral price is
where [math]C^E(t)[/math] is price a European call option with strike [math]K_2[/math] and maturity [math]T_2[/math]. Consider the Black-Scholes model,
where [math]q[/math] is the dividend rate. Recalling the Black-Scholes price for a call on a dividend-paying asset (see Section Options on Futures and Stocks with Dividends of Chapter), the time-[math]T_1[/math] payoff for the Bermuda call option is
where
It follows that for [math]t \lt T_1[/math] that the Bermuda option price [math]C^B(t,s)[/math] is given by the PDE
When pricing the Bermuda option is intuitive to think about the appropriate early-exercise rule. We learned from Section American Options and Optimality of Early Exercise that it is never optimal to exercise at time [math]T_1[/math] if [math]q=0[/math]. However if [math]q \gt 0[/math] then we need to think of a rule for when to exercise. The rule turns out to be simple: find the optimal value [math]s^e[/math] such that at time [math]t=T_1[/math],
In the next subsection we consider the American put, where there will be a time-dependent exercise rule.
Free-Boundary Problem for the American Put
Consider the Black-Scholes model,
with [math]r \gt 0[/math]. In this case it may be optimal exercise early an American put. The price [math]P^A[/math] of the put is the solution to an optimization problem,
where the [math]\tau[/math] is the optional exercise time chosen by the holder, and [math]T\wedge\tau=\min(T,\tau)[/math]. Define [math]\mathcal L[/math] to be the PDE operator,
If at time [math]t[/math] it is optimal to continue then [math]\mathcal LP^A(t,S_t)=0[/math]; if it is optimal to exercise then [math]\mathcal LP^A(t,S_t) = \mathcal L(K-S_t) \lt 0[/math] and [math]\frac{\partial}{\partial s}P^A(t,S_t) = -1[/math]. This is equivalent to finding the pair [math](P^A,s^e)[/math] such that
This is the so-called free boundary problem, which refers to the fact that we need to solve for the boundary [math]s^e(t)[/math] and the PDE's solution [math]P^A(t,s)[/math]. A straight-forward way to solve this PDE and to see the boundary is with a backward recursion on a binomial tree.
General references
Papanicolaou, Andrew (2015). "Introduction to Stochastic Differential Equations (SDEs) for Finance". arXiv:1504.05309 [q-fin.MF].