Modify the program HTSimulation so that it keeps track of the maximum of Peter's winnings in each game of 40 tosses. Have your program print out the proportion of times that your total winnings take on values [math]0,\ 2,\ 4,\ \dots,\ 40[/math]. Calculate the corresponding exact probabilities for games of two tosses and four tosses.

In an upcoming national election for the President of the United States, a pollster plans to predict the winner of the popular vote by taking a random sample of 1000 voters and declaring that the winner will be the one obtaining the most votes in his sample. Suppose that 48 percent of the voters plan to vote for the Republican candidate and 52 percent plan to vote for the Democratic candidate. To get some idea of how reasonable the pollster's plan is, write a program to make this prediction by simulation. Repeat the simulation 100 times and see how many times the pollster's prediction would come true. Repeat your experiment, assuming now that 49 percent of the population plan to vote for the Republican candidate; first with a sample of 1000 and then with a sample of 3000. (The Gallup Poll uses about 3000.) (This idea is discussed further in Central Limit Theorem.)

The psychologist Tversky and his colleagues^{[Notes 1]} say that about four out of five people will answer (a) to the following question: A certain town is served by two hospitals. In the larger hospital about 45 babies are born each day, and in the smaller hospital 15 babies are born each day. Although the overall proportion of boys is about 50 percent, the actual proportion at either hospital may be more or less than 50 percent on any day. At the end of a year, which hospital will have the greater number of days on which more than 60 percent of the babies born were boys?

• the large hospital
• the small hospital
• neither---the number of days will be about the same.

Assume that the probability that a baby is a boy is .5 (actual estimates make this more like .513). Decide, by simulation, what the right answer is to the question. Can you suggest why so many people go wrong?

Notes

You are offered the following game. A fair coin will be tossed until the first time it comes up heads. If this occurs on the [math]j[/math]th toss you are paid [math]2^j[/math] dollars. You are sure to win at least 2 dollars so you should be willing to pay to play this game---but how much? Few people would pay as much as 10 dollars to play this game. See if you can decide, by simulation, a reasonable amount that you would be willing to pay, per game, if you will be allowed to make a large number of plays of the game. Does the amount that you would be willing to pay per game depend upon the number of plays that you will be allowed?

Tversky and his colleagues^{[Notes 1]} studied the records of 48 of the Philadelphia 76ers basketball games in the 1980--81 season to see if a player had times when he was hot and every shot went in, and other times when he was cold and barely able to hit the backboard. The players estimated that they were about 25 percent more likely to make a shot after a hit than after a miss. In fact, the opposite was true---the 76ers were 6 percent more likely to score after a miss than after a hit. Tversky reports that the number of hot and cold streaks was about what one would expect by purely random effects. Assuming that a player has a fifty-fifty chance of making a shot and makes 20 shots a game, estimate by simulation the proportion of the games in which the player will have a streak of 5 or more hits.

Notes

Estimate, by simulation, the average number of children there would be in a family if all people had children until they had a boy. Do the same if all people had children until they had at least one boy and at least one girl. How many more children would you expect to find under the second scheme than under the first in 100,00 families? (Assume that boys and girls are equally likely.)

Mathematicians have been known to get some of the best ideas while sitting in a cafe, riding on a bus, or strolling in the park. In the early 1900s the famous mathematician George Pòlya lived in a hotel near the woods in Zurich. He liked to walk in the woods and think about mathematics. Pòlya describes the following incident:

At the hotel there lived also some students with whom I usually took my meals and had friendly relations. On a certain day one of them expected the visit of his fiancée, what (sic) I knew, but I did not foresee that he and his fiancée would also set out for a stroll in the woods, and then suddenly I met them there. And then I met them the same morning repeatedly, I don't remember how many times, but certainly much too often and I felt embarrassed: It looked as if I was snooping around which was, I assure you, not the case.^{[Notes 1]}

This set him to thinking about whether random walkers were destined to meet.

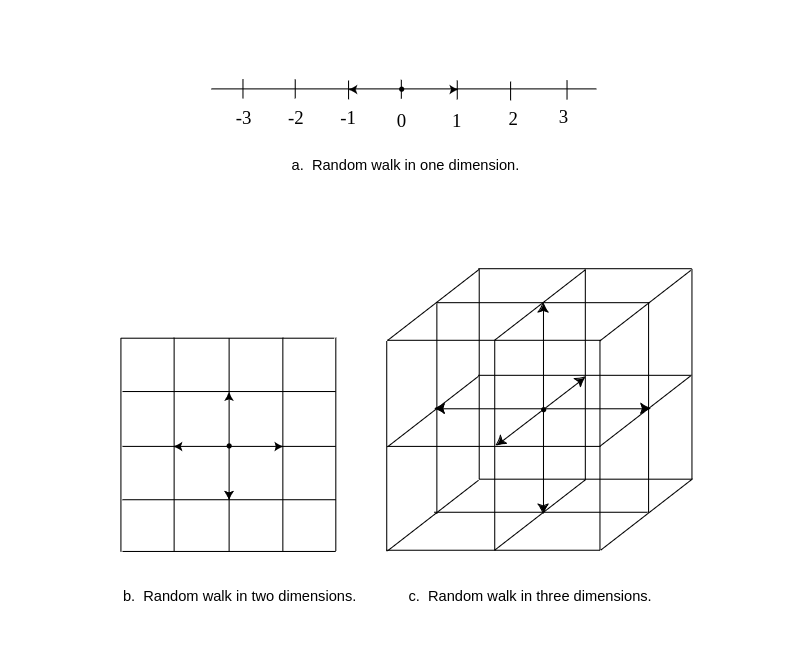
Pòlya considered random walkers in one, two, and three dimensions. In one dimension, he envisioned the walker on a very long street. At each intersection the walker flips a fair coin to decide which direction to walk next (see Figure a). In two dimensions, the walker is walking on a grid of streets, and at each intersection he chooses one of the four possible directions with equal probability (see Figure b). In three dimensions (we might better speak of a random climber), the walker moves on a three-dimensional grid, and at each intersection there are now six different directions that the walker may choose, each with equal probability (see Figure c).

The reader is referred to Random Walks in Euclidean Space, where this and related problems are discussed.

• Write a program to simulate a random walk in one dimension starting at 0. Have your program print out the lengths of the times between returns to the starting point (returns to 0). See if you can guess from this simulation the answer to the following question: Will the walker always return to his starting point eventually or might he drift away forever?
• The paths of two walkers in two dimensions who meet after [math]n[/math] steps can be considered to be a single path that starts at [math](0,0)[/math] and returns to [math](0,0)[/math] after [math]2n[/math] steps. This means that the probability that two random walkers in two dimensions meet is the same as the probability that a single walker in two dimensions ever returns to the starting point. Thus the question of whether two walkers are sure to meet is the same as the question of whether a single walker is sure to return to the starting point. Write a program to simulate a random walk in two dimensions and see if you think that the walker is sure to return to [math](0,0)[/math]. If so, Pòlya would be sure to keep meeting his friends in the park. Perhaps by now you have conjectured the answer to the question: Is a random walker in one or two dimensions sure to return to the starting point? Pòlya answered this question for dimensions one, two, and three. He established the remarkable result that the answer is yes in one and two dimensions and no in three dimensions.
• Write a program to simulate a random walk in three dimensions and see whether, from this simulation and the results of (a) and (b), you could have guessed Pòlya's result.

Notes