Using the Life Table for 1981 given in Appendix C, find the probability that a male of age 60 in 1981 lives to age 80. Find the same probability for a female.
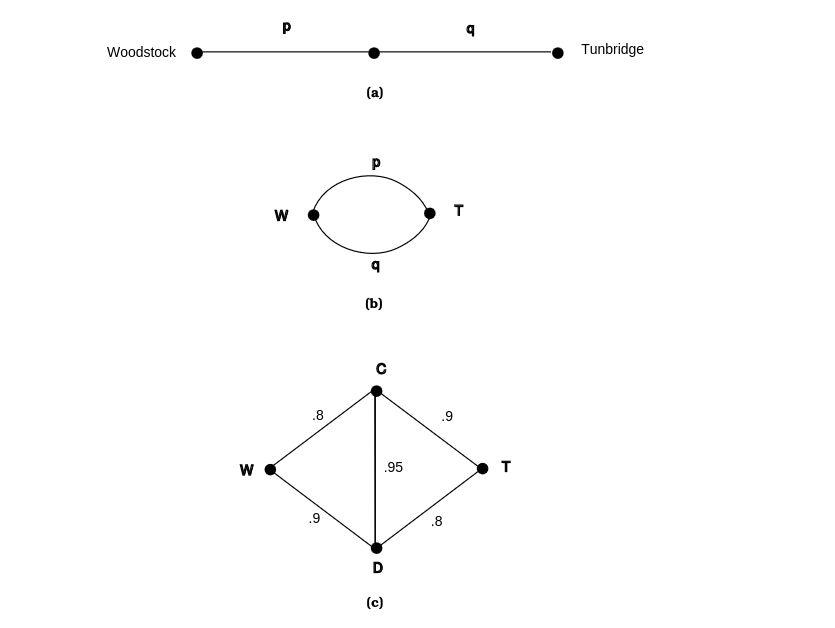
- There has been a blizzard and Helen is trying to drive from Woodstock to Tunbridge, which are connected like the top graph in Figure. Here [math]p[/math] and [math]q[/math] are the probabilities that the two roads are passable. What is the probability that Helen can get from Woodstock to Tunbridge?
- Now suppose that Woodstock and Tunbridge are connected like the middle graph in Figure. What now is the probability that she can get from [math]W[/math] to [math]T[/math]? Note that if we think of the roads as being components of a system, then in (a) and (b) we have computed the reliability of a system whose components are (a) in series and (b) in parallel.
- Now suppose [math]W[/math] and [math]T[/math] are connected like the bottom graph in Figure. Find the probability of Helen's getting from [math]W[/math] to [math]T[/math]. Hint: If the road from [math]C[/math] to [math]D[/math] is impassable, it might as well not be there at all; if it is passable, then figure out how to use part (b) twice.
Let [math]A_1[/math], [math]A_2[/math], and [math]A_3[/math] be events, and let [math]B_i[/math] represent either [math]A_i[/math] or its complement [math]\tilde A_i[/math]. Then there are eight possible choices for the triple [math](B_1, B_2, B_3)[/math]. Prove that the events [math]A_1[/math], [math]A_2[/math], [math]A_3[/math] are independent if and only if
for all eight of the possible choices for the triple [math](B_1, B_2, B_3)[/math].
Four women, A, B, C, and D, check their hats, and the hats are returned in a random manner. Let [math]\Omega[/math] be the set of all possible permutations of A, B, C, D. Let [math]X_j = 1[/math] if the [math]j[/math]th woman gets her own hat back and 0 otherwise. What is the distribution of [math]X_j[/math]? Are the [math]X_i[/math]'s mutually independent?
A box has numbers from 1 to 10. A number is drawn at random. Let [math]X_1[/math] be the number drawn. This number is replaced, and the ten numbers mixed. A second number [math]X_2[/math] is drawn. Find the distributions of [math]X_1[/math] and [math]X_2[/math]. Are [math]X_1[/math] and [math]X_2[/math] independent? Answer the same questions if the first number is not replaced before the second is drawn.
A die is thrown twice. Let [math]X_1[/math] and [math]X_2[/math] denote the outcomes. Define [math]X = \min(X_1, X_2)[/math]. Find the distribution of [math]X[/math].
Given that [math]P(X = a) = r[/math], [math]P(\max(X,Y) = a) = s[/math],and [math]P(\min(X,Y) = a) = t[/math], show that you can determine [math]u = P(Y = a)[/math] in terms of [math]r[/math], [math]s[/math], and [math]t[/math].
A fair coin is tossed three times. Let [math]X[/math] be the number of heads that turn up on the first two tosses and [math]Y[/math] the number of heads that turn up on the third toss.
Give the distribution of
- the random variables [math]X[/math] and [math]Y[/math].
- the random variable [math]Z = X + Y[/math].
- the random variable [math]W = X - Y[/math].
Assume that the random variables [math]X[/math] and [math]Y[/math] have the joint distribution given in Table.
| [math]Y[/math] | |||||
| -1 | 0 | 1 | 2 | ||
| [math]X[/math] | -1 | 0 | 1/36 | 1/6 | 1/12 |
| 0 | 1/18 | 0 | 1/18 | 0 | |
| 1 | 0 | 1/36 | 1/6 | 1/12 | |
| 2 | 1/12 | 0 | 1/12 | 1/6 |
- What is [math]P(X \geq 1\ \mbox {and\ } Y \leq 0)[/math]?
- What is the conditional probability that [math]Y \leq 0[/math] given that [math]X = 2[/math]?
- Are [math]X[/math] and [math]Y[/math] independent?
- What is the distribution of [math]Z = XY[/math]?
In the problem of points, discussed in the historical remarks in Combinations, two players, A and B, play a series of points in a game with player A winning each point with probability [math]p[/math] and player B winning each point with probability [math]q = 1 - p[/math]. The first player to win [math]N[/math] points wins the game. Assume that [math]N = 3[/math]. Let [math]X[/math] be a random variable that has the value 1 if player A wins the series and 0 otherwise. Let [math]Y[/math] be a random variable with value the number of points played in a game. Find the distribution of [math]X[/math] and [math]Y[/math] when [math]p = 1/2[/math]. Are [math]X[/math] and [math]Y[/math] independent in this case? Answer the same questions for the case [math]p = 2/3[/math].