guide:2c0f621d22: Difference between revisions
No edit summary |
mNo edit summary |
||
| (13 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<div class="d-none"> | |||
<math> | |||
% Generic syms | |||
\newcommand\defeq{:=} | |||
\newcommand{\Tt}[0]{\boldsymbol{\theta}} | |||
\newcommand{\XX}[0]{{\cal X}} | |||
\newcommand{\ZZ}[0]{{\cal Z}} | |||
\newcommand{\vx}[0]{{\bf x}} | |||
\newcommand{\vv}[0]{{\bf v}} | |||
\newcommand{\vu}[0]{{\bf u}} | |||
\newcommand{\vs}[0]{{\bf s}} | |||
\newcommand{\vm}[0]{{\bf m}} | |||
\newcommand{\vq}[0]{{\bf q}} | |||
\newcommand{\mX}[0]{{\bf X}} | |||
\newcommand{\mC}[0]{{\bf C}} | |||
\newcommand{\mA}[0]{{\bf A}} | |||
\newcommand{\mL}[0]{{\bf L}} | |||
\newcommand{\fscore}[0]{F_{1}} | |||
\newcommand{\sparsity}{s} | |||
\newcommand{\mW}[0]{{\bf W}} | |||
\newcommand{\mD}[0]{{\bf D}} | |||
\newcommand{\mZ}[0]{{\bf Z}} | |||
\newcommand{\vw}[0]{{\bf w}} | |||
\newcommand{\D}[0]{{\mathcal{D}}} | |||
\newcommand{\mP}{\mathbf{P}} | |||
\newcommand{\mQ}{\mathbf{Q}} | |||
\newcommand{\E}[0]{{\mathbb{E}}} | |||
\newcommand{\vy}[0]{{\bf y}} | |||
\newcommand{\va}[0]{{\bf a}} | |||
\newcommand{\vn}[0]{{\bf n}} | |||
\newcommand{\vb}[0]{{\bf b}} | |||
\newcommand{\vr}[0]{{\bf r}} | |||
\newcommand{\vz}[0]{{\bf z}} | |||
\newcommand{\N}[0]{{\mathcal{N}}} | |||
\newcommand{\vc}[0]{{\bf c}} | |||
\newcommand{\bm}{\boldsymbol} | |||
% Statistics and Probability Theory | |||
\newcommand{\errprob}{p_{\rm err}} | |||
\newcommand{\prob}[1]{p({#1})} | |||
\newcommand{\pdf}[1]{p({#1})} | |||
\def \expect {\mathbb{E} } | |||
% Machine Learning Symbols | |||
\newcommand{\biasterm}{B} | |||
\newcommand{\varianceterm}{V} | |||
\newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} | |||
\newcommand{\nrfolds}{k} | |||
\newcommand{\mseesterr}{E_{\rm est}} | |||
\newcommand{\bootstrapidx}{b} | |||
%\newcommand{\modeldim}{r} | |||
\newcommand{\modelidx}{l} | |||
\newcommand{\nrbootstraps}{B} | |||
\newcommand{\sampleweight}[1]{q^{(#1)}} | |||
\newcommand{\nrcategories}{K} | |||
\newcommand{\splitratio}[0]{{\rho}} | |||
\newcommand{\norm}[1]{\Vert {#1} \Vert} | |||
\newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} | |||
\newcommand{\bmx}[0]{\begin{bmatrix}} | |||
\newcommand{\emx}[0]{\end{bmatrix}} | |||
\newcommand{\T}[0]{\text{T}} | |||
\DeclareMathOperator*{\rank}{rank} | |||
%\newcommand\defeq{:=} | |||
\newcommand\eigvecS{\hat{\mathbf{u}}} | |||
\newcommand\eigvecCov{\mathbf{u}} | |||
\newcommand\eigvecCoventry{u} | |||
\newcommand{\featuredim}{n} | |||
\newcommand{\featurelenraw}{\featuredim'} | |||
\newcommand{\featurelen}{\featuredim} | |||
\newcommand{\samplingset}{\mathcal{M}} | |||
\newcommand{\samplesize}{m} | |||
\newcommand{\sampleidx}{i} | |||
\newcommand{\nractions}{A} | |||
\newcommand{\datapoint}{\vz} | |||
\newcommand{\actionidx}{a} | |||
\newcommand{\clusteridx}{c} | |||
\newcommand{\sizehypospace}{D} | |||
\newcommand{\nrcluster}{k} | |||
\newcommand{\nrseeds}{s} | |||
\newcommand{\featureidx}{j} | |||
\newcommand{\clustermean}{{\bm \mu}} | |||
\newcommand{\clustercov}{{\bm \Sigma}} | |||
\newcommand{\target}{y} | |||
\newcommand{\error}{E} | |||
\newcommand{\augidx}{b} | |||
\newcommand{\task}{\mathcal{T}} | |||
\newcommand{\nrtasks}{T} | |||
\newcommand{\taskidx}{t} | |||
\newcommand\truelabel{y} | |||
\newcommand{\polydegree}{r} | |||
\newcommand\labelvec{\vy} | |||
\newcommand\featurevec{\vx} | |||
\newcommand\feature{x} | |||
\newcommand\predictedlabel{\hat{y}} | |||
\newcommand\dataset{\mathcal{D}} | |||
\newcommand\trainset{\dataset^{(\rm train)}} | |||
\newcommand\valset{\dataset^{(\rm val)}} | |||
\newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} | |||
\newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} | |||
\newcommand{\inspace}{\mathcal{X}} | |||
\newcommand{\sigmoid}{\sigma} | |||
\newcommand{\outspace}{\mathcal{Y}} | |||
\newcommand{\hypospace}{\mathcal{H}} | |||
\newcommand{\emperror}{\widehat{L}} | |||
\newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} | |||
\newcommand{\featurespace}{\mathcal{X}} | |||
\newcommand{\labelspace}{\mathcal{Y}} | |||
\newcommand{\rawfeaturevec}{\mathbf{z}} | |||
\newcommand{\rawfeature}{z} | |||
\newcommand{\condent}{H} | |||
\newcommand{\explanation}{e} | |||
\newcommand{\explainset}{\mathcal{E}} | |||
\newcommand{\user}{u} | |||
\newcommand{\actfun}{\sigma} | |||
\newcommand{\noisygrad}{g} | |||
\newcommand{\reconstrmap}{r} | |||
\newcommand{\predictor}{h} | |||
\newcommand{\eigval}[1]{\lambda_{#1}} | |||
\newcommand{\regparam}{\lambda} | |||
\newcommand{\lrate}{\alpha} | |||
\newcommand{\edges}{\mathcal{E}} | |||
\newcommand{\generror}{E} | |||
\DeclareMathOperator{\supp}{supp} | |||
%\newcommand{\loss}[3]{L({#1},{#2},{#3})} | |||
\newcommand{\loss}[2]{L\big({#1},{#2}\big)} | |||
\newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} | |||
\newcommand{\determinant}[1]{{\rm det}({#1})} | |||
\DeclareMathOperator*{\argmax}{argmax} | |||
\DeclareMathOperator*{\argmin}{argmin} | |||
\newcommand{\itercntr}{r} | |||
\newcommand{\state}{s} | |||
\newcommand{\statespace}{\mathcal{S}} | |||
\newcommand{\timeidx}{t} | |||
\newcommand{\optpolicy}{\pi_{*}} | |||
\newcommand{\appoptpolicy}{\hat{\pi}} | |||
\newcommand{\dummyidx}{j} | |||
\newcommand{\gridsizex}{K} | |||
\newcommand{\gridsizey}{L} | |||
\newcommand{\localdataset}{\mathcal{X}} | |||
\newcommand{\reward}{r} | |||
\newcommand{\cumreward}{G} | |||
\newcommand{\return}{\cumreward} | |||
\newcommand{\action}{a} | |||
\newcommand\actionset{\mathcal{A}} | |||
\newcommand{\obstacles}{\mathcal{B}} | |||
\newcommand{\valuefunc}[1]{v_{#1}} | |||
\newcommand{\gridcell}[2]{\langle #1, #2 \rangle} | |||
\newcommand{\pair}[2]{\langle #1, #2 \rangle} | |||
\newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} | |||
\newcommand{\actionvalue}[1]{q_{#1}} | |||
\newcommand{\transition}{\mathcal{T}} | |||
\newcommand{\policy}{\pi} | |||
\newcommand{\charger}{c} | |||
\newcommand{\itervar}{k} | |||
\newcommand{\discount}{\gamma} | |||
\newcommand{\rumba}{Rumba} | |||
\newcommand{\actionnorth}{\rm N} | |||
\newcommand{\actionsouth}{\rm S} | |||
\newcommand{\actioneast}{\rm E} | |||
\newcommand{\actionwest}{\rm W} | |||
\newcommand{\chargingstations}{\mathcal{C}} | |||
\newcommand{\basisfunc}{\phi} | |||
\newcommand{\augparam}{B} | |||
\newcommand{\valerror}{E_{v}} | |||
\newcommand{\trainerror}{E_{t}} | |||
\newcommand{\foldidx}{b} | |||
\newcommand{\testset}{\dataset^{(\rm test)} } | |||
\newcommand{\testerror}{E^{(\rm test)}} | |||
\newcommand{\nrmodels}{M} | |||
\newcommand{\benchmarkerror}{E^{(\rm ref)}} | |||
\newcommand{\lossfun}{L} | |||
\newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} | |||
\newcommand{\cluster}{\mathcal{C}} | |||
\newcommand{\bayeshypothesis}{h^{*}} | |||
\newcommand{\featuremtx}{\mX} | |||
\newcommand{\weight}{w} | |||
\newcommand{\weights}{\vw} | |||
\newcommand{\regularizer}{\mathcal{R}} | |||
\newcommand{\decreg}[1]{\mathcal{R}_{#1}} | |||
\newcommand{\naturalnumbers}{\mathbb{N}} | |||
\newcommand{\featuremapvec}{{\bf \Phi}} | |||
\newcommand{\featuremap}{\phi} | |||
\newcommand{\batchsize}{B} | |||
\newcommand{\batch}{\mathcal{B}} | |||
\newcommand{\foldsize}{B} | |||
\newcommand{\nriter}{R} | |||
</math> | |||
</div> | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_ERM_idea"></span> | |||
[[File:fig_ERM_idea.jpg | 500px | thumb | ML methods learn a hypothesis <math>h \in \hypospace</math> that incur small loss | |||
when predicting the label <math>\truelabel</math> of a <span class="mw-gls mw-gls-first" data-name ="datapoint">data point</span> based on its features <math>\featurevec</math>. <span class="mw-gls mw-gls-first" data-name ="erm">Empirical risk minimization (ERM)</span> | |||
approximates the expected loss or risk by the <span class="mw-gls mw-gls-first" data-name ="emprisk">empirical risk</span> (solid curve) incurred on a | |||
finite set of labeled <span class="mw-gls" data-name ="datapoint">data point</span>s (the <span class="mw-gls mw-gls-first" data-name ="trainset">training set</span>). Note that we can compute the <span class="mw-gls" data-name ="emprisk">empirical risk</span> | |||
based on the observed <span class="mw-gls" data-name ="datapoint">data point</span>s. However, to compute the risk we would need to know | |||
the underlying <span class="mw-gls mw-gls-first" data-name ="probdist">probability distribution</span> which is rarely the case. ]] | |||
</div> | |||
Chapter [[guide:B85f6bf6f2 | Three Components of ML ]] discussed three components (see Figure [[#fig_ml_problem|fig_ml_problem]]): | |||
* <span class="mw-gls" data-name ="datapoint">data point</span>s characterized by features <math>\featurevec \in \featurespace</math> and labels <math> \truelabel \in \labelspace</math>, | |||
* a <span class="mw-gls mw-gls-first" data-name ="hypospace">hypothesis space</span> <math>\hypospace</math> of computationally feasible maps <math>h:\featurespace \rightarrow \labelspace</math>, | |||
* and a <span class="mw-gls mw-gls-first" data-name ="lossfunc">loss function</span> <math>\loss{(\featurevec,\truelabel)}{h}</math> that measuresthe discrepancy between the predicted label <math>h(\featurevec)</math> and the true label <math>\truelabel</math>. | |||
Ideally we would like to learn a hypothesis <math>h \in \hypospace</math> such that <math>\loss{(\featurevec,\truelabel)}{h}</math> is small | |||
for any <span class="mw-gls" data-name ="datapoint">data point</span> <math>(\featurevec,\truelabel)</math>. However, to implement this informal goal we need to define what | |||
is meant precisely by “any <span class="mw-gls" data-name ="datapoint">data point</span>”. Maybe the most widely used approach to the define the concept of “any <span class="mw-gls" data-name ="datapoint">data point</span>” | |||
is the <span class="mw-gls mw-gls-first" data-name ="iidasspt">i.i.d assumption</span>. | |||
The <span class="mw-gls" data-name ="iidasspt">i.i.d assumption</span> interprets <span class="mw-gls" data-name ="datapoint">data point</span>s as realizations of <span class="mw-gls mw-gls-first" data-name ="iid">independent and identically distributed (iid)</span> <span class="mw-gls mw-gls-first" data-name ="rv">random variable (RV)</span>s | |||
with a common <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>. The <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math> | |||
allows us to define the risk of a hypothesis <math>h</math> as the expectation of the <span class="mw-gls mw-gls-first" data-name ="loss">loss</span> incurred by <math>h</math> | |||
on (the realizations of) a random <span class="mw-gls" data-name ="datapoint">data point</span>. We can interpret the risk of a hypothesis as a | |||
measure for its quality in predicting the label of“any <span class="mw-gls" data-name ="datapoint">data point</span>”. | |||
If we know the <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math> from which <span class="mw-gls" data-name ="datapoint">data point</span>s are drawn (<span class="mw-gls" data-name ="iid">iid</span>), | |||
we can precisely determine the hypothesis with minimum risk. This optimal hypothesis, which is | |||
referred to as a <span class="mw-gls mw-gls-first" data-name ="bayesestimator">Bayes estimator</span>, can be read off almost directly from the posterior <span class="mw-gls" data-name ="probdist">probability distribution</span> | |||
<math>p(\truelabel|\featurevec)</math> of the label <math>\truelabel</math> given the features <math>\featurevec</math> of a <span class="mw-gls" data-name ="datapoint">data point</span>. | |||
The precise form of the <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> depends on the choice for the <span class="mw-gls" data-name ="lossfunc">loss function</span>. | |||
When using the squared error loss, the optimal hypothesis (or <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span>) is given by the posterior mean <math>h(\featurevec) = \expect \big\{ \truelabel | \featurevec \}</math> <ref name="LC">E. L. Lehmann and G. Casella. ''Theory of Point Estimation'' Springer, New York, 2nd edition, 1998</ref>. | |||
In most ML application, we do not know the true underlying <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math> from | |||
which <span class="mw-gls" data-name ="datapoint">data point</span>s are generated. Therefore, we cannot compute the <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> exactly. However, | |||
we can approximately compute this estimator by replacing the exact <span class="mw-gls" data-name ="probdist">probability distribution</span> with an estimate | |||
or approximation. Section [[#sec_ERM_Bayes | ERM for Bayes Classifiers ]] discusses a specific ML method that implements this approach. | |||
The risk of the <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> (which is the <span class="mw-gls mw-gls-first" data-name ="bayesrisk">Bayes risk</span>) provides a useful <span class="mw-gls mw-gls-first" data-name ="baseline">baseline</span> against which | |||
we can compare the average loss incurred by a ML method on a set of <span class="mw-gls" data-name ="datapoint">data point</span>s. Section [[guide:07ad9c2de8#sec_diagnosis_ML | Diagnosing ML ]] | |||
shows how to diagnose ML methods by comparing its average loss of a hypothesis on a <span class="mw-gls" data-name ="trainset">training set</span> and its | |||
average loss on a <span class="mw-gls mw-gls-first" data-name ="valset">validation set</span> with a <span class="mw-gls" data-name ="baseline">baseline</span>. | |||
Section [[#equ_sec_emp_risk_approximates_expected_loss | Approximating Risk by Empirical Risk]] motivates <span class="mw-gls mw-gls-first" data-name ="erm">empirical risk minimization (ERM)</span> by approximating | |||
the risk using the <span class="mw-gls" data-name ="emprisk">empirical risk</span> (or average loss) computed for a set of labeled (training) <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
(see Figure [[#fig_ERM_idea|fig_ERM_idea]]). This approximation is justified by the <span class="mw-gls mw-gls-first" data-name ="lln">law of large numbers</span> which characterizes the | |||
deviation between averages of <span class="mw-gls" data-name ="rv">RV</span>s and their expectation. Section [[#sec_comp_stat_ERM | Computational and Statistical Aspects of ERM ]] discusses the statistical and computational aspects of <span class="mw-gls" data-name ="erm">ERM</span>. We then specialize the <span class="mw-gls" data-name ="erm">ERM</span> for three particular ML methods arising from different combinations of <span class="mw-gls" data-name ="hypospace">hypothesis space</span> and <span class="mw-gls" data-name ="lossfunc">loss function</span>. Section [[#sec_ERM_lin_reg | ERM for Linear Regression ]] | |||
discusses <span class="mw-gls" data-name ="erm">ERM</span> for linear regression (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]). Here, <span class="mw-gls" data-name ="erm">ERM</span> amounts to minimizing a differentiable convex function, which can be done efficiently using <span class="mw-gls mw-gls-first" data-name ="gdmethods">gradient-based methods</span> (see Chapter [[guide:Cc42ad1ea4 | Gradient-Based Learning ]]). | |||
We then discuss in Section [[#sec_ERM_decision_tree | ERM for Decision Trees ]] the <span class="mw-gls" data-name ="erm">ERM</span> obtained for <span class="mw-gls mw-gls-first" data-name ="decisiontree">decision tree</span> models. The resulting <span class="mw-gls" data-name ="erm">ERM</span> problems becomes a discrete optimization problem which are typically much harder than convex optimization problems. We cannot apply <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> to solve the <span class="mw-gls" data-name ="erm">ERM</span> for <span class="mw-gls" data-name ="decisiontree">decision tree</span>s. To solve <span class="mw-gls" data-name ="erm">ERM</span> for a <span class="mw-gls" data-name ="decisiontree">decision tree</span>, we essentially must try out all possible choices for the tree structure <ref name="Hyafil1976">L. Hyafil and R. Rivest. Constructing optimal binary decision trees is np-complete. ''Information Processing Letters'' 5(1):15--17, 1976</ref>. | |||
Section [[#sec_ERM_Bayes | ERM for Bayes Classifiers ]] considers the <span class="mw-gls" data-name ="erm">ERM</span> obtained when learning a linear hypothesis | |||
using the <math>0/1</math> loss for classification problems. The resulting <span class="mw-gls" data-name ="erm">ERM</span> amounts to minimizing a non-differentiable and non-convex function. Instead of applying optimization methods to solve | |||
this <span class="mw-gls" data-name ="erm">ERM</span> instance, we will instead directly construct approximations of the <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span>. | |||
Section [[#sec_training_inference | Training and Inference Periods ]] decomposes the operation of ML methods into training periods and inference periods. The training period amounts to learning a hypothesis by solving the <span class="mw-gls" data-name ="erm">ERM</span> on a given <span class="mw-gls" data-name ="trainset">training set</span>. The resulting hypothesis is then applied to new <span class="mw-gls" data-name ="datapoint">data point</span>s, which are not contained in the <span class="mw-gls" data-name ="trainset">training set</span>. This application of a learnt hypothesis to <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span> | |||
is referred to as the inference period. Section [[#sec_online_learning | Online Learning ]] demonstrates how an online learning method | |||
can be obtained by solving the <span class="mw-gls" data-name ="erm">ERM</span> sequentially as new <span class="mw-gls" data-name ="datapoint">data point</span>s come in. Online learning methods alternate between training and inference periods whenever new data is collected. | |||
==<span id="equ_sec_emp_risk_approximates_expected_loss"/>Approximating Risk by Empirical Risk== | |||
The <span class="mw-gls" data-name ="datapoint">data point</span>s arising in many important application domains can be modelled (orapproximated) as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s with a common (joint) <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math> for the features <math>\featurevec</math> and label <math>\truelabel</math>. The <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math> used in this <span class="mw-gls" data-name ="iidasspt">i.i.d assumption</span> allows us to define the | |||
expected loss or <span class="mw-gls mw-gls-first" data-name ="risk">risk</span> of a hypothesis <math>h \in \hypospace</math> as | |||
<span id="equ_def_risk"/> | |||
<math display = "block">\begin{equation} | |||
\label{equ_def_risk} | |||
\expect \big \{ \loss{(\featurevec,\truelabel)}{h} \}. | |||
\end{equation}</math> | |||
It seems reasonable to learn a hypothesis <math>h</math> such that its risk \eqref{equ_def_risk} is minimal, | |||
<math display = "block">\begin{equation} | |||
\label{equ_def_risk_min} | |||
\bayeshypothesis \defeq \argmin_{h \in \hypospace} \expect \big \{ \loss{(\featurevec,\truelabel)}{h} \}. | |||
\end{equation}</math> | |||
We refer to any hypothesis <math>\bayeshypothesis</math> that achieves the minimum risk \eqref{equ_def_risk_min} as a <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> <ref name="LC"/>. Note that the <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> <math>\bayeshypothesis</math> depends on both, the <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math> and the <span class="mw-gls" data-name ="lossfunc">loss function</span>. When using the [[guide:B85f6bf6f2#equ_squared_loss|squared error loss]] in \eqref{equ_def_risk_min}, the <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> <math>\bayeshypothesis</math> is given by the posterior mean of <math>\truelabel</math> given the features <math>\featurevec</math> (see <ref name="papoulis">A. Papoulis and S. U. Pillai. ''Probability, Random Variables, and Stochastic Processes'' Mc-Graw Hill, New York, 4 edition, 2002</ref>{{rp|at=Ch. 7}}). | |||
Risk minimization \eqref{equ_def_risk_min} cannot be used for the design of ML methods whenever we do not know the <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>. If we do not know the <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>, which is the rule for many ML applications, we cannot evaluate the expectation in \eqref{equ_def_risk}. | |||
One exception to this rule is if the <span class="mw-gls" data-name ="datapoint">data point</span>s are synthetically generated by drawing realizations | |||
from a given <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>. | |||
The idea of <span class="mw-gls" data-name ="erm">ERM</span> is to approximate the expectation in \eqref{equ_def_risk_min} with an average loss (the <span class="mw-gls" data-name ="emprisk">empirical risk</span>) incurred on a given set of <span class="mw-gls" data-name ="datapoint">data point</span>s (the “<span class="mw-gls" data-name ="trainset">training set</span>”), | |||
<math display = "block">\begin{equation} | |||
\nonumber | |||
\dataset = \big\{ \big(\featurevec^{(1)}, \truelabel^{(1)} \big), \ldots, \big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)} \big) \}. | |||
\end{equation}</math> | |||
As discussed in Section [[guide:B85f6bf6f2#sec_empirical_risk | <span class="mw-gls" data-name ="emprisk">empirical risk</span> ]], this approximation is justified by the <span class="mw-gls" data-name ="lln">law of large numbers</span>. We obtain <span class="mw-gls" data-name ="erm">ERM</span> by replacing the risk in the minimization problem \eqref{equ_def_risk_min} with the [[guide:B85f6bf6f2#eq_def_emp_error_101 | <span class="mw-gls" data-name ="emprisk">empirical risk</span> ]], | |||
<math display="block"> | |||
\begin{align} | |||
\hat{h} & \in \argmin_{h \in \hypospace} \emperror(h|\dataset) \nonumber \\ | |||
& \label{equ_def_ERM_funs}\stackrel{\eqref{eq_def_emp_error_101}}{=} \argmin_{h \in \hypospace} (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h}. | |||
\end{align} | |||
</math> | |||
As the notation in \eqref{equ_def_ERM_funs} indicates there might be several different hypotheses that minimize <math>\emperror(h|\dataset)</math>. We denote by <math>\hat{h}</math> any of them. Mathematically, <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_ERM_funs} is just an instance of an optimization problem <ref name="BoydConvexBook">S. Boyd and L. Vandenberghe. ''Convex Optimization'' Cambridge Univ. Press, Cambridge, UK, 2004</ref>. The optimization domain in \eqref{equ_def_ERM_funs} is | |||
the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> <math>\hypospace</math> of a ML method, the objective | |||
(or cost) function is the [[guide:B85f6bf6f2#eq_def_emp_error_101 | <span class="mw-gls" data-name ="emprisk">empirical risk</span> ]]. ML methods that learn a hypothesis via <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_ERM_funs} are instances of optimization algorithms <ref name="OptMLBook">S. Sra, S. Nowozin, and S. J. Wright, editors. ''Optimization for Machine Learning'' MIT Press, 2012</ref>. | |||
<span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_ERM_funs} is a form of “learning by trial and error”. | |||
A (hypothetical) instructor (or supervisor) provides us the labels <math>\truelabel^{(\sampleidx)}</math> for the <span class="mw-gls" data-name ="datapoint">data point</span>s in <math>\dataset</math> which are characterized by features <math>\featurevec^{(\sampleidx)}</math>. This dataset serves as a <span class="mw-gls" data-name ="trainset">training set</span> in the following sense. | |||
We use a current guess for a good hypothesis <math>h</math> to predict the labels <math>\truelabel^{(\sampleidx)}</math> of the <span class="mw-gls" data-name ="datapoint">data point</span>s in <math>\dataset</math> | |||
only from their features <math>\featurevec^{(\sampleidx)}</math> . We then determine average loss <math>\emperror(h|\dataset)</math> that is incurred by the predictions <math>\hat{\truelabel}^{(\sampleidx)} = h\big( \featurevec^{(\sampleidx)} \big)</math>. If the <span class="mw-gls mw-gls-first" data-name ="trainerr">training error</span> <math>\emperror(h|\dataset)</math> | |||
is too large, we try out another hypothesis map <math>h'</math> different from <math>h</math> with the hope of achieving a smaller <span class="mw-gls" data-name ="trainerr">training error</span> <math>\emperror(h'|\dataset)</math>. | |||
We highlight that <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_ERM_funs} is motivated by the <span class="mw-gls" data-name ="lln">law of large numbers</span>. The <span class="mw-gls" data-name ="lln">law of large numbers</span>, in turn, is only | |||
useful if the <span class="mw-gls" data-name ="datapoint">data point</span>s generated within an ML application can be well modelled as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s. | |||
This <span class="mw-gls" data-name ="iidasspt">i.i.d assumption</span> is one of the most widely used working assumptions for the design and analysis of ML methods. | |||
However, there are many important application domains involving <span class="mw-gls" data-name ="datapoint">data point</span>s that clearly violate this <span class="mw-gls" data-name ="iidasspt">i.i.d assumption</span>. | |||
One example for <span class="mw-gls mw-gls-first" data-name ="noniid">non-i.i.d.</span> <span class="mw-gls mw-gls-first" data-name ="data">data</span> is time series data that consists of temporally ordered (consecutive) <span class="mw-gls" data-name ="datapoint">data point</span>s <ref name="Brockwell91">P. J. Brockwell and R. A. Davis. ''Time Series: Theory and Methods'' Springer New York, 1991</ref><ref name="Luetkepol2005">H. Lütkepohl. ''New Introduction to Multiple Time Series Analysis'' Springer, New York, 2005</ref>. Each <span class="mw-gls" data-name ="datapoint">data point</span> in a time series might represent a specific time interval or single time instants. | |||
Another example for <span class="mw-gls" data-name ="noniid">non-i.i.d.</span> data arises in active learning where ML methods | |||
actively choose (or query) new <span class="mw-gls" data-name ="datapoint">data point</span>s <ref name="Cohn1996">D. Cohn, Z. Ghahramani, and M. Jordan. Active learning with statistical models. ''J. Artif. Int. Res.'' 4(1):129--145, March 1996</ref>. For a third example of <span class="mw-gls" data-name ="noniid">non-i.i.d.</span> data, | |||
we refer to <span class="mw-gls mw-gls-first" data-name ="fl">federated learning (FL)</span> applications that involve collections (networks) of data generators with different statistical properties <ref name="pmlr-v54-mcmahan17a">B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. y Arcas. Communication-efficient learning of deep networks from decentralized | |||
data. In A. Singh and J. Zhu, editors, ''Proceedings of the 20th | |||
International Conference on Artificial Intelligence and Statistics'' | |||
volume 54 of ''Proceedings of Machine Learning Research'' pages | |||
1273--1282, Fort Lauderdale, FL, USA, 20--22 Apr 2017. PMLR</ref><ref name="JungNetExp2020">A. Jung. Networked exponential families for big data over networks. ''IEEE Access'' 8:202897--202909, 2020</ref><ref name="LocalizedLinReg2019">A. Jung and N. Tran. Localized linear regression in networked data. ''IEEE Sig. Proc. Lett.'' 26(7), Jul. 2019</ref><ref name="Tran2020">N. Tran, H. Ambos, and A. Jung. Classifying partially labeled networked data via logistic network | |||
lasso. In ''Proc. IEEE Int. Conf. on Acoustics, Speech and Signal | |||
Processing (ICASSP)'' pages 3832--3836, Barcelona, Spain, May 2020</ref><ref name="SattlerClusteredFL2020">F. Sattler, K. Müller, and W. Samek. Clustered federated learning: Model-agnostic distributed multitask | |||
optimization under privacy constraints. ''IEEE Transactions on Neural Networks and Learning Systems'' | |||
2020</ref>. | |||
A detailed discussion of ML methods for <span class="mw-gls" data-name ="noniid">non-i.i.d.</span> data is beyond the scope of this book. | |||
==<span id="sec_comp_stat_ERM"/>Computational and Statistical Aspects of ERM== | |||
Solving the optimization problem \eqref{equ_def_ERM_funs} provides two things. First, the minimizer <math>\hat{h}</math> is a predictor which performs optimal on the <span class="mw-gls" data-name ="trainset">training set</span> <math>\dataset</math>. | |||
Second, the corresponding objective value <math>\emperror(\hat{h}|\dataset)</math> (the “<span class="mw-gls" data-name ="trainerr">training error</span>”) | |||
can be used to estimate for the risk or expected loss of <math>\hat{h}</math>. However, as we will discuss | |||
in Chapter [[guide:50be9327aa | Regularization ]], for some datasets <math>\dataset</math>, the <span class="mw-gls" data-name ="trainerr">training error</span> | |||
<math>\emperror(\hat{h}|\dataset)</math> obtained for <math>\dataset</math> can be very different from the | |||
expected loss (risk) of <math>\hat{h}</math> when applied to new <span class="mw-gls" data-name ="datapoint">data point</span>s which are not contained in <math>\dataset</math>. | |||
The <span class="mw-gls" data-name ="iidasspt">i.i.d assumption</span> implies that the <span class="mw-gls" data-name ="trainerr">training error</span> <math>\emperror(h|\dataset)</math> is only a noisy approximation | |||
of the risk <math>\risk{h}</math>. The <span class="mw-gls" data-name ="erm">ERM</span> solution <math>\hat{h}</math> is a minimizer of this noisy approximation and | |||
therefore in general different from the <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> which minimizes the risk itself. | |||
Even if the hypothesis <math>\hat{h}</math> delivered by <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_ERM_funs} has | |||
small <span class="mw-gls" data-name ="trainerr">training error</span> <math>\emperror(\hat{h}|\dataset)</math>, it might have unacceptably large risk <math>\risk{\hat{h}}</math>. | |||
We refer to such a situation as overfitting and will discuss techniques for detecting and avoiding it | |||
in Chapter [[guide:07ad9c2de8 | Model Validation and Selection ]]. | |||
Many important ML methods use hypotheses that are parametrized by a parameter vector <math>\weights</math>. For | |||
each possible parameter vector, we obtain a hypothesis <math>h^{(\weights)}(\featurevec)</math>. Such a parametrization | |||
is used in <span class="mw-gls mw-gls-first" data-name ="linreg">linear regression</span> methods which learn a linear hypothesis <math>h^{(\weights)}(\featurevec) = \weights^{T} \featurevec</math> with some parameter vector <math>\weights</math>. Another example for such a parametrization is obtained from <span class="mw-gls mw-gls-first" data-name ="ann">artificial neural network (ANN)</span>s with the weights assigned to inputs of individual (artificial) neurons (see Figure [[#fig_ANN|fig_ANN]]). | |||
For ML methods that use a parametrized hypothesis <math>h^{(\weights)}(\featurevec)</math>, | |||
we can reformulate the optimization problem \eqref{equ_def_ERM_funs} | |||
as an optimization of the parameter vector, | |||
<span id="eq_def_ERM_weight"/> | |||
<math display = "block">\begin{equation} | |||
\label{eq_def_ERM_weight} | |||
\widehat{\weights} = \argmin_{\weights \in \mathbb{R}^{\featuredim}} f(\weights) \mbox{ with } f(\weights) \defeq | |||
\underbrace{(1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h^{(\weights)}}}_{\emperror\big(h^{(\weights)} |\dataset\big)}. | |||
\end{equation}</math> | |||
The objective function <math>f(\weights)</math> in \eqref{eq_def_ERM_weight} is the <span class="mw-gls" data-name ="emprisk">empirical risk</span> <math>\emperror\big(h^{(\weights)} |\dataset\big)</math> | |||
incurred by the hypothesis <math>h^{(\weights)}</math> when applied to the <span class="mw-gls" data-name ="datapoint">data point</span>s in the dataset <math>\dataset</math>. | |||
The optimization problems \eqref{eq_def_ERM_weight} and \eqref{equ_def_ERM_funs} | |||
are fully equivalent. Given the optimal parameter vector <math>\widehat{\weights}</math> solving \eqref{eq_def_ERM_weight}, | |||
the hypothesis <math>h^{(\widehat{\weights})}</math> solves \eqref{equ_def_ERM_funs}. | |||
We highlight that the precise shape of the objective function <math>f(\weights)</math> in \eqref{eq_def_ERM_weight} | |||
depends on the parametrization of the hypothesis space <math>\hypospace</math>. The parametrization is the precise | |||
rule that assigns a hypothesis map <math>h^{(\weights)}</math> to a given parameter vector <math>\weights</math>. The shape of <math>f(\weights)</math> | |||
depends also on the choice for the loss function <math>\loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h^{(\weights)}}</math>. | |||
As depicted in Figure [[#fig_diff_types_bojec|fig_diff_types_bojec]], the different combinations of parametrized <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | |||
and loss functions can result in objective functions with fundamentally different properties such that their | |||
optimization is more or less difficult. | |||
The objective function <math>f(\weights)</math> for the <span class="mw-gls" data-name ="erm">ERM</span> obtained for <span class="mw-gls" data-name ="linreg">linear regression</span> (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]) is differentiable | |||
and convex and can therefore be minimized using simple <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> (see Chapter [[guide:Cc42ad1ea4 | Gradient-Based Learning ]]). In contrast, | |||
the objective function <math>f(\weights)</math> of <span class="mw-gls" data-name ="erm">ERM</span> obtained for <span class="mw-gls mw-gls-first" data-name ="ladregression">least absolute deviation regression</span> or the <span class="mw-gls mw-gls-first" data-name ="svm">support vector machine (SVM)</span> (see Section [[guide:013ef4b5cd#sec_lad | Least Absolute Deviation Regression ]] and [[guide:013ef4b5cd#sec_SVM | Support Vector Machines ]]) | |||
is non-differentiable but still convex. The minimization of such functions is more challenging but still tractable as there exist | |||
efficient convex optimization methods which do not require differentiability of the objective function <ref name="ProximalMethods">N. Parikh and S. Boyd. Proximal algorithms. ''Foundations and Trends in Optimization'' 1(3):123--231, 2013</ref>. | |||
The objective function <math>f(\weights)</math> obtained for <span class="mw-gls" data-name ="ann">ANN</span> are typically highly non-convex with many local minima (see Figure [[#fig_diff_types_bojec|fig_diff_types_bojec]]). | |||
The optimization of non-convex objective function is in general more difficult than | |||
optimizing convex objective functions. However, it turns out that despite the non-convexity, iterative <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> | |||
can still be successfully applied to solve the resulting <span class="mw-gls" data-name ="erm">ERM</span> <ref name="Goodfellow-et-al-2016">I. Goodfellow, Y. Bengio, and A. Courville. ''Deep Learning'' MIT Press, 2016</ref>. | |||
The implementation of <span class="mw-gls" data-name ="erm">ERM</span> might be even more challenging for ML methods that use <span class="mw-gls" data-name ="decisiontree">decision tree</span>s | |||
or the [[#B85f6bf6f2#equ_def_0_1 | 0/1 loss]]. | |||
Indeed, the <span class="mw-gls" data-name ="erm">ERM</span> obtained for ML methods using <span class="mw-gls" data-name ="decisiontree">decision tree</span>s or the [[#B85f6bf6f2#equ_def_0_1 | 0/1 loss]] involve non-differentiable objective functions which are harder to minimize compared with <span class="mw-gls mw-gls-first" data-name ="smooth">smooth</span> functions (see Section [[#sec_ERM_decision_tree | ERM for Decision Trees ]]). | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_diff_types_bojec"></span> | |||
[[File:fig_diff_types_bojec.jpg | 500px | thumb | Different types of objective functions that arise in <span class="mw-gls" data-name ="erm">ERM</span> for different combinations of <span class="mw-gls" data-name ="hypospace">hypothesis space</span> and <span class="mw-gls" data-name ="lossfunc">loss function</span>. ]] | |||
</div> | |||
==<span id="sec_ERM_lin_reg"/>ERM for Linear Regression== | |||
As discussed in Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]], linear regression methods learn a linear hypothesis <math>h^{(\weights)}(\featurevec) = \weights^{T} \featurevec</math> with minimum [[guide:B85f6bf6f2#equ_squared_loss|squared error loss]]. For <span class="mw-gls" data-name ="linreg">linear regression</span>, the <span class="mw-gls" data-name ="erm">ERM</span> problem \eqref{eq_def_ERM_weight} becomes | |||
<math display="block"> | |||
\begin{align} | |||
\label{equ_def_cost_MSE} | |||
\widehat{\weights} & = \argmin_{\weights \in \mathbb{R}^{\featuredim}} (1/\samplesize) \sum_{\samplesize=1}^{\samplesize} \big(\truelabel^{(\sampleidx)} \!-\! \weights^{T} \featurevec^{(\sampleidx)} \big)^2. | |||
\end{align} | |||
</math> | |||
Here, <math>\samplesize=|\dataset|</math> denotes the <span class="mw-gls mw-gls-first" data-name ="samplesize">sample size</span> of the <span class="mw-gls" data-name ="trainset">training set</span> <math>\dataset</math>. The objective function <math>f(\weights)</math> in \eqref{equ_def_cost_MSE} is convex and smooth. Such a function can be minimized using the <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> discussed in Chapter [[guide:Cc42ad1ea4 | Gradient-Based Learning ]]. | |||
We can rewrite the <span class="mw-gls" data-name ="erm">ERM</span> problem \eqref{equ_def_cost_MSE} more concisely | |||
by stacking the labels <math>\truelabel^{(\sampleidx)}</math> and feature vectors <math>\featurevec^{(\sampleidx)}</math>, for | |||
<math>\sampleidx=1,\ldots,\samplesize</math>, into a “label vector” <math>\labelvec</math> and “feature matrix” <math>\featuremtx</math>, | |||
<span id="equ_def_vec_matrix"/> | |||
<math display="block"> | |||
\begin{align} | |||
\labelvec & = ( \truelabel^{(1)},\ldots, \truelabel^{(\samplesize)})^{T} \in \mathbb{R}^{\samplesize} \mbox{, and } \nonumber \\ | |||
\featuremtx & = \label{equ_def_vec_matrix}\begin{pmatrix} \featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \end{pmatrix}^{T}\in \mathbb{R}^{\samplesize \times \featuredim}. | |||
\end{align} | |||
</math> | |||
This allows us to rewrite the objective function in \eqref{equ_def_cost_MSE} as | |||
<math display = "block">\begin{equation} | |||
\label{equ_min_lin_pred_vec_mat} | |||
(1/\samplesize) \sum_{\samplesize=1}^{\samplesize} \big(\truelabel^{(\sampleidx)} \!-\! \weights^{T} \featurevec^{(\sampleidx)} \big)^2 = (1/\samplesize) \| \labelvec - \featuremtx\weights \|^{2}_{2}. | |||
\end{equation}</math> | |||
Inserting \eqref{equ_min_lin_pred_vec_mat} into \eqref{equ_def_cost_MSE}, | |||
allows to rewrite the <span class="mw-gls" data-name ="erm">ERM</span> problem for <span class="mw-gls" data-name ="linreg">linear regression</span> as | |||
<span id ="equ_def_cost_MSE"/> | |||
<math display="block"> | |||
\begin{align} | |||
\label{equ_def_cost_MSE_least_squard_errors} | |||
\widehat{\weights} & = \argmin_{\weights \in \mathbb{R}^{\featuredim}} (1/\samplesize) \| \labelvec - \featuremtx\weights \|^{2}_{2}. | |||
\end{align} | |||
</math> | |||
The formulation \eqref{equ_def_cost_MSE_least_squard_errors} allows for an interesting geometric interpretation of linear regression. Solving \eqref{equ_def_cost_MSE_least_squard_errors} amounts to finding a vector <math>\featuremtx\weights</math> (with feature matrix <math>\featuremtx</math> \eqref{equ_def_vec_matrix}), that is closest (in the Euclidean norm) to the label vector <math>\labelvec \in \mathbb{R}^{\samplesize}</math> \eqref{equ_def_vec_matrix}. The solution to this approximation problem is precisely the orthogonal projection of the vector <math>\labelvec</math> onto the subspace of <math>\mathbb{R}^{\samplesize}</math> that is spanned by the columns of the | |||
feature matrix <math>\featuremtx</math> (see Figure [[#fig_orthogo_ERM_linreg_norma|fig_orthogo_ERM_linreg_norma]]). | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_orthogo_ERM_linreg_norma"></span> | |||
[[File:Fig_orthogo_ERM_linreg_norma.jpg | 500px | thumb | The <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_cost_MSE_least_squard_errors} for <span class="mw-gls" data-name ="linreg">linear regression</span> amounts to an orthogonal | |||
projection of the label vector <math>\labelvec=\big(\truelabel^{(1)},\ldots,\truelabel^{(\samplesize)}\big)^{T}</math> on the | |||
subspace spanned by the columns of the feature matrix <math>\featuremtx = \big(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \big)^{T}</math>. ]] | |||
</div> | |||
To solve the optimization problem \eqref{equ_def_cost_MSE_least_squard_errors}, it is convenient to rewrite it as the quadratic problem | |||
<math display="block"> | |||
\begin{align} | |||
& \min_{\weights \in \mathbb{R}^{\featuredim}} \underbrace{(1/2) \weights^{T} \mathbf{Q} \weights - \vq^{T} \weights}_{= f(\weights)} \nonumber \\ | |||
& \mbox{ with } \mathbf{Q}= \label{equ_quadr_form_linreg}(1/\samplesize) \featuremtx^{T} \featuremtx, \mathbf{q} =(1/\samplesize) \featuremtx^{T} \labelvec. | |||
\end{align} | |||
</math> | |||
Since <math>f(\weights)</math> is a differentiable and convex function, a necessary and sufficient condition for | |||
<math>\widehat{\weights}</math> to be a minimizer <math>f(\widehat{\weights})\!=\!\min_{\weights \in \mathbb{R}^{\featuredim}} f(\weights)</math> is the '''zero-gradient condition''' <ref name="BoydConvexBook"/>{{rp|at=Sec. 4.2.3}} | |||
<math display = "block">\begin{equation} | |||
\label{equ_zero_gradient} | |||
\nabla f(\widehat{\weights}) = \mathbf{0}. | |||
\end{equation}</math> | |||
Combining \eqref{equ_quadr_form_linreg} with \eqref{equ_zero_gradient}, yields the following necessary and sufficient condition for a parameter vector <math>\widehat{\weights}</math> to solve the <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_cost_MSE}, | |||
<span id="equ_zero_gradient_lin_reg" /> | |||
<math display = "block">\begin{equation} | |||
\label{equ_zero_gradient_lin_reg} | |||
(1/\samplesize) \featuremtx^{T} \featuremtx\widehat{\weights} = (1/\samplesize) \featuremtx^{T} \labelvec. | |||
\end{equation}</math> | |||
This condition can be rewritten as | |||
<math display = "block">\begin{equation} | |||
\label{equ_zero_gradient_lin_reg_normal_condition} | |||
(1/\samplesize) \featuremtx^{T} \big( \labelvec - \featuremtx \widehat{\weights} \big) = \mathbf{0}. | |||
\end{equation}</math> | |||
As indicated in Figure [[#fig_orthogo_ERM_linreg_norma|fig_orthogo_ERM_linreg_norma]], the optimality condition | |||
\eqref{equ_zero_gradient_lin_reg_normal_condition} requires the vector | |||
<math display="block"> | |||
\big( \labelvec - \featuremtx\widehat{\vw}\big) = \big(\big(\truelabel^{(1)}-\hat{\truelabel}^{(1)}\big),\ldots,\big(\truelabel^{(\samplesize)}-\hat{\truelabel}^{(\samplesize)}\big) \big)^{T}, | |||
</math> | |||
whose entries are the prediction errors for the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span>, to be orthogonal (or normal) to the subspace spanned by the columns of the feature matrix <math>\featuremtx</math>. In view of this geometric interpretation, we refer to \eqref{equ_zero_gradient_lin_reg_normal_condition} as a “normal equation”. | |||
It can be shown that, for any given feature matrix <math>\featuremtx</math> and label vector <math>\labelvec</math>, there always | |||
exists at least one optimal parameter vector <math>\widehat{\weights}</math> which solves \eqref{equ_zero_gradient_lin_reg}. | |||
The optimal parameter vector might not be unique, i.e., there might be several different parameter vectors achieving the minimum in \eqref{equ_def_cost_MSE}. However, every vector <math>\widehat{\weights}</math> which solves \eqref{equ_zero_gradient_lin_reg} | |||
achieves the same minimum <span class="mw-gls" data-name ="emprisk">empirical risk</span> | |||
<span id="equ_emp_risk_lin_proje"/> | |||
<math display = "block">\begin{equation} | |||
\label{equ_emp_risk_lin_proje} | |||
\emperror(h^{(\widehat{\weights})} \mid \dataset) = \min_{\weights \in \mathbb{R}^{\featuredim}} \emperror(h^{(\weights)} \mid \dataset) = \| (\mathbf{I}- \mathbf{P}) \labelvec \|^{2}. | |||
\end{equation}</math> | |||
Here, we used the orthogonal projection matrix <math>\mathbf{P} \in \mathbb{R}^{\samplesize \times \samplesize}</math> | |||
on the linear span of the feature matrix <math>\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T} \in \mathbb{R}^{\samplesize \times \featuredim}</math> (see \eqref{equ_def_vec_matrix}). The linear span of a matrix <math>\mA=(\va^{(1)},\ldots,\va^{(\samplesize)}) \in \mathbb{R}^{\featuredim \times \samplesize}</math>, denoted as <math>{\rm span } \big\{\mA\}</math>, is the subspace of <math>\mathbb{R}^{\featuredim}</math> consisting of all linear combinations of the columns <math>\va^{(r)} \in \mathbb{R}^{\featuredim}</math> of <math>\mA</math>. | |||
If the columns of the feature matrix <math>\featuremtx</math> (see \eqref{equ_def_vec_matrix}) are linearly independent, | |||
which implies that the matrix <math>\featuremtx^{T} \featuremtx</math> is invertible, the projection matrix <math>\mathbf{P}</math> is given explicitly as | |||
<math display = "block">\begin{equation} | |||
\nonumber | |||
\mathbf{P} = \featuremtx \big( \featuremtx^{T} \featuremtx \big)^{-1} \featuremtx^{T}. | |||
\end{equation}</math> | |||
Moreover, the solution of \eqref{equ_zero_gradient_lin_reg} is then unique and given by | |||
<span id="equ_close_form_lin_reg"/> | |||
<math display = "block"> | |||
\begin{equation} | |||
\label{equ_close_form_lin_reg} | |||
\widehat{\weights} = \big( \featuremtx^{T} \featuremtx \big)^{-1} \featuremtx^{T} \labelvec. | |||
\end{equation}</math> | |||
The closed-form solution \eqref{equ_close_form_lin_reg} requires the inversion of the <math>\featuredim \times \featuredim</math> matrix <math>\featuremtx^{T} \featuremtx</math>. | |||
Note that formula \eqref{equ_close_form_lin_reg} is only valid if the matrix <math>\featuremtx^{T} \featuremtx</math> is invertible. | |||
The feature matrix <math>\featuremtx</math> is determined by the <span class="mw-gls" data-name ="datapoint">data point</span>s obtained in a MLapplication. Its properties are therefore not under the control of a ML method and it might well happen that the matrix <math>\featuremtx^{T} \featuremtx</math> is not invertible. As a point in case, the matrix <math>\featuremtx^{T} \featuremtx</math> cannot be invertible for any | |||
dataset containing fewer <span class="mw-gls" data-name ="datapoint">data point</span>s than the number of features used to characterize <span class="mw-gls" data-name ="datapoint">data point</span>s (this is referred to as high-dimensional data). Moreover, the matrix <math>\featuremtx^{T} \featuremtx</math> is not invertible if there two co-linear features <math>\feature_{\featureidx},\feature_{\featureidx'}</math> such that <math>\feature_{\featureidx} = \beta \feature_{\featureidx'}</math> holds for any <span class="mw-gls" data-name ="datapoint">data point</span> with some constant <math>\lrate \in \mathbb{R}</math>. | |||
Let us now consider a dataset such that the feature matrix <math>\featuremtx</math> is not full column-rank and, in turn, the matrix | |||
<math>\featuremtx^{T} \featuremtx</math> is not invertible. In this case we cannot use \eqref{equ_close_form_lin_reg} to compute | |||
the optimal parameter vector since the inverse of <math>\featuremtx^{T} \featuremtx</math> does not exist. Moreover, in this case, there | |||
are infinitely many different parameter vectors that solve \eqref{equ_zero_gradient_lin_reg}, i.e., the corresponding linear hypothesis map incurs minimum average squared error loss on the <span class="mw-gls" data-name ="trainset">training set</span>. Section [[guide:50be9327aa#sec_data_augmentation | Data Augmentation | |||
]] explains the benefits of using weights with small Euclidean norm. The parameter vector <math>\widehat{\weights}</math> solving the <span class="mw-gls" data-name ="linreg">linear regression</span> optimality condition \eqref{equ_zero_gradient_lin_reg} | |||
and having minimum Euclidean norm among all such vectors is given by | |||
<math display = "block">\begin{equation} | |||
\widehat{\weights} = \big( \featuremtx^{T} \featuremtx \big)^{\dagger} \featuremtx^{T} \labelvec. | |||
\end{equation}</math> | |||
Here, <math>\big( \featuremtx^{T} \featuremtx \big)^{\dagger}</math> denotes the pseudoinverse (or the | |||
Moore–Penrose inverse) of <math>\featuremtx^{T} \featuremtx</math> (see <ref name="golub96">G. H. Golub and C. F. Van Loan. ''Matrix Computations'' Johns Hopkins University Press, Baltimore, MD, 3rd edition, 1996</ref><ref name="Golub1980">G. Golub and C. van Loan. An analysis of the total least squares problem. ''SIAM J. Numerical Analysis'' 17(6):883--893, Dec. 1980</ref>). | |||
Computing the (pseudo-)inverse of <math>\featuremtx^{T} \featuremtx</math> can be computationally challenging for large | |||
number <math>\featuredim</math> of features. Figure [[#fig_snapshot_pixels|fig_snapshot_pixels]] depicts a simple ML problem where the | |||
number of features is already in the millions. The computational complexity of inverting the matrix <math>\featuremtx^{T} \featuremtx</math> | |||
depends crucially on its <span class="mw-gls mw-gls-first" data-name ="condnr">condition number</span>. We refer to a matrix as ill-conditioned if its <span class="mw-gls" data-name ="condnr">condition number</span> is much larger than 1. | |||
In general, ML methods do not have any control on the <span class="mw-gls" data-name ="condnr">condition number</span> of the matrix <math>\featuremtx^{T} \featuremtx</math>. Indeed, | |||
this matrix is determined solely by the (features of the) <span class="mw-gls" data-name ="datapoint">data point</span>s fed into the ML method. | |||
Section [[guide:Cc42ad1ea4#sec_GD_linear_regression | GD for Linear Regression ]] will discuss a method for computing the optimal parameter vector <math>\widehat{\weights}</math> | |||
that does not require any matrix inversion. This method, referred to as <span class="mw-gls mw-gls-first" data-name ="gd">gradient descent (GD)</span> constructs a sequence | |||
<math>\weights^{(0)}, \weights^{(1)},\ldots</math> of increasingly accurate approximations of <math>\widehat{\weights}</math>. | |||
This iterative method has two major benefits compared to evaluating the formula \eqref{equ_close_form_lin_reg} using direct matrix inversion, such as Gauss-Jordan elimination <ref name="golub96"/>. | |||
First, <span class="mw-gls" data-name ="gd">GD</span> typically requires significantly fewer arithmetic operations compared to direct matrix inversion. | |||
This is crucial in modern ML applications involving large feature matrices. Second, <span class="mw-gls" data-name ="gd">GD</span> does | |||
not break when the matrix <math>\featuremtx</math> is not full rank and the formula \eqref{equ_close_form_lin_reg} | |||
cannot be used any more. | |||
==<span id="sec_ERM_decision_tree"/>ERM for Decision Trees== | |||
Consider <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_ERM_funs} for a regression problem with <span class="mw-gls mw-gls-first" data-name ="labelspace">label space</span> <math>\labelspace=\mathbb{R}</math> and | |||
feature space <math>\featurespace= \mathbb{R}^{\featuredim}</math> and the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> defined by <span class="mw-gls" data-name ="decisiontree">decision tree</span>s(see Section [[guide:013ef4b5cd#sec_decision_trees | Decision Trees ]]). | |||
In stark contrast to <span class="mw-gls" data-name ="erm">ERM</span> for <span class="mw-gls" data-name ="linreg">linear regression</span> or <span class="mw-gls mw-gls-first" data-name ="logreg">logistic regression</span>, <span class="mw-gls" data-name ="erm">ERM</span> for <span class="mw-gls" data-name ="decisiontree">decision tree</span>s amounts to a discrete optimization problem. | |||
Consider the particular <span class="mw-gls" data-name ="hypospace">hypothesis space</span> <math>\hypospace</math> depicted in Figure [[#fig_hypospace_DT_depth_2|fig_hypospace_DT_depth_2]]. | |||
This <span class="mw-gls" data-name ="hypospace">hypothesis space</span> contains a finite number of different hypothesis maps. Each individual hypothesis map | |||
corresponds to a particular <span class="mw-gls" data-name ="decisiontree">decision tree</span>. | |||
For the small <span class="mw-gls" data-name ="hypospace">hypothesis space</span> <math>\hypospace</math> in Figure [[#fig_hypospace_DT_depth_2|fig_hypospace_DT_depth_2]], <span class="mw-gls" data-name ="erm">ERM</span> is easy. | |||
Indeed, we just have to evaluate the <span class="mw-gls" data-name ="emprisk">empirical risk</span> (“training error”) <math>\emperror(h)</math> for each hypothesis in <math>\hypospace</math> | |||
and pick the one yielding the smallest <span class="mw-gls" data-name ="emprisk">empirical risk</span>. However, when allowing for a very large (deep) <span class="mw-gls" data-name ="decisiontree">decision tree</span>, the | |||
computational complexity of exactly solving the <span class="mw-gls" data-name ="erm">ERM</span> becomes intractable <ref name="HYAFIL197615">L. Hyafil and R. L. Rivest. Constructing optimal binary decision trees is np-complete. ''Information Processing Letters'' 5(1):15--17, 1976</ref>. A popular | |||
approach to learn a <span class="mw-gls" data-name ="decisiontree">decision tree</span> is to use greedy algorithms which try to expand (grow) a given | |||
<span class="mw-gls" data-name ="decisiontree">decision tree</span> by adding new branches to leaf nodes in order to reduce the average loss on the | |||
<span class="mw-gls" data-name ="trainset">training set</span> (see <ref name="IntroSLR">G. James, D. Witten, T. Hastie, and R. Tibshirani. ''An Introduction to Statistical Learning with Applications in R'' Springer, 2013</ref>{{rp|at=Chapter 8}} for more details). | |||
{{alert-info | The idea behind many <span class="mw-gls" data-name="decisiontree">decision tree</span> learning methods is quite simple: try out expanding a <span class="mw-gls" data-name ="decisiontree">decision tree</span> by replacing a leaf node with a decision node (implementing another “test” on the feature vector) in order to reduce the overall <span class="mw-gls" data-name ="emprisk">empirical risk</span> much as possible. }} | |||
Consider the labeled dataset <math>\dataset</math> depicted in Figure [[#fig_growingatree|fig_growingatree]] and a given <span class="mw-gls" data-name ="decisiontree">decision tree</span> for | |||
predicting the label <math>\truelabel</math> based on the features <math>\featurevec</math>. We might first try a hypothesis obtained | |||
from the simple tree shown in the top of Figure [[#fig_growingatree|fig_growingatree]]. This hypothesis does not allow to achieve | |||
a small average loss on the <span class="mw-gls" data-name ="trainset">training set</span> <math>\dataset</math>. Therefore, we might grow the tree by replacing a leaf node | |||
with a decision node. According to Figure [[#fig_growingatree|fig_growingatree]], to so obtained larger <span class="mw-gls" data-name ="decisiontree">decision tree</span> provides a hypothesis that is able to perfectly predict the labels of the <span class="mw-gls" data-name ="trainset">training set</span> (it achieves zero <span class="mw-gls" data-name ="emprisk">empirical risk</span>). | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_growingatree"></span> | |||
[[File:fig_growingatree.png | 600px | thumb | Consider a given labeled dataset and the <span class="mw-gls" data-name ="decisiontree">decision tree</span> in the top row. We then grow the <span class="mw-gls" data-name ="decisiontree">decision tree</span> by expanding one of its two leaf nodes. The bottom row shows the resulting <span class="mw-gls" data-name ="decisiontree">decision tree</span>s, along with their decision boundaries. Each <span class="mw-gls" data-name ="decisiontree">decision tree</span> in the bottom row is obtained by expanding a different leaf node of the <span class="mw-gls" data-name ="decisiontree">decision tree</span> in the top row. ]] | |||
</div> | |||
One important aspect of methods that learn a <span class="mw-gls" data-name ="decisiontree">decision tree</span> by sequentially growing the tree is the question of when to stop growing. A natural stopping criterion might be obtained from the limitations in computational resources, | |||
i.e., we can only afford to use <span class="mw-gls" data-name ="decisiontree">decision tree</span>s up to certain maximum depth. Besides the computational limitations, we also face statistical limitations for the maximum size of <span class="mw-gls" data-name ="decisiontree">decision tree</span>s. ML methods that allow | |||
for very deep <span class="mw-gls" data-name ="decisiontree">decision tree</span>s, which represent highly complicated maps, tend to overfit the <span class="mw-gls" data-name ="trainset">training set</span> (see Figure [[#fig_decisiontree_overfits|fig_decisiontree_overfits]] and Chapter [[guide:50be9327aa | Regularization ]]). In particular, Even if a deep <span class="mw-gls" data-name ="decisiontree">decision tree</span> incurs small average loss on the <span class="mw-gls" data-name ="trainset">training set</span>, it might incur large loss when predicting the labels of <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. | |||
==<span id="sec_ERM_Bayes"/>ERM for Bayes Classifiers== | |||
The family of ML methods referred to as <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> uses the [[#B85f6bf6f2#equ_def_0_1 | 0/1 loss]] to measuring the quality of a classifier <math>h</math>. The resulting <span class="mw-gls" data-name ="erm">ERM</span> is | |||
<math display="block"> | |||
\begin{align} | |||
\hat{h} & = \argmin_{h \in \hypospace} (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \loss{(\featurevec^{(\sampleidx)},y^{(\sampleidx)})}{h} \nonumber \\ | |||
& \label{equ_approx_bayes_class}\stackrel{\eqref{equ_def_0_1}}{=} \argmin_{h \in \hypospace} (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \mathcal{I} ( h(\featurevec^{(\sampleidx)}) \neq y^{(\sampleidx)}). | |||
\end{align} | |||
</math> | |||
The objective function in this optimization problem is non-differentiable and non-convex (see Figure [[#fig_diff_types_bojec|fig_diff_types_bojec]]). | |||
This prevents us from using <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> (see Chapter [[guide:Cc42ad1ea4 | Gradient-Based Learning ]]) to solve \eqref{equ_approx_bayes_class}. | |||
We will now approach the <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_approx_bayes_class} via a different | |||
route by interpreting the <span class="mw-gls" data-name ="datapoint">data point</span>s <math>(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})</math> as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s with the common <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>. | |||
As discussed in Section [[guide:B85f6bf6f2#sec_lossfct | The Loss ]], the <span class="mw-gls" data-name ="emprisk">empirical risk</span> obtained using <math>0/1</math> loss approximates the error probability <math>\prob { \hat{\truelabel} \neq \truelabel }</math> with the predicted label <math>\hat{\truelabel} = 1</math> for <math>h(\featurevec) > 0</math> and <math>\hat{\truelabel} = -1</math> otherwise (see [[guide:B85f6bf6f2#equ_0_1_approx_prob | equation]]). | |||
Thus, we can approximate the <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_approx_bayes_class} as | |||
<math display="block"> | |||
\begin{align} | |||
\hat{h} & \label{equ_approx_bayes_class_approx}\stackrel{\eqref{equ_0_1_approx_prob}}{\approx}\argmin_{h \in \hypospace} \prob{ \hat{\truelabel} \neq \truelabel} . | |||
\end{align} | |||
</math> | |||
Note that the hypothesis <math>h</math>, which is the optimization variable in \eqref{equ_approx_bayes_class_approx}, enters into the objective | |||
function of \eqref{equ_approx_bayes_class_approx} via the definition of the predicted label <math>\hat{\truelabel}</math>, which is <math>\hat{\truelabel} = 1 </math> if <math>h(\featurevec) > 0</math> | |||
and <math>\hat{\truelabel} =-1</math> otherwise. | |||
It turns out that if we would know the <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>, which is required to compute <math>\prob{ \hat{\truelabel} \neq \truelabel}</math>, the solution of \eqref{equ_approx_bayes_class_approx} | |||
can be found via elementary Bayesian decision theory <ref name="PoorDetEst">H. Poor. ''An Introduction to Signal Detection and Estimation'' Springer, 2 edition, 1994</ref>. In particular, | |||
the optimal classifier <math>h(\featurevec)</math> is such that <math>\hat{\truelabel}</math> achieves the maximum “a-posteriori” | |||
probability <math>p(\hat{\truelabel}|\featurevec)</math> of the label being <math>\hat{\truelabel}</math>, given (or conditioned on) the features | |||
<math>\featurevec</math>. | |||
Since we typically do not know the <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>, we have to estimate (or approximate) it from the observed data points <math>(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})</math>. This estimation is feasible if the <span class="mw-gls" data-name ="datapoint">data point</span>s can be considered (approximated) as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s with a common <span class="mw-gls" data-name ="probdist">probability distribution</span> | |||
<math>p(\featurevec,\truelabel)</math>. We can then estimate (the parameters) of the <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math> | |||
using <span class="mw-gls mw-gls-first" data-name ="ml">maximum likelihood</span> methods (see Section [[guide:013ef4b5cd#sec_max_iikelihood | Maximum Likelihood ]]). For numeric features and labels, a widely-used parametric <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math> is the multivariate normal (Gaussian) distribution. In particular, | |||
conditioned on the label <math>\truelabel</math>, the feature vector <math>\featurevec</math> is a Gaussian random vector with | |||
mean <math>{\bm \mu}_{\truelabel}</math> and covariance <math>{\bf \Sigma}</math> {{efn | We use the shorthand <math>\mathcal{N}(\featurevec;{\bm \mu},{\bf \Sigma})</math> to denote the <span class="mw-gls mw-gls-first" data-name ="pdf">probability density function (pdf)</span> <math display="block">p(\featurevec) = \frac{1}{\sqrt{{\rm det} (2 \pi {\bf \Sigma})}} \exp\big(- (1/2) (\featurevec\!-\!{\bm \mu})^{T}{\bf \Sigma}^{-1}(\featurevec\!-\!{\bm \mu}) \big)</math>of a Gaussian random vector <math>\featurevec</math> with mean <math>{\bm \mu} = \expect \{ \featurevec \}</math> and covariance matrix <math>{\bf \Sigma} = \expect \big\{(\featurevec\!-\!{\bm \mu}) (\featurevec\!-\!{\bm \mu})^{T} \big\}</math>.}}, | |||
<math display = "block">\begin{equation} | |||
\label{equ_prob_model_Bayes} | |||
p(\featurevec|\truelabel) = \mathcal{N}(\featurevec;{\bm \mu}_{\truelabel},{\bf \Sigma}). | |||
\end{equation}</math> | |||
The conditional expectation of the features <math>\featurevec</math>, given (conditioned on) the label <math>\truelabel</math> of a data point, | |||
is <math>{\bm \mu}_{1}</math> if <math>\truelabel=1</math>, while for <math>\truelabel=-1</math> the conditional mean of <math>\featurevec</math> is <math>{\bm \mu}_{-1}</math>. | |||
In contrast, the conditional covariance matrix <math>{\bf \Sigma} = \expect\{ (\featurevec-{\bm \mu}_{\truelabel})(\featurevec-{\bm \mu}_{\truelabel})^{T}|\truelabel \}</math> of <math>\featurevec</math> is the same for both values of the label <math>\truelabel \in \{-1,1\}</math>. The conditional <span class="mw-gls" data-name ="probdist">probability distribution</span> | |||
<math>p(\featurevec|\truelabel)</math> of the feature vector, given the label <math>\truelabel</math>, is multivariate normal. In contrast, the marginal | |||
distribution of the features <math>\featurevec</math> is a <span class="mw-gls mw-gls-first" data-name ="gmm">Gaussian mixture model (GMM)</span>. We will revisit <span class="mw-gls" data-name ="gmm">GMM</span>s later in Section [[guide:1a7f020d42#sec_soft_clustering | Soft Clustering with Gaussian Mixture Models ]] where | |||
we will see that they are a great tool for <span class="mw-gls mw-gls-first" data-name ="softclustering">soft clustering</span>. | |||
For this probabilistic model of features and labels, the optimal classifier minimizing the error probability <math>\prob{\hat{\truelabel} \neq \truelabel}</math> is <math>\hat{\truelabel}\!=\!1</math> for <math>h(\featurevec)\!>\!0</math> and <math>\hat{\truelabel}\!=\!-1</math> for <math>h(\featurevec)\!\leq\!0</math> using the classifier map | |||
<math display = "block">\begin{equation} | |||
\label{equ_classif_Bayes} | |||
h(\featurevec) = \weights^{T} \featurevec \mbox{ with } \weights = {\bf \Sigma}^{-1} ({\bm \mu}_{1} - {\bm \mu}_{-1}). | |||
\end{equation}</math> | |||
Carefully note that this expression is only valid if the matrix <math>{\bf \Sigma}</math> is invertible. | |||
We cannot implement the classifier \eqref{equ_classif_Bayes} directly, since we do not know the true values of the class-specific mean vectors <math>{\bm \mu}_{1}</math>, <math>{\bm \mu}_{-1}</math> and covariance matrix <math>{\bf \Sigma}</math>. Therefore, we have to replace those unknown parameters with some estimates <math>\hat{\bm \mu}_{1}</math>, <math>\hat{\bm \mu}_{-1}</math> and <math>\widehat{\bf \Sigma}</math>. A principled approach is to use the [[guide:013ef4b5cd#equ_ML_mean_cov_Gauss | maximum likelihood estimates]]. | |||
<math display="block"> | |||
\begin{align} | |||
\hat{\bm \mu}_{1} & = (1/\samplesize_{1}) \sum_{\sampleidx=1}^{\samplesize} \mathcal{I}(y^{(\sampleidx)}=1) \featurevec^{(\sampleidx)}, \nonumber \\ | |||
\hat{\bm \mu}_{-1} & = (1/\samplesize_{-1}) \sum_{\sampleidx=1}^{\samplesize} \mathcal{I}(y^{(\sampleidx)}=-1) \featurevec^{(\sampleidx)}, \nonumber \\ | |||
\hat{\bm \mu} & = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \featurevec^{(\sampleidx)}, \nonumber \\ | |||
\mbox{and } \widehat{\bf \Sigma} & = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} (\vz^{(\sampleidx)} - \hat{\bm \mu})(\vz^{(\sampleidx)} - \hat{\bm \mu})^{T}, \label{ML_est_naive_Bayes} | |||
\end{align} | |||
</math> | |||
with <math>\samplesize_{1} = \sum_{\sampleidx=1}^{\samplesize} \mathcal{I}(\truelabel^{(\sampleidx)}=1)</math> | |||
denoting the number of datapoints with label <math>\truelabel=1</math> (<math>\samplesize_{-1}</math> is defined similarly). | |||
Inserting the estimates \eqref{ML_est_naive_Bayes} into \eqref{equ_classif_Bayes} yields the implementable classifier | |||
<math display = "block">\begin{equation} | |||
\label{equ_classif_Bayes_impl} | |||
h(\featurevec) = \weights^{T} \featurevec \mbox{ with } \weights = \widehat{\bf \Sigma}^{-1} (\hat{\bm \mu}_{1} - \hat{\bm \mu}_{-1}). | |||
\end{equation}</math> | |||
We highlight that the classifier \eqref{equ_classif_Bayes_impl} is only well-defined if the estimated covariance matrix <math>\widehat{\bf \Sigma}</math> \eqref{ML_est_naive_Bayes} is invertible. This requires | |||
to use a sufficiently large number of training datapoints such that <math>\samplesize \geq \featuredim</math>. | |||
We derived the classifier \eqref{equ_classif_Bayes_impl} as an approximate solution | |||
to the <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_approx_bayes_class}. The classifier \eqref{equ_classif_Bayes_impl} | |||
partitions the feature space <math>\mathbb{R}^{\featuredim}</math> into two half-spaces. One | |||
half-space consists of feature vectors <math>\featurevec</math> for which the hypothesis \eqref{equ_classif_Bayes_impl} | |||
is non-negative and, in turn, <math>\hat{y}=1</math>. The other half-space is constituted by feature | |||
vectors <math>\featurevec</math> for which the hypothesis \eqref{equ_classif_Bayes_impl} is negative and, in turn, | |||
<math>\hat{\truelabel}=-1</math>. Figure [[#fig_lin_dec_boundary|fig_lin_dec_boundary]] illustrates these two half-spaces and the | |||
decision boundary between them. | |||
The <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> \eqref{equ_classif_Bayes_impl} is another instance of a linear | |||
classifier like <span class="mw-gls" data-name ="logreg">logistic regression</span> and the <span class="mw-gls" data-name ="svm">SVM</span>. Each of these methods learns a | |||
linear hypothesis <math>h(\featurevec)=\weights^{T} \featurevec</math>, whose decision boundary (vectors <math>\featurevec</math> with <math>h(\featurevec)=0</math>) | |||
is a hyperplane (see Figure [[#fig_lin_dec_boundary|fig_lin_dec_boundary]]). However, these methods | |||
use different loss functions for assessing the quality of a particular linear hypothesis | |||
<math>h(\featurevec)=\weights \featurevec</math> (which defined the decision boundary via <math>h(\featurevec)=0</math>). | |||
Therefore, these three methods typically learn classifiers with different decision | |||
boundaries. | |||
For the [[guide:013ef4b5cd#equ_ML_mean_cov_Gauss | estimator]] <math>\widehat{\bf \Sigma}</math> to be accurate (close to the unknown covariance matrix) we need a number of datapoints (sample size) which is at least of the order <math>\featuredim^{2}</math>. | |||
This sample size requirement might be infeasible for applications with only few datapoints available. | |||
The maximum likelihood estimate <math>\widehat{\bf \Sigma}</math> \eqref{ML_est_naive_Bayes} | |||
is not invertible whenever <math>\samplesize < \featuredim</math>. In this case, the expression | |||
\eqref{equ_classif_Bayes_impl} becomes useless. To cope with small sample size | |||
<math>\samplesize < \featuredim</math> we can simplify the model \eqref{equ_prob_model_Bayes} | |||
by requiring the covariance to be diagonal <math>{\bf \Sigma} = {\rm diag} (\sigma_{1}^{2}, \ldots, \sigma_{\featuredim}^{2})</math>. | |||
This is equivalent to modelling the individual features <math>x_{1},\ldots,x_{\featuredim}</math> | |||
of a <span class="mw-gls" data-name ="datapoint">data point</span> as conditionally independent, given its label <math>\truelabel</math>. The resulting special case of a <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> | |||
is often referred to as a “naive Bayes” classifier. | |||
We finally highlight that the classifier \eqref{equ_classif_Bayes_impl} is obtained using the | |||
generative model \eqref{equ_prob_model_Bayes} for the data. Therefore, <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> | |||
belong to the family of generative ML methods which involve modelling the data generation. | |||
In contrast, <span class="mw-gls" data-name ="logreg">logistic regression</span> and the <span class="mw-gls" data-name ="svm">SVM</span> do not require a generative model for the | |||
<span class="mw-gls" data-name ="datapoint">data point</span>s but aim directly at finding the relation between features <math>\featurevec</math> | |||
and label <math>\truelabel</math> of a <span class="mw-gls" data-name ="datapoint">data point</span>. These methods belong therefore to the | |||
family of discriminative ML methods. | |||
Generative methods such as those learning a <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> are preferable for applications | |||
with only very limited amounts of labeled data. Indeed, having a generative model such as \eqref{equ_prob_model_Bayes} | |||
allows us to synthetically generate more labeled data by generating random features and labels | |||
according to the <span class="mw-gls" data-name ="probdist">probability distribution</span> \eqref{equ_prob_model_Bayes}. We refer to <ref name="NIPS2001_2020">A. Y. Ng and M. I. Jordan. On discriminative vs. generative classifiers: A comparison of | |||
logistic regression and naive bayes. In T. G. Dietterich, S. Becker, and Z. Ghahramani, editors, ''Advances in Neural Information Processing Systems 14'', pages 841--848. MIT Press, 2002</ref> for a more detailed comparison between generative and discriminative methods. | |||
==<span id="sec_online_learning"/>Online Learning== | |||
In it most basic form, <span class="mw-gls" data-name ="erm">ERM</span> requires a given set of labeled <span class="mw-gls" data-name ="datapoint">data point</span>s, which we refer | |||
to as the <span class="mw-gls" data-name ="trainset">training set</span>. However, some ML methods can access data only in a sequential fashion. As a point in case, consider time series data such as daily minimum and maximum | |||
temperatures recorded by a <span class="mw-gls mw-gls-first" data-name ="fmi">Finnish Meteorological Institute (FMI)</span> weather station. Such a time series consists of a | |||
sequence of <span class="mw-gls" data-name ="datapoint">data point</span>s that are generated at successive time instants. | |||
Online learning studies ML methods that learn (or optimize) a hypothesis | |||
incrementally as new data arrives. This mode of operation is quite different from ML methods | |||
that learn a hypothesis at once by solving an <span class="mw-gls" data-name ="erm">ERM</span> problem. These different operation modes corresponds to different frequencies of iterating the basic ML cycle depicted in Figure [[#fig_AlexMLBP|fig_AlexMLBP]]. | |||
Online learning methods start a new cycle in Figure [[#fig_AlexMLBP|fig_AlexMLBP]] whenever a new <span class="mw-gls" data-name ="datapoint">data point</span> arrives (e.g., we have recorded the minimum and maximum temperate of a day that just ended). | |||
We now present an online learning variant of <span class="mw-gls" data-name ="linreg">linear regression</span> (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]) which is suitable for | |||
time series data with <span class="mw-gls" data-name ="datapoint">data point</span>s <math>\big(\featurevec^{(\timeidx)},\truelabel^{(\timeidx)}\big)</math> gathered sequentially (over time). | |||
In particular, the <span class="mw-gls" data-name ="datapoint">data point</span>s <math>\big(\featurevec^{(\timeidx)},\truelabel^{(\timeidx)}\big)</math> become available (are gathered) at a discrete time instants <math>\timeidx=1,2,3\ldots</math>. | |||
Let us stack the feature vectors and labels of all <span class="mw-gls" data-name ="datapoint">data point</span>s available at time <math>\timeidx</math> into feature matrix <math>\featuremtx^{(\timeidx)}</math> and label vector <math>\labelvec^{(\timeidx)}</math>, respectively. The feature matrix and label vector for the first three time instants are | |||
<math display="block"> | |||
\begin{align} | |||
\label{equ_def_feature_label_three_instants} | |||
\timeidx&=1: \quad &\featuremtx^{(1)} & \defeq \big( \featurevec^{(1)} \big)^{T} \mbox{ , } & \labelvec^{(1)} & = \big( \truelabel^{(1)} \big)^{T} \mbox{, } \\ | |||
\timeidx&=2: \quad &\featuremtx^{(2)} & \defeq \big( \featurevec^{(1)},\featurevec^{(2)} \big)^{T} \mbox{ , } & \labelvec^{(2)} & = \big( \truelabel^{(1)},\truelabel^{(2)} \big)^{T} \mbox{, } \\ | |||
\timeidx&=3: \quad &\featuremtx^{(3)} & \defeq \big( \featurevec^{(1)},\featurevec^{(2)},\featurevec^{(3)} \big)^{T} \mbox{ , } & \labelvec^{(3} & = \big( \truelabel^{(1)},\truelabel^{(2)},\truelabel^{(3)} \big)^{T}. | |||
\end{align} | |||
</math> | |||
As detailed in Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]], <span class="mw-gls" data-name ="linreg">linear regression</span> aims at learning the weights <math>\weights</math> of a linear | |||
map <math>h(\featurevec) \defeq \weights^{T} \featurevec</math> such that the squared error loss <math>\big( \truelabel - h(\featurevec) \big)</math> is as small as possible. This informal goal of <span class="mw-gls" data-name ="linreg">linear regression</span> is made precise by the <span class="mw-gls" data-name ="erm">ERM</span> problem \eqref{equ_def_cost_MSE} which defines the optimal weights via incurring minimum average squared error loss (<span class="mw-gls" data-name ="emprisk">empirical risk</span>) on a | |||
given <span class="mw-gls" data-name ="trainset">training set</span> <math>\dataset</math>. These optimal <span class="mw-gls mw-gls-first" data-name ="weights">weights</span> are given by the solutions of \eqref{equ_zero_gradient_lin_reg_normal_condition}. | |||
When the feature vectors of datapoints in <math>\dataset</math> are linearly independent, we obtain the closed-form | |||
expression \eqref{equ_close_form_lin_reg} for the optimal <span class="mw-gls" data-name ="weights">weights</span>. | |||
Inserting the feature matrix <math>\featuremtx^{(\timeidx)}</math> and label vector <math>\labelvec^{(\timeidx)}</math> \eqref{equ_def_feature_label_three_instants} into \eqref{equ_close_form_lin_reg}, yields | |||
<math display = "block">\begin{equation} | |||
\label{equ_opt_weight_time_t} | |||
\widehat{\weights}^{(\timeidx)} = \big( \big(\featuremtx^{(\timeidx)}\big)^{T} \featuremtx^{(\timeidx)} \big)^{-1} \big(\featuremtx^{(\timeidx)}\big)^{T} \labelvec^{(\timeidx)}. | |||
\end{equation}</math> | |||
For each time instant we can evaluate the RHS of \eqref{equ_opt_weight_time_t} to | |||
obtain the parameter vector <math>\widehat{\weights}^{(\timeidx)}</math> that minimizes the average squared error loss | |||
over all <span class="mw-gls" data-name ="datapoint">data point</span>s gathered up to time <math>\timeidx</math>. | |||
However, computing <math>\widehat{\weights}^{(\timeidx)}</math> via direct evaluation of the RHS in \eqref{equ_opt_weight_time_t} for each new time instant <math>\timeidx</math> misses an opportunity for recycling computations done already at earlier time instants. | |||
Let us now show how to (partially) reuse the computations used to evaluate \eqref{equ_opt_weight_time_t} for | |||
time <math>\timeidx</math> in the evaluation of \eqref{equ_opt_weight_time_t} for the next time instant <math>\timeidx+1</math>. To this end, we first rewrite the matrix <math> \mQ^{(\timeidx)} \defeq \big(\featuremtx^{(\timeidx)}\big)^{T} \featuremtx^{(\timeidx)}</math> as | |||
<math display = "block">\begin{equation} | |||
\mQ^{(\timeidx)} = \sum_{\itercntr=1}^{\timeidx} \featurevec^{(\itercntr)} \big(\featurevec^{(\itercntr)} \big)^{T}. | |||
\end{equation}</math> | |||
Since <math>\mQ^{(\timeidx\!+\!1)} = \mQ^{(\timeidx)} + \featurevec^{(\timeidx\!+\!1)} \big(\featurevec^{(\timeidx\!+\!1)} \big)^{T}</math>, we can use a well-known identity for matrix inverses (see <ref name="Bartlett51">M. S. Bartlett. An inverse matrix adjustment arising in discriminant analysis. ''The Annals of Mathematical Statistics'' 22(1):107 -- 111, 1951</ref><ref name="MeyerSIAM73">C. Meyer. Generalized inversion of modified matrices. ''SIAM J. Appied Mathmetmatics'' 24(3), 1973</ref>) to obtain | |||
<math display = "block">\begin{equation} | |||
\label{equ_matrix_invers} | |||
\big( \mQ^{(\timeidx+1)} \big)^{-1} =\big( \mQ^{(\timeidx)} \big)^{-1} + \frac{\big( \mQ^{(\timeidx)} \big)^{-1} \featurevec^{(\timeidx+1)} \big(\featurevec^{(\timeidx+1)} \big)^{T}\big( \mQ^{(\timeidx)} \big)^{-1}}{1- \big(\featurevec^{(\timeidx+1)} \big)^{T} \big( \mQ^{(\timeidx)} \big)^{-1} \featurevec^{(\timeidx+1)} }. | |||
\end{equation}</math> | |||
Inserting \eqref{equ_matrix_invers} into \eqref{equ_opt_weight_time_t} yields the following relation between optimal parameter vectors at consecutive time instants <math>\timeidx</math> and <math>\timeidx+1</math>, | |||
<math display = "block">\begin{equation} | |||
\label{equ_def_update_recuriveLS} | |||
\widehat{\weights}^{(\timeidx+1)} =\widehat{\weights}^{(\timeidx)} - \big( \mQ^{(\timeidx+1)} \big)^{-1}\featurevec^{(\timeidx+1)} \big(\big(\featurevec^{(\timeidx+1)} \big)^{T}\widehat{\weights}^{(\timeidx)} - \truelabel^{(\timeidx+1)} \big) . | |||
\end{equation}</math> | |||
Note that neither evaluating the RHS of \eqref{equ_def_update_recuriveLS} nor evaluating the RHS | |||
of \eqref{equ_matrix_invers} requires to actually invert a matrix of with more than one entry (we can | |||
think of a scalar number as <math>1 \times 1</math> matrix). In contrast, evaluating the RHS \eqref{equ_opt_weight_time_t} | |||
requires to invert the matrix <math>\mQ^{(\timeidx)} \in \mathbb{R}^{\featurelen \times \featurelen}</math>. We | |||
obtain an online algorithm for <span class="mw-gls" data-name ="linreg">linear regression</span> via computing the updates \eqref{equ_def_update_recuriveLS} and \eqref{equ_matrix_invers} for each new time instant <math>\timeidx</math>. Another online method for <span class="mw-gls" data-name ="linreg">linear regression</span> | |||
will be discussed at the end of Section [[guide:Cc42ad1ea4#sec_sgd | Stochastic GD ]]. | |||
==Weighted ERM== | |||
Consider a ML method that uses some <span class="mw-gls" data-name ="hypospace">hypothesis space</span> <math>\hypospace</math> and <span class="mw-gls" data-name ="lossfunc">loss function</span> <math>\lossfun</math> to measure the quality predictions obtained from a specific hypothesis when applied to a <span class="mw-gls" data-name ="datapoint">data point</span>. A principled approach to learn a useful hypothesis is via <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_ERM_funs} using a <span class="mw-gls" data-name ="trainset">training set</span> | |||
<math display="block"> | |||
\dataset= \big\{ \big( \featurevec^{(1)}, \truelabel^{(1)} \big),\ldots,\big( \featurevec^{(\samplesize)}, \truelabel^{(\samplesize)} \big) \big\}. | |||
</math>. | |||
For some applications it might be useful to modify the <span class="mw-gls" data-name ="erm">ERM</span> principle \eqref{equ_def_ERM_funs} by putting different weights on the <span class="mw-gls" data-name ="datapoint">data point</span>s. In particular, for each <span class="mw-gls" data-name ="datapoint">data point</span> <math>\big( \featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)} \big)</math> | |||
we specify a non-negative weight <math>\sampleweight{\sampleidx} \in \mathbb{R}_{+}</math>. | |||
Weighted <span class="mw-gls" data-name ="erm">ERM</span> is obtained from <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_ERM_funs} by replacing the average <span class="mw-gls" data-name ="loss">loss</span> over the <span class="mw-gls" data-name ="trainset">training set</span> with a weighted average loss, | |||
<math display="block"> | |||
\begin{align} | |||
\label{equ_def_wERM_funs} | |||
\hat{h} & \in \argmin_{h \in \hypospace} \sum_{\sampleidx=1}^{\samplesize} \sampleweight{\sampleidx}\loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h}. | |||
\end{align} | |||
</math> | |||
Note that we obtain <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_ERM_funs} as the special case of weighted <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_wERM_funs} for the weights <math>\sampleweight{\sampleidx} = 1/\samplesize</math>. | |||
We might interpret the weight <math>\sampleweight{\sampleidx}</math> as a measure for the importance or relevance of | |||
the <span class="mw-gls" data-name ="datapoint">data point</span> <math>\big( \featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)} \big)</math> for the hypothesis <math>\hat{h}</math> learnt via \eqref{equ_def_wERM_funs}. The extreme case <math>\sampleweight{\sampleidx}=0</math> means that the <span class="mw-gls" data-name ="datapoint">data point</span> | |||
<math>\big( \featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)} \big)</math> becomes irrelevant for learning a hypothesis via \eqref{equ_def_wERM_funs}. | |||
This could be useful if the <span class="mw-gls" data-name ="datapoint">data point</span> <math>\big( \featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)} \big)</math> represents an outlier | |||
that violates the <span class="mw-gls" data-name ="iidasspt">i.i.d assumption</span> which is satisfied by most of the other <span class="mw-gls" data-name ="datapoint">data point</span>s. Thus, using suitable weights in \eqref{equ_def_wERM_funs} could make the resulting ML method robust against outliers in the <span class="mw-gls" data-name ="trainset">training set</span>. Note that we have discussed another strategy (via the choice for the <span class="mw-gls" data-name ="lossfunc">loss function</span>) to achieve robustness against outliers in Section [[guide:013ef4b5cd#sec_lad | Least Absolute Deviation Regression ]]. | |||
Another use-case of weighted <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_wERM_funs} is for applications where the risk of a hypothesis is defined using a <span class="mw-gls" data-name ="probdist">probability distribution</span> that is different form the <span class="mw-gls" data-name ="probdist">probability distribution</span> of the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span>. | |||
Thus, the <span class="mw-gls" data-name ="datapoint">data point</span>s conform to an <span class="mw-gls" data-name ="iidasspt">i.i.d assumption</span> with underlying <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>. | |||
However, we would like to measure the quality of a hypothesis via the expected loss or risk using a different <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p'(\featurevec,\truelabel)</math>, | |||
<math display = "block">\begin{equation} | |||
\label{equ_target_p_prime_risk} | |||
\expect_{p'} \big \{ \loss{(\featurevec,\truelabel)}{h} \} = \int \loss{(\featurevec,\truelabel)}{h} d p'(\featurevec,\truelabel) | |||
\end{equation}</math> | |||
Having a different <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p'(\featurevec,\truelabel) (\neq p (\featurevec,\truelabel)))</math> to define the overall quality (risk) of a hypothesis might be beneficial for binary classification problems with imbalanced data. | |||
Indeed, using the average loss (which approximates the risk under <math>p(\featurevec,\truelabel)</math>) might not be a useful quality measure if one class is over-represented in the <span class="mw-gls" data-name ="trainset">training set</span> (see Section [[guide:B85f6bf6f2#sec_confustion_matrix|Confusion Matrix]]). It can be shown that, under mild conditions, the weighted average loss in \eqref{equ_def_wERM_funs} approximates \eqref{equ_target_p_prime_risk} when using the weights <math>\sampleweight{\sampleidx} = p'\big(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}\big)/ p\big(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}\big)</math> <ref name="BishopBook">C. M. Bishop. ''Pattern Recognition and Machine Learning'' Springer, 2006</ref>{{rp|at=Sec. 11.1.4}}. | |||
==Notes== | |||
{{notelist}} | |||
==General References== | |||
<div class="d-flex mt-3 mb-3"> | |||
<div class="me-3"> | |||
[[File:978-981-16-8193-6.jpg | 150px | link=]] | |||
</div> | |||
<div> | |||
{{cite book | title = Machine Learning: The Basics |first = Alexander | last = Jung | publisher = Springer | location = Signapore | date = 2022 | doi = 10.1007/978-981-16-8193-6 }} | |||
{{cite arXiv |last=Jung |first=Alexander |date= |title=Machine Learning: The Basics |eprint=1805.05052 | date=2022}} | |||
</div> | |||
</div> | |||
==References== | |||
Latest revision as of 08:20, 14 June 2023
[math] % Generic syms \newcommand\defeq{:=} \newcommand{\Tt}[0]{\boldsymbol{\theta}} \newcommand{\XX}[0]{{\cal X}} \newcommand{\ZZ}[0]{{\cal Z}} \newcommand{\vx}[0]{{\bf x}} \newcommand{\vv}[0]{{\bf v}} \newcommand{\vu}[0]{{\bf u}} \newcommand{\vs}[0]{{\bf s}} \newcommand{\vm}[0]{{\bf m}} \newcommand{\vq}[0]{{\bf q}} \newcommand{\mX}[0]{{\bf X}} \newcommand{\mC}[0]{{\bf C}} \newcommand{\mA}[0]{{\bf A}} \newcommand{\mL}[0]{{\bf L}} \newcommand{\fscore}[0]{F_{1}} \newcommand{\sparsity}{s} \newcommand{\mW}[0]{{\bf W}} \newcommand{\mD}[0]{{\bf D}} \newcommand{\mZ}[0]{{\bf Z}} \newcommand{\vw}[0]{{\bf w}} \newcommand{\D}[0]{{\mathcal{D}}} \newcommand{\mP}{\mathbf{P}} \newcommand{\mQ}{\mathbf{Q}} \newcommand{\E}[0]{{\mathbb{E}}} \newcommand{\vy}[0]{{\bf y}} \newcommand{\va}[0]{{\bf a}} \newcommand{\vn}[0]{{\bf n}} \newcommand{\vb}[0]{{\bf b}} \newcommand{\vr}[0]{{\bf r}} \newcommand{\vz}[0]{{\bf z}} \newcommand{\N}[0]{{\mathcal{N}}} \newcommand{\vc}[0]{{\bf c}} \newcommand{\bm}{\boldsymbol} % Statistics and Probability Theory \newcommand{\errprob}{p_{\rm err}} \newcommand{\prob}[1]{p({#1})} \newcommand{\pdf}[1]{p({#1})} \def \expect {\mathbb{E} } % Machine Learning Symbols \newcommand{\biasterm}{B} \newcommand{\varianceterm}{V} \newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} \newcommand{\nrfolds}{k} \newcommand{\mseesterr}{E_{\rm est}} \newcommand{\bootstrapidx}{b} %\newcommand{\modeldim}{r} \newcommand{\modelidx}{l} \newcommand{\nrbootstraps}{B} \newcommand{\sampleweight}[1]{q^{(#1)}} \newcommand{\nrcategories}{K} \newcommand{\splitratio}[0]{{\rho}} \newcommand{\norm}[1]{\Vert {#1} \Vert} \newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} \newcommand{\bmx}[0]{\begin{bmatrix}} \newcommand{\emx}[0]{\end{bmatrix}} \newcommand{\T}[0]{\text{T}} \DeclareMathOperator*{\rank}{rank} %\newcommand\defeq{:=} \newcommand\eigvecS{\hat{\mathbf{u}}} \newcommand\eigvecCov{\mathbf{u}} \newcommand\eigvecCoventry{u} \newcommand{\featuredim}{n} \newcommand{\featurelenraw}{\featuredim'} \newcommand{\featurelen}{\featuredim} \newcommand{\samplingset}{\mathcal{M}} \newcommand{\samplesize}{m} \newcommand{\sampleidx}{i} \newcommand{\nractions}{A} \newcommand{\datapoint}{\vz} \newcommand{\actionidx}{a} \newcommand{\clusteridx}{c} \newcommand{\sizehypospace}{D} \newcommand{\nrcluster}{k} \newcommand{\nrseeds}{s} \newcommand{\featureidx}{j} \newcommand{\clustermean}{{\bm \mu}} \newcommand{\clustercov}{{\bm \Sigma}} \newcommand{\target}{y} \newcommand{\error}{E} \newcommand{\augidx}{b} \newcommand{\task}{\mathcal{T}} \newcommand{\nrtasks}{T} \newcommand{\taskidx}{t} \newcommand\truelabel{y} \newcommand{\polydegree}{r} \newcommand\labelvec{\vy} \newcommand\featurevec{\vx} \newcommand\feature{x} \newcommand\predictedlabel{\hat{y}} \newcommand\dataset{\mathcal{D}} \newcommand\trainset{\dataset^{(\rm train)}} \newcommand\valset{\dataset^{(\rm val)}} \newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} \newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} \newcommand{\inspace}{\mathcal{X}} \newcommand{\sigmoid}{\sigma} \newcommand{\outspace}{\mathcal{Y}} \newcommand{\hypospace}{\mathcal{H}} \newcommand{\emperror}{\widehat{L}} \newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} \newcommand{\featurespace}{\mathcal{X}} \newcommand{\labelspace}{\mathcal{Y}} \newcommand{\rawfeaturevec}{\mathbf{z}} \newcommand{\rawfeature}{z} \newcommand{\condent}{H} \newcommand{\explanation}{e} \newcommand{\explainset}{\mathcal{E}} \newcommand{\user}{u} \newcommand{\actfun}{\sigma} \newcommand{\noisygrad}{g} \newcommand{\reconstrmap}{r} \newcommand{\predictor}{h} \newcommand{\eigval}[1]{\lambda_{#1}} \newcommand{\regparam}{\lambda} \newcommand{\lrate}{\alpha} \newcommand{\edges}{\mathcal{E}} \newcommand{\generror}{E} \DeclareMathOperator{\supp}{supp} %\newcommand{\loss}[3]{L({#1},{#2},{#3})} \newcommand{\loss}[2]{L\big({#1},{#2}\big)} \newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} \newcommand{\determinant}[1]{{\rm det}({#1})} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\itercntr}{r} \newcommand{\state}{s} \newcommand{\statespace}{\mathcal{S}} \newcommand{\timeidx}{t} \newcommand{\optpolicy}{\pi_{*}} \newcommand{\appoptpolicy}{\hat{\pi}} \newcommand{\dummyidx}{j} \newcommand{\gridsizex}{K} \newcommand{\gridsizey}{L} \newcommand{\localdataset}{\mathcal{X}} \newcommand{\reward}{r} \newcommand{\cumreward}{G} \newcommand{\return}{\cumreward} \newcommand{\action}{a} \newcommand\actionset{\mathcal{A}} \newcommand{\obstacles}{\mathcal{B}} \newcommand{\valuefunc}[1]{v_{#1}} \newcommand{\gridcell}[2]{\langle #1, #2 \rangle} \newcommand{\pair}[2]{\langle #1, #2 \rangle} \newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} \newcommand{\actionvalue}[1]{q_{#1}} \newcommand{\transition}{\mathcal{T}} \newcommand{\policy}{\pi} \newcommand{\charger}{c} \newcommand{\itervar}{k} \newcommand{\discount}{\gamma} \newcommand{\rumba}{Rumba} \newcommand{\actionnorth}{\rm N} \newcommand{\actionsouth}{\rm S} \newcommand{\actioneast}{\rm E} \newcommand{\actionwest}{\rm W} \newcommand{\chargingstations}{\mathcal{C}} \newcommand{\basisfunc}{\phi} \newcommand{\augparam}{B} \newcommand{\valerror}{E_{v}} \newcommand{\trainerror}{E_{t}} \newcommand{\foldidx}{b} \newcommand{\testset}{\dataset^{(\rm test)} } \newcommand{\testerror}{E^{(\rm test)}} \newcommand{\nrmodels}{M} \newcommand{\benchmarkerror}{E^{(\rm ref)}} \newcommand{\lossfun}{L} \newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} \newcommand{\cluster}{\mathcal{C}} \newcommand{\bayeshypothesis}{h^{*}} \newcommand{\featuremtx}{\mX} \newcommand{\weight}{w} \newcommand{\weights}{\vw} \newcommand{\regularizer}{\mathcal{R}} \newcommand{\decreg}[1]{\mathcal{R}_{#1}} \newcommand{\naturalnumbers}{\mathbb{N}} \newcommand{\featuremapvec}{{\bf \Phi}} \newcommand{\featuremap}{\phi} \newcommand{\batchsize}{B} \newcommand{\batch}{\mathcal{B}} \newcommand{\foldsize}{B} \newcommand{\nriter}{R} [/math]
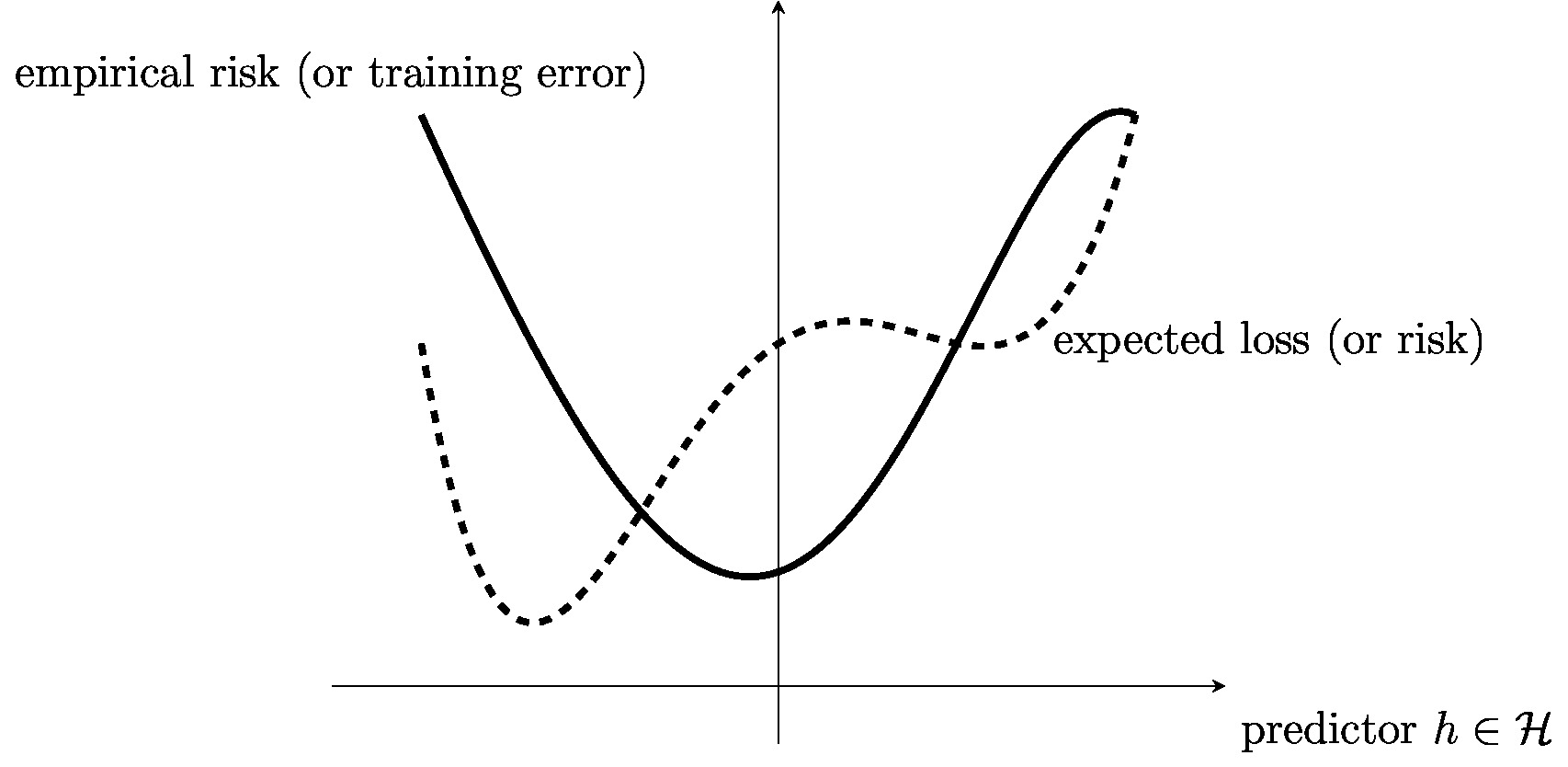
Chapter Three Components of ML discussed three components (see Figure fig_ml_problem):
- data points characterized by features [math]\featurevec \in \featurespace[/math] and labels [math] \truelabel \in \labelspace[/math],
- a hypothesis space [math]\hypospace[/math] of computationally feasible maps [math]h:\featurespace \rightarrow \labelspace[/math],
- and a loss function [math]\loss{(\featurevec,\truelabel)}{h}[/math] that measuresthe discrepancy between the predicted label [math]h(\featurevec)[/math] and the true label [math]\truelabel[/math].
Ideally we would like to learn a hypothesis [math]h \in \hypospace[/math] such that [math]\loss{(\featurevec,\truelabel)}{h}[/math] is small for any data point [math](\featurevec,\truelabel)[/math]. However, to implement this informal goal we need to define what is meant precisely by “any data point”. Maybe the most widely used approach to the define the concept of “any data point” is the i.i.d assumption.
The i.i.d assumption interprets data points as realizations of independent and identically distributed (iid) random variable (RV)s with a common probability distribution [math]p(\featurevec,\truelabel)[/math]. The probability distribution [math]p(\featurevec,\truelabel)[/math] allows us to define the risk of a hypothesis [math]h[/math] as the expectation of the loss incurred by [math]h[/math] on (the realizations of) a random data point. We can interpret the risk of a hypothesis as a measure for its quality in predicting the label of“any data point”.
If we know the probability distribution [math]p(\featurevec,\truelabel)[/math] from which data points are drawn (iid), we can precisely determine the hypothesis with minimum risk. This optimal hypothesis, which is referred to as a Bayes estimator, can be read off almost directly from the posterior probability distribution [math]p(\truelabel|\featurevec)[/math] of the label [math]\truelabel[/math] given the features [math]\featurevec[/math] of a data point. The precise form of the Bayes estimator depends on the choice for the loss function. When using the squared error loss, the optimal hypothesis (or Bayes estimator) is given by the posterior mean [math]h(\featurevec) = \expect \big\{ \truelabel | \featurevec \}[/math] [1].
In most ML application, we do not know the true underlying probability distribution [math]p(\featurevec,\truelabel)[/math] from which data points are generated. Therefore, we cannot compute the Bayes estimator exactly. However, we can approximately compute this estimator by replacing the exact probability distribution with an estimate or approximation. Section ERM for Bayes Classifiers discusses a specific ML method that implements this approach.
The risk of the Bayes estimator (which is the Bayes risk) provides a useful baseline against which we can compare the average loss incurred by a ML method on a set of data points. Section Diagnosing ML shows how to diagnose ML methods by comparing its average loss of a hypothesis on a training set and its average loss on a validation set with a baseline.
Section Approximating Risk by Empirical Risk motivates empirical risk minimization (ERM) by approximating the risk using the empirical risk (or average loss) computed for a set of labeled (training) data points (see Figure fig_ERM_idea). This approximation is justified by the law of large numbers which characterizes the deviation between averages of RVs and their expectation. Section Computational and Statistical Aspects of ERM discusses the statistical and computational aspects of ERM. We then specialize the ERM for three particular ML methods arising from different combinations of hypothesis space and loss function. Section ERM for Linear Regression discusses ERM for linear regression (see Section Linear Regression ). Here, ERM amounts to minimizing a differentiable convex function, which can be done efficiently using gradient-based methods (see Chapter Gradient-Based Learning ).
We then discuss in Section ERM for Decision Trees the ERM obtained for decision tree models. The resulting ERM problems becomes a discrete optimization problem which are typically much harder than convex optimization problems. We cannot apply gradient-based methods to solve the ERM for decision trees. To solve ERM for a decision tree, we essentially must try out all possible choices for the tree structure [2].
Section ERM for Bayes Classifiers considers the ERM obtained when learning a linear hypothesis using the [math]0/1[/math] loss for classification problems. The resulting ERM amounts to minimizing a non-differentiable and non-convex function. Instead of applying optimization methods to solve this ERM instance, we will instead directly construct approximations of the Bayes estimator.
Section Training and Inference Periods decomposes the operation of ML methods into training periods and inference periods. The training period amounts to learning a hypothesis by solving the ERM on a given training set. The resulting hypothesis is then applied to new data points, which are not contained in the training set. This application of a learnt hypothesis to data points outside the training set is referred to as the inference period. Section Online Learning demonstrates how an online learning method can be obtained by solving the ERM sequentially as new data points come in. Online learning methods alternate between training and inference periods whenever new data is collected.
Approximating Risk by Empirical Risk
The data points arising in many important application domains can be modelled (orapproximated) as realizations of iid RVs with a common (joint) probability distribution [math]p(\featurevec,\truelabel)[/math] for the features [math]\featurevec[/math] and label [math]\truelabel[/math]. The probability distribution [math]p(\featurevec,\truelabel)[/math] used in this i.i.d assumption allows us to define the expected loss or risk of a hypothesis [math]h \in \hypospace[/math] as
It seems reasonable to learn a hypothesis [math]h[/math] such that its risk \eqref{equ_def_risk} is minimal,
We refer to any hypothesis [math]\bayeshypothesis[/math] that achieves the minimum risk \eqref{equ_def_risk_min} as a Bayes estimator [1]. Note that the Bayes estimator [math]\bayeshypothesis[/math] depends on both, the probability distribution [math]p(\featurevec,\truelabel)[/math] and the loss function. When using the squared error loss in \eqref{equ_def_risk_min}, the Bayes estimator [math]\bayeshypothesis[/math] is given by the posterior mean of [math]\truelabel[/math] given the features [math]\featurevec[/math] (see [3](Ch. 7)).
Risk minimization \eqref{equ_def_risk_min} cannot be used for the design of ML methods whenever we do not know the probability distribution [math]p(\featurevec,\truelabel)[/math]. If we do not know the probability distribution [math]p(\featurevec,\truelabel)[/math], which is the rule for many ML applications, we cannot evaluate the expectation in \eqref{equ_def_risk}. One exception to this rule is if the data points are synthetically generated by drawing realizations from a given probability distribution [math]p(\featurevec,\truelabel)[/math].
The idea of ERM is to approximate the expectation in \eqref{equ_def_risk_min} with an average loss (the empirical risk) incurred on a given set of data points (the “training set”),
As discussed in Section empirical risk , this approximation is justified by the law of large numbers. We obtain ERM by replacing the risk in the minimization problem \eqref{equ_def_risk_min} with the empirical risk ,
As the notation in \eqref{equ_def_ERM_funs} indicates there might be several different hypotheses that minimize [math]\emperror(h|\dataset)[/math]. We denote by [math]\hat{h}[/math] any of them. Mathematically, ERM \eqref{equ_def_ERM_funs} is just an instance of an optimization problem [4]. The optimization domain in \eqref{equ_def_ERM_funs} is the hypothesis space [math]\hypospace[/math] of a ML method, the objective (or cost) function is the empirical risk . ML methods that learn a hypothesis via ERM \eqref{equ_def_ERM_funs} are instances of optimization algorithms [5].
ERM \eqref{equ_def_ERM_funs} is a form of “learning by trial and error”. A (hypothetical) instructor (or supervisor) provides us the labels [math]\truelabel^{(\sampleidx)}[/math] for the data points in [math]\dataset[/math] which are characterized by features [math]\featurevec^{(\sampleidx)}[/math]. This dataset serves as a training set in the following sense. We use a current guess for a good hypothesis [math]h[/math] to predict the labels [math]\truelabel^{(\sampleidx)}[/math] of the data points in [math]\dataset[/math] only from their features [math]\featurevec^{(\sampleidx)}[/math] . We then determine average loss [math]\emperror(h|\dataset)[/math] that is incurred by the predictions [math]\hat{\truelabel}^{(\sampleidx)} = h\big( \featurevec^{(\sampleidx)} \big)[/math]. If the training error [math]\emperror(h|\dataset)[/math] is too large, we try out another hypothesis map [math]h'[/math] different from [math]h[/math] with the hope of achieving a smaller training error [math]\emperror(h'|\dataset)[/math].
We highlight that ERM \eqref{equ_def_ERM_funs} is motivated by the law of large numbers. The law of large numbers, in turn, is only useful if the data points generated within an ML application can be well modelled as realizations of iid RVs. This i.i.d assumption is one of the most widely used working assumptions for the design and analysis of ML methods. However, there are many important application domains involving data points that clearly violate this i.i.d assumption.
One example for non-i.i.d. data is time series data that consists of temporally ordered (consecutive) data points [6][7]. Each data point in a time series might represent a specific time interval or single time instants. Another example for non-i.i.d. data arises in active learning where ML methods actively choose (or query) new data points [8]. For a third example of non-i.i.d. data, we refer to federated learning (FL) applications that involve collections (networks) of data generators with different statistical properties [9][10][11][12][13]. A detailed discussion of ML methods for non-i.i.d. data is beyond the scope of this book.
Computational and Statistical Aspects of ERM
Solving the optimization problem \eqref{equ_def_ERM_funs} provides two things. First, the minimizer [math]\hat{h}[/math] is a predictor which performs optimal on the training set [math]\dataset[/math]. Second, the corresponding objective value [math]\emperror(\hat{h}|\dataset)[/math] (the “training error”) can be used to estimate for the risk or expected loss of [math]\hat{h}[/math]. However, as we will discuss in Chapter Regularization , for some datasets [math]\dataset[/math], the training error [math]\emperror(\hat{h}|\dataset)[/math] obtained for [math]\dataset[/math] can be very different from the expected loss (risk) of [math]\hat{h}[/math] when applied to new data points which are not contained in [math]\dataset[/math].
The i.i.d assumption implies that the training error [math]\emperror(h|\dataset)[/math] is only a noisy approximation of the risk [math]\risk{h}[/math]. The ERM solution [math]\hat{h}[/math] is a minimizer of this noisy approximation and therefore in general different from the Bayes estimator which minimizes the risk itself. Even if the hypothesis [math]\hat{h}[/math] delivered by ERM \eqref{equ_def_ERM_funs} has small training error [math]\emperror(\hat{h}|\dataset)[/math], it might have unacceptably large risk [math]\risk{\hat{h}}[/math]. We refer to such a situation as overfitting and will discuss techniques for detecting and avoiding it in Chapter Model Validation and Selection .
Many important ML methods use hypotheses that are parametrized by a parameter vector [math]\weights[/math]. For each possible parameter vector, we obtain a hypothesis [math]h^{(\weights)}(\featurevec)[/math]. Such a parametrization is used in linear regression methods which learn a linear hypothesis [math]h^{(\weights)}(\featurevec) = \weights^{T} \featurevec[/math] with some parameter vector [math]\weights[/math]. Another example for such a parametrization is obtained from artificial neural network (ANN)s with the weights assigned to inputs of individual (artificial) neurons (see Figure fig_ANN).
For ML methods that use a parametrized hypothesis [math]h^{(\weights)}(\featurevec)[/math], we can reformulate the optimization problem \eqref{equ_def_ERM_funs} as an optimization of the parameter vector,
The objective function [math]f(\weights)[/math] in \eqref{eq_def_ERM_weight} is the empirical risk [math]\emperror\big(h^{(\weights)} |\dataset\big)[/math] incurred by the hypothesis [math]h^{(\weights)}[/math] when applied to the data points in the dataset [math]\dataset[/math]. The optimization problems \eqref{eq_def_ERM_weight} and \eqref{equ_def_ERM_funs} are fully equivalent. Given the optimal parameter vector [math]\widehat{\weights}[/math] solving \eqref{eq_def_ERM_weight}, the hypothesis [math]h^{(\widehat{\weights})}[/math] solves \eqref{equ_def_ERM_funs}.
We highlight that the precise shape of the objective function [math]f(\weights)[/math] in \eqref{eq_def_ERM_weight} depends on the parametrization of the hypothesis space [math]\hypospace[/math]. The parametrization is the precise rule that assigns a hypothesis map [math]h^{(\weights)}[/math] to a given parameter vector [math]\weights[/math]. The shape of [math]f(\weights)[/math] depends also on the choice for the loss function [math]\loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h^{(\weights)}}[/math]. As depicted in Figure fig_diff_types_bojec, the different combinations of parametrized hypothesis space and loss functions can result in objective functions with fundamentally different properties such that their optimization is more or less difficult.
The objective function [math]f(\weights)[/math] for the ERM obtained for linear regression (see Section Linear Regression ) is differentiable and convex and can therefore be minimized using simple gradient-based methods (see Chapter Gradient-Based Learning ). In contrast, the objective function [math]f(\weights)[/math] of ERM obtained for least absolute deviation regression or the support vector machine (SVM) (see Section Least Absolute Deviation Regression and Support Vector Machines ) is non-differentiable but still convex. The minimization of such functions is more challenging but still tractable as there exist efficient convex optimization methods which do not require differentiability of the objective function [14].
The objective function [math]f(\weights)[/math] obtained for ANN are typically highly non-convex with many local minima (see Figure fig_diff_types_bojec). The optimization of non-convex objective function is in general more difficult than optimizing convex objective functions. However, it turns out that despite the non-convexity, iterative gradient-based methods can still be successfully applied to solve the resulting ERM [15]. The implementation of ERM might be even more challenging for ML methods that use decision trees or the 0/1 loss. Indeed, the ERM obtained for ML methods using decision trees or the 0/1 loss involve non-differentiable objective functions which are harder to minimize compared with smooth functions (see Section ERM for Decision Trees ).
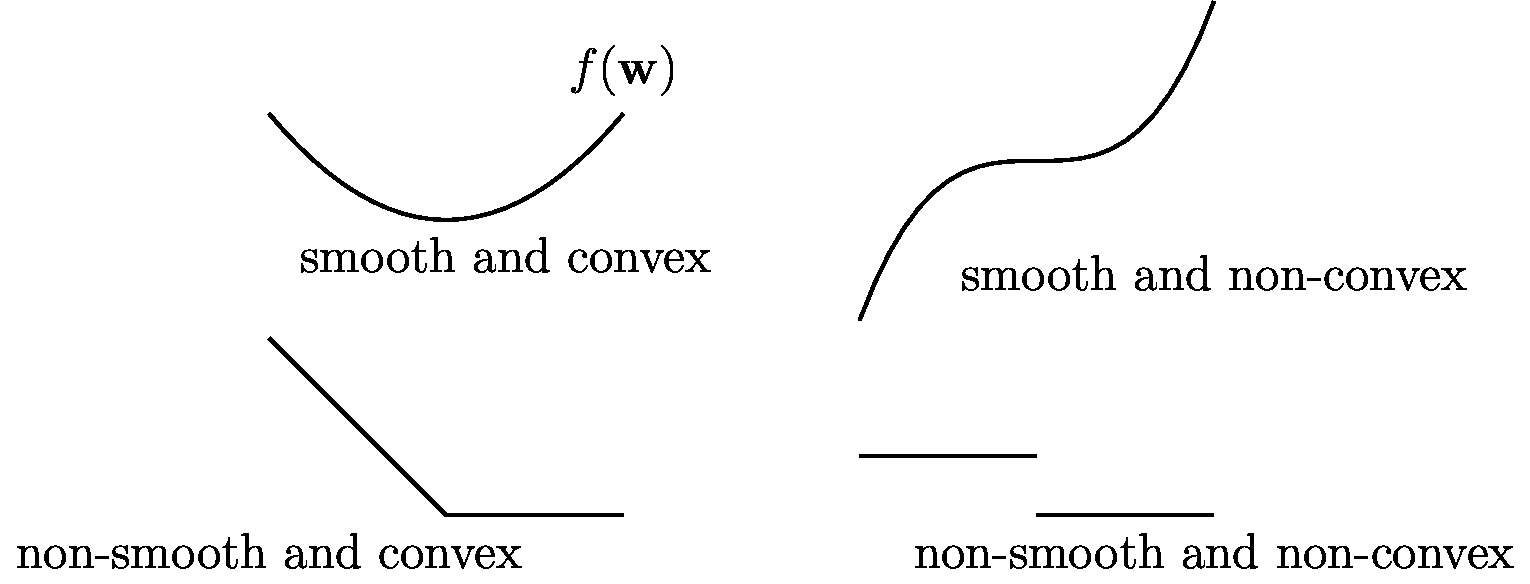
ERM for Linear Regression
As discussed in Section Linear Regression , linear regression methods learn a linear hypothesis [math]h^{(\weights)}(\featurevec) = \weights^{T} \featurevec[/math] with minimum squared error loss. For linear regression, the ERM problem \eqref{eq_def_ERM_weight} becomes
Here, [math]\samplesize=|\dataset|[/math] denotes the sample size of the training set [math]\dataset[/math]. The objective function [math]f(\weights)[/math] in \eqref{equ_def_cost_MSE} is convex and smooth. Such a function can be minimized using the gradient-based methods discussed in Chapter Gradient-Based Learning .
We can rewrite the ERM problem \eqref{equ_def_cost_MSE} more concisely by stacking the labels [math]\truelabel^{(\sampleidx)}[/math] and feature vectors [math]\featurevec^{(\sampleidx)}[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math], into a “label vector” [math]\labelvec[/math] and “feature matrix” [math]\featuremtx[/math],
This allows us to rewrite the objective function in \eqref{equ_def_cost_MSE} as
Inserting \eqref{equ_min_lin_pred_vec_mat} into \eqref{equ_def_cost_MSE}, allows to rewrite the ERM problem for linear regression as
The formulation \eqref{equ_def_cost_MSE_least_squard_errors} allows for an interesting geometric interpretation of linear regression. Solving \eqref{equ_def_cost_MSE_least_squard_errors} amounts to finding a vector [math]\featuremtx\weights[/math] (with feature matrix [math]\featuremtx[/math] \eqref{equ_def_vec_matrix}), that is closest (in the Euclidean norm) to the label vector [math]\labelvec \in \mathbb{R}^{\samplesize}[/math] \eqref{equ_def_vec_matrix}. The solution to this approximation problem is precisely the orthogonal projection of the vector [math]\labelvec[/math] onto the subspace of [math]\mathbb{R}^{\samplesize}[/math] that is spanned by the columns of the feature matrix [math]\featuremtx[/math] (see Figure fig_orthogo_ERM_linreg_norma).
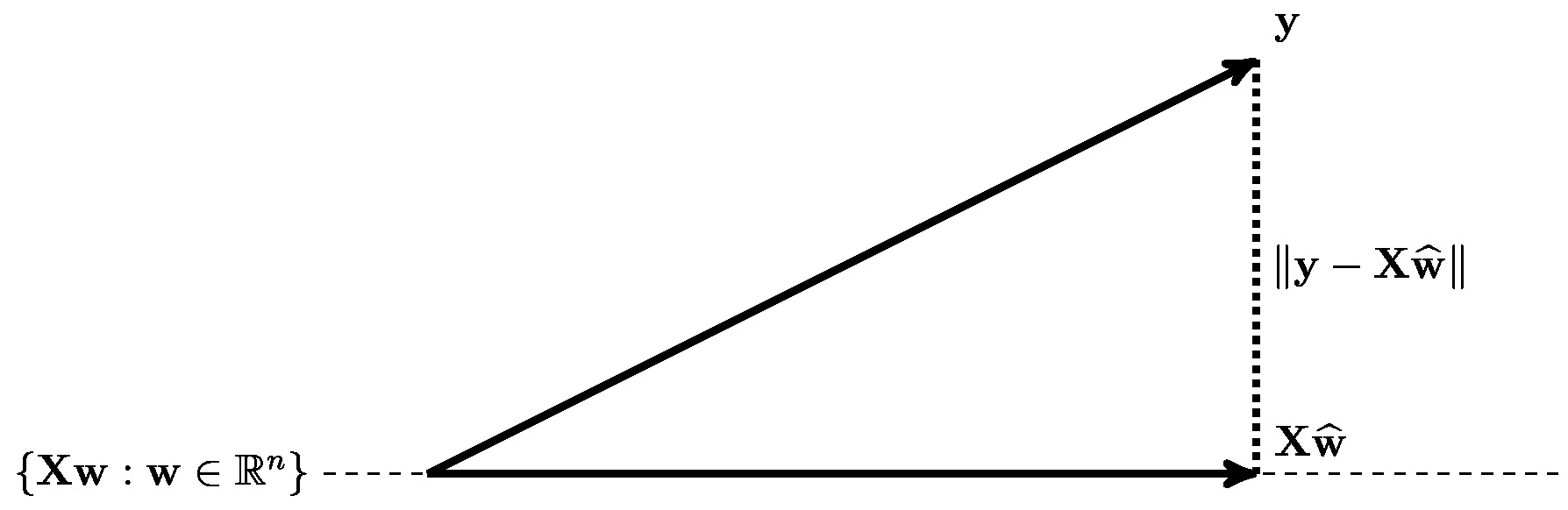
To solve the optimization problem \eqref{equ_def_cost_MSE_least_squard_errors}, it is convenient to rewrite it as the quadratic problem
Since [math]f(\weights)[/math] is a differentiable and convex function, a necessary and sufficient condition for [math]\widehat{\weights}[/math] to be a minimizer [math]f(\widehat{\weights})\!=\!\min_{\weights \in \mathbb{R}^{\featuredim}} f(\weights)[/math] is the zero-gradient condition [4](Sec. 4.2.3)
Combining \eqref{equ_quadr_form_linreg} with \eqref{equ_zero_gradient}, yields the following necessary and sufficient condition for a parameter vector [math]\widehat{\weights}[/math] to solve the ERM \eqref{equ_def_cost_MSE},
This condition can be rewritten as
As indicated in Figure fig_orthogo_ERM_linreg_norma, the optimality condition \eqref{equ_zero_gradient_lin_reg_normal_condition} requires the vector
whose entries are the prediction errors for the data points in the training set, to be orthogonal (or normal) to the subspace spanned by the columns of the feature matrix [math]\featuremtx[/math]. In view of this geometric interpretation, we refer to \eqref{equ_zero_gradient_lin_reg_normal_condition} as a “normal equation”.
It can be shown that, for any given feature matrix [math]\featuremtx[/math] and label vector [math]\labelvec[/math], there always exists at least one optimal parameter vector [math]\widehat{\weights}[/math] which solves \eqref{equ_zero_gradient_lin_reg}. The optimal parameter vector might not be unique, i.e., there might be several different parameter vectors achieving the minimum in \eqref{equ_def_cost_MSE}. However, every vector [math]\widehat{\weights}[/math] which solves \eqref{equ_zero_gradient_lin_reg} achieves the same minimum empirical risk
Here, we used the orthogonal projection matrix [math]\mathbf{P} \in \mathbb{R}^{\samplesize \times \samplesize}[/math] on the linear span of the feature matrix [math]\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T} \in \mathbb{R}^{\samplesize \times \featuredim}[/math] (see \eqref{equ_def_vec_matrix}). The linear span of a matrix [math]\mA=(\va^{(1)},\ldots,\va^{(\samplesize)}) \in \mathbb{R}^{\featuredim \times \samplesize}[/math], denoted as [math]{\rm span } \big\{\mA\}[/math], is the subspace of [math]\mathbb{R}^{\featuredim}[/math] consisting of all linear combinations of the columns [math]\va^{(r)} \in \mathbb{R}^{\featuredim}[/math] of [math]\mA[/math].
If the columns of the feature matrix [math]\featuremtx[/math] (see \eqref{equ_def_vec_matrix}) are linearly independent, which implies that the matrix [math]\featuremtx^{T} \featuremtx[/math] is invertible, the projection matrix [math]\mathbf{P}[/math] is given explicitly as
Moreover, the solution of \eqref{equ_zero_gradient_lin_reg} is then unique and given by
The closed-form solution \eqref{equ_close_form_lin_reg} requires the inversion of the [math]\featuredim \times \featuredim[/math] matrix [math]\featuremtx^{T} \featuremtx[/math].
Note that formula \eqref{equ_close_form_lin_reg} is only valid if the matrix [math]\featuremtx^{T} \featuremtx[/math] is invertible. The feature matrix [math]\featuremtx[/math] is determined by the data points obtained in a MLapplication. Its properties are therefore not under the control of a ML method and it might well happen that the matrix [math]\featuremtx^{T} \featuremtx[/math] is not invertible. As a point in case, the matrix [math]\featuremtx^{T} \featuremtx[/math] cannot be invertible for any dataset containing fewer data points than the number of features used to characterize data points (this is referred to as high-dimensional data). Moreover, the matrix [math]\featuremtx^{T} \featuremtx[/math] is not invertible if there two co-linear features [math]\feature_{\featureidx},\feature_{\featureidx'}[/math] such that [math]\feature_{\featureidx} = \beta \feature_{\featureidx'}[/math] holds for any data point with some constant [math]\lrate \in \mathbb{R}[/math].
Let us now consider a dataset such that the feature matrix [math]\featuremtx[/math] is not full column-rank and, in turn, the matrix [math]\featuremtx^{T} \featuremtx[/math] is not invertible. In this case we cannot use \eqref{equ_close_form_lin_reg} to compute the optimal parameter vector since the inverse of [math]\featuremtx^{T} \featuremtx[/math] does not exist. Moreover, in this case, there are infinitely many different parameter vectors that solve \eqref{equ_zero_gradient_lin_reg}, i.e., the corresponding linear hypothesis map incurs minimum average squared error loss on the training set. Section Data Augmentation explains the benefits of using weights with small Euclidean norm. The parameter vector [math]\widehat{\weights}[/math] solving the linear regression optimality condition \eqref{equ_zero_gradient_lin_reg} and having minimum Euclidean norm among all such vectors is given by
Here, [math]\big( \featuremtx^{T} \featuremtx \big)^{\dagger}[/math] denotes the pseudoinverse (or the Moore–Penrose inverse) of [math]\featuremtx^{T} \featuremtx[/math] (see [16][17]).
Computing the (pseudo-)inverse of [math]\featuremtx^{T} \featuremtx[/math] can be computationally challenging for large number [math]\featuredim[/math] of features. Figure fig_snapshot_pixels depicts a simple ML problem where the number of features is already in the millions. The computational complexity of inverting the matrix [math]\featuremtx^{T} \featuremtx[/math] depends crucially on its condition number. We refer to a matrix as ill-conditioned if its condition number is much larger than 1. In general, ML methods do not have any control on the condition number of the matrix [math]\featuremtx^{T} \featuremtx[/math]. Indeed, this matrix is determined solely by the (features of the) data points fed into the ML method. Section GD for Linear Regression will discuss a method for computing the optimal parameter vector [math]\widehat{\weights}[/math] that does not require any matrix inversion. This method, referred to as gradient descent (GD) constructs a sequence [math]\weights^{(0)}, \weights^{(1)},\ldots[/math] of increasingly accurate approximations of [math]\widehat{\weights}[/math]. This iterative method has two major benefits compared to evaluating the formula \eqref{equ_close_form_lin_reg} using direct matrix inversion, such as Gauss-Jordan elimination [16].
First, GD typically requires significantly fewer arithmetic operations compared to direct matrix inversion. This is crucial in modern ML applications involving large feature matrices. Second, GD does not break when the matrix [math]\featuremtx[/math] is not full rank and the formula \eqref{equ_close_form_lin_reg} cannot be used any more.
ERM for Decision Trees
Consider ERM \eqref{equ_def_ERM_funs} for a regression problem with label space [math]\labelspace=\mathbb{R}[/math] and feature space [math]\featurespace= \mathbb{R}^{\featuredim}[/math] and the hypothesis space defined by decision trees(see Section Decision Trees ). In stark contrast to ERM for linear regression or logistic regression, ERM for decision trees amounts to a discrete optimization problem. Consider the particular hypothesis space [math]\hypospace[/math] depicted in Figure fig_hypospace_DT_depth_2. This hypothesis space contains a finite number of different hypothesis maps. Each individual hypothesis map corresponds to a particular decision tree.
For the small hypothesis space [math]\hypospace[/math] in Figure fig_hypospace_DT_depth_2, ERM is easy. Indeed, we just have to evaluate the empirical risk (“training error”) [math]\emperror(h)[/math] for each hypothesis in [math]\hypospace[/math] and pick the one yielding the smallest empirical risk. However, when allowing for a very large (deep) decision tree, the computational complexity of exactly solving the ERM becomes intractable [18]. A popular approach to learn a decision tree is to use greedy algorithms which try to expand (grow) a given decision tree by adding new branches to leaf nodes in order to reduce the average loss on the training set (see [19](Chapter 8) for more details).
Consider the labeled dataset [math]\dataset[/math] depicted in Figure fig_growingatree and a given decision tree for predicting the label [math]\truelabel[/math] based on the features [math]\featurevec[/math]. We might first try a hypothesis obtained from the simple tree shown in the top of Figure fig_growingatree. This hypothesis does not allow to achieve a small average loss on the training set [math]\dataset[/math]. Therefore, we might grow the tree by replacing a leaf node with a decision node. According to Figure fig_growingatree, to so obtained larger decision tree provides a hypothesis that is able to perfectly predict the labels of the training set (it achieves zero empirical risk).
One important aspect of methods that learn a decision tree by sequentially growing the tree is the question of when to stop growing. A natural stopping criterion might be obtained from the limitations in computational resources, i.e., we can only afford to use decision trees up to certain maximum depth. Besides the computational limitations, we also face statistical limitations for the maximum size of decision trees. ML methods that allow for very deep decision trees, which represent highly complicated maps, tend to overfit the training set (see Figure fig_decisiontree_overfits and Chapter Regularization ). In particular, Even if a deep decision tree incurs small average loss on the training set, it might incur large loss when predicting the labels of data points outside the training set.
ERM for Bayes Classifiers
The family of ML methods referred to as Bayes estimator uses the 0/1 loss to measuring the quality of a classifier [math]h[/math]. The resulting ERM is
The objective function in this optimization problem is non-differentiable and non-convex (see Figure fig_diff_types_bojec). This prevents us from using gradient-based methods (see Chapter Gradient-Based Learning ) to solve \eqref{equ_approx_bayes_class}.
We will now approach the ERM \eqref{equ_approx_bayes_class} via a different route by interpreting the data points [math](\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})[/math] as realizations of iid RVs with the common probability distribution [math]p(\featurevec,\truelabel)[/math].
As discussed in Section The Loss , the empirical risk obtained using [math]0/1[/math] loss approximates the error probability [math]\prob { \hat{\truelabel} \neq \truelabel }[/math] with the predicted label [math]\hat{\truelabel} = 1[/math] for [math]h(\featurevec) \gt 0[/math] and [math]\hat{\truelabel} = -1[/math] otherwise (see equation).
Thus, we can approximate the ERM \eqref{equ_approx_bayes_class} as
Note that the hypothesis [math]h[/math], which is the optimization variable in \eqref{equ_approx_bayes_class_approx}, enters into the objective function of \eqref{equ_approx_bayes_class_approx} via the definition of the predicted label [math]\hat{\truelabel}[/math], which is [math]\hat{\truelabel} = 1 [/math] if [math]h(\featurevec) \gt 0[/math] and [math]\hat{\truelabel} =-1[/math] otherwise.
It turns out that if we would know the probability distribution [math]p(\featurevec,\truelabel)[/math], which is required to compute [math]\prob{ \hat{\truelabel} \neq \truelabel}[/math], the solution of \eqref{equ_approx_bayes_class_approx} can be found via elementary Bayesian decision theory [20]. In particular, the optimal classifier [math]h(\featurevec)[/math] is such that [math]\hat{\truelabel}[/math] achieves the maximum “a-posteriori” probability [math]p(\hat{\truelabel}|\featurevec)[/math] of the label being [math]\hat{\truelabel}[/math], given (or conditioned on) the features [math]\featurevec[/math].
Since we typically do not know the probability distribution [math]p(\featurevec,\truelabel)[/math], we have to estimate (or approximate) it from the observed data points [math](\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})[/math]. This estimation is feasible if the data points can be considered (approximated) as realizations of iid RVs with a common probability distribution [math]p(\featurevec,\truelabel)[/math]. We can then estimate (the parameters) of the probability distribution [math]p(\featurevec,\truelabel)[/math] using maximum likelihood methods (see Section Maximum Likelihood ). For numeric features and labels, a widely-used parametric probability distribution [math]p(\featurevec,\truelabel)[/math] is the multivariate normal (Gaussian) distribution. In particular, conditioned on the label [math]\truelabel[/math], the feature vector [math]\featurevec[/math] is a Gaussian random vector with mean [math]{\bm \mu}_{\truelabel}[/math] and covariance [math]{\bf \Sigma}[/math] [a],
The conditional expectation of the features [math]\featurevec[/math], given (conditioned on) the label [math]\truelabel[/math] of a data point, is [math]{\bm \mu}_{1}[/math] if [math]\truelabel=1[/math], while for [math]\truelabel=-1[/math] the conditional mean of [math]\featurevec[/math] is [math]{\bm \mu}_{-1}[/math]. In contrast, the conditional covariance matrix [math]{\bf \Sigma} = \expect\{ (\featurevec-{\bm \mu}_{\truelabel})(\featurevec-{\bm \mu}_{\truelabel})^{T}|\truelabel \}[/math] of [math]\featurevec[/math] is the same for both values of the label [math]\truelabel \in \{-1,1\}[/math]. The conditional probability distribution [math]p(\featurevec|\truelabel)[/math] of the feature vector, given the label [math]\truelabel[/math], is multivariate normal. In contrast, the marginal distribution of the features [math]\featurevec[/math] is a Gaussian mixture model (GMM). We will revisit GMMs later in Section Soft Clustering with Gaussian Mixture Models where we will see that they are a great tool for soft clustering.
For this probabilistic model of features and labels, the optimal classifier minimizing the error probability [math]\prob{\hat{\truelabel} \neq \truelabel}[/math] is [math]\hat{\truelabel}\!=\!1[/math] for [math]h(\featurevec)\!\gt\!0[/math] and [math]\hat{\truelabel}\!=\!-1[/math] for [math]h(\featurevec)\!\leq\!0[/math] using the classifier map
Carefully note that this expression is only valid if the matrix [math]{\bf \Sigma}[/math] is invertible.
We cannot implement the classifier \eqref{equ_classif_Bayes} directly, since we do not know the true values of the class-specific mean vectors [math]{\bm \mu}_{1}[/math], [math]{\bm \mu}_{-1}[/math] and covariance matrix [math]{\bf \Sigma}[/math]. Therefore, we have to replace those unknown parameters with some estimates [math]\hat{\bm \mu}_{1}[/math], [math]\hat{\bm \mu}_{-1}[/math] and [math]\widehat{\bf \Sigma}[/math]. A principled approach is to use the maximum likelihood estimates.
with [math]\samplesize_{1} = \sum_{\sampleidx=1}^{\samplesize} \mathcal{I}(\truelabel^{(\sampleidx)}=1)[/math] denoting the number of datapoints with label [math]\truelabel=1[/math] ([math]\samplesize_{-1}[/math] is defined similarly). Inserting the estimates \eqref{ML_est_naive_Bayes} into \eqref{equ_classif_Bayes} yields the implementable classifier
We highlight that the classifier \eqref{equ_classif_Bayes_impl} is only well-defined if the estimated covariance matrix [math]\widehat{\bf \Sigma}[/math] \eqref{ML_est_naive_Bayes} is invertible. This requires to use a sufficiently large number of training datapoints such that [math]\samplesize \geq \featuredim[/math].
We derived the classifier \eqref{equ_classif_Bayes_impl} as an approximate solution to the ERM \eqref{equ_approx_bayes_class}. The classifier \eqref{equ_classif_Bayes_impl} partitions the feature space [math]\mathbb{R}^{\featuredim}[/math] into two half-spaces. One half-space consists of feature vectors [math]\featurevec[/math] for which the hypothesis \eqref{equ_classif_Bayes_impl} is non-negative and, in turn, [math]\hat{y}=1[/math]. The other half-space is constituted by feature vectors [math]\featurevec[/math] for which the hypothesis \eqref{equ_classif_Bayes_impl} is negative and, in turn, [math]\hat{\truelabel}=-1[/math]. Figure fig_lin_dec_boundary illustrates these two half-spaces and the decision boundary between them.
The Bayes estimator \eqref{equ_classif_Bayes_impl} is another instance of a linear classifier like logistic regression and the SVM. Each of these methods learns a linear hypothesis [math]h(\featurevec)=\weights^{T} \featurevec[/math], whose decision boundary (vectors [math]\featurevec[/math] with [math]h(\featurevec)=0[/math]) is a hyperplane (see Figure fig_lin_dec_boundary). However, these methods use different loss functions for assessing the quality of a particular linear hypothesis [math]h(\featurevec)=\weights \featurevec[/math] (which defined the decision boundary via [math]h(\featurevec)=0[/math]). Therefore, these three methods typically learn classifiers with different decision boundaries.
For the estimator [math]\widehat{\bf \Sigma}[/math] to be accurate (close to the unknown covariance matrix) we need a number of datapoints (sample size) which is at least of the order [math]\featuredim^{2}[/math]. This sample size requirement might be infeasible for applications with only few datapoints available.
The maximum likelihood estimate [math]\widehat{\bf \Sigma}[/math] \eqref{ML_est_naive_Bayes} is not invertible whenever [math]\samplesize \lt \featuredim[/math]. In this case, the expression \eqref{equ_classif_Bayes_impl} becomes useless. To cope with small sample size [math]\samplesize \lt \featuredim[/math] we can simplify the model \eqref{equ_prob_model_Bayes} by requiring the covariance to be diagonal [math]{\bf \Sigma} = {\rm diag} (\sigma_{1}^{2}, \ldots, \sigma_{\featuredim}^{2})[/math]. This is equivalent to modelling the individual features [math]x_{1},\ldots,x_{\featuredim}[/math] of a data point as conditionally independent, given its label [math]\truelabel[/math]. The resulting special case of a Bayes estimator is often referred to as a “naive Bayes” classifier.
We finally highlight that the classifier \eqref{equ_classif_Bayes_impl} is obtained using the generative model \eqref{equ_prob_model_Bayes} for the data. Therefore, Bayes estimator belong to the family of generative ML methods which involve modelling the data generation. In contrast, logistic regression and the SVM do not require a generative model for the data points but aim directly at finding the relation between features [math]\featurevec[/math] and label [math]\truelabel[/math] of a data point. These methods belong therefore to the family of discriminative ML methods.
Generative methods such as those learning a Bayes estimator are preferable for applications with only very limited amounts of labeled data. Indeed, having a generative model such as \eqref{equ_prob_model_Bayes} allows us to synthetically generate more labeled data by generating random features and labels according to the probability distribution \eqref{equ_prob_model_Bayes}. We refer to [21] for a more detailed comparison between generative and discriminative methods.
Online Learning
In it most basic form, ERM requires a given set of labeled data points, which we refer to as the training set. However, some ML methods can access data only in a sequential fashion. As a point in case, consider time series data such as daily minimum and maximum temperatures recorded by a Finnish Meteorological Institute (FMI) weather station. Such a time series consists of a sequence of data points that are generated at successive time instants.
Online learning studies ML methods that learn (or optimize) a hypothesis incrementally as new data arrives. This mode of operation is quite different from ML methods that learn a hypothesis at once by solving an ERM problem. These different operation modes corresponds to different frequencies of iterating the basic ML cycle depicted in Figure fig_AlexMLBP. Online learning methods start a new cycle in Figure fig_AlexMLBP whenever a new data point arrives (e.g., we have recorded the minimum and maximum temperate of a day that just ended).
We now present an online learning variant of linear regression (see Section Linear Regression ) which is suitable for time series data with data points [math]\big(\featurevec^{(\timeidx)},\truelabel^{(\timeidx)}\big)[/math] gathered sequentially (over time). In particular, the data points [math]\big(\featurevec^{(\timeidx)},\truelabel^{(\timeidx)}\big)[/math] become available (are gathered) at a discrete time instants [math]\timeidx=1,2,3\ldots[/math].
Let us stack the feature vectors and labels of all data points available at time [math]\timeidx[/math] into feature matrix [math]\featuremtx^{(\timeidx)}[/math] and label vector [math]\labelvec^{(\timeidx)}[/math], respectively. The feature matrix and label vector for the first three time instants are
As detailed in Section Linear Regression , linear regression aims at learning the weights [math]\weights[/math] of a linear map [math]h(\featurevec) \defeq \weights^{T} \featurevec[/math] such that the squared error loss [math]\big( \truelabel - h(\featurevec) \big)[/math] is as small as possible. This informal goal of linear regression is made precise by the ERM problem \eqref{equ_def_cost_MSE} which defines the optimal weights via incurring minimum average squared error loss (empirical risk) on a given training set [math]\dataset[/math]. These optimal weights are given by the solutions of \eqref{equ_zero_gradient_lin_reg_normal_condition}. When the feature vectors of datapoints in [math]\dataset[/math] are linearly independent, we obtain the closed-form expression \eqref{equ_close_form_lin_reg} for the optimal weights.
Inserting the feature matrix [math]\featuremtx^{(\timeidx)}[/math] and label vector [math]\labelvec^{(\timeidx)}[/math] \eqref{equ_def_feature_label_three_instants} into \eqref{equ_close_form_lin_reg}, yields
For each time instant we can evaluate the RHS of \eqref{equ_opt_weight_time_t} to obtain the parameter vector [math]\widehat{\weights}^{(\timeidx)}[/math] that minimizes the average squared error loss over all data points gathered up to time [math]\timeidx[/math]. However, computing [math]\widehat{\weights}^{(\timeidx)}[/math] via direct evaluation of the RHS in \eqref{equ_opt_weight_time_t} for each new time instant [math]\timeidx[/math] misses an opportunity for recycling computations done already at earlier time instants.
Let us now show how to (partially) reuse the computations used to evaluate \eqref{equ_opt_weight_time_t} for time [math]\timeidx[/math] in the evaluation of \eqref{equ_opt_weight_time_t} for the next time instant [math]\timeidx+1[/math]. To this end, we first rewrite the matrix [math] \mQ^{(\timeidx)} \defeq \big(\featuremtx^{(\timeidx)}\big)^{T} \featuremtx^{(\timeidx)}[/math] as
Since [math]\mQ^{(\timeidx\!+\!1)} = \mQ^{(\timeidx)} + \featurevec^{(\timeidx\!+\!1)} \big(\featurevec^{(\timeidx\!+\!1)} \big)^{T}[/math], we can use a well-known identity for matrix inverses (see [22][23]) to obtain
Inserting \eqref{equ_matrix_invers} into \eqref{equ_opt_weight_time_t} yields the following relation between optimal parameter vectors at consecutive time instants [math]\timeidx[/math] and [math]\timeidx+1[/math],
Note that neither evaluating the RHS of \eqref{equ_def_update_recuriveLS} nor evaluating the RHS of \eqref{equ_matrix_invers} requires to actually invert a matrix of with more than one entry (we can think of a scalar number as [math]1 \times 1[/math] matrix). In contrast, evaluating the RHS \eqref{equ_opt_weight_time_t} requires to invert the matrix [math]\mQ^{(\timeidx)} \in \mathbb{R}^{\featurelen \times \featurelen}[/math]. We obtain an online algorithm for linear regression via computing the updates \eqref{equ_def_update_recuriveLS} and \eqref{equ_matrix_invers} for each new time instant [math]\timeidx[/math]. Another online method for linear regression will be discussed at the end of Section Stochastic GD .
Weighted ERM
Consider a ML method that uses some hypothesis space [math]\hypospace[/math] and loss function [math]\lossfun[/math] to measure the quality predictions obtained from a specific hypothesis when applied to a data point. A principled approach to learn a useful hypothesis is via ERM \eqref{equ_def_ERM_funs} using a training set
.
For some applications it might be useful to modify the ERM principle \eqref{equ_def_ERM_funs} by putting different weights on the data points. In particular, for each data point [math]\big( \featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)} \big)[/math] we specify a non-negative weight [math]\sampleweight{\sampleidx} \in \mathbb{R}_{+}[/math]. Weighted ERM is obtained from ERM \eqref{equ_def_ERM_funs} by replacing the average loss over the training set with a weighted average loss,
Note that we obtain ERM \eqref{equ_def_ERM_funs} as the special case of weighted ERM \eqref{equ_def_wERM_funs} for the weights [math]\sampleweight{\sampleidx} = 1/\samplesize[/math].
We might interpret the weight [math]\sampleweight{\sampleidx}[/math] as a measure for the importance or relevance of the data point [math]\big( \featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)} \big)[/math] for the hypothesis [math]\hat{h}[/math] learnt via \eqref{equ_def_wERM_funs}. The extreme case [math]\sampleweight{\sampleidx}=0[/math] means that the data point [math]\big( \featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)} \big)[/math] becomes irrelevant for learning a hypothesis via \eqref{equ_def_wERM_funs}. This could be useful if the data point [math]\big( \featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)} \big)[/math] represents an outlier that violates the i.i.d assumption which is satisfied by most of the other data points. Thus, using suitable weights in \eqref{equ_def_wERM_funs} could make the resulting ML method robust against outliers in the training set. Note that we have discussed another strategy (via the choice for the loss function) to achieve robustness against outliers in Section Least Absolute Deviation Regression .
Another use-case of weighted ERM \eqref{equ_def_wERM_funs} is for applications where the risk of a hypothesis is defined using a probability distribution that is different form the probability distribution of the data points in the training set. Thus, the data points conform to an i.i.d assumption with underlying probability distribution [math]p(\featurevec,\truelabel)[/math].
However, we would like to measure the quality of a hypothesis via the expected loss or risk using a different probability distribution [math]p'(\featurevec,\truelabel)[/math],
Having a different probability distribution [math]p'(\featurevec,\truelabel) (\neq p (\featurevec,\truelabel)))[/math] to define the overall quality (risk) of a hypothesis might be beneficial for binary classification problems with imbalanced data. Indeed, using the average loss (which approximates the risk under [math]p(\featurevec,\truelabel)[/math]) might not be a useful quality measure if one class is over-represented in the training set (see Section Confusion Matrix). It can be shown that, under mild conditions, the weighted average loss in \eqref{equ_def_wERM_funs} approximates \eqref{equ_target_p_prime_risk} when using the weights [math]\sampleweight{\sampleidx} = p'\big(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}\big)/ p\big(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}\big)[/math] [24](Sec. 11.1.4).
Notes
- We use the shorthand [math]\mathcal{N}(\featurevec;{\bm \mu},{\bf \Sigma})[/math] to denote the probability density function (pdf) [math]p(\featurevec) = \frac{1}{\sqrt{{\rm det} (2 \pi {\bf \Sigma})}} \exp\big(- (1/2) (\featurevec\!-\!{\bm \mu})^{T}{\bf \Sigma}^{-1}(\featurevec\!-\!{\bm \mu}) \big)[/math]of a Gaussian random vector [math]\featurevec[/math] with mean [math]{\bm \mu} = \expect \{ \featurevec \}[/math] and covariance matrix [math]{\bf \Sigma} = \expect \big\{(\featurevec\!-\!{\bm \mu}) (\featurevec\!-\!{\bm \mu})^{T} \big\}[/math].
General References

Jung, Alexander (2022). Machine Learning: The Basics. Signapore: Springer. doi:10.1007/978-981-16-8193-6.
Jung, Alexander (2022). "Machine Learning: The Basics". arXiv:1805.05052.
References
- 1.0 1.1 E. L. Lehmann and G. Casella. Theory of Point Estimation Springer, New York, 2nd edition, 1998
- L. Hyafil and R. Rivest. Constructing optimal binary decision trees is np-complete. Information Processing Letters 5(1):15--17, 1976
- A. Papoulis and S. U. Pillai. Probability, Random Variables, and Stochastic Processes Mc-Graw Hill, New York, 4 edition, 2002
- 4.0 4.1 S. Boyd and L. Vandenberghe. Convex Optimization Cambridge Univ. Press, Cambridge, UK, 2004
- S. Sra, S. Nowozin, and S. J. Wright, editors. Optimization for Machine Learning MIT Press, 2012
- P. J. Brockwell and R. A. Davis. Time Series: Theory and Methods Springer New York, 1991
- H. Lütkepohl. New Introduction to Multiple Time Series Analysis Springer, New York, 2005
- D. Cohn, Z. Ghahramani, and M. Jordan. Active learning with statistical models. J. Artif. Int. Res. 4(1):129--145, March 1996
- B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. y Arcas. Communication-efficient learning of deep networks from decentralized data. In A. Singh and J. Zhu, editors, Proceedings of the 20th International Conference on Artificial Intelligence and Statistics volume 54 of Proceedings of Machine Learning Research pages 1273--1282, Fort Lauderdale, FL, USA, 20--22 Apr 2017. PMLR
- A. Jung. Networked exponential families for big data over networks. IEEE Access 8:202897--202909, 2020
- A. Jung and N. Tran. Localized linear regression in networked data. IEEE Sig. Proc. Lett. 26(7), Jul. 2019
- N. Tran, H. Ambos, and A. Jung. Classifying partially labeled networked data via logistic network lasso. In Proc. IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP) pages 3832--3836, Barcelona, Spain, May 2020
- F. Sattler, K. Müller, and W. Samek. Clustered federated learning: Model-agnostic distributed multitask optimization under privacy constraints. IEEE Transactions on Neural Networks and Learning Systems 2020
- N. Parikh and S. Boyd. Proximal algorithms. Foundations and Trends in Optimization 1(3):123--231, 2013
- I. Goodfellow, Y. Bengio, and A. Courville. Deep Learning MIT Press, 2016
- 16.0 16.1 G. H. Golub and C. F. Van Loan. Matrix Computations Johns Hopkins University Press, Baltimore, MD, 3rd edition, 1996
- G. Golub and C. van Loan. An analysis of the total least squares problem. SIAM J. Numerical Analysis 17(6):883--893, Dec. 1980
- L. Hyafil and R. L. Rivest. Constructing optimal binary decision trees is np-complete. Information Processing Letters 5(1):15--17, 1976
- G. James, D. Witten, T. Hastie, and R. Tibshirani. An Introduction to Statistical Learning with Applications in R Springer, 2013
- H. Poor. An Introduction to Signal Detection and Estimation Springer, 2 edition, 1994
- A. Y. Ng and M. I. Jordan. On discriminative vs. generative classifiers: A comparison of logistic regression and naive bayes. In T. G. Dietterich, S. Becker, and Z. Ghahramani, editors, Advances in Neural Information Processing Systems 14, pages 841--848. MIT Press, 2002
- M. S. Bartlett. An inverse matrix adjustment arising in discriminant analysis. The Annals of Mathematical Statistics 22(1):107 -- 111, 1951
- C. Meyer. Generalized inversion of modified matrices. SIAM J. Appied Mathmetmatics 24(3), 1973
- C. M. Bishop. Pattern Recognition and Machine Learning Springer, 2006