guide:Cc42ad1ea4: Difference between revisions
No edit summary |
mNo edit summary |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<div class="d-none"> | |||
<math> | |||
% Generic syms | |||
\newcommand\defeq{:=} | |||
\newcommand{\Tt}[0]{\boldsymbol{\theta}} | |||
\newcommand{\XX}[0]{{\cal X}} | |||
\newcommand{\ZZ}[0]{{\cal Z}} | |||
\newcommand{\vx}[0]{{\bf x}} | |||
\newcommand{\vv}[0]{{\bf v}} | |||
\newcommand{\vu}[0]{{\bf u}} | |||
\newcommand{\vs}[0]{{\bf s}} | |||
\newcommand{\vm}[0]{{\bf m}} | |||
\newcommand{\vq}[0]{{\bf q}} | |||
\newcommand{\mX}[0]{{\bf X}} | |||
\newcommand{\mC}[0]{{\bf C}} | |||
\newcommand{\mA}[0]{{\bf A}} | |||
\newcommand{\mL}[0]{{\bf L}} | |||
\newcommand{\fscore}[0]{F_{1}} | |||
\newcommand{\sparsity}{s} | |||
\newcommand{\mW}[0]{{\bf W}} | |||
\newcommand{\mD}[0]{{\bf D}} | |||
\newcommand{\mZ}[0]{{\bf Z}} | |||
\newcommand{\vw}[0]{{\bf w}} | |||
\newcommand{\D}[0]{{\mathcal{D}}} | |||
\newcommand{\mP}{\mathbf{P}} | |||
\newcommand{\mQ}{\mathbf{Q}} | |||
\newcommand{\E}[0]{{\mathbb{E}}} | |||
\newcommand{\vy}[0]{{\bf y}} | |||
\newcommand{\va}[0]{{\bf a}} | |||
\newcommand{\vn}[0]{{\bf n}} | |||
\newcommand{\vb}[0]{{\bf b}} | |||
\newcommand{\vr}[0]{{\bf r}} | |||
\newcommand{\vz}[0]{{\bf z}} | |||
\newcommand{\N}[0]{{\mathcal{N}}} | |||
\newcommand{\vc}[0]{{\bf c}} | |||
\newcommand{\bm}{\boldsymbol} | |||
% Statistics and Probability Theory | |||
\newcommand{\errprob}{p_{\rm err}} | |||
\newcommand{\prob}[1]{p({#1})} | |||
\newcommand{\pdf}[1]{p({#1})} | |||
\def \expect {\mathbb{E} } | |||
% Machine Learning Symbols | |||
\newcommand{\biasterm}{B} | |||
\newcommand{\varianceterm}{V} | |||
\newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} | |||
\newcommand{\nrfolds}{k} | |||
\newcommand{\mseesterr}{E_{\rm est}} | |||
\newcommand{\bootstrapidx}{b} | |||
%\newcommand{\modeldim}{r} | |||
\newcommand{\modelidx}{l} | |||
\newcommand{\nrbootstraps}{B} | |||
\newcommand{\sampleweight}[1]{q^{(#1)}} | |||
\newcommand{\nrcategories}{K} | |||
\newcommand{\splitratio}[0]{{\rho}} | |||
\newcommand{\norm}[1]{\Vert {#1} \Vert} | |||
\newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} | |||
\newcommand{\bmx}[0]{\begin{bmatrix}} | |||
\newcommand{\emx}[0]{\end{bmatrix}} | |||
\newcommand{\T}[0]{\text{T}} | |||
\DeclareMathOperator*{\rank}{rank} | |||
%\newcommand\defeq{:=} | |||
\newcommand\eigvecS{\hat{\mathbf{u}}} | |||
\newcommand\eigvecCov{\mathbf{u}} | |||
\newcommand\eigvecCoventry{u} | |||
\newcommand{\featuredim}{n} | |||
\newcommand{\featurelenraw}{\featuredim'} | |||
\newcommand{\featurelen}{\featuredim} | |||
\newcommand{\samplingset}{\mathcal{M}} | |||
\newcommand{\samplesize}{m} | |||
\newcommand{\sampleidx}{i} | |||
\newcommand{\nractions}{A} | |||
\newcommand{\datapoint}{\vz} | |||
\newcommand{\actionidx}{a} | |||
\newcommand{\clusteridx}{c} | |||
\newcommand{\sizehypospace}{D} | |||
\newcommand{\nrcluster}{k} | |||
\newcommand{\nrseeds}{s} | |||
\newcommand{\featureidx}{j} | |||
\newcommand{\clustermean}{{\bm \mu}} | |||
\newcommand{\clustercov}{{\bm \Sigma}} | |||
\newcommand{\target}{y} | |||
\newcommand{\error}{E} | |||
\newcommand{\augidx}{b} | |||
\newcommand{\task}{\mathcal{T}} | |||
\newcommand{\nrtasks}{T} | |||
\newcommand{\taskidx}{t} | |||
\newcommand\truelabel{y} | |||
\newcommand{\polydegree}{r} | |||
\newcommand\labelvec{\vy} | |||
\newcommand\featurevec{\vx} | |||
\newcommand\feature{x} | |||
\newcommand\predictedlabel{\hat{y}} | |||
\newcommand\dataset{\mathcal{D}} | |||
\newcommand\trainset{\dataset^{(\rm train)}} | |||
\newcommand\valset{\dataset^{(\rm val)}} | |||
\newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} | |||
\newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} | |||
\newcommand{\inspace}{\mathcal{X}} | |||
\newcommand{\sigmoid}{\sigma} | |||
\newcommand{\outspace}{\mathcal{Y}} | |||
\newcommand{\hypospace}{\mathcal{H}} | |||
\newcommand{\emperror}{\widehat{L}} | |||
\newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} | |||
\newcommand{\featurespace}{\mathcal{X}} | |||
\newcommand{\labelspace}{\mathcal{Y}} | |||
\newcommand{\rawfeaturevec}{\mathbf{z}} | |||
\newcommand{\rawfeature}{z} | |||
\newcommand{\condent}{H} | |||
\newcommand{\explanation}{e} | |||
\newcommand{\explainset}{\mathcal{E}} | |||
\newcommand{\user}{u} | |||
\newcommand{\actfun}{\sigma} | |||
\newcommand{\noisygrad}{g} | |||
\newcommand{\reconstrmap}{r} | |||
\newcommand{\predictor}{h} | |||
\newcommand{\eigval}[1]{\lambda_{#1}} | |||
\newcommand{\regparam}{\lambda} | |||
\newcommand{\lrate}{\alpha} | |||
\newcommand{\edges}{\mathcal{E}} | |||
\newcommand{\generror}{E} | |||
\DeclareMathOperator{\supp}{supp} | |||
%\newcommand{\loss}[3]{L({#1},{#2},{#3})} | |||
\newcommand{\loss}[2]{L\big({#1},{#2}\big)} | |||
\newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} | |||
\newcommand{\determinant}[1]{{\rm det}({#1})} | |||
\DeclareMathOperator*{\argmax}{argmax} | |||
\DeclareMathOperator*{\argmin}{argmin} | |||
\newcommand{\itercntr}{r} | |||
\newcommand{\state}{s} | |||
\newcommand{\statespace}{\mathcal{S}} | |||
\newcommand{\timeidx}{t} | |||
\newcommand{\optpolicy}{\pi_{*}} | |||
\newcommand{\appoptpolicy}{\hat{\pi}} | |||
\newcommand{\dummyidx}{j} | |||
\newcommand{\gridsizex}{K} | |||
\newcommand{\gridsizey}{L} | |||
\newcommand{\localdataset}{\mathcal{X}} | |||
\newcommand{\reward}{r} | |||
\newcommand{\cumreward}{G} | |||
\newcommand{\return}{\cumreward} | |||
\newcommand{\action}{a} | |||
\newcommand\actionset{\mathcal{A}} | |||
\newcommand{\obstacles}{\mathcal{B}} | |||
\newcommand{\valuefunc}[1]{v_{#1}} | |||
\newcommand{\gridcell}[2]{\langle #1, #2 \rangle} | |||
\newcommand{\pair}[2]{\langle #1, #2 \rangle} | |||
\newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} | |||
\newcommand{\actionvalue}[1]{q_{#1}} | |||
\newcommand{\transition}{\mathcal{T}} | |||
\newcommand{\policy}{\pi} | |||
\newcommand{\charger}{c} | |||
\newcommand{\itervar}{k} | |||
\newcommand{\discount}{\gamma} | |||
\newcommand{\rumba}{Rumba} | |||
\newcommand{\actionnorth}{\rm N} | |||
\newcommand{\actionsouth}{\rm S} | |||
\newcommand{\actioneast}{\rm E} | |||
\newcommand{\actionwest}{\rm W} | |||
\newcommand{\chargingstations}{\mathcal{C}} | |||
\newcommand{\basisfunc}{\phi} | |||
\newcommand{\augparam}{B} | |||
\newcommand{\valerror}{E_{v}} | |||
\newcommand{\trainerror}{E_{t}} | |||
\newcommand{\foldidx}{b} | |||
\newcommand{\testset}{\dataset^{(\rm test)} } | |||
\newcommand{\testerror}{E^{(\rm test)}} | |||
\newcommand{\nrmodels}{M} | |||
\newcommand{\benchmarkerror}{E^{(\rm ref)}} | |||
\newcommand{\lossfun}{L} | |||
\newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} | |||
\newcommand{\cluster}{\mathcal{C}} | |||
\newcommand{\bayeshypothesis}{h^{*}} | |||
\newcommand{\featuremtx}{\mX} | |||
\newcommand{\weight}{w} | |||
\newcommand{\weights}{\vw} | |||
\newcommand{\regularizer}{\mathcal{R}} | |||
\newcommand{\decreg}[1]{\mathcal{R}_{#1}} | |||
\newcommand{\naturalnumbers}{\mathbb{N}} | |||
\newcommand{\featuremapvec}{{\bf \Phi}} | |||
\newcommand{\featuremap}{\phi} | |||
\newcommand{\batchsize}{B} | |||
\newcommand{\batch}{\mathcal{B}} | |||
\newcommand{\foldsize}{B} | |||
\newcommand{\nriter}{R} | |||
</math> | |||
</div> | |||
This chapter discusses an important family of optimization methods for solving [[ guide:2c0f621d22#eq_def_ERM_weight | <span class="mw-gls mw-gls-first" data-name ="erm">empirical risk minimization (ERM)</span>]] with a parametrized <span class="mw-gls mw-gls-first" data-name ="hypospace">hypothesis space</span> (see Chapter [[guide:2c0f621d22#sec_comp_stat_ERM | Computational and Statistical Aspects of ERM ]]). The common theme of these methods is to construct local approximations of the objective function in [[ guide:2c0f621d22#eq_def_ERM_weight | <span class="mw-gls" data-name ="erm">ERM</span>]]. These local approximations are obtained from the <span class="mw-gls mw-gls-first" data-name ="gradient">gradient</span>s of the objective function. <span class="mw-gls mw-gls-first" data-name ="gdmethods">Gradient-based methods</span> have gained popularity recently as an efficient technique for tuning the parameters of <span class="mw-gls mw-gls-first" data-name ="deepnet">deep <span class="mw-gls mw-gls-first" data-name ="ann">artificial neural network (ANN)</span> (deep net)</span>s within deep learning methods <ref name="Goodfellow-et-al-2016">I. Goodfellow, Y. Bengio, and A. Courville. ''Deep Learning'' MIT Press, 2016</ref>. | |||
Section [[#sec_basic_GD_iteration | The Basic Gradient Step ]] discusses <span class="mw-gls mw-gls-first" data-name ="gd">gradient descent (GD)</span> as the most basic form of <span class="mw-gls mw-gls-first" data-name ="gdmethods">gradient-based methods</span>. The idea | |||
of <span class="mw-gls" data-name ="gd">GD</span> is to update the weights by locally optimizing a linear approximation of the objective function. This | |||
update is referred to as a <span class="mw-gls" data-name ="gd">GD</span> step and provides the main algorithmic primitive of <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span>. | |||
One key challenge for a good use of <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> is the appropriate extend of the local | |||
approximations. This extent is controlled by a <span class="mw-gls mw-gls-first" data-name ="stepsize">step size</span> parameter that is used in the basic <span class="mw-gls" data-name ="gd">GD</span> step. | |||
Section [[#equ_sec_gd_step_size | Choosing the Learning Rate ]] discusses some approaches for choosing this <span class="mw-gls" data-name ="stepsize">step size</span>. | |||
Section [[#sec_when_to_stop | When To Stop? ]] discusses a second main challenge in using <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> which is to decide when to stop repeating the <span class="mw-gls" data-name ="gd">GD</span> steps. | |||
Section [[#sec_GD_linear_regression | GD for Linear Regression ]] and Section [[#sec_GD_logistic_regression | GD for Logistic Regression ]] spell out <span class="mw-gls" data-name ="gd">GD</span> for two instances of <span class="mw-gls" data-name ="erm">ERM</span> arising from <span class="mw-gls mw-gls-first" data-name ="linreg">linear regression</span> and <span class="mw-gls mw-gls-first" data-name ="logreg">logistic regression</span>, respectively. | |||
The beneficial effect of data normalization on the convergence speed of <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> is briefly | |||
discussed in Section [[#sec_data_normalization | Data Normalization ]]. As explained in Section [[#sec_sgd | Stochastic GD ]], the use of stochastic | |||
approximations enables <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> for applications involving massive amounts of data (“big data”). | |||
Section [[#sec_adv_gd_methods | Advanced Gradient-Based Methods ]] develops some intuition for advanced <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> that | |||
exploit the information gathered during previous iterations. | |||
==<span id="sec_basic_GD_iteration"/>The Basic Gradient Step== | |||
Let us rewrite [[ guide:2c0f621d22#eq_def_ERM_weight | <span class="mw-gls" data-name ="erm">empirical risk minimization (ERM)</span>]] as the optimization problem | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_obj_emp_risk_GD} | |||
\min_{\weights \in \mathbb{R}^{\featuredim}} f(\weights) \defeq(1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h^{(\weights)}}. | |||
\end{equation} | |||
</math> | |||
From now on we tacitly assume that each individual <span class="mw-gls mw-gls-first" data-name ="loss">loss</span> | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_componentn_loss_gd} | |||
f_{\sampleidx}(\weights) \defeq \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h^{(\weights)}} | |||
\end{equation} | |||
</math> | |||
arising in \eqref{equ_obj_emp_risk_GD} represents a <span class="mw-gls mw-gls-first" data-name ="differentiable">differentiable</span> function of the | |||
parameter vector <math>\weights</math>. Trivially, differentiability of the components \eqref{equ_def_componentn_loss_gd} | |||
implies differentiability of the overall objective function <math>f(\weights)</math> \eqref{equ_obj_emp_risk_GD}. | |||
Two important examples of <span class="mw-gls" data-name ="erm">ERM</span> involving such differentiable <span class="mw-gls mw-gls-first" data-name ="lossfunc">loss function</span>s are <span class="mw-gls" data-name ="linreg">linear regression</span> and <span class="mw-gls" data-name ="logreg">logistic regression</span>. | |||
In contrast, the [[guide:B85f6bf6f2#equ_hinge_loss | <span class="mw-gls" data-name ="hingeloss">hinge loss</span>]] used by the <span class="mw-gls mw-gls-first" data-name ="svm">support vector machine (SVM)</span> results in a non-differentiable objective | |||
function <math>f(\weights)</math> \eqref{equ_obj_emp_risk_GD}. However, it is possible to (significantly) extend the scope | |||
of <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> to non-differentiable functions by replacing the concept of a <span class="mw-gls" data-name ="gradient">gradient</span> with that | |||
of a <span class="mw-gls mw-gls-first" data-name ="subgradient">subgradient</span>. | |||
Gradient based methods are iterative. They construct a sequence of parameter vectors <math>\weights^{(0)} \rightarrow \weights^{(1)} \dots</math> | |||
that hopefully converge to a minimizer <math>\overline{\weights}</math> of <math>f(\weights)</math>, | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_opt_weight} | |||
f(\overline{\weights}) = \bar{f} \defeq \min_{\weights \in \mathbb{R}^{\featuredim}} f(\weights). | |||
\end{equation} | |||
</math> | |||
Note that there might be several different optimal parameter vectors <math>\overline{\weights}</math> that | |||
satisfy the optimality condition \eqref{equ_def_opt_weight}. We want the sequence generated | |||
by a gradient based method to converge towards any of them. The vectors <math>\weights^{(\itercntr)}</math> are | |||
(hopefully) increasingly, with increasing iteration <math>\itercntr</math>, more accurate approximation for a | |||
minimizer <math>\overline{\weights}</math> of \eqref{equ_def_opt_weight}. | |||
Since the objective function <math>f(\weights)</math> is differentiable, we can approximate it locally around the | |||
vector <math>\weights^{(\itercntr)}</math> using a tangent hyperplane that passes through the point <math>\big(\weights^{(\itercntr)},f\big(\weights^{(\itercntr)}\big) \big) \in \mathbb{R}^{\featuredim+1}</math>. The normal vector of this hyperplane is given by <math>\mathbf{n} = (\nabla f\big(\weights^{(\itercntr)}\big) ,-1)</math> | |||
(see Figure [[#fig_smooth_function|fig_smooth_function]]). The first component of the normal vector is the gradient <math>\nabla f(\weights)</math> of the objective | |||
function <math>f(\weights)</math> evaluated at the point <math>\weights^{(\itercntr)}</math>. Our main use of the gradient <math>\nabla f\big(\weights^{(\itercntr)}\big)</math> will be | |||
to construct a linear approximation <ref name="RudinBookPrinciplesMatheAnalysis">W. Rudin. ''Principles of Mathematical Analysis'' McGraw-Hill, New York, 3 edition, 1976</ref> | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_linear_approx_diff} | |||
f(\weights) \approx f\big(\weights^{(\itercntr)}\big) + \big(\weights-\weights^{(\itercntr)} \big)^{T} \nabla f\big(\weights^{(\itercntr)}\big) \mbox{ for }\weights \mbox{ sufficiently close to } \weights^{(\itercntr)}. | |||
\end{equation} | |||
</math> | |||
Requiring the objective function <math>f(\weights)</math> in \eqref{equ_linear_approx_diff} to be differentiable is the same | |||
as requiring the validity of the local linear approximation \eqref{equ_linear_approx_diff} at every possible vector <math>\weights^{(\itercntr)}</math>. | |||
It turns out that differentiability alone is not very helpful for the design and analysis of gradient based methods. | |||
Gradient based methods are most useful for finding the minimum of | |||
differentiable functions <math>f(\weights)</math> that are also <span class="mw-gls mw-gls-first" data-name ="smooth">smooth</span>. | |||
Informally, a differentiable function <math>f(\weights)</math> is smooth if the gradient <math>\nabla f(\weights)</math> does | |||
not change too rapidly as a function of the argument <math>\weights</math>. A quantitative version of the smoothness | |||
concept refers to a function as <math>\beta</math>-smooth if its gradient is Lipschitz continuous with Lipschitz | |||
constant <math>\beta> 0 </math> <ref name="CvxBubeck2015">S. Bubeck. Convex optimization. algorithms and complexity. In ''Foundations and Trends in Machine Learning'' volume 8. Now | |||
Publishers, 2015</ref>{{rp|at=Sec. 3.2}}, | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_beta_smooth} | |||
\| \nabla f(\weights) - \nabla f(\weights') \| \leq \beta \| \weights - \weights' \|. | |||
\end{equation} | |||
</math> | |||
Note that if a function <math>f(\weights)</math> is <math>\beta</math> smooth, it is also <math>\beta'</math> smooth for any <math>\beta' > \beta</math>. | |||
The smallest <math>\beta</math> such that \eqref{equ_def_beta_smooth} is satisfied depends on the features | |||
and labels of <span class="mw-gls mw-gls-first" data-name ="datapoint">data point</span>s used in \eqref{equ_obj_emp_risk_GD} as well as on the choice for the <span class="mw-gls" data-name ="lossfunc">loss function</span>. | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_smooth_function"></span> | |||
[[File:fig_smooth_function.jpg | 500px | thumb | A differentiable function <math>f(\weights)</math> can be approximated locally around a point <math>\weights^{(\itercntr)}</math> using a | |||
hyperplane whose normal vector <math>\mathbf{n} = (\nabla f\big(\weights^{(\itercntr)}\big),-1)</math> is determined by the | |||
gradient <math>\nabla f\big(\weights^{(\itercntr)}\big)</math> <ref name="RudinBookPrinciplesMatheAnalysis"/>. ]] | |||
</div> | |||
Consider a current guess or approximation <math>\weights^{(\itercntr)}</math> for the optimal parameter vector <math>\overline{\weights}</math> \eqref{equ_def_opt_weight}. | |||
We would like to find a new (better) parameter vector <math>\weights^{(\itercntr+1)}</math> that has smaller objective | |||
value <math>f(\weights^{(\itercntr+1)}) < f\big(\weights^{(\itercntr)}\big)</math> than the current guess <math>\weights^{(\itercntr)}</math>. | |||
The approximation \eqref{equ_linear_approx_diff} suggests to choose the next guess <math>\weights = \weights^{(\itercntr+1)}</math> such that <math>\big(\weights^{(\itercntr+1)}-\weights^{(\itercntr)} \big)^{T} \nabla f\big(\weights^{(\itercntr)}\big)</math> is negative. We can | |||
achieve this by the <span class="mw-gls" data-name ="gd">GD</span> step | |||
<span id="equ_def_GD_step"/> | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_GD_step} | |||
\weights^{(\itercntr\!+\!1)} = \weights^{(\itercntr)} - \lrate \nabla f(\weights^{(\itercntr)}) | |||
\end{equation} | |||
</math> | |||
with a sufficiently small <span class="mw-gls" data-name ="stepsize">step size</span> <math>\lrate>0</math>. Figure [[#fig_basic_GD_step|fig_basic_GD_step]] illustrates the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} | |||
which is the elementary computation of gradient based methods. | |||
The <span class="mw-gls" data-name ="stepsize">step size</span> <math>\lrate</math> in \eqref{equ_def_GD_step} must be sufficiently small to ensure the | |||
validity of the linear approximation \eqref{equ_linear_approx_diff}. In the context of ML, | |||
the <span class="mw-gls" data-name ="gd">GD</span> <span class="mw-gls" data-name ="stepsize">step size</span> parameter <math>\lrate</math> is also referred to as <span class="mw-gls mw-gls-first" data-name ="learnrate">learning rate</span>. Indeed, the | |||
<span class="mw-gls" data-name ="stepsize">step size</span> <math>\lrate</math> determines the amount of progress during a <span class="mw-gls" data-name ="gd">GD</span> step towards learning | |||
the optimal parameter vector <math>\overline{\weights}</math>. | |||
We need to emphasize that the interpretation of the <span class="mw-gls" data-name ="stepsize">step size</span> <math>\lrate</math> as a <span class="mw-gls" data-name ="learnrate">learning rate</span> is only | |||
useful when the <span class="mw-gls" data-name ="stepsize">step size</span> is sufficiently small. Indeed, when increasing the <span class="mw-gls" data-name ="stepsize">step size</span> <math>\lrate</math> in \eqref{equ_def_GD_step} | |||
beyond a critical value (that depends on the properties of the objective function <math>f(\weights)</math>), the iterates \eqref{equ_def_GD_step} | |||
move away from the optimal parameter vector <math>\overline{\weights}</math>. Nevertheless, from now on we will consequently | |||
use the term <span class="mw-gls" data-name ="learnrate">learning rate</span> for <math>\lrate</math>. | |||
The idea of <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> is to repeat the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} for a | |||
sufficient number of iterations (repetitions) to obtain a sufficiently accurate approximation of the | |||
optimal parameter vector <math>\overline{\weights}</math> \eqref{equ_def_opt_weight}. It turns out that this | |||
is feasible for a sufficiently small <span class="mw-gls" data-name ="learnrate">learning rate</span> and if the objective function is smooth and convex. | |||
Section [[#equ_sec_gd_step_size | Choosing the Learning Rate ]] discusses precise conditions on the <span class="mw-gls" data-name ="learnrate">learning rate</span> such that | |||
the iterates produced by the <span class="mw-gls" data-name ="gd">GD</span> step converge to the optimum parameter vector, i.e., <math>\lim_{\itercntr \rightarrow \infty} f(\weights^{(\itercntr)}) = f\big(\overline{\weights}\big)</math>. | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_basic_GD_step"></span> | |||
[[File:fig_basic_GD_step.jpg | 500px | thumb | A <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} updates a current guess or approximation <math>\weights^{(\itercntr)}</math> for the optimum parameter vector <math>\overline{\weights}</math> \eqref{equ_def_opt_weight} by adding the correction term <math>-\lrate \nabla f(\weights^{(\itercntr)})</math>. The updated parameter vector <math>\weights^{(\itercntr+1)}</math> is (typically) an improved approximation of the minimizer <math>\overline{\weights}</math>. ]] | |||
</div> | |||
To implement the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} we need to choose a useful <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math>. Moreover, | |||
executing the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} requires to compute the gradient <math>\nabla f(\weights^{(\itercntr)})</math>. | |||
Both tasks can be computationally challenging as discussed in Section [[#equ_sec_gd_step_size | Choosing the Learning Rate ]] and [[#sec_sgd | Stochastic GD ]]. | |||
For the objective function \eqref{equ_obj_emp_risk_GD} obtained in <span class="mw-gls" data-name ="linreg">linear regression</span> and <span class="mw-gls" data-name ="logreg">logistic regression</span>, we can obtain closed-form | |||
expressions for the gradient <math>\nabla f(\weights)</math> (see Section [[#sec_GD_linear_regression | GD for Linear Regression ]] and [[#sec_GD_logistic_regression | GD for Logistic Regression ]]). | |||
In general, we do not have closed-form expressions for the gradient of the objective function | |||
\eqref{equ_obj_emp_risk_GD} arising from a non-linear <span class="mw-gls" data-name ="hypospace">hypothesis space</span>. One example for such | |||
a <span class="mw-gls" data-name ="hypospace">hypothesis space</span> is obtained from a <span class="mw-gls" data-name ="ann">ANN</span>, which is used by deep learning methods (see Section [[guide:B85f6bf6f2#sec_deep_learning | Deep Learning ]]). | |||
The empirical success of deep learning methods might be partially attributed to the availability of | |||
an efficient algorithm for computing the gradient <math>\nabla f(\weights^{(\itercntr)})</math>. This algorithm | |||
is known as \index{back-propagation}back-propagation <ref name="Goodfellow-et-al-2016"/>. | |||
==<span id="equ_sec_gd_step_size"/>Choosing the Learning Rate== | |||
<div class="d-flex justify-content-center"> | |||
[[File:fig_small_large_lrate.jpg | 350px | thumb | Effect of choosing bad values for the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> in the <span class="mw-gls" data-name ="gd">GD</span> step\eqref{equ_def_GD_step}. (a) If the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> in the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} is chosen too small, the iterations make very little progress towards the optimum or even fail to reach the optimum at all. ]] | |||
[[File:fig_small_large_lrate2.jpg | 350px | thumb | Effect of choosing bad values for the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> in the <span class="mw-gls" data-name ="gd">GD</span> step\eqref{equ_def_GD_step}. (b) If the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> is chosen too large, the iterates <math>\weights^{(\itercntr)}</math> might not converge at all (it might happen that <math>f(\weights^{(\itercntr\!+\!1)}) > f(\weights^{(\itercntr)})</math>!). ]] | |||
</div> | |||
The choice of the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> in the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} has a significant impact on | |||
the performance of Algorithm [[#alg:gd_linreg|alg:gd_linreg]]. If we choose the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> too large, the <span class="mw-gls" data-name ="gd">GD</span> | |||
steps \eqref{equ_def_GD_step} diverge (see Figure [[#fig_small_large_lrate|fig_small_large_lrate]]-(b)) and, in turn, Algorithm [[#alg:gd_linreg|alg:gd_linreg]] | |||
fails to deliver a satisfactory approximation of the optimal weights <math>\overline{\weights}</math>. | |||
If we choose the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> too small (see Figure [[#fig_small_large_lrate|fig_small_large_lrate]]-(a)), the | |||
updates \eqref{equ_def_GD_step} make only very little progress towards approximating the optimal | |||
parameter vector <math>\overline{\weights}</math>. In applications that require real-time processing of data streams, it | |||
might be possible to repeat the <span class="mw-gls" data-name ="gd">GD</span> steps only for a moderate number. Thus If the <span class="mw-gls" data-name ="learnrate">learning rate</span> is chosen | |||
too small, Algorithm [[#alg:gd_linreg|alg:gd_linreg]] will fail to deliver a good approximation within an acceptable | |||
number of iterations (runtime of Algorithm [[#alg:gd_linreg|alg:gd_linreg]]). | |||
Finding a (nearly) optimal choice for the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> of <span class="mw-gls" data-name ="gd">GD</span> can be a challenging task. | |||
Many sophisticated approaches for tuning the <span class="mw-gls" data-name ="learnrate">learning rate</span> of <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> have been | |||
proposed <ref name="Goodfellow-et-al-2016"/>{{rp|at=Chapter 8}}. A detailed discussion of these approaches is | |||
beyond the scope of this book. We will instead discuss two sufficient conditions on the <span class="mw-gls" data-name ="learnrate">learning rate</span> | |||
which guarantee the convergence of the <span class="mw-gls" data-name ="gd">GD</span> iterations to the optimum of a smooth and convex objective function | |||
\eqref{equ_obj_emp_risk_GD}. | |||
The first condition applies to an objective function that is <math>\beta</math>-smooth (see \eqref{equ_def_beta_smooth}) with | |||
known constant <math>\beta</math> (not necessarily the smallest constant such that \eqref{equ_def_beta_smooth} holds). Then, | |||
the iterates <math>\weights^{(\itercntr)}</math> generated by the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} with a <span class="mw-gls" data-name ="learnrate">learning rate</span> | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_suff_cond_lrate_beta} | |||
\lrate < 2/\beta, | |||
\end{equation} | |||
</math> | |||
satisfy <ref name="nesterov04">Y. Nesterov. ''Introductory lectures on convex optimization'' volume 87 of ''Applied Optimization''. Kluwer Academic Publishers, Boston, MA, 2004. A basic course</ref>{{rp|at=Thm. 2.1.13}} | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_convergence_rate_inverse_k-GD} | |||
f \big( \weights^{(\itercntr)} \big) - \bar{f} \leq \frac{2(f \big( \weights^{(0)} \big) - \bar{f}) \sqeuclnorm{\weights^{(0)} -\overline{\weights}}}{2\sqeuclnorm{ \weights^{(0)} - \overline{\weights}}+\itercntr(f \big( \weights^{(0)} \big) -\bar{f}) \lrate(2-\beta\lrate)}. | |||
\end{equation} | |||
</math> | |||
The bound \eqref{equ_convergence_rate_inverse_k-GD} not only tells us that <span class="mw-gls" data-name ="gd">GD</span> iterates converge to an | |||
optimal parameter vector but also characterize the convergence speed or rate. The sub-optimality | |||
<math>f \big( \weights^{(\itercntr)} \big) - \min_{\weights} f(\weights)</math> in terms of objective function value | |||
decreases inversely (like “<math>1/\itercntr</math>”) with the number <math>\itercntr</math> of <span class="mw-gls" data-name ="gd">GD</span> steps \eqref{equ_def_GD_step}. | |||
Convergence bounds like \eqref{equ_convergence_rate_inverse_k-GD} can be used to specify a | |||
stopping criterion, i.e., to determine the number of <span class="mw-gls" data-name ="gd">GD</span> steps to be computed (see Section [[#sec_when_to_stop | When To Stop? ]]). | |||
The condition \eqref{equ_suff_cond_lrate_beta} and the bound \eqref{equ_convergence_rate_inverse_k-GD} is only useful | |||
if we can verify <math>\beta</math> smoothness \eqref{equ_def_beta_smooth} assumption for a reasonable constant <math>\beta</math>. | |||
Verifying \eqref{equ_convergence_rate_inverse_k-GD} only for a very large <math>\beta</math> results in the | |||
bound \eqref{equ_convergence_rate_inverse_k-GD} being too loose (pessimistic). When we use a | |||
loose bound \eqref{equ_convergence_rate_inverse_k-GD} to determine the number of <span class="mw-gls" data-name ="gd">GD</span> steps, | |||
we might compute an unnecessary large number of <span class="mw-gls" data-name ="gd">GD</span> steps \eqref{equ_def_GD_step}. | |||
One elegant approach to verify if a differentiable function <math>f(\weights)</math> is <math>\beta</math> smooth \eqref{equ_def_beta_smooth} | |||
is via the Hessian matrix <math> \nabla^{2} f(\weights) \in \mathbb{R}^{\featuredim \times \featuredim}</math> if it exists. | |||
The entries of this Hessian matrix are the second-order partial derivatives <math>\frac{\partial f(\weights)}{\partial \weight_{\featureidx} \partial \weight_{\featureidx'}}</math> | |||
of the function <math>f(\weights)</math>. | |||
Consider an objective function <math>f(\weights)</math> \eqref{equ_obj_emp_risk_GD} that is convex and twice-differentiable | |||
with <span class="mw-gls mw-gls-first" data-name ="psd">positive semi-definite (psd)</span> Hessian <math>\nabla^{2} f(\weights)</math>. If the maximum <span class="mw-gls mw-gls-first" data-name ="eigenvalue">eigenvalue</span> <math>\eigval{\rm max} \big( \nabla^{2} f(\weights) \big)</math> | |||
of the Hessian is upper bounded uniformly (for all <math>\weights</math>) by the constant <math>\beta>0</math>, then <math>f(\weights)</math> is <math>\beta</math> <span class="mw-gls" data-name ="smooth">smooth</span> \eqref{equ_def_beta_smooth} <ref name="CvxBubeck2015"/>. This implies, in turn via \eqref{equ_suff_cond_lrate_beta}, the sufficient condition | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_GD_conv_guarantee} | |||
\lrate \leq \frac{2}{\eigval{\rm max} \big( \nabla^{2} f(\weights) \big) }\mbox{ for all } \vw \in \mathbb{R}^{\featuredim} | |||
\end{equation} | |||
</math> | |||
for the <span class="mw-gls" data-name ="gd">GD</span> <span class="mw-gls" data-name ="learnrate">learning rate</span> such that the <span class="mw-gls" data-name ="gd">GD</span> steps converge to the minimum of the objective function <math>f(\weights)</math>. | |||
It is important to note that the condition \eqref{equ_GD_conv_guarantee} guarantees convergence of the <span class="mw-gls" data-name ="gd">GD</span> steps | |||
for any possible initialization <math>\weights^{(0)}</math>. Note that the usefulness of the condition \eqref{equ_GD_conv_guarantee} | |||
depends on the difficulty of computing the Hessian matrix <math>\nabla^{2} f(\weights)</math>. Section [[#sec_GD_linear_regression | GD for Linear Regression ]] | |||
and Section [[#sec_GD_logistic_regression | GD for Logistic Regression ]] will present closed-form expressions for the Hessian of the objective function \eqref{equ_obj_emp_risk_GD} obtained for <span class="mw-gls" data-name ="linreg">linear regression</span> and <span class="mw-gls" data-name ="logreg">logistic regression</span>. These closed-form expressions involve the feature vectors and labels of the <span class="mw-gls" data-name ="datapoint">data point</span>s in | |||
the <span class="mw-gls mw-gls-first" data-name ="trainset">training set</span> <math>\dataset = \big\{ \big(\featurevec^{(1)},\truelabel^{(1)} \big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)} \big) \big\}</math> used in \eqref{equ_obj_emp_risk_GD}. | |||
While it might be computationally challenging to determine the maximum (in absolute value) <span class="mw-gls" data-name ="eigenvalue">eigenvalue</span> | |||
<math>\eigval{\rm max} \big( \nabla^{2} f(\weights) \big)</math> for arbitrary <math>\weights</math>, it might still be feasible to find an | |||
upper bound <math>U</math> for it. If we know such an upper bound <math>U \geq \eigval{\rm max} \big( \nabla^{2} f(\weights) \big)</math> | |||
(valid for all <math>\weights \in \mathbb{R}^{\featuredim}</math>), the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate =1/U</math> still ensures convergence | |||
of the <span class="mw-gls" data-name ="gd">GD</span> steps \eqref{equ_def_GD_step}. | |||
Up to know we have assumed a fixed (constant) <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> that is used for each repetition of the <span class="mw-gls" data-name ="gd">GD</span> | |||
steps \eqref{equ_def_GD_step}. However, it might be useful to vary or adjust the <span class="mw-gls" data-name ="learnrate">learning rate</span> as the <span class="mw-gls" data-name ="gd">GD</span> | |||
steps \eqref{equ_def_GD_step} proceed. Thus, we might use a different <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate_{\itercntr}</math> for | |||
each iteration <math>\itercntr</math> of \eqref{equ_def_GD_step}. Such a varying <span class="mw-gls" data-name ="learnrate">learning rate</span> is useful for a variant of <span class="mw-gls" data-name ="gd">GD</span> | |||
that uses stochastic approximation (see Section [[#sec_sgd | Stochastic GD ]]). However, we might use a varying <span class="mw-gls" data-name ="learnrate">learning rate</span> also to | |||
avoid the burden of verifying <math>\beta</math> smoothness \eqref{equ_def_beta_smooth} with a tight (small) <math>\beta</math>. | |||
The <span class="mw-gls" data-name ="gd">GD</span> steps \eqref{equ_def_GD_step} with the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate_{\itercntr} \defeq 1/\itercntr</math> converge | |||
to the optimal parameter vector <math>\overline{\weights}</math> as long as we can ensure a bounded gradient | |||
<math>\| \nabla f(\weights) \| \leq U</math> for a sufficiently large neighbourhood of <math>\overline{\weights}</math> <ref name="nesterov04"/>. | |||
==When To Stop?== | |||
One main challenge in the successful application of <span class="mw-gls" data-name ="gd">GD</span> is to decide when to stop iterating | |||
(or repeating) the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step}. Maybe the most simple approach is to monitor | |||
the decrease in the objective function <math>f(\weights^{(\itercntr)})</math> and to stop if the decrease | |||
<math>f(\weights^{(\itercntr-1)})-f(\weights^{(\itercntr)})</math> falls below a threshold. However, the ultimate | |||
goal of a ML method is not to minimize the objective function <math>f(\weights)</math> in \eqref{equ_obj_emp_risk_GD}. | |||
Indeed, the objective function represents the average loss of a hypothesis <math>h^{(\weights)}</math> | |||
incurred on a <span class="mw-gls" data-name ="trainset">training set</span>. However, the ultimate goal of a ML method is to learn a parameter vector | |||
<math>\weights</math> such that the resulting hypothesis accurately predicts any <span class="mw-gls" data-name ="datapoint">data point</span>, including those | |||
outside the <span class="mw-gls" data-name ="trainset">training set</span>. | |||
We will see in Chapter [[guide:07ad9c2de8 | Model Validation and Selection ]] how to use validation | |||
techniques to probe a hypothesis outside the <span class="mw-gls" data-name ="trainset">training set</span>. These validation techniques provide a | |||
validation error <math>\tilde{f}(\weights)</math> that estimates the average loss of a hypothesis with parameter vector <math>\weights</math>. | |||
Early stopping techniques monitor the validation error <math>\tilde{f}(\weights^{(\itercntr)})</math> as the <span class="mw-gls" data-name ="gd">GD</span> iterations <math>\itercntr</math> | |||
proceed to decide when to stop iterating. | |||
Another possible stopping criterion is to use a fixed number of iterations or <span class="mw-gls" data-name ="gd">GD</span> steps. This fixed number of iterations | |||
can be chosen based on convergence bounds such as \eqref{equ_convergence_rate_inverse_k-GD} in order to | |||
guarantee a prescribed sub-optimality of the final iterate <math>\weights^{(\itercntr)}</math>. A slightly more convenient | |||
convergence bound can be obtained from \eqref{equ_convergence_rate_inverse_k-GD} when using the | |||
the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate = 1/\beta</math> in the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} <ref name="CvxBubeck2015"/>, | |||
<math display="block"> | |||
\begin{equation} | |||
f \big( \weights^{(\itercntr)} \big) -\bar{f} \leq \frac{2\beta \sqeuclnorm{\weights^{(0)} -\overline{\weights}}}{\itercntr} \mbox{ for } \itercntr=1,2,\ldots. | |||
\end{equation} | |||
</math> | |||
==<span id="sec_GD_linear_regression"/>GD for Linear Regression== | |||
We now present a gradient based method for learning the parameter vector for a linear hypothesis (see [[guide:013ef4b5cd#equ_lin_hypospace|equ_lin_hypospace]]) | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_lin_pred_GD} | |||
h^{(\weights)}(\featurevec) = \weights^{T} \featurevec. | |||
\end{equation} | |||
</math> | |||
The <span class="mw-gls" data-name ="erm">ERM</span> principle tells us to choose the parameter vector <math>\weights</math> in \eqref{equ_def_lin_pred_GD} | |||
by minimizing the average [[guide:B85f6bf6f2#equ_squared_loss|squared error loss]] | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_cost_linreg} | |||
\emperror(h^{(\weights)}| \dataset) \stackrel{\eqref{eq_def_ERM_weight}}{=} (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} (\truelabel^{(\sampleidx)} - \weights^{T} \featurevec^{(\sampleidx)})^{2}. | |||
\end{equation} | |||
</math> | |||
The average squared error loss \eqref{equ_def_cost_linreg} is computed by applying the predictor <math>h^{(\weights)}(\featurevec)</math> | |||
to labeled <span class="mw-gls" data-name ="datapoint">data point</span>s in a <span class="mw-gls" data-name ="trainset">training set</span> <math>\dataset=\{ (\featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}</math>. | |||
An optimal parameter vector <math>\overline{\weights}</math> for \eqref{equ_def_lin_pred_GD} is obtained as | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_smooth_problem_linreg} | |||
\overline{\weights} = \argmin_{\weights \in \mathbb{R}^{\featuredim}} f(\weights) \mbox{ with } f(\weights) = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big(\truelabel^{(\sampleidx)} - \weights^{T} \featurevec^{(\sampleidx)}\big)^{2}. | |||
\end{equation} | |||
</math> | |||
The objective function <math>f(\weights)</math> in \eqref{equ_smooth_problem_linreg} is convex and smooth. | |||
We can therefore use <span class="mw-gls" data-name ="gd">GD</span> \eqref{equ_def_GD_step} to solve \eqref{equ_smooth_problem_linreg} | |||
iteratively, i.e., by constructing a sequence of parameter vectors that converge to an optimal parameter vector <math>\overline{\weights}</math>. | |||
To implement <span class="mw-gls" data-name ="gd">GD</span>, we need to compute the gradient <math>\nabla f(\weights)</math>. | |||
The gradient of the objective function in \eqref{equ_smooth_problem_linreg} is given by | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_gradient_linear_regression} | |||
\nabla f(\weights) = -(2/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big(\truelabel^{(\sampleidx)} - \weights^{T} \featurevec^{(\sampleidx)} \big) \featurevec^{(\sampleidx)}. | |||
\end{equation} | |||
</math> | |||
By inserting \eqref{equ_gradient_linear_regression} into the basic <span class="mw-gls" data-name ="gd">GD</span> iteration \eqref{equ_def_GD_step}, we obtain Algorithm [[#alg:gd_linreg|alg:gd_linreg]]. | |||
<proc label="Linear regression via GD" id="alg:gd_linreg"> | |||
'''Input:''' dataset <math>\dataset=\{ (\featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}</math> ; <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate >0</math>. | |||
'''Initialize:''' set <math>\weights^{(0)}\!\defeq\!\mathbf{0}</math>; set iteration counter <math>\itercntr\!\defeq\!0</math> | |||
<ul style="list-style:numeric"> | |||
<li>'''repeat''' </li> | |||
<li class="ps-3"> <math>\itercntr \defeq \itercntr +1</math> (increase iteration counter) </li> | |||
<li class="ps-3"><math>\weights^{(\itercntr)} \defeq \weights^{(\itercntr\!-\!1)} + \lrate (2/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big(\truelabel^{(\sampleidx)} - \big(\weights^{(\itercntr\!-\!1)}\big)^{T} \featurevec^{(\sampleidx)}\big) \featurevec^{(\sampleidx)}</math> (do a GD step \eqref{equ_def_GD_step})</li> | |||
<li>'''until''' stopping criterion met</li> | |||
</ul> | |||
'''Output:''' <math>\weights^{(\itercntr)}</math> (which approximates <math>\overline{\weights}</math> in \eqref{equ_smooth_problem_linreg}) | |||
</proc> | |||
Let us have a closer look on the update in step <math>3</math> of Algorithm [[#alg:gd_linreg|alg:gd_linreg]], which is | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_update_gd_linreg} | |||
\weights^{(\itercntr)} \defeq \weights^{(\itercntr\!-\!1)} + \lrate (2/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big(\truelabel^{(\sampleidx)} - \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)} \big) \featurevec^{(\sampleidx)}. | |||
\end{equation} | |||
</math> | |||
The update \eqref{equ_update_gd_linreg} has an appealing form as it amounts to correcting the previous | |||
guess (or approximation) <math>\weights^{(\itercntr\!-\!1)}</math> for the optimal parameter vector <math>\overline{\weights}</math> | |||
by the correction term | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_corr_term_linreg} | |||
(2\lrate/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \underbrace{(\truelabel^{(\sampleidx)} - \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)})}_{e^{(\sampleidx)}} \featurevec^{(\sampleidx)}. | |||
\end{equation} | |||
</math> | |||
The correction term \eqref{equ_corr_term_linreg} is a weighted average of the feature vectors <math>\featurevec^{(\sampleidx)}</math> using weights <math>(2\lrate/\samplesize) \cdot e^{(\sampleidx)}</math>. | |||
These weights consist of the global factor <math>(2\lrate/\samplesize)</math> (that applies equally to all | |||
feature vectors <math>\featurevec^{(\sampleidx)}</math>) and a sample-specific factor <math>e^{(\sampleidx)} = (\truelabel^{(\sampleidx)} - \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)})</math>, which is the prediction (approximation) error obtained by the linear predictor <math>h^{(\weights^{(\itercntr\!-\!1)})}(\featurevec^{(\sampleidx)}) = \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)}</math> when predicting the label <math>\truelabel^{(\sampleidx)}</math> from the features <math>\featurevec^{(\sampleidx)}</math>. | |||
We can interpret the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_update_gd_linreg} as an instance of “learning by trial | |||
and error”. Indeed, the <span class="mw-gls" data-name ="gd">GD</span> step amounts to first “trying out” (trial) the predictor <math>h(\featurevec^{(\sampleidx)}) = \big(\weights^{(\itercntr\!-\!1)})^{T}\featurevec^{(\sampleidx)}</math>. The predicted values are then used to correct the weight | |||
vector <math>\weights^{(\itercntr\!-\!1)}</math> according to the error <math>e^{(\sampleidx)} = \truelabel^{(\sampleidx)} - \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)}</math>. | |||
The choice of the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> used for Algorithm [[#alg:gd_linreg|alg:gd_linreg]] can be based on the condition \eqref{equ_GD_conv_guarantee} | |||
with the Hessian <math>\nabla^{2} f(\weights)</math> of the objective function <math>f(\weights)</math> underlying <span class="mw-gls" data-name ="linreg">linear regression</span> (see \eqref{equ_smooth_problem_linreg}). | |||
This Hessian is given explicitly as | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_hessian_linreg} | |||
\nabla^{2} f(\weights) = (1/\samplesize) \featuremtx^{T} \featuremtx, | |||
\end{equation} | |||
</math>with the feature matrix <math>\featuremtx=\big(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)}\big)^{T} \in \mathbb{R}^{\samplesize \times \featuredim}</math> (see [[guide:2c0f621d22#equ_def_vec_matrix|feature matrix ]]). Note that the Hessian \eqref{equ_hessian_linreg} does not depend on the parameter vector <math>\weights</math>. | |||
Comparing \eqref{equ_hessian_linreg} with \eqref{equ_GD_conv_guarantee}, one particular strategy for choosing the <span class="mw-gls" data-name ="learnrate">learning rate</span> in Algorithm [[#alg:gd_linreg|alg:gd_linreg]] is to (i) compute the matrix product <math> \featuremtx^{T} \featuremtx</math>, (ii) compute the maximum <span class="mw-gls" data-name ="eigenvalue">eigenvalue</span> <math>\eigval{\rm max}\big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)</math> of this product and (iii) set the <span class="mw-gls" data-name ="learnrate">learning rate</span> to <math>\lrate =1/\eigval{\rm max} \big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)</math>. | |||
While it might be challenging to compute the maximum <span class="mw-gls" data-name ="eigenvalue">eigenvalue</span> <math>\eigval{\rm max} \big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)</math>, it might be easier to find an upper bound <math>U</math> for it.{{efn | The problem of computing a full eigenvalue decomposition of <math>\featuremtx^{T} \featuremtx</math> has essentially the same complexity as ERM via directly solving [[guide:2c0f621d22#equ_zero_gradient_lin_reg|equ_zero_gradient_lin_reg]], which we want to avoid by using the “cheaper” GD Algorithm [[#alg:gd_linreg|alg:gd_linreg]].}} | |||
Given such an upper bound <math>U \geq \eigval{\rm max} \big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)</math>, | |||
the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate =1/U</math> still ensures convergence of the <span class="mw-gls" data-name ="gd">GD</span> steps. Consider a dataset <math>\{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})\}_{\sampleidx=1}^{\samplesize}</math> with | |||
normalized features, i.e., <math>\| \featurevec^{(\sampleidx)}\| = 1</math> for all <math>\sampleidx =1,\ldots,\samplesize</math>. | |||
This implies, in turn, the upper bound <math>U= 1</math>, i.e., <math> 1 \geq \lambda_{\rm max} \big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)</math>. | |||
We can then ensure convergence of the iterates <math>\weights^{(\itercntr)}</math> (see \eqref{equ_update_gd_linreg}) by | |||
choosing the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate =1</math>. | |||
'''Time-Data Tradeoffs.''' | |||
The number of <span class="mw-gls" data-name ="gd">GD</span> steps required by Algorithm [[#alg:gd_linreg|alg:gd_linreg]] to ensure a prescribed | |||
sub-optimality depends crucially on the <span class="mw-gls mw-gls-first" data-name ="condnr">condition number</span> of <math>\featuremtx^{T} \featuremtx</math>. What can we say about the <span class="mw-gls" data-name ="condnr">condition number</span>? In general, we have not control over this quantity as the matrix <math>\featuremtx</math> consists of the feature vectors of arbitrary <span class="mw-gls" data-name ="datapoint">data point</span>s. However, it is often useful to model the feature vectors as realizations of <span class="mw-gls mw-gls-first" data-name ="iid">independent and identically distributed (iid)</span> random vectors. It is then possible to bound the probability of the feature matrix having a sufficiently small <span class="mw-gls" data-name ="condnr">condition number</span>. These bounds can then be used to choose the step-size such that convergence is guaranteed with sufficiently large probability. The usefulness of these bounds typically | |||
depends on the ratio <math>\featurelen/\samplesize</math>. For increasing sample-size, these bounds allow | |||
to use larger step-sizes and, in turn, result in faster convergence of GD algorithm. Thus, we obtain a trade-off between the runtime of Algorithm [[#alg:gd_linreg|alg:gd_linreg]] and the number of <span class="mw-gls" data-name ="datapoint">data point</span>s that we feed into it <ref name="Oymak2018">S. Oymak, B. Recht, and M. Soltanolkotabi. Sharp time--data tradeoffs for linear inverse problems. ''IEEE Transactions on Information Theory'' 64(6):4129--4158, June | |||
2018</ref>. | |||
==<span id="sec_GD_logistic_regression"/>GD for Logistic Regression== | |||
<span class="mw-gls mw-gls-first" data-name ="logreg">Logistic regression</span> learns a linear hypothesis <math>h^{(\weights)}</math> that is used to classify <span class="mw-gls" data-name ="datapoint">data point</span>s by predicting their binary label. The quality of such a <span class="mw-gls mw-gls-first" data-name ="linclass">linear classifier</span> is measured by the [[guide:B85f6bf6f2#equ_log_loss | <span class="mw-gls" data-name ="logloss">logistic loss</span>]]. | |||
The <span class="mw-gls" data-name ="erm">ERM</span> principle suggest to learn the parameter vector <math>\weights</math> by minimizing the average [[guide:013ef4b5cd#equ_def_emp_risk_logreg|<span class="mw-gls" data-name ="logloss">logistic loss</span>]] obtained for a <span class="mw-gls" data-name ="trainset">training set</span> <math>\dataset= \{ (\featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}</math>. | |||
The <span class="mw-gls" data-name ="trainset">training set</span> consists of <span class="mw-gls" data-name ="datapoint">data point</span>s with features <math>\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}</math> | |||
and binary labels <math>\truelabel^{(\sampleidx)} \in \{-1,1\}</math>. | |||
We can rewrite <span class="mw-gls" data-name ="erm">ERM</span> for <span class="mw-gls" data-name ="logreg">logistic regression</span> as the optimization problem | |||
<math display="block"> | |||
\begin{align} | |||
\overline{\weights}& = \argmin_{\weights \in \mathbb{R}^{\featuredim}} f(\weights) \nonumber \\ | |||
\mbox{ with } f(\weights) & = \label{equ_smooth_problem_logeg}(1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \log\big( 1\!+\!\exp \big( - \truelabel^{(\sampleidx)} \weights^{T} \featurevec^{(\sampleidx)} \big)\big). | |||
\end{align} | |||
</math> | |||
The objective function <math>f(\weights)</math> is differentiable and therefore we can use <span class="mw-gls" data-name ="gd">GD</span> \eqref{equ_def_GD_step} | |||
to solve \eqref{equ_smooth_problem_logeg}. We can write down the <span class="mw-gls" data-name ="gradient">gradient</span> of the objective function in \eqref{equ_smooth_problem_logeg} in | |||
closed-form as | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_gradient_logistic_regression} | |||
\nabla f(\weights) = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \frac{-\truelabel^{(\sampleidx)}}{1 + \exp ( \truelabel^{(\sampleidx)} \weights^{T} \featurevec^{(\sampleidx)})} \featurevec^{(\sampleidx)}. | |||
\end{equation} | |||
</math> | |||
Inserting \eqref{equ_gradient_logistic_regression} into the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} yields Algorithm [[#alg:gd_logreg|alg:gd_logreg]]. | |||
<proc label="Logistic regression via GD" id="alg:gd_logreg"> | |||
'''Input:''' labeled dataset <math>\dataset=\{ (\featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}</math> containing feature vectors | |||
<math>\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}</math> and labels <math>\truelabel^{(\sampleidx)} \in \mathbb{R}</math>; <span class="mw-gls" data-name ="gd">GD</span> learning rate <math>\lrate >0</math>. | |||
'''Initialize:''' set <math>\weights^{(0)}\!\defeq\!\mathbf{0}</math>; set iteration counter <math>\itercntr\!\defeq\!0</math> | |||
<ul style="list-style-type:decimal"> | |||
<li> | |||
'''repeat''' | |||
</li><li class="ps-3"> <math>\itercntr\!\defeq\! \itercntr\!+\!1</math> (increase iteration counter) | |||
</li><li class="ps-3"> <span id="equ_step_updat_logreg_GD"/> <math>\weights^{(\itercntr)} \defeq \weights^{(\itercntr\!-\!1)}\!+\!\lrate (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \frac{\truelabel^{(\sampleidx)}}{1\!+\!\exp \big( \truelabel^{(\sampleidx)} \big(\weights^{(\itercntr\!-\!1)}\big)^{T} \featurevec^{(\sampleidx)}\big)} \featurevec^{(\sampleidx)}</math> (do a <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step})</li> | |||
<li> | |||
'''until''' stopping criterion met | |||
</li></ul> | |||
'''Output:''' <math>\weights^{(\itercntr)}</math>, which approximates a solution <math>\overline{\weights}</math> of \eqref{equ_smooth_problem_logeg}) | |||
</proc> | |||
Let us have a closer look on the update in step [[#equ_step_updat_logreg_GD | equ_step_updat_logreg_GD]] of Algorithm [[#alg:gd_logreg|alg:gd_logreg]]. This step amounts to computing | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_update_logreg_GD} | |||
\weights^{(\itercntr)} \defeq \weights^{(\itercntr\!-\!1)} + \lrate (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \frac{\truelabel^{(\sampleidx)}}{1 + \exp \big( \truelabel^{(\sampleidx)} \big( \vw^{(\itercntr\!-\!1)} \big)^{T} \featurevec^{(\sampleidx)}\big)} \featurevec^{(\sampleidx)}. | |||
\end{equation} | |||
</math> | |||
Similar to the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_update_gd_linreg} for <span class="mw-gls" data-name ="linreg">linear regression</span>, also the <span class="mw-gls" data-name ="gd">GD</span> step | |||
\eqref{equ_update_logreg_GD} for <span class="mw-gls" data-name ="logreg">logistic regression</span> can be interpreted as an implementation of the | |||
trial-and-error principle. Indeed, \eqref{equ_update_logreg_GD} corrects the previous guess (or approximation) <math>\weights^{(\itercntr\!-\!1)}</math> for | |||
the optimal parameter vector <math>\overline{\weights}</math> by the correction term | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_correction_logreg_GD} | |||
(\lrate/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \underbrace{ \frac{\truelabel^{(\sampleidx)}}{1 + \exp ( \truelabel^{(\sampleidx)} \weights^{T} \featurevec^{(\sampleidx)})}}_{e^{(\sampleidx)}} \featurevec^{(\sampleidx)}. | |||
\end{equation} | |||
</math> | |||
The correction term \eqref{equ_correction_logreg_GD} is a weighted average of the feature vectors <math>\featurevec^{(\sampleidx)}</math>. | |||
The feature vector <math>\featurevec^{(\sampleidx)}</math> is weighted by the factor <math>(\lrate/\samplesize) \cdot e^{(\sampleidx)}</math>. | |||
These weighting factors are a product of the global factor <math>(\lrate/\samplesize)</math> that applies equally to all | |||
feature vectors <math>\featurevec^{(\sampleidx)}</math>. The global factor is multiplied by a <span class="mw-gls" data-name ="datapoint">data point</span>-specific factor | |||
<math>e^{(\sampleidx)} = \frac{\truelabel^{(\sampleidx)}}{1 + \exp ( \truelabel^{(\sampleidx)} \weights^{T} \featurevec^{(\sampleidx)})}</math>, which | |||
quantifies the error of the classifier <math>h^{(\weights^{(\itercntr\!-\!1)})}(\featurevec^{(\sampleidx)}) = \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)}</math> for a single <span class="mw-gls" data-name ="datapoint">data point</span> with true label <math>\truelabel^{(\sampleidx)} \in \{-1,1\}</math> and features <math>\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}</math>. | |||
We can use the sufficient condition \eqref{equ_GD_conv_guarantee} for the convergence of <span class="mw-gls" data-name ="gd">GD</span> steps | |||
to guide the choice of the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> in Algorithm [[#alg:gd_logreg|alg:gd_logreg]]. To apply condition | |||
\eqref{equ_GD_conv_guarantee}, we need to determine the Hessian <math>\nabla^{2} f(\weights)</math> matrix of the | |||
objective function <math>f(\weights)</math> underlying <span class="mw-gls" data-name ="logreg">logistic regression</span> (see \eqref{equ_smooth_problem_logeg}). | |||
Some basic calculus reveals (see <ref name="hastie01statisticallearning">T. Hastie, R. Tibshirani, and J. Friedman. ''The Elements of Statistical Learning'' Springer Series in Statistics. Springer, New York, NY, USA, 2001</ref>{{rp|at=Ch. 4.4.}}) | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_hessian_logreg} | |||
\nabla^{2} f(\weights) = (1/\samplesize) \mX^{T} \mD \featuremtx. | |||
\end{equation} | |||
</math> | |||
Here, we used the feature matrix <math>\featuremtx=\big(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)}\big)^{T} \in \mathbb{R}^{\samplesize \times \featuredim}</math> (see [[guide:2c0f621d22#equ_def_vec_matrix|feature matrix ]]) and the diagonal matrix <math>\mD = {\rm diag} \{d_{1},\ldots,d_{\samplesize}\} \in \mathbb{R}^{\samplesize \times \samplesize}</math> with diagonal elements | |||
<math display="block"> | |||
\begin{equation} | |||
d_{\sampleidx} = \frac{1}{1+\exp(-\weights^{T} \featurevec^{(\sampleidx)})} \bigg(1- \frac{1}{1+\exp(-\weights^{T} \featurevec^{(\sampleidx)})} \bigg). \label{equ_diag_entries_log_reg} | |||
\end{equation} | |||
</math> | |||
We highlight that, in contrast to the Hessian \eqref{equ_hessian_linreg} of the objective function | |||
arising in linear regression, the Hessian \eqref{equ_hessian_logreg} of <span class="mw-gls" data-name ="logreg">logistic regression</span> varies | |||
with the parameter vector <math>\weights</math>. This makes the analysis of Algorithm [[#alg:gd_logreg|alg:gd_logreg]] and the | |||
optimal choice for the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate</math> more difficult compared to Algorithm [[#alg:gd_linreg|alg:gd_linreg]]. | |||
At least, we can ensure convergence of \eqref{equ_update_logreg_GD} (towards a solution | |||
of \eqref{equ_smooth_problem_logeg}) for the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate=1</math> if we normalize feature vectors | |||
such that <math>\| \featurevec^{(\sampleidx)} \|=1</math>. This follows from the fact the diagonal entries | |||
\eqref{equ_diag_entries_log_reg} take values in the interval <math>[0,1]</math>. | |||
==<span id="sec_data_normalization"/>Data Normalization== | |||
The number of <span class="mw-gls" data-name ="gd">GD</span> steps \eqref{equ_def_GD_step} required to reach the minimum (within a prescribed accuracy) | |||
of the objective [[guide:2c0f621d22#equ_def_cost_MSE| function]] depends crucially on the <span class="mw-gls" data-name ="condnr">condition number</span> <ref name="CvxBubeck2015"/><ref name="JungFixedPoint">A. Jung. A fixed-point of view on gradient methods for big data. ''Frontiers in Applied Mathematics and Statistics'' 3, 2017</ref> | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_condition_number} | |||
\kappa( \featuremtx^{T} \featuremtx) \defeq \eigval{\rm max}/\eigval{\rm min}. | |||
\end{equation} | |||
</math> | |||
Here, we use the largest and smallest <span class="mw-gls" data-name ="eigenvalue">eigenvalue</span> of the matrix <math>\featuremtx^{T} \featuremtx</math>, denoted as <math> \eigval{\rm max}</math> and <math>\eigval{\rm min}</math>, respectively. The <span class="mw-gls" data-name ="condnr">condition number</span> \eqref{equ_def_condition_number} is only well-defined if the columns of the [[guide:2c0f621d22#equ_def_vec_matrix|feature matrix ]] <math>\featuremtx</math> (which are the feature vectors <math>\featurevec^{(\sampleidx)}</math>), are linearly independent. In this case the <span class="mw-gls" data-name ="condnr">condition number</span> is lower bounded as <math>1 \leq \kappa( \featuremtx^{T} \featuremtx)</math>. | |||
It can be shown that the <span class="mw-gls" data-name ="gd">GD</span> steps \eqref{equ_def_GD_step} converge faster for smaller <span class="mw-gls" data-name ="condnr">condition number</span> <math>\kappa( \featuremtx^{T} \featuremtx)</math> <ref name="JungFixedPoint"/>. Thus, <span class="mw-gls" data-name ="gd">GD</span> will be faster for datasets with a feature matrix <math>\featuremtx</math> such that <math>\kappa( \featuremtx^{T} \featuremtx) \approx 1</math>. | |||
It is therefore often beneficial to pre-process the feature vectors using a normalization (or standardization) procedure as detailed in Algorithm [[#alg_reshaping|alg_reshaping]]. | |||
<proc label="“Data Normalization”" id="alg_reshaping"> | |||
'''Input:''' labeled dataset <math>\dataset = \{(\featurevec^{(\sampleidx)},y^{(\sampleidx)})\}_{\sampleidx=1}^{\samplesize}</math> | |||
<ul style="list-style:numeric"><li> remove sample means <math>\widehat{\featurevec}=(1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \featurevec^{(\sampleidx)}</math> from features, i.e., | |||
<math display="block"> | |||
\begin{equation} | |||
\nonumber | |||
\featurevec^{(\sampleidx)} \defeq \featurevec^{(\sampleidx)} - \widehat{\featurevec} \mbox{ for } \sampleidx=1,\ldots,\samplesize | |||
\end{equation} | |||
</math> | |||
</li><li> normalise features to have unit variance, | |||
<math display="block"> | |||
\begin{equation} | |||
\nonumber | |||
\hat{\feature}^{(\sampleidx)}_{\featureidx} \defeq \feature^{(\sampleidx)}_{\featureidx}/ \hat{\sigma} \mbox{ for } \featureidx=1,\ldots,\featuredim \mbox{ and } \sampleidx=1,\ldots,\samplesize | |||
\end{equation} | |||
</math> | |||
with the empirical (sample) variance <math>\hat{\sigma}_{\featureidx}^{2} =(1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big( \feature^{(\sampleidx)}_{\featureidx} \big)^{2}</math> | |||
</li></ul> | |||
'''Output:''' normalized feature vectors <math>\{\hat{\featurevec}^{(\sampleidx)}\}_{\sampleidx=1}^{\samplesize}</math> | |||
</proc> | |||
Algorithm [[#alg_reshaping|alg_reshaping]] transforms the original feature vectors <math>\featurevec^{(\sampleidx)}</math> into new feature vectors <math>\widehat{\featurevec}^{(\sampleidx)}</math> such that the new feature matrix <math>\widehat{\featuremtx} = (\widehat{\featurevec}^{(1)},\ldots,\widehat{\featurevec}^{(\samplesize)})^{T}</math> is better conditioned than the original feature matrix, i.e., <math>\kappa( \widehat{\featuremtx}^{T} \widehat{\featuremtx}) < \kappa( \featuremtx^{T} \featuremtx)</math>. | |||
==<span id="sec_sgd"/>Stochastic GD== | |||
Consider the <span class="mw-gls" data-name ="gd">GD</span> steps \eqref{equ_def_GD_step} for minimizing the <span class="mw-gls mw-gls-first" data-name ="emprisk">empirical risk</span> \eqref{equ_obj_emp_risk_GD}. | |||
The gradient <math>\nabla f(\weights)</math> of the objective function \eqref{equ_obj_emp_risk_GD} has a particular structure. | |||
Indeed, this gradient is a sum | |||
<math display="block"> | |||
\begin{equation} | |||
\label{eq_gradient_sum} | |||
\nabla f(\weights) = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \nabla f_{\sampleidx}(\vw) \mbox{ with } f_{\sampleidx}(\weights) \defeq \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h^{(\weights)}}. | |||
\end{equation} | |||
</math> | |||
Each component of the sum \eqref{eq_gradient_sum} corresponds to one particular <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
<math>(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})</math>, for <math>\sampleidx=1,\ldots,\samplesize</math>. | |||
We need to compute a sum of the form \eqref{eq_gradient_sum} for each new <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step}. | |||
Computing the sum in \eqref{eq_gradient_sum} can be computationally challenging for at least | |||
two reasons. First, computing the sum is challenging for very large datasets with <math>\samplesize</math> | |||
in the order of billions. Second, for datasets which are stored in different data | |||
centres located all over the world, the summation would require a huge amount of | |||
network resources. Moreover, the finite transmission rate of communication networks | |||
limits the rate by which the <span class="mw-gls" data-name ="gd">GD</span> steps \eqref{equ_def_GD_step} can be executed. | |||
The idea of <span class="mw-gls mw-gls-first" data-name ="stochGD">stochastic gradient descent (SGD)</span> is to replace the exact | |||
gradient <math>\nabla f(\weights)</math> \eqref{eq_gradient_sum} by an approximation that is easier | |||
to compute than a direct evaluation of \eqref{eq_gradient_sum}. The word “stochastic” | |||
in the name <span class="mw-gls" data-name ="stochGD">SGD</span> hints already at the use of a stochastic approximation <math>\noisygrad(\weights) | |||
\approx \nabla f(\weights)</math>. It turns out that using a <span class="mw-gls" data-name ="gradient">gradient</span> approximation <math>\noisygrad(\weights)</math> | |||
can result in significant savings in computational complexity while incurring a graceful degradation | |||
in the overall optimization accuracy. The optimization accuracy (distance to minimum of <math>f(\weights)</math>) | |||
depends crucially on the “<span class="mw-gls" data-name ="gradient">gradient</span> noise” | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_gradient_noise_generic} | |||
\varepsilon \defeq \nabla f(\weights)- \noisygrad(\weights). | |||
\end{equation} | |||
</math> | |||
The elementary step of most <span class="mw-gls" data-name ="stochGD">SGD</span> methods is obtained from the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} | |||
by replacing the exact <span class="mw-gls" data-name ="gradient">gradient</span> <math>\nabla f(\weights)</math> with some stochastic approximation <math>\noisygrad(\weights)</math>, | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_SGD_update} | |||
\weights^{(\itercntr\!+\!1)} = \weights^{(\itercntr)} - \lrate_{\itercntr} \noisygrad \big( \weights^{(\itercntr)} \big), | |||
\end{equation} | |||
</math> | |||
As the notation in \eqref{equ_SGD_update} indicates, <span class="mw-gls" data-name ="stochGD">SGD</span> methods use a <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate_{\itercntr}</math> | |||
that varies between different iterations. | |||
To avoid accumulation of the <span class="mw-gls" data-name ="gradient">gradient</span> noise \eqref{equ_def_gradient_noise_generic} during the <span class="mw-gls" data-name ="stochGD">SGD</span> | |||
updates \eqref{equ_SGD_update}, <span class="mw-gls" data-name ="stochGD">SGD</span> methods typically decrease the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate_{\itercntr}</math> as | |||
the iterations proceed. The precise dependence of the <span class="mw-gls" data-name ="learnrate">learning rate</span> <math>\lrate_{\itercntr}</math> on the iteration index <math>\itercntr</math> | |||
is referred to as a <span class="mw-gls" data-name ="learnrate">learning rate</span> schedule <ref name="Goodfellow-et-al-2016"/>{{rp|at=Chapter 8}}. | |||
One possible choice for the <span class="mw-gls" data-name ="learnrate">learning rate</span> schedule is <math>\lrate_{\itercntr}\!\defeq\!1/\itercntr</math> <ref name="Murata98astatistical">N. Murata. A statistical study on on-line learning. In D. Saad, editor, ''On-line Learning in Neural Networks'' pages 63--92. Cambridge University Press, New York, NY, USA, 1998</ref>. [[exercise:0536da54e7|Exercise]] discusses conditions on the <span class="mw-gls" data-name ="learnrate">learning rate</span> schedule that guarantee convergence of the updates <span class="mw-gls" data-name ="stochGD">SGD</span> to the minimum of <math>f(\weights)</math>. | |||
The approximate (“noisy”) gradient <math>\noisygrad(\weights)</math> can be obtained by different randomization strategies. | |||
The most basic form of <span class="mw-gls" data-name ="stochGD">SGD</span> constructs the gradient approximation <math>\noisygrad(\weights)</math> by replacing the sum \eqref{eq_gradient_sum} with a randomly selected component, | |||
<math display="block"> | |||
\begin{equation} | |||
\noisygrad(\weights) \defeq \nabla f_{\hat{\sampleidx}}(\weights). | |||
\end{equation} | |||
</math> | |||
The index <math>\hat{\sampleidx}</math> is chosen randomly from the set <math>\{1,\ldots,\samplesize\}</math>. The resulting <span class="mw-gls mw-gls-first" data-name ="stochGD">Stochastic gradient descent (SGD)</span> method then repeats the update | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_SGD_update_basic_form} | |||
\weights^{(\itercntr\!+\!1)} = \weights^{(\itercntr)} - \lrate \nabla f_{\hat{\sampleidx}_{\itercntr}}(\weights^{(\itercntr)}), | |||
\end{equation} | |||
</math> | |||
sufficiently often. Every update \eqref{equ_SGD_update_basic_form} uses a “fresh” randomly chosen (drawn) index <math>\hat{\sampleidx}_{\itercntr}</math>. Formally, the indices <math>\hat{\sampleidx}_{\itercntr}</math> are realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls mw-gls-first" data-name ="rv">random variable (RV)</span>s whose common <span class="mw-gls mw-gls-first" data-name ="probdist">probability distribution</span> is the uniform distribution over the index set <math>\{1,\ldots,\samplesize\}</math>. | |||
Note that \eqref{equ_SGD_update_basic_form} replaces the summation over the <span class="mw-gls" data-name ="trainset">training set</span> during the <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step} by randomly selecting a single component of this sum. | |||
The resulting savings in computational complexity can be significant when the <span class="mw-gls" data-name ="trainset">training set</span> consists | |||
of a large number of <span class="mw-gls" data-name ="datapoint">data point</span>s that might be stored in a distributed fashion (in the “cloud”). | |||
The saving in computational complexity of <span class="mw-gls" data-name ="stochGD">SGD</span> comes at the cost of introducing a non-zero | |||
gradient noise | |||
<math display="block"> | |||
\begin{align} | |||
\varepsilon_{\itercntr} & \stackrel{\eqref{equ_def_gradient_noise_generic}}{=} \nabla f( \weights^{(\itercntr)} ) - \noisygrad \big( \weights^{(\itercntr)} \big) \nonumber \\ | |||
& = \label{equ_gradient_noise_simple_form}\nabla f( \weights^{(\itercntr)} ) - \nabla f_{\hat{\sampleidx}_{\itercntr}}(\weights). | |||
\end{align} | |||
</math> | |||
'''Mini-Batch <span class="mw-gls" data-name ="stochGD">SGD</span>.''' Let us now discuss a variant of <span class="mw-gls" data-name ="stochGD">SGD</span> that tries to reduce the approximation error (gradient noise) \eqref{equ_gradient_noise_simple_form} arising in the <span class="mw-gls" data-name ="stochGD">SGD</span> step \eqref{equ_SGD_update_basic_form}. The idea behind this variant, referred to as mini-batch <span class="mw-gls" data-name ="stochGD">SGD</span>, is quite simple. Instead of using only a single randomly selected component <math>\nabla f_{\sampleidx}(\weights)</math> (see \eqref{eq_gradient_sum}) for constructing a gradient | |||
approximation, mini-batch <span class="mw-gls" data-name ="stochGD">SGD</span> uses several randomly chosen components. | |||
We summarize mini-batch <span class="mw-gls" data-name ="stochGD">SGD</span> in Algorithm [[#alg:minibatch_gd|alg:minibatch_gd]] which requires an integer batch size <math>\batchsize</math> as input parameter. Algorithm [[#alg:minibatch_gd|alg:minibatch_gd]] repeats the <span class="mw-gls" data-name ="stochGD">SGD</span> step \eqref{equ_SGD_update} using a gradient approximation that is constructed from a randomly selected subset <math>\batch = \{ \sampleidx_{1},\ldots,\sampleidx_{\batchsize}\}</math> (a “batch”), | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_gradient_approx_mini_batch} | |||
\noisygrad \big( \weights \big) = (1/\batchsize) \sum_{\sampleidx' \in \batch} \nabla f_{\sampleidx'}(\weights). | |||
\end{equation} | |||
</math> | |||
For each new iteration of Algorithm [[#alg:minibatch_gd|alg:minibatch_gd]], a new batch <math>\batch</math> is generated by a random generator. | |||
<proc label="Mini-Batch SGD" id="alg:minibatch_gd"> | |||
'''Input:''' components <math>f_{\sampleidx}(\weights)</math>, for <math>\sampleidx=1,\ldots,\samplesize</math> of objective function <math>f(\weights)=\sum_{\sampleidx=1}^{\samplesize} f_{\sampleidx}(\weights)</math> ; batch size <math>\batchsize</math>; <span class="mw-gls" data-name ="learnrate">learning rate</span> schedule <math>\lrate_{\itercntr} >0</math>. | |||
set <math>\vw^{(0)}\!\defeq\!\mathbf{0}</math>; set iteration counter <math>\itercntr\!\defeq\!0</math> | |||
<ul style="list-style:numeric"><li> | |||
'''repeat''' | |||
</li><li class="p-3"> randomly select a batch <math>\batch = \{\sampleidx_{1},\ldots,\sampleidx_{\batchsize}\} \subseteq \{1,\ldots,\samplesize\}</math> of indices | |||
that select a subset of components <math>f_{\sampleidx}</math> | |||
</li><li class="ps-3"> compute an approximate gradient <math>\noisygrad \big( \weights^{(\itercntr)} \big)</math> using \eqref{equ_def_gradient_approx_mini_batch} | |||
</li><li class="ps-3"> <math>\itercntr \defeq \itercntr +1</math> (increase iteration counter) | |||
</li><li class="ps-3"> <math>\weights^{(\itercntr)} \defeq \weights^{(\itercntr\!-\!1)} - \lrate_{\itercntr} \noisygrad \big( \weights^{(\itercntr-1)} \big)</math> | |||
<span id="equ_sGD_step_minibtatch"/> | |||
</li><li> | |||
'''until''' stopping criterion met | |||
</li></ul>'''Output:''' <math>\weights^{(\itercntr)}</math> (which approximates <math>\argmin_{\weights \in \mathbb{R}^{\featuredim}} f(\weights)</math> )) | |||
</proc> | |||
Note that Algorithm [[#alg:minibatch_gd|alg:minibatch_gd]] includes the basic <span class="mw-gls" data-name ="stochGD">SGD</span> variant \eqref{equ_SGD_update_basic_form} | |||
as a special case for the batch size <math>\batchsize=1</math>. Another special case is <math>\batchsize= \samplesize</math>, where | |||
the <span class="mw-gls" data-name ="stochGD">SGD</span> step \ref{equ_sGD_step_minibtatch} in Algorithm [[#alg:minibatch_gd|alg:minibatch_gd]] becomes an | |||
ordinary <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step}. | |||
'''Online Learning.''' A main motivation for the <span class="mw-gls" data-name ="stochGD">SGD</span> step \eqref{equ_SGD_update_basic_form} is | |||
that a <span class="mw-gls" data-name ="trainset">training set</span> is already collected but so large that the sum in \eqref{eq_gradient_sum} is | |||
computationally intractable. Another variant of <span class="mw-gls" data-name ="stochGD">SGD</span> is obtained for sequential (time-series) data. In particular, consider | |||
<span class="mw-gls" data-name ="datapoint">data point</span>s that are gathered sequentially, one new <span class="mw-gls" data-name ="datapoint">data point</span> <math>\big( \featurevec^{(\timeidx)},\truelabel^{(\timeidx)} \big)</math> | |||
at each time instant <math>\timeidx=1,2,\ldots.</math>. With each new <span class="mw-gls" data-name ="datapoint">data point</span> <math>\big( \featurevec^{(\timeidx)},\truelabel^{(\timeidx)} \big)</math> | |||
we can access a new component <math>f_{\timeidx}(\weights) = \loss{(\featurevec^{(\timeidx)},\truelabel^{(\timeidx)})}{h^{(\weights)}}</math> (see \eqref{equ_obj_emp_risk_GD}). For sequential data, we can use a slight modification of the <span class="mw-gls" data-name ="stochGD">SGD</span> step \eqref{equ_SGD_update} | |||
to obtain an online learning method (see Section [[guide:2c0f621d22#sec_online_learning | Online Learning ]]). | |||
This online variant of <span class="mw-gls" data-name ="stochGD">SGD</span> computes, at each time instant <math>\timeidx</math>, | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_SGD_update_timeiedx} | |||
\weights^{(\timeidx)} \defeq \weights^{(\timeidx\!-\!1)} - \lrate_{\timeidx} \nabla f_{\timeidx}(\weights^{(\timeidx\!-\!1)}). | |||
\end{equation} | |||
</math> | |||
==<span id="sec_adv_gd_methods"/>Advanced Gradient-Based Methods== | |||
The main idea underlying <span class="mw-gls" data-name ="gd">GD</span> and <span class="mw-gls" data-name ="stochGD">SGD</span> is to approximate the objective function \eqref{equ_obj_emp_risk_GD} locally | |||
around a current guess or approximation <math>\weights^{(\itercntr)}</math> for the optimal weights. This | |||
local approximation is a tangent hyperplane whose normal vector is determined by the gradient | |||
<math>\nabla f (\weights^{(\itercntr)}</math>. We then obtain an updated (improved) approximation by minimizing | |||
this local approximation, i.e., by doing a <span class="mw-gls" data-name ="gd">GD</span> step \eqref{equ_def_GD_step}. | |||
The idea of advanced gradient methods <ref name="Goodfellow-et-al-2016"/>{{rp|at=Ch. 8}} is to exploit the information provided by the | |||
gradients <math>\nabla f\big(\weights^{(\itercntr')}\big)</math> at previous iterations <math>\itercntr'=1,\ldots,\itercntr</math>, | |||
to build an improved local approximation of <math>f(\weights)</math> around a current iterate <math>\weights^{(\itercntr)}</math>. | |||
Figure [[#fig_improved_local_approx|fig_improved_local_approx]] indicates such an improved local approximation of <math>f(\weights)</math> | |||
which is non-linear (e.g., quadratic). These improved local approximations can be used to adapt | |||
the <span class="mw-gls" data-name ="learnrate">learning rate</span> during the <span class="mw-gls" data-name ="gd">GD</span> steps \eqref{equ_def_GD_step}. | |||
Advanced <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> use improved local approximations to modify the <span class="mw-gls" data-name ="gradient">gradient</span> <math>\nabla f\big(\weights^{(\itercntr')}\big)</math> | |||
to obtain an improved update direction. Figure [[#fig_improved_local_approx_better_directions|fig_improved_local_approx_better_directions]] depicts the contours of an objective | |||
function <math>f(\weights)</math> for which the gradient <math>\nabla f\big(\weights^{(\itercntr)}\big)</math> points only weakly | |||
towards the optimal parameter vector <math>\overline{\weights}</math> (minimizer of <math>f(\weights)</math>). The <span class="mw-gls" data-name ="gradient">gradient</span> history <math>\nabla f\big(\weights^{(\itercntr')}\big)</math>, for<math>\itercntr'=1,\ldots,\itercntr</math>, allows to detect such an unfavourable geometry | |||
of the objective function. Moreover, the <span class="mw-gls" data-name ="gradient">gradient</span> history can be used to “correct” the | |||
update direction <math>\nabla f\big(\weights^{(\itercntr)}\big)</math> to obtain an improved update | |||
direction towards the optimum parameter vector <math>\overline{\weights}</math>. | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_improved_local_approx"></span> | |||
[[File:fig_improved_local_approx.png | 500px | thumb | Advanced <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> use the gradients at previous iterations to construct an | |||
improved (non-linear) local approximation (dashed) of the objective function <math>f(\weights)</math> (solid). ]] | |||
</div> | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_improved_local_approx_better_directions"></span> | |||
[[File:fig_improved_local_approx_better_directions.jpg | 500px | thumb | Advanced <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> use improved (non-linear) local approximations of the objective | |||
function <math>f(\weights)</math> to “nudge” the update direction towards the optimal parameter | |||
vector <math>\overline{\weights}</math>. The update direction of plain vanilla <span class="mw-gls" data-name ="gd">GD</span> \eqref{equ_def_GD_step} | |||
is the negative <span class="mw-gls" data-name ="gradient">gradient</span> <math>-\nabla f\big( \weights^{(\itercntr)}\big)</math>. For some | |||
objective functions the negative <span class="mw-gls" data-name ="gradient">gradient</span> might be only weakly correlated with | |||
the straight direction from <math>\weights^{(\itercntr)}</math> towards the optimal parameter vector (<math>\star</math>). ]] | |||
</div> | |||
==Notes== | |||
{{notelist}} | |||
==General References== | |||
<div class="d-flex mt-3 mb-3"> | |||
<div class="me-3"> | |||
[[File:978-981-16-8193-6.jpg | 150px | link=]] | |||
</div> | |||
<div> | |||
{{cite book | title = Machine Learning: The Basics |first = Alexander | last = Jung | publisher = Springer | location = Signapore | date = 2022 | doi = 10.1007/978-981-16-8193-6 }} | |||
{{cite arXiv |last=Jung |first=Alexander |date= |title=Machine Learning: The Basics |eprint=1805.05052 | date=2022}} | |||
</div> | |||
</div> | |||
==References== | |||
Latest revision as of 22:32, 20 June 2023
[math] % Generic syms \newcommand\defeq{:=} \newcommand{\Tt}[0]{\boldsymbol{\theta}} \newcommand{\XX}[0]{{\cal X}} \newcommand{\ZZ}[0]{{\cal Z}} \newcommand{\vx}[0]{{\bf x}} \newcommand{\vv}[0]{{\bf v}} \newcommand{\vu}[0]{{\bf u}} \newcommand{\vs}[0]{{\bf s}} \newcommand{\vm}[0]{{\bf m}} \newcommand{\vq}[0]{{\bf q}} \newcommand{\mX}[0]{{\bf X}} \newcommand{\mC}[0]{{\bf C}} \newcommand{\mA}[0]{{\bf A}} \newcommand{\mL}[0]{{\bf L}} \newcommand{\fscore}[0]{F_{1}} \newcommand{\sparsity}{s} \newcommand{\mW}[0]{{\bf W}} \newcommand{\mD}[0]{{\bf D}} \newcommand{\mZ}[0]{{\bf Z}} \newcommand{\vw}[0]{{\bf w}} \newcommand{\D}[0]{{\mathcal{D}}} \newcommand{\mP}{\mathbf{P}} \newcommand{\mQ}{\mathbf{Q}} \newcommand{\E}[0]{{\mathbb{E}}} \newcommand{\vy}[0]{{\bf y}} \newcommand{\va}[0]{{\bf a}} \newcommand{\vn}[0]{{\bf n}} \newcommand{\vb}[0]{{\bf b}} \newcommand{\vr}[0]{{\bf r}} \newcommand{\vz}[0]{{\bf z}} \newcommand{\N}[0]{{\mathcal{N}}} \newcommand{\vc}[0]{{\bf c}} \newcommand{\bm}{\boldsymbol} % Statistics and Probability Theory \newcommand{\errprob}{p_{\rm err}} \newcommand{\prob}[1]{p({#1})} \newcommand{\pdf}[1]{p({#1})} \def \expect {\mathbb{E} } % Machine Learning Symbols \newcommand{\biasterm}{B} \newcommand{\varianceterm}{V} \newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} \newcommand{\nrfolds}{k} \newcommand{\mseesterr}{E_{\rm est}} \newcommand{\bootstrapidx}{b} %\newcommand{\modeldim}{r} \newcommand{\modelidx}{l} \newcommand{\nrbootstraps}{B} \newcommand{\sampleweight}[1]{q^{(#1)}} \newcommand{\nrcategories}{K} \newcommand{\splitratio}[0]{{\rho}} \newcommand{\norm}[1]{\Vert {#1} \Vert} \newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} \newcommand{\bmx}[0]{\begin{bmatrix}} \newcommand{\emx}[0]{\end{bmatrix}} \newcommand{\T}[0]{\text{T}} \DeclareMathOperator*{\rank}{rank} %\newcommand\defeq{:=} \newcommand\eigvecS{\hat{\mathbf{u}}} \newcommand\eigvecCov{\mathbf{u}} \newcommand\eigvecCoventry{u} \newcommand{\featuredim}{n} \newcommand{\featurelenraw}{\featuredim'} \newcommand{\featurelen}{\featuredim} \newcommand{\samplingset}{\mathcal{M}} \newcommand{\samplesize}{m} \newcommand{\sampleidx}{i} \newcommand{\nractions}{A} \newcommand{\datapoint}{\vz} \newcommand{\actionidx}{a} \newcommand{\clusteridx}{c} \newcommand{\sizehypospace}{D} \newcommand{\nrcluster}{k} \newcommand{\nrseeds}{s} \newcommand{\featureidx}{j} \newcommand{\clustermean}{{\bm \mu}} \newcommand{\clustercov}{{\bm \Sigma}} \newcommand{\target}{y} \newcommand{\error}{E} \newcommand{\augidx}{b} \newcommand{\task}{\mathcal{T}} \newcommand{\nrtasks}{T} \newcommand{\taskidx}{t} \newcommand\truelabel{y} \newcommand{\polydegree}{r} \newcommand\labelvec{\vy} \newcommand\featurevec{\vx} \newcommand\feature{x} \newcommand\predictedlabel{\hat{y}} \newcommand\dataset{\mathcal{D}} \newcommand\trainset{\dataset^{(\rm train)}} \newcommand\valset{\dataset^{(\rm val)}} \newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} \newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} \newcommand{\inspace}{\mathcal{X}} \newcommand{\sigmoid}{\sigma} \newcommand{\outspace}{\mathcal{Y}} \newcommand{\hypospace}{\mathcal{H}} \newcommand{\emperror}{\widehat{L}} \newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} \newcommand{\featurespace}{\mathcal{X}} \newcommand{\labelspace}{\mathcal{Y}} \newcommand{\rawfeaturevec}{\mathbf{z}} \newcommand{\rawfeature}{z} \newcommand{\condent}{H} \newcommand{\explanation}{e} \newcommand{\explainset}{\mathcal{E}} \newcommand{\user}{u} \newcommand{\actfun}{\sigma} \newcommand{\noisygrad}{g} \newcommand{\reconstrmap}{r} \newcommand{\predictor}{h} \newcommand{\eigval}[1]{\lambda_{#1}} \newcommand{\regparam}{\lambda} \newcommand{\lrate}{\alpha} \newcommand{\edges}{\mathcal{E}} \newcommand{\generror}{E} \DeclareMathOperator{\supp}{supp} %\newcommand{\loss}[3]{L({#1},{#2},{#3})} \newcommand{\loss}[2]{L\big({#1},{#2}\big)} \newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} \newcommand{\determinant}[1]{{\rm det}({#1})} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\itercntr}{r} \newcommand{\state}{s} \newcommand{\statespace}{\mathcal{S}} \newcommand{\timeidx}{t} \newcommand{\optpolicy}{\pi_{*}} \newcommand{\appoptpolicy}{\hat{\pi}} \newcommand{\dummyidx}{j} \newcommand{\gridsizex}{K} \newcommand{\gridsizey}{L} \newcommand{\localdataset}{\mathcal{X}} \newcommand{\reward}{r} \newcommand{\cumreward}{G} \newcommand{\return}{\cumreward} \newcommand{\action}{a} \newcommand\actionset{\mathcal{A}} \newcommand{\obstacles}{\mathcal{B}} \newcommand{\valuefunc}[1]{v_{#1}} \newcommand{\gridcell}[2]{\langle #1, #2 \rangle} \newcommand{\pair}[2]{\langle #1, #2 \rangle} \newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} \newcommand{\actionvalue}[1]{q_{#1}} \newcommand{\transition}{\mathcal{T}} \newcommand{\policy}{\pi} \newcommand{\charger}{c} \newcommand{\itervar}{k} \newcommand{\discount}{\gamma} \newcommand{\rumba}{Rumba} \newcommand{\actionnorth}{\rm N} \newcommand{\actionsouth}{\rm S} \newcommand{\actioneast}{\rm E} \newcommand{\actionwest}{\rm W} \newcommand{\chargingstations}{\mathcal{C}} \newcommand{\basisfunc}{\phi} \newcommand{\augparam}{B} \newcommand{\valerror}{E_{v}} \newcommand{\trainerror}{E_{t}} \newcommand{\foldidx}{b} \newcommand{\testset}{\dataset^{(\rm test)} } \newcommand{\testerror}{E^{(\rm test)}} \newcommand{\nrmodels}{M} \newcommand{\benchmarkerror}{E^{(\rm ref)}} \newcommand{\lossfun}{L} \newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} \newcommand{\cluster}{\mathcal{C}} \newcommand{\bayeshypothesis}{h^{*}} \newcommand{\featuremtx}{\mX} \newcommand{\weight}{w} \newcommand{\weights}{\vw} \newcommand{\regularizer}{\mathcal{R}} \newcommand{\decreg}[1]{\mathcal{R}_{#1}} \newcommand{\naturalnumbers}{\mathbb{N}} \newcommand{\featuremapvec}{{\bf \Phi}} \newcommand{\featuremap}{\phi} \newcommand{\batchsize}{B} \newcommand{\batch}{\mathcal{B}} \newcommand{\foldsize}{B} \newcommand{\nriter}{R} [/math]
This chapter discusses an important family of optimization methods for solving empirical risk minimization (ERM) with a parametrized hypothesis space (see Chapter Computational and Statistical Aspects of ERM ). The common theme of these methods is to construct local approximations of the objective function in ERM. These local approximations are obtained from the gradients of the objective function. Gradient-based methods have gained popularity recently as an efficient technique for tuning the parameters of deep artificial neural network (ANN) (deep net)s within deep learning methods [1].
Section The Basic Gradient Step discusses gradient descent (GD) as the most basic form of gradient-based methods. The idea of GD is to update the weights by locally optimizing a linear approximation of the objective function. This update is referred to as a GD step and provides the main algorithmic primitive of gradient-based methods. One key challenge for a good use of gradient-based methods is the appropriate extend of the local approximations. This extent is controlled by a step size parameter that is used in the basic GD step. Section Choosing the Learning Rate discusses some approaches for choosing this step size. Section When To Stop? discusses a second main challenge in using gradient-based methods which is to decide when to stop repeating the GD steps.
Section GD for Linear Regression and Section GD for Logistic Regression spell out GD for two instances of ERM arising from linear regression and logistic regression, respectively. The beneficial effect of data normalization on the convergence speed of gradient-based methods is briefly discussed in Section Data Normalization . As explained in Section Stochastic GD , the use of stochastic approximations enables gradient-based methods for applications involving massive amounts of data (“big data”). Section Advanced Gradient-Based Methods develops some intuition for advanced gradient-based methods that exploit the information gathered during previous iterations.
The Basic Gradient Step
Let us rewrite empirical risk minimization (ERM) as the optimization problem
From now on we tacitly assume that each individual loss
arising in \eqref{equ_obj_emp_risk_GD} represents a differentiable function of the parameter vector [math]\weights[/math]. Trivially, differentiability of the components \eqref{equ_def_componentn_loss_gd} implies differentiability of the overall objective function [math]f(\weights)[/math] \eqref{equ_obj_emp_risk_GD}.
Two important examples of ERM involving such differentiable loss functions are linear regression and logistic regression. In contrast, the hinge loss used by the support vector machine (SVM) results in a non-differentiable objective function [math]f(\weights)[/math] \eqref{equ_obj_emp_risk_GD}. However, it is possible to (significantly) extend the scope of gradient-based methods to non-differentiable functions by replacing the concept of a gradient with that of a subgradient.
Gradient based methods are iterative. They construct a sequence of parameter vectors [math]\weights^{(0)} \rightarrow \weights^{(1)} \dots[/math] that hopefully converge to a minimizer [math]\overline{\weights}[/math] of [math]f(\weights)[/math],
Note that there might be several different optimal parameter vectors [math]\overline{\weights}[/math] that satisfy the optimality condition \eqref{equ_def_opt_weight}. We want the sequence generated by a gradient based method to converge towards any of them. The vectors [math]\weights^{(\itercntr)}[/math] are (hopefully) increasingly, with increasing iteration [math]\itercntr[/math], more accurate approximation for a minimizer [math]\overline{\weights}[/math] of \eqref{equ_def_opt_weight}.
Since the objective function [math]f(\weights)[/math] is differentiable, we can approximate it locally around the vector [math]\weights^{(\itercntr)}[/math] using a tangent hyperplane that passes through the point [math]\big(\weights^{(\itercntr)},f\big(\weights^{(\itercntr)}\big) \big) \in \mathbb{R}^{\featuredim+1}[/math]. The normal vector of this hyperplane is given by [math]\mathbf{n} = (\nabla f\big(\weights^{(\itercntr)}\big) ,-1)[/math] (see Figure fig_smooth_function). The first component of the normal vector is the gradient [math]\nabla f(\weights)[/math] of the objective function [math]f(\weights)[/math] evaluated at the point [math]\weights^{(\itercntr)}[/math]. Our main use of the gradient [math]\nabla f\big(\weights^{(\itercntr)}\big)[/math] will be to construct a linear approximation [2]
Requiring the objective function [math]f(\weights)[/math] in \eqref{equ_linear_approx_diff} to be differentiable is the same as requiring the validity of the local linear approximation \eqref{equ_linear_approx_diff} at every possible vector [math]\weights^{(\itercntr)}[/math]. It turns out that differentiability alone is not very helpful for the design and analysis of gradient based methods.
Gradient based methods are most useful for finding the minimum of differentiable functions [math]f(\weights)[/math] that are also smooth. Informally, a differentiable function [math]f(\weights)[/math] is smooth if the gradient [math]\nabla f(\weights)[/math] does not change too rapidly as a function of the argument [math]\weights[/math]. A quantitative version of the smoothness concept refers to a function as [math]\beta[/math]-smooth if its gradient is Lipschitz continuous with Lipschitz constant [math]\beta\gt 0 [/math] [3](Sec. 3.2),
Note that if a function [math]f(\weights)[/math] is [math]\beta[/math] smooth, it is also [math]\beta'[/math] smooth for any [math]\beta' \gt \beta[/math]. The smallest [math]\beta[/math] such that \eqref{equ_def_beta_smooth} is satisfied depends on the features and labels of data points used in \eqref{equ_obj_emp_risk_GD} as well as on the choice for the loss function.
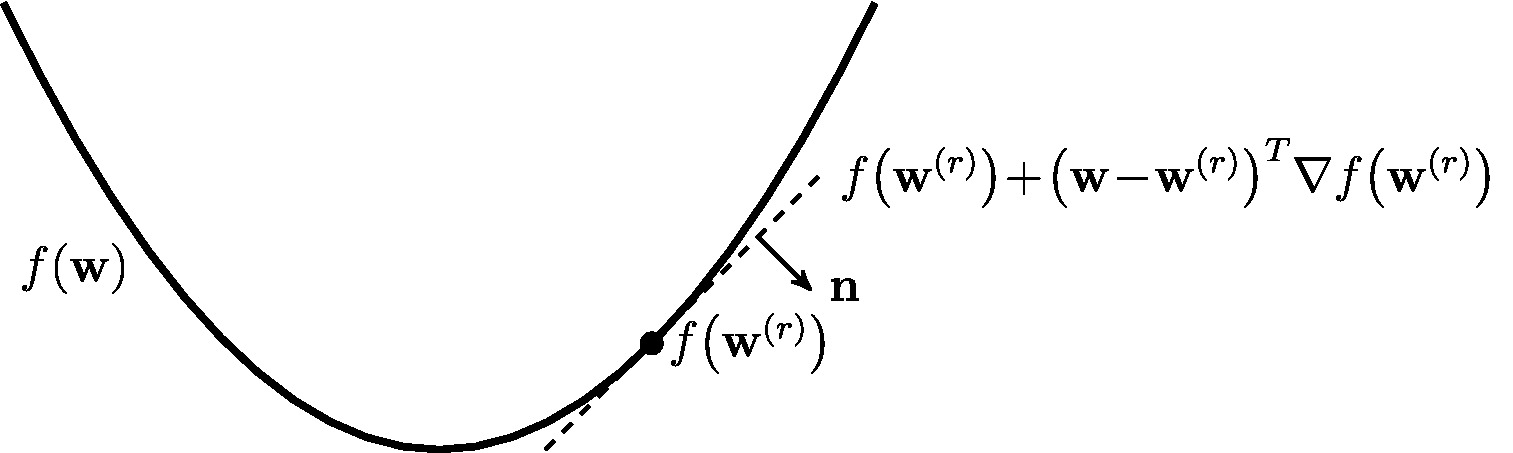
Consider a current guess or approximation [math]\weights^{(\itercntr)}[/math] for the optimal parameter vector [math]\overline{\weights}[/math] \eqref{equ_def_opt_weight}. We would like to find a new (better) parameter vector [math]\weights^{(\itercntr+1)}[/math] that has smaller objective value [math]f(\weights^{(\itercntr+1)}) \lt f\big(\weights^{(\itercntr)}\big)[/math] than the current guess [math]\weights^{(\itercntr)}[/math]. The approximation \eqref{equ_linear_approx_diff} suggests to choose the next guess [math]\weights = \weights^{(\itercntr+1)}[/math] such that [math]\big(\weights^{(\itercntr+1)}-\weights^{(\itercntr)} \big)^{T} \nabla f\big(\weights^{(\itercntr)}\big)[/math] is negative. We can achieve this by the GD step
with a sufficiently small step size [math]\lrate\gt0[/math]. Figure fig_basic_GD_step illustrates the GD step \eqref{equ_def_GD_step} which is the elementary computation of gradient based methods.
The step size [math]\lrate[/math] in \eqref{equ_def_GD_step} must be sufficiently small to ensure the validity of the linear approximation \eqref{equ_linear_approx_diff}. In the context of ML, the GD step size parameter [math]\lrate[/math] is also referred to as learning rate. Indeed, the step size [math]\lrate[/math] determines the amount of progress during a GD step towards learning the optimal parameter vector [math]\overline{\weights}[/math].
We need to emphasize that the interpretation of the step size [math]\lrate[/math] as a learning rate is only useful when the step size is sufficiently small. Indeed, when increasing the step size [math]\lrate[/math] in \eqref{equ_def_GD_step} beyond a critical value (that depends on the properties of the objective function [math]f(\weights)[/math]), the iterates \eqref{equ_def_GD_step} move away from the optimal parameter vector [math]\overline{\weights}[/math]. Nevertheless, from now on we will consequently use the term learning rate for [math]\lrate[/math].
The idea of gradient-based methods is to repeat the GD step \eqref{equ_def_GD_step} for a sufficient number of iterations (repetitions) to obtain a sufficiently accurate approximation of the optimal parameter vector [math]\overline{\weights}[/math] \eqref{equ_def_opt_weight}. It turns out that this is feasible for a sufficiently small learning rate and if the objective function is smooth and convex. Section Choosing the Learning Rate discusses precise conditions on the learning rate such that the iterates produced by the GD step converge to the optimum parameter vector, i.e., [math]\lim_{\itercntr \rightarrow \infty} f(\weights^{(\itercntr)}) = f\big(\overline{\weights}\big)[/math].
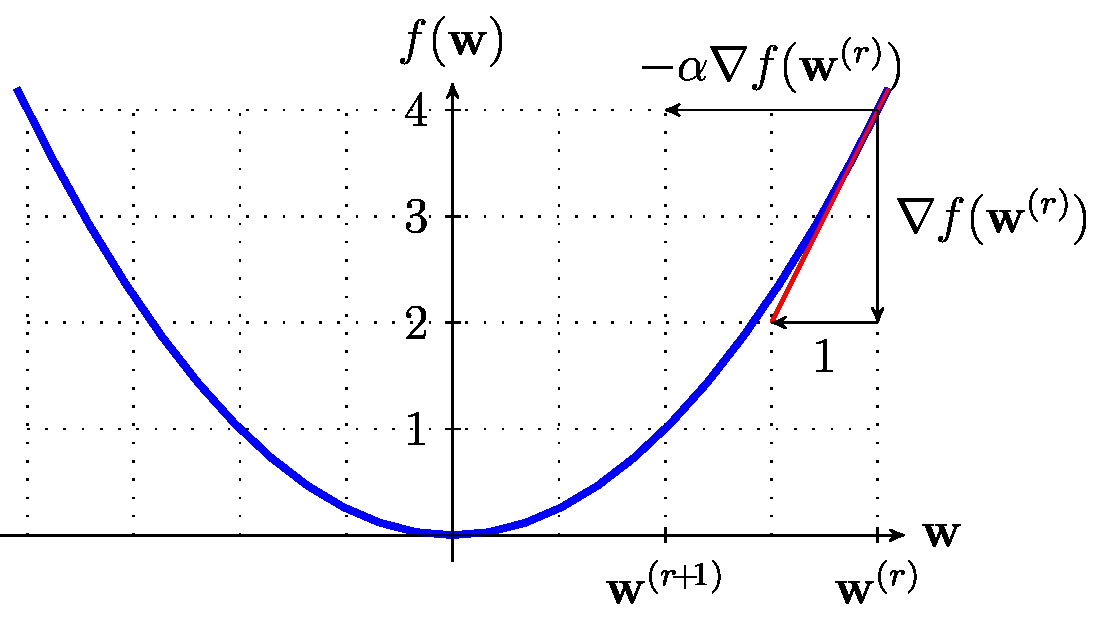
To implement the GD step \eqref{equ_def_GD_step} we need to choose a useful learning rate [math]\lrate[/math]. Moreover, executing the GD step \eqref{equ_def_GD_step} requires to compute the gradient [math]\nabla f(\weights^{(\itercntr)})[/math]. Both tasks can be computationally challenging as discussed in Section Choosing the Learning Rate and Stochastic GD . For the objective function \eqref{equ_obj_emp_risk_GD} obtained in linear regression and logistic regression, we can obtain closed-form expressions for the gradient [math]\nabla f(\weights)[/math] (see Section GD for Linear Regression and GD for Logistic Regression ).
In general, we do not have closed-form expressions for the gradient of the objective function \eqref{equ_obj_emp_risk_GD} arising from a non-linear hypothesis space. One example for such a hypothesis space is obtained from a ANN, which is used by deep learning methods (see Section Deep Learning ). The empirical success of deep learning methods might be partially attributed to the availability of an efficient algorithm for computing the gradient [math]\nabla f(\weights^{(\itercntr)})[/math]. This algorithm is known as \index{back-propagation}back-propagation [1].
Choosing the Learning Rate

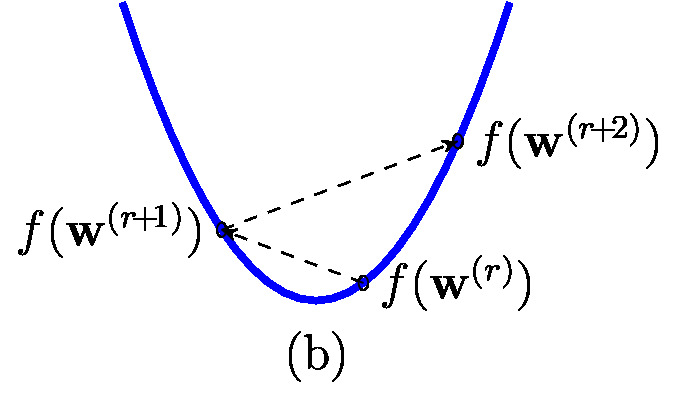
The choice of the learning rate [math]\lrate[/math] in the GD step \eqref{equ_def_GD_step} has a significant impact on the performance of Algorithm alg:gd_linreg. If we choose the learning rate [math]\lrate[/math] too large, the GD steps \eqref{equ_def_GD_step} diverge (see Figure fig_small_large_lrate-(b)) and, in turn, Algorithm alg:gd_linreg fails to deliver a satisfactory approximation of the optimal weights [math]\overline{\weights}[/math].
If we choose the learning rate [math]\lrate[/math] too small (see Figure fig_small_large_lrate-(a)), the updates \eqref{equ_def_GD_step} make only very little progress towards approximating the optimal parameter vector [math]\overline{\weights}[/math]. In applications that require real-time processing of data streams, it might be possible to repeat the GD steps only for a moderate number. Thus If the learning rate is chosen too small, Algorithm alg:gd_linreg will fail to deliver a good approximation within an acceptable number of iterations (runtime of Algorithm alg:gd_linreg).
Finding a (nearly) optimal choice for the learning rate [math]\lrate[/math] of GD can be a challenging task. Many sophisticated approaches for tuning the learning rate of gradient-based methods have been proposed [1](Chapter 8). A detailed discussion of these approaches is beyond the scope of this book. We will instead discuss two sufficient conditions on the learning rate which guarantee the convergence of the GD iterations to the optimum of a smooth and convex objective function \eqref{equ_obj_emp_risk_GD}.
The first condition applies to an objective function that is [math]\beta[/math]-smooth (see \eqref{equ_def_beta_smooth}) with known constant [math]\beta[/math] (not necessarily the smallest constant such that \eqref{equ_def_beta_smooth} holds). Then, the iterates [math]\weights^{(\itercntr)}[/math] generated by the GD step \eqref{equ_def_GD_step} with a learning rate
satisfy [4](Thm. 2.1.13)
The bound \eqref{equ_convergence_rate_inverse_k-GD} not only tells us that GD iterates converge to an optimal parameter vector but also characterize the convergence speed or rate. The sub-optimality [math]f \big( \weights^{(\itercntr)} \big) - \min_{\weights} f(\weights)[/math] in terms of objective function value decreases inversely (like “[math]1/\itercntr[/math]”) with the number [math]\itercntr[/math] of GD steps \eqref{equ_def_GD_step}. Convergence bounds like \eqref{equ_convergence_rate_inverse_k-GD} can be used to specify a stopping criterion, i.e., to determine the number of GD steps to be computed (see Section When To Stop? ).
The condition \eqref{equ_suff_cond_lrate_beta} and the bound \eqref{equ_convergence_rate_inverse_k-GD} is only useful if we can verify [math]\beta[/math] smoothness \eqref{equ_def_beta_smooth} assumption for a reasonable constant [math]\beta[/math]. Verifying \eqref{equ_convergence_rate_inverse_k-GD} only for a very large [math]\beta[/math] results in the bound \eqref{equ_convergence_rate_inverse_k-GD} being too loose (pessimistic). When we use a loose bound \eqref{equ_convergence_rate_inverse_k-GD} to determine the number of GD steps, we might compute an unnecessary large number of GD steps \eqref{equ_def_GD_step}.
One elegant approach to verify if a differentiable function [math]f(\weights)[/math] is [math]\beta[/math] smooth \eqref{equ_def_beta_smooth} is via the Hessian matrix [math] \nabla^{2} f(\weights) \in \mathbb{R}^{\featuredim \times \featuredim}[/math] if it exists. The entries of this Hessian matrix are the second-order partial derivatives [math]\frac{\partial f(\weights)}{\partial \weight_{\featureidx} \partial \weight_{\featureidx'}}[/math] of the function [math]f(\weights)[/math].
Consider an objective function [math]f(\weights)[/math] \eqref{equ_obj_emp_risk_GD} that is convex and twice-differentiable with positive semi-definite (psd) Hessian [math]\nabla^{2} f(\weights)[/math]. If the maximum eigenvalue [math]\eigval{\rm max} \big( \nabla^{2} f(\weights) \big)[/math] of the Hessian is upper bounded uniformly (for all [math]\weights[/math]) by the constant [math]\beta\gt0[/math], then [math]f(\weights)[/math] is [math]\beta[/math] smooth \eqref{equ_def_beta_smooth} [3]. This implies, in turn via \eqref{equ_suff_cond_lrate_beta}, the sufficient condition
for the GD learning rate such that the GD steps converge to the minimum of the objective function [math]f(\weights)[/math].
It is important to note that the condition \eqref{equ_GD_conv_guarantee} guarantees convergence of the GD steps for any possible initialization [math]\weights^{(0)}[/math]. Note that the usefulness of the condition \eqref{equ_GD_conv_guarantee} depends on the difficulty of computing the Hessian matrix [math]\nabla^{2} f(\weights)[/math]. Section GD for Linear Regression and Section GD for Logistic Regression will present closed-form expressions for the Hessian of the objective function \eqref{equ_obj_emp_risk_GD} obtained for linear regression and logistic regression. These closed-form expressions involve the feature vectors and labels of the data points in the training set [math]\dataset = \big\{ \big(\featurevec^{(1)},\truelabel^{(1)} \big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)} \big) \big\}[/math] used in \eqref{equ_obj_emp_risk_GD}.
While it might be computationally challenging to determine the maximum (in absolute value) eigenvalue [math]\eigval{\rm max} \big( \nabla^{2} f(\weights) \big)[/math] for arbitrary [math]\weights[/math], it might still be feasible to find an upper bound [math]U[/math] for it. If we know such an upper bound [math]U \geq \eigval{\rm max} \big( \nabla^{2} f(\weights) \big)[/math] (valid for all [math]\weights \in \mathbb{R}^{\featuredim}[/math]), the learning rate [math]\lrate =1/U[/math] still ensures convergence of the GD steps \eqref{equ_def_GD_step}.
Up to know we have assumed a fixed (constant) learning rate [math]\lrate[/math] that is used for each repetition of the GD steps \eqref{equ_def_GD_step}. However, it might be useful to vary or adjust the learning rate as the GD steps \eqref{equ_def_GD_step} proceed. Thus, we might use a different learning rate [math]\lrate_{\itercntr}[/math] for each iteration [math]\itercntr[/math] of \eqref{equ_def_GD_step}. Such a varying learning rate is useful for a variant of GD that uses stochastic approximation (see Section Stochastic GD ). However, we might use a varying learning rate also to avoid the burden of verifying [math]\beta[/math] smoothness \eqref{equ_def_beta_smooth} with a tight (small) [math]\beta[/math]. The GD steps \eqref{equ_def_GD_step} with the learning rate [math]\lrate_{\itercntr} \defeq 1/\itercntr[/math] converge to the optimal parameter vector [math]\overline{\weights}[/math] as long as we can ensure a bounded gradient [math]\| \nabla f(\weights) \| \leq U[/math] for a sufficiently large neighbourhood of [math]\overline{\weights}[/math] [4].
When To Stop?
One main challenge in the successful application of GD is to decide when to stop iterating (or repeating) the GD step \eqref{equ_def_GD_step}. Maybe the most simple approach is to monitor the decrease in the objective function [math]f(\weights^{(\itercntr)})[/math] and to stop if the decrease [math]f(\weights^{(\itercntr-1)})-f(\weights^{(\itercntr)})[/math] falls below a threshold. However, the ultimate goal of a ML method is not to minimize the objective function [math]f(\weights)[/math] in \eqref{equ_obj_emp_risk_GD}. Indeed, the objective function represents the average loss of a hypothesis [math]h^{(\weights)}[/math] incurred on a training set. However, the ultimate goal of a ML method is to learn a parameter vector [math]\weights[/math] such that the resulting hypothesis accurately predicts any data point, including those outside the training set.
We will see in Chapter Model Validation and Selection how to use validation techniques to probe a hypothesis outside the training set. These validation techniques provide a validation error [math]\tilde{f}(\weights)[/math] that estimates the average loss of a hypothesis with parameter vector [math]\weights[/math]. Early stopping techniques monitor the validation error [math]\tilde{f}(\weights^{(\itercntr)})[/math] as the GD iterations [math]\itercntr[/math] proceed to decide when to stop iterating.
Another possible stopping criterion is to use a fixed number of iterations or GD steps. This fixed number of iterations can be chosen based on convergence bounds such as \eqref{equ_convergence_rate_inverse_k-GD} in order to guarantee a prescribed sub-optimality of the final iterate [math]\weights^{(\itercntr)}[/math]. A slightly more convenient convergence bound can be obtained from \eqref{equ_convergence_rate_inverse_k-GD} when using the the learning rate [math]\lrate = 1/\beta[/math] in the GD step \eqref{equ_def_GD_step} [3],
GD for Linear Regression
We now present a gradient based method for learning the parameter vector for a linear hypothesis (see equ_lin_hypospace)
The ERM principle tells us to choose the parameter vector [math]\weights[/math] in \eqref{equ_def_lin_pred_GD} by minimizing the average squared error loss
The average squared error loss \eqref{equ_def_cost_linreg} is computed by applying the predictor [math]h^{(\weights)}(\featurevec)[/math] to labeled data points in a training set [math]\dataset=\{ (\featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}[/math]. An optimal parameter vector [math]\overline{\weights}[/math] for \eqref{equ_def_lin_pred_GD} is obtained as
The objective function [math]f(\weights)[/math] in \eqref{equ_smooth_problem_linreg} is convex and smooth. We can therefore use GD \eqref{equ_def_GD_step} to solve \eqref{equ_smooth_problem_linreg} iteratively, i.e., by constructing a sequence of parameter vectors that converge to an optimal parameter vector [math]\overline{\weights}[/math]. To implement GD, we need to compute the gradient [math]\nabla f(\weights)[/math].
The gradient of the objective function in \eqref{equ_smooth_problem_linreg} is given by
By inserting \eqref{equ_gradient_linear_regression} into the basic GD iteration \eqref{equ_def_GD_step}, we obtain Algorithm alg:gd_linreg.
Input: dataset [math]\dataset=\{ (\featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}[/math] ; learning rate [math]\lrate \gt0[/math].
Initialize: set [math]\weights^{(0)}\!\defeq\!\mathbf{0}[/math]; set iteration counter [math]\itercntr\!\defeq\!0[/math]
- repeat
- [math]\itercntr \defeq \itercntr +1[/math] (increase iteration counter)
- [math]\weights^{(\itercntr)} \defeq \weights^{(\itercntr\!-\!1)} + \lrate (2/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big(\truelabel^{(\sampleidx)} - \big(\weights^{(\itercntr\!-\!1)}\big)^{T} \featurevec^{(\sampleidx)}\big) \featurevec^{(\sampleidx)}[/math] (do a GD step \eqref{equ_def_GD_step})
- until stopping criterion met
Output: [math]\weights^{(\itercntr)}[/math] (which approximates [math]\overline{\weights}[/math] in \eqref{equ_smooth_problem_linreg})
Let us have a closer look on the update in step [math]3[/math] of Algorithm alg:gd_linreg, which is
The update \eqref{equ_update_gd_linreg} has an appealing form as it amounts to correcting the previous guess (or approximation) [math]\weights^{(\itercntr\!-\!1)}[/math] for the optimal parameter vector [math]\overline{\weights}[/math] by the correction term
The correction term \eqref{equ_corr_term_linreg} is a weighted average of the feature vectors [math]\featurevec^{(\sampleidx)}[/math] using weights [math](2\lrate/\samplesize) \cdot e^{(\sampleidx)}[/math]. These weights consist of the global factor [math](2\lrate/\samplesize)[/math] (that applies equally to all feature vectors [math]\featurevec^{(\sampleidx)}[/math]) and a sample-specific factor [math]e^{(\sampleidx)} = (\truelabel^{(\sampleidx)} - \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)})[/math], which is the prediction (approximation) error obtained by the linear predictor [math]h^{(\weights^{(\itercntr\!-\!1)})}(\featurevec^{(\sampleidx)}) = \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)}[/math] when predicting the label [math]\truelabel^{(\sampleidx)}[/math] from the features [math]\featurevec^{(\sampleidx)}[/math].
We can interpret the GD step \eqref{equ_update_gd_linreg} as an instance of “learning by trial and error”. Indeed, the GD step amounts to first “trying out” (trial) the predictor [math]h(\featurevec^{(\sampleidx)}) = \big(\weights^{(\itercntr\!-\!1)})^{T}\featurevec^{(\sampleidx)}[/math]. The predicted values are then used to correct the weight vector [math]\weights^{(\itercntr\!-\!1)}[/math] according to the error [math]e^{(\sampleidx)} = \truelabel^{(\sampleidx)} - \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)}[/math].
The choice of the learning rate [math]\lrate[/math] used for Algorithm alg:gd_linreg can be based on the condition \eqref{equ_GD_conv_guarantee} with the Hessian [math]\nabla^{2} f(\weights)[/math] of the objective function [math]f(\weights)[/math] underlying linear regression (see \eqref{equ_smooth_problem_linreg}). This Hessian is given explicitly as
with the feature matrix [math]\featuremtx=\big(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)}\big)^{T} \in \mathbb{R}^{\samplesize \times \featuredim}[/math] (see feature matrix ). Note that the Hessian \eqref{equ_hessian_linreg} does not depend on the parameter vector [math]\weights[/math].
Comparing \eqref{equ_hessian_linreg} with \eqref{equ_GD_conv_guarantee}, one particular strategy for choosing the learning rate in Algorithm alg:gd_linreg is to (i) compute the matrix product [math] \featuremtx^{T} \featuremtx[/math], (ii) compute the maximum eigenvalue [math]\eigval{\rm max}\big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)[/math] of this product and (iii) set the learning rate to [math]\lrate =1/\eigval{\rm max} \big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)[/math].
While it might be challenging to compute the maximum eigenvalue [math]\eigval{\rm max} \big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)[/math], it might be easier to find an upper bound [math]U[/math] for it.[a]
Given such an upper bound [math]U \geq \eigval{\rm max} \big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)[/math], the learning rate [math]\lrate =1/U[/math] still ensures convergence of the GD steps. Consider a dataset [math]\{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})\}_{\sampleidx=1}^{\samplesize}[/math] with normalized features, i.e., [math]\| \featurevec^{(\sampleidx)}\| = 1[/math] for all [math]\sampleidx =1,\ldots,\samplesize[/math]. This implies, in turn, the upper bound [math]U= 1[/math], i.e., [math] 1 \geq \lambda_{\rm max} \big( (1/\samplesize) \featuremtx^{T} \featuremtx \big)[/math]. We can then ensure convergence of the iterates [math]\weights^{(\itercntr)}[/math] (see \eqref{equ_update_gd_linreg}) by choosing the learning rate [math]\lrate =1[/math].
Time-Data Tradeoffs. The number of GD steps required by Algorithm alg:gd_linreg to ensure a prescribed sub-optimality depends crucially on the condition number of [math]\featuremtx^{T} \featuremtx[/math]. What can we say about the condition number? In general, we have not control over this quantity as the matrix [math]\featuremtx[/math] consists of the feature vectors of arbitrary data points. However, it is often useful to model the feature vectors as realizations of independent and identically distributed (iid) random vectors. It is then possible to bound the probability of the feature matrix having a sufficiently small condition number. These bounds can then be used to choose the step-size such that convergence is guaranteed with sufficiently large probability. The usefulness of these bounds typically depends on the ratio [math]\featurelen/\samplesize[/math]. For increasing sample-size, these bounds allow to use larger step-sizes and, in turn, result in faster convergence of GD algorithm. Thus, we obtain a trade-off between the runtime of Algorithm alg:gd_linreg and the number of data points that we feed into it [5].
GD for Logistic Regression
Logistic regression learns a linear hypothesis [math]h^{(\weights)}[/math] that is used to classify data points by predicting their binary label. The quality of such a linear classifier is measured by the logistic loss. The ERM principle suggest to learn the parameter vector [math]\weights[/math] by minimizing the average logistic loss obtained for a training set [math]\dataset= \{ (\featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}[/math]. The training set consists of data points with features [math]\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}[/math] and binary labels [math]\truelabel^{(\sampleidx)} \in \{-1,1\}[/math].
We can rewrite ERM for logistic regression as the optimization problem
The objective function [math]f(\weights)[/math] is differentiable and therefore we can use GD \eqref{equ_def_GD_step} to solve \eqref{equ_smooth_problem_logeg}. We can write down the gradient of the objective function in \eqref{equ_smooth_problem_logeg} in closed-form as
Inserting \eqref{equ_gradient_logistic_regression} into the GD step \eqref{equ_def_GD_step} yields Algorithm alg:gd_logreg.
Input: labeled dataset [math]\dataset=\{ (\featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}[/math] containing feature vectors [math]\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}[/math] and labels [math]\truelabel^{(\sampleidx)} \in \mathbb{R}[/math]; GD learning rate [math]\lrate \gt0[/math].
Initialize: set [math]\weights^{(0)}\!\defeq\!\mathbf{0}[/math]; set iteration counter [math]\itercntr\!\defeq\!0[/math]
- repeat
- [math]\itercntr\!\defeq\! \itercntr\!+\!1[/math] (increase iteration counter)
- [math]\weights^{(\itercntr)} \defeq \weights^{(\itercntr\!-\!1)}\!+\!\lrate (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \frac{\truelabel^{(\sampleidx)}}{1\!+\!\exp \big( \truelabel^{(\sampleidx)} \big(\weights^{(\itercntr\!-\!1)}\big)^{T} \featurevec^{(\sampleidx)}\big)} \featurevec^{(\sampleidx)}[/math] (do a GD step \eqref{equ_def_GD_step})
- until stopping criterion met
Output: [math]\weights^{(\itercntr)}[/math], which approximates a solution [math]\overline{\weights}[/math] of \eqref{equ_smooth_problem_logeg})
Let us have a closer look on the update in step equ_step_updat_logreg_GD of Algorithm alg:gd_logreg. This step amounts to computing
Similar to the GD step \eqref{equ_update_gd_linreg} for linear regression, also the GD step \eqref{equ_update_logreg_GD} for logistic regression can be interpreted as an implementation of the trial-and-error principle. Indeed, \eqref{equ_update_logreg_GD} corrects the previous guess (or approximation) [math]\weights^{(\itercntr\!-\!1)}[/math] for the optimal parameter vector [math]\overline{\weights}[/math] by the correction term
The correction term \eqref{equ_correction_logreg_GD} is a weighted average of the feature vectors [math]\featurevec^{(\sampleidx)}[/math]. The feature vector [math]\featurevec^{(\sampleidx)}[/math] is weighted by the factor [math](\lrate/\samplesize) \cdot e^{(\sampleidx)}[/math]. These weighting factors are a product of the global factor [math](\lrate/\samplesize)[/math] that applies equally to all feature vectors [math]\featurevec^{(\sampleidx)}[/math]. The global factor is multiplied by a data point-specific factor [math]e^{(\sampleidx)} = \frac{\truelabel^{(\sampleidx)}}{1 + \exp ( \truelabel^{(\sampleidx)} \weights^{T} \featurevec^{(\sampleidx)})}[/math], which quantifies the error of the classifier [math]h^{(\weights^{(\itercntr\!-\!1)})}(\featurevec^{(\sampleidx)}) = \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)}[/math] for a single data point with true label [math]\truelabel^{(\sampleidx)} \in \{-1,1\}[/math] and features [math]\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}[/math].
We can use the sufficient condition \eqref{equ_GD_conv_guarantee} for the convergence of GD steps to guide the choice of the learning rate [math]\lrate[/math] in Algorithm alg:gd_logreg. To apply condition \eqref{equ_GD_conv_guarantee}, we need to determine the Hessian [math]\nabla^{2} f(\weights)[/math] matrix of the objective function [math]f(\weights)[/math] underlying logistic regression (see \eqref{equ_smooth_problem_logeg}). Some basic calculus reveals (see [6](Ch. 4.4.))
Here, we used the feature matrix [math]\featuremtx=\big(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)}\big)^{T} \in \mathbb{R}^{\samplesize \times \featuredim}[/math] (see feature matrix ) and the diagonal matrix [math]\mD = {\rm diag} \{d_{1},\ldots,d_{\samplesize}\} \in \mathbb{R}^{\samplesize \times \samplesize}[/math] with diagonal elements
We highlight that, in contrast to the Hessian \eqref{equ_hessian_linreg} of the objective function arising in linear regression, the Hessian \eqref{equ_hessian_logreg} of logistic regression varies with the parameter vector [math]\weights[/math]. This makes the analysis of Algorithm alg:gd_logreg and the optimal choice for the learning rate [math]\lrate[/math] more difficult compared to Algorithm alg:gd_linreg. At least, we can ensure convergence of \eqref{equ_update_logreg_GD} (towards a solution of \eqref{equ_smooth_problem_logeg}) for the learning rate [math]\lrate=1[/math] if we normalize feature vectors such that [math]\| \featurevec^{(\sampleidx)} \|=1[/math]. This follows from the fact the diagonal entries \eqref{equ_diag_entries_log_reg} take values in the interval [math][0,1][/math].
Data Normalization
The number of GD steps \eqref{equ_def_GD_step} required to reach the minimum (within a prescribed accuracy) of the objective function depends crucially on the condition number [3][7]
Here, we use the largest and smallest eigenvalue of the matrix [math]\featuremtx^{T} \featuremtx[/math], denoted as [math] \eigval{\rm max}[/math] and [math]\eigval{\rm min}[/math], respectively. The condition number \eqref{equ_def_condition_number} is only well-defined if the columns of the feature matrix [math]\featuremtx[/math] (which are the feature vectors [math]\featurevec^{(\sampleidx)}[/math]), are linearly independent. In this case the condition number is lower bounded as [math]1 \leq \kappa( \featuremtx^{T} \featuremtx)[/math].
It can be shown that the GD steps \eqref{equ_def_GD_step} converge faster for smaller condition number [math]\kappa( \featuremtx^{T} \featuremtx)[/math] [7]. Thus, GD will be faster for datasets with a feature matrix [math]\featuremtx[/math] such that [math]\kappa( \featuremtx^{T} \featuremtx) \approx 1[/math]. It is therefore often beneficial to pre-process the feature vectors using a normalization (or standardization) procedure as detailed in Algorithm alg_reshaping.
Input: labeled dataset [math]\dataset = \{(\featurevec^{(\sampleidx)},y^{(\sampleidx)})\}_{\sampleidx=1}^{\samplesize}[/math]
- remove sample means [math]\widehat{\featurevec}=(1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \featurevec^{(\sampleidx)}[/math] from features, i.e.,
[[math]] \begin{equation} \nonumber \featurevec^{(\sampleidx)} \defeq \featurevec^{(\sampleidx)} - \widehat{\featurevec} \mbox{ for } \sampleidx=1,\ldots,\samplesize \end{equation} [[/math]]
- normalise features to have unit variance,
[[math]] \begin{equation} \nonumber \hat{\feature}^{(\sampleidx)}_{\featureidx} \defeq \feature^{(\sampleidx)}_{\featureidx}/ \hat{\sigma} \mbox{ for } \featureidx=1,\ldots,\featuredim \mbox{ and } \sampleidx=1,\ldots,\samplesize \end{equation} [[/math]]with the empirical (sample) variance [math]\hat{\sigma}_{\featureidx}^{2} =(1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big( \feature^{(\sampleidx)}_{\featureidx} \big)^{2}[/math]
Output: normalized feature vectors [math]\{\hat{\featurevec}^{(\sampleidx)}\}_{\sampleidx=1}^{\samplesize}[/math]
Algorithm alg_reshaping transforms the original feature vectors [math]\featurevec^{(\sampleidx)}[/math] into new feature vectors [math]\widehat{\featurevec}^{(\sampleidx)}[/math] such that the new feature matrix [math]\widehat{\featuremtx} = (\widehat{\featurevec}^{(1)},\ldots,\widehat{\featurevec}^{(\samplesize)})^{T}[/math] is better conditioned than the original feature matrix, i.e., [math]\kappa( \widehat{\featuremtx}^{T} \widehat{\featuremtx}) \lt \kappa( \featuremtx^{T} \featuremtx)[/math].
Stochastic GD
Consider the GD steps \eqref{equ_def_GD_step} for minimizing the empirical risk \eqref{equ_obj_emp_risk_GD}. The gradient [math]\nabla f(\weights)[/math] of the objective function \eqref{equ_obj_emp_risk_GD} has a particular structure. Indeed, this gradient is a sum
Each component of the sum \eqref{eq_gradient_sum} corresponds to one particular data points [math](\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math]. We need to compute a sum of the form \eqref{eq_gradient_sum} for each new GD step \eqref{equ_def_GD_step}.
Computing the sum in \eqref{eq_gradient_sum} can be computationally challenging for at least two reasons. First, computing the sum is challenging for very large datasets with [math]\samplesize[/math] in the order of billions. Second, for datasets which are stored in different data centres located all over the world, the summation would require a huge amount of network resources. Moreover, the finite transmission rate of communication networks limits the rate by which the GD steps \eqref{equ_def_GD_step} can be executed.
The idea of stochastic gradient descent (SGD) is to replace the exact gradient [math]\nabla f(\weights)[/math] \eqref{eq_gradient_sum} by an approximation that is easier to compute than a direct evaluation of \eqref{eq_gradient_sum}. The word “stochastic” in the name SGD hints already at the use of a stochastic approximation [math]\noisygrad(\weights) \approx \nabla f(\weights)[/math]. It turns out that using a gradient approximation [math]\noisygrad(\weights)[/math] can result in significant savings in computational complexity while incurring a graceful degradation in the overall optimization accuracy. The optimization accuracy (distance to minimum of [math]f(\weights)[/math]) depends crucially on the “gradient noise”
The elementary step of most SGD methods is obtained from the GD step \eqref{equ_def_GD_step} by replacing the exact gradient [math]\nabla f(\weights)[/math] with some stochastic approximation [math]\noisygrad(\weights)[/math],
As the notation in \eqref{equ_SGD_update} indicates, SGD methods use a learning rate [math]\lrate_{\itercntr}[/math] that varies between different iterations.
To avoid accumulation of the gradient noise \eqref{equ_def_gradient_noise_generic} during the SGD updates \eqref{equ_SGD_update}, SGD methods typically decrease the learning rate [math]\lrate_{\itercntr}[/math] as the iterations proceed. The precise dependence of the learning rate [math]\lrate_{\itercntr}[/math] on the iteration index [math]\itercntr[/math] is referred to as a learning rate schedule [1](Chapter 8). One possible choice for the learning rate schedule is [math]\lrate_{\itercntr}\!\defeq\!1/\itercntr[/math] [8]. Exercise discusses conditions on the learning rate schedule that guarantee convergence of the updates SGD to the minimum of [math]f(\weights)[/math].
The approximate (“noisy”) gradient [math]\noisygrad(\weights)[/math] can be obtained by different randomization strategies. The most basic form of SGD constructs the gradient approximation [math]\noisygrad(\weights)[/math] by replacing the sum \eqref{eq_gradient_sum} with a randomly selected component,
The index [math]\hat{\sampleidx}[/math] is chosen randomly from the set [math]\{1,\ldots,\samplesize\}[/math]. The resulting Stochastic gradient descent (SGD) method then repeats the update
sufficiently often. Every update \eqref{equ_SGD_update_basic_form} uses a “fresh” randomly chosen (drawn) index [math]\hat{\sampleidx}_{\itercntr}[/math]. Formally, the indices [math]\hat{\sampleidx}_{\itercntr}[/math] are realizations of iid random variable (RV)s whose common probability distribution is the uniform distribution over the index set [math]\{1,\ldots,\samplesize\}[/math].
Note that \eqref{equ_SGD_update_basic_form} replaces the summation over the training set during the GD step \eqref{equ_def_GD_step} by randomly selecting a single component of this sum. The resulting savings in computational complexity can be significant when the training set consists of a large number of data points that might be stored in a distributed fashion (in the “cloud”). The saving in computational complexity of SGD comes at the cost of introducing a non-zero gradient noise
Mini-Batch SGD. Let us now discuss a variant of SGD that tries to reduce the approximation error (gradient noise) \eqref{equ_gradient_noise_simple_form} arising in the SGD step \eqref{equ_SGD_update_basic_form}. The idea behind this variant, referred to as mini-batch SGD, is quite simple. Instead of using only a single randomly selected component [math]\nabla f_{\sampleidx}(\weights)[/math] (see \eqref{eq_gradient_sum}) for constructing a gradient approximation, mini-batch SGD uses several randomly chosen components.
We summarize mini-batch SGD in Algorithm alg:minibatch_gd which requires an integer batch size [math]\batchsize[/math] as input parameter. Algorithm alg:minibatch_gd repeats the SGD step \eqref{equ_SGD_update} using a gradient approximation that is constructed from a randomly selected subset [math]\batch = \{ \sampleidx_{1},\ldots,\sampleidx_{\batchsize}\}[/math] (a “batch”),
For each new iteration of Algorithm alg:minibatch_gd, a new batch [math]\batch[/math] is generated by a random generator.
Input: components [math]f_{\sampleidx}(\weights)[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math] of objective function [math]f(\weights)=\sum_{\sampleidx=1}^{\samplesize} f_{\sampleidx}(\weights)[/math] ; batch size [math]\batchsize[/math]; learning rate schedule [math]\lrate_{\itercntr} \gt0[/math].
set [math]\vw^{(0)}\!\defeq\!\mathbf{0}[/math]; set iteration counter [math]\itercntr\!\defeq\!0[/math]
- repeat
- randomly select a batch [math]\batch = \{\sampleidx_{1},\ldots,\sampleidx_{\batchsize}\} \subseteq \{1,\ldots,\samplesize\}[/math] of indices that select a subset of components [math]f_{\sampleidx}[/math]
- compute an approximate gradient [math]\noisygrad \big( \weights^{(\itercntr)} \big)[/math] using \eqref{equ_def_gradient_approx_mini_batch}
- [math]\itercntr \defeq \itercntr +1[/math] (increase iteration counter)
- [math]\weights^{(\itercntr)} \defeq \weights^{(\itercntr\!-\!1)} - \lrate_{\itercntr} \noisygrad \big( \weights^{(\itercntr-1)} \big)[/math]
- until stopping criterion met
Note that Algorithm alg:minibatch_gd includes the basic SGD variant \eqref{equ_SGD_update_basic_form}
as a special case for the batch size [math]\batchsize=1[/math]. Another special case is [math]\batchsize= \samplesize[/math], where
the SGD step \ref{equ_sGD_step_minibtatch} in Algorithm alg:minibatch_gd becomes an
ordinary GD step \eqref{equ_def_GD_step}.
Online Learning. A main motivation for the SGD step \eqref{equ_SGD_update_basic_form} is
that a training set is already collected but so large that the sum in \eqref{eq_gradient_sum} is
computationally intractable. Another variant of SGD is obtained for sequential (time-series) data. In particular, consider
data points that are gathered sequentially, one new data point [math]\big( \featurevec^{(\timeidx)},\truelabel^{(\timeidx)} \big)[/math]
at each time instant [math]\timeidx=1,2,\ldots.[/math]. With each new data point [math]\big( \featurevec^{(\timeidx)},\truelabel^{(\timeidx)} \big)[/math]
we can access a new component [math]f_{\timeidx}(\weights) = \loss{(\featurevec^{(\timeidx)},\truelabel^{(\timeidx)})}{h^{(\weights)}}[/math] (see \eqref{equ_obj_emp_risk_GD}). For sequential data, we can use a slight modification of the SGD step \eqref{equ_SGD_update}
to obtain an online learning method (see Section Online Learning ).
This online variant of SGD computes, at each time instant [math]\timeidx[/math],
Advanced Gradient-Based Methods
The main idea underlying GD and SGD is to approximate the objective function \eqref{equ_obj_emp_risk_GD} locally around a current guess or approximation [math]\weights^{(\itercntr)}[/math] for the optimal weights. This local approximation is a tangent hyperplane whose normal vector is determined by the gradient [math]\nabla f (\weights^{(\itercntr)}[/math]. We then obtain an updated (improved) approximation by minimizing this local approximation, i.e., by doing a GD step \eqref{equ_def_GD_step}.
The idea of advanced gradient methods [1](Ch. 8) is to exploit the information provided by the gradients [math]\nabla f\big(\weights^{(\itercntr')}\big)[/math] at previous iterations [math]\itercntr'=1,\ldots,\itercntr[/math], to build an improved local approximation of [math]f(\weights)[/math] around a current iterate [math]\weights^{(\itercntr)}[/math]. Figure fig_improved_local_approx indicates such an improved local approximation of [math]f(\weights)[/math] which is non-linear (e.g., quadratic). These improved local approximations can be used to adapt the learning rate during the GD steps \eqref{equ_def_GD_step}.
Advanced gradient-based methods use improved local approximations to modify the gradient [math]\nabla f\big(\weights^{(\itercntr')}\big)[/math] to obtain an improved update direction. Figure fig_improved_local_approx_better_directions depicts the contours of an objective function [math]f(\weights)[/math] for which the gradient [math]\nabla f\big(\weights^{(\itercntr)}\big)[/math] points only weakly towards the optimal parameter vector [math]\overline{\weights}[/math] (minimizer of [math]f(\weights)[/math]). The gradient history [math]\nabla f\big(\weights^{(\itercntr')}\big)[/math], for[math]\itercntr'=1,\ldots,\itercntr[/math], allows to detect such an unfavourable geometry of the objective function. Moreover, the gradient history can be used to “correct” the update direction [math]\nabla f\big(\weights^{(\itercntr)}\big)[/math] to obtain an improved update direction towards the optimum parameter vector [math]\overline{\weights}[/math].
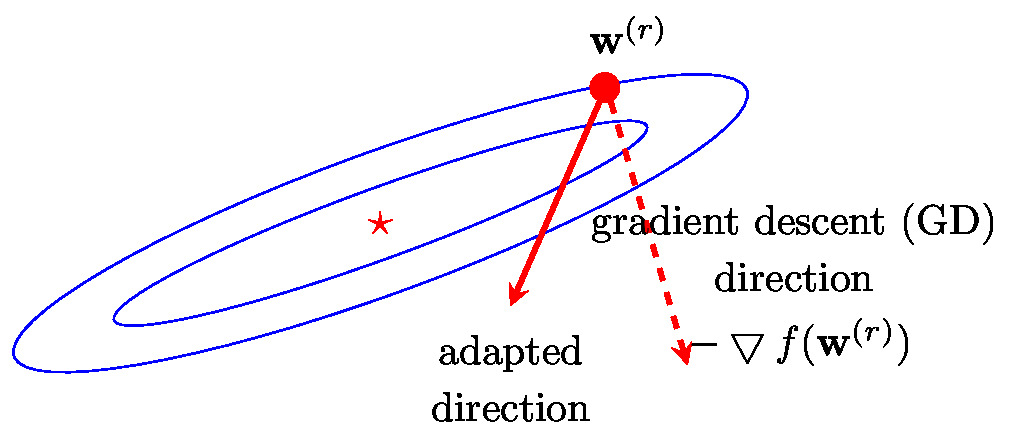
Notes
- The problem of computing a full eigenvalue decomposition of [math]\featuremtx^{T} \featuremtx[/math] has essentially the same complexity as ERM via directly solving equ_zero_gradient_lin_reg, which we want to avoid by using the “cheaper” GD Algorithm alg:gd_linreg.
General References

Jung, Alexander (2022). Machine Learning: The Basics. Signapore: Springer. doi:10.1007/978-981-16-8193-6.
Jung, Alexander (2022). "Machine Learning: The Basics". arXiv:1805.05052.
References
- Jump up to: 1.0 1.1 1.2 1.3 1.4 I. Goodfellow, Y. Bengio, and A. Courville. Deep Learning MIT Press, 2016
- Jump up to: 2.0 2.1 W. Rudin. Principles of Mathematical Analysis McGraw-Hill, New York, 3 edition, 1976
- Jump up to: 3.0 3.1 3.2 3.3 S. Bubeck. Convex optimization. algorithms and complexity. In Foundations and Trends in Machine Learning volume 8. Now Publishers, 2015
- Jump up to: 4.0 4.1 Y. Nesterov. Introductory lectures on convex optimization volume 87 of Applied Optimization. Kluwer Academic Publishers, Boston, MA, 2004. A basic course
- S. Oymak, B. Recht, and M. Soltanolkotabi. Sharp time--data tradeoffs for linear inverse problems. IEEE Transactions on Information Theory 64(6):4129--4158, June 2018
- T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning Springer Series in Statistics. Springer, New York, NY, USA, 2001
- Jump up to: 7.0 7.1 A. Jung. A fixed-point of view on gradient methods for big data. Frontiers in Applied Mathematics and Statistics 3, 2017
- N. Murata. A statistical study on on-line learning. In D. Saad, editor, On-line Learning in Neural Networks pages 63--92. Cambridge University Press, New York, NY, USA, 1998