guide:E22dac98a8: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 82: | Line 82: | ||
with intercept <math>\beta_0</math>, growth medium concentration <math>X_i</math> in petri dish <math>i</math>, and fixed growth medium effect <math>\beta_1</math>, and <math>\mathbf{Z}_i = (1, X_i)</math>, <math>\ggamma</math> the <math>2</math> dimensional random effect parameter bivariate normally distributed with zero mean and diagonal covariance matrix, and finally <math>\varepsilon_{it}\sim \mathcal{N}(0,\sigma_{\varepsilon}^2)</math> the error in the cell count of petri dish <math>i</math> at time <math>t</math>. In matrix notation the matrix <math>\mathbf{Z}</math> would comprise of <math>2n</math> columns: two columns for each cell, | with intercept <math>\beta_0</math>, growth medium concentration <math>X_i</math> in petri dish <math>i</math>, and fixed growth medium effect <math>\beta_1</math>, and <math>\mathbf{Z}_i = (1, X_i)</math>, <math>\ggamma</math> the <math>2</math> dimensional random effect parameter bivariate normally distributed with zero mean and diagonal covariance matrix, and finally <math>\varepsilon_{it}\sim \mathcal{N}(0,\sigma_{\varepsilon}^2)</math> the error in the cell count of petri dish <math>i</math> at time <math>t</math>. In matrix notation the matrix <math>\mathbf{Z}</math> would comprise of <math>2n</math> columns: two columns for each cell, | ||
<math>\mathbf{e}_i</math> and <math>X_i \mathbf{e}_i</math> (with <math>\mathbf{e}_i</math> the <math>n</math>-dimensional unit vector with a one at the <math>i</math>-th location and zeros elsewhere), corresponding to the random intercept and slope effect, respectively. | <math>\mathbf{e}_i</math> and <math>X_i \mathbf{e}_i</math> (with <math>\mathbf{e}_i</math> the <math>n</math>-dimensional unit vector with a one at the <math>i</math>-th location and zeros elsewhere), corresponding to the random intercept and slope effect, respectively. | ||
<div class="d-flex justify-content-center"> | <div class="d-flex justify-content-center"> | ||
<span id="fig:mixedModelExamples"></span> | <span id="fig:mixedModelExamples"></span> | ||
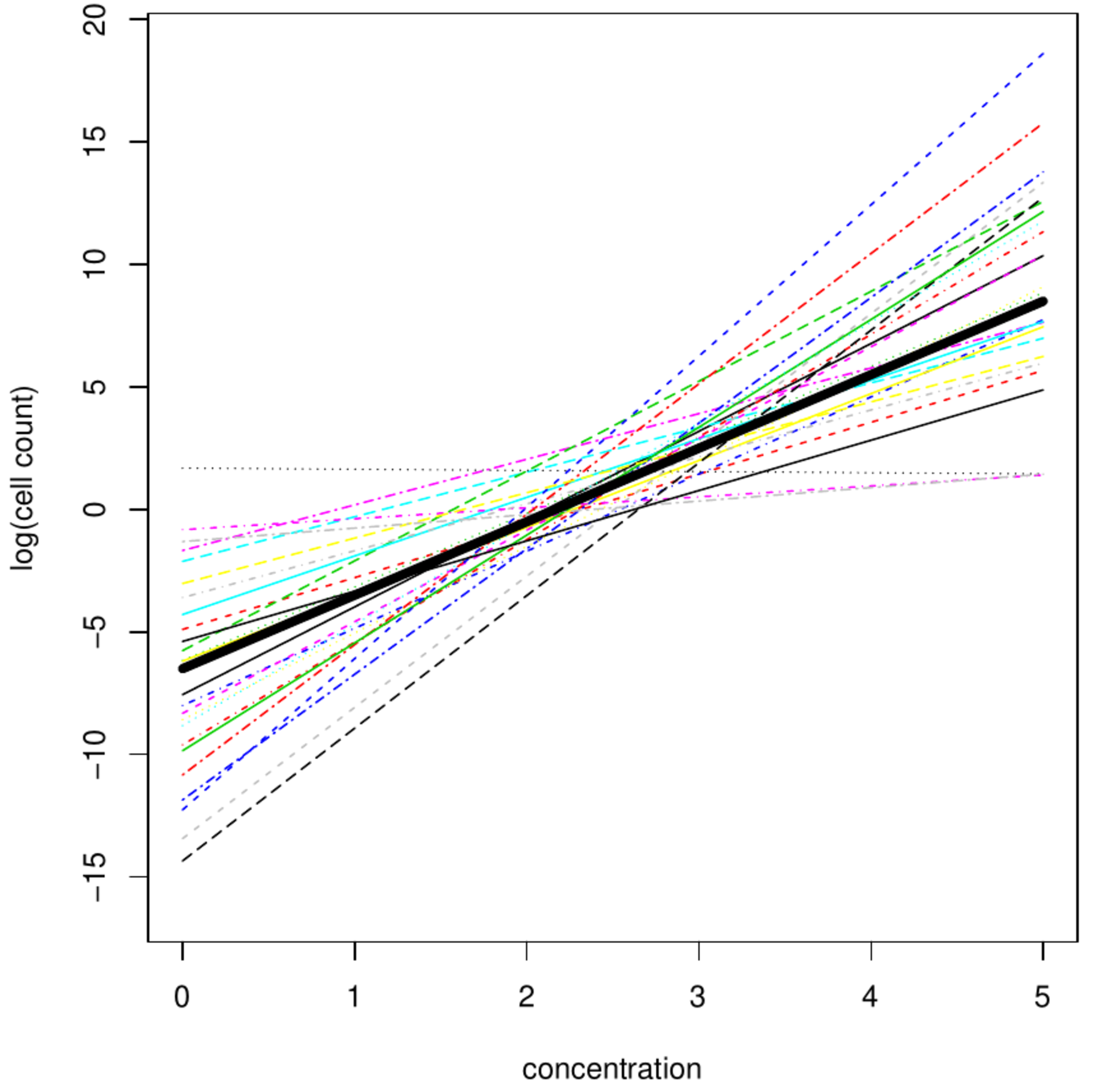
[[File:mixedModelIllustration.png | 400px | thumb | Linear regession (thick black solid line) vs. mixed model fit (thin colored and patterned lines). ]] | [[File:mixedModelIllustration.png | 400px | thumb | Linear regession (thick black solid line) vs. mixed model fit (thin colored and patterned lines). ]] | ||
</div> | </div> | ||
The fact that the number columns of <math>\mathbf{Z}</math>, i.e. the explanatory random effects, equals <math>2n</math> does not pose identifiability problems as per column only a single parameter is estimated. Finally, to illustrate the difference between the linear regression and the linear mixed model their fits on artifical data are plotted (top left panel, [[#fig:mixedModelExamples|Figure]]). Where the linear regression fit shows the ‘grand mean relationship’ between cell count and growth medium, the linear mixed model fit depicts the petri dish specific fits. | The fact that the number columns of <math>\mathbf{Z}</math>, i.e. the explanatory random effects, equals <math>2n</math> does not pose identifiability problems as per column only a single parameter is estimated. Finally, to illustrate the difference between the linear regression and the linear mixed model their fits on artifical data are plotted (top left panel, [[#fig:mixedModelExamples|Figure]]). Where the linear regression fit shows the ‘grand mean relationship’ between cell count and growth medium, the linear mixed model fit depicts the petri dish specific fits. | ||
| Line 249: | Line 251: | ||
</math> | </math> | ||
in which -- following Henderson -- <math>\mathbf{R}_{\theta}</math> and <math>\sigma_{\varepsilon}^2</math> are assumed known (for instance by virtue of maximum likelihood or REML estimation). The estimators of <math>\bbeta</math> and <math>\ggamma</math> are now the minimizers of | in which -- following Henderson -- <math>\mathbf{R}_{\theta}</math> and <math>\sigma_{\varepsilon}^2</math> are assumed known (for instance by virtue of maximum likelihood or REML estimation). The estimators of <math>\bbeta</math> and <math>\ggamma</math> are now the minimizers of ([[#mixedModel.penalizedLossFunction |loss criterion ]]). Effectively, the random effect parameter <math>\ggamma</math> is now temporarily assumed to be ‘fixed’. That is, it is temporarily treated as fixed in the derivations below that lead to the construction of the linear predictor. However, <math>\ggamma</math> is a random variable and one therefore speaks of a linear predictor rather than linear estimator. | ||
To find the estimators of <math>\bbeta</math> and <math>\ggamma</math>, defined as the minimizer of loss function, equate the partial derivatives of mixed model | To find the estimators of <math>\bbeta</math> and <math>\ggamma</math>, defined as the minimizer of loss function, equate the partial derivatives of mixed model ([[#mixedModel.penalizedLossFunction |loss function]]) with respect to <math>\bbeta</math> and <math>\ggamma</math> to zero. This yields the estimating equations (also referred to as Henderson's mixed model equations): | ||
<math display="block"> | <math display="block"> | ||
| Line 415: | Line 417: | ||
==Link to ridge regression== | ==Link to ridge regression== | ||
The link with ridge regression, implicit in the | The link with ridge regression, implicit in the exposé on the mixed model, is now explicated. Recall that ridge regression fits the linear regression model <math>\mathbf{Y} = \mathbf{X} \bbeta + \vvarepsilon</math> by means of a penalized maximum likelihood procedure, which defines -- for given penalty parameter <math>\lambda</math> -- the estimator as: | ||
<math display="block"> | <math display="block"> | ||
| Line 424: | Line 426: | ||
Constrast this to a mixed model void of covariates with fixed effects and comprising only covariates with a random effects: <math>\mathbf{Y} = \mathbf{Z} \ggamma + \vvarepsilon</math> with distributional assumptions <math>\ggamma \sim \mathcal{N}( \mathbf{0}_q, \sigma_{\gamma}^2 \mathbf{I}_{qq})</math> and | Constrast this to a mixed model void of covariates with fixed effects and comprising only covariates with a random effects: <math>\mathbf{Y} = \mathbf{Z} \ggamma + \vvarepsilon</math> with distributional assumptions <math>\ggamma \sim \mathcal{N}( \mathbf{0}_q, \sigma_{\gamma}^2 \mathbf{I}_{qq})</math> and | ||
<math>\vvarepsilon \sim \mathcal{N}(\mathbf{0}_n, \sigma_{\varepsilon}^2 \mathbf{I}_{nn})</math>. This model, when temporarily considering <math>\ggamma</math> as fixed, is fitted by the minimization of loss function ([[#mixedModel.penalizedLossFunction | | <math>\vvarepsilon \sim \mathcal{N}(\mathbf{0}_n, \sigma_{\varepsilon}^2 \mathbf{I}_{nn})</math>. This model, when temporarily considering <math>\ggamma</math> as fixed, is fitted by the minimization of loss function ([[#mixedModel.penalizedLossFunction |loss function]]). The corresponding estimator of <math>\ggamma</math> is then defined, with the current mixed model assumptions in place, as: | ||
<math display="block"> | <math display="block"> | ||
| Line 432: | Line 434: | ||
</math> | </math> | ||
The estimators are -- up to a reparamatrization of the penalty parameter -- defined identically. This should not come as a surprise after the discussion of Bayesian regression (cf. Chapter [[guide:52e4430d25 | Bayesian regression ]]) and the alert reader would already have recognized a generalized ridge loss function in | The estimators are -- up to a reparamatrization of the penalty parameter -- defined identically. This should not come as a surprise after the discussion of Bayesian regression (cf. Chapter [[guide:52e4430d25 | Bayesian regression ]]) and the alert reader would already have recognized a generalized ridge loss function in ([[#mixedModel.penalizedLossFunction |Equation ]]). The fact that we discarded the fixed effect part of the mixed model is irrelevant for the analogy as those would correspond to unpenalized covariates in the ridge regression problem. | ||
The link with ridge regression is also immenent from the linear predictor of the random effect. Recall: <math>\hat{\ggamma} = (\mathbf{Z}^{\top} \mathbf{Z} + \mathbf{R}_{\theta}^{-1})^{-1} \mathbf{Z}^{\top} (\mathbf{Y} - \mathbf{X} \bbeta)</math>. When we ignore <math>\mathbf{R}_{\theta}^{-1}</math>, the predictor reduces to a least squares estimator. But with a symmetric and positive definite matrix <math>\mathbf{R}_{\theta}^{-1}</math>, the predictor is actually of the shrinkage type as is the ridge regression estimator. This shrinkage estimator also reveals, through the term <math>(\mathbf{Z}^{\top} \mathbf{Z} + \mathbf{R}_{\theta}^{-1})^{-1}</math>, that a <math>q</math> larger than <math>n</math> does not cause identifiability problems as long as <math>\mathbf{R}_{\theta}</math> is parametrized low-dimensionally enough. | The link with ridge regression is also immenent from the linear predictor of the random effect. Recall: <math>\hat{\ggamma} = (\mathbf{Z}^{\top} \mathbf{Z} + \mathbf{R}_{\theta}^{-1})^{-1} \mathbf{Z}^{\top} (\mathbf{Y} - \mathbf{X} \bbeta)</math>. When we ignore <math>\mathbf{R}_{\theta}^{-1}</math>, the predictor reduces to a least squares estimator. But with a symmetric and positive definite matrix <math>\mathbf{R}_{\theta}^{-1}</math>, the predictor is actually of the shrinkage type as is the ridge regression estimator. This shrinkage estimator also reveals, through the term <math>(\mathbf{Z}^{\top} \mathbf{Z} + \mathbf{R}_{\theta}^{-1})^{-1}</math>, that a <math>q</math> larger than <math>n</math> does not cause identifiability problems as long as <math>\mathbf{R}_{\theta}</math> is parametrized low-dimensionally enough. | ||
| Line 569: | Line 571: | ||
An organism's internal circadian clock enables it to synchronize its activities to the earth's day-and-night cycle. The circadian clock maintains, due to environmental feedback, oscillations of approximately 24 hours. Molecularly, these oscillations reveal themselves in the fluctuation of the transcription levels of genes. The molecular core of the circadian clock is made up of <math>\pm 10</math> genes. Their behaviour (in terms of their expression patterns) is described by a dynamical system with feedback mechanisms. Linked to this core are genes that tap into the clock's rythm and use it to regulate the molecular processes. As such many genes are expected to exhibit circadian rythms. This is investigated in a mouse experiment in which the expression levels of several transcipts have been measured during two days with a resolution of one hour, resulting in a time-series of 48 time points publicly available from the <TT>R</TT>-package <TT>MetaCycle</TT>. Circadian rythms may be identified simply by eye-balling the data. But to facilitate this identification the data are smoothed to emphasize the pattern present in these data. | An organism's internal circadian clock enables it to synchronize its activities to the earth's day-and-night cycle. The circadian clock maintains, due to environmental feedback, oscillations of approximately 24 hours. Molecularly, these oscillations reveal themselves in the fluctuation of the transcription levels of genes. The molecular core of the circadian clock is made up of <math>\pm 10</math> genes. Their behaviour (in terms of their expression patterns) is described by a dynamical system with feedback mechanisms. Linked to this core are genes that tap into the clock's rythm and use it to regulate the molecular processes. As such many genes are expected to exhibit circadian rythms. This is investigated in a mouse experiment in which the expression levels of several transcipts have been measured during two days with a resolution of one hour, resulting in a time-series of 48 time points publicly available from the <TT>R</TT>-package <TT>MetaCycle</TT>. Circadian rythms may be identified simply by eye-balling the data. But to facilitate this identification the data are smoothed to emphasize the pattern present in these data. | ||
<div class="d-flex justify-content-center"> | <div id="fig:PsplinesExamples"> | ||
< | <div class="d-flex justify-content-center flex-column flex-md-row"> | ||
[[File: | [[File:BsplinesDegree1.png|400px]] | ||
[[File:BsplinesDegree2.png|400px]] | |||
</div><div class="d-flex justify-content-center flex-column flex-md-row"> | |||
[[File:PsplineFit_gene2.png|400px]] | |||
[[File:PsplineFit_gene14.png|400px]] | |||
</div> | |||
</div> | |||
<div class="figure-caption"> | |||
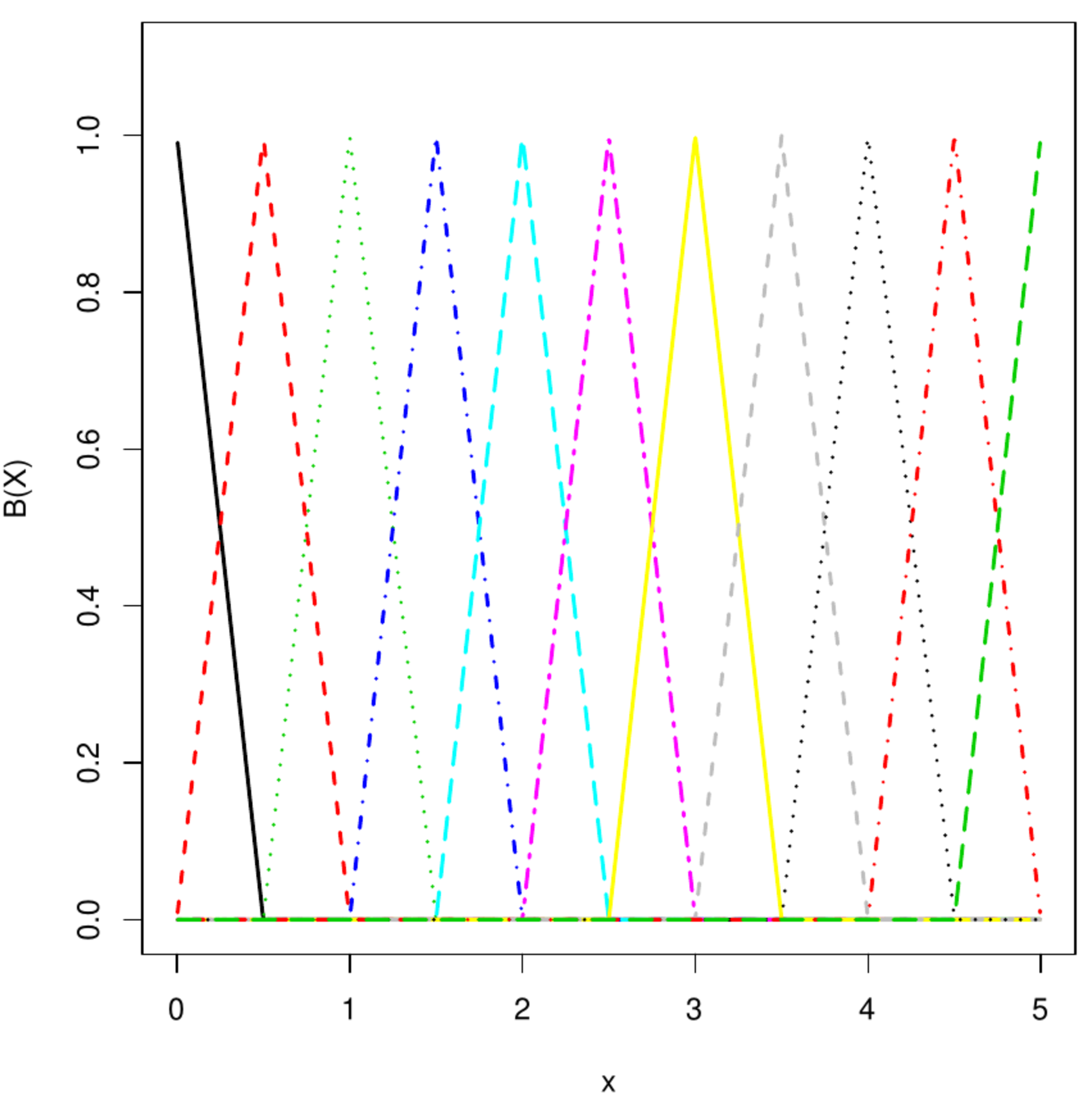
Top left and right panels: B-spline basis functions of degree 1 and 2, respectively. Bottom left and right panel: P-spline fit to transcript levels of circadian clock experiment in mice. | |||
</div> | </div> | ||
Latest revision as of 10:01, 6 July 2023
[math] \require{textmacros} \def \bbeta {\bf \beta} \def\fat#1{\mbox{\boldmath$#1$}} \def\reminder#1{\marginpar{\rule[0pt]{1mm}{11pt}}\textbf{#1}} \def\SSigma{\bf \Sigma} \def\ttheta{\bf \theta} \def\aalpha{\bf \alpha} \def\bbeta{\bf \beta} \def\ddelta{\bf \delta} \def\eeta{\bf \eta} \def\llambda{\bf \lambda} \def\ggamma{\bf \gamma} \def\nnu{\bf \nu} \def\vvarepsilon{\bf \varepsilon} \def\mmu{\bf \mu} \def\nnu{\bf \nu} \def\ttau{\bf \tau} \def\SSigma{\bf \Sigma} \def\TTheta{\bf \Theta} \def\XXi{\bf \Xi} \def\PPi{\bf \Pi} \def\GGamma{\bf \Gamma} \def\DDelta{\bf \Delta} \def\ssigma{\bf \sigma} \def\UUpsilon{\bf \Upsilon} \def\PPsi{\bf \Psi} \def\PPhi{\bf \Phi} \def\LLambda{\bf \Lambda} \def\OOmega{\bf \Omega} [/math]
Here the mixed model introduced by [1], which generalizes the linear regression model, is studied and estimated in unpenalized (!) fashion. Nonetheless, it will turn out to have an interesting connection to ridge regression. This connection may be exploited to arrive at an informed choice of the ridge penalty parameter.
The linear regression model, [math]\mathbf{Y} = \mathbf{X} \bbeta + \vvarepsilon[/math], assumes the effect of each covariate to be fixed. In certain situations it may be desirable to relax this assumption. For instance, a study may be replicated. Conditions need not be exactly constant across replications. Among others this may be due to batch effects. These may be accounted for and are then incorporated in the linear regression model. But it is not the effects of these particular batches included in the study that are of interest. Would the study have been carried out at a later date, other batches may have been involved. Hence, the included batches are thus a random draw from the population of all batches. With each batch possibly having a different effect, these effects may also be viewed as random draws from some hypothetical ‘effect’-distribution. From this point of view the effects estimated by the linear regression model are realizations from the ‘effect’-distribution. But interest is not in the particular but the general. Hence, a model that enables a generalization to the distribution of batch effects would be more suited here.
Like the linear regression model the mixed model, also called mixed effects model or random effects model, explains the variation in the response by a linear combination of the covariates. The key difference lies in the fact that the latter model distinguishes two sets of covariates, one with fixed effects and the other with random effects. In matrix notation mirroring that of the linear regression model, the mixed model can be written as:
where [math]\mathbf{Y}[/math] is the response vector of length [math]n[/math], [math]\mathbf{X}[/math] the [math](n \times p)[/math]-dimensional design matrix with the fixed vector [math]\bbeta[/math] with [math]p[/math] fixed effects, [math]\mathbf{Z}[/math] the [math](n \times q)[/math]- dimensional design matrix with an associated [math]q \times 1[/math] dimensional vector [math]\ggamma[/math] of random effects, and distributional assumptions [math]\vvarepsilon \sim \mathcal{N}( \mathbf{0}_{n}, \sigma_{\varepsilon}^2 \mathbf{I}_{nn})[/math], [math]\ggamma \sim \mathcal{N}(\mathbf{0}_{q}, \mathbf{R}_{\ttheta})[/math] and [math]\vvarepsilon[/math] and [math]\ggamma[/math] independent. In this [math]\mathbf{R}_{\ttheta}[/math] is symmetric, positive definite and parametrized by a low-dimensional parameter [math]\ttheta[/math].
The distribution of [math]\mathbf{Y}[/math] is fully defined by the mixed model and its accompanying assumptions. As [math]\mathbf{Y}[/math] is a linear combination of normally distributed random variables, it is itself normally distributed. Its mean is:
while its variance is:
in which the independence between [math]\vvarepsilon[/math] and [math]\ggamma[/math] and the standard algebra rules for the [math]\mbox{Var}(\cdot)[/math] and [math]\mbox{Cov}(\cdot)[/math] operators have been used. Put together, this yields: [math]\mathbf{Y} \sim \mathcal{N}(\mathbf{X} \bbeta, \mathbf{Z} \mathbf{R}_{\theta} \mathbf{Z}^{\top} + \sigma^2_{\varepsilon} \mathbf{I}_{nn})[/math]. Hence, the random effects term [math]\mathbf{Z} \ggamma[/math] of the mixed model does not contribute to the explanation of the mean of [math]\mathbf{Y}[/math], but aids in the decomposition of its variance around the mean. From this formulation of the model it is obvious that the random part of two distinct observations of the response are -- in general -- not independent: their covariance is given by the corresponding element of [math]\mathbf{Z} \mathbf{R}_{\theta} \mathbf{Z}^{\top}[/math]. Put differently, due to the independence assumption on the error two observations can only be (marginally) dependent through the random effect which is attenuated by the associated design matrix [math]\mathbf{Z}[/math]. To illustrate this, temporarily set [math]\mathbf{R}_{\theta} = \sigma_{\gamma}^2 \mathbf{I}_{qq}[/math]. Then, [math]\mbox{Var}(\mathbf{Y}) = \sigma_{\gamma}^2 \mathbf{Z} \mathbf{Z}^{\top} + \sigma_{\varepsilon}^2 \mathbf{I}_{nn}[/math]. From this it is obvious that two variates of [math]\mathbf{Y}[/math] are now independent if and only if the corresponding rows of [math]\mathbf{Z}[/math] are orthogonal. Moreover, two pairs of variates have the same covariance if they have the same covariate information in [math]\mathbf{Z}[/math]. Two distinct observations of the same individual have the same covariance as one of these observations with that of another individual with identical covariate information as the left-out observation on the former individual. In particular, their ‘between-covariance’ equals their individual ‘within-covariance’.
The mixed model and the linear regression model are clearly closely related: they share a common mean, a normally distributed error, and both explain the response by a linear combination of the explanatory variables. Moreover, when [math]\ggamma[/math] is known, the mixed model reduces to a linear regression model. This is seen from the conditional distribution of [math]\mathbf{Y}[/math]: [math]\mathbf{Y} \, | \, \ggamma \sim \mathcal{N}(\mathbf{X} \bbeta + \mathbf{Z} \ggamma, \sigma^2_{\varepsilon} \mathbf{I}_{nn})[/math]. Conditioning on the random effect [math]\ggamma[/math] thus pulls in the term [math]\mathbf{Z} \ggamma[/math] to the systematic, non-random explanatory part of the model. In principle, the conditioned mixed model could now be rewritten as a linear regression model by forming a new design matrix and parameter from [math]\mathbf{X}[/math] and [math]\mathbf{Z}[/math] and [math]\bbeta[/math] and [math]\ggamma[/math], respectively.
Example (Mixed model for a longitudinal study)
A longitudinal study looks into the growth rate of cells. At the beginning of the study cells are placed in [math]n[/math] petri dishes, with the same growth medium but at different concentrations. The initial number of cells in each petri dish is counted as is done at several subsequent time points. The change in cell count is believed to be -- at the log-scale -- a linear function of the concentration of the growth medium. The linear regression model may suffice. However, variation is omnipresent in biology. That is, apart from variation in the initial cell count, each cell -- even if they are from common decent -- will react (slightly?) differently to the stimulus of the growth medium. This intrinsic cell-to-cell variation in growth response may be accommodated for in the linear mixed model by the introduction of a random cell effect, both in off-set and slope. The (log) cell count of petri dish [math]i[/math] at time point [math]t[/math], denoted [math]Y_{it}[/math], is thus described by:
with intercept [math]\beta_0[/math], growth medium concentration [math]X_i[/math] in petri dish [math]i[/math], and fixed growth medium effect [math]\beta_1[/math], and [math]\mathbf{Z}_i = (1, X_i)[/math], [math]\ggamma[/math] the [math]2[/math] dimensional random effect parameter bivariate normally distributed with zero mean and diagonal covariance matrix, and finally [math]\varepsilon_{it}\sim \mathcal{N}(0,\sigma_{\varepsilon}^2)[/math] the error in the cell count of petri dish [math]i[/math] at time [math]t[/math]. In matrix notation the matrix [math]\mathbf{Z}[/math] would comprise of [math]2n[/math] columns: two columns for each cell, [math]\mathbf{e}_i[/math] and [math]X_i \mathbf{e}_i[/math] (with [math]\mathbf{e}_i[/math] the [math]n[/math]-dimensional unit vector with a one at the [math]i[/math]-th location and zeros elsewhere), corresponding to the random intercept and slope effect, respectively.
The fact that the number columns of [math]\mathbf{Z}[/math], i.e. the explanatory random effects, equals [math]2n[/math] does not pose identifiability problems as per column only a single parameter is estimated. Finally, to illustrate the difference between the linear regression and the linear mixed model their fits on artifical data are plotted (top left panel, Figure). Where the linear regression fit shows the ‘grand mean relationship’ between cell count and growth medium, the linear mixed model fit depicts the petri dish specific fits.
The mixed model was motivated by its ability to generalize to instances not included in the study. From the examples above another advantage can be deduced. E.g., the cells' effects are modelled by a single parameter (rather than one per cell). More degrees of freedom are thus left to estimate the noise level. In particular, a test for the presence of a cell effect will have more power.
The parameters of the mixed model are estimated either by means of likelihood maximization or a related procedure known as restricted maximum likelihood. Both are presented, with the exposé loosely based on [2]. First the maximum likelihood procedure is introduced, which requires the derivation of the likelihood. Hereto the assumption on the random effects is usually transformed. Let [math]\tilde{\mathbf{R}}_{\theta} = \sigma_{\varepsilon}^{-2} \mathbf{R}_{\theta}[/math], which is the covariance of the random effects parameter relevative to the error variance, and [math]\tilde{\mathbf{R}}_{\theta} = \mathbf{L}_{\theta} \mathbf{L}_{\theta}^{\top}[/math] its Cholesky decomposition. Next define the change-of-variables [math]\ggamma = \mathbf{L}_{\theta} \tilde{\ggamma}[/math]. This transforms the model to: [math]\mathbf{Y} = \mathbf{X} \bbeta + \mathbf{Z} \mathbf{L}_{\ttheta} \tilde{\ggamma} + \vvarepsilon[/math] but now with the assumption [math]\tilde{\ggamma} \sim \mathcal{N}(\mathbf{0}_{q}, \sigma_{\varepsilon}^2 \mathbf{I}_{qq})[/math]. Under this assumption the conditional likelihood, conditional on the random effects, is:
From this the unconditional likelihood is obtained through:
To evaluate the integral, the exponent needs rewriting. Hereto first note that:
Now expand the right-hand side as follows:
where [math]\mmu_{\tilde{\ggamma} \, | \mathbf{Y}} = (\mathbf{L}_{\theta}^{\top} \mathbf{Z}^{\top} \mathbf{Z} \mathbf{L}_{\theta} + \mathbf{I}_{qq})^{-1} \mathbf{L}_{\theta}^{\top} \mathbf{Z}^{\top} (\mathbf{Y} - \mathbf{X} \bbeta)[/math] and the Woodbury identity has been used in the last step. As the notation suggests [math]\mmu_{\tilde{\ggamma} \, | \mathbf{Y}}[/math] is the conditional expectation of the random effect conditional on the data: [math]\mathbb{E}(\tilde{\ggamma} \, | \, \mathbf{Y})[/math]. This may be verified from the conditional distribution [math]\tilde{\ggamma} \, | \, \mathbf{Y}[/math] when exploiting the equality derived in the preceeding display. Substitute the latter in the integral of the likelihood and use the change-of-variables: [math]\mathbf{h} = (\mathbf{L}_{\theta}^{\top} \mathbf{Z}^{\top} \mathbf{Z} \mathbf{L}_{\theta} + \mathbf{I}_{qq})^{1/2} ( \mathbf{g} - \mmu_{\tilde{\ggamma} \, | \, \mathbf{Y}} )[/math] with Jacobian [math]| (\mathbf{L}_{\theta}^{\top} \mathbf{Z}^{\top} \mathbf{Z} \mathbf{L}_{\theta} + \mathbf{I}_{qq})^{1/2} |[/math]:
where in the last step Sylvester's determinant identity has been used.
The maximum likelihood estimators of the mixed model parameters [math]\bbeta[/math], [math]\sigma_{\varepsilon}^2[/math] and [math]\tilde{\mathbf{R}}_{\theta}[/math] are found through the maximization of the logarithm of the likelihood (\ref{form.mixedModel_fullLikelihood}). Find the roots of the partial derivatives of this log-likelihood with respect to the mixed model parameters. For [math]\bbeta[/math] and [math]\sigma_{\varepsilon}^2[/math] this yields:
The former estimate can be substituted into the latter to remove its dependency on [math]\bbeta[/math]. However, both estimators still depend on [math]\ttheta[/math]. An estimator of [math]\ttheta[/math] may be found by substitution of [math]\hat{\bbeta}[/math] and [math]\hat{\sigma}_{\varepsilon}^2[/math] into the log-likelihood followed by its maximization. For general parametrizations of [math]\tilde{\mathbf{R}}_{\theta}[/math] by [math]\ttheta[/math] there are no explicit solutions. Then, resort to standard nonlinear solvers such as the Newton-Raphson algorithm and the like. With a maximum likelihood estimate of [math]\ttheta[/math] at hand, those of the other two mixed model parameters are readily obtained from the formula's above. As [math]\ttheta[/math] is unknown at the onset, it needs to be initiated followed by sequential updating of the parameter estimates until convergence.
Restricted maximum likelihood (REML) considers the fixed effect parameter [math]\bbeta[/math] as a ‘nuisance’ parameter and concentrates on the estimation of the variance components. The nuisance parameter is integrated out of the likelihood, [math]\int_{\mathbb{R}^p} L(\mathbf{Y}) d\bbeta[/math], which is referred to as the restricted likelihood. Those values of [math]\ttheta[/math] (and thereby [math]\tilde{\mathbf{R}}_{\theta}[/math]) and [math]\sigma_{\varepsilon}^2[/math] that maximize the restricted likelihood are the REML estimators. The restricted likelihood, by an argument similar to that used in the derivation of the likelihood, simplifies to:
where [math]\tilde{\mathbf{Q}}_{\theta} = \mathbf{I}_{nn} + \mathbf{Z} \tilde{\mathbf{R}}_{\theta} \mathbf{Z}^{\top}[/math] is the relative covariance (relative to the error variance) of [math]\mathbf{Y}[/math]. The REML estimators are now found by equating the partial derivatives of this restricted loglikelihood to zero and solving for [math]\sigma_{\varepsilon}^2[/math] and [math]\ttheta[/math]. The former, given the latter, is:
where the rewritten form reveals a projection matrix and, consequently, a residual sum of squares. Like the maximum likelihood estimator of [math]\ttheta[/math], its REML counterpart is generally unknown analytically and to be found numerically. Iterating between the estimation of both parameters until convergence yields the REML estimators. Obviously, REML estimation of the mixed model parameters does not produce an estimate of the fixed parameter [math]\bbeta[/math] (as it has been integrated out). Should however a point estimate be desired, then in practice the ML estimate of [math]\bbeta[/math] with the REML estimates of the other parameters is used.
An alternative way to proceed (and insightful for the present purpose) follows the original approach of Henderson, who aimed to construct a linear predictor for [math]\mathbf{Y}[/math].
A predictand is the function of the parameters that is to be predicted. A predictor is a function of the data that predicts the predictand. When this latter function is linear in the observation it is said to be a linear predictor.
In case of the mixed model the predictand is [math]\mathbf{X}_{{\mbox{{\tiny new}}}} \bbeta + \mathbf{Z}_{{\mbox{{\tiny new}}}} \ggamma[/math] for [math](n_{{\mbox{{\tiny new}}}} \times p)[/math]- and [math](n_{{\mbox{{\tiny new}}}} \times q)[/math]-dimensional design matrices [math]\mathbf{X}_{{\mbox{{\tiny new}}}}[/math] and [math]\mathbf{Z}_{{\mbox{{\tiny new}}}}[/math], respectively. Similarly, the predictor is some function of the data [math]\mathbf{Y}[/math]. When it can be expressed as [math]\mathbf{A} \mathbf{Y}[/math] for some matrix [math]\mathbf{A}[/math] it is a linear predictor.
The construction of the aforementioned linear predictor requires estimates of [math]\bbeta[/math] and [math]\ggamma[/math]. To obtain these estimates first derive the joint density of [math](\ggamma, \mathbf{Y})[/math]:
From this the likelihood is obtained and after some manipulations the loglikelihood can be shown to be proportional to:
in which -- following Henderson -- [math]\mathbf{R}_{\theta}[/math] and [math]\sigma_{\varepsilon}^2[/math] are assumed known (for instance by virtue of maximum likelihood or REML estimation). The estimators of [math]\bbeta[/math] and [math]\ggamma[/math] are now the minimizers of (loss criterion ). Effectively, the random effect parameter [math]\ggamma[/math] is now temporarily assumed to be ‘fixed’. That is, it is temporarily treated as fixed in the derivations below that lead to the construction of the linear predictor. However, [math]\ggamma[/math] is a random variable and one therefore speaks of a linear predictor rather than linear estimator.
To find the estimators of [math]\bbeta[/math] and [math]\ggamma[/math], defined as the minimizer of loss function, equate the partial derivatives of mixed model (loss function) with respect to [math]\bbeta[/math] and [math]\ggamma[/math] to zero. This yields the estimating equations (also referred to as Henderson's mixed model equations):
Solve each estimating equation for the parameters individually and find:
Note, using the Cholesky decomposition of [math]\tilde{\mathbf{R}}_{\theta}[/math] and applying the Woodbury identity twice (in both directions), that:
It thus coincides with the conditional estimate of the [math]\ggamma[/math] found in the derivation of the maximum likelihood estimator of the mixed model. This expression could also have been found by conditioning with the multivariate normal above which would have given [math]\mathbb{E}(\ggamma \, | \, \mathbf{Y})[/math].
The estimator of both [math]\bbeta[/math] and [math]\ggamma[/math] can be expressed fully and explicitly in terms of [math]\mathbf{X}[/math], [math]\mathbf{Y}[/math], [math]\mathbf{Z}[/math] and [math]\mathbf{R}_{\theta}[/math]. To obtain that of [math]\bbeta[/math] substitute the estimator of [math]\ggamma[/math] of equation (\ref{form.mixedModel_penEstOfGamma}) into that of [math]\bbeta[/math] given by equation \ref{form.mixedModel_penEstOfBeta}):
in which the Woodbury identity has been used. Now group terms and solve for [math]\bbeta[/math]:
This coincides with the maximum likelihood estimator of [math]\bbeta[/math] presented above (for known [math]\mathbf{R}_{\theta}[/math] and [math]\sigma_{\varepsilon}^2[/math]). Moreover, in the preceeding display one recognizes a generalized least squares (GLS) estimator. The GLS regression estimator is BLUE (Best Linear Unbiased Estimator) when [math]\mathbf{R}_{\theta}[/math] and [math]\sigma_{\varepsilon}[/math] are known. To find an explicit expression for [math]\ggamma[/math] use [math]\mathbf{Q}_{\theta}[/math] as previously defined and substitute the explicit expression (\ref{form.mixedModel_penEstOfBeta_explicit}) for the estimator of [math]\bbeta[/math] in the estimator of [math]\ggamma[/math], shown in display (\ref{form.mixedModel_penEstOfGamma}) above. This gives:
an explicit expression for the estimator of [math]\ggamma[/math].
The linear predictor constructed from these estimator can be shown (cf. Theorem) to be optimal, in the BLUP sense.
A Best Linear Unbiased Predictor (BLUP)
- is linear in the observations,
- is unbiased, and
- has a minimum (variance of its) predictor error, i.e. the difference among the predictor and predictand, among all unbiased linear predictors.
The predictor [math]\mathbf{X} \hat{\bbeta} + \mathbf{Z} \hat{\gamma}[/math] is the BLUP of [math]\tilde{\mathbf{Y}} = \mathbf{X} \bbeta + \mathbf{Z} \gamma[/math].
Show ProofThe predictor of [math]\mathbf{X} \hat{\bbeta} + \mathbf{Z} \hat{\ggamma}[/math] is:
Clearly, this is a linear function in [math]\mathbf{Y}[/math].
The expectation of the linear predictor is
This is also the expectation of the predictand [math]\mathbf{X} \bbeta + \mathbf{Z} \ggamma[/math]. Hence, the predictor is unbiased.
To show the predictor [math]\mathbf{B} \mathbf{Y}[/math] has minimum prediction error variance within the class of unbiased linear predictors, assume the existence of another unbiased linear predictor [math] \mathbf{A} \mathbf{Y}[/math] of [math]\mathbf{X} \bbeta + \mathbf{Z} \ggamma[/math]. The predictor error variance of the latter predictor is:
The last term vanishes as:
where the last step uses [math]\mathbf{A} \mathbf{X} = \mathbf{B} \mathbf{X}[/math], which follows from the fact that
for all [math]\bbeta \in \mathbb{R}^p[/math]. Hence,
Link to ridge regression
The link with ridge regression, implicit in the exposé on the mixed model, is now explicated. Recall that ridge regression fits the linear regression model [math]\mathbf{Y} = \mathbf{X} \bbeta + \vvarepsilon[/math] by means of a penalized maximum likelihood procedure, which defines -- for given penalty parameter [math]\lambda[/math] -- the estimator as:
Constrast this to a mixed model void of covariates with fixed effects and comprising only covariates with a random effects: [math]\mathbf{Y} = \mathbf{Z} \ggamma + \vvarepsilon[/math] with distributional assumptions [math]\ggamma \sim \mathcal{N}( \mathbf{0}_q, \sigma_{\gamma}^2 \mathbf{I}_{qq})[/math] and [math]\vvarepsilon \sim \mathcal{N}(\mathbf{0}_n, \sigma_{\varepsilon}^2 \mathbf{I}_{nn})[/math]. This model, when temporarily considering [math]\ggamma[/math] as fixed, is fitted by the minimization of loss function (loss function). The corresponding estimator of [math]\ggamma[/math] is then defined, with the current mixed model assumptions in place, as:
The estimators are -- up to a reparamatrization of the penalty parameter -- defined identically. This should not come as a surprise after the discussion of Bayesian regression (cf. Chapter Bayesian regression ) and the alert reader would already have recognized a generalized ridge loss function in (Equation ). The fact that we discarded the fixed effect part of the mixed model is irrelevant for the analogy as those would correspond to unpenalized covariates in the ridge regression problem.
The link with ridge regression is also immenent from the linear predictor of the random effect. Recall: [math]\hat{\ggamma} = (\mathbf{Z}^{\top} \mathbf{Z} + \mathbf{R}_{\theta}^{-1})^{-1} \mathbf{Z}^{\top} (\mathbf{Y} - \mathbf{X} \bbeta)[/math]. When we ignore [math]\mathbf{R}_{\theta}^{-1}[/math], the predictor reduces to a least squares estimator. But with a symmetric and positive definite matrix [math]\mathbf{R}_{\theta}^{-1}[/math], the predictor is actually of the shrinkage type as is the ridge regression estimator. This shrinkage estimator also reveals, through the term [math](\mathbf{Z}^{\top} \mathbf{Z} + \mathbf{R}_{\theta}^{-1})^{-1}[/math], that a [math]q[/math] larger than [math]n[/math] does not cause identifiability problems as long as [math]\mathbf{R}_{\theta}[/math] is parametrized low-dimensionally enough.
The following mixed model result provide an alternative approach to choice of the penalty parameter in ridge regression. It assumes a mixed model comprising of the random effects part only. Or, put differently, it assume the linear regression model [math]\mathbf{Y} = \mathbf{X} \bbeta + \vvarepsilon[/math] with [math]\bbeta \sim \mathcal{N}(\mathbf{0}_p, \sigma_{\bbeta}^2 \mathbf{I}_{pp})[/math] and [math]\varepsilon \sim \mathcal{N}(\mathbf{0}_n, \sigma_{\varepsilon}^2 \mathbf{I}_{nn})[/math].
The expected generalized cross-validation error [math]\mathbb{E}_{\bbeta} \{ \mathbb{E}_{\varepsilon} [ GCV(\lambda)] \}[/math] is minimized for [math]\lambda = \sigma_{\varepsilon}^2 / \sigma^2_{\beta}[/math].
Show ProofThe proof first finds an analytic expression of the expected [math]GCV(\lambda)[/math], then its minimum. Its expectation can be re-expressed as follows:
To get a handle on this expression, use [math](\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp})^{-1} \mathbf{X}^{\top} \mathbf{X} = \mathbf{I}_{pp} - \lambda (\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp})^{-1} = \mathbf{X}^{\top} \mathbf{X} (\mathbf{X}^{\top} \mathbf{X} + \lambda \mathbf{I}_{pp})^{-1}[/math], the cyclic property of the trace, and define [math]A(\lambda) = \sum\nolimits_{j=1}^p (d_{x,j}^2 + \lambda)^{-1}[/math], [math]B(\lambda) = \sum\nolimits_{j=1}^p (d_{x,j}^2 + \lambda)^{-2}[/math], and [math]C(\lambda) = \sum\nolimits_{j=1}^p (d_{x,j}^2 + \lambda)^{-3}[/math]. The traces in the expectation of [math]GCV(\lambda)[/math] can now be written as:
The expectation of [math]GCV(\lambda)[/math] can then be reformulated as:
Equate the derivative of this expectation w.r.t. [math]\lambda[/math] to zero, which can be seen to be proportional to:
Theorem can be extended to include unpenalized covariates. This leaves the result unaltered: the optimal (in the expected GCV sense) ridge penalty is the same signal-to-noise ratio.
We have encountered the result of Theorem before. Revisit Example which derived the mean squared error (MSE) of the ridge regression estimator when [math]\mathbf{X}[/math] is orthonormal. It was pointed out that this MSE is minized for [math]\lambda = p \sigma_{\varepsilon} / \bbeta^{\top} \bbeta[/math]. As [math]\bbeta^{\top} \bbeta /p[/math] is an estimator for [math]\sigma_{\beta}^2[/math], this implies the same optimal choice of the penalty parameter.
To point out the relevance of Theorem for the choice of the ridge penalty parameter still assume the regression parameter random. The theorem then says that the optimal penalty parameter (in the GCV sense) equals the ratio of the error variance and that of the regression parameter. Both variances can be estimated by means of the mixed model machinery (provided for instance by the lme4 package in R). These estimates may be plugged in the ratio to arrive at a choice of ridge penalty parameter (see Section Illustration: P-splines for an illustration of this usage).
REML consistency, high-dimensionally
Here a result on the asymptotic quality of the REML estimators of the random effect and error variance parameters is presented and discussed. It is the ratio of these parameters that forms the optimal choice (in the expected GCV sense) of the penalty parameter of the ridge regression estimator. As in practice the parameters are replaced by estimates to arrive at a choice for the penalty parameter, the quality of these estimators propogates to the chosen penalty parameter.
Consider the standard linear mixed model [math]\mathbf{Y} = \mathbf{X} \bbeta + \mathbf{Z} \ggamma + \vvarepsilon[/math], now with equivariant and uncorrelated random effects: [math]\ggamma \sim \mathcal{N}( \mathbf{0}_q, \sigma_{\gamma}^2 \mathbf{I}_{qq})[/math]. Write [math]\theta = \sigma_{\gamma}^2 / \sigma_{\varepsilon}^2[/math]. The REML estimators of [math]\theta[/math] and [math]\sigma_{\varepsilon}^2[/math] are to be found from the estimating equations:
where [math]\mathbf{P}_{\theta} = \tilde{\mathbf{Q}}_{\theta}^{-1} - \tilde{\mathbf{Q}}_{\theta}^{-1} \mathbf{X} (\mathbf{X}^{\top} \tilde{\mathbf{Q}}_{\theta}^{-1} \mathbf{X})^{-1} \mathbf{X}^{\top} \tilde{\mathbf{Q}}_{\theta}^{-1}[/math] and [math]\tilde{\mathbf{Q}}_{\theta} = \mathbf{I}_{nn} + \theta \mathbf{Z} \mathbf{Z}^{\top}[/math]. To arrive at the REML estimators choose initial values for the parameters. Choose one of the estimating equations substitute the initial value of the one of the parameters and solve for the other. The found root is then substituted into the other estimating equation, which is subsequently solved for the remaining parameter. Iterate between these two steps until convergence. The discussion of the practical evaluation of a root for [math]\theta[/math] from these estimating equations in a high-dimensional context is postponed to the next section.
The employed linear mixed model assumes that each of the [math]q[/math] covariates included as a column in [math]\mathbf{Z}[/math] contributes to the variation of the response. However, it may be that only a fraction of these covariates exerts any influence on the response. That is, the random effect parameter [math]\ggamma[/math] is sparse, which could be operationalized as [math]\ggamma[/math] having [math]q_0[/math] zero elements while the remaining [math]q_{c} = q - q_0[/math] elements are non-zero. Only for the latter [math]q_{c}[/math] elements of [math]\ggamma[/math] the normal assumption makes sense, but is invalid for the [math]q_0[/math] zeros in [math]\ggamma[/math]. The posed mixed model is then misspecified.
The next theorem states that the REML estimators of [math]\theta = \sigma_{\gamma}^2 / \sigma_{\varepsilon}^2[/math] and [math]\sigma_{\varepsilon}^2[/math] are consistent (possibly after adjustment, see the theorem), even under the above mentioned misspecification.
Let [math]\mathbf{Z}[/math] be standardized column-wise and with its unstandardized entries i.i.d. from a sub-Gaussian distribution. Furthermore, assume that [math]n, q, q_{c} \rightarrow \infty[/math] such that
where [math]\tau, \omega \in (0, 1][/math]. Finally, suppose that [math]\sigma_{\varepsilon}^2[/math] and [math]\sigma_{\gamma}^2[/math] are positive. Then:
- The ‘adjusted’ REML estimator of the variance ratio [math] \sigma_{\gamma}^2 / \sigma_{\varepsilon}^2[/math] is consistent:
[[math]] \begin{eqnarray*} \frac{q}{ q_{c}} \widehat{(\sigma_{\gamma}^2 / \sigma_{\varepsilon}^2)} \stackrel{P}{\longrightarrow} \sigma_{\gamma}^2 / \sigma_{\varepsilon}^2. \end{eqnarray*} [[/math]]
- The REML estimator of the error variance is consistent: [math]\hat{\sigma}_{\varepsilon}^2 \stackrel{P}{\longrightarrow} \sigma_{\varepsilon}^2[/math].
Before the interpretation and implication of Theorem are discussed, its conditions for the consistency result are reviewed:
- The standardization and distribution assumption on the design matrix of the random effects has no direct practical interpretation. These conditions warrant the applicability of certain results from random matrix theory upon which the proof of the theorem hinges.
- The positive variance assumption [math]\sigma_{\varepsilon}^2, \sigma_{\gamma}^2 \gt 0[/math], in particular that of the random effect parameter, effectively states that some -- possibly misspecified -- form of the mixed model applies.
- Practically most relevant are the conditions on the sample size, random effect dimension, and sparsity. The [math]\tau[/math] and [math]\omega[/math] in Theorem are the limiting ratio's of the sample size [math]n[/math] and non-zero random effects [math] q_{c}[/math], respectively, to the total number of random effects [math]q[/math]. The number of random effects thus exceeds the sample size, as long as the latter grows (in the limit) at some fixed rate with the former. Independently, the model may be misspecified. The sparsity condition only requires that (in the limit) a fraction of the random effects is nonzero.
Now discuss the interpretation and relevance of the theorem:
- Theorem complements the classical low-dimensional consistency results on the REML estimator.
- Theorem shows that not all (i.e. consistency) is lost when the model is misspecified.
- The practical relevance of the part i) of Theorem is limited as the number of nonzero random effects [math]q_{c}[/math], or [math]\omega[/math] for that matter, is usually unknown. Consequently, the REML estimator of the variance ratio [math]\sigma_{\gamma}^2 / \sigma_{\varepsilon}^2[/math] cannot be adjusted correctly to achieve asymptotically unbiasedness and -- thereby -- consistency
- Part ii) in its own right may not seem very useful. But it is surprising that high-dimensionally (i.e. when the dimension of the random effect parameter exceeds the sample size) the standard (that is, derived for low-dimensional data) REML estimator of [math]\sigma_{\varepsilon}^2[/math] is consistent. Beyond this surprise, a good estimator of [math]\sigma_{\varepsilon}^2[/math] indicates how much of the variation in the response cannot be attributed to the covariates represented by the columns [math]\mathbf{Z}[/math]. A good indication of the noise level in the data finds use at many place. In particular, it is helpful in deciding on the order of the penalty parameter.
- Theorem suggests to choose the ridge penalty parameter equal to the ratio of the error variance and that of the random effects. Confronted with data the reciprocal of the REML estimator of [math]\theta = \sigma_{\gamma}^2 / \sigma_{\varepsilon}^2[/math] may be used as value for the penalty parameter. Without the adjustment for the fraction of nonzero random effects, this value is off. But in the worst case this value is an over-estimation of the optimal (in the GCV sense) ridge penalty parameter. Consequently, too much penalization is applied and the ridge regression estimate of the regression parameter is conservative as it shrinks the elements too much to zero.
Illustration: P-splines
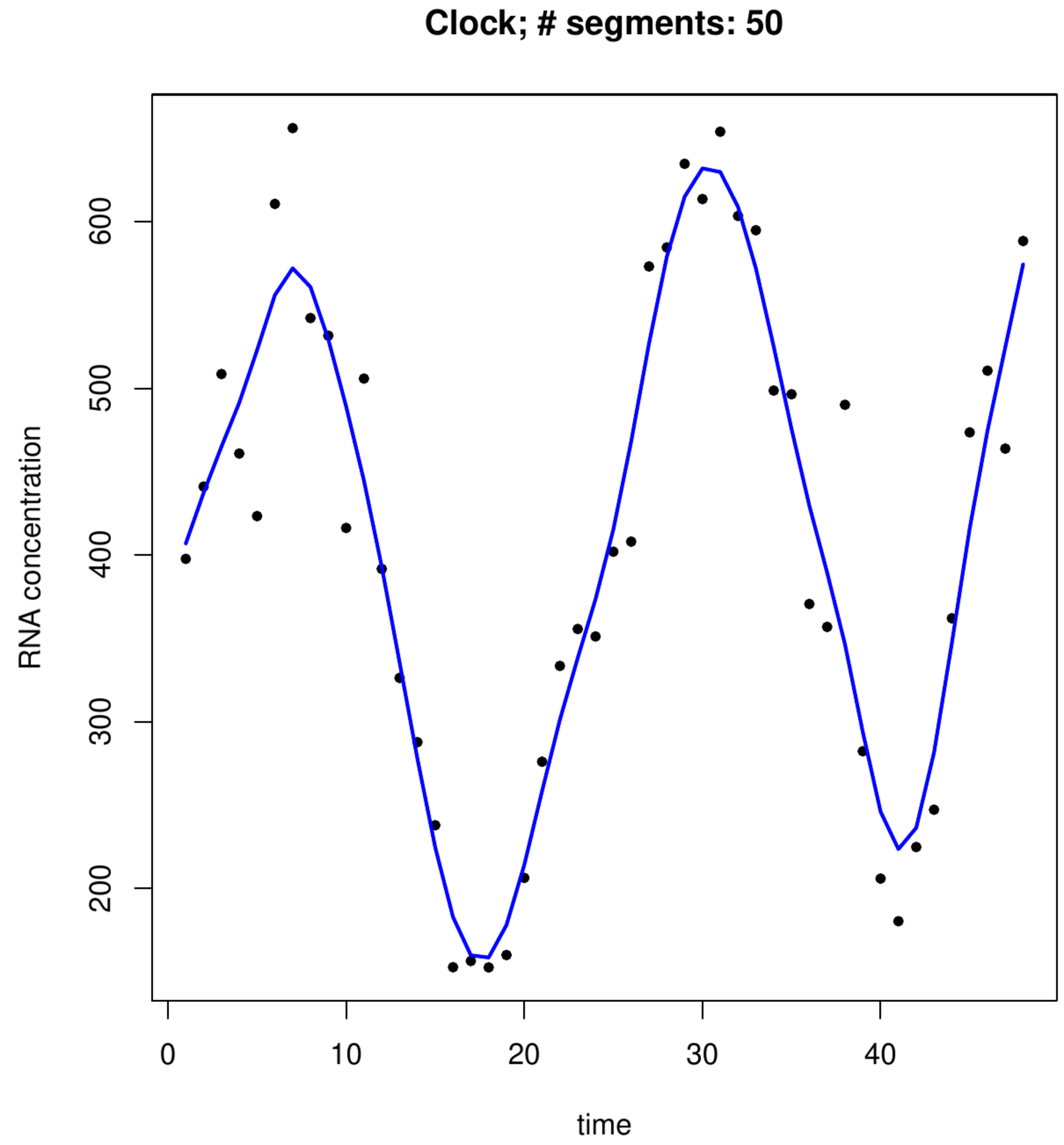
An organism's internal circadian clock enables it to synchronize its activities to the earth's day-and-night cycle. The circadian clock maintains, due to environmental feedback, oscillations of approximately 24 hours. Molecularly, these oscillations reveal themselves in the fluctuation of the transcription levels of genes. The molecular core of the circadian clock is made up of [math]\pm 10[/math] genes. Their behaviour (in terms of their expression patterns) is described by a dynamical system with feedback mechanisms. Linked to this core are genes that tap into the clock's rythm and use it to regulate the molecular processes. As such many genes are expected to exhibit circadian rythms. This is investigated in a mouse experiment in which the expression levels of several transcipts have been measured during two days with a resolution of one hour, resulting in a time-series of 48 time points publicly available from the R-package MetaCycle. Circadian rythms may be identified simply by eye-balling the data. But to facilitate this identification the data are smoothed to emphasize the pattern present in these data.
Top left and right panels: B-spline basis functions of degree 1 and 2, respectively. Bottom left and right panel: P-spline fit to transcript levels of circadian clock experiment in mice.
Smooothing refers to nonparametric -- in the sense that parameters have no tangible interpretation -- description of a curve. For instance, one may wish to learn some general functional relationship between two variable, [math]X[/math] and [math]Y[/math], from data. Statistically, the model [math]Y= f(X) + \varepsilon[/math], for unknown and general function [math]f(\cdot)[/math], is to be fitted to paired observations [math]\{ (y_i, x_i) \}_{i=1}^n[/math]. Here we use P-splines, penalized B-splines with B for Basis [4].
A B-spline is formed through a linear combination of (pieces of) polynomial basis functions of degree [math]r[/math]. For their construction specify the interval [math][x_{\mbox{{\tiny start}}}, x_{\mbox{{\tiny end}}}][/math] on which the function is to be learned/approximated. Let [math]\{ t_j \}_{j=0}^{m+2r}[/math] be a grid, overlapping the interval, of equidistantly placed points called knots given by [math]t_j = x_{\mbox{{\tiny start}}} + (j- r) h[/math] for all [math]j=0, \ldots, m+2r[/math] with [math]h = \tfrac{1}{m}(x_{\mbox{{\tiny end}}} - x_{\mbox{{\tiny start}}})[/math]. The B-spline base functions are then defined as:
where [math]\Delta^r[f_j(\cdot)][/math] is the [math]r[/math]-th difference operator applied to [math]f_j(\cdot)[/math]. For [math]r=1[/math]: [math]\Delta[f_j(\cdot)] = f_j(\cdot) - f_{j-1}(\cdot)[/math], while [math]r=2[/math]: [math]\Delta^2[f_j(\cdot)] = \Delta \{ \Delta [f_j(\cdot)] \} = \Delta[f_j(\cdot) - f_{j-1}(\cdot)] = f_j(\cdot) - 2f_{j-1}(\cdot) + f_{j-2}(\cdot)[/math], et cetera. The top right and bottom left panels of Figure show a [math]1^{\mbox{{\tiny st}}}[/math] and [math]2^{\mbox{{\tiny nd}}}[/math] degree B-spline basis functions. A P-spline is a curve of the form [math]\sum_{j=0}^{m+2r} \alpha_j B_j(x; r)[/math] fitted to the data by means of penalized least squares minimization. The least squares are [math]\| \mathbf{Y} - \mathbf{B} \aalpha \|_2^2[/math] where [math]\mathbf{B}[/math] is a [math]n \times (m + 2r)[/math]-dimensional matrix with the [math]j[/math]-th column equalling [math](B_j(x_i; r), B_j(x_2; r), \ldots, B_j(x_{n}; r))^{\top}[/math]. The employed penalty is of the ridge type: the sum of the squared difference among contiguous [math]\alpha_j[/math]. Let [math]\mathbf{D}[/math] be the first order differencing matrix. The penalty can then be written as [math]\| \mathbf{D} \alpha \|_2^2 = \sum_{j=2}^{m+2r} (\alpha_j - \alpha_{j-1})^2[/math]. A second order difference matrix would amount to [math]\| \mathbf{D} \alpha \|_2^2 = \sum_{j=3}^{m+2r} (\alpha_j - 2 \alpha_{j-1} + \alpha_{j-2})^2[/math]. [5] points out how P-splines may be interpret as a mixed model. Hereto choose [math]\tilde{\mathbf{X}}[/math] such that its columns span the null space of [math]\mathbf{D}^{\top} \mathbf{D}[/math], which comprises a single column representing the intercept when [math]\mathbf{D}[/math] is a first order differencing matrix, and [math]\tilde{\mathbf{Z}} = \mathbf{D}^{\top} (\mathbf{D} \mathbf{D}^{\top})^{-1}[/math]. Then, for any [math]\aalpha[/math]:
This parametrization simplifies the employed penalty to:
where [math]\mathbf{D} \tilde{\mathbf{X}} \bbeta[/math] has vanished by the construction of [math]\tilde{\mathbf{X}}[/math]. Hence, the penalty only affects the random effect parameter, leaving the fixed effect parameter unshrunken. The resulting loss function, [math]\| \mathbf{Y} - \mathbf{X} \bbeta - \mathbf{Z} \ggamma \|_2^2 + \lambda \| \gamma \|_2^2[/math], coincides for suitably chosen [math]\lambda[/math] to that of the mixed model (as will become apparent later). The bottom panels of Figure shows the flexibility of this approach.
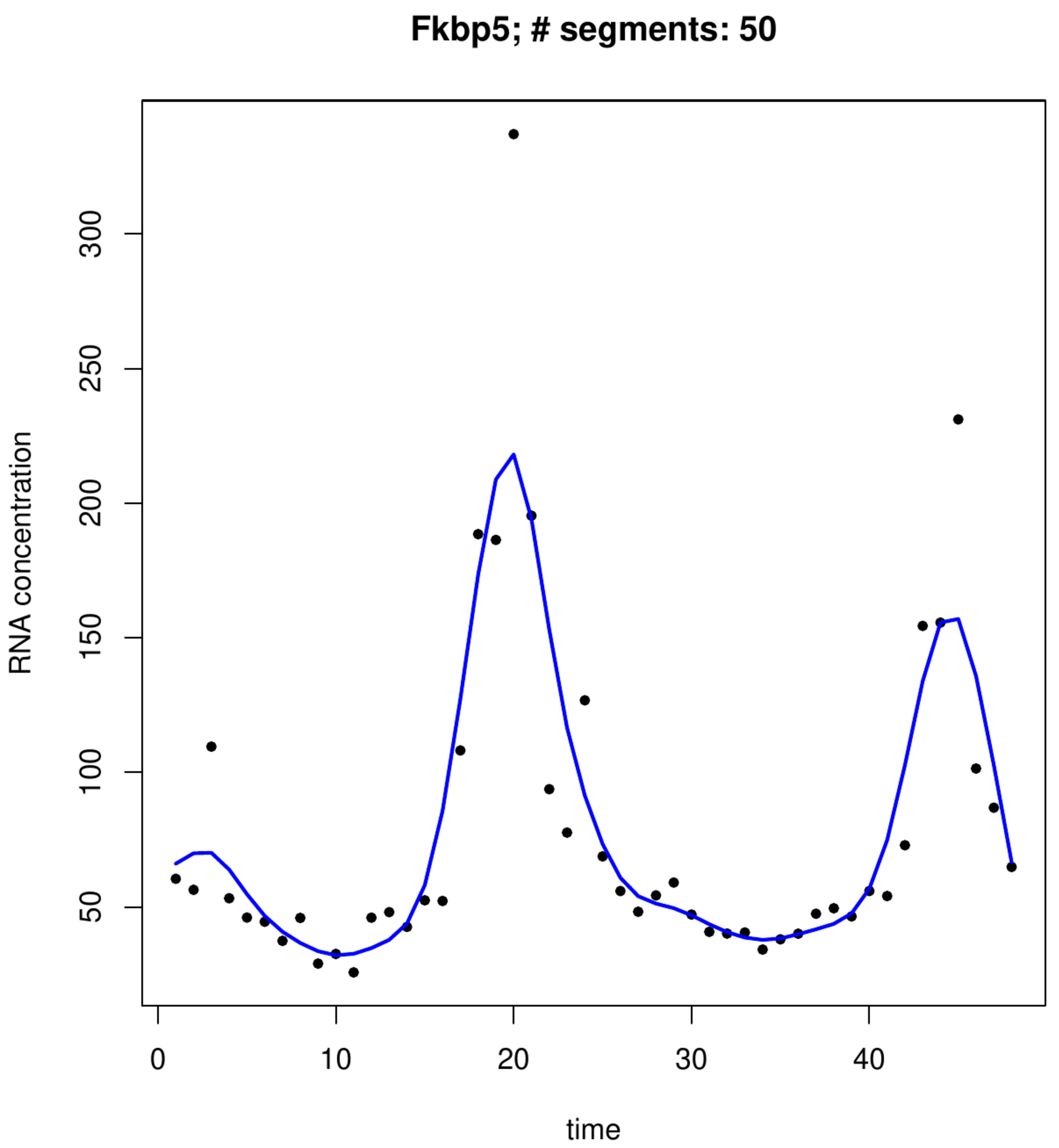
The following R-script fits a P-spline to a gene's transcript levels of the circadian clock study in mice. It uses a basis of [math]m=50[/math] truncated polynomial functions of degree [math]r=3[/math] (cubic), which is generated first alongside several auxillary matrices. This basis forms, after post-multiplication with a projection matrix onto the space spanned by the columns of the difference matrix [math]\mathbf{D}[/math], the design matrix for the random coefficient of the mixed model [math]\mathbf{Y} = \mathbf{X} \bbeta + \mathbf{Z} \ggamma + \vvarepsilon[/math] with [math]\ggamma \sim \mathcal{N}(\mathbf{0}_q, \sigma_{\gamma}^2 \mathbf{I}_{qq})[/math] and [math]\vvarepsilon \sim \mathcal{N}(\mathbf{0}_n, \sigma_{\varepsilon}^2 \mathbf{I}_{nn})[/math]. The variance parameters of this model are then estimated by means of restricted maximum likelihood (REML). The final P-spline fit is obtained from the linear predictor using, in line with Theorem, [math]\lambda = \sigma_{\varepsilon}^2 / \sigma_{\gamma}^2[/math] in which the REML estimates of these variance parameters are substituted. The resulting P-spline fit of two transcripts is shown in the bottom panels of Figure.
# load libraries
library(gridExtra)
library(MetaCycle)
library(MASS)
#------------------------------------------------------------------------------
# intermezzo: declaration of functions used analysis
#------------------------------------------------------------------------------
tpower <- function(x, knots, p) {
# function for evaluation of truncated p-th
# power functions positions x, given knots
return((x - knots)^p * (x > knots))
}
bbase <- function(x, m, r) {
# function for B-spline basis generation
# evaluated at the extremes of x
# with m segments and spline degree r
h <- (max(x) - min(x))/m
knots <- min(x) + (c(0:(m+2*r)) - r) * h
P <- outer(x, knots, tpower, r)
D <- diff(diag(m+2*r+1), diff=r+1) / (gamma(r+1) * h^r)
return((-1)^(r+1) * P %*% t(D))
}
thetaEstEqREML <- function(theta, Z, Y, X, sigma2e){
# function for REML estimation:
# estimating equation of theta
QthetaInv <- solve(diag(length(Y)) + theta * Z %*% t(Z))
Ptheta <- QthetaInv -
QthetaInv %*% X %*%
solve(t(X) %*% QthetaInv %*% X) %*% t(X) %*% QthetaInv
return(sum(diag(Ptheta %*% Z %*% t(Z))) -
as.numeric(t(Y) %*% Ptheta %*% Z %*% t(Z) %*% Ptheta %*% Y) / sigma2e)
}
#------------------------------------------------------------------------------
# load data
data(cycMouseLiverRNA)
id <- 14
Y <- as.numeric(cycMouseLiverRNA[id,-1])
X <- 1:length(Y)
# set P-spline parameters
m <- 50
r <- 3
B <- bbase(X, m=m, r=r)
# prepare some matrices
D <- diff(diag(m+r), diff = 2)
Z <- B %*% t(D) %*% solve(D %*% t(D))
X <- B %*% Null(t(D) %*% D)
# initiate
theta <- 1
for (k in 1:100){
# for-loop, alternating between theta and error variance estimation
thetaPrev <- theta
QthetaInv <- solve(diag(length(Y)) + theta * Z %*% t(Z))
Ptheta <- QthetaInv -
QthetaInv %*% X %*%
solve(t(X) %*% QthetaInv %*% X) %*% t(X) %*% QthetaInv
sigma2e <- t(Y) %*% Ptheta %*% Y / (length(Y)-2)
theta <- uniroot(thetaEstEqREML, c(0, 100000),
Z=Z, Y=Y, X=X, sigma2e=sigma2e)$root
if (abs(theta - thetaPrev) < 10^(-5)){ break }
}
# P-spline fit
bgHat <- solve(t(cbind(X, Z)) %*% cbind(X, Z) +
diag(c(rep(0, ncol(X)), rep(1/theta, ncol(Z))))) %*%
t(cbind(X, Z)) %*% Y
# plot fit
plot(Y, pch=20, xlab="time", ylab="RNA concentration",
main=paste(strsplit(cycMouseLiverRNA[id,1], "_")[[1]][1],
"; # segments: ", m, sep=""))
lines(cbind(X, Z) %*% bgHat, col="blue", lwd=2)
The fitted splines displayed Figure nicely match the data. From the circadian clock perspective it is especially the fit in the right-hand side bottom panel that displays the archetypical sinusoidal behaviour associated by the layman with the sought-for rythm. Close inspection of the fits reveals some minor discontinuities in the derivative of the spline fit. These minor discontinuities are indicative of a little overfitting, due to too large an estimate of [math]\sigma_{\gamma}^2[/math]. This appears to be due to numerical instability of the solution of the estimating equations of the REML estimators of the mixed model's variance parameter estimators when [math]m[/math] is large compared to the sample size [math]n[/math].
General References
van Wieringen, Wessel N. (2021). "Lecture notes on ridge regression". arXiv:1509.09169 [stat.ME].
References
- Henderson, C. (1953).Estimation of variance and covariance components.Biometrics, 9(2), 226--252
- Bates, D. and DebRoy, S. (2004).Linear mixed models and penalized least squares.Journal of Multivariate Analysis, 91(1), 1--17
- 3.0 3.1 Jiang, J., Li, C., Paul, D., Yang, C., and Zhao, H. (2016).On high-dimensional misspecified mixed model analysis in genome-wide association study.The Annals of Statistics, 44(5), 2127--2160
- Eilers, P. and Marx, B. (1996).Flexible smoothing with b-splines and penalties.Statistical Science, 11(2), 89--102
- Eilers, P. (1999).Discussion on: The analysis of designed experiments and longitudinal data by using smoothing splines.Journal of the Royal Statistical Society: Series C (Applied Statistics), 48(3), 307--308