guide:A618cf4c07: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 6: | Line 6: | ||
\newcommand{\NA}{{\rm NA}} | \newcommand{\NA}{{\rm NA}} | ||
\newcommand{\mathds}{\mathbb}</math></div> | \newcommand{\mathds}{\mathbb}</math></div> | ||
In this chapter, we describe the discrete probability distributions and the continuous | In this chapter, we describe the discrete probability distributions and the continuous probability densities that occur most often in the analysis of experiments. We will also show how one simulates these distributions and densities on a computer. | ||
probability densities that occur most often in the analysis of experiments. We will | |||
also show how one simulates these distributions and densities on a computer. | |||
===Discrete Uniform Distribution=== | ===Discrete Uniform Distribution=== | ||
In Chapter | In Chapter [[guide:4f3a4e96c3|Discrete Probability Distributions]], we saw that in many cases, we assume that all outcomes of an | ||
experiment are equally likely. If <math>X</math> is a random variable which represents the | experiment are equally likely. If <math>X</math> is a random variable which represents the | ||
outcome of an experiment of this type, then we say that <math>X</math> is uniformly distributed. | outcome of an experiment of this type, then we say that <math>X</math> is uniformly distributed. | ||
| Line 20: | Line 18: | ||
can be simulated on a computer using the program ''' GeneralSimulation'''. However, in | can be simulated on a computer using the program ''' GeneralSimulation'''. However, in | ||
this case, a faster algorithm can be used instead. (This algorithm was described in | this case, a faster algorithm can be used instead. (This algorithm was described in | ||
Chapter | Chapter [[guide:4f3a4e96c3|Discrete Probability Distributions]]; we repeat the description here for completeness.) The expression | ||
<math display="block"> | <math display="block"> | ||
| Line 35: | Line 33: | ||
If the sample space is a countably infinite set, such as the set of positive | If the sample space is a countably infinite set, such as the set of positive | ||
integers, then it is not possible to have an experiment which is uniform on this set | integers, then it is not possible to have an experiment which is uniform on this set | ||
(see | (see [[exercise:457d6175f2 |Exercise]]). If the sample space is an uncountable set, with | ||
positive, finite length, such as | positive, finite length, such as the interval <math>[0, 1]</math>, then we use continuous density functions (see [[guide:D26a5cb8f7|Important Densities]]). | ||
the interval <math>[0, 1]</math>, then we use continuous density functions (see | |||
===Binomial Distribution=== | ===Binomial Distribution=== | ||
The binomial distribution with parameters <math>n</math>, <math>p</math>, and <math>k</math> was defined in | The binomial distribution with parameters <math>n</math>, <math>p</math>, and <math>k</math> was defined in | ||
Chapter | Chapter [[guide:1cf65e65b3|Combinatorics]]. It is the distribution of the random variable which counts the | ||
number of heads which occur when a coin is tossed <math>n</math> times, assuming that on any one | number of heads which occur when a coin is tossed <math>n</math> times, assuming that on any one | ||
toss, the probability that a head occurs is <math>p</math>. The distribution function is given | toss, the probability that a head occurs is <math>p</math>. The distribution function is given | ||
| Line 54: | Line 51: | ||
One straightforward way to simulate a binomial random variable <math>X</math> is to compute | One straightforward way to simulate a binomial random variable <math>X</math> is to compute | ||
the sum of <math>n</math> independent <math>0-1</math> random variables, each of which take on the value 1 | the sum of <math>n</math> independent <math>0-1</math> random variables, each of which take on the value 1 | ||
with probability <math>p</math>. | with probability <math>p</math>. This method requires <math>n</math> calls to a random number generator to | ||
obtain one value of the random variable. When <math>n</math> is relatively large (say at least | obtain one value of the random variable. When <math>n</math> is relatively large (say at least | ||
30), the Central Limit Theorem (see | 30), the Central Limit Theorem (see \ref{} ) implies that the binomial | ||
distribution is well-approximated by the corresponding normal density function (which | distribution is well-approximated by the corresponding normal density function (which | ||
is defined in | is defined in [[guide:D26a5cb8f7|Important Densities]]) with parameters <math>\mu = np</math> and | ||
<math>\sigma = \sqrt{npq}</math>. Thus, in this case we can compute a value <math>Y</math> of a normal | <math>\sigma = \sqrt{npq}</math>. Thus, in this case we can compute a value <math>Y</math> of a normal | ||
random variable with these parameters, and if <math>-1/2 \le Y < n+1/2</math>, we can use the | random variable with these parameters, and if <math>-1/2 \le Y < n+1/2</math>, we can use the | ||
| Line 67: | Line 64: | ||
</math> | </math> | ||
to represent the random variable <math>X</math>. If <math>Y < -1/2</math> or <math>Y | to represent the random variable <math>X</math>. If <math>Y < -1/2</math> or <math>Y | ||
> n + 1/2</math>, we reject <math>Y</math> and compute another value. We will see in the next section | > n + 1/2</math>, we reject <math>Y</math> and compute another value. We will see in the next section how we can quickly simulate normal random variables. | ||
how we can quickly simulate normal random variables. | |||
===Geometric Distribution=== | ===Geometric Distribution=== | ||
| Line 76: | Line 71: | ||
\choice{The probability measure for a process that requires an infinite number of trials is | \choice{The probability measure for a process that requires an infinite number of trials is | ||
determined in terms of probabilities that require only a finite number of trials<ref group="Notes" >See | determined in terms of probabilities that require only a finite number of trials<ref group="Notes" >See | ||
Section 2.2 of the complete Grinstead-Snell book</ref> | Section 2.2 of the complete Grinstead-Snell book</ref> We showed in Section \ref{sec 2.2} how to assign a | ||
probability distribution to the infinite tree. | probability distribution to the infinite tree. Thus, we can determine the distribution for any random | ||
variable <math>X</math> relating to the experiment provided | variable <math>X</math> relating to the experiment provided | ||
<math>P(X = a)</math> can be computed in terms of a finite number of trials. For example, let <math>T</math> be | <math>P(X = a)</math> can be computed in terms of a finite number of trials. For example, let <math>T</math> be | ||
| Line 107: | Line 102: | ||
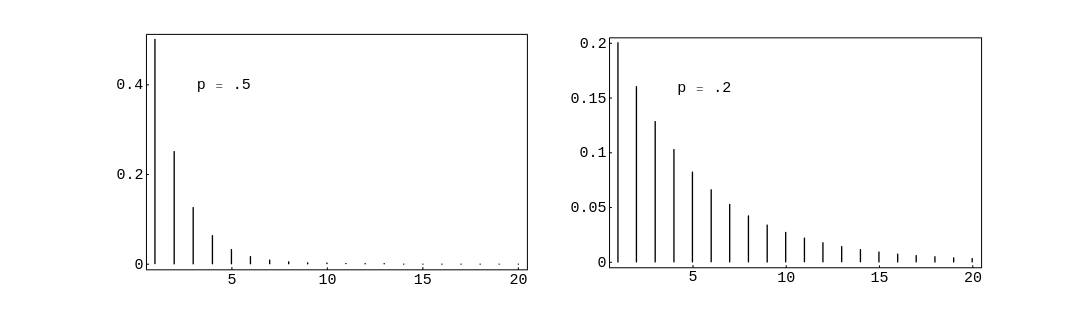
In | In [[#fig 5.4|Figure]] we have plotted this distribution using the program ''' | ||
GeometricPlot''' for the cases <math>p = .5</math> and <math>p = .2</math>. We see that as <math>p</math> decreases we | GeometricPlot''' for the cases <math>p = .5</math> and <math>p = .2</math>. We see that as <math>p</math> decreases we | ||
are more likely to get large values for <math>T</math>, as would be expected. In both cases, the | are more likely to get large values for <math>T</math>, as would be expected. In both cases, the | ||
| Line 115: | Line 110: | ||
\frac {P(T = j + 1)}{P(T = j)} = q < 1\ . | \frac {P(T = j + 1)}{P(T = j)} = q < 1\ . | ||
</math> | </math> | ||
<div id=" | <div id="fig 5.4" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig5-4. | [[File:guide_e6d15_PSfig5-4.png | 600px | thumb | Geometric distributions. ]] | ||
</div> | </div> | ||
| Line 151: | Line 146: | ||
</math> | </math> | ||
Thus, <math>Y</math> is geometrically distributed with parameter <math>p</math>. To | Thus, <math>Y</math> is geometrically distributed with parameter <math>p</math>. To | ||
generate <math>Y</math>, all we have to do is solve | generate <math>Y</math>, all we have to do is solve Equation \ref{eq 5.3} for <math>Y</math>. We obtain | ||
<math display="block"> | <math display="block"> | ||
| Line 202: | Line 197: | ||
and is also obeyed by the exponential distribution. (Fortunately, not too many | and is also obeyed by the exponential distribution. (Fortunately, not too many | ||
service stations have this property.) | service stations have this property.) | ||
===Negative Binomial Distribution=== | ===Negative Binomial Distribution=== | ||
Suppose we are given a coin which has probability <math>p</math> of coming up heads when it is | Suppose we are given a coin which has probability <math>p</math> of coming up heads when it is tossed. We fix a positive integer <math>k</math>, and toss the coin until the <math>k</math>th head appears. We let <math>X</math> represent the number of tosses. When <math>k = 1</math>, <math>X</math> is geometrically distributed. For a general <math>k</math>, we say that <math>X</math> has a negative binomial | ||
tossed. We fix a positive integer <math>k</math>, and toss the coin until the <math>k</math>th head | distribution. We now calculate the probability distribution of <math>X</math>. If <math>X = x</math>, then it must be true that there were exactly <math>k-1</math> heads thrown in the first <math>x-1</math> tosses,and a head must have been thrown on the <math>x</math>th toss. There are | ||
appears. We let <math>X</math> represent the number of tosses. When <math>k = 1</math>, <math>X</math> is | |||
geometrically distributed. For a general <math>k</math>, we say that <math>X</math> has a negative binomial | |||
distribution. We now calculate the probability distribution of <math>X</math>. If <math>X = x</math>, then | |||
it must be true that there were exactly <math>k-1</math> heads thrown in the first <math>x-1</math> tosses, | |||
and a head must have been thrown on the <math>x</math>th toss. There are | |||
<math display="block"> | <math display="block"> | ||
| Line 217: | Line 206: | ||
</math> | </math> | ||
sequences of length <math>x</math> with these properties, and each of | sequences of length <math>x</math> with these properties, and each of them is assigned the same probability, namely | ||
them is assigned the same | |||
probability, namely | |||
<math display="block"> | <math display="block"> | ||
| Line 236: | Line 223: | ||
One can simulate this on a computer by simulating the tossing of a coin. | One can simulate this on a computer by simulating the tossing of a coin. The following algorithm is, in general, much faster. We note that <math>X</math> can be understood as the sum of <math>k</math> outcomes of a geometrically distributed experiment with parameter <math>p</math>. | ||
following algorithm is, in general, much faster. We note that <math>X</math> can be understood | |||
as the sum of <math>k</math> outcomes of a geometrically distributed experiment with parameter <math>p</math>. | |||
Thus, we can use the following sum as a means of generating <math>X</math>: | Thus, we can use the following sum as a means of generating <math>X</math>: | ||
| Line 257: | Line 242: | ||
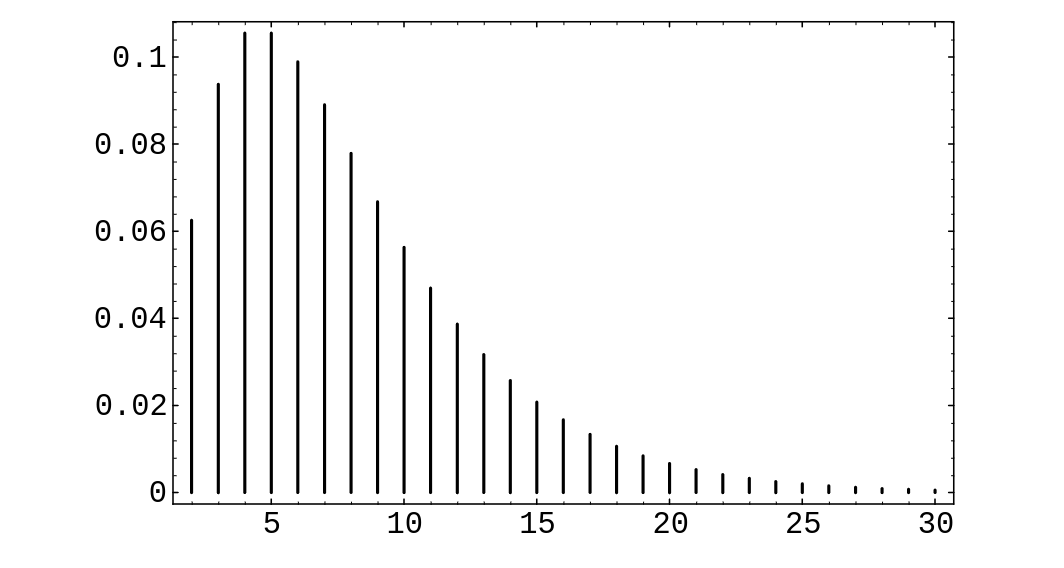
In | In [[#fig 7.2|Figure]] we give a graph of the distribution for <math>k = 2</math> and <math>p = .25</math>. | ||
Note that the distribution is quite asymmetric, with a long tail reflecting the fact that | Note that the distribution is quite asymmetric, with a long tail reflecting the fact that | ||
large values of <math>x</math> are possible. | large values of <math>x</math> are possible. | ||
<div id=" | <div id="fig 7.2" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig7-2-1. | [[File:guide_e6d15_PSfig7-2-1.png | 400px | thumb |Negative binomial distribution with <math>k = 2</math> and <math>p = .25</math>. ]] | ||
</div> | </div> | ||
===Poisson Distribution=== | ===Poisson Distribution=== | ||
| Line 280: | Line 264: | ||
model this situation so that we can consider the probabilities of events such as more | model this situation so that we can consider the probabilities of events such as more | ||
than 10 phone calls occurring in a 5-minute time interval. Presumably, in our | than 10 phone calls occurring in a 5-minute time interval. Presumably, in our | ||
example, there would be more incoming calls between 6:00 and 7:00 | example, there would be more incoming calls between 6:00 and 7:00 P.M. than | ||
between 4:00 and 5:00 | between 4:00 and 5:00 A.M., and this fact would certainly affect the above | ||
probability. Thus, to have a hope of computing such probabilities, we must assume that the | probability. Thus, to have a hope of computing such probabilities, we must assume that the | ||
average rate, i.e., the average number of occurrences per minute, is a constant. This rate we | average rate, i.e., the average number of occurrences per minute, is a constant. This rate we | ||
| Line 293: | Line 277: | ||
Our next assumption is that the number of occurrences in two | Our next assumption is that the number of occurrences in two | ||
non-overlapping time intervals are independent. In our example, this | non-overlapping time intervals are independent. In our example, this | ||
means that the events that there are <math>j</math> calls between 5:00 and 5:15 | means that the events that there are <math>j</math> calls between 5:00 and 5:15 P.M. and <math>k</math> | ||
calls between 6:00 and 6:15 | calls between 6:00 and 6:15 P.M. on the same day are independent. | ||
| Line 327: | Line 311: | ||
occurrences in a given time interval. We want to calculate the distribution of <math>X</math>. | occurrences in a given time interval. We want to calculate the distribution of <math>X</math>. | ||
For ease of calculation, we will assume that the time interval is of length 1; for | For ease of calculation, we will assume that the time interval is of length 1; for | ||
time intervals of arbitrary length <math>t</math>, see | time intervals of arbitrary length <math>t</math>, see [[exercise:D793d2a774 |Exercise]]. We know that | ||
<math display="block"> | <math display="block"> | ||
| Line 352: | Line 336: | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
The above distribution is the Poisson distribution. We note that it | The above distribution is the Poisson distribution. We note that it must be checked that the distribution given in equation \ref{eq 5.1} really ''is'' a distribution, i.e., that its values are non-negative and sum to 1. (See [[exercise:65d6310ccf |Exercise]].) | ||
must be checked that the distribution given in | |||
distribution, i.e., that its values are non-negative and sum to 1. (See | |||
The Poisson distribution is used as an approximation to the binomial distribution when the parameters <math>n</math> and <math>p</math> are large and small, respectively (see [[#exam 5.3 |Example]] and [[#exam 5.5 |Example]]). However, the Poisson distribution also arises in situations where it may not be easy to interpret or measure the parameters <math>n</math> and <math>p</math> (see [[#exam 5.5.5 |Example]]). | |||
<span id="exam 5.3"/> | <span id="exam 5.3"/> | ||
'''Example''' | '''Example''' | ||
| Line 460: | Line 436: | ||
that receive exactly <math>j</math> hits is then <math>100 \cdot p(j)</math>. It is easy to write a program | that receive exactly <math>j</math> hits is then <math>100 \cdot p(j)</math>. It is easy to write a program | ||
''' LondonBombs''' to simulate this situation and compare the expected number of | ''' LondonBombs''' to simulate this situation and compare the expected number of | ||
squares with <math>j</math> hits with the observed number. In | squares with <math>j</math> hits with the observed number. In [[exercise:9f18a63405 |Exercise]] you are asked to compare the actual observed data with that predicted by the Poisson distribution. | ||
asked to compare the actual observed data with that predicted by the Poisson | |||
distribution. | |||
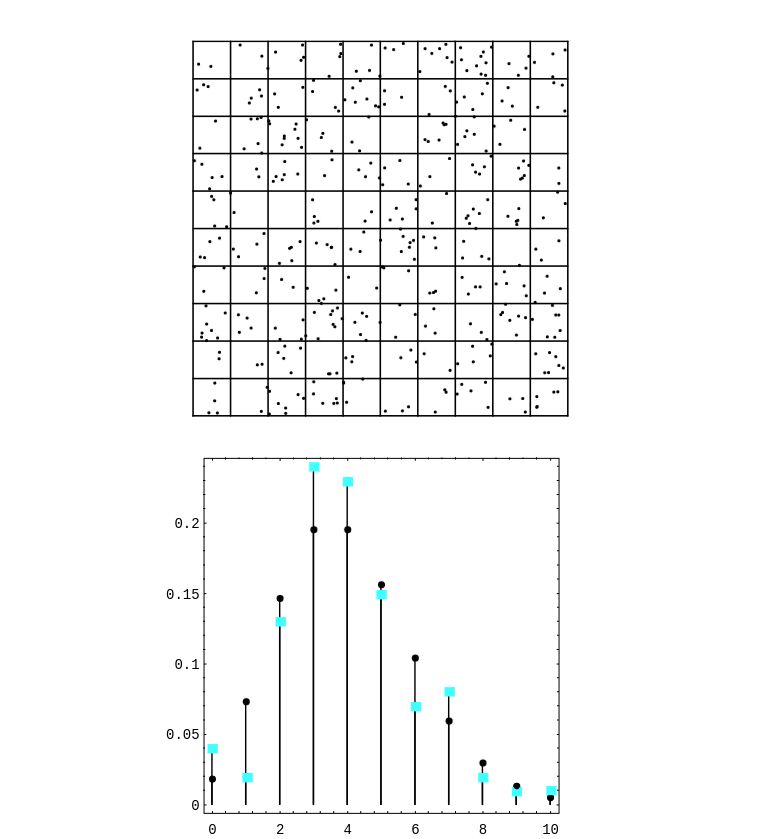
In | In [[#fig 5.1.5|Figure]], we have shown the simulated hits, together with a spike graph | ||
showing both the observed and predicted frequencies. The observed frequencies are shown | showing both the observed and predicted frequencies. The observed frequencies are shown | ||
as squares, and the predicted frequencies are shown as dots. | as squares, and the predicted frequencies are shown as dots. | ||
<div id=" | |||
[[File:guide_e6d15_PSfig5-1-5. | <div id="fig 5.1.5" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig5-1-5.png | 600px | thumb | Flying bomb hits. ]] | |||
</div> | </div> | ||
If the reader would rather not consider flying bombs, he is invited to | If the reader would rather not consider flying bombs, he is invited to instead consider an analogous situation involving cookies and raisins. We assume that | ||
instead consider an analogous situation involving cookies and raisins. We assume that | we have made enough cookie dough for 500 cookies. We put 600 raisins in the dough, and mix it thoroughly. One way to look at this situation is that we have 500 cookies, and after placing the cookies in a grid on the table, we throw 600 raisins at the cookies. (See [[exercise:30cffe3184 |Exercise]].) | ||
we have made enough cookie dough for 500 cookies. We put 600 raisins in the dough, | |||
and mix it thoroughly. One way to look at this situation is that we have 500 cookies, | |||
and after placing the cookies in a grid on the table, we throw 600 raisins at the | |||
cookies. (See | |||
<span id="exam 5.5.5"/> | <span id="exam 5.5.5"/> | ||
'''Example''' | '''Example''' | ||
| Line 493: | Line 465: | ||
to model the situation using the Poisson distribution than the binomial distribution. | to model the situation using the Poisson distribution than the binomial distribution. | ||
To simulate a Poisson random variable on a computer, a good way is to take advantage of the relationship between the Poisson distribution and the exponential density. This relationship and the resulting simulation algorithm will be described in the next section. | |||
To simulate a Poisson random variable on a computer, a good way is to take | |||
advantage of the relationship between the Poisson distribution and the exponential | |||
density. This relationship and the resulting simulation algorithm will be described | |||
in the next section. | |||
===Hypergeometric Distribution=== | ===Hypergeometric Distribution=== | ||
| Line 521: | Line 489: | ||
This distribution can be generalized to the case where there are more than two types | This distribution can be generalized to the case where there are more than two types | ||
of objects. (See | of objects. (See [[exercise:1de6f93eb1 |Exercise]].) | ||
| Line 529: | Line 497: | ||
<math>k</math> are much larger than <math>n</math>, then whether we choose our sample with or without | <math>k</math> are much larger than <math>n</math>, then whether we choose our sample with or without | ||
replacement should not affect the probabilities very much, and the experiment | replacement should not affect the probabilities very much, and the experiment | ||
consisting of choosing with replacement yields a binomially distributed random | consisting of choosing with replacement yields a binomially distributed random variable (see [[exercise:44e18f4b7e |Exercise]]). | ||
variable (see | |||
An example of how this distribution might be used is given in | An example of how this distribution might be used is given in [[exercise:0ae7247be4 |Exercise]] and | ||
[[exercise:0ae7247be4 |Exercise]]. We now give another example involving the hypergeometric | [[exercise:0ae7247be4 |Exercise]]. We now give another example involving the hypergeometric | ||
distribution. It illustrates a statistical test called Fisher's Exact Test. | distribution. It illustrates a statistical test called Fisher's Exact Test. | ||
<span id="exam 5.6"/> | <span id="exam 5.6"/> | ||
'''Example''' | '''Example''' | ||
as eye color and hair color, and to ask whether there is an association between the | as eye color and hair color, and to ask whether there is an association between the two traits. Two traits are associated if knowing the value of one of the traits for a given person allows us to predict the value of the other trait for that person. The stronger the association, the more accurate the predictions become. If there is no association between the traits, then we say that the traits are independent. In this example, we will use the traits of gender and political party, and we will assume that there are only two possible genders, female and male, and only two possible political | ||
two traits. Two traits are associated if knowing the value of one of the traits for a | |||
given person allows us to predict the value of the other trait for that person. The | |||
stronger the association, the more accurate the predictions become. If there is no | |||
association between the traits, then we say that the traits are independent. In this | |||
example, we will use the traits of gender and political party, and we will assume that | |||
there are only two possible genders, female and male, and only two possible political | |||
parties, Democratic and Republican. | parties, Democratic and Republican. | ||
Suppose that we have collected data concerning these traits. To test whether there is an association between the traits, we first assume that there is no | |||
Suppose that we have collected data concerning these traits. To test whether | association between the two traits. This gives rise to an “expected” data set, in which knowledge of the value of one trait is of no help in predicting the value of the other trait. Our collected data set usually differs from this expected data set. If it differs by quite a bit, then we would tend to reject the assumption of independence of the traits. To nail down what is meant by “quite a bit,” we decide which possible data sets differ from the expected data set by at least as much as ours does, and then we compute the probability that any of these data sets would occur under the assumption of independence of traits. If this probability is small, then it is unlikely that the difference between our collected data set and the expected data set | ||
there is an association between the traits, we first assume that there is no | |||
association between the two traits. This gives rise to an “expected” data set, in | |||
which knowledge of the value of one trait is of no help in predicting the value of the | |||
other trait. Our collected data set usually differs from this expected data set. If | |||
it differs by quite a bit, then we would tend to reject the assumption of independence | |||
of the traits. To nail down what is meant by “quite a bit,” we decide which | |||
possible data sets differ from the expected data set by at least as much as ours does, | |||
and then we compute the probability that any of these data sets would occur under the | |||
assumption of independence of traits. If this probability is small, then it is | |||
unlikely that the difference between our collected data set and the expected data set | |||
is due entirely to chance. | is due entirely to chance. | ||
Suppose that we have collected the data shown in [[#table 5.2 |Table]]. | Suppose that we have collected the data shown in [[#table 5.2 |Table]]. | ||
| Line 639: | Line 588: | ||
We are now ready to decide whether our actual data differs from the expected data | We are now ready to decide whether our actual data differs from the expected data set by an amount which is greater than could be reasonably attributed to chance alone. We note that the expected number of female Democrats is 18, but the actual number in our data is 24. The other data sets which differ from the expected data set by more than ours correspond to those where the number of female Democrats equals 25, | ||
set by an amount which is greater than could be reasonably attributed to chance | |||
alone. We note that the expected number of female Democrats is 18, but the actual | |||
number in our data is 24. The other data sets which differ from the expected data set | |||
by more than ours correspond to those where the number of female Democrats equals 25, | |||
26, 27, or 28. Thus, to obtain the required probability, we sum the expression in | 26, 27, or 28. Thus, to obtain the required probability, we sum the expression in | ||
[[#eq 5.65 |(]]) from <math>a = 24</math> to <math>a = 28</math>. We obtain a value of <math>.000395</math>. Thus, we | [[#eq 5.65 |(]]) from <math>a = 24</math> to <math>a = 28</math>. We obtain a value of <math>.000395</math>. Thus, we | ||
should reject the hypothesis that the two traits are independent. | should reject the hypothesis that the two traits are independent. | ||
Finally, we turn to the question of how to simulate a hypergeometric random variable <math>X</math>. Let us assume that the parameters for <math>X</math> are <math>N</math>, <math>k</math>, and <math>n</math>. We imagine that we have a set of <math>N</math> balls, labelled from 1 to <math>N</math>. We decree that the first <math>k</math> of these balls are red, and the rest are blue. Suppose that we have chosen | |||
Finally, we turn to the question of how to simulate a hypergeometric random | |||
variable <math>X</math>. Let us assume that the parameters for <math>X</math> are <math>N</math>, <math>k</math>, and <math>n</math>. We | |||
imagine that we have a set of <math>N</math> balls, labelled from 1 to <math>N</math>. We decree that the | |||
first <math>k</math> of these balls are red, and the rest are blue. Suppose that we have chosen | |||
<math>m</math> balls, and that <math>j</math> of them are red. Then there are <math>k-j</math> red balls left, and | <math>m</math> balls, and that <math>j</math> of them are red. Then there are <math>k-j</math> red balls left, and | ||
<math>N-m</math> balls left. Thus, our next choice will be red with probability | <math>N-m</math> balls left. Thus, our next choice will be red with probability | ||
| Line 695: | Line 636: | ||
while if one were to use the actual numbers, the leading digits would roughly follow the Benford | while if one were to use the actual numbers, the leading digits would roughly follow the Benford | ||
distribution. As an example, Nigrini analyzed President Clinton's tax returns | distribution. As an example, Nigrini analyzed President Clinton's tax returns | ||
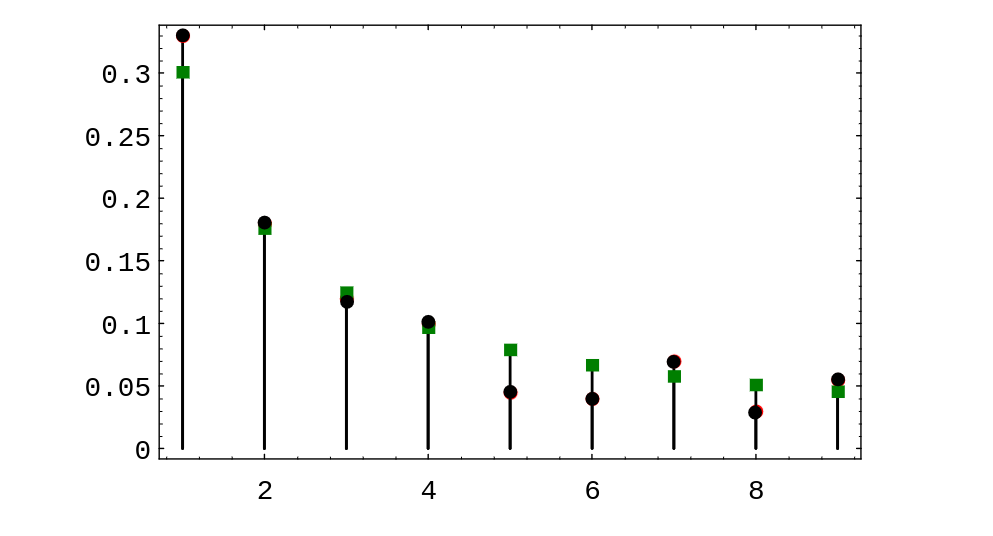
for a 13-year period. In | for a 13-year period. In [[#fig 5.1.6|Figure]], the Benford distribution values are shown as | ||
squares, and the President's tax return data are shown as circles. One sees that in this example, the | squares, and the President's tax return data are shown as circles. One sees that in this example, the | ||
Benford distribution fits the data very well. | Benford distribution fits the data very well. | ||
<div id=" | |||
[[File:guide_e6d15_PSfig5-1-6. | <div id="fig 5.1.6" class="d-flex justify-content-center"> | ||
[[File:guide_e6d15_PSfig5-1-6.png | 400px | thumb |Leading digits in President Clinton's tax returns.]] | |||
</div> | </div> | ||
| Line 709: | Line 651: | ||
frequency diminishes up to 9.”<ref group="Notes" >S. Newcomb, “Note on the frequency of use of the different | frequency diminishes up to 9.”<ref group="Notes" >S. Newcomb, “Note on the frequency of use of the different | ||
digits in natural numbers,” ''American Journal of Mathematics,'' vol.\ 4 (1881), pgs.\ 39-40.</ref> | digits in natural numbers,” ''American Journal of Mathematics,'' vol.\ 4 (1881), pgs.\ 39-40.</ref> | ||
==General references== | |||
{{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | {{cite web |url=https://math.dartmouth.edu/~prob/prob/prob.pdf |title=Grinstead and Snell’s Introduction to Probability |last=Doyle |first=Peter G.|date=2006 |access-date=June 6, 2024}} | ||
==Notes== | ==Notes== | ||
{{Reflist|group=Notes}} | {{Reflist|group=Notes}} | ||
Revision as of 22:08, 10 June 2024
In this chapter, we describe the discrete probability distributions and the continuous probability densities that occur most often in the analysis of experiments. We will also show how one simulates these distributions and densities on a computer.
Discrete Uniform Distribution
In Chapter Discrete Probability Distributions, we saw that in many cases, we assume that all outcomes of an experiment are equally likely. If [math]X[/math] is a random variable which represents the outcome of an experiment of this type, then we say that [math]X[/math] is uniformly distributed. If the sample space [math]S[/math] is of size [math]n[/math], where [math]0 \lt n \lt \infty[/math], then the distribution function [math]m(\omega)[/math] is defined to be [math]1/n[/math] for all [math]\omega \in S[/math]. As is the case with all of the discrete probability distributions discussed in this chapter, this experiment can be simulated on a computer using the program GeneralSimulation. However, in this case, a faster algorithm can be used instead. (This algorithm was described in Chapter Discrete Probability Distributions; we repeat the description here for completeness.) The expression
takes on as a value each integer between 1 and [math]n[/math] with probability [math]1/n[/math] (the notation [math]\lfloor x \rfloor[/math] denotes the greatest integer not exceeding [math]x[/math]). Thus, if the possible outcomes of the experiment are labelled [math]\omega_1\ \omega_2,\ \ldots,\ \omega_n[/math], then we use the above expression to represent the subscript of the output of the experiment.
If the sample space is a countably infinite set, such as the set of positive
integers, then it is not possible to have an experiment which is uniform on this set
(see Exercise). If the sample space is an uncountable set, with
positive, finite length, such as the interval [math][0, 1][/math], then we use continuous density functions (see Important Densities).
Binomial Distribution
The binomial distribution with parameters [math]n[/math], [math]p[/math], and [math]k[/math] was defined in Chapter Combinatorics. It is the distribution of the random variable which counts the number of heads which occur when a coin is tossed [math]n[/math] times, assuming that on any one toss, the probability that a head occurs is [math]p[/math]. The distribution function is given by the formula
where [math]q = 1 - p[/math].
One straightforward way to simulate a binomial random variable [math]X[/math] is to compute
the sum of [math]n[/math] independent [math]0-1[/math] random variables, each of which take on the value 1
with probability [math]p[/math]. This method requires [math]n[/math] calls to a random number generator to
obtain one value of the random variable. When [math]n[/math] is relatively large (say at least
30), the Central Limit Theorem (see \ref{} ) implies that the binomial
distribution is well-approximated by the corresponding normal density function (which
is defined in Important Densities) with parameters [math]\mu = np[/math] and
[math]\sigma = \sqrt{npq}[/math]. Thus, in this case we can compute a value [math]Y[/math] of a normal
random variable with these parameters, and if [math]-1/2 \le Y \lt n+1/2[/math], we can use the
value
to represent the random variable [math]X[/math]. If [math]Y \lt -1/2[/math] or [math]Y \gt n + 1/2[/math], we reject [math]Y[/math] and compute another value. We will see in the next section how we can quickly simulate normal random variables.
Geometric Distribution
Consider a Bernoulli trials process continued for an infinite number of trials; for example, a coin tossed an infinite sequence of times. \choice{The probability measure for a process that requires an infinite number of trials is determined in terms of probabilities that require only a finite number of trials[Notes 1] We showed in Section \ref{sec 2.2} how to assign a probability distribution to the infinite tree. Thus, we can determine the distribution for any random variable [math]X[/math] relating to the experiment provided [math]P(X = a)[/math] can be computed in terms of a finite number of trials. For example, let [math]T[/math] be the number of trials up to and including the first success. Then
and in general,
To show that this is a distribution, we must show that
The left-hand expression is just a geometric series with first term [math]p[/math] and common ratio [math]q[/math], so its sum is
which equals 1.
In Figure we have plotted this distribution using the program
GeometricPlot for the cases [math]p = .5[/math] and [math]p = .2[/math]. We see that as [math]p[/math] decreases we
are more likely to get large values for [math]T[/math], as would be expected. In both cases, the
most probable value for [math]T[/math] is 1. This will always be true since
In general, if [math]0 \lt p \lt 1[/math], and [math]q = 1 - p[/math], then we say that the random variable [math]T[/math]
has a geometric distribution if
for [math]j = 1,\ 2,\ 3,\ \ldots[/math] .
To simulate the geometric distribution with parameter [math]p[/math], we can simply compute
a sequence of random numbers in [math][0, 1)[/math], stopping when an entry does not exceed [math]p[/math].
However, for small values of
[math]p[/math], this is time-consuming (taking, on the average, [math]1/p[/math] steps). We now describe a
method whose running time does not depend upon the size of [math]p[/math]. Define [math]Y[/math] to be the smallest integer
satisfying the inequality
Then we have
Thus, [math]Y[/math] is geometrically distributed with parameter [math]p[/math]. To generate [math]Y[/math], all we have to do is solve Equation \ref{eq 5.3} for [math]Y[/math]. We obtain
where the notation [math]\lceil x \rceil[/math] means the least integer which is greater than or equal to [math]x[/math]. Since [math]\log(1-rnd)[/math] and [math]\log(rnd)[/math] are identically distributed, [math]Y[/math] can also be generated using the equation
Example The geometric distribution plays an important role in the theory of queues, or waiting lines. For example, suppose a line of customers waits for service at a counter. It is often assumed that, in each small time unit, either 0 or 1 new customers arrive at the counter. The probability that a customer arrives is [math]p[/math] and that no customer arrives is [math]q = 1 - p[/math]. Then the time [math]T[/math] until the next arrival has a geometric distribution. It is natural to ask for the probability that no customer arrives in the next [math]k[/math] time units, that is, for [math]P(T \gt k)[/math]. This is given by
This probability can also be found by noting that we are asking for no successes (i.e., arrivals) in a sequence of [math]k[/math] consecutive time units, where the probability of a success in any one time unit is [math]p[/math]. Thus, the probability is just [math]q^k[/math], since arrivals in any two time units are independent events.
It is often assumed that the length of time required to service a customer also has a
geometric distribution but with a different value for [math]p[/math]. This implies a rather
special property of the service time. To see this, let us compute the conditional
probability
Thus, the probability that the customer's service takes [math]s[/math] more time units is independent of the length of time [math]r[/math] that the customer has already been served. Because of this interpretation, this property is called the “memoryless” property, and is also obeyed by the exponential distribution. (Fortunately, not too many service stations have this property.)
Negative Binomial Distribution
Suppose we are given a coin which has probability [math]p[/math] of coming up heads when it is tossed. We fix a positive integer [math]k[/math], and toss the coin until the [math]k[/math]th head appears. We let [math]X[/math] represent the number of tosses. When [math]k = 1[/math], [math]X[/math] is geometrically distributed. For a general [math]k[/math], we say that [math]X[/math] has a negative binomial distribution. We now calculate the probability distribution of [math]X[/math]. If [math]X = x[/math], then it must be true that there were exactly [math]k-1[/math] heads thrown in the first [math]x-1[/math] tosses,and a head must have been thrown on the [math]x[/math]th toss. There are
sequences of length [math]x[/math] with these properties, and each of them is assigned the same probability, namely
Therefore, if we define
then
One can simulate this on a computer by simulating the tossing of a coin. The following algorithm is, in general, much faster. We note that [math]X[/math] can be understood as the sum of [math]k[/math] outcomes of a geometrically distributed experiment with parameter [math]p[/math].
Thus, we can use the following sum as a means of generating [math]X[/math]:
Example distribution for the number of tosses is [math]u(x, 2, p)[/math]. Thus the probability that [math]x[/math] tosses are needed to obtain two heads is found by letting [math]k = 2[/math] in the above formula. We obtain
for [math]x = 2, 3, \ldots\ [/math].
In Figure we give a graph of the distribution for [math]k = 2[/math] and [math]p = .25[/math].
Note that the distribution is quite asymmetric, with a long tail reflecting the fact that
large values of [math]x[/math] are possible.
Poisson Distribution
The Poisson distribution arises in many situations. It is safe to say that it is one of the three most important discrete probability distributions (the other two being the uniform and the binomial distributions). The Poisson distribution can be viewed as arising from the binomial distribution or from the exponential density. We shall now explain its connection with the former; its connection with the latter will be explained in the next section.
Suppose that we have a situation in which a certain kind of occurrence happens at
random over a period of time. For example, the occurrences that we are interested in
might be incoming telephone calls to a police station in a large city. We want to
model this situation so that we can consider the probabilities of events such as more
than 10 phone calls occurring in a 5-minute time interval. Presumably, in our
example, there would be more incoming calls between 6:00 and 7:00 P.M. than
between 4:00 and 5:00 A.M., and this fact would certainly affect the above
probability. Thus, to have a hope of computing such probabilities, we must assume that the
average rate, i.e., the average number of occurrences per minute, is a constant. This rate we
will denote by
[math]\lambda[/math]. (Thus, in a given 5-minute time interval, we would expect about
[math]5\lambda[/math] occurrences.) This means that if we were to apply our model to the two
time periods given above, we would simply use different rates for the two time
periods, thereby obtaining two different probabilities for the given event.
Our next assumption is that the number of occurrences in two
non-overlapping time intervals are independent. In our example, this
means that the events that there are [math]j[/math] calls between 5:00 and 5:15 P.M. and [math]k[/math]
calls between 6:00 and 6:15 P.M. on the same day are independent.
We can use the binomial distribution to model this situation. We imagine that a
given time interval is broken up into [math]n[/math] subintervals of equal length. If the
subintervals are sufficiently short, we can assume that two or more occurrences happen
in one subinterval with a probability which is negligible in comparison with the
probability of at most one occurrence. Thus, in each subinterval, we are assuming
that there is either 0 or 1 occurrence. This means that the sequence of subintervals
can be thought of as a sequence of Bernoulli trials, with a success corresponding to
an occurrence in the subinterval.
To decide upon the proper value of [math]p[/math], the probability of an occurrence in a
given subinterval, we reason as follows. On the average, there are [math]\lambda t[/math]
occurrences in a time interval of length
[math]t[/math]. If this time interval is divided into [math]n[/math] subintervals, then we would expect,
using the Bernoulli trials interpretation, that there should be [math]np[/math] occurrences.
Thus, we want
so
We now wish to consider the random variable [math]X[/math], which counts the number of
occurrences in a given time interval. We want to calculate the distribution of [math]X[/math].
For ease of calculation, we will assume that the time interval is of length 1; for
time intervals of arbitrary length [math]t[/math], see Exercise. We know that
For large [math]n[/math], this is approximately [math]e^{-\lambda}[/math]. It is easy to calculate that for any fixed [math]k[/math], we have
which, for large [math]n[/math] (and therefore small [math]p[/math]) is approximately [math]\lambda/k[/math]. Thus, we have
and in general,
The above distribution is the Poisson distribution. We note that it must be checked that the distribution given in equation \ref{eq 5.1} really is a distribution, i.e., that its values are non-negative and sum to 1. (See Exercise.)
The Poisson distribution is used as an approximation to the binomial distribution when the parameters [math]n[/math] and [math]p[/math] are large and small, respectively (see Example and Example). However, the Poisson distribution also arises in situations where it may not be easy to interpret or measure the parameters [math]n[/math] and [math]p[/math] (see Example).
Example mistake per 1000 words. Assume that he is setting a book with 100 words to a page. Let [math]S_{100}[/math] be the number of mistakes that he makes on a single page. Then the exact probability distribution for [math]S_{100}[/math] would be obtained by considering [math]S_{100}[/math] as a result of 100 Bernoulli trials with [math]p = 1/1000[/math]. The expected value of [math]S_{100}[/math] is [math]\lambda = 100(1/1000) = .1[/math]. The exact probability that [math]S_{100} = j[/math] is [math]b(100,1/1000,j)[/math], and the Poisson approximation is
In Table we give, for various values of [math]n[/math] and [math]p[/math], the exact values computed by the binomial distribution and the Poisson approximation.
| Poisson | Binomial | Poisson | Binomial | Poisson | Binomial | |
| [math]n = 100[/math] | [math]n = 100[/math] | [math]n = 1000[/math] | ||||
| [math]j[/math] | [math]\lambda = .1[/math] | [math]p = .001[/math] | [math]\lambda = 1[/math] | [math]p = .01[/math] | [math]\lambda = 10[/math] | [math]p = .01[/math] |
| 0 | .9048 | .9048 | .3679 | .3660 | .0000 | .0000 |
| 1 | .0905 | .0905 | .3679 | .3697 | .0005 | .0004 |
| 2 | .0045 | .0045 | .1839 | .1849 | .0023 | .0022 |
| 3 | .0002 | .0002 | .0613 | .0610 | .0076 | .0074 |
| 4 | .0000 | .0000 | .0153 | .0149 | .0189 | .0186 |
| 5 | .0031 | .0029 | .0378 | .0374 | ||
| 6 | .0005 | .0005 | .0631 | .0627 | ||
| 7 | .0001 | .0001 | .0901 | .0900 | ||
| 8 | .0000 | .0000 | .1126 | .1128 | ||
| 9 | .1251 | .1256 | ||||
| 10 | .1251 | .1257 | ||||
| 11 | .1137 | .1143 | ||||
| 12 | .0948 | .0952 | ||||
| 13 | .0729 | .0731 | ||||
| 14 | .0521 | .0520 | ||||
| 15 | .0347 | .0345 | ||||
| 16 | .0217 | .0215 | ||||
| 17 | .0128 | .0126 | ||||
| 18 | .0071 | .0069 | ||||
| 19 | .0037 | .0036 | ||||
| 20 | .0019 | .0018 | ||||
| 21 | .0009 | .0009 | ||||
| 22 | .0004 | .0004 | ||||
| 23 | .0002 | .0002 | ||||
| 24 | .0001 | .0001 | ||||
| 25 | .0000 | .0000 |
Example discusses the statistics of flying bomb hits in the south of London during the Second World War.
Assume that you live in a district of size 10 blocks by 10 blocks so that the total
district is divided into 100 small squares. How likely is it that the square in which
you live will receive no hits if the total area is hit by 400 bombs?
We assume that a particular bomb will hit your square with probability 1/100. Since
there are 400 bombs, we can regard the number of hits that your square receives as the
number of successes in a Bernoulli trials process with
[math]n = 400[/math] and [math]p = 1/100[/math]. Thus we can use the Poisson distribution with [math]\lambda = 400
\cdot 1/100 = 4[/math] to approximate the probability that your square will receive
[math]j[/math] hits. This probability is [math]p(j) = e^{-4} 4^j/j![/math]. The expected number of squares
that receive exactly [math]j[/math] hits is then [math]100 \cdot p(j)[/math]. It is easy to write a program
LondonBombs to simulate this situation and compare the expected number of
squares with [math]j[/math] hits with the observed number. In Exercise you are asked to compare the actual observed data with that predicted by the Poisson distribution.
In Figure, we have shown the simulated hits, together with a spike graph
showing both the observed and predicted frequencies. The observed frequencies are shown
as squares, and the predicted frequencies are shown as dots.
If the reader would rather not consider flying bombs, he is invited to instead consider an analogous situation involving cookies and raisins. We assume that we have made enough cookie dough for 500 cookies. We put 600 raisins in the dough, and mix it thoroughly. One way to look at this situation is that we have 500 cookies, and after placing the cookies in a grid on the table, we throw 600 raisins at the cookies. (See Exercise.)
Example the average human has 40 white blood cells. Let [math]X[/math] be the random variable which gives the number of white blood cells in a random sample of size [math]A[/math] from a random individual. We can think of [math]X[/math] as binomially distributed with each white blood cell in the body representing a trial. If a given white blood cell turns up in the sample, then the trial corresponding to that blood cell was a success. Then [math]p[/math] should be taken as the ratio of [math]A[/math] to the total amount of blood in the individual, and [math]n[/math] will be the number of white blood cells in the individual. Of course, in practice, neither of these parameters is very easy to measure accurately, but presumably the number 40 is easy to measure. But for the average human, we then have [math]40 = np[/math], so we can think of [math]X[/math] as being Poisson distributed, with parameter [math]\lambda = 40[/math]. In this case, it is easier to model the situation using the Poisson distribution than the binomial distribution.
To simulate a Poisson random variable on a computer, a good way is to take advantage of the relationship between the Poisson distribution and the exponential density. This relationship and the resulting simulation algorithm will be described in the next section.
Hypergeometric Distribution
Suppose that we have a set of [math]N[/math] balls, of which [math]k[/math] are red and [math]N-k[/math] are blue. We choose [math]n[/math] of these balls, without replacement, and define [math]X[/math] to be the number of red balls in our sample. The distribution of [math]X[/math] is called the hypergeometric distribution. We note that this distribution depends upon three parameters, namely [math]N[/math], [math]k[/math], and [math]n[/math]. There does not seem to be a standard notation for this distribution; we will use the notation [math]h(N, k, n, x)[/math] to denote [math]P(X = x)[/math]. This probability can be found by noting that there are
This distribution can be generalized to the case where there are more than two types of objects. (See Exercise.)
If we let [math]N[/math] and [math]k[/math] tend to [math]\infty[/math], in such a way that the ratio
[math]k/N[/math] remains fixed, then the hypergeometric distribution tends to the binomial
distribution with parameters [math]n[/math] and [math]p = k/N[/math]. This is reasonable because if [math]N[/math] and
[math]k[/math] are much larger than [math]n[/math], then whether we choose our sample with or without
replacement should not affect the probabilities very much, and the experiment
consisting of choosing with replacement yields a binomially distributed random variable (see Exercise).
An example of how this distribution might be used is given in Exercise and Exercise. We now give another example involving the hypergeometric distribution. It illustrates a statistical test called Fisher's Exact Test.
Example as eye color and hair color, and to ask whether there is an association between the two traits. Two traits are associated if knowing the value of one of the traits for a given person allows us to predict the value of the other trait for that person. The stronger the association, the more accurate the predictions become. If there is no association between the traits, then we say that the traits are independent. In this example, we will use the traits of gender and political party, and we will assume that there are only two possible genders, female and male, and only two possible political parties, Democratic and Republican.
Suppose that we have collected data concerning these traits. To test whether there is an association between the traits, we first assume that there is no association between the two traits. This gives rise to an “expected” data set, in which knowledge of the value of one trait is of no help in predicting the value of the other trait. Our collected data set usually differs from this expected data set. If it differs by quite a bit, then we would tend to reject the assumption of independence of the traits. To nail down what is meant by “quite a bit,” we decide which possible data sets differ from the expected data set by at least as much as ours does, and then we compute the probability that any of these data sets would occur under the assumption of independence of traits. If this probability is small, then it is unlikely that the difference between our collected data set and the expected data set is due entirely to chance.
Suppose that we have collected the data shown in Table.
| Democrat | Republican | ||
| Female | 24 | 4 | 28 |
| Male | 8 | 14 | 22 |
| 32 | 18 | 50 |
The row and column sums are called marginal totals, or marginals. In what follows, we will denote the row sums by [math]t_{11}[/math] and [math]t_{12}[/math], and the column sums by [math]t_{21}[/math] and [math]t_{22}[/math]. The [math]ij[/math]th entry in the table will be denoted by [math]s_{ij}[/math]. Finally, the size of the data set will be denoted by [math]n[/math]. Thus, a general data table will look as shown in Table.
| Democrat | Republican | ||
| Female | [math]s_{11}[/math] | [math]s_{12}[/math] | [math]t_{11}[/math] |
| Male | [math]s_{21}[/math] | [math]s_{22}[/math] | [math]t_{12}[/math] |
| [math]t_{21}[/math] | [math]t_{22}[/math] | [math]n[/math] |
We now explain the model which will be used to construct the “expected” data set. In the model, we assume that the two traits are independent. We then put [math]t_{21}[/math] yellow balls and [math]t_{22}[/math] green balls, corresponding to the Democratic and Republican marginals, into an urn. We draw [math]t_{11}[/math] balls, without replacement, from the urn, and call these balls females. The [math]t_{12}[/math] balls remaining in the urn are called males. In the specific case under consideration, the probability of getting the actual data under this model is given by the expression
We are now ready to construct the expected data set. If we choose 28 balls out of
50, we should expect to see, on the average, the same percentage of yellow balls in
our sample as in the urn. Thus, we should expect to see, on the average, [math]28(32/50)
= 17.92 \approx 18[/math] yellow balls in our sample. (See Exercise.)
The other expected values are computed in exactly the same way. Thus, the
expected data set is shown in Table.
| Democrat | Republican | ||
| Female | 18 | 10 | 28 |
| Male | 14 | 8 | 22 |
| 32 | 18 | 50 |
We note that the value of [math]s_{11}[/math] determines the other three values in the table, since the marginals are all fixed. Thus, in considering the possible data sets that could appear in this model, it is enough to consider the various possible values of [math]s_{11}[/math]. In the specific case at hand, what is the probability of drawing exactly [math]a[/math] yellow balls, i.e., what is the probability that [math]s_{11} = a[/math]? It is
We are now ready to decide whether our actual data differs from the expected data set by an amount which is greater than could be reasonably attributed to chance alone. We note that the expected number of female Democrats is 18, but the actual number in our data is 24. The other data sets which differ from the expected data set by more than ours correspond to those where the number of female Democrats equals 25,
26, 27, or 28. Thus, to obtain the required probability, we sum the expression in
() from [math]a = 24[/math] to [math]a = 28[/math]. We obtain a value of [math].000395[/math]. Thus, we
should reject the hypothesis that the two traits are independent.
Finally, we turn to the question of how to simulate a hypergeometric random variable [math]X[/math]. Let us assume that the parameters for [math]X[/math] are [math]N[/math], [math]k[/math], and [math]n[/math]. We imagine that we have a set of [math]N[/math] balls, labelled from 1 to [math]N[/math]. We decree that the first [math]k[/math] of these balls are red, and the rest are blue. Suppose that we have chosen [math]m[/math] balls, and that [math]j[/math] of them are red. Then there are [math]k-j[/math] red balls left, and [math]N-m[/math] balls left. Thus, our next choice will be red with probability
Benford Distribution
Our next example of a distribution comes from the study of leading digits in data sets. It turns out that many data sets that occur “in real life” have the property that the first digits of the data are not uniformly distributed over the set [math]\{1, 2, \ldots, 9\}[/math]. Rather, it appears that the digit 1 is most likely to occur, and that the distribution is monotonically decreasing on the set of possible digits. The Benford distribution appears, in many cases, to fit such data. Many explanations have been given for the occurrence of this distribution. Possibly the most convincing explanation is that this distribution is the only one that is invariant under a change of scale. If one thinks of certain data sets as somehow “naturally occurring,” then the distribution should be unaffected by which units are chosen in which to represent the data, i.e., the distribution should be invariant under change of scale.
Theodore Hill[Notes 2] gives a general
description of the Benford distribution, when one considers the first
[math]d[/math] digits of integers in a data set. We will restrict our attention to the first digit. In this
case, the Benford distribution has distribution function
Mark Nigrini[Notes 3] has advocated the use of the Benford distribution as a means of
testing suspicious financial records such as bookkeeping entries,
checks, and tax returns. His idea is that if someone were to “make up” numbers
in these cases, the person would probably produce numbers that are fairly uniformly distributed,
while if one were to use the actual numbers, the leading digits would roughly follow the Benford
distribution. As an example, Nigrini analyzed President Clinton's tax returns
for a 13-year period. In Figure, the Benford distribution values are shown as
squares, and the President's tax return data are shown as circles. One sees that in this example, the
Benford distribution fits the data very well.
This distribution was discovered by the astronomer Simon Newcomb who stated the
following in his paper on the subject: “That the ten digits do not occur with equal frequency must
be evident to anyone making use of logarithm tables, and noticing how much faster the first pages
wear out than the last ones. The first significant figure is oftener 1 than any other digit, and the
frequency diminishes up to 9.”[Notes 4]
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.
Notes
- See Section 2.2 of the complete Grinstead-Snell book
- T. P. Hill, “The Significant Digit Phenomenon,” American Mathematical Monthly, vol.\ 102, no.\ 4 (April 1995), pgs. 322-327.
- M. Nigrini, “Detecting Biases and Irregularities in Tabulated Data,” working paper
- S. Newcomb, “Note on the frequency of use of the different digits in natural numbers,” American Journal of Mathematics, vol.\ 4 (1881), pgs.\ 39-40.