guide:07ad9c2de8: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 195: | Line 195: | ||
<span id="fig_bars_val_sel"></span> | <span id="fig_bars_val_sel"></span> | ||
[[File:fig_bars_val_sel.jpg | 500px | thumb | We can diagnose a ML method by comparing its <span class="mw-gls mw-gls-first" data-name ="trainerr">training error</span> | [[File:fig_bars_val_sel.jpg | 500px | thumb | We can diagnose a ML method by comparing its <span class="mw-gls mw-gls-first" data-name ="trainerr">training error</span> | ||
with its <span class="mw-gls mw-gls-first" data-name ="valerr">validation error</span>. Ideally both are on the same level as a <span class="mw-gls mw-gls-first" data-name ="baseline">baseline</span> (or | with its <span class="mw-gls mw-gls-first" data-name ="valerr">validation error</span>. Ideally both are on the same level as a <span class="mw-gls mw-gls-first" data-name ="baseline">baseline</span> (or benchmark error level). ]] | ||
</div> | </div> | ||
Chapter [[guide:2c0f621d22 | Empirical Risk Minimization ]] discussed <span class="mw-gls mw-gls-first" data-name ="erm">empirical risk minimization (ERM)</span> as a principled approach to learning a good hypothesis | Chapter [[guide:2c0f621d22 | Empirical Risk Minimization ]] discussed <span class="mw-gls mw-gls-first" data-name ="erm">empirical risk minimization (ERM)</span> as a principled approach to learning a good hypothesis out of a <span class="mw-gls mw-gls-first" data-name ="hypospace">hypothesis space</span> or <span class="mw-gls mw-gls-first" data-name ="model">model</span>. <span class="mw-gls" data-name ="erm">ERM</span> based methods learn a hypothesis | ||
out of a <span class="mw-gls mw-gls-first" data-name ="hypospace">hypothesis space</span> or <span class="mw-gls mw-gls-first" data-name ="model">model</span>. <span class="mw-gls" data-name ="erm">ERM</span> based methods learn a hypothesis | <math>\hat{h} \in \hypospace</math> that incurs minimum average loss on a set of labeled <span class="mw-gls mw-gls-first" data-name ="datapoint">data point</span>s that serve as the <span class="mw-gls mw-gls-first" data-name ="trainset">training set</span>. | ||
<math>\hat{h} \in \hypospace</math> | |||
that incurs minimum average loss on a set of labeled <span class="mw-gls mw-gls-first" data-name ="datapoint">data point</span>s that serve as the <span class="mw-gls mw-gls-first" data-name ="trainset">training set</span>. | |||
We refer to the average loss incurred by a hypothesis on the <span class="mw-gls" data-name ="trainset">training set</span> as the <span class="mw-gls" data-name ="trainerr">training error</span>. | We refer to the average loss incurred by a hypothesis on the <span class="mw-gls" data-name ="trainset">training set</span> as the <span class="mw-gls" data-name ="trainerr">training error</span>. | ||
The minimum average <span class="mw-gls mw-gls-first" data-name ="loss">loss</span> achieved by a hypothesis that solves the <span class="mw-gls" data-name ="erm">ERM</span> might be referred to as | The minimum average <span class="mw-gls mw-gls-first" data-name ="loss">loss</span> achieved by a hypothesis that solves the <span class="mw-gls" data-name ="erm">ERM</span> might be referred to as the <span class="mw-gls" data-name ="trainerr">training error</span> of the overall ML method. This overall ML method is defined by the choice of | ||
the <span class="mw-gls" data-name ="trainerr">training error</span> of the overall ML method. This overall ML method is defined by the choice of | |||
<span class="mw-gls" data-name ="hypospace">hypothesis space</span> (or <span class="mw-gls" data-name ="model">model</span>) and <span class="mw-gls mw-gls-first" data-name ="lossfunc">loss function</span> (see Chapter [[guide:013ef4b5cd | The Landscape of ML ]]). | <span class="mw-gls" data-name ="hypospace">hypothesis space</span> (or <span class="mw-gls" data-name ="model">model</span>) and <span class="mw-gls mw-gls-first" data-name ="lossfunc">loss function</span> (see Chapter [[guide:013ef4b5cd | The Landscape of ML ]]). | ||
<span class="mw-gls mw-gls-first" data-name ="erm">Empirical risk minimization (ERM)</span> is sensible only if the <span class="mw-gls" data-name ="trainerr">training error</span> of a hypothesis is an reliable approximation | <span class="mw-gls mw-gls-first" data-name ="erm">Empirical risk minimization (ERM)</span> is sensible only if the <span class="mw-gls" data-name ="trainerr">training error</span> of a hypothesis is an reliable approximation for its loss incurred on <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. Whether the training error of a hypothesis is a reliable approximation for its <span class="mw-gls" data-name ="loss">loss</span> on <span class="mw-gls" data-name ="datapoint">data point</span>s outside the | ||
for its loss incurred on <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. Whether the training | <span class="mw-gls" data-name ="trainset">training set</span> depends on both, the statistical properties of the <span class="mw-gls" data-name ="datapoint">data point</span>s generated by an ML application and on the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> used by the ML method. | ||
error of a hypothesis is a reliable approximation for its <span class="mw-gls" data-name ="loss">loss</span> on <span class="mw-gls" data-name ="datapoint">data point</span>s outside the | |||
<span class="mw-gls" data-name ="trainset">training set</span> depends on both, the statistical properties of the <span class="mw-gls" data-name ="datapoint">data point</span>s generated | |||
by an ML application and on the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> used by the ML method. | |||
ML methods often use <span class="mw-gls" data-name ="hypospace">hypothesis space</span>s with a large <span class="mw-gls mw-gls-first" data-name ="effdim">effective dimension</span> (see Section [[guide:B85f6bf6f2#sec_hypo_space | The Model ]]). As an example | ML methods often use <span class="mw-gls" data-name ="hypospace">hypothesis space</span>s with a large <span class="mw-gls mw-gls-first" data-name ="effdim">effective dimension</span> (see Section [[guide:B85f6bf6f2#sec_hypo_space | The Model ]]). As an example consider <span class="mw-gls mw-gls-first" data-name ="linreg">linear regression</span> (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]) with <span class="mw-gls" data-name ="datapoint">data point</span>s having a large number | ||
consider <span class="mw-gls mw-gls-first" data-name ="linreg">linear regression</span> (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]) with <span class="mw-gls" data-name ="datapoint">data point</span>s having a large number | <math>\featuredim</math> of features (this setting is referred to as the <span class="mw-gls mw-gls-first" data-name ="highdimregime">high-dimensional regime</span>). The <span class="mw-gls" data-name ="effdim">effective dimension</span> of the [[guide:013ef4b5cd#equ_lin_hypospace|linear hypothesis space]], which is used by <span class="mw-gls" data-name ="linreg">linear regression</span>, is equal to the number | ||
<math>\featuredim</math> of | |||
features (this setting is referred to as the <span class="mw-gls mw-gls-first" data-name ="highdimregime">high-dimensional regime</span>). The <span class="mw-gls" data-name ="effdim">effective dimension</span> of the [[guide:013ef4b5cd#equ_lin_hypospace|linear hypothesis space]], which is used by <span class="mw-gls" data-name ="linreg">linear regression</span>, is equal to the number | |||
<math>\featuredim</math> of features. Modern technology allows to collect a huge number of features about individual <span class="mw-gls" data-name ="datapoint">data point</span>s which implies, in turn, that the <span class="mw-gls" data-name ="effdim">effective dimension</span> of [[guide:013ef4b5cd#equ_lin_hypospace|equ_lin_hypospace]] is large. Another example of a high-dimensional <span class="mw-gls" data-name ="hypospace">hypothesis space</span> arises in deep learning methods using a <span class="mw-gls" data-name ="hypospace">hypothesis space</span> are constituted by all maps represented by an <span class="mw-gls mw-gls-first" data-name ="ann">artificial neural network (ANN)</span> | <math>\featuredim</math> of features. Modern technology allows to collect a huge number of features about individual <span class="mw-gls" data-name ="datapoint">data point</span>s which implies, in turn, that the <span class="mw-gls" data-name ="effdim">effective dimension</span> of [[guide:013ef4b5cd#equ_lin_hypospace|equ_lin_hypospace]] is large. Another example of a high-dimensional <span class="mw-gls" data-name ="hypospace">hypothesis space</span> arises in deep learning methods using a <span class="mw-gls" data-name ="hypospace">hypothesis space</span> are constituted by all maps represented by an <span class="mw-gls mw-gls-first" data-name ="ann">artificial neural network (ANN)</span> | ||
with billions of tunable <span class="mw-gls mw-gls-first" data-name ="parameters">parameters</span>. | with billions of tunable <span class="mw-gls mw-gls-first" data-name ="parameters">parameters</span>. | ||
A high-dimensional <span class="mw-gls" data-name ="hypospace">hypothesis space</span> is very likely to contain a hypothesis that perfectly | A high-dimensional <span class="mw-gls" data-name ="hypospace">hypothesis space</span> is very likely to contain a hypothesis that perfectly fits any given <span class="mw-gls" data-name ="trainset">training set</span>. Such a hypothesis achieves a very small <span class="mw-gls" data-name ="trainerr">training error</span> but might incur a large loss when predicting the labels of a <span class="mw-gls" data-name ="datapoint">data point</span> that is not included in <span class="mw-gls" data-name ="trainset">training set</span>. | ||
fits any given <span class="mw-gls" data-name ="trainset">training set</span>. Such a hypothesis achieves a very small <span class="mw-gls" data-name ="trainerr">training error</span> but might | |||
incur a large loss when predicting the labels of a <span class="mw-gls" data-name ="datapoint">data point</span> that is not included in <span class="mw-gls" data-name ="trainset">training set</span>. | |||
Thus, the (minimum) <span class="mw-gls" data-name ="trainerr">training error</span> achieved by a hypothesis learnt by <span class="mw-gls" data-name ="erm">ERM</span> can be misleading. | Thus, the (minimum) <span class="mw-gls" data-name ="trainerr">training error</span> achieved by a hypothesis learnt by <span class="mw-gls" data-name ="erm">ERM</span> can be misleading. | ||
We say that a ML method, such as <span class="mw-gls" data-name ="linreg">linear regression</span> using too many features, overfits the <span class="mw-gls" data-name ="trainset">training set</span> | We say that a ML method, such as <span class="mw-gls" data-name ="linreg">linear regression</span> using too many features, overfits the <span class="mw-gls" data-name ="trainset">training set</span> | ||
when it learns a hypothesis (e.g., via <span class="mw-gls" data-name ="erm">ERM</span>) that has small <span class="mw-gls" data-name ="trainerr">training error</span> but incurs | when it learns a hypothesis (e.g., via <span class="mw-gls" data-name ="erm">ERM</span>) that has small <span class="mw-gls" data-name ="trainerr">training error</span> but incurs much larger loss outside the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
much larger loss outside the <span class="mw-gls" data-name ="trainset">training set</span>. | |||
Section [[#sec_overfitting_sec_6 | Overfitting ]] shows that <span class="mw-gls" data-name ="linreg">linear regression</span> will overfit a <span class="mw-gls" data-name ="trainset">training set</span> | Section [[#sec_overfitting_sec_6 | Overfitting ]] shows that <span class="mw-gls" data-name ="linreg">linear regression</span> will overfit a <span class="mw-gls" data-name ="trainset">training set</span> | ||
as soon as the number of features of a <span class="mw-gls" data-name ="datapoint">data point</span> exceeds the size of the <span class="mw-gls" data-name ="trainset">training set</span>. | as soon as the number of features of a <span class="mw-gls" data-name ="datapoint">data point</span> exceeds the size of the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
Section [[#sec_validate_predictor | Validation ]] demonstrates how to validate a learnt hypothesis by | Section [[#sec_validate_predictor | Validation ]] demonstrates how to validate a learnt hypothesis by computing its average loss on <span class="mw-gls" data-name ="datapoint">data point</span>s which are not contained in the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
computing its average loss on <span class="mw-gls" data-name ="datapoint">data point</span>s which are not contained in the <span class="mw-gls" data-name ="trainset">training set</span>. | |||
We refer to the set of <span class="mw-gls" data-name ="datapoint">data point</span>s used to validate the learnt hypothesis as a <span class="mw-gls mw-gls-first" data-name ="valset">validation set</span>. | We refer to the set of <span class="mw-gls" data-name ="datapoint">data point</span>s used to validate the learnt hypothesis as a <span class="mw-gls mw-gls-first" data-name ="valset">validation set</span>. | ||
If a ML method overfits the <span class="mw-gls" data-name ="trainset">training set</span>, it learns a hypothesis whose <span class="mw-gls" data-name ="trainerr">training error</span> is much | If a ML method overfits the <span class="mw-gls" data-name ="trainset">training set</span>, it learns a hypothesis whose <span class="mw-gls" data-name ="trainerr">training error</span> is much smaller than its <span class="mw-gls" data-name ="valerr">validation error</span>. We can detect if a ML method overfits by comparing its <span class="mw-gls" data-name ="trainerr">training error</span> with its <span class="mw-gls" data-name ="valerr">validation error</span> (see Figure [[#fig_bars_val_sel|fig_bars_val_sel]]). | ||
smaller than its <span class="mw-gls" data-name ="valerr">validation error</span>. We can detect if a ML method overfits by comparing its <span class="mw-gls" data-name ="trainerr">training error</span> with | |||
its <span class="mw-gls" data-name ="valerr">validation error</span> (see Figure [[#fig_bars_val_sel|fig_bars_val_sel]]). | |||
We can use the <span class="mw-gls" data-name ="valerr">validation error</span> not only to detect if a ML method overfits. The <span class="mw-gls" data-name ="valerr">validation error</span> | We can use the <span class="mw-gls" data-name ="valerr">validation error</span> not only to detect if a ML method overfits. The <span class="mw-gls" data-name ="valerr">validation error</span> | ||
can also be used as a quality measure for the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> or <span class="mw-gls" data-name ="model">model</span> used by the ML method. | can also be used as a quality measure for the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> or <span class="mw-gls" data-name ="model">model</span> used by the ML method. | ||
This is analogous to the concept of a <span class="mw-gls" data-name ="lossfunc">loss function</span> that allows us to evaluate the quality | This is analogous to the concept of a <span class="mw-gls" data-name ="lossfunc">loss function</span> that allows us to evaluate the quality of a hypothesis | ||
of a hypothesis | <math>h\!\in\!\hypospace</math>. Section [[#sec_modsel | Model Selection ]] shows how to select between ML methods using different <span class="mw-gls" data-name ="model">model</span>s by comparing their <span class="mw-gls" data-name ="valerr">validation error</span>s. | ||
<math>h\!\in\!\hypospace</math>. Section [[#sec_modsel | Model Selection ]] shows how to select between | |||
ML methods using different <span class="mw-gls" data-name ="model">model</span>s by comparing their <span class="mw-gls" data-name ="valerr">validation error</span>s. | |||
Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]] uses a simple probabilistic model for the data to study the | Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]] uses a simple probabilistic model for the data to study the relation between the <span class="mw-gls" data-name ="trainerr">training error</span> of a learnt hypothesis and its expected loss (see [[guide:2c0f621d22#equ_def_risk|risk]]). | ||
relation between the <span class="mw-gls" data-name ="trainerr">training error</span> of a learnt hypothesis and its expected loss (see [[guide:2c0f621d22#equ_def_risk|risk]]). | |||
This probabilistic analysis reveals the interplay between the data, the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | This probabilistic analysis reveals the interplay between the data, the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | ||
and the resulting <span class="mw-gls" data-name ="trainerr">training error</span> and <span class="mw-gls" data-name ="valerr">validation error</span> of a ML method. | and the resulting <span class="mw-gls" data-name ="trainerr">training error</span> and <span class="mw-gls" data-name ="valerr">validation error</span> of a ML method. | ||
| Line 258: | Line 240: | ||
As indicated in Figure [[#fig_bars_val_sel|fig_bars_val_sel]], for some ML applications, we might have a | As indicated in Figure [[#fig_bars_val_sel|fig_bars_val_sel]], for some ML applications, we might have a | ||
<span class="mw-gls" data-name ="baseline">baseline</span> (or benchmark) for the achievable performance | <span class="mw-gls" data-name ="baseline">baseline</span> (or benchmark) for the achievable performance of ML methods. Such a <span class="mw-gls" data-name ="baseline">baseline</span> might be obtained from existing ML methods, human performance levels or from a probabilistic model (see Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]]). Section [[#sec_diagnosis_ML | Diagnosing ML ]] details how the comparison between <span class="mw-gls" data-name ="trainerr">training error</span>, <span class="mw-gls" data-name ="valerr">validation error</span> and (if available) a <span class="mw-gls" data-name ="baseline">baseline</span> | ||
of ML methods. Such a <span class="mw-gls" data-name ="baseline">baseline</span> might be obtained from existing ML methods, human performance | informs possible improvements for a ML method. These improvements might be obtained by collecting more <span class="mw-gls" data-name ="datapoint">data point</span>s, using more features of <span class="mw-gls" data-name ="datapoint">data point</span>s or by changing the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> (or <span class="mw-gls" data-name ="model">model</span>). | ||
levels or from a probabilistic model (see Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]]). Section [[#sec_diagnosis_ML | Diagnosing ML ]] details | |||
how the comparison between <span class="mw-gls" data-name ="trainerr">training error</span>, <span class="mw-gls" data-name ="valerr">validation error</span> and (if available) a <span class="mw-gls" data-name ="baseline">baseline</span> | |||
informs possible improvements for a ML method. These improvements might be obtained by | |||
collecting more <span class="mw-gls" data-name ="datapoint">data point</span>s, using more features of <span class="mw-gls" data-name ="datapoint">data point</span>s or by changing the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> (or <span class="mw-gls" data-name ="model">model</span>). | |||
Having a <span class="mw-gls" data-name ="baseline">baseline</span> for the expected <span class="mw-gls" data-name ="loss">loss</span>, such as the <span class="mw-gls mw-gls-first" data-name ="bayesrisk">Bayes risk</span>, allows to tell if a ML | Having a <span class="mw-gls" data-name ="baseline">baseline</span> for the expected <span class="mw-gls" data-name ="loss">loss</span>, such as the <span class="mw-gls mw-gls-first" data-name ="bayesrisk">Bayes risk</span>, allows to tell if a ML method already provides satisfactory results. If the <span class="mw-gls" data-name ="trainerr">training error</span> and the <span class="mw-gls" data-name ="valerr">validation error</span> of a ML method are close to the <span class="mw-gls" data-name ="baseline">baseline</span>, there might be little point in trying to further improve the ML method. | ||
method already provides satisfactory results. If the <span class="mw-gls" data-name ="trainerr">training error</span> and the <span class="mw-gls" data-name ="valerr">validation error</span> of a ML method | |||
are close to the <span class="mw-gls" data-name ="baseline">baseline</span>, there might be little point in trying to further improve the ML method. | |||
==<span id="sec_overfitting_sec_6"/>Overfitting== | ==<span id="sec_overfitting_sec_6"/>Overfitting== | ||
We now have a closer look at the occurrence of overfitting in <span class="mw-gls" data-name ="linreg">linear regression</span> methods. As discussed in | We now have a closer look at the occurrence of overfitting in <span class="mw-gls" data-name ="linreg">linear regression</span> methods. As discussed in Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]], <span class="mw-gls" data-name ="linreg">linear regression</span> methods learn a linear hypothesis | ||
Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]], <span class="mw-gls" data-name ="linreg">linear regression</span> methods learn a linear hypothesis | <math>h(\featurevec) = \weights^{T} \featurevec</math> which is parametrized by the parameter vector | ||
<math>h(\featurevec) = \weights^{T} \featurevec</math> | |||
which is parametrized by the parameter vector | |||
<math>\weights \in \mathbb{R}^{\featurelen}</math>. | <math>\weights \in \mathbb{R}^{\featurelen}</math>. | ||
The learnt hypothesis is then used to predict the numeric label | The learnt hypothesis is then used to predict the numeric label | ||
<math>\truelabel \in \mathbb{R}</math> | <math>\truelabel \in \mathbb{R}</math> of a <span class="mw-gls" data-name ="datapoint">data point</span> based on its feature vector | ||
of a <span class="mw-gls" data-name ="datapoint">data point</span> based on its feature vector | |||
<math>\featurevec \in \mathbb{R}^{\featurelen}</math>. | <math>\featurevec \in \mathbb{R}^{\featurelen}</math>. | ||
<span class="mw-gls mw-gls-first" data-name ="linreg">Linear regression</span> aims at finding a parameter vector | <span class="mw-gls mw-gls-first" data-name ="linreg">Linear regression</span> aims at finding a parameter vector | ||
<math>\widehat{\vw}</math> with minimum | <math>\widehat{\vw}</math> with minimum average squared error loss incurred on a <span class="mw-gls" data-name ="trainset">training set</span> | ||
average squared error loss incurred on a <span class="mw-gls" data-name ="trainset">training set</span> | |||
<math display="block">\dataset = \big\{ \big(\featurevec^{(1)},\truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big) \big\}.</math> | |||
<math display="block"> | |||
\dataset = \big\{ \big(\featurevec^{(1)},\truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big) \big\}. | |||
</math> | |||
The <span class="mw-gls" data-name ="trainset">training set</span> | The <span class="mw-gls" data-name ="trainset">training set</span> | ||
| Line 298: | Line 273: | ||
<math>\truelabel^{(\sampleidx)}</math>, respectively, | <math>\truelabel^{(\sampleidx)}</math>, respectively, | ||
of the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> into the feature matrix | of the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> into the feature matrix | ||
<math>\featuremtx=(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T}</math> | <math>\featuremtx=(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T}</math> and label vector <math>\labelvec=(\truelabel^{(1)},\ldots,\truelabel^{(\samplesize)})^{T}</math>. | ||
and label vector <math>\labelvec=(\truelabel^{(1)},\ldots,\truelabel^{(\samplesize)})^{T}</math>. | |||
The [[guide:2c0f621d22#equ_emp_risk_lin_proje | <span class="mw-gls" data-name ="erm">ERM</span> ]] of <span class="mw-gls" data-name ="linreg">linear regression</span> is solved by any parameter vector <math>\widehat{\weights}</math> that solves [[guide:2c0f621d22#equ_zero_gradient_lin_reg|equ_zero_gradient_lin_reg]]. The (minimum) <span class="mw-gls" data-name ="trainerr">training error</span> of the hypothesis <math>h^{(\widehat{\weights})}</math> is obtained as | The [[guide:2c0f621d22#equ_emp_risk_lin_proje | <span class="mw-gls" data-name ="erm">ERM</span> ]] of <span class="mw-gls" data-name ="linreg">linear regression</span> is solved by any parameter vector <math>\widehat{\weights}</math> that solves [[guide:2c0f621d22#equ_zero_gradient_lin_reg|equ_zero_gradient_lin_reg]]. The (minimum) <span class="mw-gls" data-name ="trainerr">training error</span> of the hypothesis <math>h^{(\widehat{\weights})}</math> is obtained as | ||
<math display="block"> | <math display="block"> | ||
\begin{align} | \begin{align} | ||
\emperror(h^{(\widehat{\weights})} \mid \dataset) & \stackrel{\eqref{eq_def_ERM_weight}}{=} | \emperror(h^{(\widehat{\weights})} \mid \dataset) & \stackrel{\eqref{eq_def_ERM_weight}}{=} | ||
| Line 308: | Line 284: | ||
& \stackrel{\eqref{equ_emp_risk_lin_proje}}{=} \sqeuclnorm{ (\mathbf{I}- \mathbf{P}) \labelvec }. | & \stackrel{\eqref{equ_emp_risk_lin_proje}}{=} \sqeuclnorm{ (\mathbf{I}- \mathbf{P}) \labelvec }. | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
Here, we used the orthogonal projection matrix | Here, we used the orthogonal projection matrix | ||
<math>\mathbf{P}</math> on the linear span | <math>\mathbf{P}</math> on the linear span | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\nonumber | \nonumber | ||
| Line 317: | Line 296: | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
of the feature matrix | of the feature matrix | ||
<math>\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T} \in \mathbb{R}^{ \samplesize \times \featuredim}</math>. | <math>\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T} \in \mathbb{R}^{ \samplesize \times \featuredim}</math>. | ||
In many ML applications we have access to a huge number of individual features to characterize a <span class="mw-gls" data-name ="datapoint">data point</span>. | In many ML applications we have access to a huge number of individual features to characterize a <span class="mw-gls" data-name ="datapoint">data point</span>. | ||
As a point in case, consider a <span class="mw-gls" data-name ="datapoint">data point</span> which is a snapshot obtained from a modern smartphone camera. These | As a point in case, consider a <span class="mw-gls" data-name ="datapoint">data point</span> which is a snapshot obtained from a modern smartphone camera. These cameras have a resolution of several megapixels. Here, we can use millions of pixel colour intensities as its features. | ||
cameras have a resolution of several megapixels. Here, we can use millions of pixel colour intensities as its features. | |||
For such applications, it is common to have more features for <span class="mw-gls" data-name ="datapoint">data point</span>s than the size of the <span class="mw-gls" data-name ="trainset">training set</span>, | For such applications, it is common to have more features for <span class="mw-gls" data-name ="datapoint">data point</span>s than the size of the <span class="mw-gls" data-name ="trainset">training set</span>, | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_condition_overfitting} | \label{equ_condition_overfitting} | ||
\featuredim \geq \samplesize. | \featuredim \geq \samplesize. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
Whenever \eqref{equ_condition_overfitting} holds, the feature vectors | Whenever \eqref{equ_condition_overfitting} holds, the feature vectors | ||
<math>\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}</math> | <math>\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}</math> of the <span class="mw-gls" data-name ="datapoint">data point</span>s in | ||
of the <span class="mw-gls" data-name ="datapoint">data point</span>s in | |||
<math>\dataset</math> are typically linearly independent. As a case in point, if the feature vectors | <math>\dataset</math> are typically linearly independent. As a case in point, if the feature vectors | ||
<math>\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}</math> are realizations of <span class="mw-gls mw-gls-first" data-name ="iid">independent and identically distributed (iid)</span> <span class="mw-gls mw-gls-first" data-name ="rv">random variable (RV)</span>s with a | <math>\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}</math> are realizations of <span class="mw-gls mw-gls-first" data-name ="iid">independent and identically distributed (iid)</span> <span class="mw-gls mw-gls-first" data-name ="rv">random variable (RV)</span>s with a continuous <span class="mw-gls" data-name ="probdist">probability distribution</span>, these vectors are linearly independent with probability one <ref name="Muirhead1982">R. Muirhead. ''Aspects of Multivariate Statistical Theory'' John Wiley \& Sons Inc., 1982</ref>. | ||
continuous <span class="mw-gls" data-name ="probdist">probability distribution</span>, these vectors are linearly independent with probability one <ref name="Muirhead1982">R. Muirhead. ''Aspects of Multivariate Statistical Theory'' John Wiley \& Sons Inc., 1982</ref>. | |||
If the feature vectors | If the feature vectors | ||
<math>\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}</math> | <math>\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}</math> are linearly independent, the span of the feature matrix | ||
are linearly independent, the span of the feature matrix | <math>\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T}</math> coincides with | ||
<math>\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T}</math> | |||
coincides with | |||
<math>\mathbb{R}^{\samplesize}</math> which implies, in turn, | <math>\mathbb{R}^{\samplesize}</math> which implies, in turn, | ||
<math>\mathbf{P} = \mathbf{I}</math>. | <math>\mathbf{P} = \mathbf{I}</math>. | ||
Inserting <math>\mathbf{P} = \mathbf{I}</math> into [[guide:2c0f621d22#equ_emp_risk_lin_proje | equ_emp_risk_lin_proje ]] yields | Inserting <math>\mathbf{P} = \mathbf{I}</math> into [[guide:2c0f621d22#equ_emp_risk_lin_proje | equ_emp_risk_lin_proje ]] yields | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{eq_zero_trianing_error} | \label{eq_zero_trianing_error} | ||
\emperror(h^{(\widehat{\weights})} \mid \dataset) = 0. | \emperror(h^{(\widehat{\weights})} \mid \dataset) = 0. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
As soon as the number <math>\samplesize= | \dataset|</math> of training <span class="mw-gls" data-name ="datapoint">data point</span>s does | |||
not exceed the number <math>\featuredim</math> of features that characterize <span class="mw-gls" data-name ="datapoint">data point</span>s, there | As soon as the number <math>\samplesize= | \dataset|</math> of training <span class="mw-gls" data-name ="datapoint">data point</span>s does not exceed the number <math>\featuredim</math> of features that characterize <span class="mw-gls" data-name ="datapoint">data point</span>s, there is (with probability one) a linear predictor <math>h^{(\widehat{\weights})}</math> achieving zero <span class="mw-gls" data-name ="trainerr">training error</span>(!). | ||
is (with probability one) a linear predictor <math>h^{(\widehat{\weights})}</math> achieving zero <span class="mw-gls" data-name ="trainerr">training error</span>(!). | |||
While the hypothesis <math>h^{(\widehat{\weights})}</math> achieves zero <span class="mw-gls" data-name ="trainerr">training error</span>, it will typically incur a | While the hypothesis <math>h^{(\widehat{\weights})}</math> achieves zero <span class="mw-gls" data-name ="trainerr">training error</span>, it will typically incur a non-zero average prediction error <math>\truelabel - h^{(\widehat{\weights})}(\featurevec)</math> on <span class="mw-gls" data-name ="datapoint">data point</span>s | ||
non-zero average prediction error <math>\truelabel - h^{(\widehat{\weights})}(\featurevec)</math> on <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
<math>(\featurevec,\truelabel)</math> outside the <span class="mw-gls" data-name ="trainset">training set</span> (see Figure [[#fig_polyn_training|fig_polyn_training]]). Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]] will make this statement more precise by using a probabilistic model for the <span class="mw-gls" data-name ="datapoint">data point</span>s within and outside the <span class="mw-gls" data-name ="trainset">training set</span>. | <math>(\featurevec,\truelabel)</math> outside the <span class="mw-gls" data-name ="trainset">training set</span> (see Figure [[#fig_polyn_training|fig_polyn_training]]). Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]] will make this statement more precise by using a probabilistic model for the <span class="mw-gls" data-name ="datapoint">data point</span>s within and outside the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
Note that \eqref{eq_zero_trianing_error} also applies if the features | Note that \eqref{eq_zero_trianing_error} also applies if the features | ||
<math>\featurevec</math> and labels | <math>\featurevec</math> and labels | ||
<math>y</math> | <math>y</math> of <span class="mw-gls" data-name ="datapoint">data point</span>s are completely unrelated. Consider an ML problem with | ||
of <span class="mw-gls" data-name ="datapoint">data point</span>s are completely unrelated. Consider an ML problem with | |||
<span class="mw-gls" data-name ="datapoint">data point</span>s whose labels | <span class="mw-gls" data-name ="datapoint">data point</span>s whose labels | ||
<math>\truelabel</math> and features are realizations of a <span class="mw-gls" data-name ="rv">RV</span> that are statistically | <math>\truelabel</math> and features are realizations of a <span class="mw-gls" data-name ="rv">RV</span> that are statistically independent. Thus, in a very strong sense, the features | ||
independent. Thus, in a very strong sense, the features | <math>\featurevec</math> contain no information about the label of a <span class="mw-gls" data-name ="datapoint">data point</span>. Nevertheless, as soon as the number of features exceeds the size of the <span class="mw-gls" data-name ="trainset">training set</span>, such that \eqref{equ_condition_overfitting} holds, <span class="mw-gls" data-name ="linreg">linear regression</span> methods will learn a hypothesis with zero <span class="mw-gls" data-name ="trainerr">training error</span>. | ||
<math>\featurevec</math> contain no information | |||
about the label of a <span class="mw-gls" data-name ="datapoint">data point</span>. Nevertheless, as soon as the number of features exceeds | |||
the size of the <span class="mw-gls" data-name ="trainset">training set</span>, such that \eqref{equ_condition_overfitting} holds, <span class="mw-gls" data-name ="linreg">linear regression</span> methods | |||
will learn a hypothesis with zero <span class="mw-gls" data-name ="trainerr">training error</span>. | |||
We can easily extend the above discussion about the occurrence of overfitting in linear | We can easily extend the above discussion about the occurrence of overfitting in linear regression to other methods that combine <span class="mw-gls" data-name ="linreg">linear regression</span> with a feature map. | ||
regression to other methods that combine <span class="mw-gls" data-name ="linreg">linear regression</span> with a feature map. | |||
Polynomial regression, using <span class="mw-gls" data-name ="datapoint">data point</span>s with a single feature | Polynomial regression, using <span class="mw-gls" data-name ="datapoint">data point</span>s with a single feature | ||
<math>z</math>, combines linear | <math>z</math>, combines linear regression with the <span class="mw-gls mw-gls-first" data-name ="featuremap">feature map</span> | ||
regression with the <span class="mw-gls mw-gls-first" data-name ="featuremap">feature map</span> | <math>\rawfeature \mapsto \featuremapvec(\rawfeature) \defeq \big(\rawfeature^{0},\ldots,\rawfeature^{\featurelen-1}\big)^{T}</math> as discussed in Section [[guide:013ef4b5cd#sec_polynomial_regression | Polynomial Regression ]]. | ||
<math>\rawfeature \mapsto \featuremapvec(\rawfeature) \defeq \big(\rawfeature^{0},\ldots,\rawfeature^{\featurelen-1}\big)^{T}</math> | |||
as discussed in Section [[guide:013ef4b5cd#sec_polynomial_regression | Polynomial Regression ]]. | |||
It can be shown that whenever \eqref{equ_condition_overfitting} holds and the features | It can be shown that whenever \eqref{equ_condition_overfitting} holds and the features | ||
| Line 395: | Line 365: | ||
by minimizing its average loss on a <span class="mw-gls" data-name ="trainset">training set</span> (blue crosses). Using high-degree polynomials | by minimizing its average loss on a <span class="mw-gls" data-name ="trainset">training set</span> (blue crosses). Using high-degree polynomials | ||
(large | (large | ||
<math>\featurelen</math>) results in a small <span class="mw-gls" data-name ="trainerr">training error</span>. However, the learnt high-degree polynomial | <math>\featurelen</math>) results in a small <span class="mw-gls" data-name ="trainerr">training error</span>. However, the learnt high-degree polynomial performs poorly on <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span> (orange dots). ]] | ||
</div> | </div> | ||
| Line 417: | Line 386: | ||
on the <span class="mw-gls" data-name ="valset">validation set</span> | on the <span class="mw-gls" data-name ="valset">validation set</span> | ||
<math>\valset</math>. The average loss | <math>\valset</math>. The average loss | ||
<math>\emperror(\hat{h}| \valset)</math> obtained on the validation | <math>\emperror(\hat{h}| \valset)</math> obtained on the validation set is the <span class="mw-gls" data-name ="valerr">validation error</span>. Note that | ||
<math>\hat{h}</math> depends on the <span class="mw-gls" data-name ="trainset">training set</span> | <math>\hat{h}</math> depends on the <span class="mw-gls" data-name ="trainset">training set</span> | ||
<math>\trainset</math> but is completely | <math>\trainset</math> but is completely independent of the <span class="mw-gls" data-name ="valset">validation set</span> | ||
<math>\valset</math>. ]] | <math>\valset</math>. ]] | ||
</div> | </div> | ||
| Line 427: | Line 394: | ||
Consider an ML method that uses [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]] to learn a hypothesis | Consider an ML method that uses [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]] to learn a hypothesis | ||
<math>\hat{h} \in \hypospace</math> out of the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> <math>\hypospace</math>. The discussion in Section [[#sec_overfitting_sec_6 | Overfitting ]] revealed that the <span class="mw-gls" data-name ="trainerr">training error</span> of a learnt hypothesis | <math>\hat{h} \in \hypospace</math> out of the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> <math>\hypospace</math>. The discussion in Section [[#sec_overfitting_sec_6 | Overfitting ]] revealed that the <span class="mw-gls" data-name ="trainerr">training error</span> of a learnt hypothesis | ||
<math>\hat{h}</math> can be a poor indicator for the performance of <math>\hat{h}</math> for <span class="mw-gls" data-name ="datapoint">data point</span>s | <math>\hat{h}</math> can be a poor indicator for the performance of <math>\hat{h}</math> for <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. The hypothesis <math>\hat{h}</math> tends to “look better” on the <span class="mw-gls" data-name ="trainset">training set</span> over which it has been tuned within <span class="mw-gls" data-name ="erm">ERM</span>.The basic idea of validating the predictor | ||
outside the <span class="mw-gls" data-name ="trainset">training set</span>. The hypothesis <math>\hat{h}</math> tends to “look better” on the <span class="mw-gls" data-name ="trainset">training set</span> over which it has been tuned within <span class="mw-gls" data-name ="erm">ERM</span>.The basic idea of validating the predictor | |||
<math>\hat{h}</math> is simple: | <math>\hat{h}</math> is simple: | ||
| Line 434: | Line 400: | ||
* then we compute the average <span class="mw-gls" data-name ="loss">loss</span> of <math>\hat{h}</math> on <span class="mw-gls" data-name ="datapoint">data point</span>s that do not belong to the <span class="mw-gls" data-name ="trainset">training set</span>. | * then we compute the average <span class="mw-gls" data-name ="loss">loss</span> of <math>\hat{h}</math> on <span class="mw-gls" data-name ="datapoint">data point</span>s that do not belong to the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
Thus, validation means to compute the average <span class="mw-gls" data-name ="loss">loss</span> of a hypothesis using <span class="mw-gls" data-name ="datapoint">data point</span>s that | Thus, validation means to compute the average <span class="mw-gls" data-name ="loss">loss</span> of a hypothesis using <span class="mw-gls" data-name ="datapoint">data point</span>s that have not been used in <span class="mw-gls" data-name ="erm">ERM</span> to learn that hypothesis. | ||
have not been used in <span class="mw-gls" data-name ="erm">ERM</span> to learn that hypothesis. | |||
Assume we have access to a dataset of | Assume we have access to a dataset of | ||
<math>\samplesize</math> <span class="mw-gls" data-name ="datapoint">data point</span>s, | <math>\samplesize</math> <span class="mw-gls" data-name ="datapoint">data point</span>s, | ||
<math display="block">\dataset = \big\{ \big(\featurevec^{(1)},\truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big) \big\}.</math> | |||
<math display="block"> | |||
\dataset = \big\{ \big(\featurevec^{(1)},\truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big) \big\}. | |||
</math> | |||
Each <span class="mw-gls" data-name ="datapoint">data point</span> is characterized by a feature vector | Each <span class="mw-gls" data-name ="datapoint">data point</span> is characterized by a feature vector | ||
<math>\featurevec^{(\sampleidx)}</math> and a label | <math>\featurevec^{(\sampleidx)}</math> and a label | ||
<math>\truelabel^{(\sampleidx)}</math>. | <math>\truelabel^{(\sampleidx)}</math>. | ||
Algorithm [[#alg:validated_ERM|alg:validated_ERM]] outlines how to learn and validate a hypothesis | Algorithm [[#alg:validated_ERM|alg:validated_ERM]] outlines how to learn and validate a hypothesis | ||
<math>h\in \hypospace</math> | <math>h\in \hypospace</math> by splitting the dataset | ||
by splitting the dataset | |||
<math>\dataset</math> into a <span class="mw-gls" data-name ="trainset">training set</span> and a <span class="mw-gls" data-name ="valset">validation set</span>. The random shuffling in step | <math>\dataset</math> into a <span class="mw-gls" data-name ="trainset">training set</span> and a <span class="mw-gls" data-name ="valset">validation set</span>. The random shuffling in step | ||
[[#alg_shuffle_step|alg_shuffle_step]] of Algorithm [[#alg:validated_ERM|alg:validated_ERM]] ensures the <span class="mw-gls mw-gls-first" data-name ="iidasspt">i.i.d. assumption</span> for the shuffled data. | [[#alg_shuffle_step|alg_shuffle_step]] of Algorithm [[#alg:validated_ERM|alg:validated_ERM]] ensures the <span class="mw-gls mw-gls-first" data-name ="iidasspt">i.i.d. assumption</span> for the shuffled data. | ||
| Line 459: | Line 427: | ||
'''Input:''' model <math>\hypospace</math>, loss function <math>\lossfun</math>, dataset <math>\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}</math>; split ratio <math>\splitratio</math> | '''Input:''' model <math>\hypospace</math>, loss function <math>\lossfun</math>, dataset <math>\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}</math>; split ratio <math>\splitratio</math> | ||
<ul style="list-style: | <ul style="list-style-type:decimal"> | ||
<li><span id="alg_shuffle_step"/> randomly shuffle the <span class="mw-gls" data-name ="datapoint">data point</span>s in | <li><span id="alg_shuffle_step"/> randomly shuffle the <span class="mw-gls" data-name ="datapoint">data point</span>s in | ||
| Line 467: | Line 435: | ||
<math>\samplesize_{t}\!=\! \lceil\splitratio \samplesize\rceil</math> <span class="mw-gls" data-name ="datapoint">data point</span>s, | <math>\samplesize_{t}\!=\! \lceil\splitratio \samplesize\rceil</math> <span class="mw-gls" data-name ="datapoint">data point</span>s, | ||
<math display="block">\trainset = \big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize_{t})}, \truelabel^{(\samplesize_{t})}\big) \big\}.</math> | |||
<math display="block"> | |||
\trainset = \big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize_{t})}, \truelabel^{(\samplesize_{t})}\big) \big\}.</math> | |||
</li><li> create the <span class="mw-gls" data-name ="valset">validation set</span> | </li><li> create the <span class="mw-gls" data-name ="valset">validation set</span> | ||
<math>\valset</math> by the | <math>\valset | ||
</math> | |||
by the | |||
<math>\samplesize_v = \samplesize - \samplesize_t</math> remaining <span class="mw-gls" data-name ="datapoint">data point</span>s, | <math>\samplesize_v = \samplesize - \samplesize_t</math> remaining <span class="mw-gls" data-name ="datapoint">data point</span>s, | ||
<math display="block">\valset = \big\{ \big(\featurevec^{(\samplesize_{t}+1)}, \truelabel^{(\samplesize_{t}+1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}.</math> | |||
<math display="block"> | |||
\valset = \big\{ \big(\featurevec^{(\samplesize_{t}+1)}, \truelabel^{(\samplesize_{t}+1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}.</math> | |||
</li><li> <span id="equ_step_train_val_ERM"/>learn hypothesis | </li><li> <span id="equ_step_train_val_ERM"/>learn hypothesis | ||
<math>\hat{h}</math> via <span class="mw-gls" data-name ="erm">ERM</span> on the <span class="mw-gls" data-name ="trainset">training set</span>, | <math>\hat{h} | ||
<math display="block"> | </math> | ||
via <span class="mw-gls" data-name ="erm">ERM</span> on the <span class="mw-gls" data-name ="trainset">training set</span>, | |||
<math display="block"> | |||
\begin{equation} | \begin{equation} | ||
\label{equ_def_hat_h_fitting} | \label{equ_def_hat_h_fitting} | ||
| Line 506: | Line 486: | ||
The choice of the split ratio | The choice of the split ratio | ||
<math>\splitratio \approx \samplesize_{t}/ \samplesize</math> in Algorithm [[#alg:validated_ERM|alg:validated_ERM]] | <math>\splitratio \approx \samplesize_{t}/ \samplesize | ||
is often based on trial and error. We try out different choices for the split ratio and pick the one with the smallest <span class="mw-gls" data-name ="valerr">validation error</span>. It is difficult to make a precise statement on how to choose the split ratio which applies broadly <ref name="Larsen1999">J. Larsen and C. Goutte. On optimal data split for generalization estimation and model | </math> | ||
in Algorithm [[#alg:validated_ERM|alg:validated_ERM]] | |||
is often based on trial and error. We try out different choices for the split ratio and pick the one with the smallest <span class="mw-gls" data-name ="valerr">validation error</span>. It is difficult to make a precise statement on how to choose the split ratio which applies broadly <ref name="Larsen1999">J. Larsen and C. Goutte. On optimal data split for generalization estimation and model selection. In ''IEEE Workshop on Neural Networks for Signal Process'' 1999</ref>. This difficulty stems from the fact that the optimal choice for | |||
<math>\rho</math> depends on the precise statistical properties of the <span class="mw-gls" data-name ="datapoint">data point</span>s. | <math>\rho</math> depends on the precise statistical properties of the <span class="mw-gls" data-name ="datapoint">data point</span>s. | ||
One approach to determine the required size of the <span class="mw-gls" data-name ="valset">validation set</span> is to use a probabilistic model for the <span class="mw-gls" data-name ="datapoint">data point</span>s. | One approach to determine the required size of the <span class="mw-gls" data-name ="valset">validation set</span> is to use a probabilistic model for the <span class="mw-gls" data-name ="datapoint">data point</span>s. | ||
The <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span> is maybe the most widely used probabilistic model within ML. Here, we interpret <span class="mw-gls" data-name ="datapoint">data point</span>s | The <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span> is maybe the most widely used probabilistic model within ML. Here, we interpret <span class="mw-gls" data-name ="datapoint">data point</span>s as the realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s. These <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s have a common (joint) <span class="mw-gls" data-name ="probdist">probability distribution</span> | ||
as the realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s. These <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s have a common (joint) <span class="mw-gls" data-name ="probdist">probability distribution</span> | |||
<math>p(\featurevec,\truelabel)</math> over possible features | <math>p(\featurevec,\truelabel)</math> over possible features | ||
| Line 519: | Line 500: | ||
<math>\truelabel</math> of a <span class="mw-gls" data-name ="datapoint">data point</span>. | <math>\truelabel</math> of a <span class="mw-gls" data-name ="datapoint">data point</span>. | ||
Under the <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>, the <span class="mw-gls" data-name ="valerr">validation error</span> | Under the <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>, the <span class="mw-gls" data-name ="valerr">validation error</span> | ||
<math>\valerror</math> \eqref{equ_def_training_val_val} also becomes a realization | <math>\valerror</math> \eqref{equ_def_training_val_val} also becomes a realization of a <span class="mw-gls" data-name ="rv">RV</span>. The expectation (or mean) | ||
of a <span class="mw-gls" data-name ="rv">RV</span>. The expectation (or mean) | |||
<math>\expect \{ \valerror \}</math> of this <span class="mw-gls" data-name ="rv">RV</span> is precisely the <span class="mw-gls mw-gls-first" data-name ="risk">risk</span> | <math>\expect \{ \valerror \}</math> of this <span class="mw-gls" data-name ="rv">RV</span> is precisely the <span class="mw-gls mw-gls-first" data-name ="risk">risk</span> | ||
<math>\expect\{ \loss{(\featurevec,\truelabel)} {\hat{h}} \}</math> of <math>\hat{h}</math> (see [[guide:2c0f621d22#equ_def_risk|<span class="mw-gls" data-name ="risk">risk</span>]]). | <math>\expect\{ \loss{(\featurevec,\truelabel)} {\hat{h}} \}</math> of <math>\hat{h}</math> (see [[guide:2c0f621d22#equ_def_risk|<span class="mw-gls" data-name ="risk">risk</span>]]). | ||
Within the above <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>, the <span class="mw-gls" data-name ="valerr">validation error</span> | Within the above <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>, the <span class="mw-gls" data-name ="valerr">validation error</span> | ||
<math>\valerror</math> becomes a realization of a <span class="mw-gls" data-name ="rv">RV</span> that | <math>\valerror</math> becomes a realization of a <span class="mw-gls" data-name ="rv">RV</span> that fluctuates around its mean | ||
fluctuates around its mean | |||
<math>\expect \{ \valerror \}</math>. We can quantify this fluctuation using the variance | <math>\expect \{ \valerror \}</math>. We can quantify this fluctuation using the variance | ||
<math display="block">\sigma_{\valerror}^{2} \defeq \expect \big\{ \big( \valerror -\expect \{ \valerror \}\big)^{2} \big\}.</math> | <math display="block"> | ||
\sigma_{\valerror}^{2} \defeq \expect \big\{ \big( \valerror -\expect \{ \valerror \}\big)^{2} \big\}. | |||
</math> | |||
Note that the validation error is the average of the realizations | Note that the validation error is the average of the realizations | ||
<math>\loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}</math> | <math>\loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}</math> of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s. The <span class="mw-gls" data-name ="probdist">probability distribution</span> of the <span class="mw-gls" data-name ="rv">RV</span> | ||
of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s. The <span class="mw-gls" data-name ="probdist">probability distribution</span> of the <span class="mw-gls" data-name ="rv">RV</span> | <math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math> is determined by the <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>, the choice of loss function and the hypothesis <math>\hat{h}</math>. In general, we do not know <math>p(\featurevec,\truelabel)</math> and, in turn, also do not know the <span class="mw-gls" data-name ="probdist">probability distribution</span> of <math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math>. | ||
<math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math> is determined by the <span class="mw-gls" data-name ="probdist">probability distribution</span> <math>p(\featurevec,\truelabel)</math>, the choice of loss function and the | |||
hypothesis <math>\hat{h}</math>. In general, we do not know <math>p(\featurevec,\truelabel)</math> and, in turn, also do not know | |||
the <span class="mw-gls" data-name ="probdist">probability distribution</span> of <math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math>. | |||
If we know an upper bound <math>U</math> on the variance of the (random) loss | If we know an upper bound <math>U</math> on the variance of the (random) loss | ||
| Line 541: | Line 520: | ||
we can bound the variance of | we can bound the variance of | ||
<math>\valerror</math> as | <math>\valerror</math> as | ||
<math display="block"> \sigma_{\valerror}^{2} \leq U/\samplesize_{v}.</math> We can then, in turn, | |||
<math display="block"> | |||
\sigma_{\valerror}^{2} \leq U/\samplesize_{v}. | |||
</math> | |||
We can then, in turn, | |||
ensure that the variance | ensure that the variance | ||
<math>\sigma_{\valerror}^{2}</math> of the validation error | <math>\sigma_{\valerror}^{2}</math> of the validation error | ||
| Line 548: | Line 532: | ||
<math>\eta</math>, say | <math>\eta</math>, say | ||
<math>\eta = (1/100) \trainerror^2</math>, by using a <span class="mw-gls" data-name ="valset">validation set</span> of size | <math>\eta = (1/100) \trainerror^2</math>, by using a <span class="mw-gls" data-name ="valset">validation set</span> of size | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_lower_bound_variance} | \label{equ_lower_bound_variance} | ||
\samplesize_{v} \geq U/ \eta. | \samplesize_{v} \geq U/ \eta. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
The lower bound \eqref{equ_lower_bound_variance} is only useful if we can determine an upper | The lower bound \eqref{equ_lower_bound_variance} is only useful if we can determine an upper bound | ||
bound | |||
<math>U</math> on the variance of the <span class="mw-gls" data-name ="rv">RV</span> | <math>U</math> on the variance of the <span class="mw-gls" data-name ="rv">RV</span> | ||
<math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math> where | <math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math> where | ||
| Line 562: | Line 547: | ||
with <span class="mw-gls" data-name ="probdist">probability distribution</span> | with <span class="mw-gls" data-name ="probdist">probability distribution</span> | ||
<math>p(\featurevec,\truelabel)</math>. An upper bound on the variance of | <math>p(\featurevec,\truelabel)</math>. An upper bound on the variance of | ||
<math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math> | <math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math> can be derived using probability theory if we know an accurate probabilistic model | ||
can be derived using probability theory if we know an accurate probabilistic model | <math>p(\featurevec,\truelabel)</math> for the <span class="mw-gls" data-name ="datapoint">data point</span>s. Such a probabilistic model might be provided by application-specific scientific fields such as biology or psychology. Another option is to estimate the variance of | ||
<math>p(\featurevec,\truelabel)</math> | <math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math> using the sample variance of the actual loss values | ||
for the <span class="mw-gls" data-name ="datapoint">data point</span>s. Such a probabilistic model might be provided by application-specific scientific | <math>\loss{(\featurevec^{(1)},\truelabel^{(1)})}{\hat{h}},\ldots, \loss{(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)})}{\hat{h}}</math> obtained for the dataset | ||
fields such as biology or psychology. Another option is to estimate the variance of | |||
<math>\loss{(\featurevec,\truelabel)}{\hat{h}}</math> | |||
using the sample variance of the actual loss values | |||
<math>\loss{(\featurevec^{(1)},\truelabel^{(1)})}{\hat{h}},\ldots, \loss{(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)})}{\hat{h}}</math> | |||
obtained for the dataset | |||
<math>\dataset</math>. | <math>\dataset</math>. | ||
| Line 577: | Line 557: | ||
Algorithm [[#alg:validated_ERM|alg:validated_ERM]] uses the most basic form of splitting a given dataset | Algorithm [[#alg:validated_ERM|alg:validated_ERM]] uses the most basic form of splitting a given dataset | ||
<math>\dataset</math> into a <span class="mw-gls" data-name ="trainset">training set</span> | <math>\dataset</math> into a <span class="mw-gls" data-name ="trainset">training set</span> | ||
and a <span class="mw-gls" data-name ="valset">validation set</span>. Many variations and extensions of this basic splitting approach have been proposed | and a <span class="mw-gls" data-name ="valset">validation set</span>. Many variations and extensions of this basic splitting approach have been proposed and studied (see <ref name="Efron97">B. Efron and R. Tibshirani. Improvements on cross-validation: The 632+ bootstrap method. ''Journal of the American Statistical Association'' | ||
and studied (see <ref name="Efron97">B. Efron and R. Tibshirani. Improvements on cross-validation: The 632+ bootstrap method. ''Journal of the American Statistical Association'' | 92(438):548--560, 1997</ref> and Section [[#sec_the_bootsrap | The Bootstrap ]]). One very popular extension of the single split into <span class="mw-gls" data-name ="trainset">training set</span> and <span class="mw-gls" data-name ="valset">validation set</span> is known as <span class="mw-gls mw-gls-first" data-name ="kCV"> | ||
92(438):548--560, 1997</ref> and Section [[#sec_the_bootsrap | The Bootstrap ]]). One very popular extension of the single | |||
split into <span class="mw-gls" data-name ="trainset">training set</span> and <span class="mw-gls" data-name ="valset">validation set</span> is known as <span class="mw-gls mw-gls-first" data-name ="kCV"> | |||
<math>k</math>-fold cross-validation ( | <math>k</math>-fold cross-validation ( | ||
<math>k</math>-fold CV)</span> <ref name="hastie01statisticallearning">T. Hastie, R. Tibshirani, and J. Friedman. ''The Elements of Statistical Learning'' Springer Series in Statistics. Springer, New York, NY, USA, 2001</ref>{{rp|at=Sec. 7.10}}. | <math>k</math>-fold CV)</span> <ref name="hastie01statisticallearning">T. Hastie, R. Tibshirani, and J. Friedman. ''The Elements of Statistical Learning'' Springer Series in Statistics. Springer, New York, NY, USA, 2001</ref>{{rp|at=Sec. 7.10}}. | ||
| Line 593: | Line 571: | ||
[[File:fig_k_fold_CV.jpg | 500px | thumb | Illustration of | [[File:fig_k_fold_CV.jpg | 500px | thumb | Illustration of | ||
<math>\nrfolds</math>-fold CV for | <math>\nrfolds</math>-fold CV for | ||
<math>\nrfolds=5</math>. We evenly partition the entire | <math>\nrfolds=5</math>. We evenly partition the entire dataset | ||
<math>\dataset</math> into | <math>\dataset</math> into | ||
<math>\nrfolds=5</math> subsets (or folds) | <math>\nrfolds=5</math> subsets (or folds) | ||
<math>\dataset_{1},\ldots,\dataset_{5}</math>. We then | <math>\dataset_{1},\ldots,\dataset_{5}</math>. We then repeat the validated <span class="mw-gls" data-name ="erm">ERM</span> Algorithm [[#alg:validated_ERM|alg:validated_ERM]] for | ||
<math>\nrfolds=5</math> times. The | <math>\nrfolds=5</math> times. The | ||
<math>\foldidx</math>th | <math>\foldidx</math>th repetition uses the | ||
<math>\foldidx</math>th fold | <math>\foldidx</math>th fold | ||
<math>\dataset_{\foldidx}</math> as the <span class="mw-gls" data-name ="valset">validation set</span> and the remaining | <math>\dataset_{\foldidx}</math> as the <span class="mw-gls" data-name ="valset">validation set</span> and the remaining | ||
| Line 613: | Line 588: | ||
The average (over all <math>\nrfolds</math> folds) <span class="mw-gls" data-name ="valerr">validation error</span> delivered by <span class="mw-gls" data-name ="kCV"> | The average (over all <math>\nrfolds</math> folds) <span class="mw-gls" data-name ="valerr">validation error</span> delivered by <span class="mw-gls" data-name ="kCV"> | ||
<math>k</math>-fold CV</span> tends to better estimate the expected loss or [[guide:2c0f621d22#equ_def_risk| risk]] compared to the <span class="mw-gls" data-name ="valerr">validation error</span> obtained from a single split in Algorithm [[#alg:validated_ERM|alg:validated_ERM]]. Consider a dataset that consists of a relatively small number | <math>k</math>-fold CV</span> tends to better estimate the expected loss or [[guide:2c0f621d22#equ_def_risk| risk]] compared to the <span class="mw-gls" data-name ="valerr">validation error</span> obtained from a single split in Algorithm [[#alg:validated_ERM|alg:validated_ERM]]. Consider a dataset that consists of a relatively small number of <span class="mw-gls" data-name ="datapoint">data point</span>s. If we use a single split of this small dataset into a <span class="mw-gls" data-name ="trainset">training set</span> and <span class="mw-gls" data-name ="valset">validation set</span>, we might be very unlucky and choose <span class="mw-gls" data-name ="datapoint">data point</span>s for the <span class="mw-gls" data-name ="valset">validation set</span> which are <span class="mw-gls mw-gls-first" data-name ="outlier">outlier</span>s and not representative for the statistical properties of most <span class="mw-gls" data-name ="datapoint">data point</span>s. The effect of such an unlucky split is typically averaged out when using <span class="mw-gls" data-name ="kCV"> | ||
of <span class="mw-gls" data-name ="datapoint">data point</span>s. If we use a single split of this small dataset into a <span class="mw-gls" data-name ="trainset">training set</span> and <span class="mw-gls" data-name ="valset">validation set</span>, we might be very unlucky and choose <span class="mw-gls" data-name ="datapoint">data point</span>s for the <span class="mw-gls" data-name ="valset">validation set</span> which are <span class="mw-gls mw-gls-first" data-name ="outlier">outlier</span>s | |||
and not representative for the statistical properties of most <span class="mw-gls" data-name ="datapoint">data point</span>s. The effect of such an unlucky split is typically averaged out when using <span class="mw-gls" data-name ="kCV"> | |||
<math>k</math>-fold CV</span>. | <math>k</math>-fold CV</span>. | ||
| Line 624: | Line 597: | ||
<math>\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}</math>; number | <math>\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}</math>; number | ||
<math>\nrfolds</math> of folds | <math>\nrfolds</math> of folds | ||
<ul style="list-style: | <ul style="list-style-type:decimal"><li> randomly shuffle the <span class="mw-gls" data-name ="datapoint">data point</span>s in | ||
<math>\dataset</math> <span id="alg_shuffle_step_kCV"/> | <math>\dataset</math> <span id="alg_shuffle_step_kCV"/> | ||
</li><li> divide the shuffled dataset | </li><li> divide the shuffled dataset | ||
| Line 632: | Line 605: | ||
of size | of size | ||
<math>\foldsize=\lceil\samplesize/\nrfolds\rceil</math>, | <math>\foldsize=\lceil\samplesize/\nrfolds\rceil</math>, | ||
<math display="block"> | |||
<math display="block"> | |||
\begin{equation} | \begin{equation} | ||
\dataset_{1}\!=\!\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots, \big(\featurevec^{(\foldsize)}, \truelabel^{(\foldsize)}\big)\} ,\ldots,\dataset_{k}\!=\!\big\{ \big(\featurevec^{((\nrfolds\!-\!1)\foldsize+1)}, \truelabel^{((\nrfolds\!-\!1)\foldsize+1)}\big),\ldots, \big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big)\} | \dataset_{1}\!=\!\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots, \big(\featurevec^{(\foldsize)}, \truelabel^{(\foldsize)}\big)\} ,\ldots,\dataset_{k}\!=\!\big\{ \big(\featurevec^{((\nrfolds\!-\!1)\foldsize+1)}, \truelabel^{((\nrfolds\!-\!1)\foldsize+1)}\big),\ldots, \big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big)\} | ||
| Line 642: | Line 617: | ||
</li> | </li> | ||
<li class="ps-3"> | <li class="ps-3"> | ||
use <math>\foldidx</math>th fold as the validation set | use <math>\foldidx | ||
</math> | |||
th fold as the validation set | |||
<math>\valset=\dataset_{\foldidx}</math> | <math>\valset=\dataset_{\foldidx}</math> | ||
</li> | </li> | ||
| Line 651: | Line 629: | ||
learn hypothesis | learn hypothesis | ||
<math>\hat{h}</math> via <span class="mw-gls" data-name ="erm">ERM</span> on the <span class="mw-gls" data-name ="trainset">training set</span>, | <math>\hat{h}</math> via <span class="mw-gls" data-name ="erm">ERM</span> on the <span class="mw-gls" data-name ="trainset">training set</span>, | ||
<math display="block"> | |||
<math display="block"> | |||
\begin{equation} | \begin{equation} | ||
\label{equ_def_hat_h_fitting_cv} | \label{equ_def_hat_h_fitting_cv} | ||
| Line 676: | Line 656: | ||
<li>'''end for'''</li> | <li>'''end for'''</li> | ||
<li> | <li> | ||
compute average training and validation errors <math display="block">\trainerror \defeq (1/\nrfolds) \sum_{\foldidx=1}^{\nrfolds} \trainerror^{(\foldidx)}\mbox{, and }\valerror \defeq (1/\nrfolds) \sum_{\foldidx=1}^{\nrfolds} \valerror^{(\foldidx)}</math> | compute average training and validation errors | ||
<math>\hat{h} \defeq \hat{h}^{(\foldidx)}</math> for some | <math display="block"> | ||
<math>\foldidx \in \{1,\ldots,\nrfolds\}</math> | \trainerror \defeq (1/\nrfolds) \sum_{\foldidx=1}^{\nrfolds} \trainerror^{(\foldidx)}\mbox{, and }\valerror \defeq (1/\nrfolds) \sum_{\foldidx=1}^{\nrfolds} \valerror^{(\foldidx)} | ||
</math> | |||
</li> | |||
<li> pick a learnt hypothesis <math>\hat{h} \defeq \hat{h}^{(\foldidx)}</math>for some <math>\foldidx \in \{1,\ldots,\nrfolds\}</math> | |||
</li> | |||
</ul> | |||
'''Output:''' learnt hypothesis <math>\hat{h}</math>; average <span class="mw-gls" data-name ="trainerr">training error</span> <math>\trainerror</math>; average validation error <math>\valerror</math> | '''Output:''' learnt hypothesis <math>\hat{h}</math>; average <span class="mw-gls" data-name ="trainerr">training error</span> <math>\trainerror</math>; average validation error <math>\valerror</math> | ||
| Line 688: | Line 673: | ||
===Imbalanced Data=== | ===Imbalanced Data=== | ||
The simple validation approach discussed above requires the validation set to be | The simple validation approach discussed above requires the validation set to be a good representative for the overall statistical properties of the data. This might not be the case in applications with discrete valued labels and some of the label values being very rare. We might then be interested in having a good estimate of the conditional risks | ||
a good representative for the overall statistical properties of the data. This might | |||
not be the case in applications with discrete valued labels and some of the label | |||
values being very rare. We might then be interested in having a good estimate of | |||
the conditional risks | |||
<math>\expect \{ \loss{(\featurevec,\truelabel)}{h} | \truelabel=\truelabel'\}</math> where | <math>\expect \{ \loss{(\featurevec,\truelabel)}{h} | \truelabel=\truelabel'\}</math> where | ||
<math>\truelabel'</math> is one of the rare | <math>\truelabel'</math> is one of the rare label values. This is more than requiring a good estimate for the risk | ||
label values. This is more than requiring a good estimate for the risk | |||
<math>\expect \{ \loss{(\featurevec,\truelabel)}{h} \}</math>. | <math>\expect \{ \loss{(\featurevec,\truelabel)}{h} \}</math>. | ||
| Line 702: | Line 682: | ||
<math>\truelabel \in \{-1,1\}</math>. | <math>\truelabel \in \{-1,1\}</math>. | ||
Assume we aim at learning a hypothesis | Assume we aim at learning a hypothesis | ||
<math>h(\featurevec) = \weights^{T} \featurevec</math> to classify <span class="mw-gls" data-name ="datapoint">data point</span>s | <math>h(\featurevec) = \weights^{T} \featurevec</math> to classify <span class="mw-gls" data-name ="datapoint">data point</span>s as | ||
as | |||
<math>\hat{\truelabel}=1</math> if | <math>\hat{\truelabel}=1</math> if | ||
<math>h(\featurevec) \geq 0</math> while | <math>h(\featurevec) \geq 0</math> while | ||
<math>\hat{\truelabel}=-1</math> otherwise. The learning is based | <math>\hat{\truelabel}=-1</math> otherwise. The learning is based on a dataset | ||
on a dataset | |||
<math>\dataset</math> which contains only one single (!) <span class="mw-gls" data-name ="datapoint">data point</span> with | <math>\dataset</math> which contains only one single (!) <span class="mw-gls" data-name ="datapoint">data point</span> with | ||
<math>\truelabel=-1</math>. If | <math>\truelabel=-1</math>. If we then split the dataset into training and validation set, it is with high probability that the validation set does not include any <span class="mw-gls" data-name ="datapoint">data point</span> with label value | ||
we then split the dataset into training and validation set, it is with high probability that | <math>\truelabel=-1</math>. This cannot happen when using | ||
the validation set does not include any <span class="mw-gls" data-name ="datapoint">data point</span> with label value | |||
<math>\truelabel=-1</math>. This cannot happen | |||
when using | |||
<math>\nrfolds</math>-fold CV since the single <span class="mw-gls" data-name ="datapoint">data point</span> must be in one of the validation folds. | <math>\nrfolds</math>-fold CV since the single <span class="mw-gls" data-name ="datapoint">data point</span> must be in one of the validation folds. | ||
However, even the applicability of <span class="mw-gls" data-name ="kCV"> | However, even the applicability of <span class="mw-gls" data-name ="kCV"> | ||
| Line 722: | Line 697: | ||
To learn and validate a hypothesis with imbalanced data, it might be useful to to generate synthetic | To learn and validate a hypothesis with imbalanced data, it might be useful to to generate synthetic | ||
<span class="mw-gls" data-name ="datapoint">data point</span>s to enlarge the minority class. This can be done using <span class="mw-gls mw-gls-first" data-name ="dataug">data augmentation</span> techniques which we discuss in Section [[guide:50be9327aa#sec_data_augmentation | Data Augmentation ]]. Another option is to choose a <span class="mw-gls" data-name ="lossfunc">loss function</span> that takes the different frequencies of label values into account. Let us illustrate this approach in what | <span class="mw-gls" data-name ="datapoint">data point</span>s to enlarge the minority class. This can be done using <span class="mw-gls mw-gls-first" data-name ="dataug">data augmentation</span> techniques which we discuss in Section [[guide:50be9327aa#sec_data_augmentation | Data Augmentation ]]. Another option is to choose a <span class="mw-gls" data-name ="lossfunc">loss function</span> that takes the different frequencies of label values into account. Let us illustrate this approach in what follows by an illustrative example. | ||
follows by an illustrative example. | |||
Consider an imbalanced dataset of size <math>\samplesize=100</math>, which contains | Consider an imbalanced dataset of size <math>\samplesize=100</math>, which contains | ||
<math>90</math> <span class="mw-gls" data-name ="datapoint">data point</span>s with | <math>90</math> <span class="mw-gls" data-name ="datapoint">data point</span>s with label | ||
label | |||
<math>\truelabel=1</math> but only | <math>\truelabel=1</math> but only | ||
<math>10</math> <span class="mw-gls" data-name ="datapoint">data point</span>s with label | <math>10</math> <span class="mw-gls" data-name ="datapoint">data point</span>s with label | ||
<math>\truelabel=-1</math>. We might want to | <math>\truelabel=-1</math>. We might want to put more weight on wrong predictions obtained for <span class="mw-gls" data-name ="datapoint">data point</span>s from the minority class (with true label value | ||
put more weight on wrong predictions obtained for <span class="mw-gls" data-name ="datapoint">data point</span>s from the minority class (with true label | |||
value | |||
<math>\truelabel=-1</math>). This can be done by using a much larger value for the <span class="mw-gls" data-name ="loss">loss</span> | <math>\truelabel=-1</math>). This can be done by using a much larger value for the <span class="mw-gls" data-name ="loss">loss</span> | ||
<math>\loss{(\featurevec,\truelabel=-1)}{h(\featurevec)=1}</math> | <math>\loss{(\featurevec,\truelabel=-1)}{h(\featurevec)=1}</math> than for the <span class="mw-gls" data-name ="loss">loss</span> | ||
than for the <span class="mw-gls" data-name ="loss">loss</span> | <math>\loss{(\featurevec,\truelabel=1)}{h(\featurevec)=-1}</math> incurred by incorrectly predicting the label of a <span class="mw-gls" data-name ="datapoint">data point</span> from the majority class (with true label value | ||
<math>\loss{(\featurevec,\truelabel=1)}{h(\featurevec)=-1}</math> incurred by incorrectly | |||
predicting the label of a <span class="mw-gls" data-name ="datapoint">data point</span> from the majority class (with true label value | |||
<math>\truelabel=1</math>). | <math>\truelabel=1</math>). | ||
==<span id="sec_modsel"/>Model Selection== | ==<span id="sec_modsel"/>Model Selection== | ||
Chapter [[guide:013ef4b5cd | The Landscape of ML ]] illustrated how many well-known ML methods are obtained | Chapter [[guide:013ef4b5cd | The Landscape of ML ]] illustrated how many well-known ML methods are obtained by different combinations of a <span class="mw-gls" data-name ="hypospace">hypothesis space</span> or <span class="mw-gls" data-name ="model">model</span>, <span class="mw-gls" data-name ="lossfunc">loss function</span> and data representation. | ||
by different combinations of a <span class="mw-gls" data-name ="hypospace">hypothesis space</span> or <span class="mw-gls" data-name ="model">model</span>, <span class="mw-gls" data-name ="lossfunc">loss function</span> and data representation. | While for many ML applications there is often a natural choice for the <span class="mw-gls" data-name ="lossfunc">loss function</span> and data representation, the right choice for the <span class="mw-gls" data-name ="model">model</span> is typically less obvious. We now discuss how to use the validation methods of Section [[#sec_validate_predictor | Validation ]] to choose between different candidate models. | ||
While for many ML applications there is often a natural choice for the <span class="mw-gls" data-name ="lossfunc">loss function</span> and data | |||
representation, the right choice for the <span class="mw-gls" data-name ="model">model</span> is typically less obvious. We now discuss how | |||
to use the validation methods of Section [[#sec_validate_predictor | Validation ]] to choose between different | |||
candidate models. | |||
Consider <span class="mw-gls" data-name ="datapoint">data point</span>s characterized by a single numeric feature | Consider <span class="mw-gls" data-name ="datapoint">data point</span>s characterized by a single numeric feature | ||
| Line 754: | Line 719: | ||
If we suspect that the relation between feature | If we suspect that the relation between feature | ||
<math>\feature</math> and label | <math>\feature</math> and label | ||
<math>\truelabel</math> is non-linear, we might use | <math>\truelabel</math> is non-linear, we might use polynomial regression which is discussed in Section [[guide:013ef4b5cd#sec_polynomial_regression | Polynomial Regression ]]. Polynomial regression uses the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | ||
polynomial regression which is discussed in Section [[guide:013ef4b5cd#sec_polynomial_regression | Polynomial Regression ]]. Polynomial | <math>\hypospace_{\rm poly}^{(\featuredim)}</math> with some maximum degree | ||
regression uses the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | |||
<math>\hypospace_{\rm poly}^{(\featuredim)}</math> with some maximum | |||
degree | |||
<math>\featuredim</math>. Different choices for the maximum degree | <math>\featuredim</math>. Different choices for the maximum degree | ||
<math>\featuredim</math> yield a different | <math>\featuredim</math> yield a different | ||
| Line 778: | Line 740: | ||
<math>\mu_{2}= 20</math>. | <math>\mu_{2}= 20</math>. | ||
Algorithm [[#alg:model_selection|alg:model_selection]] summarizes a simple method to choose between different candidate | Algorithm [[#alg:model_selection|alg:model_selection]] summarizes a simple method to choose between different candidate models | ||
models | <math>\hypospace^{(1)},\hypospace^{(2)},\ldots,\hypospace^{(\nrmodels)}</math>. The idea is to first learn and validate a hypothesis | ||
<math>\hypospace^{(1)},\hypospace^{(2)},\ldots,\hypospace^{(\nrmodels)}</math>. The idea is to first learn | |||
and validate a hypothesis | |||
<math>\hat{h}^{(\modelidx)}</math> separately for each model | <math>\hat{h}^{(\modelidx)}</math> separately for each model | ||
<math>\hypospace^{(\modelidx)}</math> | <math>\hypospace^{(\modelidx)}</math> using Algorithm [[#alg:kfoldCV_ERM|alg:kfoldCV_ERM]]. For each model | ||
using Algorithm [[#alg:kfoldCV_ERM|alg:kfoldCV_ERM]]. For each model | |||
<math>\hypospace^{(\modelidx)}</math>, we learn the hypothesis | <math>\hypospace^{(\modelidx)}</math>, we learn the hypothesis | ||
| Line 790: | Line 749: | ||
<math>\valerror^{(\modelidx)}</math> \eqref{equ_def_training_val_val}. We then choose the hypothesis | <math>\valerror^{(\modelidx)}</math> \eqref{equ_def_training_val_val}. We then choose the hypothesis | ||
<math>\hat{h}^{(\hat{\modelidx})}</math> | <math>\hat{h}^{(\hat{\modelidx})}</math> from those model | ||
from those model | |||
<math>\hypospace^{(\hat{\modelidx})}</math> which resulted in the smallest <span class="mw-gls" data-name ="valerr">validation error</span> | <math>\hypospace^{(\hat{\modelidx})}</math> which resulted in the smallest <span class="mw-gls" data-name ="valerr">validation error</span> | ||
<math>\valerror^{(\hat{\modelidx})} = \min_{\modelidx=1,\ldots,\nrmodels} \valerror^{(\modelidx)}</math>. | <math>\valerror^{(\hat{\modelidx})} = \min_{\modelidx=1,\ldots,\nrmodels} \valerror^{(\modelidx)}</math>. | ||
| Line 799: | Line 757: | ||
The quality of a particular hypothesis | The quality of a particular hypothesis | ||
<math>h</math> is measured using the (average) loss incurred on some <span class="mw-gls" data-name ="trainset">training set</span>. | <math>h</math> is measured using the (average) loss incurred on some <span class="mw-gls" data-name ="trainset">training set</span>. | ||
We use the same principle for model selection but on a higher level. Instead of learning a hypothesis | We use the same principle for model selection but on a higher level. Instead of learning a hypothesis within a <span class="mw-gls" data-name ="hypospace">hypothesis space</span>, we choose (or learn) a <span class="mw-gls" data-name ="hypospace">hypothesis space</span> within a set of candidate | ||
within a <span class="mw-gls" data-name ="hypospace">hypothesis space</span>, we choose (or learn) a <span class="mw-gls" data-name ="hypospace">hypothesis space</span> within a set of candidate | |||
<span class="mw-gls" data-name ="hypospace">hypothesis space</span>s. The quality of a given <span class="mw-gls" data-name ="hypospace">hypothesis space</span> is measured by the validation error \eqref{equ_def_training_val_val}. | <span class="mw-gls" data-name ="hypospace">hypothesis space</span>s. The quality of a given <span class="mw-gls" data-name ="hypospace">hypothesis space</span> is measured by the validation error \eqref{equ_def_training_val_val}. | ||
To determine the validation error of a <span class="mw-gls" data-name ="hypospace">hypothesis space</span>, we first learn the hypothesis | To determine the validation error of a <span class="mw-gls" data-name ="hypospace">hypothesis space</span>, we first learn the hypothesis | ||
| Line 806: | Line 763: | ||
<span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_hat_h_fitting} on the <span class="mw-gls" data-name ="trainset">training set</span>. Then, we obtain the <span class="mw-gls" data-name ="valerr">validation error</span> as the average loss of <math>\hat{h}</math> on the <span class="mw-gls" data-name ="valset">validation set</span>. | <span class="mw-gls" data-name ="erm">ERM</span> \eqref{equ_def_hat_h_fitting} on the <span class="mw-gls" data-name ="trainset">training set</span>. Then, we obtain the <span class="mw-gls" data-name ="valerr">validation error</span> as the average loss of <math>\hat{h}</math> on the <span class="mw-gls" data-name ="valset">validation set</span>. | ||
The final hypothesis <math>\hat{h}</math> delivered by the model selection Algorithm [[#alg:model_selection|alg:model_selection]] not | The final hypothesis <math>\hat{h}</math> delivered by the model selection Algorithm [[#alg:model_selection|alg:model_selection]] not only depends on the <span class="mw-gls" data-name ="trainset">training set</span> used in <span class="mw-gls" data-name ="erm">ERM</span> (see \eqref{equ_def_hat_h_fitting_cv}). This hypothesis <math>\hat{h}</math> has also been chosen based on its validation error which is the average loss on the <span class="mw-gls" data-name ="valset">validation set</span> in \eqref{equ_def_training_val_val_cv}. | ||
only depends on the <span class="mw-gls" data-name ="trainset">training set</span> used in <span class="mw-gls" data-name ="erm">ERM</span> (see \eqref{equ_def_hat_h_fitting_cv}). This hypothesis <math>\hat{h}</math> has also been chosen based on its validation error which is the average loss on the <span class="mw-gls" data-name ="valset">validation set</span> in \eqref{equ_def_training_val_val_cv}. | Indeed, we compared this validation error with the <span class="mw-gls" data-name ="valerr">validation error</span>s of other models to pick the model <math>\hypospace^{(\hat{\modelidx})}</math> (see step [[#step_pick_optimal_model |step_pick_optimal_model]]) which contains | ||
Indeed, we compared this validation error with the <span class="mw-gls" data-name ="valerr">validation error</span>s of other models to pick the | |||
model <math>\hypospace^{(\hat{\modelidx})}</math> (see step [[#step_pick_optimal_model |step_pick_optimal_model]]) which contains | |||
<math>\hat{h}</math>. Since we used the <span class="mw-gls" data-name ="valerr">validation error</span> \eqref{equ_def_training_val_val_cv} of | <math>\hat{h}</math>. Since we used the <span class="mw-gls" data-name ="valerr">validation error</span> \eqref{equ_def_training_val_val_cv} of | ||
<math>\hat{h}</math> to learn it, we cannot use this <span class="mw-gls" data-name ="valerr">validation error</span> as a good indicator for the general performance of | <math>\hat{h}</math> to learn it, we cannot use this <span class="mw-gls" data-name ="valerr">validation error</span> as a good indicator for the general performance of | ||
<math>\hat{h}</math>. | <math>\hat{h}</math>. | ||
To estimate the general performance of the final hypothesis <math>\hat{h}</math> delivered by Algorithm [[#alg:model_selection|alg:model_selection]] we | To estimate the general performance of the final hypothesis <math>\hat{h}</math> delivered by Algorithm [[#alg:model_selection|alg:model_selection]] we must try it out on a test set. The test set, which is constructed in step [[#equ_construct_test_set_algmodsel | equ_construct_test_set_algmodsel]] | ||
must try it out on a test set. The test set, which is constructed in step [[#equ_construct_test_set_algmodsel | equ_construct_test_set_algmodsel]] | of Algorithm [[#alg:model_selection|alg:model_selection]], consists of <span class="mw-gls" data-name ="datapoint">data point</span>s that are neither contained in the <span class="mw-gls" data-name ="trainset">training set</span> \eqref{equ_def_hat_h_fitting_cv} nor the <span class="mw-gls" data-name ="valset">validation set</span> \eqref{equ_def_training_val_val_cv} used for training and validating the candidate models <math>\hypospace^{(1)},\ldots,\hypospace^{(\nrmodels)}</math>. | ||
of Algorithm [[#alg:model_selection|alg:model_selection]], consists of <span class="mw-gls" data-name ="datapoint">data point</span>s that are neither contained | |||
in the <span class="mw-gls" data-name ="trainset">training set</span> \eqref{equ_def_hat_h_fitting_cv} nor the <span class="mw-gls" data-name ="valset">validation set</span> \eqref{equ_def_training_val_val_cv} used for training and validating the candidate models <math>\hypospace^{(1)},\ldots,\hypospace^{(\nrmodels)}</math>. | |||
The average loss of the final hypothesis on the test set is referred to as the test error. The test error is computed in the step [[#step_compute_test_error_mod_selection|step_compute_test_error_mod_selection]] of Algorithm [[#alg:model_selection|alg:model_selection]]. | The average loss of the final hypothesis on the test set is referred to as the test error. The test error is computed in the step [[#step_compute_test_error_mod_selection|step_compute_test_error_mod_selection]] of Algorithm [[#alg:model_selection|alg:model_selection]]. | ||
| Line 830: | Line 783: | ||
<math>\nrfolds</math> of folds, <span class="mw-gls mw-gls-first" data-name ="testset">test set</span> fraction | <math>\nrfolds</math> of folds, <span class="mw-gls mw-gls-first" data-name ="testset">test set</span> fraction | ||
<math>\rho</math> | <math>\rho</math> | ||
<ul style="list-style: | <ul style="list-style-type:decimal"><li> randomly shuffle the <span class="mw-gls" data-name ="datapoint">data point</span>s in | ||
<math>\dataset</math> <span id="alg_shuffle_step_model-sel"/> | <math>\dataset</math> <span id="alg_shuffle_step_model-sel"/> | ||
</li><li> determine size | </li><li> determine size | ||
| Line 836: | Line 789: | ||
</li><li> construct a <span class="mw-gls" data-name ="testset">test set</span><span id-"equ_construct_test_set_algmodsel"/> | </li><li> construct a <span class="mw-gls" data-name ="testset">test set</span><span id-"equ_construct_test_set_algmodsel"/> | ||
<math display="block">\testset= \big\{\big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize')}, \truelabel^{(\samplesize')}\big) \big\}</math> | |||
<math display="block"> | |||
\testset= \big\{\big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize')}, \truelabel^{(\samplesize')}\big) \big\}</math> | |||
| Line 849: | Line 804: | ||
<math>\dataset=\dataset^{(\rm trainval)}</math>, | <math>\dataset=\dataset^{(\rm trainval)}</math>, | ||
<span class="mw-gls" data-name ="lossfunc">loss function</span> | <span class="mw-gls" data-name ="lossfunc">loss function</span> | ||
<math>\lossfun</math> | <math>\lossfun | ||
</math> | |||
and | |||
<math>\nrfolds</math> folds | <math>\nrfolds</math> folds | ||
</li> | </li> | ||
| Line 869: | Line 826: | ||
</li><li> compute ''' test error''' <span id=step_compute_test_error_mod_selection/> | </li><li> compute ''' test error''' <span id=step_compute_test_error_mod_selection/> | ||
<math display="block"> | |||
<math display="block"> | |||
\begin{equation} | \begin{equation} | ||
\label{equ_def_training_error_val_test} | \label{equ_def_training_error_val_test} | ||
| Line 881: | Line 840: | ||
Sometimes it is beneficial to use different loss functions for the training and the validation of a hypothesis. | Sometimes it is beneficial to use different loss functions for the training and the validation of a hypothesis. | ||
As an example, consider <span class="mw-gls mw-gls-first" data-name ="logreg">logistic regression</span> and the <span class="mw-gls mw-gls-first" data-name ="svm">support vector machine (SVM)</span> which have been discussed in Sections [[guide:013ef4b5cd#sec_LogReg | Logistic Regression ]] and | As an example, consider <span class="mw-gls mw-gls-first" data-name ="logreg">logistic regression</span> and the <span class="mw-gls mw-gls-first" data-name ="svm">support vector machine (SVM)</span> which have been discussed in Sections [[guide:013ef4b5cd#sec_LogReg | Logistic Regression ]] and | ||
[[guide:013ef4b5cd#sec_SVM | Support Vector Machines ]], respectively. Both methods use the same model which is the space of linear hypothesis | [[guide:013ef4b5cd#sec_SVM | Support Vector Machines ]], respectively. Both methods use the same model which is the space of linear hypothesis maps <math>h(\featurevec) = \weights^{T} \featurevec</math>. The main difference between these two methods is in their choice for the <span class="mw-gls" data-name ="lossfunc">loss function</span>. <span class="mw-gls mw-gls-first" data-name ="logreg">Logistic regression</span> minimizes the (average) [[guide:B85f6bf6f2#equ_log_loss | <span class="mw-gls mw-gls-first" data-name ="logloss">logistic loss</span>]]on the <span class="mw-gls" data-name ="trainset">training set</span> to learn the hypothesis <math>h^{(1)}(\featurevec)= \big( \weights^{(1)} \big)^{T} \featurevec | ||
maps <math>h(\featurevec) = \weights^{T} \featurevec</math>. The main difference between these two methods is in their choice for the <span class="mw-gls" data-name ="lossfunc">loss function</span>. <span class="mw-gls mw-gls-first" data-name ="logreg">Logistic regression</span> minimizes the (average) [[guide:B85f6bf6f2#equ_log_loss | <span class="mw-gls mw-gls-first" data-name ="logloss">logistic loss</span>]]on the <span class="mw-gls" data-name ="trainset">training set</span> to learn the | </math> | ||
hypothesis <math>h^{(1)}(\featurevec)= \big( \weights^{(1)} \big)^{T} \featurevec </math> with a parameter vector | |||
with a parameter vector | |||
<math>\weights^{(1)}</math>. The <span class="mw-gls" data-name ="svm">SVM</span> instead minimizes the (average) [[guide:B85f6bf6f2#equ_hinge_loss | <span class="mw-gls" data-name ="hingeloss">hinge loss</span>]] on the <span class="mw-gls" data-name ="trainset">training set</span> to learn the hypothesis <math>h^{(2)}(\featurevec) = \big( \weights^{(2)} \big)^{T} \featurevec</math> with a parameter vector <math>\weights^{(2)}</math>. It is inconvenient to compare the usefulness of the two hypotheses <math>h^{(1)}(\featurevec)</math> and <math>h^{(2)}(\featurevec)</math> using different <span class="mw-gls" data-name ="lossfunc">loss function</span>s to compute their <span class="mw-gls" data-name ="valerr">validation error</span>s. This comparison is more convenient if we instead compute the <span class="mw-gls" data-name ="valerr">validation error</span>s for <math>h^{(1)}(\featurevec)</math> and <math>h^{(2)}(\featurevec)</math> using the average [[#B85f6bf6f2#equ_def_0_1 | 0/1 loss]]. | <math>\weights^{(1)}</math>. The <span class="mw-gls" data-name ="svm">SVM</span> instead minimizes the (average) [[guide:B85f6bf6f2#equ_hinge_loss | <span class="mw-gls" data-name ="hingeloss">hinge loss</span>]] on the <span class="mw-gls" data-name ="trainset">training set</span> to learn the hypothesis <math>h^{(2)}(\featurevec) = \big( \weights^{(2)} \big)^{T} \featurevec</math> with a parameter vector <math>\weights^{(2)}</math>. It is inconvenient to compare the usefulness of the two hypotheses <math>h^{(1)}(\featurevec)</math> and <math>h^{(2)}(\featurevec)</math> using different <span class="mw-gls" data-name ="lossfunc">loss function</span>s to compute their <span class="mw-gls" data-name ="valerr">validation error</span>s. This comparison is more convenient if we instead compute the <span class="mw-gls" data-name ="valerr">validation error</span>s for <math>h^{(1)}(\featurevec)</math> and <math>h^{(2)}(\featurevec)</math> using the average [[#B85f6bf6f2#equ_def_0_1 | 0/1 loss]]. | ||
Algorithm [[#alg:model_selection|alg:model_selection]] requires as one of its inputs a given list of candidate models. The | Algorithm [[#alg:model_selection|alg:model_selection]] requires as one of its inputs a given list of candidate models. The longer this list, the more computation is required from Algorithm [[#alg:model_selection|alg:model_selection]]. Sometimes it is possible to prune the list of candidate models by removing models that are very unlikely to have minimum validation error. | ||
longer this list, the more computation is required from Algorithm [[#alg:model_selection|alg:model_selection]]. Sometimes | |||
it is possible to prune the list of candidate models by removing models that are very unlikely to have | |||
minimum validation error. | |||
Consider polynomial regression which uses as the model the space <math>\hypospace_{\rm poly}^{(r)}</math> | Consider polynomial regression which uses as the model the space <math>\hypospace_{\rm poly}^{(r)}</math> of polynomials with maximum degree <math>\polydegree</math> (see [[guide:013ef4b5cd#equ_def_poly_hyposapce |equ_def_poly_hyposapce]]). For <math>\polydegree=1</math>, | ||
of polynomials with maximum degree <math>\polydegree</math> (see [[guide:013ef4b5cd#equ_def_poly_hyposapce |equ_def_poly_hyposapce]]). For <math>\polydegree=1</math>, | |||
<math>\hypospace_{\rm poly}^{(\polydegree)}</math> is the space of polynomials with maximum degree one (which are linear maps), | <math>\hypospace_{\rm poly}^{(\polydegree)}</math> is the space of polynomials with maximum degree one (which are linear maps), | ||
<math>h(\feature)=\weight_{2}\feature+\weight_{1}</math>. For | <math>h(\feature)=\weight_{2}\feature+\weight_{1}</math>. For | ||
<math>\polydegree=2</math>, | <math>\polydegree=2</math>, | ||
<math>\hypospace_{\rm poly}^{(\polydegree)}</math> is the | <math>\hypospace_{\rm poly}^{(\polydegree)}</math> is the space of polynomials with maximum degree two, | ||
space of polynomials with maximum degree two, | <math>h(\feature)=\weight_{3}\feature^2 +\weight_{2}\feature+\weight_{1}.</math> The polynomial degree | ||
<math>h(\feature)=\weight_{3}\feature^2 +\weight_{2}\feature+\weight_{1}.</math> | <math>\polydegree</math> parametrizes a nested set of models, | ||
<math display="block">\hypospace_{\rm poly}^{(\polydegree)} \subset \hypospace_{\rm poly}^{(\polydegree)} \subset \ldots.</math> | <math display="block"> | ||
\hypospace_{\rm poly}^{(\polydegree)} \subset \hypospace_{\rm poly}^{(\polydegree)} \subset \ldots. | |||
</math> | |||
For each degree | For each degree | ||
<math>\polydegree</math>, we learn a hypothesis | <math>\polydegree</math>, we learn a hypothesis | ||
<math>h^{(r)} \in \hypospace_{\rm poly}^{(\polydegree)}</math> with minimum average | <math>h^{(r)} \in \hypospace_{\rm poly}^{(\polydegree)}</math> with minimum average loss (<span class="mw-gls" data-name ="trainerr">training error</span>) | ||
loss (<span class="mw-gls" data-name ="trainerr">training error</span>) | <math>\trainerror^{(\polydegree)}</math> on a <span class="mw-gls" data-name ="trainset">training set</span> (see \eqref{equ_def_training_error_val}). To validate the learnt hypothesis | ||
<math>\trainerror^{(\polydegree)}</math> on a <span class="mw-gls" data-name ="trainset">training set</span> (see \eqref{equ_def_training_error_val}). To validate | |||
the learnt hypothesis | |||
<math>h^{(\polydegree)}</math>, we compute its average loss (<span class="mw-gls" data-name ="valerr">validation error</span>) | <math>h^{(\polydegree)}</math>, we compute its average loss (<span class="mw-gls" data-name ="valerr">validation error</span>) | ||
<math>\valerror^{(\polydegree)}</math> | <math>\valerror^{(\polydegree)}</math> on a <span class="mw-gls" data-name ="valset">validation set</span> (see \eqref{equ_def_training_val_val}). | ||
on a <span class="mw-gls" data-name ="valset">validation set</span> (see \eqref{equ_def_training_val_val}). | |||
Figure [[#fig_trainvalvsdegree|fig_trainvalvsdegree]] depicts the typical dependency of the training and validation errors on the | Figure [[#fig_trainvalvsdegree|fig_trainvalvsdegree]] depicts the typical dependency of the training and validation errors on the polynomial degree | ||
polynomial degree | |||
<math>\polydegree</math>. The <span class="mw-gls" data-name ="trainerr">training error</span> | <math>\polydegree</math>. The <span class="mw-gls" data-name ="trainerr">training error</span> | ||
<math>\trainerror^{(\polydegree)}</math> decreases monotonically | <math>\trainerror^{(\polydegree)}</math> decreases monotonically with increasing polynomial degree | ||
with increasing polynomial degree | <math>\polydegree</math>. To illustrate this monotonic decrease, we consider the two specific choices | ||
<math>\polydegree</math>. To illustrate this monotonic decrease, we consider the two specific | |||
choices | |||
<math>\polydegree=3</math> and | <math>\polydegree=3</math> and | ||
<math>\polydegree=5</math> with corresponding models | <math>\polydegree=5</math> with corresponding models | ||
<math>\hypospace^{(\polydegree)}_{\rm poly}</math> | <math>\hypospace^{(\polydegree)}_{\rm poly}</math> and | ||
and | |||
<math>\hypospace^{(\polydegree)}_{\rm poly}</math>. Note that | <math>\hypospace^{(\polydegree)}_{\rm poly}</math>. Note that | ||
<math>\hypospace^{(3)}_{\rm poly} \subset \hypospace^{(5)}_{\rm poly}</math> | <math>\hypospace^{(3)}_{\rm poly} \subset \hypospace^{(5)}_{\rm poly}</math> since any polynomial with degree not exceeding | ||
since any polynomial with degree not exceeding | |||
<math>3</math> is also a polynomial with degree not exceeding | <math>3</math> is also a polynomial with degree not exceeding | ||
<math>5</math>. | <math>5</math>. | ||
Therefore, the <span class="mw-gls" data-name ="trainerr">training error</span> \eqref{equ_def_training_error_val} obtained when minimizing over the larger | Therefore, the <span class="mw-gls" data-name ="trainerr">training error</span> \eqref{equ_def_training_error_val} obtained when minimizing over the larger model | ||
model | |||
<math> \hypospace^{(5)}_{\rm poly}</math> can only decrease but never increase compared to \eqref{equ_def_training_error_val} | <math> \hypospace^{(5)}_{\rm poly}</math> can only decrease but never increase compared to \eqref{equ_def_training_error_val} | ||
using the smaller model | using the smaller model | ||
<math> \hypospace^{(3)}_{\rm poly}</math> | <math> \hypospace^{(3)}_{\rm poly}</math> Figure [[#fig_trainvalvsdegree|fig_trainvalvsdegree]] indicates that the validation error | ||
Figure [[#fig_trainvalvsdegree|fig_trainvalvsdegree]] indicates that the validation error | |||
<math>\valerror^{(\polydegree)}</math> (see \eqref{equ_def_training_val_val}) | <math>\valerror^{(\polydegree)}</math> (see \eqref{equ_def_training_val_val}) | ||
behaves very different compared to the <span class="mw-gls" data-name ="trainerr">training error</span> | behaves very different compared to the <span class="mw-gls" data-name ="trainerr">training error</span> | ||
<math>\trainerror^{(\polydegree)}</math>. Starting with degree | <math>\trainerror^{(\polydegree)}</math>. Starting with degree | ||
<math>\polydegree=0</math>, the validation error | <math>\polydegree=0</math>, the validation error first decreases with increasing degree | ||
first decreases with increasing degree | |||
<math>\polydegree</math>. As soon as the degree | <math>\polydegree</math>. As soon as the degree | ||
<math>\polydegree</math> is increased | <math>\polydegree</math> is increased beyond a critical value, the validation error starts to increase with increasing | ||
beyond a critical value, the validation error starts to increase with increasing | <math>\polydegree</math>. For very large values of | ||
<math>\polydegree</math>. For very large | <math>\polydegree</math>, the <span class="mw-gls" data-name ="trainerr">training error</span> becomes almost negligible while the validation error becomes very large. In this regime, polynomial regression overfits the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
values of | |||
<math>\polydegree</math>, the <span class="mw-gls" data-name ="trainerr">training error</span> becomes almost negligible while the validation error becomes | |||
very large. In this regime, polynomial regression overfits the <span class="mw-gls" data-name ="trainset">training set</span>. | |||
Figure [[#fig_polyregdegree9|fig_polyregdegree9]] illustrates the overfitting of polynomial regression when using a maximum | Figure [[#fig_polyregdegree9|fig_polyregdegree9]] illustrates the overfitting of polynomial regression when using a maximum degree that is too large. In particular, Figure [[#fig_polyregdegree9|fig_polyregdegree9]] depicts a learnt hypothesis which is a degree | ||
degree that is too large. In particular, Figure [[#fig_polyregdegree9|fig_polyregdegree9]] depicts a learnt hypothesis which is a degree | <math>9</math> polynomial that fits very well the <span class="mw-gls" data-name ="trainset">training set</span>, resulting in a very small <span class="mw-gls" data-name ="trainerr">training error</span>. To achieve this low <span class="mw-gls" data-name ="trainerr">training error</span> | ||
<math>9</math> | |||
polynomial that fits very well the <span class="mw-gls" data-name ="trainset">training set</span>, resulting in a very small <span class="mw-gls" data-name ="trainerr">training error</span>. To achieve this low <span class="mw-gls" data-name ="trainerr">training error</span> | |||
the resulting polynomial has an unreasonable high rate of change for feature values | the resulting polynomial has an unreasonable high rate of change for feature values | ||
<math>\feature \approx 0</math>. This results in | <math>\feature \approx 0</math>. This results in large prediction errors for <span class="mw-gls" data-name ="datapoint">data point</span>s with feature values | ||
large prediction errors for <span class="mw-gls" data-name ="datapoint">data point</span>s with feature values | |||
<math>x \approx 0</math>. | <math>x \approx 0</math>. | ||
| Line 969: | Line 908: | ||
[[File:fig_polyregdegree9.png | 500px | thumb | A hypothesis | [[File:fig_polyregdegree9.png | 500px | thumb | A hypothesis | ||
<math>\hat{h}</math> which is a polynomial with degree not larger than | <math>\hat{h}</math> which is a polynomial with degree not larger than | ||
<math>\polydegree=9</math>. The | <math>\polydegree=9</math>. The hypothesis has been learnt by minimizing the average loss on the <span class="mw-gls" data-name ="trainset">training set</span>. Note the rapid change of | ||
<math>\hat{h}</math> for feature values | |||
<math>\hat{h}</math> for feature | |||
<math>\feature \approx 0</math>. ]] | <math>\feature \approx 0</math>. ]] | ||
</div> | </div> | ||
| Line 983: | Line 920: | ||
''More Data Beats Clever Algorithms ?; More Data Beats Clever Feature Selection?'' | ''More Data Beats Clever Algorithms ?; More Data Beats Clever Feature Selection?'' | ||
A key challenge in ML is to ensure that a hypothesis that predicts well the labels on a <span class="mw-gls" data-name ="trainset">training set</span> (which has | A key challenge in ML is to ensure that a hypothesis that predicts well the labels on a <span class="mw-gls" data-name ="trainset">training set</span> (which has been used to learn that hypothesis) will also predict well the labels of <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
been used to learn that hypothesis) will also predict well the labels of <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. | |||
We say that a ML method generalizes well if it learns a hypothesis | We say that a ML method generalizes well if it learns a hypothesis | ||
<math>\hat{h}</math> that performs not significantly | <math>\hat{h}</math> that performs not significantly worse on <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. In other words, the loss incurred by | ||
worse on <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. In other words, the loss incurred by | |||
<math>\hat{h}</math> for | <math>\hat{h}</math> for | ||
<span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span> is not much larger than the average <span class="mw-gls" data-name ="loss">loss</span> of | <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span> is not much larger than the average <span class="mw-gls" data-name ="loss">loss</span> of | ||
<math>\hat{h}</math> incurred | <math>\hat{h}</math> incurred on the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
on the <span class="mw-gls" data-name ="trainset">training set</span>. | |||
We now study the generalization of <span class="mw-gls" data-name ="linreg">linear regression</span> methods (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]) using an <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>. | We now study the generalization of <span class="mw-gls" data-name ="linreg">linear regression</span> methods (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]) using an <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>. | ||
In particular, we interpret <span class="mw-gls" data-name ="datapoint">data point</span>s as <span class="mw-gls" data-name ="iid">iid</span> realizations of <span class="mw-gls" data-name ="rv">RV</span>s that have the same distribution as | In particular, we interpret <span class="mw-gls" data-name ="datapoint">data point</span>s as <span class="mw-gls" data-name ="iid">iid</span> realizations of <span class="mw-gls" data-name ="rv">RV</span>s that have the same distribution as a random <span class="mw-gls" data-name ="datapoint">data point</span> | ||
a random <span class="mw-gls" data-name ="datapoint">data point</span> | |||
<math>\datapoint=(\featurevec,\truelabel)</math>. The feature vector | <math>\datapoint=(\featurevec,\truelabel)</math>. The feature vector | ||
<math>\featurevec</math> is then a | <math>\featurevec</math> is then a realization of a standard Gaussian <span class="mw-gls" data-name ="rv">RV</span> with zero mean and covariance being the identity matrix, i.e., | ||
realization of a standard Gaussian <span class="mw-gls" data-name ="rv">RV</span> with zero mean and covariance | |||
being the identity matrix, i.e., | |||
<math>\featurevec \sim \mathcal{N}(\mathbf{0}, \mathbf{I})</math>. | <math>\featurevec \sim \mathcal{N}(\mathbf{0}, \mathbf{I})</math>. | ||
| Line 1,005: | Line 936: | ||
<math>\truelabel</math> of a random <span class="mw-gls" data-name ="datapoint">data point</span> is related to its features | <math>\truelabel</math> of a random <span class="mw-gls" data-name ="datapoint">data point</span> is related to its features | ||
<math>\featurevec</math> via a linear Gaussian model | <math>\featurevec</math> via a linear Gaussian model | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_linear_obs_model} | \label{equ_linear_obs_model} | ||
\truelabel = \overline{\weights}^{T} \featurevec + \varepsilon \mbox{, with noise } \varepsilon \sim \mathcal{N}(0,\sigma^{2}). | \truelabel = \overline{\weights}^{T} \featurevec + \varepsilon \mbox{, with noise } \varepsilon \sim \mathcal{N}(0,\sigma^{2}). | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
We assume the noise variance | We assume the noise variance | ||
<math>\sigma^{2}</math> fixed and known. This is a simplifying assumption and in | <math>\sigma^{2}</math> fixed and known. This is a simplifying assumption and in practice we would need to estimate the noise variance from data <ref name="Cohen2002">I. Cohen and B. Berdugo. Noise estimation by minima controlled recursive averaging for robust speech enhancement. ''IEEE Sig. Proc. Lett.'' 9(1):12--15, Jan. 2002</ref>. Note that, within our probabilistic model, the error component | ||
practice we would need to estimate the noise variance from data <ref name="Cohen2002">I. Cohen and B. Berdugo. Noise estimation by minima controlled recursive averaging for robust | <math>\varepsilon</math> in \eqref{equ_linear_obs_model} is intrinsic to the data and cannot be overcome by any ML method. We highlight that the probabilistic model for the observed <span class="mw-gls" data-name ="datapoint">data point</span>s is just a modelling assumption. This assumption allows us to study some fundamental behaviour of ML methods. There are principled methods (“statistical tests”) that allow to determine if a given dataset can be accurately modelled using \eqref{equ_linear_obs_model} <ref name="HuberApproxModels">P. Huber. Approximate models. In C. Huber-Carol, N. Balakrishnan, M. Nikulin, and M. Mesbah, | ||
editors, ''Goodness-of-Fit Tests and Model Validity. Statistics for Industry and Technology. Birkhäuser, Boston, MA, 2002</ref>. | |||
our probabilistic model, the error component | |||
<math>\varepsilon</math> in \eqref{equ_linear_obs_model} is intrinsic | |||
to the data and cannot be overcome by any ML method. We highlight that the probabilistic model for | |||
the observed <span class="mw-gls" data-name ="datapoint">data point</span>s is just a modelling assumption. This assumption allows us to study some | |||
fundamental behaviour of ML methods. There are principled methods (“statistical tests”) that allow to | |||
determine if a given dataset can be accurately modelled using \eqref{equ_linear_obs_model} <ref name="HuberApproxModels">P. Huber. Approximate models. In C. Huber-Carol, N. Balakrishnan, M. Nikulin, and M. Mesbah, | |||
editors, ''Goodness-of-Fit Tests and Model Validity. Statistics for | |||
We predict the label | We predict the label | ||
<math>\truelabel</math> from the features | <math>\truelabel</math> from the features | ||
<math>\featurevec</math> using a linear hypothesis | <math>\featurevec</math> using a linear hypothesis | ||
<math>h(\featurevec)</math> | <math>h(\featurevec)</math> that depends only on the first | ||
that depends only on the first | |||
<math>\modelidx</math> features | <math>\modelidx</math> features | ||
<math>\feature_{1},\ldots,\feature_{\modelidx}</math>. Thus, we | <math>\feature_{1},\ldots,\feature_{\modelidx}</math>. Thus, we use the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | ||
use the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | |||
<span id="equ_generalization_hypospace_r"/> | <span id="equ_generalization_hypospace_r"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_generalization_hypospace_r} | \label{equ_generalization_hypospace_r} | ||
| Line 1,041: | Line 967: | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
Note that each element | Note that each element | ||
<math>h^{(\weights)} \in \hypospace^{(\modelidx)}</math> corresponds to a particular | <math>h^{(\weights)} \in \hypospace^{(\modelidx)}</math> corresponds to a particular choice of the parameter vector | ||
choice of the parameter vector | |||
<math>\weights \in \mathbb{R}^{\modelidx}</math>. | <math>\weights \in \mathbb{R}^{\modelidx}</math>. | ||
The model parameter | The model parameter | ||
<math>\modelidx \in \{0,\ldots,\featuredim\}</math> coincides with the <span class="mw-gls" data-name ="effdim">effective dimension</span> of | <math>\modelidx \in \{0,\ldots,\featuredim\}</math> coincides with the <span class="mw-gls" data-name ="effdim">effective dimension</span> of the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | ||
the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | |||
<math>\hypospace^{(\modelidx)}</math>. For | <math>\hypospace^{(\modelidx)}</math>. For | ||
<math>\modelidx< \featuredim</math>, the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | <math>\modelidx< \featuredim</math>, the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> | ||
<math>\hypospace^{(\modelidx)}</math> | <math>\hypospace^{(\modelidx)}</math> is a proper (strict) subset of the space of [[guide:B85f6bf6f2#equ_def_hypo_linear_pred|linear hypothesis maps]] used within <span class="mw-gls" data-name ="linreg">linear regression</span> (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]). Moreover, the parameter <math>\modelidx</math> indexes a nested sequence of models, | ||
is a proper (strict) subset of the space of [[guide:B85f6bf6f2#equ_def_hypo_linear_pred|linear hypothesis maps]] used within <span class="mw-gls" data-name ="linreg">linear regression</span> (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]). Moreover, the parameter <math>\modelidx</math> indexes a nested sequence of models, | |||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\hypospace^{(0)} \subseteq \hypospace^{(1)} \subseteq \ldots \subseteq \hypospace^{(\featuredim)}. \nonumber | \hypospace^{(0)} \subseteq \hypospace^{(1)} \subseteq \ldots \subseteq \hypospace^{(\featuredim)}. \nonumber | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
The quality of a particular predictor | The quality of a particular predictor | ||
<math>h^{(\weights)} \in \hypospace^{(\modelidx)}</math> is measured via the | <math>h^{(\weights)} \in \hypospace^{(\modelidx)}</math> is measured via the average squared error | ||
average squared error | |||
<math>\emperror (h^{(\weights)} \mid \trainset)</math> incurred on the labeled <span class="mw-gls" data-name ="trainset">training set</span> | <math>\emperror (h^{(\weights)} \mid \trainset)</math> incurred on the labeled <span class="mw-gls" data-name ="trainset">training set</span> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_def_train_set_prob_analysis_generatlization} | \label{equ_def_train_set_prob_analysis_generatlization} | ||
\trainset= \{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big), \ldots, \big(\featurevec^{(\samplesize_{t})}, \truelabel^{(\samplesize_{t})}\big) \}. | \trainset= \{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big), \ldots, \big(\featurevec^{(\samplesize_{t})}, \truelabel^{(\samplesize_{t})}\big) \}. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
We interpret <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> | We interpret <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> | ||
<math>\trainset</math> as well as any other <span class="mw-gls" data-name ="datapoint">data point</span> | <math>\trainset</math> as well as any other <span class="mw-gls" data-name ="datapoint">data point</span> | ||
outside the <span class="mw-gls" data-name ="trainset">training set</span> as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s with a common <span class="mw-gls" data-name ="probdist">probability distribution</span>. This | outside the <span class="mw-gls" data-name ="trainset">training set</span> as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s with a common <span class="mw-gls" data-name ="probdist">probability distribution</span>. This common <span class="mw-gls" data-name ="probdist">probability distribution</span> is a multivariate normal (Gaussian) distribution, | ||
common <span class="mw-gls" data-name ="probdist">probability distribution</span> is a multivariate normal (Gaussian) distribution, | |||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_toy_model_iid} | \label{equ_toy_model_iid} | ||
\featurevec, \featurevec^{(\sampleidx)} \mbox{iid with } \featurevec, \featurevec^{(\sampleidx)} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}). | \featurevec, \featurevec^{(\sampleidx)} \mbox{iid with } \featurevec, \featurevec^{(\sampleidx)} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}). | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
The labels | The labels | ||
<math>\truelabel^{(\sampleidx)},\truelabel</math> are related to the features of <span class="mw-gls" data-name ="datapoint">data point</span>s via (see \eqref{equ_linear_obs_model}) | <math>\truelabel^{(\sampleidx)},\truelabel</math> are related to the features of <span class="mw-gls" data-name ="datapoint">data point</span>s via (see \eqref{equ_linear_obs_model}) | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_labels_training_data} | \label{equ_labels_training_data} | ||
\truelabel^{(\sampleidx)} = \overline{\weights}^{T} \featurevec^{(\sampleidx)} + \varepsilon^{(\sampleidx)}\mbox{, and } \truelabel = \overline{\weights}^{T} \featurevec + \varepsilon. | \truelabel^{(\sampleidx)} = \overline{\weights}^{T} \featurevec^{(\sampleidx)} + \varepsilon^{(\sampleidx)}\mbox{, and } \truelabel = \overline{\weights}^{T} \featurevec + \varepsilon. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
Here, the noise terms | Here, the noise terms | ||
<math>\varepsilon, \varepsilon^{(\sampleidx)} \sim \mathcal{N}(0,\sigma^{2})</math> are realizations | <math>\varepsilon, \varepsilon^{(\sampleidx)} \sim \mathcal{N}(0,\sigma^{2})</math> are realizations of <span class="mw-gls" data-name ="iid">iid</span> Gaussian <span class="mw-gls" data-name ="rv">RV</span>s with zero mean and variance | ||
of <span class="mw-gls" data-name ="iid">iid</span> Gaussian <span class="mw-gls" data-name ="rv">RV</span>s with zero mean and variance | |||
<math>\sigma^{2}</math>. | <math>\sigma^{2}</math>. | ||
Chapter [[guide:2c0f621d22 | Empirical Risk Minimization ]] showed that the <span class="mw-gls" data-name ="trainerr">training error</span> | Chapter [[guide:2c0f621d22 | Empirical Risk Minimization ]] showed that the <span class="mw-gls" data-name ="trainerr">training error</span> | ||
<math>\emperror (h^{(\weights)} \mid \trainset)</math> is | <math>\emperror (h^{(\weights)} \mid \trainset)</math> is minimized by the predictor | ||
minimized by the predictor | |||
<math>h^{(\widehat{\weights})}(\featurevec) = \widehat{\weights}^{T} \mathbf{I}_{\modelidx \times \featuredim} \featurevec</math>, | <math>h^{(\widehat{\weights})}(\featurevec) = \widehat{\weights}^{T} \mathbf{I}_{\modelidx \times \featuredim} \featurevec</math>, | ||
that uses the parameter vector | that uses the parameter vector | ||
<span id="equ_optimal_weight_closed_form"/> | <span id="equ_optimal_weight_closed_form"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_optimal_weight_closed_form} | \label{equ_optimal_weight_closed_form} | ||
\widehat{\weights} = \big(\big(\featuremtx^{(\modelidx)}\big)^{T} \featuremtx^{(\modelidx)} \big)^{-1} \big(\featuremtx^{(\modelidx)}\big)^{T} \labelvec. | \widehat{\weights} = \big(\big(\featuremtx^{(\modelidx)}\big)^{T} \featuremtx^{(\modelidx)} \big)^{-1} \big(\featuremtx^{(\modelidx)}\big)^{T} \labelvec. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
Here we used the (restricted) feature matrix | Here we used the (restricted) feature matrix | ||
<math>\mX^{(\modelidx)}</math> and the label vector | <math>\mX^{(\modelidx)}</math> and the label vector | ||
<math>\labelvec</math> defined as, respectively, | <math>\labelvec</math> defined as, respectively, | ||
<math display="block"> | <math display="block"> | ||
\begin{align} | \begin{align} | ||
| Line 1,114: | Line 1,050: | ||
\label{equ_def_feature_matrix_r} \vy& \!=\!\big(\truelabel^{(1)},\ldots,\truelabel^{(\samplesize_{\rm t})}\big)^{T}\!\in\!\mathbb{R}^{\samplesize_{\rm t}}. | \label{equ_def_feature_matrix_r} \vy& \!=\!\big(\truelabel^{(1)},\ldots,\truelabel^{(\samplesize_{\rm t})}\big)^{T}\!\in\!\mathbb{R}^{\samplesize_{\rm t}}. | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
It will be convenient to tolerate a slight abuse of notation and denote both, | It will be convenient to tolerate a slight abuse of notation and denote both, | ||
the length- | the length- | ||
<math>\modelidx</math> vector \eqref{equ_optimal_weight_closed_form} as well as the | <math>\modelidx</math> vector \eqref{equ_optimal_weight_closed_form} as well as the zero-padded parameter vector | ||
zero-padded parameter vector | |||
<math>\big(\widehat{\weights}^{T},\mathbf{0}^{T}\big)^{T} \in \mathbb{R}^{\featuredim}</math>, | <math>\big(\widehat{\weights}^{T},\mathbf{0}^{T}\big)^{T} \in \mathbb{R}^{\featuredim}</math>, | ||
by | by | ||
<math>\widehat{\weights}</math>. This allows us to write | <math>\widehat{\weights}</math>. This allows us to write | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
h^{(\widehat{\weights})}(\featurevec) = \widehat{\weights}^{T} \featurevec. | h^{(\widehat{\weights})}(\featurevec) = \widehat{\weights}^{T} \featurevec. | ||
| Line 1,129: | Line 1,066: | ||
</math> | </math> | ||
We highlight that the formula \eqref{equ_optimal_weight_closed_form} for the optimal weight | We highlight that the formula \eqref{equ_optimal_weight_closed_form} for the optimal weight vector | ||
vector | |||
<math>\widehat{\weights}</math> is only valid if the matrix | <math>\widehat{\weights}</math> is only valid if the matrix | ||
<math>\big(\featuremtx^{(\modelidx)}\big)^{T} \featuremtx^{(\modelidx)}</math> | <math>\big(\featuremtx^{(\modelidx)}\big)^{T} \featuremtx^{(\modelidx)}</math> is invertible. Within our toy model (see \eqref{equ_toy_model_iid}), this is true with probability one whenever | ||
is invertible. Within our toy model (see \eqref{equ_toy_model_iid}), this is true with probability one | |||
whenever | |||
<math>\samplesize_{\rm t} \geq \modelidx</math>. Indeed, for | <math>\samplesize_{\rm t} \geq \modelidx</math>. Indeed, for | ||
<math>\samplesize_{\rm t} \geq \modelidx</math> the | <math>\samplesize_{\rm t} \geq \modelidx</math> the truncated feature vectors | ||
truncated feature vectors | |||
<math>\mathbf{I}_{\modelidx \times \featuredim} \featurevec^{(1)}, \ldots, \mathbf{I}_{\modelidx \times \featuredim} \featurevec^{(\samplesize_{t})}</math>, | <math>\mathbf{I}_{\modelidx \times \featuredim} \featurevec^{(1)}, \ldots, \mathbf{I}_{\modelidx \times \featuredim} \featurevec^{(\samplesize_{t})}</math>, | ||
which are <span class="mw-gls" data-name ="iid">iid</span> realizations of a Gaussian <span class="mw-gls" data-name ="rv">RV</span>, are linearly independent with probability one <ref name="BertsekasProb">D. Bertsekas and J. Tsitsiklis. ''Introduction to Probability'' Athena Scientific, 2 edition, 2008</ref><ref name="Gallager13">R. G. Gallager. ''Stochastic Processes: Theory for Applications'' Cambridge University Press, 2013</ref>. | which are <span class="mw-gls" data-name ="iid">iid</span> realizations of a Gaussian <span class="mw-gls" data-name ="rv">RV</span>, are linearly independent with probability one <ref name="BertsekasProb">D. Bertsekas and J. Tsitsiklis. ''Introduction to Probability'' Athena Scientific, 2 edition, 2008</ref><ref name="Gallager13">R. G. Gallager. ''Stochastic Processes: Theory for Applications'' Cambridge University Press, 2013</ref>. | ||
In what follows, we consider the case | In what follows, we consider the case | ||
<math>\samplesize_{\rm t} > \modelidx</math> such that the | <math>\samplesize_{\rm t} > \modelidx</math> such that the formula \eqref{equ_optimal_weight_closed_form} is valid (with probability one). The more challenging <span class="mw-gls" data-name ="highdimregime">high-dimensional regime</span> | ||
formula \eqref{equ_optimal_weight_closed_form} is valid (with probability one). The more | <math>\samplesize_{\rm t} \leq \modelidx</math> will be studied in Chapter [[guide:50be9327aa | Regularization ]]. | ||
challenging <span class="mw-gls" data-name ="highdimregime">high-dimensional regime</span> | |||
<math>\samplesize_{\rm t} \leq \modelidx</math> will be | |||
studied in Chapter [[guide:50be9327aa | Regularization ]]. | |||
The optimal parameter vector | The optimal parameter vector | ||
| Line 1,152: | Line 1,082: | ||
depends on the <span class="mw-gls" data-name ="trainset">training set</span> | depends on the <span class="mw-gls" data-name ="trainset">training set</span> | ||
<math>\trainset</math> via the feature matrix | <math>\trainset</math> via the feature matrix | ||
<math>\featuremtx^{(\modelidx)}</math> | <math>\featuremtx^{(\modelidx)}</math> and label vector <math>\labelvec</math> (see \eqref{equ_def_feature_matrix_r}). Therefore, | ||
and label vector <math>\labelvec</math> (see \eqref{equ_def_feature_matrix_r}). Therefore, | |||
since we model the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> as realizations of <span class="mw-gls" data-name ="rv">RV</span>s, the parameter vector | since we model the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> as realizations of <span class="mw-gls" data-name ="rv">RV</span>s, the parameter vector | ||
<math>\widehat{\weights}</math> | <math>\widehat{\weights}</math> | ||
\eqref{equ_optimal_weight_closed_form} is the realization of a <span class="mw-gls" data-name ="rv">RV</span>. For each specific | \eqref{equ_optimal_weight_closed_form} is the realization of a <span class="mw-gls" data-name ="rv">RV</span>. For each specific realization of the <span class="mw-gls" data-name ="trainset">training set</span> | ||
realization of the <span class="mw-gls" data-name ="trainset">training set</span> | <math>\trainset</math>, we obtain a specific realization of the optimal parameter vector | ||
<math>\trainset</math>, we obtain a specific realization of the | |||
optimal parameter vector | |||
<math>\widehat{\weights}</math>. | <math>\widehat{\weights}</math>. | ||
| Line 1,165: | Line 1,092: | ||
<math>\truelabel^{(\sampleidx)}</math> of the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> <math>\dataset</math>. | <math>\truelabel^{(\sampleidx)}</math> of the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> <math>\dataset</math>. | ||
The parameter vector <math>\widehat{\vw}</math> delivered by [[guide:2c0f621d22#equ_def_cost_MSE|<span class="mw-gls" data-name ="erm">ERM</span> ]] typically | The parameter vector <math>\widehat{\vw}</math> delivered by [[guide:2c0f621d22#equ_def_cost_MSE|<span class="mw-gls" data-name ="erm">ERM</span> ]] typically results in a non-zero <span class="mw-gls mw-gls-first" data-name ="esterr">estimation error</span> | ||
results in a non-zero <span class="mw-gls mw-gls-first" data-name ="esterr">estimation error</span> | |||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_def_est_error} | \label{equ_def_est_error} | ||
\Delta \weights \defeq \widehat{\weights} - \overline{\weights}. | \Delta \weights \defeq \widehat{\weights} - \overline{\weights}. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
The <span class="mw-gls" data-name ="esterr">estimation error</span> \eqref{equ_def_est_error} is the realization of a <span class="mw-gls" data-name ="rv">RV</span> since the learnt parameter vector <math>\widehat{\weights}</math> (see \eqref{equ_optimal_weight_closed_form}) is itself a realization of a <span class="mw-gls" data-name ="rv">RV</span>. | The <span class="mw-gls" data-name ="esterr">estimation error</span> \eqref{equ_def_est_error} is the realization of a <span class="mw-gls" data-name ="rv">RV</span> since the learnt parameter vector <math>\widehat{\weights}</math> (see \eqref{equ_optimal_weight_closed_form}) is itself a realization of a <span class="mw-gls" data-name ="rv">RV</span>. | ||
| Line 1,180: | Line 1,108: | ||
The prediction accuracy of <math>h^{(\widehat{\weights})}</math>, using the learnt parameter vector \eqref{equ_optimal_weight_closed_form}, | The prediction accuracy of <math>h^{(\widehat{\weights})}</math>, using the learnt parameter vector \eqref{equ_optimal_weight_closed_form}, | ||
depends crucially on the <span class="mw-gls mw-gls-first" data-name ="msee">mean squared estimation error (MSEE)</span> | depends crucially on the <span class="mw-gls mw-gls-first" data-name ="msee">mean squared estimation error (MSEE)</span> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_def_est_err} | \label{equ_def_est_err} | ||
| Line 1,190: | Line 1,120: | ||
We will next decompose the <span class="mw-gls" data-name ="msee">MSEE</span> | We will next decompose the <span class="mw-gls" data-name ="msee">MSEE</span> | ||
<math>\mseesterr</math> into two components, which are referred to as a <span class="mw-gls mw-gls-first" data-name ="variance">variance</span> term and a <span class="mw-gls mw-gls-first" data-name ="bias">bias</span> term. The variance term quantifies the random fluctuations or the | <math>\mseesterr</math> into two components, which are referred to as a <span class="mw-gls mw-gls-first" data-name ="variance">variance</span> term and a <span class="mw-gls mw-gls-first" data-name ="bias">bias</span> term. The variance term quantifies the random fluctuations or the parameter vector obtained from <span class="mw-gls" data-name ="erm">ERM</span> on the <span class="mw-gls" data-name ="trainset">training set</span> \eqref{equ_def_train_set_prob_analysis_generatlization}. | ||
parameter vector obtained from <span class="mw-gls" data-name ="erm">ERM</span> on the <span class="mw-gls" data-name ="trainset">training set</span> \eqref{equ_def_train_set_prob_analysis_generatlization}. | The <span class="mw-gls" data-name ="bias">bias</span> term characterizes the systematic (or expected) deviation between the true parameter vector <math>\overline{\weights}</math> (see \eqref{equ_linear_obs_model}) and the (expectation of the) | ||
The <span class="mw-gls" data-name ="bias">bias</span> term characterizes the systematic (or expected) deviation between the true parameter | |||
vector <math>\overline{\weights}</math> (see \eqref{equ_linear_obs_model}) and the (expectation of the) | |||
learnt parameter vector <math>\widehat{\weights}</math>. | learnt parameter vector <math>\widehat{\weights}</math>. | ||
Let us start with rewriting \eqref{equ_def_est_err} using elementary manipulations as <math display="block"> | Let us start with rewriting \eqref{equ_def_est_err} using elementary manipulations as | ||
<math display="block"> | |||
\begin{align} | \begin{align} | ||
\mseesterr & \stackrel{\eqref{equ_def_est_err}}{=} \expect \big\{ \sqeuclnorm{\widehat{\weights} - \overline{\weights}} \big \}\big \} \nonumber \\[2mm] | \mseesterr & \stackrel{\eqref{equ_def_est_err}}{=} \expect \big\{ \sqeuclnorm{\widehat{\weights} - \overline{\weights}} \big \}\big \} \nonumber \\[2mm] | ||
| Line 1,202: | Line 1,132: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
We can develop the last expression further by expanding the squared Euclidean norm, | We can develop the last expression further by expanding the squared Euclidean norm, | ||
<math display="block"> | <math display="block"> | ||
\begin{align} | \begin{align} | ||
\mseesterr &= \expect \big\{ \sqeuclnorm{\widehat{\weights} - \expect \{ \widehat{\weights} \} } \big\} - 2 \expect \big \{ \big( \widehat{\weights} - \expect \big\{ \widehat{\weights} \big\} \big)^{T} \big( \overline{\weights} - \expect \big\{ \widehat{\weights} \big\} \big) \big\} + \expect \big\{ \sqeuclnorm{\overline{\weights} - \expect \big\{ \widehat{\weights} \big\} } \big\}\nonumber \\[4mm] | \mseesterr &= \expect \big\{ \sqeuclnorm{\widehat{\weights} - \expect \{ \widehat{\weights} \} } \big\} - 2 \expect \big \{ \big( \widehat{\weights} - \expect \big\{ \widehat{\weights} \big\} \big)^{T} \big( \overline{\weights} - \expect \big\{ \widehat{\weights} \big\} \big) \big\} + \expect \big\{ \sqeuclnorm{\overline{\weights} - \expect \big\{ \widehat{\weights} \big\} } \big\}\nonumber \\[4mm] | ||
| Line 1,210: | Line 1,143: | ||
+ \underbrace{ \expect \big\{ \sqeuclnorm{ \overline{\weights} - \expect \{ \widehat{\weights} \} } \big\} }_{\mbox{bias } \biasterm^2}. | + \underbrace{ \expect \big\{ \sqeuclnorm{ \overline{\weights} - \expect \{ \widehat{\weights} \} } \big\} }_{\mbox{bias } \biasterm^2}. | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
The first component in \eqref{equ_bias_var_decomp} represents the (expected) <span class="mw-gls" data-name ="variance">variance</span> of the | |||
learnt parameter vector | The first component in \eqref{equ_bias_var_decomp} represents the (expected) <span class="mw-gls" data-name ="variance">variance</span> of the learnt parameter vector | ||
<math>\widehat{\weights}</math> \eqref{equ_optimal_weight_closed_form}. | <math>\widehat{\weights}</math> \eqref{equ_optimal_weight_closed_form}. | ||
Note that, within our probabilistic model, the <span class="mw-gls" data-name ="trainset">training set</span> \eqref{equ_def_train_set_prob_analysis_generatlization} is | Note that, within our probabilistic model, the <span class="mw-gls" data-name ="trainset">training set</span> \eqref{equ_def_train_set_prob_analysis_generatlization} is the realization of a <span class="mw-gls" data-name ="rv">RV</span> since it is constituted by <span class="mw-gls" data-name ="datapoint">data point</span>s that are <span class="mw-gls" data-name ="iid">iid</span> realizations of <span class="mw-gls" data-name ="rv">RV</span>s | ||
the realization of a <span class="mw-gls" data-name ="rv">RV</span> since it is constituted by <span class="mw-gls" data-name ="datapoint">data point</span>s that are <span class="mw-gls" data-name ="iid">iid</span> realizations of <span class="mw-gls" data-name ="rv">RV</span>s | |||
(see \eqref{equ_toy_model_iid} and \eqref{equ_linear_obs_model}). | (see \eqref{equ_toy_model_iid} and \eqref{equ_linear_obs_model}). | ||
| Line 1,222: | Line 1,154: | ||
<math>\widehat{\weights}</math> is computed from a randomly fluctuating <span class="mw-gls" data-name ="trainset">training set</span> via \eqref{equ_optimal_weight_closed_form} | <math>\widehat{\weights}</math> is computed from a randomly fluctuating <span class="mw-gls" data-name ="trainset">training set</span> via \eqref{equ_optimal_weight_closed_form} | ||
and is therefore itself fluctuating around its expectation | and is therefore itself fluctuating around its expectation | ||
<math>\expect \big \{\widehat{\weights}\}</math>. The <span class="mw-gls" data-name ="bias">bias</span> term | <math>\expect \big \{\widehat{\weights}\}</math>. The <span class="mw-gls" data-name ="bias">bias</span> term is the Euclidean distance between this expectation | ||
is the Euclidean distance between this expectation | <math>\expect \big \{\widehat{\weights}\}</math> and the true parameter vector | ||
<math>\expect \big \{\widehat{\weights}\}</math> and the true parameter | |||
vector | |||
<math>\overline{\weights}</math> relating features and label of a <span class="mw-gls" data-name ="datapoint">data point</span> via \eqref{equ_linear_obs_model}. | <math>\overline{\weights}</math> relating features and label of a <span class="mw-gls" data-name ="datapoint">data point</span> via \eqref{equ_linear_obs_model}. | ||
| Line 1,236: | Line 1,166: | ||
<math>\biasterm^{2}</math> typically decreases with increasing | <math>\biasterm^{2}</math> typically decreases with increasing | ||
<math>\modelidx</math> while the variance | <math>\modelidx</math> while the variance | ||
<math>\varianceterm</math> | <math>\varianceterm</math> increases with increasing | ||
increases with increasing | |||
<math>\modelidx</math>. | <math>\modelidx</math>. | ||
In particular, the <span class="mw-gls" data-name ="bias">bias</span> term is given as | In particular, the <span class="mw-gls" data-name ="bias">bias</span> term is given as | ||
<span id="equ_def_bias_term"/> | <span id="equ_def_bias_term"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_def_bias_term} | \label{equ_def_bias_term} | ||
\biasterm^{2} = \sqeuclnorm{\overline{\weights} - \expect \{ \widehat{\weights} \} } = \sum_{\featureidx=\modelidx+1}^{\featuredim} \overline{\weight}_{\featureidx}^2, | \biasterm^{2} = \sqeuclnorm{\overline{\weights} - \expect \{ \widehat{\weights} \} } = \sum_{\featureidx=\modelidx+1}^{\featuredim} \overline{\weight}_{\featureidx}^2, | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
The <span class="mw-gls" data-name ="bias">bias</span> term \eqref{equ_def_bias_term} is zero if and only if | The <span class="mw-gls" data-name ="bias">bias</span> term \eqref{equ_def_bias_term} is zero if and only if | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_def_zero_bias_weght_elements} | \label{equ_def_zero_bias_weght_elements} | ||
\overline{\weight}_{\featureidx}=0 \mbox{ for any index } \featureidx=\modelidx+1,\ldots,\featuredim. | \overline{\weight}_{\featureidx}=0 \mbox{ for any index } \featureidx=\modelidx+1,\ldots,\featuredim. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
The necessary and sufficient condition \eqref{equ_def_zero_bias_weght_elements} | The necessary and sufficient condition \eqref{equ_def_zero_bias_weght_elements} | ||
| Line 1,265: | Line 1,199: | ||
While the model parameter | While the model parameter | ||
<math>\modelidx</math> is under control, the true parameter vector | <math>\modelidx</math> is under control, the true parameter vector | ||
<math>\overline{\weights}</math> | <math>\overline{\weights}</math> is not under our control but determined by the underlying data generation process. | ||
is not under our control but determined by the underlying data generation process. | The only way to ensure \eqref{equ_def_zero_bias_weght_elements} for every possible parameter vector | ||
The only way to ensure \eqref{equ_def_zero_bias_weght_elements} for every possible | |||
parameter vector | |||
<math>\overline{\weights}</math> in \eqref{equ_linear_obs_model} is to use | <math>\overline{\weights}</math> in \eqref{equ_linear_obs_model} is to use | ||
<math>\modelidx=\featuredim</math>, i.e., | <math>\modelidx=\featuredim</math>, i.e., | ||
| Line 1,276: | Line 1,208: | ||
When using the model | When using the model | ||
<math>\hypospace^{(\modelidx)}</math> with | <math>\hypospace^{(\modelidx)}</math> with | ||
<math>\modelidx < \featuredim</math>, we cannot guarantee | <math>\modelidx < \featuredim</math>, we cannot guarantee a zero <span class="mw-gls" data-name ="bias">bias</span> term since we have no control over the true underlying parameter vector | ||
a zero <span class="mw-gls" data-name ="bias">bias</span> term since we have no control over the true underlying parameter vector | <math>\overline{\weights}</math> in \eqref{equ_linear_obs_model}. In general, the <span class="mw-gls" data-name ="bias">bias</span> term decreases with an increasing model size | ||
<math>\overline{\weights}</math> | <math>\modelidx</math> (see Figure [[#fig_bias_variance|fig_bias_variance]]). We highlight that the <span class="mw-gls" data-name ="bias">bias</span> term does not depend on the variance | ||
in \eqref{equ_linear_obs_model}. In general, the <span class="mw-gls" data-name ="bias">bias</span> term decreases with an | |||
increasing model size | |||
<math>\modelidx</math> (see Figure [[#fig_bias_variance|fig_bias_variance]]). We highlight that | |||
the <span class="mw-gls" data-name ="bias">bias</span> term does not depend on the variance | |||
<math>\sigma^{2}</math> of the noise | <math>\sigma^{2}</math> of the noise | ||
<math>\varepsilon</math> | <math>\varepsilon</math> in our toy model \eqref{equ_linear_obs_model}. | ||
in our toy model \eqref{equ_linear_obs_model}. | |||
Let us now consider the <span class="mw-gls" data-name ="variance">variance</span> term in \eqref{equ_bias_var_decomp}. Using the statistical | Let us now consider the <span class="mw-gls" data-name ="variance">variance</span> term in \eqref{equ_bias_var_decomp}. Using the statistical independence of the features and labels of <span class="mw-gls" data-name ="datapoint">data point</span>s (see \eqref{equ_linear_obs_model}, | ||
independence of the features and labels of <span class="mw-gls" data-name ="datapoint">data point</span>s (see \eqref{equ_linear_obs_model}, | |||
\eqref{equ_toy_model_iid} and \eqref{equ_labels_training_data}), one can show that {{efn |This derivation is not very difficult but rather lengthy. For more details about the derivation of \eqref{equ_variance_term_toy_model} we refer to the literature <ref name="BertsekasProb"/><ref name="Luetkepol2005">H. Lütkepohl. ''New Introduction to Multiple Time Series Analysis'' Springer, New York, 2005</ref>.}} | \eqref{equ_toy_model_iid} and \eqref{equ_labels_training_data}), one can show that {{efn |This derivation is not very difficult but rather lengthy. For more details about the derivation of \eqref{equ_variance_term_toy_model} we refer to the literature <ref name="BertsekasProb"/><ref name="Luetkepol2005">H. Lütkepohl. ''New Introduction to Multiple Time Series Analysis'' Springer, New York, 2005</ref>.}} | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_variance_term_toy_model} | \label{equ_variance_term_toy_model} | ||
\varianceterm = \expect \big\{ \sqeuclnorm{\widehat{\weights} - \expect\{ \widehat{\weights} \} } \big\} = \big( \biasterm^2+ \sigma^{2}\big) \mbox{tr} \left\{ \expect \left\{\big( \big(\featuremtx^{(\modelidx)}\big)^{T} \featuremtx^{(\modelidx)} \big)^{-1} \right\} \right\}. | \varianceterm = \expect \big\{ \sqeuclnorm{\widehat{\weights} - \expect\{ \widehat{\weights} \} } \big\} = \big( \biasterm^2+ \sigma^{2}\big) \mbox{tr} \left\{ \expect \left\{\big( \big(\featuremtx^{(\modelidx)}\big)^{T} \featuremtx^{(\modelidx)} \big)^{-1} \right\} \right\}. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
By \eqref{equ_toy_model_iid}, the matrix | By \eqref{equ_toy_model_iid}, the matrix | ||
<math>\left(\big(\featuremtx^{(\modelidx)}\big)^{T} \mX^{(\modelidx)} \right)^{-1}</math> is | <math>\left(\big(\featuremtx^{(\modelidx)}\big)^{T} \mX^{(\modelidx)} \right)^{-1}</math> is a realization of a (matrix-valued) <span class="mw-gls" data-name ="rv">RV</span> with an inverse Wishart distribution <ref name="Mardia1979">K. V. Mardia, J. T. Kent, and J. M. Bibby. ''Multivariate Analysis'' Academic Press, 1979</ref>. | ||
a realization of a (matrix-valued) <span class="mw-gls" data-name ="rv">RV</span> with an inverse Wishart distribution <ref name="Mardia1979">K. V. Mardia, J. T. Kent, and J. M. Bibby. ''Multivariate Analysis'' Academic Press, 1979</ref>. | |||
For | For | ||
<math>\samplesize_{\rm t} > \modelidx+1</math>, its expectation is given as | <math>\samplesize_{\rm t} > \modelidx+1</math>, its expectation is given as | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_expr_expect_inv-wishart} | \label{equ_expr_expect_inv-wishart} | ||
\expect\{ \big(\big(\featuremtx^{(\modelidx)} \big)^{T} \featuremtx^{(\modelidx)} \big)^{-1} \} = 1/(\samplesize_{\rm t}-\modelidx-1) \mathbf{I}. | \expect\{ \big(\big(\featuremtx^{(\modelidx)} \big)^{T} \featuremtx^{(\modelidx)} \big)^{-1} \} = 1/(\samplesize_{\rm t}-\modelidx-1) \mathbf{I}. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
By inserting \eqref{equ_expr_expect_inv-wishart} and | By inserting \eqref{equ_expr_expect_inv-wishart} and | ||
| Line 1,312: | Line 1,242: | ||
<span id="equ_formulae_variance_toy_model"/> | <span id="equ_formulae_variance_toy_model"/> | ||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_formulae_variance_toy_model} | \label{equ_formulae_variance_toy_model} | ||
\varianceterm = \expect \left\{ \sqeuclnorm{\widehat{\weights} - \expect\left\{ \widehat{\weights} \right\}} \right\} = \big( \biasterm^{2} +\sigma^{2}\big) \modelidx/(\samplesize_{\rm t}-\modelidx-1). | \varianceterm = \expect \left\{ \sqeuclnorm{\widehat{\weights} - \expect\left\{ \widehat{\weights} \right\}} \right\} = \big( \biasterm^{2} +\sigma^{2}\big) \modelidx/(\samplesize_{\rm t}-\modelidx-1). | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
The <span class="mw-gls" data-name ="variance">variance</span> \eqref{equ_formulae_variance_toy_model} typically increases with increasing | The <span class="mw-gls" data-name ="variance">variance</span> \eqref{equ_formulae_variance_toy_model} typically increases with increasing model complexity <math>\modelidx</math> (see Figure [[#fig_bias_variance|fig_bias_variance]]). In contrast, the <span class="mw-gls" data-name ="bias">bias</span> term | ||
model complexity <math>\modelidx</math> (see Figure [[#fig_bias_variance|fig_bias_variance]]). In contrast, the <span class="mw-gls" data-name ="bias">bias</span> term | |||
\eqref{equ_def_bias_term} decreases with increasing <math>\modelidx</math>. | \eqref{equ_def_bias_term} decreases with increasing <math>\modelidx</math>. | ||
The opposite dependence of <span class="mw-gls" data-name ="variance">variance</span> and <span class="mw-gls" data-name ="bias">bias</span> on the model complexity results in a <span class="mw-gls" data-name ="bias">bias</span>-<span class="mw-gls" data-name ="variance">variance</span> trade-off. Choosing a model (<span class="mw-gls" data-name ="hypospace">hypothesis space</span>) with small <span class="mw-gls" data-name ="bias">bias</span> will typically result in large <span class="mw-gls" data-name ="variance">variance</span> and vice versa. In general, the | The opposite dependence of <span class="mw-gls" data-name ="variance">variance</span> and <span class="mw-gls" data-name ="bias">bias</span> on the model complexity results in a <span class="mw-gls" data-name ="bias">bias</span>-<span class="mw-gls" data-name ="variance">variance</span> trade-off. Choosing a model (<span class="mw-gls" data-name ="hypospace">hypothesis space</span>) with small <span class="mw-gls" data-name ="bias">bias</span> will typically result in large <span class="mw-gls" data-name ="variance">variance</span> and vice versa. In general, the choice of model must balance between a small <span class="mw-gls" data-name ="variance">variance</span> and a small <span class="mw-gls" data-name ="bias">bias</span>. | ||
choice of model must balance between a small <span class="mw-gls" data-name ="variance">variance</span> and a small <span class="mw-gls" data-name ="bias">bias</span>. | |||
<div class="d-flex justify-content-center"> | <div class="d-flex justify-content-center"> | ||
| Line 1,335: | Line 1,265: | ||
Consider a <span class="mw-gls" data-name ="linreg">linear regression</span> method that learns the linear hypothesis | Consider a <span class="mw-gls" data-name ="linreg">linear regression</span> method that learns the linear hypothesis | ||
<math>h(\featurevec) = \widehat{\weights}^{T} \featurevec</math> using | <math>h(\featurevec) = \widehat{\weights}^{T} \featurevec</math> using the parameter vector \eqref{equ_optimal_weight_closed_form}. The parameter vector | ||
the parameter vector \eqref{equ_optimal_weight_closed_form}. The parameter vector | |||
<math>\widehat{\weights}^{T}</math> \eqref{equ_optimal_weight_closed_form} | <math>\widehat{\weights}^{T}</math> \eqref{equ_optimal_weight_closed_form} | ||
results in a linear hypothesis with minimum <span class="mw-gls" data-name ="trainerr">training error</span>, i.e., minimum average loss on the <span class="mw-gls" data-name ="trainset">training set</span>. | results in a linear hypothesis with minimum <span class="mw-gls" data-name ="trainerr">training error</span>, i.e., minimum average loss on the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
However, the ultimate goal of ML is to find a hypothesis that predicts well the label of any <span class="mw-gls" data-name ="datapoint">data point</span>. | However, the ultimate goal of ML is to find a hypothesis that predicts well the label of any <span class="mw-gls" data-name ="datapoint">data point</span>. | ||
In particular, we want the hypothesis | In particular, we want the hypothesis | ||
<math>h(\featurevec) = \widehat{\weights}^{T} \featurevec</math> to generalize | <math>h(\featurevec) = \widehat{\weights}^{T} \featurevec</math> to generalize well to <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. | ||
well to <span class="mw-gls" data-name ="datapoint">data point</span>s outside the <span class="mw-gls" data-name ="trainset">training set</span>. | |||
We quantify the generalization capability of | We quantify the generalization capability of | ||
<math>h(\featurevec) = \widehat{\weights}^{T} \featurevec</math> by | <math>h(\featurevec) = \widehat{\weights}^{T} \featurevec</math> by its expected prediction loss | ||
its expected prediction loss | |||
<math display="block"> | <math display="block"> | ||
\begin{equation} | \begin{equation} | ||
\label{equ_def_expected_pred_loss} | \label{equ_def_expected_pred_loss} | ||
\error_{\rm pred} = \expect \big\{ \big( \truelabel - \underbrace{\widehat{\weights}^{T} \featurevec}_{ = \hat{\truelabel}} \big)^2 \big\}. | \error_{\rm pred} = \expect \big\{ \big( \truelabel - \underbrace{\widehat{\weights}^{T} \featurevec}_{ = \hat{\truelabel}} \big)^2 \big\}. | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
Note that | Note that | ||
<math>\error_{\rm pred}</math> is a measure for the performance of a ML method and not of a specific hypothesis. | <math>\error_{\rm pred}</math> is a measure for the performance of a ML method and not of a specific hypothesis. | ||
| Line 1,358: | Line 1,288: | ||
<math>\widehat{\weights}</math> is not fixed but depends on the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span>. These | <math>\widehat{\weights}</math> is not fixed but depends on the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span>. These | ||
<span class="mw-gls" data-name ="datapoint">data point</span>s are modelled as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s and, in turn, the learnt parameter vector | <span class="mw-gls" data-name ="datapoint">data point</span>s are modelled as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s and, in turn, the learnt parameter vector | ||
<math>\widehat{\weights}</math> | <math>\widehat{\weights}</math> becomes a realization of a <span class="mw-gls" data-name ="rv">RV</span>. Thus, in some sense, the expected prediction loss \eqref{equ_def_expected_pred_loss} characterizes the overall ML method that reads in a <span class="mw-gls" data-name ="trainset">training set</span> and delivers (learn) a linear hypothesis with parameter vector | ||
becomes a realization of a <span class="mw-gls" data-name ="rv">RV</span>. Thus, in some sense, the expected prediction loss \eqref{equ_def_expected_pred_loss} characterizes | |||
the overall ML method that reads in a <span class="mw-gls" data-name ="trainset">training set</span> and delivers (learn) a linear hypothesis with parameter vector | |||
<math>\widehat{\weights}</math> \eqref{equ_optimal_weight_closed_form}. In contrast, the [[guide:2c0f621d22#equ_def_risk| <span class="mw-gls" data-name ="risk">risk</span>]] introduced in Chapter [[guide:2c0f621d22 | Empirical Risk Minimization ]] characterizes the performance of a specific (fixed) hypothesis | <math>\widehat{\weights}</math> \eqref{equ_optimal_weight_closed_form}. In contrast, the [[guide:2c0f621d22#equ_def_risk| <span class="mw-gls" data-name ="risk">risk</span>]] introduced in Chapter [[guide:2c0f621d22 | Empirical Risk Minimization ]] characterizes the performance of a specific (fixed) hypothesis | ||
<math>h</math> without taking into account a learning process that delivered <math>h</math> based on <span class="mw-gls mw-gls-first" data-name ="data">data</span>. | <math>h</math> without taking into account a learning process that delivered <math>h</math> based on <span class="mw-gls mw-gls-first" data-name ="data">data</span>. | ||
Let us now relate the expected prediction loss \eqref{equ_def_expected_pred_loss} of the linear | Let us now relate the expected prediction loss \eqref{equ_def_expected_pred_loss} of the linear hypothesis | ||
hypothesis | |||
<math>h(\featurevec) = \widehat{\weights}^{T} \featurevec</math> to the <span class="mw-gls" data-name ="bias">bias</span> and <span class="mw-gls" data-name ="variance">variance</span> | <math>h(\featurevec) = \widehat{\weights}^{T} \featurevec</math> to the <span class="mw-gls" data-name ="bias">bias</span> and <span class="mw-gls" data-name ="variance">variance</span> | ||
of \eqref{equ_optimal_weight_closed_form}, | of \eqref{equ_optimal_weight_closed_form}, | ||
<span id = "equ_decomp_E_pred_toy_model"/> | |||
<math display="block"> | <math display="block"> | ||
\begin{align} | \begin{align} | ||
| Line 1,377: | Line 1,307: | ||
& \label{equ_decomp_E_pred_toy_model}\stackrel{\eqref{equ_bias_var_decomp}}{=} \biasterm^{2} + \varianceterm + \sigma^{2}. | & \label{equ_decomp_E_pred_toy_model}\stackrel{\eqref{equ_bias_var_decomp}}{=} \biasterm^{2} + \varianceterm + \sigma^{2}. | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
Here, step (a) uses the law of iterated expectation (see, e.g., <ref name="BertsekasProb"/>). Step (b) uses that | |||
the feature vector | Here, step (a) uses the law of iterated expectation (see, e.g., <ref name="BertsekasProb"/>). Step (b) uses that the feature vector | ||
<math>\featurevec</math> of a “new” <span class="mw-gls" data-name ="datapoint">data point</span> is a realization of a <span class="mw-gls" data-name ="rv">RV</span> which is | <math>\featurevec</math> of a “new” <span class="mw-gls" data-name ="datapoint">data point</span> is a realization of a <span class="mw-gls" data-name ="rv">RV</span> which is statistically independent of the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> | ||
statistically independent of the <span class="mw-gls" data-name ="datapoint">data point</span>s in the <span class="mw-gls" data-name ="trainset">training set</span> | <math>\trainset</math>. We also used our assumption that | ||
<math>\trainset</math>. We also used | <math>\featurevec</math> is the realization of a <span class="mw-gls" data-name ="rv">RV</span> with zero mean and covariance matrix | ||
our assumption that | |||
<math>\featurevec</math> is the realization of a <span class="mw-gls" data-name ="rv">RV</span> with zero mean and covariance | |||
matrix | |||
<math>\expect \{ \featurevec \featurevec^{T}\}=\mathbf{I}</math> (see \eqref{equ_toy_model_iid}). | <math>\expect \{ \featurevec \featurevec^{T}\}=\mathbf{I}</math> (see \eqref{equ_toy_model_iid}). | ||
According to \eqref{equ_decomp_E_pred_toy_model}, the average (expected) prediction error <math>\error_{\rm pred}</math> is the sum of three components: (i) the bias | According to \eqref{equ_decomp_E_pred_toy_model}, the average (expected) prediction error <math>\error_{\rm pred}</math> is the sum of three components: (i) the bias | ||
<math>\biasterm^{2}</math>, (ii) the variance <math>\varianceterm</math> and (iii) the noise variance <math>\sigma^{2}</math>. Figure [[#fig_bias_variance|fig_bias_variance]] illustrates the typical dependency of the bias and variance on the model \eqref{equ_generalization_hypospace_r}, | <math>\biasterm^{2}</math>, (ii) the variance <math>\varianceterm</math> and (iii) the noise variance <math>\sigma^{2}</math>. Figure [[#fig_bias_variance|fig_bias_variance]] illustrates the typical dependency of the bias and variance on the model \eqref{equ_generalization_hypospace_r}, | ||
which is parametrized by the model complexity <math>\modelidx</math>. Note that the model complexity parameter <math>\modelidx</math> | which is parametrized by the model complexity <math>\modelidx</math>. Note that the model complexity parameter <math>\modelidx</math> in \eqref{equ_generalization_hypospace_r} coincides with the effective model dimension <math>\effdim{\hypospace^{(\modelidx)}}</math> (see Section [[guide:B85f6bf6f2#sec_hypo_space | The Model ]]). | ||
in \eqref{equ_generalization_hypospace_r} coincides with the effective model dimension <math>\effdim{\hypospace^{(\modelidx)}}</math> (see Section [[guide:B85f6bf6f2#sec_hypo_space | The Model ]]). | |||
The bias and variance, whose sum is the estimation error | The bias and variance, whose sum is the estimation error | ||
| Line 1,398: | Line 1,324: | ||
We highlight that our statistical analysis, resulting the formulas for bias \eqref{equ_def_bias_term}, <span class="mw-gls" data-name ="variance">variance</span> \eqref{equ_formulae_variance_toy_model} and the average prediction error \eqref{equ_decomp_E_pred_toy_model}, applies only if the observed <span class="mw-gls" data-name ="datapoint">data point</span>s can be well modelled using the probabilistic model specified by \eqref{equ_linear_obs_model}, \eqref{equ_toy_model_iid} | We highlight that our statistical analysis, resulting the formulas for bias \eqref{equ_def_bias_term}, <span class="mw-gls" data-name ="variance">variance</span> \eqref{equ_formulae_variance_toy_model} and the average prediction error \eqref{equ_decomp_E_pred_toy_model}, applies only if the observed <span class="mw-gls" data-name ="datapoint">data point</span>s can be well modelled using the probabilistic model specified by \eqref{equ_linear_obs_model}, \eqref{equ_toy_model_iid} | ||
and \eqref{equ_labels_training_data}. The validity of this probabilistic model can to be verified by principled | and \eqref{equ_labels_training_data}. The validity of this probabilistic model can to be verified by principled statistical model validation techniques <ref name="Young93">K. Young. Bayesian diagnostics for checking assumptions of normality. ''Journal of Statistical Computation and Simulation'' 47(3--4):167 | ||
statistical model validation techniques <ref name="Young93">K. Young. Bayesian diagnostics for checking assumptions of normality. ''Journal of Statistical Computation and Simulation'' 47(3--4):167 | |||
-- 180, 1993</ref><ref name="Vasicek76">O. Vasicek. A test for normality based on sample entropy. ''Journal of the Royal Statistical Society. Series B | -- 180, 1993</ref><ref name="Vasicek76">O. Vasicek. A test for normality based on sample entropy. ''Journal of the Royal Statistical Society. Series B | ||
(Methodological)'' 38(1):54--59, 1976</ref>. Section [[#sec_the_bootsrap | The Bootstrap ]] discusses a fundamentally different approach to analyzing the statistical properties of a ML method. Instead of a probabilistic model, this approach uses random sampling | (Methodological)'' 38(1):54--59, 1976</ref>. Section [[#sec_the_bootsrap | The Bootstrap ]] discusses a fundamentally different approach to analyzing the statistical properties of a ML method. Instead of a probabilistic model, this approach uses random sampling techniques to synthesize <span class="mw-gls" data-name ="iid">iid</span> copies of given (small) <span class="mw-gls" data-name ="datapoint">data point</span>s. We can approximate the expectation of some relevant quantity, such as the loss <math>\loss{\big(\featurevec,\truelabel \big) }{h}</math>, using an average over synthetic data <ref name="hastie01statisticallearning"/>. | ||
techniques to synthesize <span class="mw-gls" data-name ="iid">iid</span> copies of given (small) <span class="mw-gls" data-name ="datapoint">data point</span>s. We can approximate the expectation of some relevant quantity, such as the loss <math>\loss{\big(\featurevec,\truelabel \big) }{h}</math>, using an average over | |||
synthetic data <ref name="hastie01statisticallearning"/>. | |||
The qualitative behaviour of estimation error in Figure [[#fig_bias_variance|fig_bias_variance]] depends on the definition for the model complexity. | The qualitative behaviour of estimation error in Figure [[#fig_bias_variance|fig_bias_variance]] depends on the definition for the model complexity. | ||
Our concept of <span class="mw-gls" data-name ="effdim">effective dimension</span> (see Section [[guide:B85f6bf6f2#sec_hypo_space | The Model ]]) coincides with most other notions of model complexity | Our concept of <span class="mw-gls" data-name ="effdim">effective dimension</span> (see Section [[guide:B85f6bf6f2#sec_hypo_space | The Model ]]) coincides with most other notions of model complexity for the linear <span class="mw-gls" data-name ="hypospace">hypothesis space</span> \eqref{equ_generalization_hypospace_r}. However, for more complicated models such as deep nets it is often not obvious how <span class="mw-gls" data-name ="effdim">effective dimension</span> is related to more tangible quantities such as total number of tunable <span class="mw-gls mw-gls-first" data-name ="weights">weights</span> or the number of artificial neurons. Indeed, the <span class="mw-gls" data-name ="effdim">effective dimension</span> might also depend on the specific learning algorithm such as <span class="mw-gls mw-gls-first" data-name ="stochGD">stochastic gradient descent (SGD)</span>. Therefore, for deep nets, if we would plot estimation error against number of tunable <span class="mw-gls" data-name ="weights">weights</span> we might observe a behaviour of estimation error fundamentally different from the shape in Figure [[#fig_bias_variance|fig_bias_variance]]. One example for such un-intuitive behaviour is known as “double descent phenomena” <ref name="Belkin15849">M. Belkin, D. Hsu, S. Ma, and S. Mandal. Reconciling modern machine-learning practice and the classical bias–variance trade-off. ''Proceedings of the National Academy of Sciences'' | ||
for the linear <span class="mw-gls" data-name ="hypospace">hypothesis space</span> \eqref{equ_generalization_hypospace_r}. However, for more complicated models | |||
such as deep nets it is often not obvious how <span class="mw-gls" data-name ="effdim">effective dimension</span> is related to more tangible quantities such | |||
as total number of tunable <span class="mw-gls mw-gls-first" data-name ="weights">weights</span> or the number of artificial neurons. Indeed, the <span class="mw-gls" data-name ="effdim">effective dimension</span> might also depend | |||
on the specific learning algorithm such as <span class="mw-gls mw-gls-first" data-name ="stochGD">stochastic gradient descent (SGD)</span>. Therefore, for deep nets, if we would plot estimation error | |||
against number of tunable <span class="mw-gls" data-name ="weights">weights</span> we might observe a behaviour of estimation error fundamentally different from | |||
the shape in Figure [[#fig_bias_variance|fig_bias_variance]]. One example for such un-intuitive behaviour is known as “double descent phenomena” <ref name="Belkin15849">M. Belkin, D. Hsu, S. Ma, and S. Mandal. Reconciling modern machine-learning practice and the classical bias–variance trade-off. ''Proceedings of the National Academy of Sciences'' | |||
116(32):15849--15854, 2019</ref>. | 116(32):15849--15854, 2019</ref>. | ||
| Line 1,422: | Line 1,339: | ||
Consider learning a hypothesis | Consider learning a hypothesis | ||
<math>\hat{h} \in \hypospace</math> by minimizing the | <math>\hat{h} \in \hypospace</math> by minimizing the average loss incurred on a <span class="mw-gls mw-gls-first" data-name ="dataset">dataset</span> | ||
average loss incurred on a <span class="mw-gls mw-gls-first" data-name ="dataset">dataset</span> | |||
<math>\dataset=\{ \big(\featurevec^{(1)},\truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big)\}</math>. | <math>\dataset=\{ \big(\featurevec^{(1)},\truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big)\}</math>. | ||
The <span class="mw-gls" data-name ="datapoint">data point</span>s | The <span class="mw-gls" data-name ="datapoint">data point</span>s | ||
<math>\big(\featurevec^{(\sampleidx))},\truelabel^{(\sampleidx)}\big)</math> are modelled | <math>\big(\featurevec^{(\sampleidx))},\truelabel^{(\sampleidx)}\big)</math> are modelled as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s. Let use denote the (common) probability distribution of these <span class="mw-gls" data-name ="rv">RV</span>s by | ||
as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s. Let use denote the (common) probability | |||
distribution of these <span class="mw-gls" data-name ="rv">RV</span>s by | |||
<math>p(\featurevec,\truelabel)</math>. | <math>p(\featurevec,\truelabel)</math>. | ||
| Line 1,434: | Line 1,348: | ||
<math>\big(\featurevec^{(\sampleidx))},\truelabel^{(\sampleidx)}\big)</math> as realizations of | <math>\big(\featurevec^{(\sampleidx))},\truelabel^{(\sampleidx)}\big)</math> as realizations of | ||
<span class="mw-gls" data-name ="rv">RV</span>s, also the learnt hypothesis | <span class="mw-gls" data-name ="rv">RV</span>s, also the learnt hypothesis | ||
<math>\hat{h}</math> is a realization | <math>\hat{h}</math> is a realization of a <span class="mw-gls" data-name ="rv">RV</span>. Indeed, the hypothesis | ||
of a <span class="mw-gls" data-name ="rv">RV</span>. Indeed, the hypothesis | <math>\hat{h}</math> is obtained by solving an optimization [[guide:Cc42ad1ea4#equ_def_ERM_funs | problem]] that involves realizations of <span class="mw-gls" data-name ="rv">RV</span>s. The bootstrap is a method for estimating | ||
<math>\hat{h}</math> is obtained by | |||
solving an optimization [[guide:Cc42ad1ea4#equ_def_ERM_funs | problem]] that involves | |||
realizations of <span class="mw-gls" data-name ="rv">RV</span>s. The bootstrap is a method for estimating | |||
(parameters of) the <span class="mw-gls" data-name ="probdist">probability distribution</span> | (parameters of) the <span class="mw-gls" data-name ="probdist">probability distribution</span> | ||
<math>p(\hat{h})</math> <ref name="hastie01statisticallearning"/>. | <math>p(\hat{h})</math> <ref name="hastie01statisticallearning"/>. | ||
| Line 1,444: | Line 1,355: | ||
Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]] used a probabilistic model for <span class="mw-gls" data-name ="datapoint">data point</span>s to derive (the parameters of) | Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]] used a probabilistic model for <span class="mw-gls" data-name ="datapoint">data point</span>s to derive (the parameters of) | ||
the <span class="mw-gls" data-name ="probdist">probability distribution</span> | the <span class="mw-gls" data-name ="probdist">probability distribution</span> | ||
<math>p(\hat{h})</math>. Note that the analysis in Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]] only applies to | <math>p(\hat{h})</math>. Note that the analysis in Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]] only applies to the specific probabilistic model \eqref{equ_toy_model_iid}, \eqref{equ_labels_training_data}. In contrast, | ||
the specific probabilistic model \eqref{equ_toy_model_iid}, \eqref{equ_labels_training_data}. In contrast, | |||
the <span class="mw-gls" data-name ="bootstrap">bootstrap</span> can be used for <span class="mw-gls" data-name ="datapoint">data point</span>s drawn from an arbitrary <span class="mw-gls" data-name ="probdist">probability distribution</span>. | the <span class="mw-gls" data-name ="bootstrap">bootstrap</span> can be used for <span class="mw-gls" data-name ="datapoint">data point</span>s drawn from an arbitrary <span class="mw-gls" data-name ="probdist">probability distribution</span>. | ||
The core idea behind the <span class="mw-gls" data-name ="bootstrap">bootstrap</span> is to use the <span class="mw-gls" data-name ="histogram">histogram</span> | The core idea behind the <span class="mw-gls" data-name ="bootstrap">bootstrap</span> is to use the <span class="mw-gls" data-name ="histogram">histogram</span> | ||
<math>\hat{p}(\datapoint)</math> | <math>\hat{p}(\datapoint)</math> of the <span class="mw-gls" data-name ="datapoint">data point</span>s in | ||
of the <span class="mw-gls" data-name ="datapoint">data point</span>s in | |||
<math>\dataset</math> to generate | <math>\dataset</math> to generate | ||
<math>\nrbootstraps</math> new datasets | <math>\nrbootstraps</math> new datasets | ||
| Line 1,456: | Line 1,365: | ||
Each dataset is constructed such that is has the same size as the original dataset | Each dataset is constructed such that is has the same size as the original dataset | ||
<math>\dataset</math>. | <math>\dataset</math>. | ||
For each dataset <math>\dataset^{(\bootstrapidx)}</math>, we solve a separate [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]] to obtain the hypothesis <math>\hat{h}^{(\bootstrapidx)}</math>. The hypothesis <math>\hat{h}^{(\bootstrapidx)}</math> is a realization | For each dataset <math>\dataset^{(\bootstrapidx)}</math>, we solve a separate [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]] to obtain the hypothesis <math>\hat{h}^{(\bootstrapidx)}</math>. The hypothesis <math>\hat{h}^{(\bootstrapidx)}</math> is a realization of a <span class="mw-gls" data-name ="rv">RV</span> whose distribution is determined by the <span class="mw-gls" data-name ="histogram">histogram</span> | ||
of a <span class="mw-gls" data-name ="rv">RV</span> whose distribution is determined by the <span class="mw-gls" data-name ="histogram">histogram</span> | |||
<math>\hat{p}(\datapoint)</math> as well as the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> and the <span class="mw-gls" data-name ="lossfunc">loss function</span> used in the [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]]. | <math>\hat{p}(\datapoint)</math> as well as the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> and the <span class="mw-gls" data-name ="lossfunc">loss function</span> used in the [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]]. | ||
| Line 1,464: | Line 1,372: | ||
''diagnose ML methods by comparing <span class="mw-gls" data-name ="trainerr">training error</span> with <span class="mw-gls" data-name ="valerr">validation error</span> and (if available) some <span class="mw-gls" data-name ="baseline">baseline</span>; <span class="mw-gls" data-name ="baseline">baseline</span> can be obtained via the <span class="mw-gls" data-name ="bayesrisk">Bayes risk</span> when using a probabilistic model (such as the <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>) or human performance or the performance of existing ML methods ("experts" in regret framework)'' | ''diagnose ML methods by comparing <span class="mw-gls" data-name ="trainerr">training error</span> with <span class="mw-gls" data-name ="valerr">validation error</span> and (if available) some <span class="mw-gls" data-name ="baseline">baseline</span>; <span class="mw-gls" data-name ="baseline">baseline</span> can be obtained via the <span class="mw-gls" data-name ="bayesrisk">Bayes risk</span> when using a probabilistic model (such as the <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>) or human performance or the performance of existing ML methods ("experts" in regret framework)'' | ||
In what follows, we tacitly assume that <span class="mw-gls" data-name ="datapoint">data point</span>s can (to a good approximation) be | In what follows, we tacitly assume that <span class="mw-gls" data-name ="datapoint">data point</span>s can (to a good approximation) be interpreted as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s (see Section [[guide:B85f6bf6f2#equ_prob_models_data | Probabilistic Models for Data ]]). | ||
interpreted as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s (see Section [[guide:B85f6bf6f2#equ_prob_models_data | Probabilistic Models for Data ]]). | This “<span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>” underlies [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]] as the guiding principle for learning a hypothesis with small [[guide:2c0f621d22#equ_def_risk|<span class="mw-gls" data-name ="risk">risk</span>]]. This assumption also motivates to use the average loss \eqref{equ_def_training_val_val} on a <span class="mw-gls" data-name ="valset">validation set</span> as an estimate for the <span class="mw-gls" data-name ="risk">risk</span>. More fundamentally, we need the <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span> to define the concept of <span class="mw-gls" data-name ="risk">risk</span> as a measure for how well a hypothesis predicts the labels of arbitrary <span class="mw-gls" data-name ="datapoint">data point</span>s. | ||
This “<span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>” underlies [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]] as the guiding principle for learning a hypothesis with small [[guide:2c0f621d22#equ_def_risk|<span class="mw-gls" data-name ="risk">risk</span>]]. This assumption also motivates to use the average loss \eqref{equ_def_training_val_val} on a <span class="mw-gls" data-name ="valset">validation set</span> as an estimate for | |||
the <span class="mw-gls" data-name ="risk">risk</span>. More fundamentally, we need the <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span> to define the concept of <span class="mw-gls" data-name ="risk">risk</span> as a measure for how well a hypothesis predicts the labels of arbitrary <span class="mw-gls" data-name ="datapoint">data point</span>s. | |||
Consider a ML method which uses Algorithm [[#alg:validated_ERM|alg:validated_ERM]] (or Algorithm [[#alg:kfoldCV_ERM|alg:kfoldCV_ERM]]) | Consider a ML method which uses Algorithm [[#alg:validated_ERM|alg:validated_ERM]] (or Algorithm [[#alg:kfoldCV_ERM|alg:kfoldCV_ERM]]) | ||
| Line 1,474: | Line 1,380: | ||
<math>\hat{h}</math>, these algorithms also deliver the <span class="mw-gls" data-name ="trainerr">training error</span> | <math>\hat{h}</math>, these algorithms also deliver the <span class="mw-gls" data-name ="trainerr">training error</span> | ||
<math>\trainerror</math> and the validation | <math>\trainerror</math> and the validation error | ||
error | <math>\valerror</math>. As we will see shortly, we can diagnose ML methods to some extent just by comparing training with validation errors. This diagnosis is further enabled if we know a | ||
<math>\valerror</math>. As we will see shortly, we can diagnose ML methods to some extent just | |||
by comparing training with validation errors. This diagnosis is further enabled if we know a | |||
<span class="mw-gls" data-name ="baseline">baseline</span> | <span class="mw-gls" data-name ="baseline">baseline</span> | ||
<math>\benchmarkerror</math> . | <math>\benchmarkerror</math> . | ||
One important source of a <span class="mw-gls" data-name ="baseline">baseline</span> | One important source of a <span class="mw-gls" data-name ="baseline">baseline</span> | ||
<math>\benchmarkerror</math> are probabilistic models | <math>\benchmarkerror</math> are probabilistic models for the <span class="mw-gls" data-name ="datapoint">data point</span>s (see Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]]). Given a probabilistic model, which specifies the <span class="mw-gls" data-name ="probdist">probability distribution</span> | ||
for the <span class="mw-gls" data-name ="datapoint">data point</span>s (see Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]]). Given a probabilistic model, which | |||
specifies the <span class="mw-gls" data-name ="probdist">probability distribution</span> | |||
<math>p(\featurevec,\truelabel)</math> of the features and label of <span class="mw-gls" data-name ="datapoint">data point</span>s, | <math>p(\featurevec,\truelabel)</math> of the features and label of <span class="mw-gls" data-name ="datapoint">data point</span>s, | ||
we can compute the minimum achievable [[guide:2c0f621d22#equ_def_risk|<span class="mw-gls" data-name ="risk">risk</span>]]. Indeed, the minimum | we can compute the minimum achievable [[guide:2c0f621d22#equ_def_risk|<span class="mw-gls" data-name ="risk">risk</span>]]. Indeed, the minimum achievable risk is precisely the expected loss of the <span class="mw-gls mw-gls-first" data-name ="bayesestimator">Bayes estimator</span> | ||
achievable risk is precisely the expected loss of the <span class="mw-gls mw-gls-first" data-name ="bayesestimator">Bayes estimator</span> | <math>\hat{h}(\featurevec)</math> of the label | ||
<math>\hat{h}(\featurevec)</math> | |||
of the label | |||
<math>\truelabel</math>, given the features | <math>\truelabel</math>, given the features | ||
<math>\featurevec</math> of a <span class="mw-gls" data-name ="datapoint">data point</span>. The <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> | <math>\featurevec</math> of a <span class="mw-gls" data-name ="datapoint">data point</span>. The <span class="mw-gls" data-name ="bayesestimator">Bayes estimator</span> | ||
<math>\hat{h}(\featurevec)</math> is fully determined by the <span class="mw-gls" data-name ="probdist">probability distribution</span> | <math>\hat{h}(\featurevec)</math> is fully determined by the <span class="mw-gls" data-name ="probdist">probability distribution</span> | ||
<math>p(\featurevec,\truelabel)</math> of | <math>p(\featurevec,\truelabel)</math> of the features and label of a (random) <span class="mw-gls" data-name ="datapoint">data point</span> <ref name="LC">E. L. Lehmann and G. Casella. ''Theory of Point Estimation'' Springer, New York, 2nd edition, 1998</ref>{{rp|at=Chapter 4}}. | ||
the features and label of a (random) <span class="mw-gls" data-name ="datapoint">data point</span> <ref name="LC">E. L. Lehmann and G. Casella. ''Theory of Point Estimation'' Springer, New York, 2nd edition, 1998</ref>{{rp|at=Chapter 4}}. | |||
A further potential source for a <span class="mw-gls" data-name ="baseline">baseline</span> | A further potential source for a <span class="mw-gls" data-name ="baseline">baseline</span> | ||
<math>\benchmarkerror</math> is an existing, but for some reason | <math>\benchmarkerror</math> is an existing, but for some reason unsuitable, ML method. This existing ML method might be computationally too expensive to be used for the ML application at end. However, we might still use its statistical properties as a benchmark. | ||
unsuitable, ML method. This existing ML method might be computationally too expensive to be used | The We might also use the performance of human experts as a <span class="mw-gls" data-name ="baseline">baseline</span>. | ||
for the ML application at end. However, we might still use its statistical properties as a benchmark. | If we want to develop a ML method that detects certain type of skin cancers from images of the skin, a benchmark might be the current classification accuracy achieved by experienced dermatologists <ref name="Esteva2017">A. Esteva, B. Kuprel, R. A. Novoa, J. Ko, S. M. Swetter, H. M. Blau, and S. Thrun. Dermatologist-level classification of skin cancer with deep neural networks. ''Nature'' 542, 2017</ref>. | ||
The | |||
We might also use the performance of human experts as a <span class="mw-gls" data-name ="baseline">baseline</span>. | |||
If we want to develop a ML method that detects certain type of skin cancers from | |||
images of the skin, a benchmark might be the current classification accuracy | |||
achieved by experienced dermatologists <ref name="Esteva2017">A. Esteva, B. Kuprel, R. A. Novoa, J. Ko, S. M. Swetter, H. M. Blau, and | |||
We can diagnose a ML method by comparing the <span class="mw-gls" data-name ="trainerr">training error</span> | We can diagnose a ML method by comparing the <span class="mw-gls" data-name ="trainerr">training error</span> | ||
<math>\trainerror</math> | <math>\trainerror</math> with the validation error | ||
with the validation error | |||
<math>\valerror</math> and (if available) the benchmark | <math>\valerror</math> and (if available) the benchmark | ||
<math>\benchmarkerror</math>. | <math>\benchmarkerror</math>. | ||
| Line 1,518: | Line 1,408: | ||
<ul> | <ul> | ||
<li> | <li> | ||
<math>\trainerror \approx \valerror \approx \benchmarkerror</math>: The <span class="mw-gls" data-name ="trainerr">training error</span> is on the same level as the validation error and the benchmark error. There is not much to improve here since the validation error is already on the desired error level. Moreover, the <span class="mw-gls" data-name ="trainerr">training error</span> is not much smaller than the validation error which indicates that | <math>\trainerror \approx \valerror \approx \benchmarkerror</math>: The <span class="mw-gls" data-name ="trainerr">training error</span> is on the same level as the validation error and the benchmark error. There is not much to improve here since the validation error is already on the desired error level. Moreover, the <span class="mw-gls" data-name ="trainerr">training error</span> is not much smaller than the validation error which indicates that there is no overfitting. It seems we have obtained a ML method that achieves the benchmark error level. | ||
there is no overfitting. It seems we have obtained a ML method that achieves the benchmark error level. | |||
</li> | </li> | ||
| Line 1,528: | Line 1,417: | ||
<li class="mt-3"> | <li class="mt-3"> | ||
<math>\trainerror \approx \valerror\gg \benchmarkerror</math>: The <span class="mw-gls" data-name ="trainerr">training error</span> is on the same level as the <span class="mw-gls" data-name ="valerr">validation error</span>and both are significantly larger than the <span class="mw-gls" data-name ="baseline">baseline</span>. Since the <span class="mw-gls" data-name ="trainerr">training error</span> is not much smaller than the <span class="mw-gls" data-name ="valerr">validation error</span>, the learnt hypothesis seems to not overfit the <span class="mw-gls" data-name ="trainset">training set</span>. However, the <span class="mw-gls" data-name ="trainerr">training error</span> achieved by the learnt hypothesis is significantly larger than the benchmark error level. There can be several reasons for this to happen. First, it might be that the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> used by the ML method is too small, i.e., it does not include a hypothesis that provides a good approximation for the relation between features and label of a <span class="mw-gls" data-name ="datapoint">data point</span>. The remedy for this situation is to use a larger <span class="mw-gls" data-name ="hypospace">hypothesis space</span>, e.g., by including more features in a linear model, using higher polynomial degrees in polynomial regression, using deeper <span class="mw-gls" data-name ="decisiontree">decision tree</span>s or having larger <span class="mw-gls" data-name ="ann">ANN</span>s (<span class="mw-gls mw-gls-first" data-name ="deepnet">deep <span class="mw-gls" data-name ="ann">ANN</span> (deep net)</span>s). Another reason for the <span class="mw-gls" data-name ="trainerr">training error</span> being too large is that the optimization algorithm used to solve [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]] is not working properly. When using <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> (see Section [[guide:Cc42ad1ea4#sec_GD_linear_regression | GD for Linear Regression ]]) to solve <span class="mw-gls" data-name ="erm">ERM</span>, one reason for <math>\trainerror \gg \benchmarkerror</math> could be that the <span class="mw-gls mw-gls-first" data-name ="learnrate">learning rate</span> <math>\lrate</math> in the <span class="mw-gls" data-name ="gd">GD</span> step | <math>\trainerror \approx \valerror\gg \benchmarkerror</math>: The <span class="mw-gls" data-name ="trainerr">training error</span> is on the same level as the <span class="mw-gls" data-name ="valerr">validation error</span>and both are significantly larger than the <span class="mw-gls" data-name ="baseline">baseline</span>. Since the <span class="mw-gls" data-name ="trainerr">training error</span> is not much smaller than the <span class="mw-gls" data-name ="valerr">validation error</span>, the learnt hypothesis seems to not overfit the <span class="mw-gls" data-name ="trainset">training set</span>. However, the <span class="mw-gls" data-name ="trainerr">training error</span> achieved by the learnt hypothesis is significantly larger than the benchmark error level. There can be several reasons for this to happen. First, it might be that the <span class="mw-gls" data-name ="hypospace">hypothesis space</span> used by the ML method is too small, i.e., it does not include a hypothesis that provides a good approximation for the relation between features and label of a <span class="mw-gls" data-name ="datapoint">data point</span>. The remedy for this situation is to use a larger <span class="mw-gls" data-name ="hypospace">hypothesis space</span>, e.g., by including more features in a linear model, using higher polynomial degrees in polynomial regression, using deeper <span class="mw-gls" data-name ="decisiontree">decision tree</span>s or having larger <span class="mw-gls" data-name ="ann">ANN</span>s (<span class="mw-gls mw-gls-first" data-name ="deepnet">deep <span class="mw-gls" data-name ="ann">ANN</span> (deep net)</span>s). Another reason for the <span class="mw-gls" data-name ="trainerr">training error</span> being too large is that the optimization algorithm used to solve [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]] is not working properly. When using <span class="mw-gls" data-name ="gdmethods">gradient-based methods</span> (see Section [[guide:Cc42ad1ea4#sec_GD_linear_regression | GD for Linear Regression ]]) to solve <span class="mw-gls" data-name ="erm">ERM</span>, one reason for <math>\trainerror \gg \benchmarkerror</math> could be that the <span class="mw-gls mw-gls-first" data-name ="learnrate">learning rate</span> <math>\lrate</math> in the [[guide:Cc42ad1ea4#equ_def_GD_step|<span class="mw-gls" data-name ="gd">GD</span> step]] is chosen too small or too large (see Figure [[#fig_small_large_lrate|fig_small_large_lrate]]-(b)). This can be solved by adjusting the <span class="mw-gls" data-name ="learnrate">learning rate</span> by trying out several different values and using the one resulting in the smallest <span class="mw-gls" data-name ="trainerr">training error</span>. Another option is derive optimal values for the <span class="mw-gls" data-name ="learnrate">learning rate</span> based on a probabilistic model for how the <span class="mw-gls" data-name ="datapoint">data point</span>s are generated. One example for such a probabilistic model is the <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span> that has been used in Section [[#sec_gen_linreg | A Probabilistic Analysis of Generalization ]] to analyze <span class="mw-gls" data-name ="linreg">linear regression</span> methods. | ||
</li> | </li> | ||
<li class="mt-3"> | <li class="mt-3"> | ||
<math>\trainerror \gg \valerror </math>: The <span class="mw-gls" data-name ="trainerr">training error</span> is significantly larger than the <span class="mw-gls" data-name ="valerr">validation error</span> (see Exercise | <math>\trainerror \gg \valerror </math>: The <span class="mw-gls" data-name ="trainerr">training error</span> is significantly larger than the <span class="mw-gls" data-name ="valerr">validation error</span> (see [[exercise:609eec77ba|Exercise]]). The idea of [[guide:Cc42ad1ea4#equ_def_ERM_funs | <span class="mw-gls" data-name ="erm">ERM</span>]] is to approximate the [[guide:2c0f621d22#equ_def_risk|risk]] of a hypothesis by its average loss on a <span class="mw-gls" data-name ="trainset">training set</span> <math>\dataset = \{ (\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}</math>.The mathematical underpinning for this approximation is the <span class="mw-gls mw-gls-first" data-name ="lln">law of large numbers</span> which characterizes the average of (realizations of) <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s. The quality and usefulness of this approximation depends on the validity of two conditions. First, the <span class="mw-gls" data-name ="datapoint">data point</span>s used for computing the average loss should be such that they would be typically obtained as realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s with a common <span class="mw-gls" data-name ="probdist">probability distribution</span>. Second, the number of <span class="mw-gls" data-name ="datapoint">data point</span>s used for computing the average <span class="mw-gls" data-name ="loss">loss</span> must be sufficiently large. Whenever the <span class="mw-gls" data-name ="datapoint">data point</span>s behave different than the the realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s or if the size of the <span class="mw-gls" data-name ="trainset">training set</span> or <span class="mw-gls" data-name ="valset">validation set</span> is too small, the interpretation (comparison) of <span class="mw-gls" data-name ="trainerr">training error</span> and <span class="mw-gls" data-name ="valerr">validation error</span>s becomes more difficult. As an extreme case, it might then be that the <span class="mw-gls" data-name ="valerr">validation error</span> consists of <span class="mw-gls" data-name ="datapoint">data point</span>s for which every hypothesis incurs small average loss. Here, we might try to increase the size of the <span class="mw-gls" data-name ="valset">validation set</span> by collecting more labeled <span class="mw-gls" data-name ="datapoint">data point</span>s or by using <span class="mw-gls" data-name ="dataug">data augmentation</span> (see Section [[guide:50be9327aa#sec_data_augmentation | Data Augmentation ]]). If the size of <span class="mw-gls" data-name ="trainset">training set</span> and <span class="mw-gls" data-name ="valset">validation set</span> are large but we still obtain <math>\trainerror \gg \valerror </math>, one should verify if <span class="mw-gls" data-name ="datapoint">data point</span>s in these sets conform to the <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span>. There are principled statistical methods that allow to test if an <span class="mw-gls" data-name ="iidasspt">i.i.d. assumption</span> is satisfied (see <ref name="Luetkepol2005"/> and references therein). | ||
</li> | </li> | ||
</ul> | </ul> | ||
| Line 1,538: | Line 1,427: | ||
==Notes== | ==Notes== | ||
{{notelist}} | {{notelist}} | ||
==General References== | |||
<div class="d-flex mt-3 mb-3"> | |||
<div class="me-3"> | |||
[[File:978-981-16-8193-6.jpg | 150px | link=]] | |||
</div> | |||
<div> | |||
{{cite book | title = Machine Learning: The Basics |first = Alexander | last = Jung | publisher = Springer | location = Signapore | date = 2022 | doi = 10.1007/978-981-16-8193-6 }} | |||
{{cite arXiv |last=Jung |first=Alexander |date= |title=Machine Learning: The Basics |eprint=1805.05052 | date=2022}} | |||
</div> | |||
</div> | |||
==References== | ==References== | ||
Latest revision as of 14:57, 6 July 2023
[math] % Generic syms \newcommand\defeq{:=} \newcommand{\Tt}[0]{\boldsymbol{\theta}} \newcommand{\XX}[0]{{\cal X}} \newcommand{\ZZ}[0]{{\cal Z}} \newcommand{\vx}[0]{{\bf x}} \newcommand{\vv}[0]{{\bf v}} \newcommand{\vu}[0]{{\bf u}} \newcommand{\vs}[0]{{\bf s}} \newcommand{\vm}[0]{{\bf m}} \newcommand{\vq}[0]{{\bf q}} \newcommand{\mX}[0]{{\bf X}} \newcommand{\mC}[0]{{\bf C}} \newcommand{\mA}[0]{{\bf A}} \newcommand{\mL}[0]{{\bf L}} \newcommand{\fscore}[0]{F_{1}} \newcommand{\sparsity}{s} \newcommand{\mW}[0]{{\bf W}} \newcommand{\mD}[0]{{\bf D}} \newcommand{\mZ}[0]{{\bf Z}} \newcommand{\vw}[0]{{\bf w}} \newcommand{\D}[0]{{\mathcal{D}}} \newcommand{\mP}{\mathbf{P}} \newcommand{\mQ}{\mathbf{Q}} \newcommand{\E}[0]{{\mathbb{E}}} \newcommand{\vy}[0]{{\bf y}} \newcommand{\va}[0]{{\bf a}} \newcommand{\vn}[0]{{\bf n}} \newcommand{\vb}[0]{{\bf b}} \newcommand{\vr}[0]{{\bf r}} \newcommand{\vz}[0]{{\bf z}} \newcommand{\N}[0]{{\mathcal{N}}} \newcommand{\vc}[0]{{\bf c}} \newcommand{\bm}{\boldsymbol} % Statistics and Probability Theory \newcommand{\errprob}{p_{\rm err}} \newcommand{\prob}[1]{p({#1})} \newcommand{\pdf}[1]{p({#1})} \def \expect {\mathbb{E} } % Machine Learning Symbols \newcommand{\biasterm}{B} \newcommand{\varianceterm}{V} \newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} \newcommand{\nrfolds}{k} \newcommand{\mseesterr}{E_{\rm est}} \newcommand{\bootstrapidx}{b} %\newcommand{\modeldim}{r} \newcommand{\modelidx}{l} \newcommand{\nrbootstraps}{B} \newcommand{\sampleweight}[1]{q^{(#1)}} \newcommand{\nrcategories}{K} \newcommand{\splitratio}[0]{{\rho}} \newcommand{\norm}[1]{\Vert {#1} \Vert} \newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} \newcommand{\bmx}[0]{\begin{bmatrix}} \newcommand{\emx}[0]{\end{bmatrix}} \newcommand{\T}[0]{\text{T}} \DeclareMathOperator*{\rank}{rank} %\newcommand\defeq{:=} \newcommand\eigvecS{\hat{\mathbf{u}}} \newcommand\eigvecCov{\mathbf{u}} \newcommand\eigvecCoventry{u} \newcommand{\featuredim}{n} \newcommand{\featurelenraw}{\featuredim'} \newcommand{\featurelen}{\featuredim} \newcommand{\samplingset}{\mathcal{M}} \newcommand{\samplesize}{m} \newcommand{\sampleidx}{i} \newcommand{\nractions}{A} \newcommand{\datapoint}{\vz} \newcommand{\actionidx}{a} \newcommand{\clusteridx}{c} \newcommand{\sizehypospace}{D} \newcommand{\nrcluster}{k} \newcommand{\nrseeds}{s} \newcommand{\featureidx}{j} \newcommand{\clustermean}{{\bm \mu}} \newcommand{\clustercov}{{\bm \Sigma}} \newcommand{\target}{y} \newcommand{\error}{E} \newcommand{\augidx}{b} \newcommand{\task}{\mathcal{T}} \newcommand{\nrtasks}{T} \newcommand{\taskidx}{t} \newcommand\truelabel{y} \newcommand{\polydegree}{r} \newcommand\labelvec{\vy} \newcommand\featurevec{\vx} \newcommand\feature{x} \newcommand\predictedlabel{\hat{y}} \newcommand\dataset{\mathcal{D}} \newcommand\trainset{\dataset^{(\rm train)}} \newcommand\valset{\dataset^{(\rm val)}} \newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} \newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} \newcommand{\inspace}{\mathcal{X}} \newcommand{\sigmoid}{\sigma} \newcommand{\outspace}{\mathcal{Y}} \newcommand{\hypospace}{\mathcal{H}} \newcommand{\emperror}{\widehat{L}} \newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} \newcommand{\featurespace}{\mathcal{X}} \newcommand{\labelspace}{\mathcal{Y}} \newcommand{\rawfeaturevec}{\mathbf{z}} \newcommand{\rawfeature}{z} \newcommand{\condent}{H} \newcommand{\explanation}{e} \newcommand{\explainset}{\mathcal{E}} \newcommand{\user}{u} \newcommand{\actfun}{\sigma} \newcommand{\noisygrad}{g} \newcommand{\reconstrmap}{r} \newcommand{\predictor}{h} \newcommand{\eigval}[1]{\lambda_{#1}} \newcommand{\regparam}{\lambda} \newcommand{\lrate}{\alpha} \newcommand{\edges}{\mathcal{E}} \newcommand{\generror}{E} \DeclareMathOperator{\supp}{supp} %\newcommand{\loss}[3]{L({#1},{#2},{#3})} \newcommand{\loss}[2]{L\big({#1},{#2}\big)} \newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} \newcommand{\determinant}[1]{{\rm det}({#1})} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\itercntr}{r} \newcommand{\state}{s} \newcommand{\statespace}{\mathcal{S}} \newcommand{\timeidx}{t} \newcommand{\optpolicy}{\pi_{*}} \newcommand{\appoptpolicy}{\hat{\pi}} \newcommand{\dummyidx}{j} \newcommand{\gridsizex}{K} \newcommand{\gridsizey}{L} \newcommand{\localdataset}{\mathcal{X}} \newcommand{\reward}{r} \newcommand{\cumreward}{G} \newcommand{\return}{\cumreward} \newcommand{\action}{a} \newcommand\actionset{\mathcal{A}} \newcommand{\obstacles}{\mathcal{B}} \newcommand{\valuefunc}[1]{v_{#1}} \newcommand{\gridcell}[2]{\langle #1, #2 \rangle} \newcommand{\pair}[2]{\langle #1, #2 \rangle} \newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} \newcommand{\actionvalue}[1]{q_{#1}} \newcommand{\transition}{\mathcal{T}} \newcommand{\policy}{\pi} \newcommand{\charger}{c} \newcommand{\itervar}{k} \newcommand{\discount}{\gamma} \newcommand{\rumba}{Rumba} \newcommand{\actionnorth}{\rm N} \newcommand{\actionsouth}{\rm S} \newcommand{\actioneast}{\rm E} \newcommand{\actionwest}{\rm W} \newcommand{\chargingstations}{\mathcal{C}} \newcommand{\basisfunc}{\phi} \newcommand{\augparam}{B} \newcommand{\valerror}{E_{v}} \newcommand{\trainerror}{E_{t}} \newcommand{\foldidx}{b} \newcommand{\testset}{\dataset^{(\rm test)} } \newcommand{\testerror}{E^{(\rm test)}} \newcommand{\nrmodels}{M} \newcommand{\benchmarkerror}{E^{(\rm ref)}} \newcommand{\lossfun}{L} \newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} \newcommand{\cluster}{\mathcal{C}} \newcommand{\bayeshypothesis}{h^{*}} \newcommand{\featuremtx}{\mX} \newcommand{\weight}{w} \newcommand{\weights}{\vw} \newcommand{\regularizer}{\mathcal{R}} \newcommand{\decreg}[1]{\mathcal{R}_{#1}} \newcommand{\naturalnumbers}{\mathbb{N}} \newcommand{\featuremapvec}{{\bf \Phi}} \newcommand{\featuremap}{\phi} \newcommand{\batchsize}{B} \newcommand{\batch}{\mathcal{B}} \newcommand{\foldsize}{B} \newcommand{\nriter}{R} [/math]
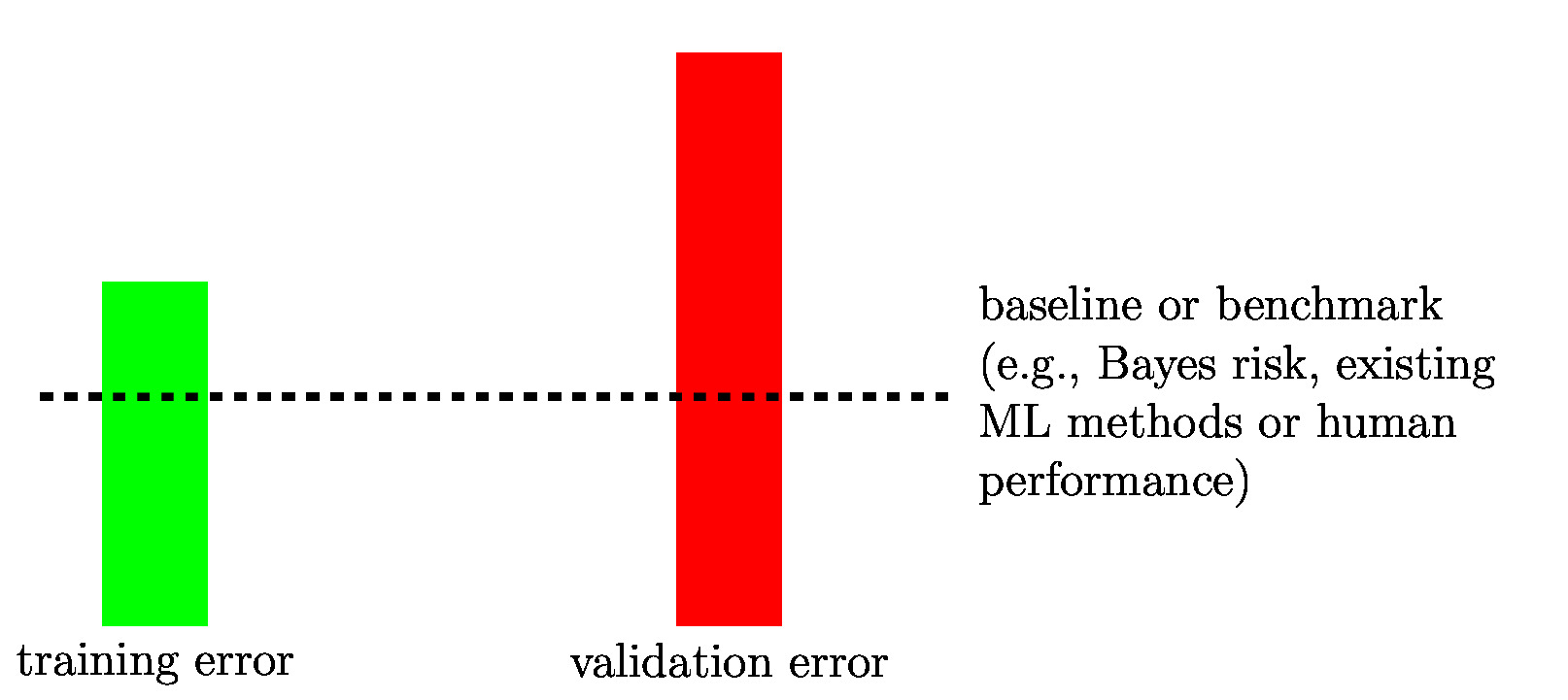
Chapter Empirical Risk Minimization discussed empirical risk minimization (ERM) as a principled approach to learning a good hypothesis out of a hypothesis space or model. ERM based methods learn a hypothesis [math]\hat{h} \in \hypospace[/math] that incurs minimum average loss on a set of labeled data points that serve as the training set. We refer to the average loss incurred by a hypothesis on the training set as the training error. The minimum average loss achieved by a hypothesis that solves the ERM might be referred to as the training error of the overall ML method. This overall ML method is defined by the choice of hypothesis space (or model) and loss function (see Chapter The Landscape of ML ).
Empirical risk minimization (ERM) is sensible only if the training error of a hypothesis is an reliable approximation for its loss incurred on data points outside the training set. Whether the training error of a hypothesis is a reliable approximation for its loss on data points outside the training set depends on both, the statistical properties of the data points generated by an ML application and on the hypothesis space used by the ML method.
ML methods often use hypothesis spaces with a large effective dimension (see Section The Model ). As an example consider linear regression (see Section Linear Regression ) with data points having a large number [math]\featuredim[/math] of features (this setting is referred to as the high-dimensional regime). The effective dimension of the linear hypothesis space, which is used by linear regression, is equal to the number [math]\featuredim[/math] of features. Modern technology allows to collect a huge number of features about individual data points which implies, in turn, that the effective dimension of equ_lin_hypospace is large. Another example of a high-dimensional hypothesis space arises in deep learning methods using a hypothesis space are constituted by all maps represented by an artificial neural network (ANN) with billions of tunable parameters.
A high-dimensional hypothesis space is very likely to contain a hypothesis that perfectly fits any given training set. Such a hypothesis achieves a very small training error but might incur a large loss when predicting the labels of a data point that is not included in training set. Thus, the (minimum) training error achieved by a hypothesis learnt by ERM can be misleading. We say that a ML method, such as linear regression using too many features, overfits the training set when it learns a hypothesis (e.g., via ERM) that has small training error but incurs much larger loss outside the training set.
Section Overfitting shows that linear regression will overfit a training set
as soon as the number of features of a data point exceeds the size of the training set.
Section Validation demonstrates how to validate a learnt hypothesis by computing its average loss on data points which are not contained in the training set.
We refer to the set of data points used to validate the learnt hypothesis as a validation set.
If a ML method overfits the training set, it learns a hypothesis whose training error is much smaller than its validation error. We can detect if a ML method overfits by comparing its training error with its validation error (see Figure fig_bars_val_sel).
We can use the validation error not only to detect if a ML method overfits. The validation error can also be used as a quality measure for the hypothesis space or model used by the ML method. This is analogous to the concept of a loss function that allows us to evaluate the quality of a hypothesis [math]h\!\in\!\hypospace[/math]. Section Model Selection shows how to select between ML methods using different models by comparing their validation errors.
Section A Probabilistic Analysis of Generalization uses a simple probabilistic model for the data to study the relation between the training error of a learnt hypothesis and its expected loss (see risk). This probabilistic analysis reveals the interplay between the data, the hypothesis space and the resulting training error and validation error of a ML method.
Section The Bootstrap discusses the bootstrap as a simulation based alternative to the probabilistic analysis of Section A Probabilistic Analysis of Generalization . While Section A Probabilistic Analysis of Generalization assumes a specific probability distribution of the data points, the bootstrap does not require the specification of a probability distribution underlying the data.
As indicated in Figure fig_bars_val_sel, for some ML applications, we might have a
baseline (or benchmark) for the achievable performance of ML methods. Such a baseline might be obtained from existing ML methods, human performance levels or from a probabilistic model (see Section A Probabilistic Analysis of Generalization ). Section Diagnosing ML details how the comparison between training error, validation error and (if available) a baseline
informs possible improvements for a ML method. These improvements might be obtained by collecting more data points, using more features of data points or by changing the hypothesis space (or model).
Having a baseline for the expected loss, such as the Bayes risk, allows to tell if a ML method already provides satisfactory results. If the training error and the validation error of a ML method are close to the baseline, there might be little point in trying to further improve the ML method.
Overfitting
We now have a closer look at the occurrence of overfitting in linear regression methods. As discussed in Section Linear Regression , linear regression methods learn a linear hypothesis [math]h(\featurevec) = \weights^{T} \featurevec[/math] which is parametrized by the parameter vector [math]\weights \in \mathbb{R}^{\featurelen}[/math]. The learnt hypothesis is then used to predict the numeric label [math]\truelabel \in \mathbb{R}[/math] of a data point based on its feature vector [math]\featurevec \in \mathbb{R}^{\featurelen}[/math]. Linear regression aims at finding a parameter vector [math]\widehat{\vw}[/math] with minimum average squared error loss incurred on a training set
The training set [math]\dataset[/math] consists of [math]\samplesize[/math] data points [math]\big(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}\big)[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math], with known label values [math]\truelabel^{(\sampleidx)}[/math]. We stack the feature vectors [math]\featurevec^{(\sampleidx)}[/math] and labels [math]\truelabel^{(\sampleidx)}[/math], respectively, of the data points in the training set into the feature matrix [math]\featuremtx=(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T}[/math] and label vector [math]\labelvec=(\truelabel^{(1)},\ldots,\truelabel^{(\samplesize)})^{T}[/math].
The ERM of linear regression is solved by any parameter vector [math]\widehat{\weights}[/math] that solves equ_zero_gradient_lin_reg. The (minimum) training error of the hypothesis [math]h^{(\widehat{\weights})}[/math] is obtained as
Here, we used the orthogonal projection matrix [math]\mathbf{P}[/math] on the linear span
of the feature matrix [math]\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T} \in \mathbb{R}^{ \samplesize \times \featuredim}[/math].
In many ML applications we have access to a huge number of individual features to characterize a data point. As a point in case, consider a data point which is a snapshot obtained from a modern smartphone camera. These cameras have a resolution of several megapixels. Here, we can use millions of pixel colour intensities as its features. For such applications, it is common to have more features for data points than the size of the training set,
Whenever \eqref{equ_condition_overfitting} holds, the feature vectors [math]\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}[/math] of the data points in [math]\dataset[/math] are typically linearly independent. As a case in point, if the feature vectors
[math]\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}[/math] are realizations of independent and identically distributed (iid) random variable (RV)s with a continuous probability distribution, these vectors are linearly independent with probability one [1].
If the feature vectors [math]\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}[/math] are linearly independent, the span of the feature matrix [math]\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T}[/math] coincides with [math]\mathbb{R}^{\samplesize}[/math] which implies, in turn, [math]\mathbf{P} = \mathbf{I}[/math]. Inserting [math]\mathbf{P} = \mathbf{I}[/math] into equ_emp_risk_lin_proje yields
As soon as the number [math]\samplesize= | \dataset|[/math] of training data points does not exceed the number [math]\featuredim[/math] of features that characterize data points, there is (with probability one) a linear predictor [math]h^{(\widehat{\weights})}[/math] achieving zero training error(!).
While the hypothesis [math]h^{(\widehat{\weights})}[/math] achieves zero training error, it will typically incur a non-zero average prediction error [math]\truelabel - h^{(\widehat{\weights})}(\featurevec)[/math] on data points [math](\featurevec,\truelabel)[/math] outside the training set (see Figure fig_polyn_training). Section A Probabilistic Analysis of Generalization will make this statement more precise by using a probabilistic model for the data points within and outside the training set.
Note that \eqref{eq_zero_trianing_error} also applies if the features [math]\featurevec[/math] and labels [math]y[/math] of data points are completely unrelated. Consider an ML problem with data points whose labels [math]\truelabel[/math] and features are realizations of a RV that are statistically independent. Thus, in a very strong sense, the features [math]\featurevec[/math] contain no information about the label of a data point. Nevertheless, as soon as the number of features exceeds the size of the training set, such that \eqref{equ_condition_overfitting} holds, linear regression methods will learn a hypothesis with zero training error.
We can easily extend the above discussion about the occurrence of overfitting in linear regression to other methods that combine linear regression with a feature map. Polynomial regression, using data points with a single feature [math]z[/math], combines linear regression with the feature map [math]\rawfeature \mapsto \featuremapvec(\rawfeature) \defeq \big(\rawfeature^{0},\ldots,\rawfeature^{\featurelen-1}\big)^{T}[/math] as discussed in Section Polynomial Regression .
It can be shown that whenever \eqref{equ_condition_overfitting} holds and the features
[math]\rawfeature^{(1)},\ldots,\rawfeature^{(\samplesize)}[/math] of the training set are all different, the feature vectors [math]\featurevec^{(1)}\defeq \featuremapvec \big(\rawfeature^{(1)}\big),\ldots, \featurevec^{(\samplesize)}\defeq \featuremapvec \big(\rawfeature^{(\samplesize)}\big)[/math] are linearly independent. This implies, in turn, that polynomial regression is guaranteed to find a hypothesis with zero training error whenever [math]\samplesize \leq \featurelen[/math] and the data points in the training set have different feature values.
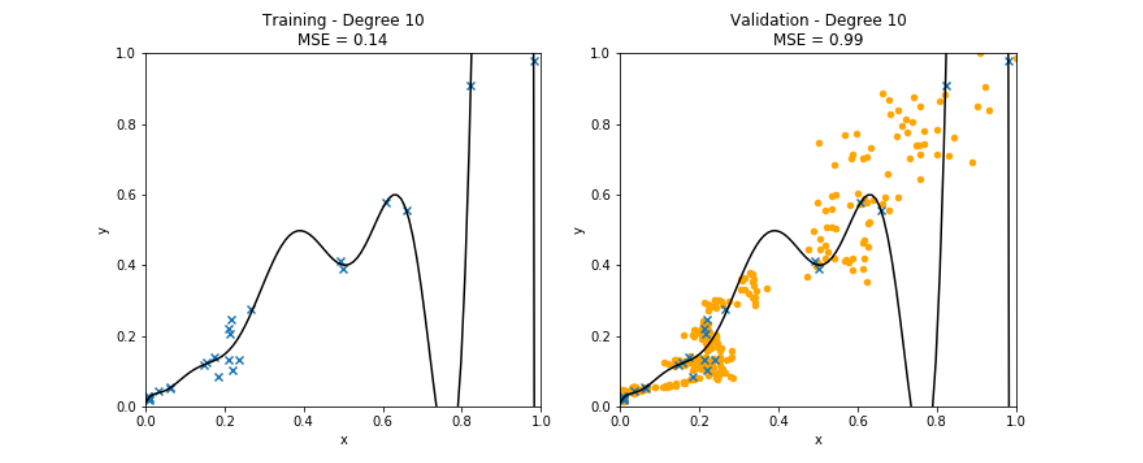
Validation
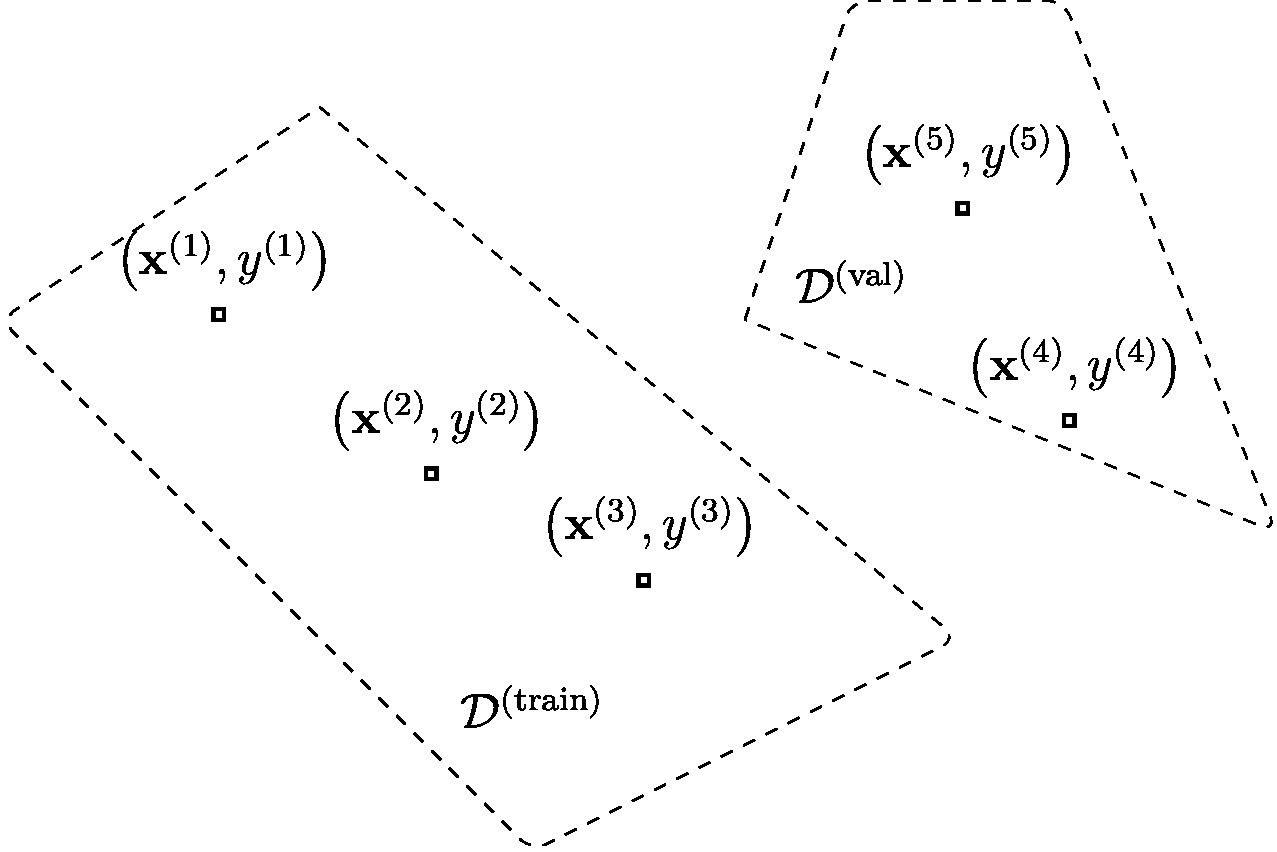
Consider an ML method that uses ERM to learn a hypothesis [math]\hat{h} \in \hypospace[/math] out of the hypothesis space [math]\hypospace[/math]. The discussion in Section Overfitting revealed that the training error of a learnt hypothesis [math]\hat{h}[/math] can be a poor indicator for the performance of [math]\hat{h}[/math] for data points outside the training set. The hypothesis [math]\hat{h}[/math] tends to “look better” on the training set over which it has been tuned within ERM.The basic idea of validating the predictor [math]\hat{h}[/math] is simple:
- first we learn a hypothesis [math]\hat{h}[/math] using ERM on a training set and
- then we compute the average loss of [math]\hat{h}[/math] on data points that do not belong to the training set.
Thus, validation means to compute the average loss of a hypothesis using data points that have not been used in ERM to learn that hypothesis.
Assume we have access to a dataset of [math]\samplesize[/math] data points,
Each data point is characterized by a feature vector [math]\featurevec^{(\sampleidx)}[/math] and a label [math]\truelabel^{(\sampleidx)}[/math]. Algorithm alg:validated_ERM outlines how to learn and validate a hypothesis [math]h\in \hypospace[/math] by splitting the dataset [math]\dataset[/math] into a training set and a validation set. The random shuffling in step alg_shuffle_step of Algorithm alg:validated_ERM ensures the i.i.d. assumption for the shuffled data. Section The Size of the Validation Set shows next how the i.i.d. assumption ensures that the validation error \eqref{equ_def_training_val_val} approximates the expected loss of the hypothesis [math]\hat{h}[/math]. The hypothesis [math]\hat{h}[/math] is learnt via ERM on the training set during step equ_step_train_val_ERM of Algorithm alg:validated_ERM.
Input: model [math]\hypospace[/math], loss function [math]\lossfun[/math], dataset [math]\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}[/math]; split ratio [math]\splitratio[/math]
- randomly shuffle the data points in [math]\dataset[/math]
- create the training set
[math]\trainset[/math] using the first
[math]\samplesize_{t}\!=\! \lceil\splitratio \samplesize\rceil[/math] data points,
[[math]] \trainset = \big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize_{t})}, \truelabel^{(\samplesize_{t})}\big) \big\}.[[/math]]
- create the validation set
[math]\valset
[/math]
by the
[math]\samplesize_v = \samplesize - \samplesize_t[/math] remaining data points,
[[math]] \valset = \big\{ \big(\featurevec^{(\samplesize_{t}+1)}, \truelabel^{(\samplesize_{t}+1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}.[[/math]]
- learn hypothesis
[math]\hat{h}
[/math]
via ERM on the training set,
[[math]] \begin{equation} \label{equ_def_hat_h_fitting} \hat{h} \defeq \argmin_{h\in \hypospace} \emperror\big(h| \trainset \big) \end{equation} [[/math]]
- compute the training error
[[math]] \begin{equation} \label{equ_def_training_error_val} \trainerror \defeq \emperror\big(\hat{h}| \trainset \big) = (1/\samplesize_{t}) \sum_{\sampleidx=1}^{\samplesize_{t}} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}. \end{equation} [[/math]]
- compute the validation error
[[math]] \begin{equation} \label{equ_def_training_val_val} \valerror \defeq \emperror\big(\hat{h}| \valset \big)= (1/\samplesize_{v}) \sum_{\sampleidx=\samplesize_{t}+1}^{\samplesize} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}. \end{equation} [[/math]]
Output: learnt hypothesis [math]\hat{h}[/math], training error [math]\trainerror[/math], validation error [math]\valerror[/math]
The Size of the Validation Set
The choice of the split ratio [math]\splitratio \approx \samplesize_{t}/ \samplesize [/math]
in Algorithm alg:validated_ERM is often based on trial and error. We try out different choices for the split ratio and pick the one with the smallest validation error. It is difficult to make a precise statement on how to choose the split ratio which applies broadly [2]. This difficulty stems from the fact that the optimal choice for [math]\rho[/math] depends on the precise statistical properties of the data points.
One approach to determine the required size of the validation set is to use a probabilistic model for the data points. The i.i.d. assumption is maybe the most widely used probabilistic model within ML. Here, we interpret data points as the realizations of iid RVs. These iid RVs have a common (joint) probability distribution
[math]p(\featurevec,\truelabel)[/math] over possible features [math]\featurevec[/math] and labels [math]\truelabel[/math] of a data point. Under the i.i.d. assumption, the validation error [math]\valerror[/math] \eqref{equ_def_training_val_val} also becomes a realization of a RV. The expectation (or mean) [math]\expect \{ \valerror \}[/math] of this RV is precisely the risk [math]\expect\{ \loss{(\featurevec,\truelabel)} {\hat{h}} \}[/math] of [math]\hat{h}[/math] (see risk).
Within the above i.i.d. assumption, the validation error [math]\valerror[/math] becomes a realization of a RV that fluctuates around its mean [math]\expect \{ \valerror \}[/math]. We can quantify this fluctuation using the variance
Note that the validation error is the average of the realizations [math]\loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}[/math] of iid RVs. The probability distribution of the RV [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math] is determined by the probability distribution [math]p(\featurevec,\truelabel)[/math], the choice of loss function and the hypothesis [math]\hat{h}[/math]. In general, we do not know [math]p(\featurevec,\truelabel)[/math] and, in turn, also do not know the probability distribution of [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math].
If we know an upper bound [math]U[/math] on the variance of the (random) loss [math]\loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}[/math], we can bound the variance of [math]\valerror[/math] as
We can then, in turn, ensure that the variance [math]\sigma_{\valerror}^{2}[/math] of the validation error [math]\valerror[/math] does not exceed a given threshold
[math]\eta[/math], say [math]\eta = (1/100) \trainerror^2[/math], by using a validation set of size
The lower bound \eqref{equ_lower_bound_variance} is only useful if we can determine an upper bound [math]U[/math] on the variance of the RV [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math] where [math]\big(\featurevec,\truelabel\big)[/math] is a RV with probability distribution [math]p(\featurevec,\truelabel)[/math]. An upper bound on the variance of [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math] can be derived using probability theory if we know an accurate probabilistic model [math]p(\featurevec,\truelabel)[/math] for the data points. Such a probabilistic model might be provided by application-specific scientific fields such as biology or psychology. Another option is to estimate the variance of [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math] using the sample variance of the actual loss values [math]\loss{(\featurevec^{(1)},\truelabel^{(1)})}{\hat{h}},\ldots, \loss{(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)})}{\hat{h}}[/math] obtained for the dataset [math]\dataset[/math].
k-Fold Cross Validation
Algorithm alg:validated_ERM uses the most basic form of splitting a given dataset [math]\dataset[/math] into a training set and a validation set. Many variations and extensions of this basic splitting approach have been proposed and studied (see [3] and Section The Bootstrap ). One very popular extension of the single split into training set and validation set is known as [math]k[/math]-fold cross-validation ( [math]k[/math]-fold CV) [4](Sec. 7.10). We summarize [math]k[/math]-fold CV in Algorithm alg:kfoldCV_ERM below.
Figure fig_k_fold_CV illustrates the key principle behind [math]k[/math]-fold CV. First, we divide the entire dataset evenly into [math]\nrfolds[/math] subsets which are referred to as “folds”. The learning (via ERM) and validation of a hypothesis out of a given hypothesis space [math]\hypospace[/math] is then repeated [math]\nrfolds[/math] times.

During each repetition, we use one fold as the validation set and the remaining [math]\nrfolds-1[/math] folds as a training set. We then average the values of the training error and validation error obtained for each repetition (fold).
The average (over all [math]\nrfolds[/math] folds) validation error delivered by [math]k[/math]-fold CV tends to better estimate the expected loss or risk compared to the validation error obtained from a single split in Algorithm alg:validated_ERM. Consider a dataset that consists of a relatively small number of data points. If we use a single split of this small dataset into a training set and validation set, we might be very unlucky and choose data points for the validation set which are outliers and not representative for the statistical properties of most data points. The effect of such an unlucky split is typically averaged out when using [math]k[/math]-fold CV.
Input: model [math]\hypospace[/math], loss function [math]\lossfun[/math], dataset [math]\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}[/math]; number [math]\nrfolds[/math] of folds
- randomly shuffle the data points in [math]\dataset[/math]
- divide the shuffled dataset
[math]\dataset[/math] into
[math]\nrfolds[/math] folds
[math]\dataset_{1},\ldots,\dataset_{\nrfolds}[/math]
of size
[math]\foldsize=\lceil\samplesize/\nrfolds\rceil[/math],
[[math]] \begin{equation} \dataset_{1}\!=\!\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots, \big(\featurevec^{(\foldsize)}, \truelabel^{(\foldsize)}\big)\} ,\ldots,\dataset_{k}\!=\!\big\{ \big(\featurevec^{((\nrfolds\!-\!1)\foldsize+1)}, \truelabel^{((\nrfolds\!-\!1)\foldsize+1)}\big),\ldots, \big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big)\} \end{equation} [[/math]]
- For fold index [math]\foldidx=1,\ldots,\nrfolds[/math] do
- use [math]\foldidx [/math] th fold as the validation set [math]\valset=\dataset_{\foldidx}[/math]
- use rest as the training set [math]\trainset=\dataset \setminus \dataset_{\foldidx}[/math]
-
learn hypothesis
[math]\hat{h}[/math] via ERM on the training set,
[[math]] \begin{equation} \label{equ_def_hat_h_fitting_cv} \hat{h}^{(\foldidx)} \defeq \argmin_{h\in \hypospace} \emperror\big(h| \trainset \big) \end{equation} [[/math]]
- compute the training error
[[math]] \begin{equation} \label{equ_def_training_error_val_cv} \trainerror^{(\foldidx)} \defeq \emperror\big(\hat{h}| \trainset \big) = (1/\big|\trainset\big|) \sum_{\sampleidx \in \trainset} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h}. \end{equation} [[/math]]
- compute validation error
[[math]] \begin{equation} \label{equ_def_training_val_val_cv} \valerror^{(\foldidx)} \defeq \emperror\big(\hat{h}| \valset \big)= (1/\big|\valset\big|) \sum_{\sampleidx \in \valset} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}. \end{equation} [[/math]]
- end for
-
compute average training and validation errors
[[math]] \trainerror \defeq (1/\nrfolds) \sum_{\foldidx=1}^{\nrfolds} \trainerror^{(\foldidx)}\mbox{, and }\valerror \defeq (1/\nrfolds) \sum_{\foldidx=1}^{\nrfolds} \valerror^{(\foldidx)} [[/math]]
- pick a learnt hypothesis [math]\hat{h} \defeq \hat{h}^{(\foldidx)}[/math]for some [math]\foldidx \in \{1,\ldots,\nrfolds\}[/math]
Output: learnt hypothesis [math]\hat{h}[/math]; average training error [math]\trainerror[/math]; average validation error [math]\valerror[/math]
Imbalanced Data
The simple validation approach discussed above requires the validation set to be a good representative for the overall statistical properties of the data. This might not be the case in applications with discrete valued labels and some of the label values being very rare. We might then be interested in having a good estimate of the conditional risks [math]\expect \{ \loss{(\featurevec,\truelabel)}{h} | \truelabel=\truelabel'\}[/math] where [math]\truelabel'[/math] is one of the rare label values. This is more than requiring a good estimate for the risk [math]\expect \{ \loss{(\featurevec,\truelabel)}{h} \}[/math].
Consider data points characterized by a feature vector [math]\featurevec[/math] and binary label [math]\truelabel \in \{-1,1\}[/math]. Assume we aim at learning a hypothesis [math]h(\featurevec) = \weights^{T} \featurevec[/math] to classify data points as [math]\hat{\truelabel}=1[/math] if [math]h(\featurevec) \geq 0[/math] while [math]\hat{\truelabel}=-1[/math] otherwise. The learning is based on a dataset [math]\dataset[/math] which contains only one single (!) data point with [math]\truelabel=-1[/math]. If we then split the dataset into training and validation set, it is with high probability that the validation set does not include any data point with label value [math]\truelabel=-1[/math]. This cannot happen when using [math]\nrfolds[/math]-fold CV since the single data point must be in one of the validation folds. However, even the applicability of [math]k[/math]-fold CV for such an imbalanced dataset is limited since we evaluate the performance of a hypothesis [math]h(\featurevec)[/math] using only one single data point with [math]\truelabel=-1[/math]. The resulting validation error will be dominated by the loss of [math]h(\featurevec)[/math] incurred on data points from the majority class (those with true label value [math]\truelabel=1[/math]).
To learn and validate a hypothesis with imbalanced data, it might be useful to to generate synthetic data points to enlarge the minority class. This can be done using data augmentation techniques which we discuss in Section Data Augmentation . Another option is to choose a loss function that takes the different frequencies of label values into account. Let us illustrate this approach in what follows by an illustrative example.
Consider an imbalanced dataset of size [math]\samplesize=100[/math], which contains [math]90[/math] data points with label [math]\truelabel=1[/math] but only [math]10[/math] data points with label [math]\truelabel=-1[/math]. We might want to put more weight on wrong predictions obtained for data points from the minority class (with true label value [math]\truelabel=-1[/math]). This can be done by using a much larger value for the loss [math]\loss{(\featurevec,\truelabel=-1)}{h(\featurevec)=1}[/math] than for the loss [math]\loss{(\featurevec,\truelabel=1)}{h(\featurevec)=-1}[/math] incurred by incorrectly predicting the label of a data point from the majority class (with true label value [math]\truelabel=1[/math]).
Model Selection
Chapter The Landscape of ML illustrated how many well-known ML methods are obtained by different combinations of a hypothesis space or model, loss function and data representation. While for many ML applications there is often a natural choice for the loss function and data representation, the right choice for the model is typically less obvious. We now discuss how to use the validation methods of Section Validation to choose between different candidate models.
Consider data points characterized by a single numeric feature [math]\feature\in \mathbb{R}[/math] and numeric label [math]\truelabel\in \mathbb{R}[/math]. If we suspect that the relation between feature [math]\feature[/math] and label [math]\truelabel[/math] is non-linear, we might use polynomial regression which is discussed in Section Polynomial Regression . Polynomial regression uses the hypothesis space [math]\hypospace_{\rm poly}^{(\featuredim)}[/math] with some maximum degree [math]\featuredim[/math]. Different choices for the maximum degree [math]\featuredim[/math] yield a different hypothesis space: [math]\hypospace^{(1)} = \mathcal{H}_{\rm poly}^{(0)},\hypospace^{(2)} = \mathcal{H}_{\rm poly}^{(1)},\ldots,\hypospace^{(\nrmodels)} = \hypospace_{\rm poly}^{(\nrmodels)}[/math].
Another ML method that learns non-linear hypothesis map is Gaussian basis regression (see Section Gaussian Basis Regression ). Here, different choices for the variance [math]\sigma[/math] and shifts [math]\mu[/math] of the Gaussian basis function result in different hypothesis spaces. For example, [math]\hypospace^{(1)} = \mathcal{H}^{(2)}_{\rm Gauss}[/math] with [math]\sigma=1[/math] and [math]\mu_{1}=1[/math] and [math]\mu_{2}=2[/math], [math]\hypospace^{(2)} = \hypospace^{(2)}_{\rm Gauss}[/math] with [math]\sigma = 1/10[/math], [math]\mu_{1}=10[/math], [math]\mu_{2}= 20[/math].
Algorithm alg:model_selection summarizes a simple method to choose between different candidate models [math]\hypospace^{(1)},\hypospace^{(2)},\ldots,\hypospace^{(\nrmodels)}[/math]. The idea is to first learn and validate a hypothesis [math]\hat{h}^{(\modelidx)}[/math] separately for each model [math]\hypospace^{(\modelidx)}[/math] using Algorithm alg:kfoldCV_ERM. For each model [math]\hypospace^{(\modelidx)}[/math], we learn the hypothesis
[math]\hat{h}^{(\modelidx)}[/math] via ERM \eqref{equ_def_hat_h_fitting} and then compute its validation error
[math]\valerror^{(\modelidx)}[/math] \eqref{equ_def_training_val_val}. We then choose the hypothesis [math]\hat{h}^{(\hat{\modelidx})}[/math] from those model [math]\hypospace^{(\hat{\modelidx})}[/math] which resulted in the smallest validation error [math]\valerror^{(\hat{\modelidx})} = \min_{\modelidx=1,\ldots,\nrmodels} \valerror^{(\modelidx)}[/math].
The workflow of Algorithm alg:model_selection is similar to the workflow of ERM. Remember that the idea of ERM is to learn a hypothesis out of a set of different candidates (the hypothesis space). The quality of a particular hypothesis [math]h[/math] is measured using the (average) loss incurred on some training set. We use the same principle for model selection but on a higher level. Instead of learning a hypothesis within a hypothesis space, we choose (or learn) a hypothesis space within a set of candidate hypothesis spaces. The quality of a given hypothesis space is measured by the validation error \eqref{equ_def_training_val_val}. To determine the validation error of a hypothesis space, we first learn the hypothesis [math]\hat{h} \in \hypospace[/math] via ERM \eqref{equ_def_hat_h_fitting} on the training set. Then, we obtain the validation error as the average loss of [math]\hat{h}[/math] on the validation set.
The final hypothesis [math]\hat{h}[/math] delivered by the model selection Algorithm alg:model_selection not only depends on the training set used in ERM (see \eqref{equ_def_hat_h_fitting_cv}). This hypothesis [math]\hat{h}[/math] has also been chosen based on its validation error which is the average loss on the validation set in \eqref{equ_def_training_val_val_cv}. Indeed, we compared this validation error with the validation errors of other models to pick the model [math]\hypospace^{(\hat{\modelidx})}[/math] (see step step_pick_optimal_model) which contains [math]\hat{h}[/math]. Since we used the validation error \eqref{equ_def_training_val_val_cv} of [math]\hat{h}[/math] to learn it, we cannot use this validation error as a good indicator for the general performance of [math]\hat{h}[/math].
To estimate the general performance of the final hypothesis [math]\hat{h}[/math] delivered by Algorithm alg:model_selection we must try it out on a test set. The test set, which is constructed in step equ_construct_test_set_algmodsel of Algorithm alg:model_selection, consists of data points that are neither contained in the training set \eqref{equ_def_hat_h_fitting_cv} nor the validation set \eqref{equ_def_training_val_val_cv} used for training and validating the candidate models [math]\hypospace^{(1)},\ldots,\hypospace^{(\nrmodels)}[/math]. The average loss of the final hypothesis on the test set is referred to as the test error. The test error is computed in the step step_compute_test_error_mod_selection of Algorithm alg:model_selection.
Input: list of candidate models [math]\hypospace^{(1)},\ldots,\hypospace^{(\nrmodels)}[/math], loss function [math]\lossfun[/math], dataset [math]\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}[/math]; number [math]\nrfolds[/math] of folds, test set fraction [math]\rho[/math]
- randomly shuffle the data points in [math]\dataset[/math]
- determine size [math]\samplesize' \defeq \lceil \rho \samplesize \rceil[/math] of test set
- construct a test set
[[math]] \testset= \big\{\big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize')}, \truelabel^{(\samplesize')}\big) \big\}[[/math]]
- construct a training set and a validation set,
[[math]]\dataset^{(\rm trainval)} = \big\{\big(\featurevec^{(\samplesize'+1)}, \truelabel^{(\samplesize'+1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}[[/math]]
- For [math] \modelidx=1,\ldots,\nrmodels[/math] do
- run Algorithm alg:kfoldCV_ERM using [math]\hypospace=\hypospace^{(\modelidx)}[/math], dataset [math]\dataset=\dataset^{(\rm trainval)}[/math], loss function [math]\lossfun [/math] and [math]\nrfolds[/math] folds
- Algorithm alg:kfoldCV_ERM delivers hypothesis [math]\hat{h}[/math] and validation error [math]\valerror[/math]
- store learnt hypothesis [math]\hat{h}^{(\modelidx)}\defeq\hat{h}[/math] and validation error [math]\valerror^{(\modelidx)}\defeq\valerror[/math]
- end for
- pick model [math]\hypospace^{(\hat{\modelidx})}[/math] with minimum validation error [math]\valerror^{(\hat{\modelidx})}\!=\!\min_{\modelidx=1,\ldots,\nrmodels}\valerror^{(\modelidx)}[/math] \label{step_pick_optimal_model}
- define optimal hypothesis [math]\hat{h}= \hat{h}^{(\hat{\modelidx})}[/math]
- compute test error
[[math]] \begin{equation} \label{equ_def_training_error_val_test} \testerror \defeq \emperror\big(\hat{h}| \testset \big) = (1/\big|\testset\big|) \sum_{\sampleidx \in \testset} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}. \end{equation} [[/math]]
Sometimes it is beneficial to use different loss functions for the training and the validation of a hypothesis.
As an example, consider logistic regression and the support vector machine (SVM) which have been discussed in Sections Logistic Regression and
Support Vector Machines , respectively. Both methods use the same model which is the space of linear hypothesis maps [math]h(\featurevec) = \weights^{T} \featurevec[/math]. The main difference between these two methods is in their choice for the loss function. Logistic regression minimizes the (average) logistic losson the training set to learn the hypothesis [math]h^{(1)}(\featurevec)= \big( \weights^{(1)} \big)^{T} \featurevec
[/math]
with a parameter vector [math]\weights^{(1)}[/math]. The SVM instead minimizes the (average) hinge loss on the training set to learn the hypothesis [math]h^{(2)}(\featurevec) = \big( \weights^{(2)} \big)^{T} \featurevec[/math] with a parameter vector [math]\weights^{(2)}[/math]. It is inconvenient to compare the usefulness of the two hypotheses [math]h^{(1)}(\featurevec)[/math] and [math]h^{(2)}(\featurevec)[/math] using different loss functions to compute their validation errors. This comparison is more convenient if we instead compute the validation errors for [math]h^{(1)}(\featurevec)[/math] and [math]h^{(2)}(\featurevec)[/math] using the average 0/1 loss.
Algorithm alg:model_selection requires as one of its inputs a given list of candidate models. The longer this list, the more computation is required from Algorithm alg:model_selection. Sometimes it is possible to prune the list of candidate models by removing models that are very unlikely to have minimum validation error.
Consider polynomial regression which uses as the model the space [math]\hypospace_{\rm poly}^{(r)}[/math] of polynomials with maximum degree [math]\polydegree[/math] (see equ_def_poly_hyposapce). For [math]\polydegree=1[/math],
[math]\hypospace_{\rm poly}^{(\polydegree)}[/math] is the space of polynomials with maximum degree one (which are linear maps), [math]h(\feature)=\weight_{2}\feature+\weight_{1}[/math]. For [math]\polydegree=2[/math], [math]\hypospace_{\rm poly}^{(\polydegree)}[/math] is the space of polynomials with maximum degree two, [math]h(\feature)=\weight_{3}\feature^2 +\weight_{2}\feature+\weight_{1}.[/math] The polynomial degree [math]\polydegree[/math] parametrizes a nested set of models,
For each degree [math]\polydegree[/math], we learn a hypothesis [math]h^{(r)} \in \hypospace_{\rm poly}^{(\polydegree)}[/math] with minimum average loss (training error) [math]\trainerror^{(\polydegree)}[/math] on a training set (see \eqref{equ_def_training_error_val}). To validate the learnt hypothesis [math]h^{(\polydegree)}[/math], we compute its average loss (validation error) [math]\valerror^{(\polydegree)}[/math] on a validation set (see \eqref{equ_def_training_val_val}).
Figure fig_trainvalvsdegree depicts the typical dependency of the training and validation errors on the polynomial degree [math]\polydegree[/math]. The training error [math]\trainerror^{(\polydegree)}[/math] decreases monotonically with increasing polynomial degree [math]\polydegree[/math]. To illustrate this monotonic decrease, we consider the two specific choices [math]\polydegree=3[/math] and [math]\polydegree=5[/math] with corresponding models [math]\hypospace^{(\polydegree)}_{\rm poly}[/math] and [math]\hypospace^{(\polydegree)}_{\rm poly}[/math]. Note that [math]\hypospace^{(3)}_{\rm poly} \subset \hypospace^{(5)}_{\rm poly}[/math] since any polynomial with degree not exceeding [math]3[/math] is also a polynomial with degree not exceeding [math]5[/math]. Therefore, the training error \eqref{equ_def_training_error_val} obtained when minimizing over the larger model [math] \hypospace^{(5)}_{\rm poly}[/math] can only decrease but never increase compared to \eqref{equ_def_training_error_val} using the smaller model [math] \hypospace^{(3)}_{\rm poly}[/math] Figure fig_trainvalvsdegree indicates that the validation error [math]\valerror^{(\polydegree)}[/math] (see \eqref{equ_def_training_val_val}) behaves very different compared to the training error [math]\trainerror^{(\polydegree)}[/math]. Starting with degree [math]\polydegree=0[/math], the validation error first decreases with increasing degree [math]\polydegree[/math]. As soon as the degree [math]\polydegree[/math] is increased beyond a critical value, the validation error starts to increase with increasing [math]\polydegree[/math]. For very large values of [math]\polydegree[/math], the training error becomes almost negligible while the validation error becomes very large. In this regime, polynomial regression overfits the training set.
Figure fig_polyregdegree9 illustrates the overfitting of polynomial regression when using a maximum degree that is too large. In particular, Figure fig_polyregdegree9 depicts a learnt hypothesis which is a degree [math]9[/math] polynomial that fits very well the training set, resulting in a very small training error. To achieve this low training error the resulting polynomial has an unreasonable high rate of change for feature values [math]\feature \approx 0[/math]. This results in large prediction errors for data points with feature values [math]x \approx 0[/math].
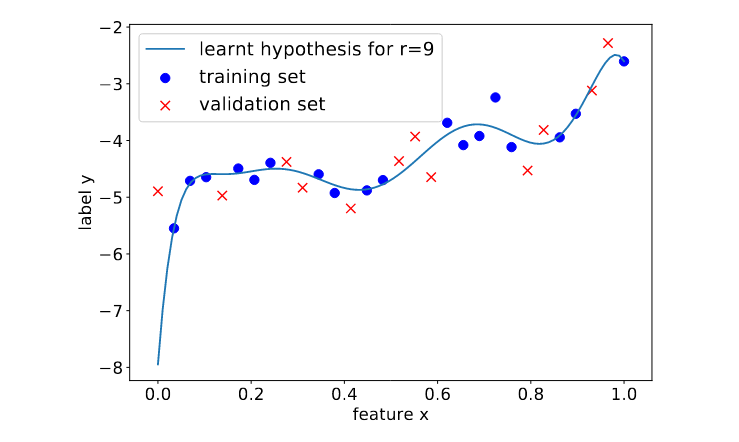
A Probabilistic Analysis of Generalization
More Data Beats Clever Algorithms ?; More Data Beats Clever Feature Selection?
A key challenge in ML is to ensure that a hypothesis that predicts well the labels on a training set (which has been used to learn that hypothesis) will also predict well the labels of data points outside the training set. We say that a ML method generalizes well if it learns a hypothesis [math]\hat{h}[/math] that performs not significantly worse on data points outside the training set. In other words, the loss incurred by [math]\hat{h}[/math] for data points outside the training set is not much larger than the average loss of [math]\hat{h}[/math] incurred on the training set.
We now study the generalization of linear regression methods (see Section Linear Regression ) using an i.i.d. assumption. In particular, we interpret data points as iid realizations of RVs that have the same distribution as a random data point [math]\datapoint=(\featurevec,\truelabel)[/math]. The feature vector [math]\featurevec[/math] is then a realization of a standard Gaussian RV with zero mean and covariance being the identity matrix, i.e., [math]\featurevec \sim \mathcal{N}(\mathbf{0}, \mathbf{I})[/math].
The label [math]\truelabel[/math] of a random data point is related to its features [math]\featurevec[/math] via a linear Gaussian model
We assume the noise variance [math]\sigma^{2}[/math] fixed and known. This is a simplifying assumption and in practice we would need to estimate the noise variance from data [5]. Note that, within our probabilistic model, the error component [math]\varepsilon[/math] in \eqref{equ_linear_obs_model} is intrinsic to the data and cannot be overcome by any ML method. We highlight that the probabilistic model for the observed data points is just a modelling assumption. This assumption allows us to study some fundamental behaviour of ML methods. There are principled methods (“statistical tests”) that allow to determine if a given dataset can be accurately modelled using \eqref{equ_linear_obs_model} [6].
We predict the label [math]\truelabel[/math] from the features [math]\featurevec[/math] using a linear hypothesis [math]h(\featurevec)[/math] that depends only on the first [math]\modelidx[/math] features [math]\feature_{1},\ldots,\feature_{\modelidx}[/math]. Thus, we use the hypothesis space
Note that each element [math]h^{(\weights)} \in \hypospace^{(\modelidx)}[/math] corresponds to a particular choice of the parameter vector [math]\weights \in \mathbb{R}^{\modelidx}[/math].
The model parameter [math]\modelidx \in \{0,\ldots,\featuredim\}[/math] coincides with the effective dimension of the hypothesis space [math]\hypospace^{(\modelidx)}[/math]. For [math]\modelidx\lt \featuredim[/math], the hypothesis space [math]\hypospace^{(\modelidx)}[/math] is a proper (strict) subset of the space of linear hypothesis maps used within linear regression (see Section Linear Regression ). Moreover, the parameter [math]\modelidx[/math] indexes a nested sequence of models,
The quality of a particular predictor [math]h^{(\weights)} \in \hypospace^{(\modelidx)}[/math] is measured via the average squared error [math]\emperror (h^{(\weights)} \mid \trainset)[/math] incurred on the labeled training set
We interpret data points in the training set [math]\trainset[/math] as well as any other data point outside the training set as realizations of iid RVs with a common probability distribution. This common probability distribution is a multivariate normal (Gaussian) distribution,
The labels [math]\truelabel^{(\sampleidx)},\truelabel[/math] are related to the features of data points via (see \eqref{equ_linear_obs_model})
Here, the noise terms [math]\varepsilon, \varepsilon^{(\sampleidx)} \sim \mathcal{N}(0,\sigma^{2})[/math] are realizations of iid Gaussian RVs with zero mean and variance [math]\sigma^{2}[/math].
Chapter Empirical Risk Minimization showed that the training error [math]\emperror (h^{(\weights)} \mid \trainset)[/math] is minimized by the predictor [math]h^{(\widehat{\weights})}(\featurevec) = \widehat{\weights}^{T} \mathbf{I}_{\modelidx \times \featuredim} \featurevec[/math], that uses the parameter vector
Here we used the (restricted) feature matrix [math]\mX^{(\modelidx)}[/math] and the label vector [math]\labelvec[/math] defined as, respectively,
It will be convenient to tolerate a slight abuse of notation and denote both, the length- [math]\modelidx[/math] vector \eqref{equ_optimal_weight_closed_form} as well as the zero-padded parameter vector [math]\big(\widehat{\weights}^{T},\mathbf{0}^{T}\big)^{T} \in \mathbb{R}^{\featuredim}[/math], by [math]\widehat{\weights}[/math]. This allows us to write
We highlight that the formula \eqref{equ_optimal_weight_closed_form} for the optimal weight vector [math]\widehat{\weights}[/math] is only valid if the matrix [math]\big(\featuremtx^{(\modelidx)}\big)^{T} \featuremtx^{(\modelidx)}[/math] is invertible. Within our toy model (see \eqref{equ_toy_model_iid}), this is true with probability one whenever [math]\samplesize_{\rm t} \geq \modelidx[/math]. Indeed, for [math]\samplesize_{\rm t} \geq \modelidx[/math] the truncated feature vectors [math]\mathbf{I}_{\modelidx \times \featuredim} \featurevec^{(1)}, \ldots, \mathbf{I}_{\modelidx \times \featuredim} \featurevec^{(\samplesize_{t})}[/math], which are iid realizations of a Gaussian RV, are linearly independent with probability one [7][8].
In what follows, we consider the case [math]\samplesize_{\rm t} \gt \modelidx[/math] such that the formula \eqref{equ_optimal_weight_closed_form} is valid (with probability one). The more challenging high-dimensional regime [math]\samplesize_{\rm t} \leq \modelidx[/math] will be studied in Chapter Regularization .
The optimal parameter vector [math]\widehat{\weights}[/math] (see \eqref{equ_optimal_weight_closed_form}) depends on the training set [math]\trainset[/math] via the feature matrix [math]\featuremtx^{(\modelidx)}[/math] and label vector [math]\labelvec[/math] (see \eqref{equ_def_feature_matrix_r}). Therefore, since we model the data points in the training set as realizations of RVs, the parameter vector [math]\widehat{\weights}[/math] \eqref{equ_optimal_weight_closed_form} is the realization of a RV. For each specific realization of the training set [math]\trainset[/math], we obtain a specific realization of the optimal parameter vector [math]\widehat{\weights}[/math].
The probabilistic model \eqref{equ_linear_obs_model} relates the features [math]\featurevec[/math] of a data point to its label [math]\truelabel[/math] via some (unknown) true parameter vector [math]\overline{\weights}[/math]. Intuitively, the best linear hypothesis would be [math]h(\featurevec) =\widehat{\weights}^{T} \featurevec[/math] with parameter vector [math]\widehat{\weights} = \overline{\weights}[/math]. However, in general this will not be achievable since we have to compute [math]\widehat{\weights}[/math] based on the features [math]\featurevec^{(\sampleidx)}[/math] and noisy labels [math]\truelabel^{(\sampleidx)}[/math] of the data points in the training set [math]\dataset[/math].
The parameter vector [math]\widehat{\vw}[/math] delivered by ERM typically results in a non-zero estimation error
The estimation error \eqref{equ_def_est_error} is the realization of a RV since the learnt parameter vector [math]\widehat{\weights}[/math] (see \eqref{equ_optimal_weight_closed_form}) is itself a realization of a RV.
The Bias and Variance Decomposition. The prediction accuracy of [math]h^{(\widehat{\weights})}[/math], using the learnt parameter vector \eqref{equ_optimal_weight_closed_form}, depends crucially on the mean squared estimation error (MSEE)
We will next decompose the MSEE [math]\mseesterr[/math] into two components, which are referred to as a variance term and a bias term. The variance term quantifies the random fluctuations or the parameter vector obtained from ERM on the training set \eqref{equ_def_train_set_prob_analysis_generatlization}. The bias term characterizes the systematic (or expected) deviation between the true parameter vector [math]\overline{\weights}[/math] (see \eqref{equ_linear_obs_model}) and the (expectation of the) learnt parameter vector [math]\widehat{\weights}[/math].
Let us start with rewriting \eqref{equ_def_est_err} using elementary manipulations as
We can develop the last expression further by expanding the squared Euclidean norm,
The first component in \eqref{equ_bias_var_decomp} represents the (expected) variance of the learnt parameter vector [math]\widehat{\weights}[/math] \eqref{equ_optimal_weight_closed_form}. Note that, within our probabilistic model, the training set \eqref{equ_def_train_set_prob_analysis_generatlization} is the realization of a RV since it is constituted by data points that are iid realizations of RVs (see \eqref{equ_toy_model_iid} and \eqref{equ_linear_obs_model}).
The second component in \eqref{equ_bias_var_decomp} is referred to as a bias term. The parameter vector [math]\widehat{\weights}[/math] is computed from a randomly fluctuating training set via \eqref{equ_optimal_weight_closed_form} and is therefore itself fluctuating around its expectation [math]\expect \big \{\widehat{\weights}\}[/math]. The bias term is the Euclidean distance between this expectation [math]\expect \big \{\widehat{\weights}\}[/math] and the true parameter vector [math]\overline{\weights}[/math] relating features and label of a data point via \eqref{equ_linear_obs_model}.
The bias term [math]\biasterm^{2}[/math] and the variance [math]\varianceterm[/math] in \eqref{equ_bias_var_decomp} both depend on the model complexity parameter [math]\modelidx[/math] but in a fundamentally different manner. The bias term [math]\biasterm^{2}[/math] typically decreases with increasing [math]\modelidx[/math] while the variance [math]\varianceterm[/math] increases with increasing [math]\modelidx[/math]. In particular, the bias term is given as
The bias term \eqref{equ_def_bias_term} is zero if and only if
The necessary and sufficient condition \eqref{equ_def_zero_bias_weght_elements} for zero bias is equivalent to [math]h^{(\overline{\weights})} \in \hypospace^{(\modelidx)}[/math]. Note that the condition \eqref{equ_def_zero_bias_weght_elements} depends on both, the model parameter [math]\modelidx[/math] and the true parameter vector [math]\overline{\weights}[/math]. While the model parameter [math]\modelidx[/math] is under control, the true parameter vector [math]\overline{\weights}[/math] is not under our control but determined by the underlying data generation process. The only way to ensure \eqref{equ_def_zero_bias_weght_elements} for every possible parameter vector [math]\overline{\weights}[/math] in \eqref{equ_linear_obs_model} is to use [math]\modelidx=\featuredim[/math], i.e., to use all available features [math]\feature_{1},\ldots,\feature_{\featuredim}[/math] of a data point.
When using the model [math]\hypospace^{(\modelidx)}[/math] with [math]\modelidx \lt \featuredim[/math], we cannot guarantee a zero bias term since we have no control over the true underlying parameter vector [math]\overline{\weights}[/math] in \eqref{equ_linear_obs_model}. In general, the bias term decreases with an increasing model size [math]\modelidx[/math] (see Figure fig_bias_variance). We highlight that the bias term does not depend on the variance [math]\sigma^{2}[/math] of the noise [math]\varepsilon[/math] in our toy model \eqref{equ_linear_obs_model}.
Let us now consider the variance term in \eqref{equ_bias_var_decomp}. Using the statistical independence of the features and labels of data points (see \eqref{equ_linear_obs_model}, \eqref{equ_toy_model_iid} and \eqref{equ_labels_training_data}), one can show that [a]
By \eqref{equ_toy_model_iid}, the matrix [math]\left(\big(\featuremtx^{(\modelidx)}\big)^{T} \mX^{(\modelidx)} \right)^{-1}[/math] is a realization of a (matrix-valued) RV with an inverse Wishart distribution [10]. For [math]\samplesize_{\rm t} \gt \modelidx+1[/math], its expectation is given as
By inserting \eqref{equ_expr_expect_inv-wishart} and [math]\mbox{tr} \{ \mathbf{I} \} = \modelidx[/math] into \eqref{equ_variance_term_toy_model},
The variance \eqref{equ_formulae_variance_toy_model} typically increases with increasing model complexity [math]\modelidx[/math] (see Figure fig_bias_variance). In contrast, the bias term \eqref{equ_def_bias_term} decreases with increasing [math]\modelidx[/math].
The opposite dependence of variance and bias on the model complexity results in a bias-variance trade-off. Choosing a model (hypothesis space) with small bias will typically result in large variance and vice versa. In general, the choice of model must balance between a small variance and a small bias.
Generalization.
Consider a linear regression method that learns the linear hypothesis [math]h(\featurevec) = \widehat{\weights}^{T} \featurevec[/math] using the parameter vector \eqref{equ_optimal_weight_closed_form}. The parameter vector [math]\widehat{\weights}^{T}[/math] \eqref{equ_optimal_weight_closed_form} results in a linear hypothesis with minimum training error, i.e., minimum average loss on the training set. However, the ultimate goal of ML is to find a hypothesis that predicts well the label of any data point. In particular, we want the hypothesis [math]h(\featurevec) = \widehat{\weights}^{T} \featurevec[/math] to generalize well to data points outside the training set.
We quantify the generalization capability of [math]h(\featurevec) = \widehat{\weights}^{T} \featurevec[/math] by its expected prediction loss
Note that [math]\error_{\rm pred}[/math] is a measure for the performance of a ML method and not of a specific hypothesis. Indeed, the learnt parameter vector [math]\widehat{\weights}[/math] is not fixed but depends on the data points in the training set. These data points are modelled as realizations of iid RVs and, in turn, the learnt parameter vector [math]\widehat{\weights}[/math] becomes a realization of a RV. Thus, in some sense, the expected prediction loss \eqref{equ_def_expected_pred_loss} characterizes the overall ML method that reads in a training set and delivers (learn) a linear hypothesis with parameter vector [math]\widehat{\weights}[/math] \eqref{equ_optimal_weight_closed_form}. In contrast, the risk introduced in Chapter Empirical Risk Minimization characterizes the performance of a specific (fixed) hypothesis [math]h[/math] without taking into account a learning process that delivered [math]h[/math] based on data.
Let us now relate the expected prediction loss \eqref{equ_def_expected_pred_loss} of the linear hypothesis [math]h(\featurevec) = \widehat{\weights}^{T} \featurevec[/math] to the bias and variance of \eqref{equ_optimal_weight_closed_form},
Here, step (a) uses the law of iterated expectation (see, e.g., [7]). Step (b) uses that the feature vector [math]\featurevec[/math] of a “new” data point is a realization of a RV which is statistically independent of the data points in the training set [math]\trainset[/math]. We also used our assumption that [math]\featurevec[/math] is the realization of a RV with zero mean and covariance matrix [math]\expect \{ \featurevec \featurevec^{T}\}=\mathbf{I}[/math] (see \eqref{equ_toy_model_iid}).
According to \eqref{equ_decomp_E_pred_toy_model}, the average (expected) prediction error [math]\error_{\rm pred}[/math] is the sum of three components: (i) the bias [math]\biasterm^{2}[/math], (ii) the variance [math]\varianceterm[/math] and (iii) the noise variance [math]\sigma^{2}[/math]. Figure fig_bias_variance illustrates the typical dependency of the bias and variance on the model \eqref{equ_generalization_hypospace_r}, which is parametrized by the model complexity [math]\modelidx[/math]. Note that the model complexity parameter [math]\modelidx[/math] in \eqref{equ_generalization_hypospace_r} coincides with the effective model dimension [math]\effdim{\hypospace^{(\modelidx)}}[/math] (see Section The Model ).
The bias and variance, whose sum is the estimation error [math]\error_{\rm est}[/math], can be influenced by varying the model complexity [math]\modelidx[/math] which is a design parameter. The noise variance [math]\sigma^{2}[/math] is the intrinsic accuracy limit of our toy model \eqref{equ_linear_obs_model} and is not under the control of the ML engineer. It is impossible for any ML method (no matter how computationally expensive) to achieve, on average, a prediction error smaller than the noise variance [math]\sigma^{2}[/math]. Carefully note that this statement only applies if the data points arising in a ML application can be (reasonably well) modelled as realizations of iid RVs.
We highlight that our statistical analysis, resulting the formulas for bias \eqref{equ_def_bias_term}, variance \eqref{equ_formulae_variance_toy_model} and the average prediction error \eqref{equ_decomp_E_pred_toy_model}, applies only if the observed data points can be well modelled using the probabilistic model specified by \eqref{equ_linear_obs_model}, \eqref{equ_toy_model_iid} and \eqref{equ_labels_training_data}. The validity of this probabilistic model can to be verified by principled statistical model validation techniques [11][12]. Section The Bootstrap discusses a fundamentally different approach to analyzing the statistical properties of a ML method. Instead of a probabilistic model, this approach uses random sampling techniques to synthesize iid copies of given (small) data points. We can approximate the expectation of some relevant quantity, such as the loss [math]\loss{\big(\featurevec,\truelabel \big) }{h}[/math], using an average over synthetic data [4].
The qualitative behaviour of estimation error in Figure fig_bias_variance depends on the definition for the model complexity. Our concept of effective dimension (see Section The Model ) coincides with most other notions of model complexity for the linear hypothesis space \eqref{equ_generalization_hypospace_r}. However, for more complicated models such as deep nets it is often not obvious how effective dimension is related to more tangible quantities such as total number of tunable weights or the number of artificial neurons. Indeed, the effective dimension might also depend on the specific learning algorithm such as stochastic gradient descent (SGD). Therefore, for deep nets, if we would plot estimation error against number of tunable weights we might observe a behaviour of estimation error fundamentally different from the shape in Figure fig_bias_variance. One example for such un-intuitive behaviour is known as “double descent phenomena” [13].
The Bootstrap
basic idea of bootstrap: use histogram of dataset as the underlying probability distribution; generate new data points by random sampling (with replacement) from that distribution.
Consider learning a hypothesis [math]\hat{h} \in \hypospace[/math] by minimizing the average loss incurred on a dataset [math]\dataset=\{ \big(\featurevec^{(1)},\truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big)\}[/math]. The data points [math]\big(\featurevec^{(\sampleidx))},\truelabel^{(\sampleidx)}\big)[/math] are modelled as realizations of iid RVs. Let use denote the (common) probability distribution of these RVs by [math]p(\featurevec,\truelabel)[/math].
If we interpret the data points [math]\big(\featurevec^{(\sampleidx))},\truelabel^{(\sampleidx)}\big)[/math] as realizations of RVs, also the learnt hypothesis [math]\hat{h}[/math] is a realization of a RV. Indeed, the hypothesis [math]\hat{h}[/math] is obtained by solving an optimization problem that involves realizations of RVs. The bootstrap is a method for estimating (parameters of) the probability distribution [math]p(\hat{h})[/math] [4].
Section A Probabilistic Analysis of Generalization used a probabilistic model for data points to derive (the parameters of) the probability distribution [math]p(\hat{h})[/math]. Note that the analysis in Section A Probabilistic Analysis of Generalization only applies to the specific probabilistic model \eqref{equ_toy_model_iid}, \eqref{equ_labels_training_data}. In contrast, the bootstrap can be used for data points drawn from an arbitrary probability distribution.
The core idea behind the bootstrap is to use the histogram [math]\hat{p}(\datapoint)[/math] of the data points in [math]\dataset[/math] to generate [math]\nrbootstraps[/math] new datasets [math]\dataset^{(1)},\ldots,\dataset^{(\nrbootstraps)}[/math]. Each dataset is constructed such that is has the same size as the original dataset [math]\dataset[/math]. For each dataset [math]\dataset^{(\bootstrapidx)}[/math], we solve a separate ERM to obtain the hypothesis [math]\hat{h}^{(\bootstrapidx)}[/math]. The hypothesis [math]\hat{h}^{(\bootstrapidx)}[/math] is a realization of a RV whose distribution is determined by the histogram [math]\hat{p}(\datapoint)[/math] as well as the hypothesis space and the loss function used in the ERM.
Diagnosing ML
diagnose ML methods by comparing training error with validation error and (if available) some baseline; baseline can be obtained via the Bayes risk when using a probabilistic model (such as the i.i.d. assumption) or human performance or the performance of existing ML methods ("experts" in regret framework)
In what follows, we tacitly assume that data points can (to a good approximation) be interpreted as realizations of iid RVs (see Section Probabilistic Models for Data ). This “i.i.d. assumption” underlies ERM as the guiding principle for learning a hypothesis with small risk. This assumption also motivates to use the average loss \eqref{equ_def_training_val_val} on a validation set as an estimate for the risk. More fundamentally, we need the i.i.d. assumption to define the concept of risk as a measure for how well a hypothesis predicts the labels of arbitrary data points.
Consider a ML method which uses Algorithm alg:validated_ERM (or Algorithm alg:kfoldCV_ERM) to learn and validate the hypothesis [math]\hat{h} \in \hypospace[/math]. Besides the learnt hypothesis
[math]\hat{h}[/math], these algorithms also deliver the training error [math]\trainerror[/math] and the validation error [math]\valerror[/math]. As we will see shortly, we can diagnose ML methods to some extent just by comparing training with validation errors. This diagnosis is further enabled if we know a baseline [math]\benchmarkerror[/math] .
One important source of a baseline [math]\benchmarkerror[/math] are probabilistic models for the data points (see Section A Probabilistic Analysis of Generalization ). Given a probabilistic model, which specifies the probability distribution [math]p(\featurevec,\truelabel)[/math] of the features and label of data points, we can compute the minimum achievable risk. Indeed, the minimum achievable risk is precisely the expected loss of the Bayes estimator [math]\hat{h}(\featurevec)[/math] of the label [math]\truelabel[/math], given the features [math]\featurevec[/math] of a data point. The Bayes estimator
[math]\hat{h}(\featurevec)[/math] is fully determined by the probability distribution [math]p(\featurevec,\truelabel)[/math] of the features and label of a (random) data point [14](Chapter 4).
A further potential source for a baseline [math]\benchmarkerror[/math] is an existing, but for some reason unsuitable, ML method. This existing ML method might be computationally too expensive to be used for the ML application at end. However, we might still use its statistical properties as a benchmark. The We might also use the performance of human experts as a baseline. If we want to develop a ML method that detects certain type of skin cancers from images of the skin, a benchmark might be the current classification accuracy achieved by experienced dermatologists [15].
We can diagnose a ML method by comparing the training error [math]\trainerror[/math] with the validation error [math]\valerror[/math] and (if available) the benchmark [math]\benchmarkerror[/math].
- [math]\trainerror \approx \valerror \approx \benchmarkerror[/math]: The training error is on the same level as the validation error and the benchmark error. There is not much to improve here since the validation error is already on the desired error level. Moreover, the training error is not much smaller than the validation error which indicates that there is no overfitting. It seems we have obtained a ML method that achieves the benchmark error level.
- [math]\valerror \gg \trainerror[/math]: The validation error is significantly larger than the training error. It seems that the ERM results in a hypothesis [math]\hat{h}[/math] that overfits the training set. The loss incurred by [math]\hat{h}[/math] on data points outside the training set, such as those in the validation set, is significantly worse. This is an indicator for overfitting which can be addressed either by reducing the effective dimension of the hypothesis space or by increasing the size of the training set. To reduce the effective dimension of the hypothesis space we have different options depending on the used model. We might use a small number of features in a linear model, a smaller maximum depth of decision trees (Section Decision Trees ) or a fewer layers in an ANN (Section Deep Learning ). One very elegant means for reducing the effective dimension of a hypothesis space is by limiting the number of gradient descent (GD) steps used in gradient-based methods. This optimization based shrinking of a hypothesis space is referred to as early stopping. More generally, we can reduce the effective dimension of a hypothesis space via regularization techniques (see Chapter Regularization ).
- [math]\trainerror \approx \valerror\gg \benchmarkerror[/math]: The training error is on the same level as the validation errorand both are significantly larger than the baseline. Since the training error is not much smaller than the validation error, the learnt hypothesis seems to not overfit the training set. However, the training error achieved by the learnt hypothesis is significantly larger than the benchmark error level. There can be several reasons for this to happen. First, it might be that the hypothesis space used by the ML method is too small, i.e., it does not include a hypothesis that provides a good approximation for the relation between features and label of a data point. The remedy for this situation is to use a larger hypothesis space, e.g., by including more features in a linear model, using higher polynomial degrees in polynomial regression, using deeper decision trees or having larger ANNs (deep ANN (deep net)s). Another reason for the training error being too large is that the optimization algorithm used to solve ERM is not working properly. When using gradient-based methods (see Section GD for Linear Regression ) to solve ERM, one reason for [math]\trainerror \gg \benchmarkerror[/math] could be that the learning rate [math]\lrate[/math] in the GD step is chosen too small or too large (see Figure fig_small_large_lrate-(b)). This can be solved by adjusting the learning rate by trying out several different values and using the one resulting in the smallest training error. Another option is derive optimal values for the learning rate based on a probabilistic model for how the data points are generated. One example for such a probabilistic model is the i.i.d. assumption that has been used in Section A Probabilistic Analysis of Generalization to analyze linear regression methods.
- [math]\trainerror \gg \valerror [/math]: The training error is significantly larger than the validation error (see Exercise). The idea of ERM is to approximate the risk of a hypothesis by its average loss on a training set [math]\dataset = \{ (\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}[/math].The mathematical underpinning for this approximation is the law of large numbers which characterizes the average of (realizations of) iid RVs. The quality and usefulness of this approximation depends on the validity of two conditions. First, the data points used for computing the average loss should be such that they would be typically obtained as realizations of iid RVs with a common probability distribution. Second, the number of data points used for computing the average loss must be sufficiently large. Whenever the data points behave different than the the realizations of iid RVs or if the size of the training set or validation set is too small, the interpretation (comparison) of training error and validation errors becomes more difficult. As an extreme case, it might then be that the validation error consists of data points for which every hypothesis incurs small average loss. Here, we might try to increase the size of the validation set by collecting more labeled data points or by using data augmentation (see Section Data Augmentation ). If the size of training set and validation set are large but we still obtain [math]\trainerror \gg \valerror [/math], one should verify if data points in these sets conform to the i.i.d. assumption. There are principled statistical methods that allow to test if an i.i.d. assumption is satisfied (see [9] and references therein).
Notes
General References

Jung, Alexander (2022). Machine Learning: The Basics. Signapore: Springer. doi:10.1007/978-981-16-8193-6.
Jung, Alexander (2022). "Machine Learning: The Basics". arXiv:1805.05052.
References
- R. Muirhead. Aspects of Multivariate Statistical Theory John Wiley \& Sons Inc., 1982
- J. Larsen and C. Goutte. On optimal data split for generalization estimation and model selection. In IEEE Workshop on Neural Networks for Signal Process 1999
- B. Efron and R. Tibshirani. Improvements on cross-validation: The 632+ bootstrap method. Journal of the American Statistical Association 92(438):548--560, 1997
- Jump up to: 4.0 4.1 4.2 T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning Springer Series in Statistics. Springer, New York, NY, USA, 2001
- I. Cohen and B. Berdugo. Noise estimation by minima controlled recursive averaging for robust speech enhancement. IEEE Sig. Proc. Lett. 9(1):12--15, Jan. 2002
- P. Huber. Approximate models. In C. Huber-Carol, N. Balakrishnan, M. Nikulin, and M. Mesbah, editors, Goodness-of-Fit Tests and Model Validity. Statistics for Industry and Technology. Birkhäuser, Boston, MA, 2002
- Jump up to: 7.0 7.1 7.2 D. Bertsekas and J. Tsitsiklis. Introduction to Probability Athena Scientific, 2 edition, 2008
- R. G. Gallager. Stochastic Processes: Theory for Applications Cambridge University Press, 2013
- Jump up to: 9.0 9.1 H. Lütkepohl. New Introduction to Multiple Time Series Analysis Springer, New York, 2005
- K. V. Mardia, J. T. Kent, and J. M. Bibby. Multivariate Analysis Academic Press, 1979
- K. Young. Bayesian diagnostics for checking assumptions of normality. Journal of Statistical Computation and Simulation 47(3--4):167 -- 180, 1993
- O. Vasicek. A test for normality based on sample entropy. Journal of the Royal Statistical Society. Series B (Methodological) 38(1):54--59, 1976
- M. Belkin, D. Hsu, S. Ma, and S. Mandal. Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proceedings of the National Academy of Sciences 116(32):15849--15854, 2019
- E. L. Lehmann and G. Casella. Theory of Point Estimation Springer, New York, 2nd edition, 1998
- A. Esteva, B. Kuprel, R. A. Novoa, J. Ko, S. M. Swetter, H. M. Blau, and S. Thrun. Dermatologist-level classification of skin cancer with deep neural networks. Nature 542, 2017