guide:E4fd10ce73: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 12: | Line 12: | ||
===Average Value=== | ===Average Value=== | ||
A die is rolled. If an odd number turns up, we win an amount equal to this number; | A die is rolled. If an odd number turns up, we win an amount equal to this number; if an even number turns up, we lose an amount equal to this number. For example, if a two turns up we lose 2, and if a three comes up we win 3. We want to decide if this is a reasonable game to play. We first try simulation. The program ''' Die''' carries out this simulation. | ||
if an even number turns up, we lose an amount equal to this number. For example, if | |||
a two turns up we lose 2, and if a three comes up we win 3. We want to decide if | |||
this is a reasonable game to play. We first try simulation. The program ''' Die''' carries out this simulation. | |||
The program prints the frequency and the relative frequency with which each outcome occurs. It also calculates the average winnings. We have run the program twice. The results are shown in [[#table 6.1 |Table]]. | |||
The program prints the frequency and the relative frequency with which each outcome | |||
occurs. It also calculates the average winnings. We have run the program twice. The results are | |||
shown in [[#table 6.1 |Table]]. | |||
<span id="table 6.1"/> | <span id="table 6.1"/> | ||
{| class="table text-center" | |||
|+ Frequencies for dice game. | |||
! | |||
! colspan="2" |n = 100 | |||
! colspan="2" |n = 10000 | |||
|- | |||
| Winning || Frequency || Relative Frequency || Frequency || Relative Frequency | |||
|- | |||
| 1 || 17 || .17 || 1681 || .1681 | |||
|- | |||
| -2 || 17|| .17 || 1678 || .1678 | |||
|- | |||
| 3 || 16 || 0.16 || 1626 || .1626 | |||
|- | |||
| -4 || 18 ||.18 ||1696 || .1696 | |||
|- | |||
| 5 || 16 || .16 || 1686 || .1686 | |||
|- | |||
| -6 || 16 || .16 || 1633 || .1633 | |||
|} | |||
In the first run we have played the game 100 times. In this run our average gain is <math>-.57</math>. It looks as if the game is unfavorable, and we wonder how unfavorable it really is. To get a better idea, we have played the game 10,00 times. In this case our average gain is <math>-.4949</math>. | |||
We note that the relative frequency of each of the six possible outcomes is quite | We note that the relative frequency of each of the six possible outcomes is quite close to the probability 1/6 for this outcome. This corresponds to our frequency interpretation of probability. It also suggests that for very large numbers of plays, our average gain should be | ||
close to the probability 1/6 for this outcome. This corresponds to our frequency | |||
interpretation of probability. It also suggests that for very large numbers of | |||
plays, our average gain should be | |||
<math display="block"> | <math display="block"> | ||
| Line 59: | Line 50: | ||
\end{eqnarray*} | \end{eqnarray*} | ||
</math> | </math> | ||
This agrees quite well with our average gain for 10,00 plays. | |||
We note that the value we have chosen for the average gain is obtained by taking the | This agrees quite well with our average gain for 10,00 plays. We note that the value we have chosen for the average gain is obtained by taking the | ||
possible outcomes, multiplying by the probability, and adding the results. This | possible outcomes, multiplying by the probability, and adding the results. This suggests the following definition for the expected outcome of an experiment. | ||
suggests the following definition for the expected outcome of an experiment. | |||
===Expected Value=== | ===Expected Value=== | ||
| Line 245: | Line 235: | ||
|+ Tossing a coin three times. | |+ Tossing a coin three times. | ||
|- | |- | ||
!X !! Y | |||
|- | |- | ||
|HHH || 1 | |HHH || 1 | ||
| Line 718: | Line 708: | ||
</div> | </div> | ||
It is interesting to note that the more romantic option (c) is less favorable than option (a) (see Exercise | It is interesting to note that the more romantic option (c) is less favorable than option (a) (see [[exercise:D4dd17835d|Exercise]]). | ||
If you bet 1~dollar on the number 17, then the distribution function for your winnings <math>X</math> is | If you bet 1~dollar on the number 17, then the distribution function for your winnings <math>X</math> is | ||
| Line 746: | Line 736: | ||
theorem.}} | theorem.}} | ||
{{proofcard|Theorem|thm_6.5|Let <math>X</math> be a random variable with sample space | {{proofcard|Theorem|thm_6.5|Let <math>X</math> be a random variable with sample space | ||
<math>\Omega</math>. If <math>F_1</math>, <math>F_2 | <math>\Omega</math>. If <math>F_1</math>, <math>F_2, \ldots, F_r</math> are events such that <math>F_i \cap F_j = | ||
\emptyset</math> for <math>i \ne j</math> and <math>\Omega = \cup_j F_j</math>, then | \emptyset</math> for <math>i \ne j</math> and <math>\Omega = \cup_j F_j</math>, then | ||
| Line 872: | Line 862: | ||
Pascal first observed that if each player has only one game to win, then the stake of 64 pistoles should be divided evenly. Then he considered the case where one player has won two games and the other one. | Pascal first observed that if each player has only one game to win, then the stake of 64 pistoles should be divided evenly. Then he considered the case where one player has won two games and the other one. | ||
<blockquote> Then consider, Sir, if the first man wins, he gets 64 pistoles, if he | <blockquote> Then consider, Sir, if the first man wins, he gets 64 pistoles, if he loses he gets 32. Thus if they do not wish to risk this last game, but wish to | ||
loses he gets 32. Thus if they do not wish to risk this last game, but wish to | separate without playing it, the first man must say: “I am certain to get 32 pistoles, even if I lose I still get them; but as for the other 32 pistoles, | ||
separate without playing it, the first man must say: “I am certain to get | perhaps I will get them, perhaps you will get them, the chances are equal. Let us then divide these 32 pistoles in half and give one half to me as well as my 32 which are mine for sure.” He will then have 48 pistoles and the other 16.<ref group="Notes" >Quoted in F. N. David, ''Games, Gods and Gambling'' (London: Griffin, 1962), p. 231.</ref> | ||
32 pistoles, even if I lose I still get them; but as for the other 32 pistoles, | |||
perhaps I will get them, perhaps you will get them, the chances are equal. Let us | |||
then divide these 32 pistoles in half and give one half to me as well as my 32 which | |||
are mine for sure.” He will then have 48 pistoles and the other 16.<ref group="Notes" >Quoted | |||
in F. N. David, ''Games, Gods and Gambling'' (London: Griffin, 1962), p. 231.</ref> | |||
</blockquote> | </blockquote> | ||
| Line 886: | Line 871: | ||
certain symmetric situations and uses this to deduce the expected for the general situation. | certain symmetric situations and uses this to deduce the expected for the general situation. | ||
He does this in steps. His first proposition is | He does this in steps. His first proposition is | ||
<blockquote> Prop. I. If I expect <math>a</math> or <math>b</math>, either of which, with equal | <blockquote> Prop. I. If I expect <math>a</math> or <math>b</math>, either of which, with equal probability, may fall to me, then my Expectation is worth <math>(a + b)/2</math>, that is, the half Sum of <math>a</math> and <math>b</math>.<ref group="Notes" >C. Huygens, ''Calculating in Games of Chance,'' translation attributed to John Arbuthnot (London, 1692), p. 34.</ref> | ||
probability, may fall to me, then my Expectation is worth <math>(a + b)/2</math>, that is, the | |||
half Sum of | |||
<math>a</math> and <math>b</math>.<ref group="Notes" >C. Huygens, ''Calculating in Games of Chance,'' translation | |||
attributed to John Arbuthnot (London, 1692), p. 34.</ref> | |||
</blockquote> | </blockquote> | ||
Huygens proved this as follows: Assume that two player A and B play a game in which | Huygens proved this as follows: Assume that two player A and B play a game in which | ||
| Line 907: | Line 888: | ||
loser 3 --- a game in which the value is obviously 5. | loser 3 --- a game in which the value is obviously 5. | ||
Huygens' second proposition is | Huygens' second proposition is | ||
<blockquote> Prop. II. If I expect <math>a</math>, <math>b</math>, or <math>c</math>, either of which, with equal | <blockquote> Prop. II. If I expect <math>a</math>, <math>b</math>, or <math>c</math>, either of which, with equal facility, may happen, then the Value of my Expectation is <math>(a + b + c)/3</math>, or the third of the Sum of <math>a</math>, <math>b</math>, and <math>c</math>.<ref group="Notes" >ibid., p. 35.</ref> | ||
facility, may happen, then the Value of my Expectation is <math>(a + b + c)/3</math>, or the | |||
third of the Sum of <math>a</math>, <math>b</math>, and <math>c</math>.<ref group="Notes" >ibid., p. 35.</ref> | |||
</blockquote> | </blockquote> | ||
His argument here is similar. Three players, A, B, and C, each stake | His argument here is similar. Three players, A, B, and C, each stake | ||
| Line 1,004: | Line 983: | ||
<span id="table 6.4"/> | <span id="table 6.4"/> | ||
{| class="table" | |||
|+Payoffs. | |||
! !! God does not exist !! God exists | |||
|- | |||
| || <math>p</math> || <math>1 - p</math> | |||
|- | |||
| believe || <math>-u</math> || <math>v </math> | |||
|- | |||
| not believe || 0 || <math>-x</math> | |||
|} | |||
</ | |||
Here <math>-u</math> represents the cost to you of passing up some worldly pleasures as a consequence of believing that God exists. If you do not believe, and God is a vengeful God, you will lose <math>x</math>. If God exists and you do believe you will gain v. Now to determine which strategy is best you should compare the two expected values | Here <math>-u</math> represents the cost to you of passing up some worldly pleasures as a consequence of believing that God exists. If you do not believe, and God is a vengeful God, you will lose <math>x</math>. If God exists and you do believe you will gain v. Now to determine which strategy is best you should compare the two expected values | ||
| Line 1,045: | Line 1,016: | ||
|+ Graunt's mortality data. | |+ Graunt's mortality data. | ||
|- | |- | ||
!Age !! Survivors | |||
|- | |- | ||
|0 || 100 | |0 || 100 | ||
| Line 1,067: | Line 1,036: | ||
|76 || 1 | |76 || 1 | ||
|} | |} | ||
As Hacking observes, Graunt apparently constructed this table by assuming that after | |||
the age of 6 there is a constant probability of about 5/8 of surviving for another | As Hacking observes, Graunt apparently constructed this table by assuming that after the age of 6 there is a constant probability of about 5/8 of surviving for another decade.<ref group="Notes" >ibid., p. 109.</ref> For example, of the 64 people who survive to age 6, | ||
decade.<ref group="Notes" >ibid., p. 109.</ref> For example, of the 64 people who survive to age 6, | |||
5/8 of 64 or 40 survive to 16, 5/8 of these 40 or 25 survive to 26, and so forth. Of | 5/8 of 64 or 40 survive to 16, 5/8 of these 40 or 25 survive to 26, and so forth. Of | ||
course, he rounded off his figures to the nearest whole person. | course, he rounded off his figures to the nearest whole person. | ||
Latest revision as of 03:33, 16 June 2024
When a large collection of numbers is assembled, as in a census, we are usually interested not in the individual numbers, but rather in certain descriptive quantities such as the average or the median. In general, the same is true for the probability distribution of a numerically-valued random variable. In this and in the next section, we shall discuss two such descriptive quantities: the expected value and the variance. Both of these quantities apply only to numerically-valued random variables, and so we assume, in these sections, that all random variables have numerical values. To give some intuitive justification for our definition, we consider the following game.
Average Value
A die is rolled. If an odd number turns up, we win an amount equal to this number; if an even number turns up, we lose an amount equal to this number. For example, if a two turns up we lose 2, and if a three comes up we win 3. We want to decide if this is a reasonable game to play. We first try simulation. The program Die carries out this simulation.
The program prints the frequency and the relative frequency with which each outcome occurs. It also calculates the average winnings. We have run the program twice. The results are shown in Table.
| n = 100 | n = 10000 | |||
|---|---|---|---|---|
| Winning | Frequency | Relative Frequency | Frequency | Relative Frequency |
| 1 | 17 | .17 | 1681 | .1681 |
| -2 | 17 | .17 | 1678 | .1678 |
| 3 | 16 | 0.16 | 1626 | .1626 |
| -4 | 18 | .18 | 1696 | .1696 |
| 5 | 16 | .16 | 1686 | .1686 |
| -6 | 16 | .16 | 1633 | .1633 |
In the first run we have played the game 100 times. In this run our average gain is [math]-.57[/math]. It looks as if the game is unfavorable, and we wonder how unfavorable it really is. To get a better idea, we have played the game 10,00 times. In this case our average gain is [math]-.4949[/math].
We note that the relative frequency of each of the six possible outcomes is quite close to the probability 1/6 for this outcome. This corresponds to our frequency interpretation of probability. It also suggests that for very large numbers of plays, our average gain should be
This agrees quite well with our average gain for 10,00 plays. We note that the value we have chosen for the average gain is obtained by taking the possible outcomes, multiplying by the probability, and adding the results. This suggests the following definition for the expected outcome of an experiment.
Expected Value
Let [math]X[/math] be a numerically-valued discrete random variable with sample space [math]\Omega[/math] and distribution function [math]m(x)[/math]. The expected value [math]E(X)[/math] is defined by
Example Let an experiment consist of tossing a fair coin three times. Let [math]X[/math] denote the number of heads which appear. Then the possible values of [math]X[/math] are [math]0, 1, 2[/math] and [math]3[/math]. The corresponding probabilities are [math]1/8, 3/8, 3/8,[/math] and [math]1/8[/math]. Thus, the expected value of [math]X[/math] equals
Later in this section we shall see a quicker way to compute this expected value, based on the fact that [math]X[/math] can be written as a sum of simpler random variables.
Example Suppose that we toss a fair coin until a head first comes up, and let [math]X[/math] represent the number of tosses which were made. Then the possible values of [math]X[/math] are [math]1, 2, \ldots[/math], and the distribution function of [math]X[/math] is defined by
(This is just the geometric distribution with parameter [math]1/2[/math].) Thus, we have
Example (Example continued) Suppose that we flip a coin until a head first appears, and if the number of tosses equals
[math]n[/math], then we are paid [math]2^n[/math] dollars. What is the expected value of the payment?
We let [math]Y[/math] represent the payment. Then,
for [math]n \ge 1[/math]. Thus,
which is a divergent sum. Thus, [math]Y[/math] has no expectation. This example is called the St. Petersburg Paradox.
The fact that the above sum is infinite suggests that a player should be willing to pay any fixed amount per game for the privilege of playing this game. The reader is asked to consider how much he or she would be willing to pay for this privilege. It is unlikely that the reader's answer is more than 10 dollars; therein lies the paradox.
In the early history of probability, various mathematicians gave ways to resolve
this paradox. One idea (due to G. Cramer) consists of assuming that the amount
of money in the world is finite. He thus assumes that there is some fixed value of [math]n[/math] such
that if the number of tosses equals or exceeds [math]n[/math], the payment is [math]2^n[/math] dollars.
The reader is asked to show in Exercise that the expected value of
the payment is now finite.
Daniel Bernoulli and Cramer also considered another way to
assign value to the payment. Their idea was that the value of a payment is some function of the
payment; such a function is now called a utility function. Examples of
reasonable utility functions might include the square-root function or the logarithm function. In
both cases, the value of [math]2n[/math] dollars is less than twice the value of [math]n[/math] dollars. It can
easily be shown that in both cases, the expected utility of the payment is finite (see Exercise).
Example Let [math]T[/math] be the time for the first success in a Bernoulli trials process. Then we take as sample space [math]\Omega[/math] the integers [math]1,~2,~\ldots\ [/math] and assign the geometric distribution
Thus,
Now if [math]|x| \lt 1[/math], then
Differentiating this formula, we get
so
In particular, we see that if we toss a fair coin a sequence of times, the expected time until the first heads is 1/(1/2) = 2. If we roll a die a sequence of times, the expected number of rolls until the first six is 1/(1/6) = 6.
Interpretation of Expected Value
In statistics, one is frequently concerned with the average value of a set of data. The following example shows that the ideas of average value and expected value are very closely related.
Example The heights, in inches, of the women on the Swarthmore basketball team are 5' 9”, 5' 9”, 5' 6”, 5' 8”, 5' 11”, 5' 5”, 5' 7”, 5' 6”, 5' 6”, 5' 7”, 5' 10”, and 6' 0”.
A statistician would compute the average height (in inches) as follows:
One can also interpret this number as the expected value of a random variable. To see this, let an experiment consist of choosing one of the women at random, and let [math]X[/math] denote her height. Then the expected value of [math]X[/math] equals 67.9.
Of course, just as with the frequency interpretation of probability, to interpret expected value as an average outcome requires further justification. We know that for any finite experiment the average of the outcomes is not predictable. However, we shall eventually prove that the average will usually be close to [math]E(X)[/math] if we repeat the experiment a large number of times. We first need to develop some properties of the expected value. Using these properties, and those of the concept of the variance to be introduced in the next section, we shall be able to prove the Law of Large Numbers. This theorem will justify mathematically both our frequency concept of probability and the interpretation of expected value as the average value to be expected in a large number of experiments.
Expectation of a Function of a Random Variable
Suppose that [math]X[/math] is a discrete random variable with sample space [math]\Omega[/math], and [math]\phi(x)[/math] is a real-valued function with domain [math]\Omega[/math]. Then [math]\phi(X)[/math] is a real-valued random variable. One way to determine the expected value of [math]\phi(X)[/math] is to first determine the distribution function of this random variable, and then use the definition of expectation. However, there is a better way to compute the expected value of [math]\phi(X)[/math], as demonstrated in the next example.
Example Suppose a coin is tossed 9 times, with the result
The first set of three heads is called a run. There are three more runs in this sequence, namely the next four tails, the next head, and the next tail. We do not consider the first two tosses to constitute a run, since the third toss has the same value as the first two.
Now suppose an experiment consists of tossing a fair coin three times. Find the
expected number of runs. It will be helpful to think of two random variables, [math]X[/math]
and [math]Y[/math], associated with this experiment. We let [math]X[/math] denote the sequence of heads
and tails that results when the experiment is performed, and [math]Y[/math] denote the number of
runs in the outcome
[math]X[/math]. The possible outcomes of [math]X[/math] and the corresponding values of [math]Y[/math] are
shown in Table.
| X | Y |
|---|---|
| HHH | 1 |
| HHT | 2 |
| HTH | 3 |
| HTT | 2 |
| THH | 2 |
| THT | 3 |
| TTH | 2 |
| TTT | 1 |
To calculate [math]E(Y)[/math] using the definition of expectation, we first must find the distribution function [math]m(y)[/math] of [math]Y[/math] i.e., we group together those values of [math]X[/math] with a common value of [math]Y[/math] and add their probabilities. In this case, we calculate that the distribution function of [math]Y[/math] is: [math]m(1) = 1/4,\ m(2) = 1/2,[/math] and [math]m(3) = 1/4[/math]. One easily finds that [math]E(Y) = 2[/math].
Now suppose we didn't group the values of [math]X[/math] with a common [math]Y[/math]-value, but
instead, for each
[math]X[/math]-value [math]x[/math], we multiply the probability of [math]x[/math] and the corresponding value of [math]Y[/math],
and add the results. We obtain
which equals 2.
This illustrates the following general principle. If [math]X[/math] and [math]Y[/math] are two random
variables, and [math]Y[/math] can be written as a function of [math]X[/math], then one can compute the
expected value of [math]Y[/math] using the distribution function of [math]X[/math].
If [math]X[/math] is a discrete random variable with sample space [math]\Omega[/math] and distribution function [math]m(x)[/math], and if [math]\phi : \Omega \to \mat{\rm R}[/math] is a function, then
The proof of this theorem is straightforward, involving nothing more than grouping values of [math]X[/math] with a common [math]Y[/math]-value, as in Example.
The Sum of Two Random Variables
Many important results in probability theory concern sums of random variables. We first consider what it means to add two random variables.
Example Let [math]Y[/math] be the number of fixed points in a random coin comes up heads and 0 if the coin comes up tails. Then, we roll a die and let [math]Y[/math] denote the face that comes up. What does [math]X+Y[/math] mean, and what is its distribution? This question is easily answered in this case, by considering, as we did in Chapter Conditional Probability, the joint random variable [math]Z = (X,Y)[/math], whose outcomes are ordered pairs of the form [math](x, y)[/math], where [math]0 \le x \le 1[/math] and [math]1 \le y \le 6[/math]. The description of the experiment makes it reasonable to assume that [math]X[/math] and [math]Y[/math] are independent, so the distribution function of [math]Z[/math] is uniform, with [math]1/12[/math] assigned to each outcome. Now it is an easy matter to find the set of outcomes of [math]X+Y[/math], and its distribution function.
In Example, the random variable [math]X[/math] denoted the number of heads which occur when a fair coin is tossed three times. It is natural to think of [math]X[/math] as the sum of the random variables [math]X_1, X_2, X_3[/math], where [math]X_i[/math] is defined to be 1 if the [math]i[/math]th toss comes up heads, and 0 if the [math]i[/math]th toss comes up tails. The expected values of the [math]X_i[/math]'s are extremely easy to compute. It turns out that the expected value of [math]X[/math] can be obtained by simply adding the expected values of the [math]X_i[/math]'s. This fact is stated in the following theorem.
Let [math]X[/math] and [math]Y[/math] be random variables with finite expected values. Then
Let the sample spaces of [math]X[/math] and [math]Y[/math] be denoted by [math]\Omega_X[/math] and [math]\Omega_Y[/math], and suppose that
It is easy to prove by mathematical induction that the expected value of the sum of any finite number of random variables is the sum of the expected values of the individual random variables.
It is important to note that mutual independence of the summands was not needed
as a hypothesis in the Theorem and its generalization. The fact that expectations add, whether or not the summands are mutually independent, is sometimes referred to as the First Fundamental Mystery of Probability.
Example Let [math]Y[/math] be the number of fixed points in a random permutation of the set [math]\{a,b,c\}[/math]. To find the expected value of [math]Y[/math], it is helpful to consider the basic random variable associated with this experiment, namely the random variable [math]X[/math] which represents the random permutation. There are six possible outcomes of [math]X[/math], and we assign to each of them the probability [math]1/6[/math] see Table. Then we can calculate [math]E(Y)[/math] using Theorem, as
| [math]X[/math] | [math]Y[/math] | |
| [math]a\;\;\;b\;\;\; c[/math] | 3 | |
| [math]a\;\;\; c\;\;\; b[/math] | 1 | |
| [math]b\;\;\; a\;\;\; c[/math] | 1 | |
| [math]b\;\;\; c\;\;\; a[/math] | 0 | |
| [math]c\;\;\;a\;\;\; b[/math] | 0 | |
| [math]c\;\;\; b\;\;\; a[/math] | 1 |
We now give a very quick way to calculate the average number of fixed points in
a random permutation of the set [math]\{1, 2, 3, \ldots, n\}[/math]. Let [math]Z[/math] denote the random
permutation. For each [math]i[/math], [math]1 \le i \le n[/math], let [math]X_i[/math] equal 1 if [math]Z[/math] fixes [math]i[/math], and
0 otherwise. So if we let [math]F[/math] denote the number of fixed points in [math]Z[/math], then
Bernoulli Trials
Let [math]S_n[/math] be the number of successes in [math]n[/math] Bernoulli trials with probability [math]p[/math] for success on each trial. Then the expected number of successes is [math]np[/math]. That is,
Let [math]X_j[/math] be a random variable which has the value 1 if the [math]j[/math]th outcome is a success and 0 if it is a failure. Then, for each [math]X_j[/math],
Poisson Distribution
Recall that the Poisson distribution with parameter [math]\lambda[/math] was obtained as a limit of binomial distributions with parameters [math]n[/math] and [math]p[/math], where it was assumed that [math]np = \lambda[/math], and [math]n \rightarrow \infty[/math]. Since for each [math]n[/math], the corresponding binomial distribution has expected value [math]\lambda[/math], it is reasonable to guess that the expected value of a Poisson distribution with parameter [math]\lambda[/math] also has expectation equal to [math]\lambda[/math]. This is in fact the case, and the reader is invited to show this (see Exercise).
Independence
If [math]X[/math] and [math]Y[/math] are two random variables, it is not true in general that [math]E(X \cdot Y) = E(X)E(Y)[/math]. However, this is true if [math]X[/math] and [math]Y[/math] are independent.
If [math]X[/math] and [math]Y[/math] are independent random variables, then
Suppose that
But if [math]X[/math] and [math]Y[/math] are independent,
Example A coin is tossed twice. [math]X_i = 1[/math] if the [math]i[/math]th toss is heads and 0 otherwise. We know that [math]X_1[/math] and [math]X_2[/math] are independent. They each have expected value 1/2. Thus [math]E(X_1 \cdot X_2) = E(X_1) E(X_2) = (1/2)(1/2) = 1/4[/math].
We next give a simple example to show that the expected values need not multiply if the random variables are not independent.
Example Consider a single toss of a coin. We define the random variable [math]X[/math] to be 1 if heads turns up and 0 if tails turns up, and we set [math]Y = 1 - X[/math]. Then [math]E(X) = E(Y) = 1/2[/math]. But [math]X \cdot Y = 0[/math] for either outcome. Hence, [math]E(X \cdot Y) = 0 \ne E(X) E(Y)[/math].
We return to our records example of Permutations for another application of the result that the expected value of the sum of random variables is the sum of the expected values of the individual random variables.
Records
Example We start keeping snowfall records this year and want to find the expected number of records that will occur in the next [math]n[/math] years. The first year is necessarily a record. The second year will be a record if the snowfall in the second year is greater than that in the first year. By symmetry, this probability is 1/2. More generally, let [math]X_j[/math] be 1 if the [math]j[/math]th year is a record and 0 otherwise. To find [math]E(X_j)[/math], we need only find the probability that the [math]j[/math]th year is a record. But the record snowfall for the first [math]j[/math] years is equally likely to fall in any one of these years, so [math]E(X_j) = 1/j[/math]. Therefore, if [math]S_n[/math] is the total number of records observed in the first [math]n[/math] years,
Craps
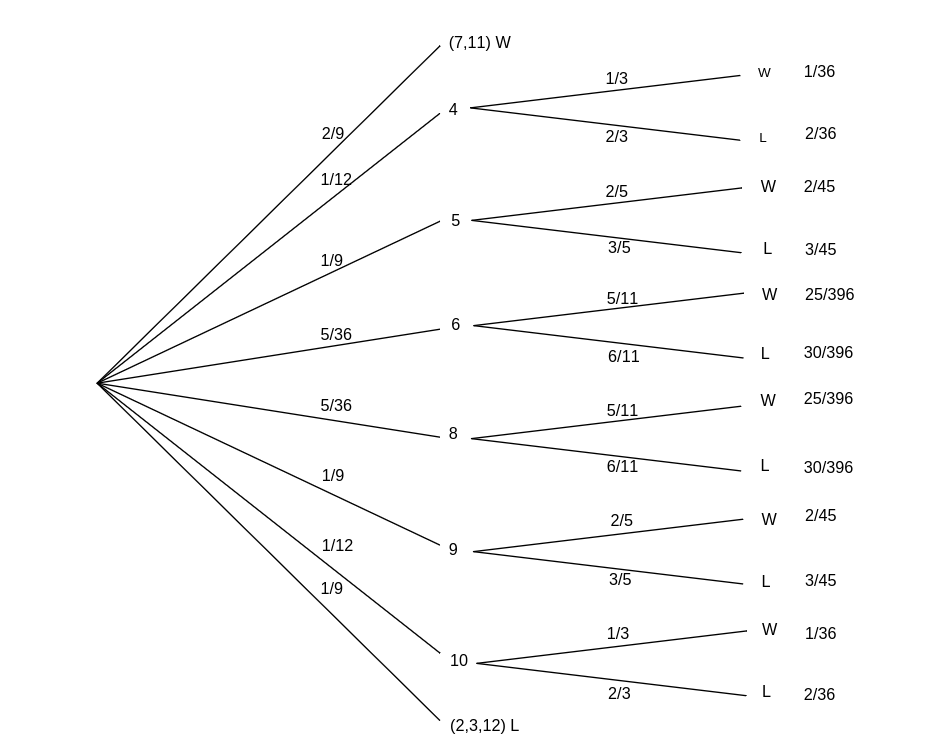
Example In the game of craps, the player makes a bet and rolls a pair of dice. If the sum of the numbers is 7 or 11 the player wins, if it is 2, 3, or 12 the player loses. If any other number results, say [math]r[/math], then [math]r[/math] becomes the player's point and he continues to roll until either [math]r[/math] or 7 occurs. If [math]r[/math] comes up first he wins, and if 7 comes up first he loses. The program Craps simulates playing this game a number of times.
We have run the program for 1000 plays in which the player bets 1 dollar each time. The player's average winnings were [math]-.006[/math]. The game of craps would seem to be only slightly unfavorable. Let us calculate the expected winnings on a single play and see if this is the case. We construct a two-stage tree measure as shown in
The first stage represents the possible sums for his first roll. The second stage represents the possible outcomes for the game if it has not ended on the first roll. In this stage we are representing the possible outcomes of a sequence of rolls required to determine the final outcome. The branch probabilities for the first stage are computed in the usual way assuming all 36 possibilites for outcomes for the pair of dice are equally likely. For the second stage we assume that the game will eventually end, and we compute the conditional probabilities for obtaining either the point or a 7. For example, assume that the player's point is 6. Then the game will end when one of the eleven pairs, [math](1,5)[/math], [math](2,4)[/math], [math](3,3)[/math], [math](4,2)[/math], [math](5,1)[/math], [math](1,6)[/math], [math](2,5)[/math], [math](3,4)[/math], [math](4,3)[/math], [math](5,2)[/math], [math](6,1)[/math], occurs. We assume that each of these possible pairs has the same probability. Then the player wins in the first five cases and loses in the last six. Thus the probability of winning is 5/11 and the probability of losing is 6/11. From the path probabilities, we can find the probability that the player wins 1 dollar; it is 244/495. The probability of losing is then 251/495. Thus if [math]X[/math] is his winning for a dollar bet,
Roulette
Example In Las Vegas, a roulette wheel has 38 slots numbered [math]0,\ 00,\ 1,\ 2,\ \ldots,\ 36[/math]. The [math]0[/math] and [math]00[/math] slots are green, and half of the remaining 36 slots are red and half are black. A croupier spins the wheel and throws an ivory ball. If you bet 1 dollar on red, you win 1 dollar if the ball stops in a red slot, and otherwise you lose a dollar. We wish to calculate the expected value of your winnings, if you bet 1 dollar on red.
Let [math]X[/math] be the random variable which denotes your winnings in a 1 dollar bet on red in Las Vegas
roulette. Then the distribution of [math]X[/math] is given by
We now consider the roulette game in Monte Carlo, and follow the treatment of
Sagan.[Notes 1] In the roulette game in Monte Carlo there is only one 0. If you
bet 1 franc on red and a 0 turns up, then, depending upon the casino, one or more of the following
options may be offered:
(a) You get 1/2 of your bet back, and the casino gets the other half of your bet.
(b) Your bet is put “in prison,” which we will denote by [math]P_1[/math]. If red comes up on the next turn,
you get your bet back (but you don't win any money). If black or 0 comes up, you lose your bet.
(c) Your bet is put in prison [math]P_1[/math], as before. If red comes up on the next turn, you get
your bet back, and if black comes up on the next turn, then you lose your bet. If a 0
comes up on the next turn, then your bet is put into double prison, which we will denote by
[math]P_2[/math]. If your bet is in double prison, and if red comes up on the next turn, then your bet is
moved back to prison [math]P_1[/math] and the game proceeds as before. If your bet is in double prison, and
if black or 0 come up on the next turn, then you lose your bet. We refer the reader to
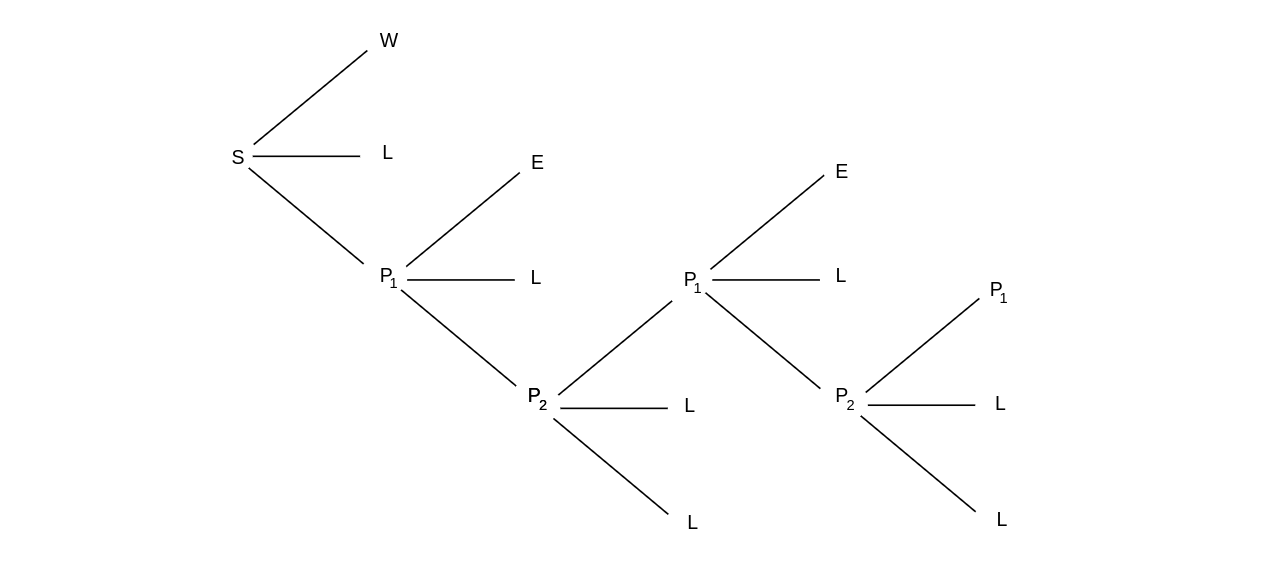
Figure, where a tree for this option is shown. In this figure, [math]S[/math] is the
starting position, [math]W[/math] means that you win your bet, [math]L[/math] means that you lose your bet, and [math]E[/math] means
that you break even.
It is interesting to compare the expected winnings of a 1 franc bet on red, under each
of these three options. We leave the first two calculations as an exercise
(see Exercise).
Suppose that you choose to play alternative (c).
The calculation for this case illustrates the way that the early French probabilists worked problems
like this.
Suppose you bet on red, you choose alternative (c), and a 0 comes up. Your
possible future outcomes are shown in the tree diagram in Figure.
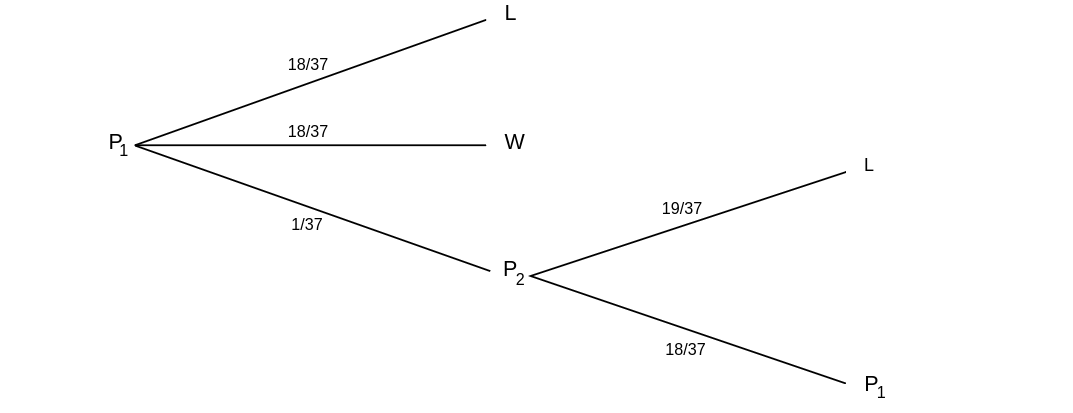
Assume that your money is in the first prison and let [math]x[/math] be the probability that you
lose your franc. From the tree diagram we see that
To find the probability that you win when you bet on red, note that you can only win if
red comes up on the first turn, and this happens with probability 18/37.
Thus your expected winnings are
It is interesting to note that the more romantic option (c) is less favorable than option (a) (see Exercise).
If you bet 1~dollar on the number 17, then the distribution function for your winnings [math]X[/math] is
and the expected winnings are
Thus, at Monte Carlo different bets have different expected values. In Las Vegas almost all bets have the same expected value of [math]-2/38 = -.0526[/math] (see Exercise and Exercise).
Conditional Expectation
If [math]F[/math] is any event and [math]X[/math] is a random variable with sample space [math]\Omega = \{x_1, x_2, \ldots\}[/math], then the conditional expectation given [math]F[/math] is defined by
Let [math]X[/math] be a random variable with sample space [math]\Omega[/math]. If [math]F_1[/math], [math]F_2, \ldots, F_r[/math] are events such that [math]F_i \cap F_j = \emptyset[/math] for [math]i \ne j[/math] and [math]\Omega = \cup_j F_j[/math], then
We have
Example In the game of craps, the player makes a bet and rolls a pair of dice. We can think of a single play as a two-stage process. The first stage consists of a single roll of a pair of dice. The play is over if this roll is a 2, 3, 7, 11, or 12. Otherwise, the player's point is established, and the second stage begins. This second stage consists of a sequence of rolls which ends when either the player's point or a 7 is rolled. We record the outcomes of this two-stage experiment using the random variables [math]X[/math] and [math]S[/math], where [math]X[/math] denotes the first roll, and [math]S[/math] denotes the number of rolls in the second stage of the experiment (of course, [math]S[/math] is sometimes equal to 0). Note that [math]T = S+1[/math]. Then by Theorem
Martingales
We can extend the notion of fairness to a player playing a sequence of games by using the concept of conditional expectation.
Example Let [math]S_1,S_2, \ldots,S_n[/math] be Peter's accumulated fortune in playing heads or tails (see Example). Then
We note that Peter's expected fortune after the next play is equal to his present fortune. When this occurs, we say the game is fair. A fair game is also called a martingale. If the coin is biased and comes up heads with probability
[math]p[/math] and tails with probability [math]q = 1 - p[/math], then
Thus, if [math]p \lt q[/math], this game is unfavorable, and if [math]p \gt q[/math], it is favorable.
If you are in a casino, you will see players adopting elaborate systems of play to try to make unfavorable games favorable. Two such systems, the martingale doubling system and the more conservative Labouchere system, were described in Exercise and Exercise.
Unfortunately, such systems cannot change even a fair game into a favorable game. Even so, it is a favorite pastime of many people to develop systems of play for gambling games and for other games such as the stock market. We close this section with a simple illustration of such a system.
Stock Prices
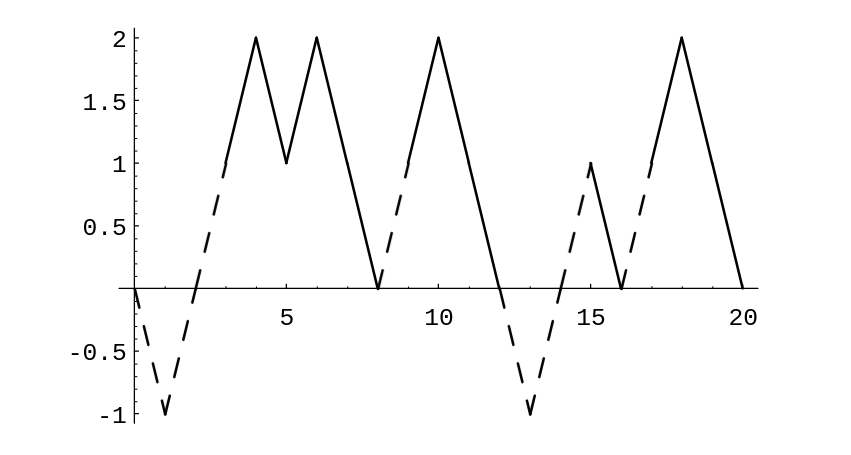
Example Let us assume that a stock increases or decreases in value each day by 1 dollar, each with probability 1/2. Then we can identify this simplified model with our familiar game of heads or tails. We assume that a buyer, Mr.\ Ace, adopts the following strategy. He buys the stock on the first day at its price [math]V[/math]. He then waits until the price of the stock increases by one to [math]V + 1[/math] and sells. He then continues to watch the stock until its price falls back to [math]V[/math]. He buys again and waits until it goes up to [math]V + 1[/math] and sells. Thus he holds the stock in intervals during which it increases by 1 dollar. In each such interval, he makes a profit of 1 dollar. However, we assume that he can do this only for a finite number of trading days. Thus he can lose if, in the last interval that he holds the stock, it does not get back up to [math]V + 1[/math]; and this is the only way he can lose. In Figure we illustrate a typical history if Mr.\ Ace must stop in twenty days.
Mr. Ace holds the stock under his system during the days indicated by broken lines. We note that for the history shown in Figure, his system nets him a gain of 4 dollars.
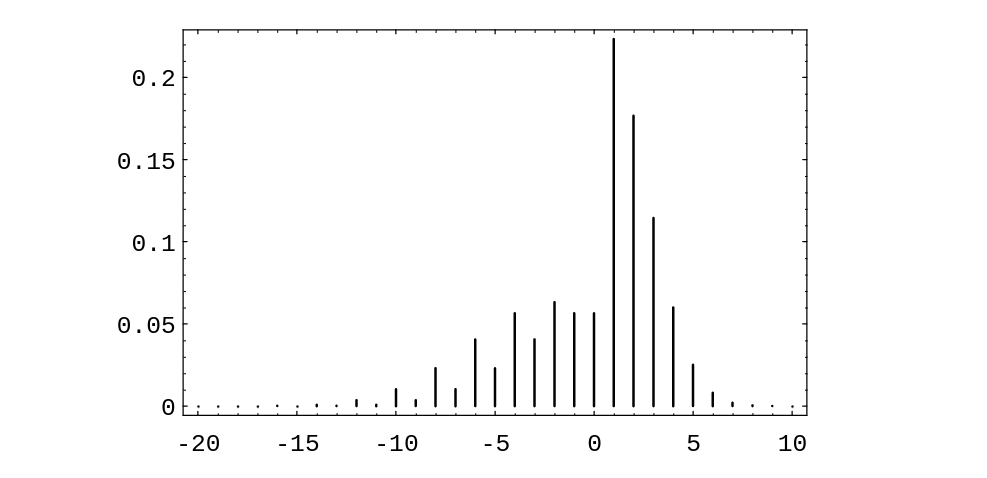
We have written a program StockSystem to simulate the fortune of Mr. Ace if he uses his sytem over an [math]n[/math]-day period. If one runs this program a large number of times, for [math]n = 20[/math], say, one finds that his expected winnings are very close to 0, but the probability that he is ahead after 20 days is significantly greater than 1/2. For small values of [math]n[/math], the exact distribution of winnings can be calculated. The distribution for the case [math]n = 20[/math] is shown in Figure. Using this distribution, it is easy to calculate that the expected value of his winnings is exactly 0. This is another instance of the fact that a fair game (a martingale) remains fair under quite general systems of play.
Although the expected value of his winnings is 0, the probability that Mr.\ Ace is ahead after 20 days is about .610. Thus, he would be able to tell his friends that his system gives him a better chance of being ahead than that of someone who simply buys the stock and holds it, if our simple random model is correct. There have been a number of studies to determine how random the stock market is.
Historical Remarks
With the Law of Large Numbers to bolster the frequency interpretation of probability, we find it natural to justify the definition of expected value in terms of the average outcome over a large number of repetitions of the experiment. The concept of expected value was used before it was formally defined; and when it was used, it was considered not as an average value but rather as the appropriate value for a gamble. For example recall, from the Historical Remarks section of Chapter Discrete Probability Distributions, section Discrete Probability Distributions, Pascal's way of finding the value of a three-game series that had to be called off before it is finished.
Pascal first observed that if each player has only one game to win, then the stake of 64 pistoles should be divided evenly. Then he considered the case where one player has won two games and the other one.
Then consider, Sir, if the first man wins, he gets 64 pistoles, if he loses he gets 32. Thus if they do not wish to risk this last game, but wish to
separate without playing it, the first man must say: “I am certain to get 32 pistoles, even if I lose I still get them; but as for the other 32 pistoles, perhaps I will get them, perhaps you will get them, the chances are equal. Let us then divide these 32 pistoles in half and give one half to me as well as my 32 which are mine for sure.” He will then have 48 pistoles and the other 16.[Notes 2]
Note that Pascal reduced the problem to a symmetric bet in which each player gets the same amount and takes it as obvious that in this case the stakes should be divided equally. The first systematic study of expected value appears in Huygens' book. Like Pascal, Huygens find the value of a gamble by assuming that the answer is obvious for certain symmetric situations and uses this to deduce the expected for the general situation. He does this in steps. His first proposition is
Prop. I. If I expect [math]a[/math] or [math]b[/math], either of which, with equal probability, may fall to me, then my Expectation is worth [math](a + b)/2[/math], that is, the half Sum of [math]a[/math] and [math]b[/math].[Notes 3]
Huygens proved this as follows: Assume that two player A and B play a game in which each player puts up a stake of [math](a + b)/2[/math] with an equal chance of winning the total stake. Then the value of the game to each player is [math](a + b)/2[/math]. For example, if the game had to be called off clearly each player should just get back his original stake. Now, by symmetry, this value is not changed if we add the condition that the winner of the game has to pay the loser an amount [math]b[/math] as a consolation prize. Then for player A the value is still [math](a + b)/2[/math]. But what are his possible outcomes for the modified game? If he wins he gets the total stake [math]a + b[/math] and must pay B an amount [math]b[/math] so ends up with [math]a[/math]. If he loses he gets an amount [math]b[/math] from player B. Thus player A wins [math]a[/math] or [math]b[/math] with equal chances and the value to him is [math](a + b)/2[/math]. Huygens illustrated this proof in terms of an example. If you are offered a game in which you have an equal chance of winning 2 or 8, the expected value is 5, since this game is equivalent to the game in which each player stakes 5 and agrees to pay the loser 3 --- a game in which the value is obviously 5. Huygens' second proposition is
Prop. II. If I expect [math]a[/math], [math]b[/math], or [math]c[/math], either of which, with equal facility, may happen, then the Value of my Expectation is [math](a + b + c)/3[/math], or the third of the Sum of [math]a[/math], [math]b[/math], and [math]c[/math].[Notes 4]
His argument here is similar. Three players, A, B, and C, each stake
in a game they have an equal chance of winning. The value of this game to player A is clearly the amount he has staked. Further, this value is not changed if A enters into an agreement with B that if one of them wins he pays the other a consolation prize of [math]b[/math] and with C that if one of them wins he pays the other a consolation prize of [math]c[/math]. By symmetry these agreements do not change the value of the game. In this modified game, if A wins he wins the total stake [math]a + b + c[/math] minus the consolation prizes [math]b + c[/math] giving him a final winning of [math]a[/math]. If B wins, A wins [math]b[/math] and if C wins, A wins [math]c[/math]. Thus A finds himself in a game with value [math](a + b + c)/3[/math] and with outcomes [math]a[/math], [math]b[/math], and [math]c[/math] occurring with equal chance. This proves Proposition II.
More generally, this reasoning shows that if there are [math]n[/math] outcomes
all occurring with the same probability, the expected value is
In his third proposition Huygens considered the case where you win [math]a[/math] or [math]b[/math] but with unequal probabilities. He assumed there are [math]p[/math] chances of winning [math]a[/math], and [math]q[/math] chances of winning [math]b[/math], all having the same probability. He then showed that the expected value is
Thus, instead of defining the expected value as a weighted average, Huygens assumed
that the expected value of certain symmetric gambles are known and deduced the other
values from these. Although this requires a good deal of clever manipulation,
Huygens ended up with values that agree with those given by our modern definition of
expected value. One advantage of this method is that it gives a justification for
the expected value in cases where it is not reasonable to assume that you can repeat
the experiment a large number of times, as for example, in betting that at least two
presidents died on the same day of the year. (In fact, three did; all were signers
of the Declaration of Independence, and all three died on July 4.)
In his book, Huygens calculated the expected value of games using techniques similar
to those which we used in computing the expected value for roulette at Monte Carlo.
For example, his proposition XIV is:
Prop. XIV. If I were playing with another by turns, with two Dice, on
this Condition, that if I throw 7 I gain, and if he throws 6 he gains allowing him the first Throw: To find the proportion of my Hazard to his.[Notes 5]
A modern description of this game is as follows. Huygens and his opponent take
turns rolling a die. The game is over if Huygens rolls a 7 or his opponent rolls a
6. His opponent rolls first. What is the probability that Huygens wins the game?
To solve this problem Huygens let
[math]x[/math] be his chance of winning when his opponent threw first and [math]y[/math] his chance of
winning when he threw first. Then on the first roll his opponent wins on 5 out of
the 36 possibilities. Thus,
| God does not exist | God exists | |
|---|---|---|
| [math]p[/math] | [math]1 - p[/math] | |
| believe | [math]-u[/math] | [math]v [/math] |
| not believe | 0 | [math]-x[/math] |
Here [math]-u[/math] represents the cost to you of passing up some worldly pleasures as a consequence of believing that God exists. If you do not believe, and God is a vengeful God, you will lose [math]x[/math]. If God exists and you do believe you will gain v. Now to determine which strategy is best you should compare the two expected values
| Age | Survivors |
|---|---|
| 0 | 100 |
| 6 | 64 |
| 16 | 40 |
| 26 | 25 |
| 36 | 16 |
| 46 | 10 |
| 56 | 6 |
| 66 | 3 |
| 76 | 1 |
As Hacking observes, Graunt apparently constructed this table by assuming that after the age of 6 there is a constant probability of about 5/8 of surviving for another decade.[Notes 8] For example, of the 64 people who survive to age 6, 5/8 of 64 or 40 survive to 16, 5/8 of these 40 or 25 survive to 26, and so forth. Of course, he rounded off his figures to the nearest whole person. Clearly, a constant mortality rate cannot be correct throughout the whole range, and later tables provided by Halley were more realistic in this respect.[Notes 9] A terminal annuity provides a fixed amount of money during a period of [math]n[/math] years. To determine the price of a terminal annuity one needs only to know the appropriate interest rate. A life annuity provides a fixed amount during each year of the buyer's life. The appropriate price for a life annuity is the expected value of the terminal annuity evaluated for the random lifetime of the buyer. Thus, the work of Huygens in introducing expected value and the work of Graunt and Halley in determining mortality tables led to a more rational method for pricing annuities. This was one of the first serious uses of probability theory outside the gambling houses. Although expected value plays a role now in every branch of science, it retains its importance in the casino. In 1962, Edward Thorp's book Beat the Dealer[Notes 10] provided the reader with a strategy for playing the popular casino game of blackjack that would assure the player a positive expected winning. This book forevermore changed the belief of the casinos that they could not be beat.
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.
Notes
- H. Sagan, Markov Chains in Monte Carlo, Math. Mag., vol. 54, no. 1 (1981), pp. 3-10.
- Quoted in F. N. David, Games, Gods and Gambling (London: Griffin, 1962), p. 231.
- C. Huygens, Calculating in Games of Chance, translation attributed to John Arbuthnot (London, 1692), p. 34.
- ibid., p. 35.
- ibid., p. 47.
- Quoted in I. Hacking, The Emergence of Probability (Cambridge: Cambridge Univ. Press, 1975).
- ibid., p. 108.
- ibid., p. 109.
- E. Halley, “An Estimate of The Degrees of Mortality of Mankind,” Phil. Trans. Royal. Soc., vol. 17 (1693), pp. 596--610; 654--656.
- E. Thorp, Beat the Dealer (New York: Random House, 1962).