guide:4f25e79970: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 1: | Line 1: | ||
<div class="d-none"> | |||
<math> | |||
\( | |||
% Generic syms | |||
\newcommand\defeq{:=} | |||
\newcommand{\Tt}[0]{\boldsymbol{\theta}} | |||
\newcommand{\XX}[0]{{\cal X}} | |||
\newcommand{\ZZ}[0]{{\cal Z}} | |||
\newcommand{\vx}[0]{{\bf x}} | |||
\newcommand{\vv}[0]{{\bf v}} | |||
\newcommand{\vu}[0]{{\bf u}} | |||
\newcommand{\vs}[0]{{\bf s}} | |||
\newcommand{\vm}[0]{{\bf m}} | |||
\newcommand{\vq}[0]{{\bf q}} | |||
\newcommand{\mX}[0]{{\bf X}} | |||
\newcommand{\mC}[0]{{\bf C}} | |||
\newcommand{\mA}[0]{{\bf A}} | |||
\newcommand{\mL}[0]{{\bf L}} | |||
\newcommand{\fscore}[0]{F_{1}} | |||
\newcommand{\sparsity}{s} | |||
\newcommand{\mW}[0]{{\bf W}} | |||
\newcommand{\mD}[0]{{\bf D}} | |||
\newcommand{\mZ}[0]{{\bf Z}} | |||
\newcommand{\vw}[0]{{\bf w}} | |||
\newcommand{\D}[0]{{\mathcal{D}}} | |||
\newcommand{\mP}{\mathbf{P}} | |||
\newcommand{\mQ}{\mathbf{Q}} | |||
\newcommand{\E}[0]{{\mathbb{E}}} | |||
\newcommand{\vy}[0]{{\bf y}} | |||
\newcommand{\va}[0]{{\bf a}} | |||
\newcommand{\vn}[0]{{\bf n}} | |||
\newcommand{\vb}[0]{{\bf b}} | |||
\newcommand{\vr}[0]{{\bf r}} | |||
\newcommand{\vz}[0]{{\bf z}} | |||
\newcommand{\N}[0]{{\mathcal{N}}} | |||
\newcommand{\vc}[0]{{\bf c}} | |||
\newcommand{\bm}{\boldsymbol} | |||
% Statistics and Probability Theory | |||
\newcommand{\errprob}{p_{\rm err}} | |||
\newcommand{\prob}[1]{p({#1})} | |||
\newcommand{\pdf}[1]{p({#1})} | |||
\def \expect {\mathbb{E} } | |||
% Machine Learning Symbols | |||
\newcommand{\biasterm}{B} | |||
\newcommand{\varianceterm}{V} | |||
\newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} | |||
\newcommand{\nrfolds}{k} | |||
\newcommand{\mseesterr}{E_{\rm est}} | |||
\newcommand{\bootstrapidx}{b} | |||
%\newcommand{\modeldim}{r} | |||
\newcommand{\modelidx}{l} | |||
\newcommand{\nrbootstraps}{B} | |||
\newcommand{\sampleweight}[1]{q^{(#1)}} | |||
\newcommand{\nrcategories}{K} | |||
\newcommand{\splitratio}[0]{{\rho}} | |||
\newcommand{\norm}[1]{\Vert {#1} \Vert} | |||
\newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} | |||
\newcommand{\bmx}[0]{\begin{bmatrix}} | |||
\newcommand{\emx}[0]{\end{bmatrix}} | |||
\newcommand{\T}[0]{\text{T}} | |||
\DeclareMathOperator*{\rank}{rank} | |||
%\newcommand\defeq{:=} | |||
\newcommand\eigvecS{\hat{\mathbf{u}}} | |||
\newcommand\eigvecCov{\mathbf{u}} | |||
\newcommand\eigvecCoventry{u} | |||
\newcommand{\featuredim}{n} | |||
\newcommand{\featurelenraw}{\featuredim'} | |||
\newcommand{\featurelen}{\featuredim} | |||
\newcommand{\samplingset}{\mathcal{M}} | |||
\newcommand{\samplesize}{m} | |||
\newcommand{\sampleidx}{i} | |||
\newcommand{\nractions}{A} | |||
\newcommand{\datapoint}{\vz} | |||
\newcommand{\actionidx}{a} | |||
\newcommand{\clusteridx}{c} | |||
\newcommand{\sizehypospace}{D} | |||
\newcommand{\nrcluster}{k} | |||
\newcommand{\nrseeds}{s} | |||
\newcommand{\featureidx}{j} | |||
\newcommand{\clustermean}{{\bm \mu}} | |||
\newcommand{\clustercov}{{\bm \Sigma}} | |||
\newcommand{\target}{y} | |||
\newcommand{\error}{E} | |||
\newcommand{\augidx}{b} | |||
\newcommand{\task}{\mathcal{T}} | |||
\newcommand{\nrtasks}{T} | |||
\newcommand{\taskidx}{t} | |||
\newcommand\truelabel{y} | |||
\newcommand{\polydegree}{r} | |||
\newcommand\labelvec{\vy} | |||
\newcommand\featurevec{\vx} | |||
\newcommand\feature{x} | |||
\newcommand\predictedlabel{\hat{y}} | |||
\newcommand\dataset{\mathcal{D}} | |||
\newcommand\trainset{\dataset^{(\rm train)}} | |||
\newcommand\valset{\dataset^{(\rm val)}} | |||
\newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} | |||
\newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} | |||
\newcommand{\inspace}{\mathcal{X}} | |||
\newcommand{\sigmoid}{\sigma} | |||
\newcommand{\outspace}{\mathcal{Y}} | |||
\newcommand{\hypospace}{\mathcal{H}} | |||
\newcommand{\emperror}{\widehat{L}} | |||
\newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} | |||
\newcommand{\featurespace}{\mathcal{X}} | |||
\newcommand{\labelspace}{\mathcal{Y}} | |||
\newcommand{\rawfeaturevec}{\mathbf{z}} | |||
\newcommand{\rawfeature}{z} | |||
\newcommand{\condent}{H} | |||
\newcommand{\explanation}{e} | |||
\newcommand{\explainset}{\mathcal{E}} | |||
\newcommand{\user}{u} | |||
\newcommand{\actfun}{\sigma} | |||
\newcommand{\noisygrad}{g} | |||
\newcommand{\reconstrmap}{r} | |||
\newcommand{\predictor}{h} | |||
\newcommand{\eigval}[1]{\lambda_{#1}} | |||
\newcommand{\regparam}{\lambda} | |||
\newcommand{\lrate}{\alpha} | |||
\newcommand{\edges}{\mathcal{E}} | |||
\newcommand{\generror}{E} | |||
\DeclareMathOperator{\supp}{supp} | |||
%\newcommand{\loss}[3]{L({#1},{#2},{#3})} | |||
\newcommand{\loss}[2]{L\big({#1},{#2}\big)} | |||
\newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} | |||
\newcommand{\determinant}[1]{{\rm det}({#1})} | |||
\DeclareMathOperator*{\argmax}{argmax} | |||
\DeclareMathOperator*{\argmin}{argmin} | |||
\newcommand{\itercntr}{r} | |||
\newcommand{\state}{s} | |||
\newcommand{\statespace}{\mathcal{S}} | |||
\newcommand{\timeidx}{t} | |||
\newcommand{\optpolicy}{\pi_{*}} | |||
\newcommand{\appoptpolicy}{\hat{\pi}} | |||
\newcommand{\dummyidx}{j} | |||
\newcommand{\gridsizex}{K} | |||
\newcommand{\gridsizey}{L} | |||
\newcommand{\localdataset}{\mathcal{X}} | |||
\newcommand{\reward}{r} | |||
\newcommand{\cumreward}{G} | |||
\newcommand{\return}{\cumreward} | |||
\newcommand{\action}{a} | |||
\newcommand\actionset{\mathcal{A}} | |||
\newcommand{\obstacles}{\mathcal{B}} | |||
\newcommand{\valuefunc}[1]{v_{#1}} | |||
\newcommand{\gridcell}[2]{\langle #1, #2 \rangle} | |||
\newcommand{\pair}[2]{\langle #1, #2 \rangle} | |||
\newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} | |||
\newcommand{\actionvalue}[1]{q_{#1}} | |||
\newcommand{\transition}{\mathcal{T}} | |||
\newcommand{\policy}{\pi} | |||
\newcommand{\charger}{c} | |||
\newcommand{\itervar}{k} | |||
\newcommand{\discount}{\gamma} | |||
\newcommand{\rumba}{Rumba} | |||
\newcommand{\actionnorth}{\rm N} | |||
\newcommand{\actionsouth}{\rm S} | |||
\newcommand{\actioneast}{\rm E} | |||
\newcommand{\actionwest}{\rm W} | |||
\newcommand{\chargingstations}{\mathcal{C}} | |||
\newcommand{\basisfunc}{\phi} | |||
\newcommand{\augparam}{B} | |||
\newcommand{\valerror}{E_{v}} | |||
\newcommand{\trainerror}{E_{t}} | |||
\newcommand{\foldidx}{b} | |||
\newcommand{\testset}{\dataset^{(\rm test)} } | |||
\newcommand{\testerror}{E^{(\rm test)}} | |||
\newcommand{\nrmodels}{M} | |||
\newcommand{\benchmarkerror}{E^{(\rm ref)}} | |||
\newcommand{\lossfun}{L} | |||
\newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} | |||
\newcommand{\cluster}{\mathcal{C}} | |||
\newcommand{\bayeshypothesis}{h^{*}} | |||
\newcommand{\featuremtx}{\mX} | |||
\newcommand{\weight}{w} | |||
\newcommand{\weights}{\vw} | |||
\newcommand{\regularizer}{\mathcal{R}} | |||
\newcommand{\decreg}[1]{\mathcal{R}_{#1}} | |||
\newcommand{\naturalnumbers}{\mathbb{N}} | |||
\newcommand{\featuremapvec}{{\bf \Phi}} | |||
\newcommand{\featuremap}{\phi} | |||
\newcommand{\batchsize}{B} | |||
\newcommand{\batch}{\mathcal{B}} | |||
\newcommand{\foldsize}{B} | |||
\newcommand{\nriter}{R} | |||
% Machine Learning from Networked Data | |||
\newcommand{\nodesigvec}{\mathbf{u}} | |||
\newcommand{\edgesigvec}{\mathbf{f}} | |||
\newcommand{\edgesig}{f} | |||
\newcommand{\edgeweight}{A} | |||
\newcommand{\edgeweights}{\mA} | |||
\newcommand{\edgeidx}{e} | |||
\newcommand{\edgesigs}{\mathbb{R}^{\edges \times \featuredim}} | |||
\newcommand{\graph}{\mathcal{G}} | |||
\newcommand{\nodes}{\mathcal{V}} | |||
\newcommand{\degreemtx}{\mathbf{D}} | |||
\newcommand{\incidencemtx}{\mathbf{B}} | |||
\newcommand{\nodedegree}[1]{d^{(#1)}} | |||
\newcommand{\nodeidx}{i} | |||
\newcommand{\nrnodes}{n} | |||
\newcommand{\nodesigs}{\mathbb{R}^{\nodes \times \featuredim }} | |||
\newcommand{\naturalspace}{\mathcal{N}} | |||
\newcommand{\gindex}[1][i]{^{(#1)}} | |||
\newcommand{\gsignal}{\vw} | |||
\newcommand{\trueweights}{\overline{\vw}} | |||
\newcommand{\vt}{\mathbf{t}} | |||
\newcommand{\FIM}{\mathbf{F}} | |||
\newcommand{\FIMentry}{F} | |||
\newcommand{\edge}[2]{\{#1,#2\}} | |||
\newcommand{\directededge}[2]{\left(#1,#2\right)} | |||
</math> | |||
</div> | |||
<blockquote> | |||
“Solving Problems By Changing the Viewpoint.” | |||
</blockquote> | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_dimred"></span> | |||
[[File:fig_dimred.jpg | 500px | thumb | Dimensionality reduction methods aim at finding a map | |||
<math>h</math> which maximally | |||
compresses the raw data while still allowing to accurately reconstruct the original | |||
datapoint from a small number of features | |||
<math>x_{1},\ldots,x_{\featuredim}</math>. ]] | |||
</div> | |||
Chapter [[guide:B85f6bf6f2 | Three Components of ML ]] defined features as those properties of a <span class="mw-gls mw-gls-first" data-name ="datapoint">data point</span> that can | |||
be measured or computed easily. Sometimes the choice of features follows naturally from the | |||
available hard- and software. For example, we might use the numeric measurement | |||
<math>\rawfeature \in \mathbb{R}</math> | |||
delivered by a sensing device as a feature. However, we could augment this single feature with | |||
new features such as the powers | |||
<math>\rawfeature^{2}</math> and | |||
<math>\rawfeature^{3}</math> or adding a constant | |||
<math>\rawfeature+5</math>. | |||
Each of these computations produces a new feature. Which of these additional features are most useful? | |||
Feature learning methods automate the choice of finding good features. These methods learn a hypothesis | |||
map that reads in some representation of a <span class="mw-gls" data-name ="datapoint">data point</span> and transforms it to a set of features. Feature learning | |||
methods differ in the precise format of the original data representation as well as the format of the delivered features. | |||
This chapter mainly discusses feature learning methods that require <span class="mw-gls" data-name ="datapoint">data point</span>s being represented by | |||
<math>\featurelenraw</math> | |||
numeric raw features and deliver a set of | |||
<math>\featurelen</math> new numeric features. We will denote the raw features and the learnt | |||
new features by | |||
<math>\rawfeaturevec=\big(\rawfeature_{1},\ldots,\rawfeature_{\featurelenraw} \big)^{T} \in \mathbb{R}^{\featurelenraw}</math> and | |||
<math>\featurevec=\big(\feature_{1},\ldots,\feature_{\featurelen}\big)^{T} \in \mathbb{R}^{\featurelen}</math>, respectively. | |||
Many ML application domains generate <span class="mw-gls" data-name ="datapoint">data point</span>s for which can access a huge number of raw features. | |||
Consider <span class="mw-gls" data-name ="datapoint">data point</span>s being snapshots generated by a smartphone. It seems natural to use the pixel colour intensities | |||
as the raw features of the snapshot. Since modern smartphone have “Megapixel cameras”, the pixel intensities would | |||
provide us with millions of raw features. It might seem a good idea to use as many raw features of a <span class="mw-gls" data-name ="datapoint">data point</span> as possible | |||
since more features should offer more information about a <span class="mw-gls" data-name ="datapoint">data point</span> and its label | |||
<math>\truelabel</math>. There are, however, | |||
two pitfalls in using an unnecessarily large number of features. The first one is a computational pitfall and the second one | |||
is a statistical pitfall. | |||
Computationally, using very long feature vectors | |||
<math>\featurevec \in \mathbb{R}^{\featuredim}</math> (with | |||
<math>\featuredim</math> being billions), | |||
might result in prohibitive computational resource requirements (bandwidth, storage, time) of the resulting ML method. | |||
Statistically, using a large number of features makes the resulting ML methods more prone to | |||
overfitting. For example, <span class="mw-gls mw-gls-first" data-name ="linreg">linear regression</span> will typically overfit when using feature vectors | |||
<math>\featurevec\!\in\!\mathbb{R}^{\featuredim}</math> | |||
whose length | |||
<math>\featuredim</math> exceeds the number | |||
<math>\samplesize</math> of labeled <span class="mw-gls" data-name ="datapoint">data point</span>s used | |||
for training (see Chapter [[guide:50be9327aa | Regularization ]]). | |||
Both from a computational and a statistical perspective, it is beneficial to use only the maximum necessary | |||
amount of features. The challenge is to select those features which carry most of the relevant | |||
information required for the prediction of the label | |||
<math>\truelabel</math>. Finding the most relevant features | |||
out of a huge number of raw features is the goal of dimensionality reduction methods. | |||
Dimensionality reduction methods form an important sub-class of feature learning methods. | |||
These methods learn a hypothesis | |||
<math>h(\rawfeaturevec)</math> that maps a long raw feature vector | |||
<math>\rawfeaturevec \in \mathbb{R}^{\featurelenraw}</math> to a new (short) feature vector | |||
<math>\featurevec \in \mathbb{R}^{\featurelen}</math> | |||
with | |||
<math>\featurelen \ll \featurelenraw</math>. | |||
Beside avoiding overfitting and coping with limited computational resources, dimensionality reduction | |||
can also be useful for data visualization. Indeed, if the resulting feature vector has length | |||
<math>\featurelen=2</math>, | |||
we depict <span class="mw-gls" data-name ="datapoint">data point</span>s in the two-dimensional plane in form of a <span class="mw-gls mw-gls-first" data-name ="scatterplot">scatterplot</span>. | |||
We will discuss the basic idea underlying dimensionality reduction methods in Section [[guide:4f25e79970#sec_dim_red | Basic Principle of Dimensionality Reduction ]]. | |||
Section [[guide:4f25e79970#sec_pca | Principal Component Analysis ]] presents one particular example of a dimensionality reduction method that computes | |||
relevant features by a linear transformation of the raw feature vector. Section [[guide:4f25e79970#sec_lda | Feature Learning for Labeled Data ]] discusses a method | |||
for dimensionality reduction that exploits the availability of labelled <span class="mw-gls" data-name ="datapoint">data point</span>s. Section [[guide:4f25e79970#equ_random_projections | Random Projections ]] | |||
shows how randomness can be used to obtain computationally cheap dimensionality reduction . | |||
Most of this chapter discusses dimensionality reduction methods that determine a small number | |||
of relevant features from a large set of raw features. However, sometimes it might be useful to go | |||
the opposite direction. There are applications where it might be beneficial to construct a large (even infinite) | |||
number of new features from a small set of raw features. Section [[guide:4f25e79970#sec_dim_increas | Dimensionality Increase ]] will showcase | |||
how computing additional features can help to improve the prediction accuracy of ML methods. | |||
==<span id="sec_dim_red"/>Basic Principle of Dimensionality Reduction== | |||
The efficiency of ML methods depends crucially on the choice of features that are used to characterize <span class="mw-gls" data-name ="datapoint">data point</span>s. | |||
Ideally we would like to have a small number of highly relevant features to characterize <span class="mw-gls" data-name ="datapoint">data point</span>s. If we use too | |||
many features we risk to waste computations on exploring irrelevant features. If we use too few features | |||
we might not have enough information to predict the label of a <span class="mw-gls" data-name ="datapoint">data point</span>. For a given number | |||
<math>\featurelen</math> | |||
of features, dimensionality reduction methods aim at learning an (in a certain sense) optimal map from the <span class="mw-gls" data-name ="datapoint">data point</span> | |||
to a feature vector of length | |||
<math>\featurelen</math>. | |||
Figure [[#fig_dimred|fig_dimred]] illustrates the basic idea of dimensionality reduction methods. Their goal | |||
is to learn (or find) a “compression” map | |||
<math>h(\cdot): \mathbb{R}^{\featurelenraw} \rightarrow \mathbb{R}^{\featuredim}</math> | |||
that transforms a (long) raw feature vector | |||
<math>\rawfeaturevec \in \mathbb{R}^{\featurelenraw}</math> to a (short) feature vector | |||
<math>\featurevec=(\feature_{1},\ldots,\feature_{\featuredim})^{T} \defeq h(\rawfeaturevec)</math> (typically | |||
<math>\featuredim \ll \featurelenraw</math>). | |||
The new feature vector | |||
<math>\featurevec = h(\rawfeaturevec)</math> serves as a compressed representation (or code) | |||
for the original feature vector | |||
<math>\rawfeaturevec</math>. We can reconstruct the raw feature vector using a | |||
reconstruction map | |||
<math>\reconstrmap(\cdot): \mathbb{R}^{\featurelen} \rightarrow \mathbb{R}^{\featurelenraw}</math>. | |||
The reconstructed raw features | |||
<math>\widehat{\rawfeaturevec} \defeq \reconstrmap(\featurevec) = \reconstrmap(h(\rawfeaturevec))</math> | |||
will typically differ from the original raw feature vector | |||
<math>\rawfeaturevec</math>. In general, we obtain a non-zero reconstruction error | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_reconst_error} | |||
\underbrace{\widehat{\rawfeaturevec}}_{=\reconstrmap(h(\rawfeaturevec)))} - \rawfeaturevec. | |||
\end{equation} | |||
</math> | |||
Dimensionality reduction methods learn a compression map | |||
<math>h(\cdot)</math> such that the reconstruction error \eqref{equ_def_reconst_error} | |||
is minimized. In particular, for a dataset | |||
<math>\dataset = \big\{ \rawfeaturevec^{(1)},\ldots,\rawfeaturevec^{(\samplesize)} \big\}</math>, | |||
we measure the quality of a pair of compression map | |||
<math>h</math> and reconstruction map | |||
<math>\reconstrmap</math> by the average reconstruction error | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_emp_error_dimred} | |||
\emperror\big(h,\reconstrmap| \dataset \big) \defeq (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \loss{\rawfeaturevec^{(\sampleidx)}}{\reconstrmap\big(h\big(\rawfeaturevec^{(\sampleidx)}\big)\big)}. | |||
\end{equation} | |||
</math> | |||
Here, | |||
<math>\loss{\rawfeaturevec}{\reconstrmap\big(h\big(\rawfeaturevec^{(\sampleidx)}\big)}</math> denotes a loss function that is used | |||
to measure the reconstruction error | |||
<math>\underbrace{\reconstrmap\big(h\big(\rawfeaturevec^{(\sampleidx)}\big)\big)}_{\widehat{\rawfeaturevec}} - \rawfeaturevec</math>. | |||
Different choices for the loss function in \eqref{equ_def_emp_error_dimred} result in different dimensionality | |||
reduction methods. One widely-used choice for the loss is the squared Euclidean norm | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_squared_eucl_norm} | |||
\loss{\rawfeaturevec}{g\big(h\big(\rawfeaturevec\big)\big)} \defeq \big\| \rawfeaturevec -g\big(h\big(\rawfeaturevec\big)\big) \big\|^{2}_{2}. | |||
\end{equation} | |||
</math> | |||
Practical dimensionality reduction methods have only finite computational resources. Any practical | |||
method must therefore restrict the set of possible compression and reconstruction maps to small | |||
subsets | |||
<math>\hypospace</math> and | |||
<math>\hypospace^{*}</math>, respectively. These subsets are the <span class="mw-gls mw-gls-first" data-name ="hypospace">hypothesis space</span>s | |||
for the compression map | |||
<math>h \in \hypospace</math> and the reconstruction map | |||
<math>\reconstrmap \in \hypospace^{*}</math>. | |||
Feature learning methods differ in their choice for these <span class="mw-gls" data-name ="hypospace">hypothesis space</span>s. | |||
Dimensionality reduction methods learn a compression map by solving | |||
<math display="block"> | |||
\begin{align} | |||
\hat{h} & = \argmin_{h \in \hypospace} \min_{\reconstrmap \in \hypospace^{*}} \emperror\big(h,\reconstrmap| \dataset \big) \nonumber \\ & \label{equ_optimaization_dimred}\stackrel{\eqref{equ_def_emp_error_dimred}}{=} \argmin_{h \in \hypospace} \min_{\reconstrmap\in \hypospace^{*}} (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \loss{\rawfeaturevec^{(\sampleidx)}}{\reconstrmap\big(h\big(\rawfeaturevec^{(\sampleidx)}\big)\big)}. | |||
\end{align} | |||
</math> | |||
We can interpret \eqref{equ_optimaization_dimred} as a (typically non-linear) approximation problem. | |||
The optimal compression map | |||
<math>\hat{h}</math> is such that the reconstruction | |||
<math>\reconstrmap(\hat{h}(\rawfeaturevec))</math>, | |||
with a suitably chosen reconstruction map | |||
<math>\reconstrmap</math>, approximates the original raw feature vector | |||
<math>\rawfeaturevec</math> | |||
as good as possible. Note that we use a single compression map | |||
<math>h(\cdot)</math> and a single | |||
reconstruction map | |||
<math>\reconstrmap(\cdot)</math> for all <span class="mw-gls" data-name ="datapoint">data point</span>s in the dataset | |||
<math>\dataset</math>. | |||
We obtain variety of dimensionality methods by using different choices for the <span class="mw-gls" data-name ="hypospace">hypothesis space</span>s | |||
<math>\hypospace, \hypospace^{*}</math> | |||
and loss function in \eqref{equ_optimaization_dimred}. Section [[guide:4f25e79970#sec_pca | Principal Component Analysis ]] discusses a method that solves \eqref{equ_optimaization_dimred} | |||
for | |||
<math>\hypospace, \hypospace^{*}</math> constituted by linear maps and the loss \eqref{equ_def_squared_eucl_norm}. Deep autoencoders | |||
are another family of dimensionality reduction methods that solve \eqref{equ_optimaization_dimred} with | |||
<math>\hypospace, \hypospace^{*}</math> constituted by non-linear maps that are represented by deep neural | |||
networks <ref name="Goodfellow-et-al-2016"/>{{rp|at=Ch. 14}}. | |||
==<span id="sec_pca"/>Principal Component Analysis== | |||
We now consider the special case of dimensionality reduction where the compression and reconstruction map | |||
are required to be linear maps. Consider a <span class="mw-gls" data-name ="datapoint">data point</span> which is characterized by a (typically very long) | |||
raw feature vector | |||
<math>\rawfeaturevec\!=\!\big( \rawfeature_{1},\ldots,\rawfeature_{\featurelenraw} \big)^{T} \!\in\! \mathbb{R}^{\featurelenraw}</math> | |||
of length | |||
<math>\featurelenraw</math>. The length | |||
<math>\featurelenraw</math> of the raw feature vector might be easily of | |||
the order of millions. To obtain a small set of relevant features | |||
<math>\featurevec\!=\!\big(\feature_{1},\ldots,\feature_{\featuredim} \big)^{T}\!\in\! \mathbb{R}^{\featuredim}</math>, we apply a linear transformation to the raw feature vector, | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_feat_learning_matrix} | |||
\featurevec = \mathbf{W} \rawfeaturevec. | |||
\end{equation} | |||
</math> | |||
Here, the “compression” matrix | |||
<math>\mathbf{W} \in \mathbb{R}^{\featuredim \times \featurelenraw}</math> maps | |||
(in a linear fashion) the (long) raw feature vector | |||
<math>\rawfeaturevec \in \mathbb{R}^{\featurelenraw}</math> to the (shorter) | |||
feature vector | |||
<math>\featurevec \in \mathbb{R}^{\featuredim}</math>. | |||
It is reasonable to choose the compression matrix | |||
<math>\mathbf{W} \in \mathbb{R}^{\featuredim \times \featurelenraw}</math> | |||
in \eqref{equ_feat_learning_matrix} such that the resulting features | |||
<math>\featurevec \in \mathbb{R}^{\featuredim}</math> | |||
allow to approximate the original <span class="mw-gls" data-name ="datapoint">data point</span> | |||
<math>\rawfeaturevec \in \mathbb{R}^{\featurelenraw}</math> as | |||
accurate as possible. We can approximate (or recover) the <span class="mw-gls" data-name ="datapoint">data point</span> | |||
<math>\rawfeaturevec \in \mathbb{R}^{\featurelenraw}</math> | |||
back from the features | |||
<math>\featurevec</math> by applying a reconstruction operator | |||
<math>\mathbf{R} \in \mathbb{R}^{\featurelenraw \times \featuredim}</math>, which is | |||
chosen such that | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_approx_linear_PCA} | |||
\rawfeaturevec \approx \mathbf{R} \featurevec \stackrel{\eqref{equ_feat_learning_matrix}}{=} \mathbf{R} \mathbf{W} \rawfeaturevec. | |||
\end{equation} | |||
</math> | |||
The approximation error | |||
<math>\emperror \big( \mathbf{W},\mathbf{R} \mid \dataset\big)</math> resulting | |||
when \eqref{equ_approx_linear_PCA} is applied to each <span class="mw-gls" data-name ="datapoint">data point</span> in a | |||
dataset | |||
<math>\dataset= \{ \rawfeaturevec^{(\sampleidx)}\}_{\sampleidx=1}^{\samplesize}</math> is then | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_app_error_PCA} | |||
\emperror \big( \mathbf{W},\mathbf{R} \mid \dataset\big) = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \| \rawfeaturevec^{(\sampleidx)} - \mathbf{R} \mathbf{W} \rawfeaturevec^{(\sampleidx)} \|^{2}. | |||
\end{equation} | |||
</math> | |||
One can verify that the approximation error | |||
<math>\emperror \big( \mathbf{W},\mathbf{R} \mid \dataset\big)</math> | |||
can only by minimal if the compression matrix | |||
<math>\mathbf{W}</math> is of the form | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_PCA_W} | |||
\mathbf{W} = \mathbf{W}_{\rm PCA} \defeq \big( \eigvecCov^{(1)},\ldots, \eigvecCov^{(\featuredim)} \big)^{T} \in \mathbb{R}^{\featuredim \times \featurelenraw}, | |||
\end{equation} | |||
</math> | |||
with | |||
<math>\featuredim</math> orthonormal vectors | |||
<math>\eigvecCov^{(\featureidx)}</math>, for | |||
<math>\featureidx=1,\ldots,\featuredim</math>. | |||
The vectors | |||
<math>\eigvecCov^{(\featureidx)}</math> are the <span class="mw-gls mw-gls-first" data-name ="eigenvector">eigenvector</span>s corresponding to the | |||
<math>\featuredim</math> largest | |||
<span class="mw-gls mw-gls-first" data-name ="eigenvalue">eigenvalue</span>s of the sample covariance matrix | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_Q_PCA} | |||
\mQ \defeq (1/\samplesize) \mathbf{Z}^{T} \mathbf{Z} \in \mathbb{R}^{\featurelenraw \times \featurelenraw}. | |||
\end{equation} | |||
</math> | |||
Here we used the data matrix | |||
<math>\mathbf{Z}\!=\!\big( \rawfeaturevec^{(1)}, \ldots, \rawfeaturevec^{(\samplesize)} \big)^{T}\!\in\!\mathbb{R}^{\samplesize \times \featurelenraw}</math>.\footnote{Some authors define the data matrix as | |||
<math>\mZ\!=\!\big( \widetilde{\rawfeaturevec}^{(1)}, \ldots, \widetilde{\rawfeaturevec}^{(\samplesize)} \big)^{T}\!\in\!\mathbb{R}^{\samplesize \times D}</math> using “centered” <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
<math>\rawfeaturevec^{(\sampleidx)} - \widehat{\vm}</math> | |||
obtained by subtracting the average | |||
<math>\widehat{\vm} = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \rawfeaturevec^{(\sampleidx)}</math>.} | |||
It can be verified easily, using the definition \eqref{equ_def_Q_PCA}, that the matrix | |||
<math>\mathbf{Q}</math> is <span class="mw-gls mw-gls-first" data-name ="psd">positive semi-definite (psd)</span>. As a <span class="mw-gls" data-name ="psd">psd</span> matrix, | |||
<math>\mQ</math> has an <span class="mw-gls mw-gls-first" data-name ="evd">eigenvalue decomposition (EVD)</span> of the form <ref name="Strang2007"/> | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_EVD_Q_PCA} | |||
\mQ=\big(\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelenraw)}\big) \begin{pmatrix}\eigval{1} & \ldots & 0 \\ 0 & \ddots & 0 \\ 0 & \ldots & \eigval{\featurelenraw} | |||
\end{pmatrix} \big(\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelenraw)}\big)^{T} | |||
\end{equation} | |||
</math> | |||
with real-valued <span class="mw-gls" data-name ="eigenvalue">eigenvalue</span>s | |||
<math>\eigval{1} \geq \eigval{2}\geq \ldots \geq \eigval{\featurelenraw} \geq 0</math> | |||
and orthonormal <span class="mw-gls" data-name ="eigenvector">eigenvector</span>s | |||
<math>\{ \eigvecCov^{(\featureidx)} \}_{\featureidx=1}^{\featurelenraw}</math>. | |||
The feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math> are obtained by applying the compression matrix | |||
<math>\mathbf{W}_{\rm PCA}</math> | |||
\eqref{equ_def_PCA_W} to the raw feature vectors | |||
<math>\rawfeaturevec^{(\sampleidx)}</math>. We refer to the entries of the | |||
learnt feature vector | |||
<math>\featurevec^{(\sampleidx)}= \mW_{\rm PCA} \rawfeaturevec^{(\sampleidx)}</math> (see \eqref{equ_def_PCA_W}) | |||
as the principal components (PC) of the raw feature vectors | |||
<math>\rawfeaturevec^{(\sampleidx)}</math>. Algorithm [[#alg_PCA | alg_PCA ]] | |||
summarizes the overall procedure of determining the compression matrix \eqref{equ_def_PCA_W} and computing | |||
the learnt feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math>. This procedure is known as <span class="mw-gls mw-gls-first" data-name ="pca">principal component analysis (PCA)</span>. | |||
<proc label="PCA" id="alg_PCA"> | |||
'''Input:''' dataset <math>\dataset=\{ \rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw} \}_{\sampleidx=1}^{\samplesize}</math>; number <math>\featuredim</math> of PCs. | |||
<ul style="list-style:numeric"> | |||
<li> compute the <span class="mw-gls" data-name ="evd">EVD</span> \eqref{equ_EVD_Q_PCA} to obtain orthonormal <span class="mw-gls" data-name ="eigenvector">eigenvector</span>s | |||
<math>\big(\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelenraw)}\big)</math> | |||
corresponding to (decreasingly ordered) eigenvalues | |||
<math>\eigval{1} \geq \eigval{2} \geq \ldots \geq \eigval{\featurelenraw} \geq 0</math> | |||
</li><li> construct compression matrix | |||
<math>\mW_{\rm PCA} \defeq \big( \eigvecCov^{(1)},\ldots, \eigvecCov^{(\featuredim)} \big)^{T} \in \mathbb{R}^{\featuredim \times \featurelenraw}</math> | |||
</li><li> compute feature vector | |||
<math>\featurevec^{(\sampleidx)} = \mW_{\rm PCA} \rawfeaturevec^{(\sampleidx)}</math> whose entries are PC of | |||
<math>\rawfeaturevec^{(\sampleidx)}</math> | |||
</li><li> compute approximation error | |||
<math>\emperror^{(\rm PCA)} = \sum_{\featureidx = \featuredim+1}^{\featurelenraw} \eigval{\featureidx}</math> (see \eqref{equ_approx_error_PCA}). | |||
</li> | |||
</ul> | |||
'''Output:''' | |||
<math>\featurevec^{(\sampleidx)}</math>, for | |||
<math>\sampleidx=1,\ldots,\samplesize</math>, and the approximation error | |||
<math>\emperror^{(\rm PCA)}</math>. | |||
</proc> | |||
The length <math>\featuredim \in \{0,\ldots,\featurelenraw)</math> of the delivered feature vectors <math>\featurevec^{(\sampleidx)}</math>, | |||
for <math>\sampleidx=1,\ldots,\samplesize</math>, is an input (or hyper-) parameter of Algorithm [[#alg_PCA | alg_PCA ]]. Two extreme cases | |||
are <math>\featuredim=0</math> (maximum compression) and <math>\featuredim=\featurelenraw</math> (no compression). | |||
We finally note that the choice for the orthonormal <span class="mw-gls" data-name ="eigenvector">eigenvector</span>s in \eqref{equ_def_PCA_W} | |||
might not be unique. Depending on the sample covariance matrix <math>\mQ</math>, there might different sets | |||
of orthonormal vectors that correspond to the same eigenvalue of <math>\mQ</math>. Thus, for a given length | |||
<math>\featuredim</math> of the new feature vectors, there might be several different matrices | |||
<math>\mW</math> that achieve the same (optimal) reconstruction error <math>\emperror^{(\rm PCA)}</math>. | |||
Computationally, Algorithm [[#alg_PCA | alg_PCA ]] essentially amounts to an <span class="mw-gls" data-name ="evd">EVD</span> of the sample covariance matrix | |||
<math>\mQ</math> | |||
\eqref{equ_def_Q_PCA}. The <span class="mw-gls" data-name ="evd">EVD</span> of | |||
<math>\mQ</math> provides not only the optimal compression matrix | |||
<math>\mW_{\rm PCA}</math> but also the measure | |||
<math>\emperror^{(\rm PCA)}</math> for the information loss incurred by | |||
replacing the original <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
<math>\rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}</math> | |||
with the shorter feature vector | |||
<math>\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}</math>. | |||
We quantify this information loss by the approximation error obtained when using the compression | |||
matrix | |||
<math>\mathbf{W}_{\rm PCA}</math> (and corresponding reconstruction matrix | |||
<math>\mathbf{R}_{\rm opt} = \mathbf{W}_{\rm PCA}^{T}</math>), | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_approx_error_PCA} | |||
\emperror^{(\rm PCA)} \defeq \emperror \big( \mathbf{W}_{\rm PCA},\underbrace{\mathbf{R}_{\rm opt}}_{=\mathbf{W}_{\rm PCA}^{T}}\mid \dataset\big) = \sum_{\featureidx = \featuredim+1}^{\featurelenraw} \eigval{\featureidx}. | |||
\end{equation} | |||
</math> | |||
As depicted in Figure [[#fig_ellbow_PCA|fig_ellbow_PCA]], the approximation error | |||
<math>\emperror^{(\rm PCA)}</math> decreases with increasing | |||
number | |||
<math>\featuredim</math> of PCs used for the new features \eqref{equ_feat_learning_matrix}. For the extreme case | |||
<math>\featuredim\!=\!0</math>, | |||
where we completely ignore the raw feature vectors | |||
<math>\rawfeaturevec^{(\sampleidx)}</math>, the optimal reconstruction error is | |||
<math>\emperror^{(\rm PCA)} = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big\| \rawfeaturevec^{(\sampleidx)} \big\|^{2}</math>. | |||
The other extreme case <math>\featuredim\!=\!\featurelenraw</math> allows to use the raw features directly as the new features <math>\featurevec^{(\sampleidx)}\!=\!\rawfeaturevec^{(\sampleidx)}</math>. This extreme case means no compression at all, and trivially results in a zero reconstruction error <math>\emperror^{(\rm PCA)}\!=\!0</math>. | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_ellbow_PCA"></span> | |||
[[File:fig_ellbow_PCA.jpg | 500px | thumb | Reconstruction error | |||
<math>\emperror^{(\rm PCA)}</math> (see \eqref{equ_approx_error_PCA}) | |||
of <span class="mw-gls" data-name ="pca">PCA</span> for varying number | |||
<math>\featuredim</math> of PCs. ]] | |||
</div> | |||
===Combining PCA with linear regression === | |||
One important use case of <span class="mw-gls" data-name ="pca">PCA</span> is as a pre-processing step within an overall ML problem | |||
such as <span class="mw-gls" data-name ="linreg">linear regression</span> (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]). As discussed in Chapter | |||
[[guide:50be9327aa | Regularization ]], <span class="mw-gls" data-name ="linreg">linear regression</span> methods are prone to overfitting | |||
whenever the <span class="mw-gls" data-name ="datapoint">data point</span>s are characterized by raw feature vectors | |||
<math>\rawfeaturevec</math> | |||
whose length | |||
<math>\featurelenraw</math> exceeds the number | |||
<math>\samplesize</math> of labeled <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
used in <span class="mw-gls mw-gls-first" data-name ="erm">empirical risk minimization (ERM)</span>. | |||
One simple but powerful strategy to avoid overfitting is to preprocess the raw | |||
features | |||
<math>\rawfeaturevec^{(\sampleidx)}\in \mathbb{R}^{\featurelenraw}</math>, for | |||
<math>\sampleidx=1,\ldots,\samplesize</math> | |||
by applying <span class="mw-gls" data-name ="pca">PCA</span>. Indeed, <span class="mw-gls" data-name ="pca">PCA</span> Algorithm [[#alg_PCA | alg_PCA ]] delivers feature vectors | |||
<math>\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}</math> of prescribed length | |||
<math>\featuredim</math>. Thus, | |||
choosing the parameter | |||
<math>\featuredim</math> such that | |||
<math>\featuredim < \samplesize</math> will typically prevent the follow-up <span class="mw-gls" data-name ="linreg">linear regression</span> method from overfitting. | |||
===How To Choose Number of PC?=== | |||
There are several aspects which can guide the choice for the number <math>\featuredim</math> of PCs to be used as features. | |||
* To generate data visualizations we might use either <math>\featuredim=2</math> or <math>\featuredim=3</math>. | |||
* We should choose <math>\featuredim</math> sufficiently small such that the overall ML method fits the available computational resources. | |||
* Consider using <span class="mw-gls" data-name ="pca">PCA</span> as a pre-processing for <span class="mw-gls" data-name ="linreg">linear regression</span> (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]]). In particular, we can use the learnt feature vectors <math>\featurevec^{(\sampleidx)}</math> delivered by <span class="mw-gls" data-name ="pca">PCA</span> as the feature vectors of <span class="mw-gls" data-name ="datapoint">data point</span>s in plain <span class="mw-gls" data-name ="linreg">linear regression</span> methods. To avoid overfitting, we should choose <math>\featuredim < \samplesize</math> (see Chapter [[guide:50be9327aa | Regularization ]]). | |||
* Choose <math>\featuredim</math> large enough such that the resulting approximation error <math>\emperror^{(\rm PCA)}</math> is reasonably small (see Figure [[#fig_ellbow_PCA|fig_ellbow_PCA]]). | |||
===Data Visualisation=== | |||
If we use <span class="mw-gls" data-name ="pca">PCA</span> with <math>\featuredim=2</math>, we obtain feature vectors | |||
<math>\featurevec^{(\sampleidx)} = \mW_{\rm PCA} \rawfeaturevec^{(\sampleidx)}</math> (see \eqref{equ_feat_learning_matrix}) which can be depicted as points in a <span class="mw-gls" data-name ="scatterplot">scatterplot</span> (see Section [[guide:B85f6bf6f2#equ_subsection_scatterplot | Scatterplot ]]). | |||
As an example, consider <span class="mw-gls" data-name ="datapoint">data point</span>s <math>\datapoint^{(\sampleidx)}</math> obtained from historic recordings of Bitcoin statistics. Each <span class="mw-gls" data-name ="datapoint">data point</span> | |||
<math>\datapoint^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}</math> is a vector of length | |||
<math>\featurelenraw=6</math>. It is difficult to visualise points in an <span class="mw-gls mw-gls-first" data-name ="euclidspace">Euclidean space</span> | |||
<math>\mathbb{R}^{\featurelenraw}</math> of dimension | |||
<math>\featurelenraw > 2</math>. | |||
Therefore, we apply <span class="mw-gls" data-name ="pca">PCA</span> with | |||
<math>\featuredim=2</math> which results in feature vectors | |||
<math>\featurevec^{(\sampleidx)} \in \mathbb{R}^{2}</math>. | |||
These new feature vectors (of length | |||
<math>2</math>) can be depicted conveniently as the <span class="mw-gls" data-name ="scatterplot">scatterplot</span> in Figure [[#fig_scatterplot_visualization|fig_scatterplot_visualization]]. | |||
<div class="d-flex justify-content-center"> | |||
<span id="fig_scatterplot_visualization"></span> | |||
[[File:fig_scatterplot_visualization.jpg | 500px | thumb | A <span class="mw-gls" data-name ="scatterplot">scatterplot</span> of <span class="mw-gls" data-name ="datapoint">data point</span>s with feature vectors | |||
<math>\featurevec^{(\sampleidx)} = \big(\feature_{1}^{(\sampleidx)},\feature_{2}^{(\sampleidx)}\big)^{T}</math> | |||
whose entries are the first two PCs of the Bitcoin statistics | |||
<math>\rawfeaturevec^{(\sampleidx)}</math> of the | |||
<math>\sampleidx</math>-th day. ]] | |||
</div> | |||
===Extensions of PCA=== | |||
We now briefly discuss variants and extensions of the basic <span class="mw-gls" data-name ="pca">PCA</span> method. | |||
{| class="table" | |||
|- | |||
! Variant/extension !! Description | |||
|- | |||
| Kernel <span class="mw-gls" data-name ="pca">PCA</span> <ref name="hastie01statisticallearning"/>{{rp|at=Ch.14.5.4}} || The <span class="mw-gls" data-name ="pca">PCA</span> method is most effective if the raw feature vectors of <span class="mw-gls" data-name ="datapoint">data point</span>s are concentrated around a <math>\featurelen</math>-dimensional linear subspace of <math>\mathbb{R}^{\featurelenraw}</math>. Kernel <span class="mw-gls" data-name ="pca">PCA</span> extends <span class="mw-gls" data-name ="pca">PCA</span> to <span class="mw-gls" data-name ="datapoint">data point</span>s that are located near a low-dimensional manifold which might be highly non-linear. This is achieved by applying <span class="mw-gls" data-name ="pca">PCA</span> to transformed feature vectors instead of the original raw feature vectors. Kernel <span class="mw-gls" data-name ="pca">PCA</span> first applies a (typically non-linear) feature map <math>\featuremap</math> to the raw feature vectors <math>\rawfeaturevec^{(\sampleidx)}</math> (see Section [[guide:013ef4b5cd#sec_kernel_methods | Kernel Methods ]]) and applies <span class="mw-gls" data-name ="pca">PCA</span> to the transformed feature vectors <math>\featuremap \big( \rawfeaturevec^{(\sampleidx)} \big)</math>, for <math>\sampleidx=1,\ldots,\samplesize</math>. | |||
|- | |||
| Robust <span class="mw-gls" data-name ="pca">PCA</span> <ref name="RobustPCA"/> || The basic <span class="mw-gls" data-name ="pca">PCA</span> Algorithm [[#alg_PCA | alg_PCA ]] is sensitive to <span class="mw-gls mw-gls-first" data-name ="outlier">outlier</span>s, i.e., a small number of <span class="mw-gls" data-name ="datapoint">data point</span>s with significantly different statistical properties than the bulk of <span class="mw-gls" data-name ="datapoint">data point</span>s. This sensitivity might be attributed to the properties of the squared Euclidean norm \eqref{equ_def_squared_eucl_norm} which is used in <span class="mw-gls" data-name ="pca">PCA</span> to measure the reconstruction error \eqref{equ_def_reconst_error}. We have seen in Chapter [[guide:013ef4b5cd | The Landscape of ML ]] that <span class="mw-gls" data-name ="linreg">linear regression</span> (see Section [[guide:013ef4b5cd#sec_lin_reg | Linear Regression ]] and [[guide:013ef4b5cd#sec_lad | Least Absolute Deviation Regression ]]) can be made robust against outliers by replacing the squared error loss with another <span class="mw-gls mw-gls-first" data-name ="lossfunc">loss function</span>. In a similar spirit, robust <span class="mw-gls" data-name ="pca">PCA</span> replaces the squared Euclidean norm with another norm that is less sensitive to having very large reconstruction errors \eqref{equ_def_reconst_error} for a small number of <span class="mw-gls" data-name ="datapoint">data point</span>s (which are outliers). | |||
|- | |||
| Sparse <span class="mw-gls" data-name ="pca">PCA</span> <ref name="hastie01statisticallearning"/>{{rp|at=Ch.14.5.5}} || The basic <span class="mw-gls" data-name ="pca">PCA</span> method transforms the raw feature vector <math>\rawfeaturevec^{(\sampleidx)}</math> of a <span class="mw-gls" data-name ="datapoint">data point</span> to a new (shorter) feature vector <math>\featurevec^{(\sampleidx)}</math>. In general each entry <math>\feature^{(\sampleidx)}_{\featureidx}</math> of the new feature vector will depend on each entry of the raw feature vector <math>\rawfeaturevec^{(\sampleidx)}</math>. More precisely, the new feature <math>\feature^{(\sampleidx)}_{\featureidx}</math> depends on all raw features <math>\rawfeature^{(\sampleidx)}_{\featureidx'}</math> for which the corresponding entry <math>W_{\featureidx,\featureidx'}</math> of the matrix <math>\mW= \mW_{\rm PCA}</math> \eqref{equ_def_PCA_W} is non-zero. For most <span class="mw-gls mw-gls-first" data-name ="dataset">dataset</span>s, all entries of the matrix <math>\mW_{\rm PCA}</math> will typically be non-zero. In some applications of linear dimensionality reduction we would like to construct new features that depend only on a small subset of raw features. Equivalently we would like to learn a linear compression map <math>\mW</math> \eqref{equ_feat_learning_matrix} such that each row of <math>\mW</math> contains only few non-zero entries. To this end, sparse <span class="mw-gls" data-name ="pca">PCA</span> enforces the rows of the compression matrix <math>\mW</math> to contain only a small number of non-zero entries. This enforcement can be implement either using additional constraints on <math>\mW</math> or by adding a penalty term to the reconstruction error \eqref{equ_app_error_PCA}. | |||
|- | |||
| Probabilistic <span class="mw-gls" data-name ="pca">PCA</span> <ref name="Roweis98emalgorithms"/><ref name="probabilistic-principal-component-analysis"/> || We have motivated <span class="mw-gls" data-name ="pca">PCA</span> as a method for learning an optimal linear compression map (matrix) \eqref{equ_feat_learning_matrix} | |||
such that the compressed feature vectors allows to linearly reconstruct the original raw feature vector | |||
with minimum reconstruction error \eqref{equ_app_error_PCA}. Another interpretation of <span class="mw-gls" data-name ="pca">PCA</span> is that of | |||
a method that learns a subspace of | |||
<math>\mathbb{R}^{\featurelenraw}</math> that best fits the distribution of | |||
the raw feature vectors | |||
<math>\rawfeaturevec^{(\sampleidx)}</math>, for | |||
<math>\sampleidx=1,\ldots,\samplesize</math>. This optimal subspace is | |||
precisely the subspace spanned by the rows of | |||
<math>\mathbf{W}_{\rm PCA}</math> \eqref{equ_def_PCA_W}. | |||
<span class="mw-gls mw-gls-first" data-name ="ppca">Probabilistic PCA (PPCA)</span> interprets the raw feature vectors | |||
<math>\rawfeaturevec^{(\sampleidx)}</math> | |||
as realizations of <span class="mw-gls mw-gls-first" data-name ="iid">independent and identically distributed (iid)</span> <span class="mw-gls mw-gls-first" data-name ="rv">random variable (RV)</span>s. These realizations are modelled as | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_PPCA_model} | |||
\rawfeaturevec^{(\sampleidx)} = \mW^{T} \featurevec^{(\sampleidx)} + \bm{\varepsilon}^{(\sampleidx)} \mbox{, for } \sampleidx=1,\ldots,\samplesize. | |||
\end{equation} | |||
</math> | |||
Here, | |||
<math>\mW \in \mathbb{R}^{\featuredim \times \featurelenraw}</math> is some unknown matrix with orthonormal rows. The rows of | |||
<math>\mW</math> span | |||
the subspace around which the raw features are concentrated. The vectors | |||
<math>\featurevec^{(\sampleidx)}</math> in \eqref{equ_def_PPCA_model} | |||
are realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s whose common probability distribution is | |||
<math>\mathcal{N}(\mathbf{0}, \mathbf{I})</math>. The | |||
vectors | |||
<math>\bm{\varepsilon}^{(\sampleidx)}</math> are realizations of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s whose common probability distribution is | |||
<math>\mathcal{N}(\mathbf{0}, \sigma^{2} \mathbf{I})</math> with some fixed but unknown variance | |||
<math>\sigma^{2}</math>. Note that | |||
<math>\mW</math> and | |||
<math>\sigma^{2}</math> parametrize | |||
the joint probability distribution of the feature vectors | |||
<math> \rawfeaturevec^{(\sampleidx)}</math> via \eqref{equ_def_PPCA_model}. | |||
<span class="mw-gls" data-name ="ppca">PPCA</span> amounts to maximum likelihood estimation (see Section [[guide:013ef4b5cd#sec_max_iikelihood | Maximum Likelihood ]]) of the parameters | |||
<math>\mW</math> and | |||
<math>\sigma^{2}</math>. | |||
This maximum likelihood estimation problem can be solved using computationally efficient estimation techniques such as <span class="mw-gls mw-gls-first" data-name ="em">expectation maximization (EM)</span> <ref name="probabilistic-principal-component-analysis"/>{{rp|at=Appendix B}}. The implementation of <span class="mw-gls mw-gls-first" data-name ="ppca">probabilistic PCA (PPCA)</span> via <span class="mw-gls" data-name ="em">EM</span> also offers a principled approach | |||
to handle missing data. Roughly speaking, the <span class="mw-gls" data-name ="em">EM</span> method allows to use the probabilistic model \eqref{equ_def_PPCA_model} | |||
to estimate missing raw features <ref name="probabilistic-principal-component-analysis"/>{{rp|at=Sec.\ 4.1}}. | |||
|} | |||
==Feature Learning for Non-Numeric Data== | |||
We have motivated dimensionality reduction methods as transformations of (very long) raw feature vectors | |||
to a new (shorter) feature vector | |||
<math>\featurevec</math> such that it allows to reconstruct the raw features | |||
<math>\rawfeaturevec</math> with minimum reconstruction | |||
error \eqref{equ_def_reconst_error}. To make this requirement precise we need to define a measure for the size | |||
of the reconstruction error and specify the class of possible reconstruction maps. <span class="mw-gls mw-gls-first" data-name ="pca">Principal component analysis (PCA)</span> uses the squared Euclidean | |||
norm \eqref{equ_app_error_PCA} to measure the reconstruction error and only allows for linear reconstruction | |||
maps \eqref{equ_approx_linear_PCA}. | |||
Alternatively, we can view dimensionality reduction as the generation of new feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math> | |||
that maintain the intrinsic geometry of the <span class="mw-gls" data-name ="datapoint">data point</span>s with their raw feature vectors | |||
<math>\rawfeaturevec^{(\sampleidx)}</math>. | |||
Different dimensionality reduction methods use different concepts for characterizing the “intrinsic geometry” of <span class="mw-gls" data-name ="datapoint">data point</span>s. | |||
<span class="mw-gls" data-name ="pca">PCA</span> defines the intrinsic geometry of <span class="mw-gls" data-name ="datapoint">data point</span>s using the squared Euclidean distances between feature vectors. | |||
Indeed, <span class="mw-gls" data-name ="pca">PCA</span> produces feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math> such that for <span class="mw-gls" data-name ="datapoint">data point</span>s whose raw feature vectors | |||
have small squared Euclidean distance, also the new feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math> will have small squared | |||
Euclidean distance. | |||
Some application domains generate <span class="mw-gls" data-name ="datapoint">data point</span>s for which the Euclidean distances between raw feature vectors | |||
does not reflect the intrinsic geometry of <span class="mw-gls" data-name ="datapoint">data point</span>s. As a point in case, consider <span class="mw-gls" data-name ="datapoint">data point</span>s representing scientific | |||
articles which can be characterized by the relative frequencies of words from some given set of relevant words (dictionary). | |||
A small Euclidean distance between the resulting raw feature vectors typically does not imply that the corresponding | |||
text documents are similar. Instead, the similarity between two articles might depend on the number of authors that | |||
are contained in author lists of both papers. We can represent the similarities between all articles using a similarity | |||
graph whose nodes represent <span class="mw-gls" data-name ="datapoint">data point</span>s which are connected by an edge (link) if they are similar (see Figure [[#fig_connect_clustering|fig_connect_clustering]]). | |||
Consider a dataset | |||
<math>\dataset = \big(\datapoint^{(1)},\ldots,\datapoint^{(\samplesize)} \big)</math> whose intrinsic geometry is | |||
characterized by an unweighted <span class="mw-gls mw-gls-first" data-name ="simgraph">similarity graph</span> | |||
<math>\graph = \big(\nodes \defeq \{1,\ldots,\samplesize\},\edges\big)</math>. | |||
The node | |||
<math>\sampleidx \in \nodes</math> represents the | |||
<math>\sampleidx</math>-th <span class="mw-gls" data-name ="datapoint">data point</span> | |||
<math>\datapoint^{(\sampleidx)}</math>. Two | |||
nodes are connected by an undirected edge if the corresponding <span class="mw-gls" data-name ="datapoint">data point</span>s are similar. | |||
We would like to find short feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math>, for | |||
<math>\sampleidx=1,\ldots,\samplesize</math>, such | |||
that two <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
<math>\sampleidx,\sampleidx'</math>, whose feature vectors | |||
<math>\featurevec^{(\sampleidx)}, \featurevec^{(\sampleidx')}</math> | |||
have small Euclidean distance, are well-connected to each other. This informal requirement must be made | |||
precise by a measure for how well two nodes of an undirected graph are connected. We refer the | |||
reader to literature on network theory for an overview and details of various connectivity | |||
measures <ref name="NewmannBook"/>. | |||
Let us discuss a simple but powerful technique to map the nodes | |||
<math>\sampleidx \in \nodes</math> of an | |||
undirected graph | |||
<math>\graph</math> to (short) feature vectors | |||
<math>\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}</math>. | |||
This map is such that the Euclidean distances between the feature vectors of two nodes reflect their connectivity | |||
within | |||
<math>\graph</math>. This technique uses the <span class="mw-gls mw-gls-first" data-name ="LapMat">Laplacian matrix</span> | |||
<math>\mL \in \mathbb{R}^{(\sampleidx)}</math> | |||
which is defined for an undirected graph | |||
<math>\graph</math> (with node set | |||
<math>\nodes = \{1,\ldots,\samplesize\}</math>) element-wise | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_laplacian_sim_graph} | |||
L_{\sampleidx,\nodeidx'} \defeq \begin{cases} - 1 & \mbox{ , if } \{\sampleidx,\sampleidx'\} \in \edges \\ | |||
\nodedegree{\sampleidx} & \mbox{ , if } \sampleidx=\sampleidx' \\ | |||
0 & \mbox{ otherwise.} \end{cases}. | |||
\end{equation} | |||
</math> | |||
Here, | |||
<math>\nodedegree{\sampleidx} \defeq \big| \{ \sampleidx': \{\sampleidx,\sampleidx'\} \in \edges \} \big|</math> | |||
denotes the number of neighbours (the degree) of node | |||
<math>\sampleidx \in \nodes</math>. It can be shown | |||
that the <span class="mw-gls" data-name ="LapMat">Laplacian matrix</span> | |||
<math>\mL</math> is <span class="mw-gls" data-name ="psd">psd</span> <ref name="Luxburg2007"/>{{rp|at=Proposition 1}}. | |||
Therefore we can find a set of orthonormal <span class="mw-gls" data-name ="eigenvector">eigenvector</span>s | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_eigvec_alap_featLearn} | |||
\eigvecCov^{(1)},\ldots,\eigvecCov^{(\samplesize)} \in \mathbb{R}^{\samplesize} | |||
\end{equation} | |||
</math> | |||
with corresponding (ordered in a non-decreasing fashion) <span class="mw-gls" data-name ="eigenvalue">eigenvalue</span>s | |||
<math>\eigval{1} \leq \ldots \leq \eigval{\samplesize}</math> of | |||
<math>\mL</math>. | |||
For a given number | |||
<math>\featuredim</math>, we construct the feature vector | |||
<math display="block">\featurevec^{(\sampleidx)} \defeq \big( \eigvecCoventry_{\sampleidx}^{(1)},\ldots,\eigvecCoventry_{\sampleidx}^{(\featurelen)} \big)^{T}</math> | |||
for the | |||
<math>\sampleidx</math>th <span class="mw-gls" data-name ="datapoint">data point</span>. Here, we used the entries of of the first | |||
<math>\featuredim</math> eigenvectors \eqref{equ_def_eigvec_alap_featLearn}. | |||
It can be shown that the Euclidean distances between the feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math>, for | |||
<math>\sampleidx=1,\ldots,\samplesize</math>, | |||
reflect the connectivities between <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
<math>\sampleidx=1,\ldots,\samplesize</math> in the <span class="mw-gls" data-name ="simgraph">similarity graph</span> | |||
<math>\graph</math>. | |||
For a more precise statement of this informal claim we refer to the excellent tutorial <ref name="Luxburg2007"/>. | |||
To summarize, we can construct numeric feature vectors for (non-numeric ) <span class="mw-gls" data-name ="datapoint">data point</span>s via the <span class="mw-gls" data-name ="eigenvector">eigenvector</span>s | |||
of the <span class="mw-gls" data-name ="LapMat">Laplacian matrix</span> of a <span class="mw-gls" data-name ="simgraph">similarity graph</span> for the <span class="mw-gls" data-name ="datapoint">data point</span>s. Algorithm [[#alg_dimred_discrete | alg_dimred_discrete ]] summarizes this | |||
feature learning method which requires as its input a <span class="mw-gls" data-name ="simgraph">similarity graph</span> for the <span class="mw-gls" data-name ="datapoint">data point</span>s and the desired number | |||
<math>\featurelen</math> | |||
of numeric features. Note that Algorithm [[#alg_dimred_discrete | alg_dimred_discrete ]] does not make any use of the Euclidean distances | |||
between raw feature vectors and uses solely the <span class="mw-gls" data-name ="simgraph">similarity graph</span> | |||
<math>\graph</math> to determine the intrinsic geometry of <math>\dataset</math>. | |||
<proc label="Feature Learning for Non-Numeric Data" id="alg_dimred_discrete"> | |||
'''Input:''' <span class="mw-gls" data-name ="dataset">dataset</span> | |||
<math>\dataset=\{ \rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw} \}_{\sampleidx=1}^{\samplesize}</math>; | |||
<span class="mw-gls" data-name ="simgraph">similarity graph</span> | |||
<math>\graph</math>; | |||
number | |||
<math>\featuredim</math> of features to be constructed for each <span class="mw-gls" data-name ="datapoint">data point</span>. | |||
<ul style="list-style:numeric"><li> construct the <span class="mw-gls" data-name ="LapMat">Laplacian matrix</span> | |||
<math>\mL</math> of the <span class="mw-gls" data-name ="simgraph">similarity graph</span> (see \eqref{equ_def_laplacian_sim_graph}) | |||
</li><li> compute <span class="mw-gls" data-name ="evd">EVD</span> of | |||
<math>\mL</math> to obtain | |||
<math>\featurelen</math> orthonormal <span class="mw-gls" data-name ="eigenvector">eigenvector</span>s \eqref{equ_def_eigvec_alap_featLearn} | |||
corresponding to the smallest <span class="mw-gls" data-name ="eigenvalue">eigenvalue</span>s of | |||
<math>\mL</math> | |||
</li><li> for each <span class="mw-gls" data-name ="datapoint">data point</span> | |||
<math>\sampleidx</math>, construct feature vector | |||
<math display="block"> | |||
\begin{equation} | |||
\featurevec^{(\sampleidx)} \defeq \big( \eigvecCoventry^{(1)}_{\sampleidx}, \ldots, \eigvecCoventry^{(\featurelen)}_{\sampleidx} \big)^{T} \in \mathbb{R}^{\featurelen} | |||
\end{equation} | |||
</math> | |||
</li></ul>'''Output:''' <math>\featurevec^{(\sampleidx)}</math>, for <math>\sampleidx=1,\ldots,\samplesize</math> | |||
</proc> | |||
==<span id="sec_lda"/>Feature Learning for Labeled Data== | |||
We have discussed <span class="mw-gls" data-name ="pca">PCA</span> as a linear dimensionality reduction method. <span class="mw-gls" data-name ="pca">PCA</span> learns a compression matrix | |||
that maps raw features | |||
<math>\rawfeaturevec^{(\sampleidx)}</math> of <span class="mw-gls" data-name ="datapoint">data point</span>s to new (much shorter) feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math>. The feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math> determined by <span class="mw-gls" data-name ="pca">PCA</span> depend solely | |||
on the raw feature vectors | |||
<math>\rawfeaturevec^{(\sampleidx)}</math> of a given dataset | |||
<math>\dataset</math>. In particular, <span class="mw-gls" data-name ="pca">PCA</span> determines | |||
the compression matrix such that the new features allow for a linear reconstruction \eqref{equ_approx_linear_PCA} | |||
with minimum reconstruction error \eqref{equ_app_error_PCA}. | |||
For some application domains we might not only have access to raw feature vectors but also to the label | |||
values | |||
<math>\truelabel^{(\sampleidx)}</math> of the <span class="mw-gls" data-name ="datapoint">data point</span>s in | |||
<math>\dataset</math>. Indeed, dimensionality reduction | |||
methods might be used as pre-processing step within a regression or classification problem that involves a labeled <span class="mw-gls mw-gls-first" data-name ="trainset">training set</span>. | |||
However, in its basic form, <span class="mw-gls" data-name ="pca">PCA</span> (see Algorithm [[#alg_PCA | alg_PCA ]]) does not allow to exploit the information | |||
provided by available labels | |||
<math>\truelabel^{(\sampleidx)}</math> of <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
<math>\rawfeaturevec^{(\sampleidx)}</math>. | |||
For some datasets, <span class="mw-gls" data-name ="pca">PCA</span> might deliver feature vectors that are not very relevant for the overall task of | |||
predicting the label of a <span class="mw-gls" data-name ="datapoint">data point</span>. | |||
Let us now discuss a modification of <span class="mw-gls" data-name ="pca">PCA</span> that exploits the information provided by available labels of the | |||
<span class="mw-gls" data-name ="datapoint">data point</span>s. The idea is to learn a linear construction map (matrix) | |||
<math>\mW</math> such that the new feature vectors | |||
<math>\featurevec^{(\sampleidx)} = \mW \rawfeaturevec^{(\sampleidx)}</math> allow to predict the label | |||
<math>\truelabel^{(\sampleidx)}</math> | |||
as good as possible. We restrict the prediction to be linear, | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_lin_predictor_dimred} | |||
\hat{\truelabel}^{(\sampleidx)} \defeq \vr^{T} \featurevec^{(\sampleidx)} = \vr^{T} \mW \rawfeaturevec^{(\sampleidx)}, | |||
\end{equation} | |||
</math> | |||
with some weight vector | |||
<math>\vr \in \mathbb{R}^{\featuredim}</math>. | |||
While <span class="mw-gls" data-name ="pca">PCA</span> is motivated by minimizing the reconstruction error \eqref{equ_def_reconst_error}, we now aim | |||
at minimizing the prediction error | |||
<math>\hat{\truelabel}^{(\sampleidx)} - \truelabel^{(\sampleidx)}</math>. In particular, we assess | |||
the usefulness of a given pair of construction map | |||
<math>\mW</math> and predictor | |||
<math>\vr</math> (see \eqref{equ_lin_predictor_dimred}), | |||
using the <span class="mw-gls mw-gls-first" data-name ="emprisk">empirical risk</span> | |||
<math display="block"> | |||
\begin{align} | |||
\emperror \big( \mathbf{W},\mathbf{r} \mid \dataset\big) & \defeq (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big( \truelabel^{(\sampleidx)} - \hat{\truelabel}^{(\sampleidx)} \big)^{2} \nonumber \\ | |||
& \label{equ_lda_prediction_error} \stackrel{\eqref{equ_lin_predictor_dimred}}{=} (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big( \truelabel^{(\sampleidx)} - \mathbf{r}^{T} \mathbf{W} \rawfeaturevec^{(\sampleidx)} \big)^{2}. | |||
\end{align} | |||
</math> | |||
to guide the learning of a compressing matrix <math>\mW</math> and corresponding linear predictor <span class="mw-gls mw-gls-first" data-name ="weights">weights</span> | |||
<math>\vr</math> (\eqref{equ_lin_predictor_dimred}). | |||
The optimal matrix | |||
<math>\mW</math> that minimizes the <span class="mw-gls" data-name ="emprisk">empirical risk</span> \eqref{equ_lda_prediction_error} can be obtained via | |||
the <span class="mw-gls" data-name ="evd">EVD</span> \eqref{equ_EVD_Q_PCA} of the sample covariance matrix | |||
<math>\mQ</math> \eqref{equ_def_Q_PCA}. Note that we have | |||
used the <span class="mw-gls" data-name ="evd">EVD</span> of | |||
<math>\mQ</math> already for <span class="mw-gls" data-name ="pca">PCA</span> in Section [[guide:4f25e79970#sec_pca | Principal Component Analysis ]] (see \eqref{equ_def_PCA_W}). Remember that <span class="mw-gls" data-name ="pca">PCA</span> uses the <math>\featuredim</math> eigenvectors <math>\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelen)}</math> corresponding to the <math>\featurelen</math> largest eigenvalues of <math>\mQ</math>. In contrast, to minimize \eqref{equ_lda_prediction_error}, we need to use a different set of eigenvectors in the rows of <math>\mW</math> in general. To find the right set of | |||
<math>\featuredim</math> eigenvectors, we need the sample cross-correlation vector | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_cross_correlation_PCA} | |||
\vq \defeq (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \truelabel^{(\sampleidx)} \rawfeaturevec^{(\sampleidx)}. | |||
\end{equation} | |||
</math> | |||
The entry <math>q_{\featureidx}</math> of the vector <math>\vq</math> estimates the correlation between the raw | |||
feature <math>\rawfeature^{(\sampleidx)}_{\featureidx}</math> and the label <math>\truelabel^{(\sampleidx)}</math>. | |||
We then define the index set | |||
<math display="block"> | |||
\begin{equation} | |||
\mathcal{S} \defeq \{ \featureidx_{1},\ldots,\featureidx_{\featurelen}\} \mbox{ such that } \big(q_{\featureidx}\big)^2/\eigval{\featureidx} \geq \big(q_{\featureidx'}\big)^2/\eigval{\featureidx'} \mbox{ for any } \featureidx \in \mathcal{S}, \featureidx' \in \{1,\ldots,\featurelenraw\} \notin \mathcal{S}. | |||
\end{equation} | |||
</math> | |||
It can then be shown that the rows of the optimal compression matrix <math>\mW</math> are the <span class="mw-gls" data-name ="eigenvector">eigenvector</span>s | |||
<math>\eigvecCov^{(\featureidx)}</math> with | |||
<math>\featureidx \in \mathcal{S}</math>. We summarize the overall feature learning method | |||
in Algorithm [[#alg_PCA_labeled | alg_PCA_labeled ]]. | |||
<proc label="Linear Feature Learning for Labeled Data" id="alg_PCA_labeled"> | |||
'''Input:''' dataset | |||
<math> \big(\rawfeaturevec^{(1)},\truelabel^{(1)} \big),\ldots,\big(\rawfeaturevec^{(\samplesize)},\truelabel^{(\samplesize)} \big)</math> with raw features | |||
<math>\rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}</math> and numeric labels | |||
<math>\truelabel^{(\sampleidx)} \in \mathbb{R}</math> ; length | |||
<math>\featuredim</math> of new feature vectors. | |||
<ul style="list-style:numeric"><li> compute <span class="mw-gls" data-name ="evd">EVD</span> \eqref{equ_EVD_Q_PCA} of the sample covariance matrix \eqref{equ_def_Q_PCA} to obtain orthonormal eigenvectors | |||
<math>\big(\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelenraw)}\big)</math> | |||
corresponding to (decreasingly ordered) eigenvalues | |||
<math>\eigval{1}\geq \eigval{2}\geq \ldots \geq \eigval{\featurelenraw} \geq 0</math> | |||
</li><li> compute the sample cross-correlation vector \eqref{equ_cross_correlation_PCA} and, in turn, the sequence | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_sequence_cross_cov_matrix} | |||
\big(q_{1}\big)^2/\eigval{1}, \ldots, \big(q_{\featurelenraw}\big)^2/\eigval{\featurelenraw} | |||
\end{equation} | |||
</math> | |||
</li><li> determine indices | |||
<math>\featureidx_{1},\ldots,\featureidx_{\featurelen}</math> of | |||
<math>\featurelen</math> largest elements in \eqref{equ_sequence_cross_cov_matrix} | |||
</li><li> construct compression matrix | |||
<math>\mW \defeq \big( \eigvecCov^{(\featureidx_{1})},\ldots, \eigvecCov^{(\featureidx_{\featuredim})} \big)^{T} \in \mathbb{R}^{\featuredim \times \featurelenraw}</math> | |||
</li><li> compute feature vector | |||
<math>\featurevec^{(\sampleidx)} = \mW \rawfeaturevec^{(\sampleidx)}</math> | |||
</li></ul>'''Output:''' <math>\featurevec^{(\sampleidx)}</math>, for <math>\sampleidx=1,\ldots,\samplesize</math>, and compression matrix <math>\mW</math>. | |||
</proc> | |||
The main focus of this section is on regression problems that involve <span class="mw-gls" data-name ="datapoint">data point</span>s with numeric labels | |||
(e.g., from the <span class="mw-gls mw-gls-first" data-name ="labelspace">label space</span> <math>\labelspace = \mathbb{R}</math>). Given the raw features and labels of the <span class="mw-gls" data-name ="datapoint">data point</span> | |||
in the dataset <math>\dataset</math>, Algorithm [[#alg_PCA_labeled | alg_PCA_labeled ]] determines new feature vectors | |||
<math>\featurevec^{(\sampleidx)}</math> that allow to linearly predict a numeric label with minimum squared error. A similar approach can be used for | |||
classification problems involving <span class="mw-gls" data-name ="datapoint">data point</span>s with a finite <span class="mw-gls" data-name ="labelspace">label space</span> <math>\labelspace</math>. Linear (or Fisher) discriminant analysis aims at constructing a compression matrix | |||
<math>\mW</math> such that the learnt features <math>\featurevec = \mW \rawfeaturevec</math> of a <span class="mw-gls" data-name ="datapoint">data point</span> allow to predict its label <math>\truelabel</math> as accurately as possible <ref name="hastie01statisticallearning"/>. | |||
==Privacy-Preserving Feature Learning== | |||
Many important application domains of ML involve sensitive data that is subject to data protection law <ref name="Wachter:2019wn"/>. | |||
Consider a health-care provider (such as a hospital) holding a large database of patient records. From a ML perspective this | |||
databases is nothing but a (typically large) set of <span class="mw-gls" data-name ="datapoint">data point</span>s representing individual patients. The <span class="mw-gls" data-name ="datapoint">data point</span>s | |||
are characterized by many features including personal identifiers (name, social security number), bio-physical parameters | |||
as well as examination results . We could apply ML to learn a predictor for the risk of particular disease given the features of a <span class="mw-gls" data-name ="datapoint">data point</span>. | |||
Given large patient databases, the ML methods might not be implemented locally at the hospital but using cloud computing. | |||
However, data protection requirements might prohibit the transfer of raw patient records that allow to match individuals with | |||
bio-physical properties. In this case we might apply feature learning methods to construct new features for each patient such | |||
that they allow to learn an accurate hypothesis for predicting a disease but do not allow to identify sensitive properties of the | |||
patient such as its name or a social security number. | |||
Let us formalize the above application by characterizing each <span class="mw-gls" data-name ="datapoint">data point</span> (patient in the hospital database) using raw feature | |||
vector | |||
<math>\rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}</math> and a sensitive numeric property | |||
<math>\pi^{(\sampleidx)}</math>. | |||
We would like to find a compression map | |||
<math>\mW</math> such that the resulting features | |||
<math>\featurevec^{(\sampleidx)} = \mW \rawfeaturevec^{(\sampleidx)}</math> | |||
do not allow to accurately predict the sensitive property | |||
<math>\pi^{(\sampleidx)}</math>. The prediction of the sensitive property | |||
is restricted to be a linear | |||
<math>\hat{\pi}^{(\sampleidx)} \defeq \vr^{T} \featurevec^{(\sampleidx)}</math> with some weight vector | |||
<math>\vr</math>. | |||
Similar to Section [[guide:4f25e79970#sec_lda | Feature Learning for Labeled Data ]] we want to find a compression matrix | |||
<math>\mW</math> that transforms, in a linear fashion, the | |||
raw feature vector | |||
<math>\rawfeaturevec \in \mathbb{R}^{\featurelenraw}</math> to a new feature vector | |||
<math>\featurevec \in \mathbb{R}^{\featurelen}</math>. | |||
However the design criterion for the optimal compression matrix | |||
<math>\mW</math> was different in Section [[guide:4f25e79970#sec_lda | Feature Learning for Labeled Data ]] where | |||
the new feature vectors should allow for an accurate linear prediction of the label. In contrast, here we want to construct | |||
feature vectors such that there is no accurate linear predictor of the sensitive property | |||
<math>\pi^{(\sampleidx)}</math>. | |||
As in Section [[guide:4f25e79970#sec_lda | Feature Learning for Labeled Data ]], the optimal compression matrix | |||
<math>\mW</math> is given row-wise by the <span class="mw-gls" data-name ="eigenvector">eigenvector</span>s of the | |||
sample covariance matrix \eqref{equ_def_Q_PCA}. However, the choice of which eigenvectors to use is different | |||
and based on the entries of the sample cross-correlation vector | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_cross_correlation_privacypreseringPCA} | |||
\vc \defeq (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \pi^{(\sampleidx)} \rawfeaturevec^{(\sampleidx)}. | |||
\end{equation} | |||
</math> | |||
We summarize the construction of the optimal privacy-preserving compression matrix and corresponding new | |||
feature vectors in Algorithm [[#alg_PCA_privacypreserving | alg_PCA_privacypreserving ]]. | |||
<proc label="Privacy Preserving Feature Learning" id="alg_PCA_privacypreserving"> | |||
'''Input:''' dataset | |||
<math> \big(\rawfeaturevec^{(1)},\truelabel^{(1)} \big),\ldots,\big(\rawfeaturevec^{(\samplesize)},\truelabel^{(\samplesize)} \big)</math>; each | |||
<span class="mw-gls" data-name ="datapoint">data point</span> characterized by raw features | |||
<math>\rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}</math> and (numeric) sensitive property | |||
<math>\pi^{(\sampleidx)} \in \mathbb{R}</math>; number | |||
<math>\featuredim</math> of new features. | |||
<ul style="list-style:numeric"><li> compute the <span class="mw-gls" data-name ="evd">EVD</span> \eqref{equ_EVD_Q_PCA} of the sample covariance matrix \eqref{equ_def_Q_PCA} to obtain orthonormal eigenvectors | |||
<math>\big(\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelenraw)}\big)</math> | |||
corresponding to (decreasingly ordered) eigenvalues | |||
<math>\eigval{1} \geq \eigval{2} \geq \ldots \geq \eigval{\featurelenraw} \geq 0</math> | |||
</li><li> compute the sample cross-correlation vector \eqref{equ_cross_correlation_privacypreseringPCA} and, in turn, the sequence | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_sequence_cross_cov_matrix_privacypreserving} | |||
\big(c_{1}\big)^2/\eigval{1}, \ldots, \big(c_{\featurelenraw}\big)^2/\eigval{\featurelenraw} | |||
\end{equation} | |||
</math> | |||
</li><li> determine indices | |||
<math>\featureidx_{1},\ldots,\featureidx_{\featurelen}</math> of | |||
<math>\featurelen</math> smallest elements in \eqref{equ_sequence_cross_cov_matrix_privacypreserving} | |||
</li><li> construct compression matrix | |||
<math>\mW \defeq \big( \eigvecCov^{(\featureidx_{1})},\ldots, \eigvecCov^{(\featureidx_{\featuredim})} \big)^{T} \in \mathbb{R}^{\featuredim \times \featurelenraw}</math> | |||
</li><li> compute feature vector | |||
<math>\featurevec^{(\sampleidx)} = \mW \rawfeaturevec^{(\sampleidx)}</math> | |||
</li></ul>'''Output:''' feature vectors <math>\featurevec^{(\sampleidx)}</math>, for <math>\sampleidx=1,\ldots,\samplesize</math>, and compression matrix <math>\mW</math>. | |||
</proc> | |||
Algorithm [[#alg_PCA_privacypreserving | alg_PCA_privacypreserving ]] learns a map <math>\mW</math> to extract privacy-preserving features out of the raw feature vector | |||
of a <span class="mw-gls" data-name ="datapoint">data point</span>. These new features are privacy-preserving as they do not allow to accurately predict (in a linear fashion) a | |||
sensitive property <math>\pi</math> of the <span class="mw-gls" data-name ="datapoint">data point</span>. Another formalization for the preservation of privacy can be obtained using information-theoretic concepts. This information-theoretic approach interprets <span class="mw-gls" data-name ="datapoint">data point</span>s, their feature vector and sensitive property, as realizations of <span class="mw-gls" data-name ="rv">RV</span>s. It is then possible to use the mutual information between new features | |||
<math>\featurevec</math> and the sensitive (private) property | |||
<math>\pi</math> as an optimization criterion for learning a compression map | |||
<math>h</math> (Section [[guide:4f25e79970#sec_dim_red | Basic Principle of Dimensionality Reduction ]]). The resulting feature learning method (referred | |||
to as privacy-funnel) differs from Algorithm [[#alg_PCA_privacypreserving | alg_PCA_privacypreserving ]] not only in the optimization criterion for the compression map | |||
but also in that it allows it to be non-linear <ref name="MakhdoumiFunnel2014"/><ref name="Shkel2021"/>. | |||
==<span id="equ_random_projections"/>Random Projections== | |||
Note that <span class="mw-gls" data-name ="pca">PCA</span> uses an <span class="mw-gls" data-name ="evd">EVD</span> of the sample covariance matrix | |||
<math>\mathbf{Q}</math> \eqref{equ_def_Q_PCA}. | |||
The computational complexity (e.g., measured by number of multiplications and additions) for computing this <span class="mw-gls" data-name ="evd">EVD</span> | |||
is lower bounded by | |||
<math>\featuredim \min\{ \featurelenraw^{2}, \samplesize^{2} \}</math> <ref name="golub96"/><ref name="TippingProbPCA"/>. | |||
This computational complexity can be prohibitive for ML applications with | |||
<math>\featurelenraw</math> | |||
and | |||
<math>\samplesize</math> being of the order of millions or even billions. | |||
There is a computationally cheap alternative to <span class="mw-gls" data-name ="pca">PCA</span> (Algorithm [[#alg_PCA | alg_PCA ]]) for finding a useful | |||
compression matrix | |||
<math>\mathbf{W}</math> in \eqref{equ_feat_learning_matrix}. This alternative is | |||
to construct the compression matrix | |||
<math>\mathbf{W}</math> entry-wise | |||
<math display="block"> | |||
\begin{equation} | |||
\label{equ_def_iid_random_matrix} | |||
W_{\featureidx,\featureidx'} \defeq a_{\featureidx,\featureidx'} \mbox{ with } a_{\featureidx,\featureidx'} \sim \prob{a}. | |||
\end{equation} | |||
</math> | |||
The matrix entries \eqref{equ_def_iid_random_matrix} are realizations | |||
<math>a_{i,j}</math> of <span class="mw-gls" data-name ="iid">iid</span> <span class="mw-gls" data-name ="rv">RV</span>s | |||
with some common probability distribution | |||
<math>\prob{a}</math>. Different choices for the probability distribution | |||
<math>\prob{a}</math> | |||
have been studied in the literature <ref name="RauhutFoucartCS"/>. The Bernoulli distribution is used to obtain a compression | |||
matrix with binary entries. Another popular choice for | |||
<math>\prob{a}</math> is the multivariate normal (Gaussian) distribution. | |||
Consider <span class="mw-gls" data-name ="datapoint">data point</span>s whose raw feature vectors | |||
<math>\rawfeaturevec</math> are located near a | |||
<math>\sparsity</math>-dimensional subspace | |||
of | |||
<math>\mathbb{R}^{\featurelenraw}</math>. The feature vectors | |||
<math>\featurevec</math> obtained via \eqref{equ_feat_learning_matrix} using | |||
a random matrix \eqref{equ_def_iid_random_matrix} allows to reconstruct the raw feature vectors | |||
<math>\rawfeaturevec</math> | |||
with high probability whenever | |||
<math display="block"> | |||
\begin{equation} | |||
\featuredim \geq C \sparsity \log \featurelenraw. | |||
\end{equation} | |||
</math> | |||
The constant | |||
<math>C</math> depends on the maximum tolerated reconstruction error | |||
<math>\eta</math> (such that | |||
<math>\| \widehat{\rawfeaturevec} - \rawfeaturevec \|_{2}^{2} \leq \eta</math> for any <span class="mw-gls" data-name ="datapoint">data point</span>) and the probability | |||
that the features | |||
<math>\featurevec</math> (see \eqref{equ_def_iid_random_matrix}) allow for a maximum reconstruction | |||
error | |||
<math>\eta</math> <ref name="RauhutFoucartCS"/>{{rp|at=Theorem 9.27.}}. | |||
==<span id="sec_dim_increas"/>Dimensionality Increase== | |||
The focus of this chapter is on dimensionality reduction methods that learn a <span class="mw-gls mw-gls-first" data-name ="featuremap">feature map</span> delivering new feature | |||
vectors which are (significantly) shorter than the raw feature vectors. However, it might sometimes be beneficial to | |||
learn a <span class="mw-gls" data-name ="featuremap">feature map</span> that delivers new feature vectors which are longer than the raw feature vectors. We have already | |||
discussed two examples for such feature learning methods in Sections [[guide:013ef4b5cd#sec_polynomial_regression | Polynomial Regression ]] and [[guide:013ef4b5cd#sec_kernel_methods | Kernel Methods ]]. | |||
Polynomial regression maps a single raw feature | |||
<math>\rawfeature</math> to a feature vector containing the powers of the raw feature | |||
<math>z</math>. | |||
This allows to use apply linear predictor maps to the new feature vectors to obtain predictions that depend non-linearly | |||
on the raw feature | |||
<math>\rawfeature</math>. Kernel methods might even use a <span class="mw-gls" data-name ="featuremap">feature map</span> that delivers feature vectors belonging to | |||
an infinite-dimensional <span class="mw-gls mw-gls-first" data-name ="hilbertspace">Hilbert space</span> <ref name="LearningKernelsBook"/>. | |||
Mapping raw feature vectors into higher-dimensional (or even infinite-dimensional) spaces might be useful if the | |||
intrinsic geometry of the <span class="mw-gls" data-name ="datapoint">data point</span>s is simpler when looked at in the higher-dimensional space. Consider a | |||
binary classification problem where <span class="mw-gls" data-name ="datapoint">data point</span>s are highly inter-winded in the original feature space (see Figure [[#fig_kernelmethods|fig_kernelmethods]]). | |||
Loosely speaking, mapping into higher-dimensional_feature_space_might "flatten-out" a non-linear decision boundary | |||
between <span class="mw-gls" data-name ="datapoint">data point</span>s. We can then apply linear classifiers to the higher-dimensional features to achieve accurate | |||
predictions. | |||
==References== | |||
Revision as of 00:55, 11 June 2023
[math] \( % Generic syms \newcommand\defeq{:=} \newcommand{\Tt}[0]{\boldsymbol{\theta}} \newcommand{\XX}[0]{{\cal X}} \newcommand{\ZZ}[0]{{\cal Z}} \newcommand{\vx}[0]{{\bf x}} \newcommand{\vv}[0]{{\bf v}} \newcommand{\vu}[0]{{\bf u}} \newcommand{\vs}[0]{{\bf s}} \newcommand{\vm}[0]{{\bf m}} \newcommand{\vq}[0]{{\bf q}} \newcommand{\mX}[0]{{\bf X}} \newcommand{\mC}[0]{{\bf C}} \newcommand{\mA}[0]{{\bf A}} \newcommand{\mL}[0]{{\bf L}} \newcommand{\fscore}[0]{F_{1}} \newcommand{\sparsity}{s} \newcommand{\mW}[0]{{\bf W}} \newcommand{\mD}[0]{{\bf D}} \newcommand{\mZ}[0]{{\bf Z}} \newcommand{\vw}[0]{{\bf w}} \newcommand{\D}[0]{{\mathcal{D}}} \newcommand{\mP}{\mathbf{P}} \newcommand{\mQ}{\mathbf{Q}} \newcommand{\E}[0]{{\mathbb{E}}} \newcommand{\vy}[0]{{\bf y}} \newcommand{\va}[0]{{\bf a}} \newcommand{\vn}[0]{{\bf n}} \newcommand{\vb}[0]{{\bf b}} \newcommand{\vr}[0]{{\bf r}} \newcommand{\vz}[0]{{\bf z}} \newcommand{\N}[0]{{\mathcal{N}}} \newcommand{\vc}[0]{{\bf c}} \newcommand{\bm}{\boldsymbol} % Statistics and Probability Theory \newcommand{\errprob}{p_{\rm err}} \newcommand{\prob}[1]{p({#1})} \newcommand{\pdf}[1]{p({#1})} \def \expect {\mathbb{E} } % Machine Learning Symbols \newcommand{\biasterm}{B} \newcommand{\varianceterm}{V} \newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} \newcommand{\nrfolds}{k} \newcommand{\mseesterr}{E_{\rm est}} \newcommand{\bootstrapidx}{b} %\newcommand{\modeldim}{r} \newcommand{\modelidx}{l} \newcommand{\nrbootstraps}{B} \newcommand{\sampleweight}[1]{q^{(#1)}} \newcommand{\nrcategories}{K} \newcommand{\splitratio}[0]{{\rho}} \newcommand{\norm}[1]{\Vert {#1} \Vert} \newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} \newcommand{\bmx}[0]{\begin{bmatrix}} \newcommand{\emx}[0]{\end{bmatrix}} \newcommand{\T}[0]{\text{T}} \DeclareMathOperator*{\rank}{rank} %\newcommand\defeq{:=} \newcommand\eigvecS{\hat{\mathbf{u}}} \newcommand\eigvecCov{\mathbf{u}} \newcommand\eigvecCoventry{u} \newcommand{\featuredim}{n} \newcommand{\featurelenraw}{\featuredim'} \newcommand{\featurelen}{\featuredim} \newcommand{\samplingset}{\mathcal{M}} \newcommand{\samplesize}{m} \newcommand{\sampleidx}{i} \newcommand{\nractions}{A} \newcommand{\datapoint}{\vz} \newcommand{\actionidx}{a} \newcommand{\clusteridx}{c} \newcommand{\sizehypospace}{D} \newcommand{\nrcluster}{k} \newcommand{\nrseeds}{s} \newcommand{\featureidx}{j} \newcommand{\clustermean}{{\bm \mu}} \newcommand{\clustercov}{{\bm \Sigma}} \newcommand{\target}{y} \newcommand{\error}{E} \newcommand{\augidx}{b} \newcommand{\task}{\mathcal{T}} \newcommand{\nrtasks}{T} \newcommand{\taskidx}{t} \newcommand\truelabel{y} \newcommand{\polydegree}{r} \newcommand\labelvec{\vy} \newcommand\featurevec{\vx} \newcommand\feature{x} \newcommand\predictedlabel{\hat{y}} \newcommand\dataset{\mathcal{D}} \newcommand\trainset{\dataset^{(\rm train)}} \newcommand\valset{\dataset^{(\rm val)}} \newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} \newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} \newcommand{\inspace}{\mathcal{X}} \newcommand{\sigmoid}{\sigma} \newcommand{\outspace}{\mathcal{Y}} \newcommand{\hypospace}{\mathcal{H}} \newcommand{\emperror}{\widehat{L}} \newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} \newcommand{\featurespace}{\mathcal{X}} \newcommand{\labelspace}{\mathcal{Y}} \newcommand{\rawfeaturevec}{\mathbf{z}} \newcommand{\rawfeature}{z} \newcommand{\condent}{H} \newcommand{\explanation}{e} \newcommand{\explainset}{\mathcal{E}} \newcommand{\user}{u} \newcommand{\actfun}{\sigma} \newcommand{\noisygrad}{g} \newcommand{\reconstrmap}{r} \newcommand{\predictor}{h} \newcommand{\eigval}[1]{\lambda_{#1}} \newcommand{\regparam}{\lambda} \newcommand{\lrate}{\alpha} \newcommand{\edges}{\mathcal{E}} \newcommand{\generror}{E} \DeclareMathOperator{\supp}{supp} %\newcommand{\loss}[3]{L({#1},{#2},{#3})} \newcommand{\loss}[2]{L\big({#1},{#2}\big)} \newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} \newcommand{\determinant}[1]{{\rm det}({#1})} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\itercntr}{r} \newcommand{\state}{s} \newcommand{\statespace}{\mathcal{S}} \newcommand{\timeidx}{t} \newcommand{\optpolicy}{\pi_{*}} \newcommand{\appoptpolicy}{\hat{\pi}} \newcommand{\dummyidx}{j} \newcommand{\gridsizex}{K} \newcommand{\gridsizey}{L} \newcommand{\localdataset}{\mathcal{X}} \newcommand{\reward}{r} \newcommand{\cumreward}{G} \newcommand{\return}{\cumreward} \newcommand{\action}{a} \newcommand\actionset{\mathcal{A}} \newcommand{\obstacles}{\mathcal{B}} \newcommand{\valuefunc}[1]{v_{#1}} \newcommand{\gridcell}[2]{\langle #1, #2 \rangle} \newcommand{\pair}[2]{\langle #1, #2 \rangle} \newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} \newcommand{\actionvalue}[1]{q_{#1}} \newcommand{\transition}{\mathcal{T}} \newcommand{\policy}{\pi} \newcommand{\charger}{c} \newcommand{\itervar}{k} \newcommand{\discount}{\gamma} \newcommand{\rumba}{Rumba} \newcommand{\actionnorth}{\rm N} \newcommand{\actionsouth}{\rm S} \newcommand{\actioneast}{\rm E} \newcommand{\actionwest}{\rm W} \newcommand{\chargingstations}{\mathcal{C}} \newcommand{\basisfunc}{\phi} \newcommand{\augparam}{B} \newcommand{\valerror}{E_{v}} \newcommand{\trainerror}{E_{t}} \newcommand{\foldidx}{b} \newcommand{\testset}{\dataset^{(\rm test)} } \newcommand{\testerror}{E^{(\rm test)}} \newcommand{\nrmodels}{M} \newcommand{\benchmarkerror}{E^{(\rm ref)}} \newcommand{\lossfun}{L} \newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} \newcommand{\cluster}{\mathcal{C}} \newcommand{\bayeshypothesis}{h^{*}} \newcommand{\featuremtx}{\mX} \newcommand{\weight}{w} \newcommand{\weights}{\vw} \newcommand{\regularizer}{\mathcal{R}} \newcommand{\decreg}[1]{\mathcal{R}_{#1}} \newcommand{\naturalnumbers}{\mathbb{N}} \newcommand{\featuremapvec}{{\bf \Phi}} \newcommand{\featuremap}{\phi} \newcommand{\batchsize}{B} \newcommand{\batch}{\mathcal{B}} \newcommand{\foldsize}{B} \newcommand{\nriter}{R} % Machine Learning from Networked Data \newcommand{\nodesigvec}{\mathbf{u}} \newcommand{\edgesigvec}{\mathbf{f}} \newcommand{\edgesig}{f} \newcommand{\edgeweight}{A} \newcommand{\edgeweights}{\mA} \newcommand{\edgeidx}{e} \newcommand{\edgesigs}{\mathbb{R}^{\edges \times \featuredim}} \newcommand{\graph}{\mathcal{G}} \newcommand{\nodes}{\mathcal{V}} \newcommand{\degreemtx}{\mathbf{D}} \newcommand{\incidencemtx}{\mathbf{B}} \newcommand{\nodedegree}[1]{d^{(#1)}} \newcommand{\nodeidx}{i} \newcommand{\nrnodes}{n} \newcommand{\nodesigs}{\mathbb{R}^{\nodes \times \featuredim }} \newcommand{\naturalspace}{\mathcal{N}} \newcommand{\gindex}[1][i]{^{(#1)}} \newcommand{\gsignal}{\vw} \newcommand{\trueweights}{\overline{\vw}} \newcommand{\vt}{\mathbf{t}} \newcommand{\FIM}{\mathbf{F}} \newcommand{\FIMentry}{F} \newcommand{\edge}[2]{\{#1,#2\}} \newcommand{\directededge}[2]{\left(#1,#2\right)} [/math]
“Solving Problems By Changing the Viewpoint.”
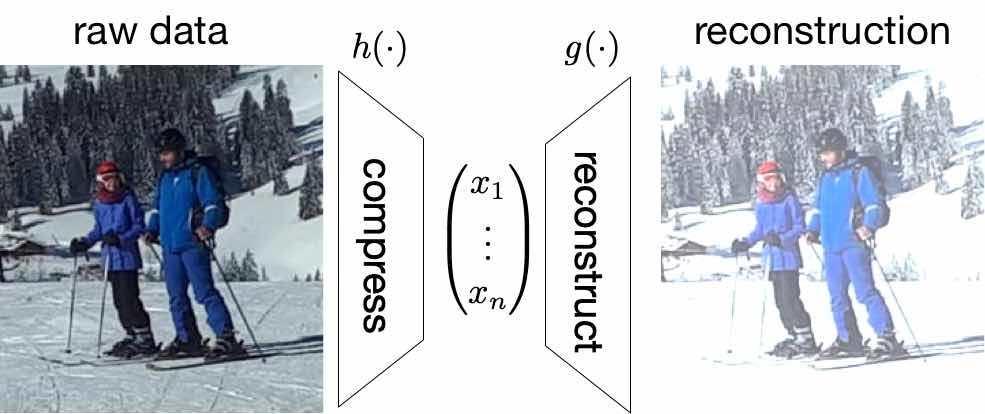
Chapter Three Components of ML defined features as those properties of a data point that can
be measured or computed easily. Sometimes the choice of features follows naturally from the
available hard- and software. For example, we might use the numeric measurement
[math]\rawfeature \in \mathbb{R}[/math]
delivered by a sensing device as a feature. However, we could augment this single feature with
new features such as the powers
[math]\rawfeature^{2}[/math] and
[math]\rawfeature^{3}[/math] or adding a constant
[math]\rawfeature+5[/math].
Each of these computations produces a new feature. Which of these additional features are most useful?
Feature learning methods automate the choice of finding good features. These methods learn a hypothesis map that reads in some representation of a data point and transforms it to a set of features. Feature learning methods differ in the precise format of the original data representation as well as the format of the delivered features. This chapter mainly discusses feature learning methods that require data points being represented by [math]\featurelenraw[/math] numeric raw features and deliver a set of [math]\featurelen[/math] new numeric features. We will denote the raw features and the learnt new features by [math]\rawfeaturevec=\big(\rawfeature_{1},\ldots,\rawfeature_{\featurelenraw} \big)^{T} \in \mathbb{R}^{\featurelenraw}[/math] and [math]\featurevec=\big(\feature_{1},\ldots,\feature_{\featurelen}\big)^{T} \in \mathbb{R}^{\featurelen}[/math], respectively.
Many ML application domains generate data points for which can access a huge number of raw features. Consider data points being snapshots generated by a smartphone. It seems natural to use the pixel colour intensities as the raw features of the snapshot. Since modern smartphone have “Megapixel cameras”, the pixel intensities would provide us with millions of raw features. It might seem a good idea to use as many raw features of a data point as possible since more features should offer more information about a data point and its label [math]\truelabel[/math]. There are, however, two pitfalls in using an unnecessarily large number of features. The first one is a computational pitfall and the second one is a statistical pitfall.
Computationally, using very long feature vectors [math]\featurevec \in \mathbb{R}^{\featuredim}[/math] (with [math]\featuredim[/math] being billions), might result in prohibitive computational resource requirements (bandwidth, storage, time) of the resulting ML method. Statistically, using a large number of features makes the resulting ML methods more prone to overfitting. For example, linear regression will typically overfit when using feature vectors [math]\featurevec\!\in\!\mathbb{R}^{\featuredim}[/math] whose length [math]\featuredim[/math] exceeds the number [math]\samplesize[/math] of labeled data points used for training (see Chapter Regularization ).
Both from a computational and a statistical perspective, it is beneficial to use only the maximum necessary amount of features. The challenge is to select those features which carry most of the relevant information required for the prediction of the label [math]\truelabel[/math]. Finding the most relevant features out of a huge number of raw features is the goal of dimensionality reduction methods. Dimensionality reduction methods form an important sub-class of feature learning methods. These methods learn a hypothesis [math]h(\rawfeaturevec)[/math] that maps a long raw feature vector
[math]\rawfeaturevec \in \mathbb{R}^{\featurelenraw}[/math] to a new (short) feature vector [math]\featurevec \in \mathbb{R}^{\featurelen}[/math] with [math]\featurelen \ll \featurelenraw[/math].
Beside avoiding overfitting and coping with limited computational resources, dimensionality reduction can also be useful for data visualization. Indeed, if the resulting feature vector has length [math]\featurelen=2[/math], we depict data points in the two-dimensional plane in form of a scatterplot.
We will discuss the basic idea underlying dimensionality reduction methods in Section Basic Principle of Dimensionality Reduction . Section Principal Component Analysis presents one particular example of a dimensionality reduction method that computes relevant features by a linear transformation of the raw feature vector. Section Feature Learning for Labeled Data discusses a method for dimensionality reduction that exploits the availability of labelled data points. Section Random Projections shows how randomness can be used to obtain computationally cheap dimensionality reduction .
Most of this chapter discusses dimensionality reduction methods that determine a small number of relevant features from a large set of raw features. However, sometimes it might be useful to go the opposite direction. There are applications where it might be beneficial to construct a large (even infinite) number of new features from a small set of raw features. Section Dimensionality Increase will showcase how computing additional features can help to improve the prediction accuracy of ML methods.
Basic Principle of Dimensionality Reduction
The efficiency of ML methods depends crucially on the choice of features that are used to characterize data points. Ideally we would like to have a small number of highly relevant features to characterize data points. If we use too many features we risk to waste computations on exploring irrelevant features. If we use too few features we might not have enough information to predict the label of a data point. For a given number [math]\featurelen[/math] of features, dimensionality reduction methods aim at learning an (in a certain sense) optimal map from the data point to a feature vector of length [math]\featurelen[/math].
Figure fig_dimred illustrates the basic idea of dimensionality reduction methods. Their goal is to learn (or find) a “compression” map [math]h(\cdot): \mathbb{R}^{\featurelenraw} \rightarrow \mathbb{R}^{\featuredim}[/math] that transforms a (long) raw feature vector [math]\rawfeaturevec \in \mathbb{R}^{\featurelenraw}[/math] to a (short) feature vector
[math]\featurevec=(\feature_{1},\ldots,\feature_{\featuredim})^{T} \defeq h(\rawfeaturevec)[/math] (typically [math]\featuredim \ll \featurelenraw[/math]).
The new feature vector [math]\featurevec = h(\rawfeaturevec)[/math] serves as a compressed representation (or code) for the original feature vector [math]\rawfeaturevec[/math]. We can reconstruct the raw feature vector using a reconstruction map [math]\reconstrmap(\cdot): \mathbb{R}^{\featurelen} \rightarrow \mathbb{R}^{\featurelenraw}[/math]. The reconstructed raw features [math]\widehat{\rawfeaturevec} \defeq \reconstrmap(\featurevec) = \reconstrmap(h(\rawfeaturevec))[/math] will typically differ from the original raw feature vector [math]\rawfeaturevec[/math]. In general, we obtain a non-zero reconstruction error
Dimensionality reduction methods learn a compression map [math]h(\cdot)[/math] such that the reconstruction error \eqref{equ_def_reconst_error} is minimized. In particular, for a dataset [math]\dataset = \big\{ \rawfeaturevec^{(1)},\ldots,\rawfeaturevec^{(\samplesize)} \big\}[/math], we measure the quality of a pair of compression map [math]h[/math] and reconstruction map [math]\reconstrmap[/math] by the average reconstruction error
Here, [math]\loss{\rawfeaturevec}{\reconstrmap\big(h\big(\rawfeaturevec^{(\sampleidx)}\big)}[/math] denotes a loss function that is used to measure the reconstruction error [math]\underbrace{\reconstrmap\big(h\big(\rawfeaturevec^{(\sampleidx)}\big)\big)}_{\widehat{\rawfeaturevec}} - \rawfeaturevec[/math]. Different choices for the loss function in \eqref{equ_def_emp_error_dimred} result in different dimensionality reduction methods. One widely-used choice for the loss is the squared Euclidean norm
Practical dimensionality reduction methods have only finite computational resources. Any practical method must therefore restrict the set of possible compression and reconstruction maps to small subsets [math]\hypospace[/math] and [math]\hypospace^{*}[/math], respectively. These subsets are the hypothesis spaces for the compression map [math]h \in \hypospace[/math] and the reconstruction map [math]\reconstrmap \in \hypospace^{*}[/math]. Feature learning methods differ in their choice for these hypothesis spaces.
Dimensionality reduction methods learn a compression map by solving
We can interpret \eqref{equ_optimaization_dimred} as a (typically non-linear) approximation problem. The optimal compression map [math]\hat{h}[/math] is such that the reconstruction [math]\reconstrmap(\hat{h}(\rawfeaturevec))[/math], with a suitably chosen reconstruction map [math]\reconstrmap[/math], approximates the original raw feature vector [math]\rawfeaturevec[/math] as good as possible. Note that we use a single compression map [math]h(\cdot)[/math] and a single reconstruction map [math]\reconstrmap(\cdot)[/math] for all data points in the dataset [math]\dataset[/math].
We obtain variety of dimensionality methods by using different choices for the hypothesis spaces [math]\hypospace, \hypospace^{*}[/math] and loss function in \eqref{equ_optimaization_dimred}. Section Principal Component Analysis discusses a method that solves \eqref{equ_optimaization_dimred} for [math]\hypospace, \hypospace^{*}[/math] constituted by linear maps and the loss \eqref{equ_def_squared_eucl_norm}. Deep autoencoders are another family of dimensionality reduction methods that solve \eqref{equ_optimaization_dimred} with
[math]\hypospace, \hypospace^{*}[/math] constituted by non-linear maps that are represented by deep neural networks [1](Ch. 14).
Principal Component Analysis
We now consider the special case of dimensionality reduction where the compression and reconstruction map are required to be linear maps. Consider a data point which is characterized by a (typically very long) raw feature vector [math]\rawfeaturevec\!=\!\big( \rawfeature_{1},\ldots,\rawfeature_{\featurelenraw} \big)^{T} \!\in\! \mathbb{R}^{\featurelenraw}[/math] of length [math]\featurelenraw[/math]. The length [math]\featurelenraw[/math] of the raw feature vector might be easily of the order of millions. To obtain a small set of relevant features [math]\featurevec\!=\!\big(\feature_{1},\ldots,\feature_{\featuredim} \big)^{T}\!\in\! \mathbb{R}^{\featuredim}[/math], we apply a linear transformation to the raw feature vector,
Here, the “compression” matrix [math]\mathbf{W} \in \mathbb{R}^{\featuredim \times \featurelenraw}[/math] maps (in a linear fashion) the (long) raw feature vector [math]\rawfeaturevec \in \mathbb{R}^{\featurelenraw}[/math] to the (shorter) feature vector [math]\featurevec \in \mathbb{R}^{\featuredim}[/math].
It is reasonable to choose the compression matrix
[math]\mathbf{W} \in \mathbb{R}^{\featuredim \times \featurelenraw}[/math]
in \eqref{equ_feat_learning_matrix} such that the resulting features
[math]\featurevec \in \mathbb{R}^{\featuredim}[/math]
allow to approximate the original data point
[math]\rawfeaturevec \in \mathbb{R}^{\featurelenraw}[/math] as
accurate as possible. We can approximate (or recover) the data point
[math]\rawfeaturevec \in \mathbb{R}^{\featurelenraw}[/math]
back from the features
[math]\featurevec[/math] by applying a reconstruction operator
[math]\mathbf{R} \in \mathbb{R}^{\featurelenraw \times \featuredim}[/math], which is
chosen such that
The approximation error [math]\emperror \big( \mathbf{W},\mathbf{R} \mid \dataset\big)[/math] resulting when \eqref{equ_approx_linear_PCA} is applied to each data point in a dataset [math]\dataset= \{ \rawfeaturevec^{(\sampleidx)}\}_{\sampleidx=1}^{\samplesize}[/math] is then
One can verify that the approximation error [math]\emperror \big( \mathbf{W},\mathbf{R} \mid \dataset\big)[/math] can only by minimal if the compression matrix [math]\mathbf{W}[/math] is of the form
with [math]\featuredim[/math] orthonormal vectors [math]\eigvecCov^{(\featureidx)}[/math], for [math]\featureidx=1,\ldots,\featuredim[/math]. The vectors [math]\eigvecCov^{(\featureidx)}[/math] are the eigenvectors corresponding to the [math]\featuredim[/math] largest eigenvalues of the sample covariance matrix
Here we used the data matrix [math]\mathbf{Z}\!=\!\big( \rawfeaturevec^{(1)}, \ldots, \rawfeaturevec^{(\samplesize)} \big)^{T}\!\in\!\mathbb{R}^{\samplesize \times \featurelenraw}[/math].\footnote{Some authors define the data matrix as [math]\mZ\!=\!\big( \widetilde{\rawfeaturevec}^{(1)}, \ldots, \widetilde{\rawfeaturevec}^{(\samplesize)} \big)^{T}\!\in\!\mathbb{R}^{\samplesize \times D}[/math] using “centered” data points [math]\rawfeaturevec^{(\sampleidx)} - \widehat{\vm}[/math] obtained by subtracting the average [math]\widehat{\vm} = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \rawfeaturevec^{(\sampleidx)}[/math].} It can be verified easily, using the definition \eqref{equ_def_Q_PCA}, that the matrix [math]\mathbf{Q}[/math] is positive semi-definite (psd). As a psd matrix, [math]\mQ[/math] has an eigenvalue decomposition (EVD) of the form [2]
with real-valued eigenvalues [math]\eigval{1} \geq \eigval{2}\geq \ldots \geq \eigval{\featurelenraw} \geq 0[/math] and orthonormal eigenvectors [math]\{ \eigvecCov^{(\featureidx)} \}_{\featureidx=1}^{\featurelenraw}[/math].
The feature vectors [math]\featurevec^{(\sampleidx)}[/math] are obtained by applying the compression matrix [math]\mathbf{W}_{\rm PCA}[/math] \eqref{equ_def_PCA_W} to the raw feature vectors [math]\rawfeaturevec^{(\sampleidx)}[/math]. We refer to the entries of the learnt feature vector [math]\featurevec^{(\sampleidx)}= \mW_{\rm PCA} \rawfeaturevec^{(\sampleidx)}[/math] (see \eqref{equ_def_PCA_W}) as the principal components (PC) of the raw feature vectors [math]\rawfeaturevec^{(\sampleidx)}[/math]. Algorithm alg_PCA summarizes the overall procedure of determining the compression matrix \eqref{equ_def_PCA_W} and computing the learnt feature vectors [math]\featurevec^{(\sampleidx)}[/math]. This procedure is known as principal component analysis (PCA).
Input: dataset [math]\dataset=\{ \rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw} \}_{\sampleidx=1}^{\samplesize}[/math]; number [math]\featuredim[/math] of PCs.
- compute the EVD \eqref{equ_EVD_Q_PCA} to obtain orthonormal eigenvectors [math]\big(\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelenraw)}\big)[/math] corresponding to (decreasingly ordered) eigenvalues [math]\eigval{1} \geq \eigval{2} \geq \ldots \geq \eigval{\featurelenraw} \geq 0[/math]
- construct compression matrix [math]\mW_{\rm PCA} \defeq \big( \eigvecCov^{(1)},\ldots, \eigvecCov^{(\featuredim)} \big)^{T} \in \mathbb{R}^{\featuredim \times \featurelenraw}[/math]
- compute feature vector [math]\featurevec^{(\sampleidx)} = \mW_{\rm PCA} \rawfeaturevec^{(\sampleidx)}[/math] whose entries are PC of [math]\rawfeaturevec^{(\sampleidx)}[/math]
- compute approximation error [math]\emperror^{(\rm PCA)} = \sum_{\featureidx = \featuredim+1}^{\featurelenraw} \eigval{\featureidx}[/math] (see \eqref{equ_approx_error_PCA}).
Output: [math]\featurevec^{(\sampleidx)}[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math], and the approximation error [math]\emperror^{(\rm PCA)}[/math].
The length [math]\featuredim \in \{0,\ldots,\featurelenraw)[/math] of the delivered feature vectors [math]\featurevec^{(\sampleidx)}[/math],
for [math]\sampleidx=1,\ldots,\samplesize[/math], is an input (or hyper-) parameter of Algorithm alg_PCA . Two extreme cases
are [math]\featuredim=0[/math] (maximum compression) and [math]\featuredim=\featurelenraw[/math] (no compression).
We finally note that the choice for the orthonormal eigenvectors in \eqref{equ_def_PCA_W}
might not be unique. Depending on the sample covariance matrix [math]\mQ[/math], there might different sets
of orthonormal vectors that correspond to the same eigenvalue of [math]\mQ[/math]. Thus, for a given length
[math]\featuredim[/math] of the new feature vectors, there might be several different matrices
[math]\mW[/math] that achieve the same (optimal) reconstruction error [math]\emperror^{(\rm PCA)}[/math].
Computationally, Algorithm alg_PCA essentially amounts to an EVD of the sample covariance matrix [math]\mQ[/math] \eqref{equ_def_Q_PCA}. The EVD of [math]\mQ[/math] provides not only the optimal compression matrix
[math]\mW_{\rm PCA}[/math] but also the measure [math]\emperror^{(\rm PCA)}[/math] for the information loss incurred by replacing the original data points [math]\rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}[/math] with the shorter feature vector [math]\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}[/math]. We quantify this information loss by the approximation error obtained when using the compression matrix [math]\mathbf{W}_{\rm PCA}[/math] (and corresponding reconstruction matrix
[math]\mathbf{R}_{\rm opt} = \mathbf{W}_{\rm PCA}^{T}[/math]),
As depicted in Figure fig_ellbow_PCA, the approximation error [math]\emperror^{(\rm PCA)}[/math] decreases with increasing number [math]\featuredim[/math] of PCs used for the new features \eqref{equ_feat_learning_matrix}. For the extreme case [math]\featuredim\!=\!0[/math], where we completely ignore the raw feature vectors [math]\rawfeaturevec^{(\sampleidx)}[/math], the optimal reconstruction error is
[math]\emperror^{(\rm PCA)} = (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big\| \rawfeaturevec^{(\sampleidx)} \big\|^{2}[/math]. The other extreme case [math]\featuredim\!=\!\featurelenraw[/math] allows to use the raw features directly as the new features [math]\featurevec^{(\sampleidx)}\!=\!\rawfeaturevec^{(\sampleidx)}[/math]. This extreme case means no compression at all, and trivially results in a zero reconstruction error [math]\emperror^{(\rm PCA)}\!=\!0[/math].
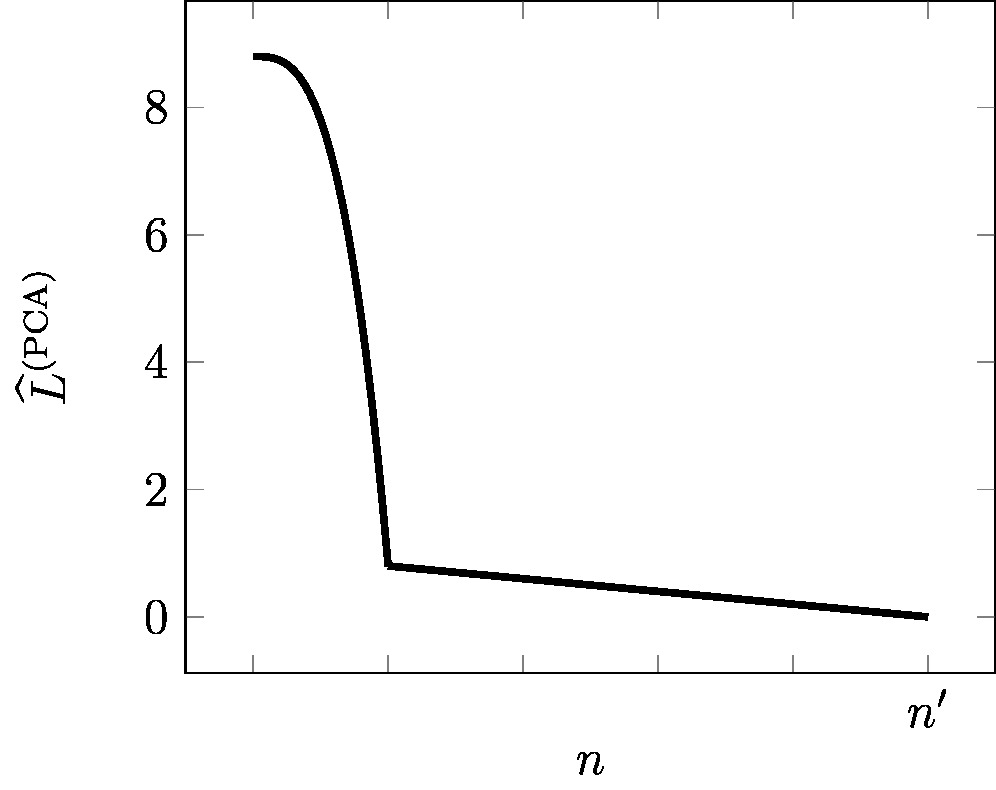
Combining PCA with linear regression
One important use case of PCA is as a pre-processing step within an overall ML problem such as linear regression (see Section Linear Regression ). As discussed in Chapter Regularization , linear regression methods are prone to overfitting whenever the data points are characterized by raw feature vectors [math]\rawfeaturevec[/math] whose length [math]\featurelenraw[/math] exceeds the number [math]\samplesize[/math] of labeled data points used in empirical risk minimization (ERM).
One simple but powerful strategy to avoid overfitting is to preprocess the raw features [math]\rawfeaturevec^{(\sampleidx)}\in \mathbb{R}^{\featurelenraw}[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math] by applying PCA. Indeed, PCA Algorithm alg_PCA delivers feature vectors
[math]\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}[/math] of prescribed length [math]\featuredim[/math]. Thus, choosing the parameter [math]\featuredim[/math] such that [math]\featuredim \lt \samplesize[/math] will typically prevent the follow-up linear regression method from overfitting.
How To Choose Number of PC?
There are several aspects which can guide the choice for the number [math]\featuredim[/math] of PCs to be used as features.
- To generate data visualizations we might use either [math]\featuredim=2[/math] or [math]\featuredim=3[/math].
- We should choose [math]\featuredim[/math] sufficiently small such that the overall ML method fits the available computational resources.
- Consider using PCA as a pre-processing for linear regression (see Section Linear Regression ). In particular, we can use the learnt feature vectors [math]\featurevec^{(\sampleidx)}[/math] delivered by PCA as the feature vectors of data points in plain linear regression methods. To avoid overfitting, we should choose [math]\featuredim \lt \samplesize[/math] (see Chapter Regularization ).
- Choose [math]\featuredim[/math] large enough such that the resulting approximation error [math]\emperror^{(\rm PCA)}[/math] is reasonably small (see Figure fig_ellbow_PCA).
Data Visualisation
If we use PCA with [math]\featuredim=2[/math], we obtain feature vectors [math]\featurevec^{(\sampleidx)} = \mW_{\rm PCA} \rawfeaturevec^{(\sampleidx)}[/math] (see \eqref{equ_feat_learning_matrix}) which can be depicted as points in a scatterplot (see Section Scatterplot ).
As an example, consider data points [math]\datapoint^{(\sampleidx)}[/math] obtained from historic recordings of Bitcoin statistics. Each data point [math]\datapoint^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}[/math] is a vector of length [math]\featurelenraw=6[/math]. It is difficult to visualise points in an Euclidean space [math]\mathbb{R}^{\featurelenraw}[/math] of dimension [math]\featurelenraw \gt 2[/math]. Therefore, we apply PCA with [math]\featuredim=2[/math] which results in feature vectors [math]\featurevec^{(\sampleidx)} \in \mathbb{R}^{2}[/math]. These new feature vectors (of length [math]2[/math]) can be depicted conveniently as the scatterplot in Figure fig_scatterplot_visualization.
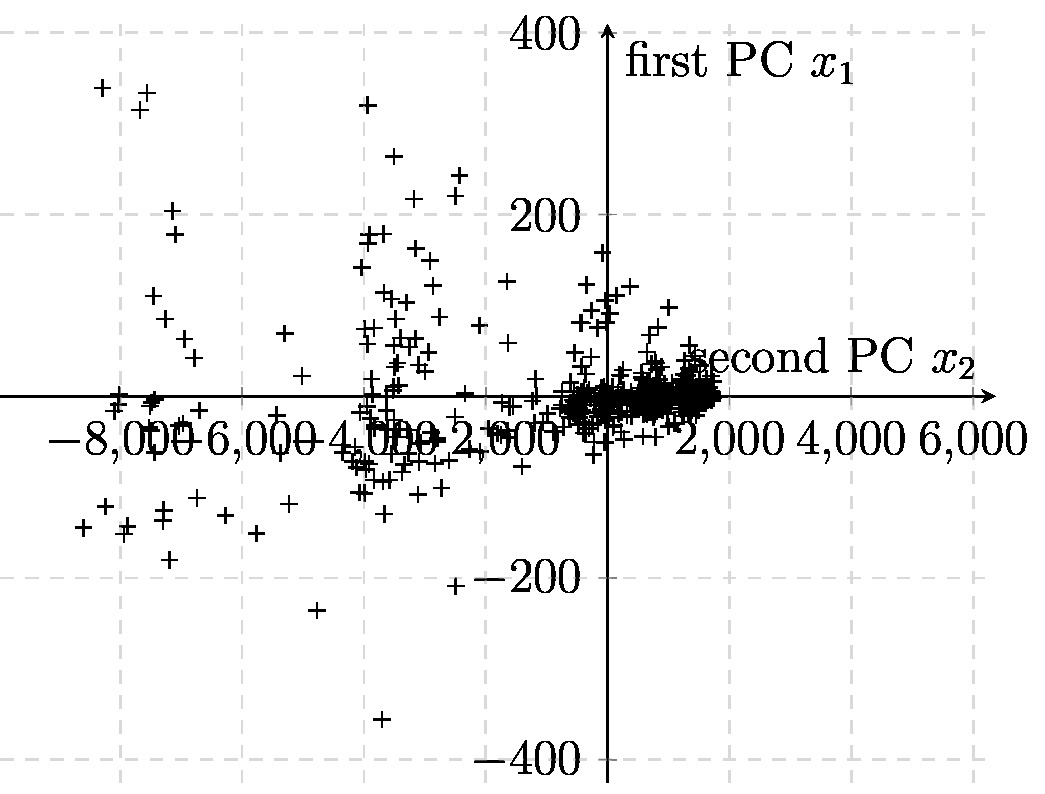
Extensions of PCA
We now briefly discuss variants and extensions of the basic PCA method.
| Variant/extension | Description |
|---|---|
| Kernel PCA [3](Ch.14.5.4) | The PCA method is most effective if the raw feature vectors of data points are concentrated around a [math]\featurelen[/math]-dimensional linear subspace of [math]\mathbb{R}^{\featurelenraw}[/math]. Kernel PCA extends PCA to data points that are located near a low-dimensional manifold which might be highly non-linear. This is achieved by applying PCA to transformed feature vectors instead of the original raw feature vectors. Kernel PCA first applies a (typically non-linear) feature map [math]\featuremap[/math] to the raw feature vectors [math]\rawfeaturevec^{(\sampleidx)}[/math] (see Section Kernel Methods ) and applies PCA to the transformed feature vectors [math]\featuremap \big( \rawfeaturevec^{(\sampleidx)} \big)[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math]. |
| Robust PCA [4] | The basic PCA Algorithm alg_PCA is sensitive to outliers, i.e., a small number of data points with significantly different statistical properties than the bulk of data points. This sensitivity might be attributed to the properties of the squared Euclidean norm \eqref{equ_def_squared_eucl_norm} which is used in PCA to measure the reconstruction error \eqref{equ_def_reconst_error}. We have seen in Chapter The Landscape of ML that linear regression (see Section Linear Regression and Least Absolute Deviation Regression ) can be made robust against outliers by replacing the squared error loss with another loss function. In a similar spirit, robust PCA replaces the squared Euclidean norm with another norm that is less sensitive to having very large reconstruction errors \eqref{equ_def_reconst_error} for a small number of data points (which are outliers). |
| Sparse PCA [3](Ch.14.5.5) | The basic PCA method transforms the raw feature vector [math]\rawfeaturevec^{(\sampleidx)}[/math] of a data point to a new (shorter) feature vector [math]\featurevec^{(\sampleidx)}[/math]. In general each entry [math]\feature^{(\sampleidx)}_{\featureidx}[/math] of the new feature vector will depend on each entry of the raw feature vector [math]\rawfeaturevec^{(\sampleidx)}[/math]. More precisely, the new feature [math]\feature^{(\sampleidx)}_{\featureidx}[/math] depends on all raw features [math]\rawfeature^{(\sampleidx)}_{\featureidx'}[/math] for which the corresponding entry [math]W_{\featureidx,\featureidx'}[/math] of the matrix [math]\mW= \mW_{\rm PCA}[/math] \eqref{equ_def_PCA_W} is non-zero. For most datasets, all entries of the matrix [math]\mW_{\rm PCA}[/math] will typically be non-zero. In some applications of linear dimensionality reduction we would like to construct new features that depend only on a small subset of raw features. Equivalently we would like to learn a linear compression map [math]\mW[/math] \eqref{equ_feat_learning_matrix} such that each row of [math]\mW[/math] contains only few non-zero entries. To this end, sparse PCA enforces the rows of the compression matrix [math]\mW[/math] to contain only a small number of non-zero entries. This enforcement can be implement either using additional constraints on [math]\mW[/math] or by adding a penalty term to the reconstruction error \eqref{equ_app_error_PCA}. |
| Probabilistic PCA [5][6] | We have motivated PCA as a method for learning an optimal linear compression map (matrix) \eqref{equ_feat_learning_matrix}
such that the compressed feature vectors allows to linearly reconstruct the original raw feature vector with minimum reconstruction error \eqref{equ_app_error_PCA}. Another interpretation of PCA is that of a method that learns a subspace of [math]\mathbb{R}^{\featurelenraw}[/math] that best fits the distribution of the raw feature vectors [math]\rawfeaturevec^{(\sampleidx)}[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math]. This optimal subspace is precisely the subspace spanned by the rows of [math]\mathbf{W}_{\rm PCA}[/math] \eqref{equ_def_PCA_W}. Probabilistic PCA (PPCA) interprets the raw feature vectors [math]\rawfeaturevec^{(\sampleidx)}[/math] as realizations of independent and identically distributed (iid) random variable (RV)s. These realizations are modelled as [[math]]
\begin{equation}
\label{equ_def_PPCA_model}
\rawfeaturevec^{(\sampleidx)} = \mW^{T} \featurevec^{(\sampleidx)} + \bm{\varepsilon}^{(\sampleidx)} \mbox{, for } \sampleidx=1,\ldots,\samplesize.
\end{equation}
[[/math]]
Here,
[math]\mW \in \mathbb{R}^{\featuredim \times \featurelenraw}[/math] is some unknown matrix with orthonormal rows. The rows of
[math]\mW[/math] span
the subspace around which the raw features are concentrated. The vectors
[math]\featurevec^{(\sampleidx)}[/math] in \eqref{equ_def_PPCA_model}
are realizations of iid RVs whose common probability distribution is
[math]\mathcal{N}(\mathbf{0}, \mathbf{I})[/math]. The
vectors
[math]\bm{\varepsilon}^{(\sampleidx)}[/math] are realizations of iid RVs whose common probability distribution is
[math]\mathcal{N}(\mathbf{0}, \sigma^{2} \mathbf{I})[/math] with some fixed but unknown variance
[math]\sigma^{2}[/math]. Note that
[math]\mW[/math] and
[math]\sigma^{2}[/math] parametrize
the joint probability distribution of the feature vectors
[math] \rawfeaturevec^{(\sampleidx)}[/math] via \eqref{equ_def_PPCA_model}.
PPCA amounts to maximum likelihood estimation (see Section Maximum Likelihood ) of the parameters
[math]\mW[/math] and
[math]\sigma^{2}[/math].
This maximum likelihood estimation problem can be solved using computationally efficient estimation techniques such as expectation maximization (EM) [6](Appendix B). The implementation of probabilistic PCA (PPCA) via EM also offers a principled approach
to handle missing data. Roughly speaking, the EM method allows to use the probabilistic model \eqref{equ_def_PPCA_model}
to estimate missing raw features [6](Sec.\ 4.1).
|
Feature Learning for Non-Numeric Data
We have motivated dimensionality reduction methods as transformations of (very long) raw feature vectors to a new (shorter) feature vector [math]\featurevec[/math] such that it allows to reconstruct the raw features [math]\rawfeaturevec[/math] with minimum reconstruction error \eqref{equ_def_reconst_error}. To make this requirement precise we need to define a measure for the size of the reconstruction error and specify the class of possible reconstruction maps. Principal component analysis (PCA) uses the squared Euclidean norm \eqref{equ_app_error_PCA} to measure the reconstruction error and only allows for linear reconstruction maps \eqref{equ_approx_linear_PCA}.
Alternatively, we can view dimensionality reduction as the generation of new feature vectors [math]\featurevec^{(\sampleidx)}[/math] that maintain the intrinsic geometry of the data points with their raw feature vectors [math]\rawfeaturevec^{(\sampleidx)}[/math]. Different dimensionality reduction methods use different concepts for characterizing the “intrinsic geometry” of data points. PCA defines the intrinsic geometry of data points using the squared Euclidean distances between feature vectors. Indeed, PCA produces feature vectors [math]\featurevec^{(\sampleidx)}[/math] such that for data points whose raw feature vectors have small squared Euclidean distance, also the new feature vectors [math]\featurevec^{(\sampleidx)}[/math] will have small squared Euclidean distance.
Some application domains generate data points for which the Euclidean distances between raw feature vectors does not reflect the intrinsic geometry of data points. As a point in case, consider data points representing scientific articles which can be characterized by the relative frequencies of words from some given set of relevant words (dictionary). A small Euclidean distance between the resulting raw feature vectors typically does not imply that the corresponding text documents are similar. Instead, the similarity between two articles might depend on the number of authors that are contained in author lists of both papers. We can represent the similarities between all articles using a similarity graph whose nodes represent data points which are connected by an edge (link) if they are similar (see Figure fig_connect_clustering).
Consider a dataset [math]\dataset = \big(\datapoint^{(1)},\ldots,\datapoint^{(\samplesize)} \big)[/math] whose intrinsic geometry is characterized by an unweighted similarity graph [math]\graph = \big(\nodes \defeq \{1,\ldots,\samplesize\},\edges\big)[/math]. The node [math]\sampleidx \in \nodes[/math] represents the [math]\sampleidx[/math]-th data point [math]\datapoint^{(\sampleidx)}[/math]. Two nodes are connected by an undirected edge if the corresponding data points are similar.
We would like to find short feature vectors [math]\featurevec^{(\sampleidx)}[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math], such that two data points [math]\sampleidx,\sampleidx'[/math], whose feature vectors [math]\featurevec^{(\sampleidx)}, \featurevec^{(\sampleidx')}[/math] have small Euclidean distance, are well-connected to each other. This informal requirement must be made precise by a measure for how well two nodes of an undirected graph are connected. We refer the reader to literature on network theory for an overview and details of various connectivity measures [7].
Let us discuss a simple but powerful technique to map the nodes [math]\sampleidx \in \nodes[/math] of an undirected graph [math]\graph[/math] to (short) feature vectors [math]\featurevec^{(\sampleidx)} \in \mathbb{R}^{\featuredim}[/math]. This map is such that the Euclidean distances between the feature vectors of two nodes reflect their connectivity within [math]\graph[/math]. This technique uses the Laplacian matrix [math]\mL \in \mathbb{R}^{(\sampleidx)}[/math] which is defined for an undirected graph [math]\graph[/math] (with node set [math]\nodes = \{1,\ldots,\samplesize\}[/math]) element-wise
Here, [math]\nodedegree{\sampleidx} \defeq \big| \{ \sampleidx': \{\sampleidx,\sampleidx'\} \in \edges \} \big|[/math] denotes the number of neighbours (the degree) of node [math]\sampleidx \in \nodes[/math]. It can be shown that the Laplacian matrix [math]\mL[/math] is psd [8](Proposition 1). Therefore we can find a set of orthonormal eigenvectors
with corresponding (ordered in a non-decreasing fashion) eigenvalues [math]\eigval{1} \leq \ldots \leq \eigval{\samplesize}[/math] of [math]\mL[/math].
For a given number [math]\featuredim[/math], we construct the feature vector
for the [math]\sampleidx[/math]th data point. Here, we used the entries of of the first [math]\featuredim[/math] eigenvectors \eqref{equ_def_eigvec_alap_featLearn}. It can be shown that the Euclidean distances between the feature vectors [math]\featurevec^{(\sampleidx)}[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math], reflect the connectivities between data points [math]\sampleidx=1,\ldots,\samplesize[/math] in the similarity graph [math]\graph[/math]. For a more precise statement of this informal claim we refer to the excellent tutorial [8].
To summarize, we can construct numeric feature vectors for (non-numeric ) data points via the eigenvectors of the Laplacian matrix of a similarity graph for the data points. Algorithm alg_dimred_discrete summarizes this feature learning method which requires as its input a similarity graph for the data points and the desired number [math]\featurelen[/math] of numeric features. Note that Algorithm alg_dimred_discrete does not make any use of the Euclidean distances between raw feature vectors and uses solely the similarity graph [math]\graph[/math] to determine the intrinsic geometry of [math]\dataset[/math].
Input: dataset [math]\dataset=\{ \rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw} \}_{\sampleidx=1}^{\samplesize}[/math]; similarity graph [math]\graph[/math]; number [math]\featuredim[/math] of features to be constructed for each data point.
- construct the Laplacian matrix [math]\mL[/math] of the similarity graph (see \eqref{equ_def_laplacian_sim_graph})
- compute EVD of [math]\mL[/math] to obtain [math]\featurelen[/math] orthonormal eigenvectors \eqref{equ_def_eigvec_alap_featLearn} corresponding to the smallest eigenvalues of [math]\mL[/math]
- for each data point
[math]\sampleidx[/math], construct feature vector
[[math]] \begin{equation} \featurevec^{(\sampleidx)} \defeq \big( \eigvecCoventry^{(1)}_{\sampleidx}, \ldots, \eigvecCoventry^{(\featurelen)}_{\sampleidx} \big)^{T} \in \mathbb{R}^{\featurelen} \end{equation} [[/math]]
Feature Learning for Labeled Data
We have discussed PCA as a linear dimensionality reduction method. PCA learns a compression matrix that maps raw features [math]\rawfeaturevec^{(\sampleidx)}[/math] of data points to new (much shorter) feature vectors
[math]\featurevec^{(\sampleidx)}[/math]. The feature vectors [math]\featurevec^{(\sampleidx)}[/math] determined by PCA depend solely on the raw feature vectors [math]\rawfeaturevec^{(\sampleidx)}[/math] of a given dataset [math]\dataset[/math]. In particular, PCA determines the compression matrix such that the new features allow for a linear reconstruction \eqref{equ_approx_linear_PCA} with minimum reconstruction error \eqref{equ_app_error_PCA}.
For some application domains we might not only have access to raw feature vectors but also to the label values [math]\truelabel^{(\sampleidx)}[/math] of the data points in [math]\dataset[/math]. Indeed, dimensionality reduction methods might be used as pre-processing step within a regression or classification problem that involves a labeled training set. However, in its basic form, PCA (see Algorithm alg_PCA ) does not allow to exploit the information provided by available labels [math]\truelabel^{(\sampleidx)}[/math] of data points [math]\rawfeaturevec^{(\sampleidx)}[/math]. For some datasets, PCA might deliver feature vectors that are not very relevant for the overall task of predicting the label of a data point.
Let us now discuss a modification of PCA that exploits the information provided by available labels of the data points. The idea is to learn a linear construction map (matrix) [math]\mW[/math] such that the new feature vectors
[math]\featurevec^{(\sampleidx)} = \mW \rawfeaturevec^{(\sampleidx)}[/math] allow to predict the label [math]\truelabel^{(\sampleidx)}[/math] as good as possible. We restrict the prediction to be linear,
with some weight vector [math]\vr \in \mathbb{R}^{\featuredim}[/math].
While PCA is motivated by minimizing the reconstruction error \eqref{equ_def_reconst_error}, we now aim at minimizing the prediction error [math]\hat{\truelabel}^{(\sampleidx)} - \truelabel^{(\sampleidx)}[/math]. In particular, we assess the usefulness of a given pair of construction map [math]\mW[/math] and predictor [math]\vr[/math] (see \eqref{equ_lin_predictor_dimred}), using the empirical risk
to guide the learning of a compressing matrix [math]\mW[/math] and corresponding linear predictor weights [math]\vr[/math] (\eqref{equ_lin_predictor_dimred}).
The optimal matrix [math]\mW[/math] that minimizes the empirical risk \eqref{equ_lda_prediction_error} can be obtained via the EVD \eqref{equ_EVD_Q_PCA} of the sample covariance matrix [math]\mQ[/math] \eqref{equ_def_Q_PCA}. Note that we have used the EVD of [math]\mQ[/math] already for PCA in Section Principal Component Analysis (see \eqref{equ_def_PCA_W}). Remember that PCA uses the [math]\featuredim[/math] eigenvectors [math]\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelen)}[/math] corresponding to the [math]\featurelen[/math] largest eigenvalues of [math]\mQ[/math]. In contrast, to minimize \eqref{equ_lda_prediction_error}, we need to use a different set of eigenvectors in the rows of [math]\mW[/math] in general. To find the right set of [math]\featuredim[/math] eigenvectors, we need the sample cross-correlation vector
The entry [math]q_{\featureidx}[/math] of the vector [math]\vq[/math] estimates the correlation between the raw feature [math]\rawfeature^{(\sampleidx)}_{\featureidx}[/math] and the label [math]\truelabel^{(\sampleidx)}[/math]. We then define the index set
It can then be shown that the rows of the optimal compression matrix [math]\mW[/math] are the eigenvectors
[math]\eigvecCov^{(\featureidx)}[/math] with [math]\featureidx \in \mathcal{S}[/math]. We summarize the overall feature learning method in Algorithm alg_PCA_labeled .
Input: dataset [math] \big(\rawfeaturevec^{(1)},\truelabel^{(1)} \big),\ldots,\big(\rawfeaturevec^{(\samplesize)},\truelabel^{(\samplesize)} \big)[/math] with raw features [math]\rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}[/math] and numeric labels [math]\truelabel^{(\sampleidx)} \in \mathbb{R}[/math] ; length [math]\featuredim[/math] of new feature vectors.
- compute EVD \eqref{equ_EVD_Q_PCA} of the sample covariance matrix \eqref{equ_def_Q_PCA} to obtain orthonormal eigenvectors [math]\big(\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelenraw)}\big)[/math] corresponding to (decreasingly ordered) eigenvalues [math]\eigval{1}\geq \eigval{2}\geq \ldots \geq \eigval{\featurelenraw} \geq 0[/math]
- compute the sample cross-correlation vector \eqref{equ_cross_correlation_PCA} and, in turn, the sequence
[[math]] \begin{equation} \label{equ_sequence_cross_cov_matrix} \big(q_{1}\big)^2/\eigval{1}, \ldots, \big(q_{\featurelenraw}\big)^2/\eigval{\featurelenraw} \end{equation} [[/math]]
- determine indices [math]\featureidx_{1},\ldots,\featureidx_{\featurelen}[/math] of [math]\featurelen[/math] largest elements in \eqref{equ_sequence_cross_cov_matrix}
- construct compression matrix [math]\mW \defeq \big( \eigvecCov^{(\featureidx_{1})},\ldots, \eigvecCov^{(\featureidx_{\featuredim})} \big)^{T} \in \mathbb{R}^{\featuredim \times \featurelenraw}[/math]
- compute feature vector [math]\featurevec^{(\sampleidx)} = \mW \rawfeaturevec^{(\sampleidx)}[/math]
The main focus of this section is on regression problems that involve data points with numeric labels (e.g., from the label space [math]\labelspace = \mathbb{R}[/math]). Given the raw features and labels of the data point in the dataset [math]\dataset[/math], Algorithm alg_PCA_labeled determines new feature vectors [math]\featurevec^{(\sampleidx)}[/math] that allow to linearly predict a numeric label with minimum squared error. A similar approach can be used for classification problems involving data points with a finite label space [math]\labelspace[/math]. Linear (or Fisher) discriminant analysis aims at constructing a compression matrix [math]\mW[/math] such that the learnt features [math]\featurevec = \mW \rawfeaturevec[/math] of a data point allow to predict its label [math]\truelabel[/math] as accurately as possible [3].
Privacy-Preserving Feature Learning
Many important application domains of ML involve sensitive data that is subject to data protection law [9]. Consider a health-care provider (such as a hospital) holding a large database of patient records. From a ML perspective this databases is nothing but a (typically large) set of data points representing individual patients. The data points are characterized by many features including personal identifiers (name, social security number), bio-physical parameters as well as examination results . We could apply ML to learn a predictor for the risk of particular disease given the features of a data point.
Given large patient databases, the ML methods might not be implemented locally at the hospital but using cloud computing. However, data protection requirements might prohibit the transfer of raw patient records that allow to match individuals with bio-physical properties. In this case we might apply feature learning methods to construct new features for each patient such that they allow to learn an accurate hypothesis for predicting a disease but do not allow to identify sensitive properties of the patient such as its name or a social security number.
Let us formalize the above application by characterizing each data point (patient in the hospital database) using raw feature vector [math]\rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}[/math] and a sensitive numeric property [math]\pi^{(\sampleidx)}[/math]. We would like to find a compression map [math]\mW[/math] such that the resulting features [math]\featurevec^{(\sampleidx)} = \mW \rawfeaturevec^{(\sampleidx)}[/math] do not allow to accurately predict the sensitive property [math]\pi^{(\sampleidx)}[/math]. The prediction of the sensitive property is restricted to be a linear [math]\hat{\pi}^{(\sampleidx)} \defeq \vr^{T} \featurevec^{(\sampleidx)}[/math] with some weight vector [math]\vr[/math].
Similar to Section Feature Learning for Labeled Data we want to find a compression matrix [math]\mW[/math] that transforms, in a linear fashion, the raw feature vector [math]\rawfeaturevec \in \mathbb{R}^{\featurelenraw}[/math] to a new feature vector [math]\featurevec \in \mathbb{R}^{\featurelen}[/math]. However the design criterion for the optimal compression matrix [math]\mW[/math] was different in Section Feature Learning for Labeled Data where the new feature vectors should allow for an accurate linear prediction of the label. In contrast, here we want to construct feature vectors such that there is no accurate linear predictor of the sensitive property [math]\pi^{(\sampleidx)}[/math].
As in Section Feature Learning for Labeled Data , the optimal compression matrix [math]\mW[/math] is given row-wise by the eigenvectors of the sample covariance matrix \eqref{equ_def_Q_PCA}. However, the choice of which eigenvectors to use is different and based on the entries of the sample cross-correlation vector
We summarize the construction of the optimal privacy-preserving compression matrix and corresponding new feature vectors in Algorithm alg_PCA_privacypreserving .
Input: dataset [math] \big(\rawfeaturevec^{(1)},\truelabel^{(1)} \big),\ldots,\big(\rawfeaturevec^{(\samplesize)},\truelabel^{(\samplesize)} \big)[/math]; each data point characterized by raw features [math]\rawfeaturevec^{(\sampleidx)} \in \mathbb{R}^{\featurelenraw}[/math] and (numeric) sensitive property [math]\pi^{(\sampleidx)} \in \mathbb{R}[/math]; number [math]\featuredim[/math] of new features.
- compute the EVD \eqref{equ_EVD_Q_PCA} of the sample covariance matrix \eqref{equ_def_Q_PCA} to obtain orthonormal eigenvectors [math]\big(\eigvecCov^{(1)},\ldots,\eigvecCov^{(\featurelenraw)}\big)[/math] corresponding to (decreasingly ordered) eigenvalues [math]\eigval{1} \geq \eigval{2} \geq \ldots \geq \eigval{\featurelenraw} \geq 0[/math]
- compute the sample cross-correlation vector \eqref{equ_cross_correlation_privacypreseringPCA} and, in turn, the sequence
[[math]] \begin{equation} \label{equ_sequence_cross_cov_matrix_privacypreserving} \big(c_{1}\big)^2/\eigval{1}, \ldots, \big(c_{\featurelenraw}\big)^2/\eigval{\featurelenraw} \end{equation} [[/math]]
- determine indices [math]\featureidx_{1},\ldots,\featureidx_{\featurelen}[/math] of [math]\featurelen[/math] smallest elements in \eqref{equ_sequence_cross_cov_matrix_privacypreserving}
- construct compression matrix [math]\mW \defeq \big( \eigvecCov^{(\featureidx_{1})},\ldots, \eigvecCov^{(\featureidx_{\featuredim})} \big)^{T} \in \mathbb{R}^{\featuredim \times \featurelenraw}[/math]
- compute feature vector [math]\featurevec^{(\sampleidx)} = \mW \rawfeaturevec^{(\sampleidx)}[/math]
Algorithm alg_PCA_privacypreserving learns a map [math]\mW[/math] to extract privacy-preserving features out of the raw feature vector
of a data point. These new features are privacy-preserving as they do not allow to accurately predict (in a linear fashion) a
sensitive property [math]\pi[/math] of the data point. Another formalization for the preservation of privacy can be obtained using information-theoretic concepts. This information-theoretic approach interprets data points, their feature vector and sensitive property, as realizations of RVs. It is then possible to use the mutual information between new features
[math]\featurevec[/math] and the sensitive (private) property
[math]\pi[/math] as an optimization criterion for learning a compression map
[math]h[/math] (Section Basic Principle of Dimensionality Reduction ). The resulting feature learning method (referred
to as privacy-funnel) differs from Algorithm alg_PCA_privacypreserving not only in the optimization criterion for the compression map
but also in that it allows it to be non-linear [10][11].
Random Projections
Note that PCA uses an EVD of the sample covariance matrix [math]\mathbf{Q}[/math] \eqref{equ_def_Q_PCA}. The computational complexity (e.g., measured by number of multiplications and additions) for computing this EVD is lower bounded by [math]\featuredim \min\{ \featurelenraw^{2}, \samplesize^{2} \}[/math] [12][13]. This computational complexity can be prohibitive for ML applications with [math]\featurelenraw[/math] and [math]\samplesize[/math] being of the order of millions or even billions.
There is a computationally cheap alternative to PCA (Algorithm alg_PCA ) for finding a useful compression matrix [math]\mathbf{W}[/math] in \eqref{equ_feat_learning_matrix}. This alternative is to construct the compression matrix [math]\mathbf{W}[/math] entry-wise
The matrix entries \eqref{equ_def_iid_random_matrix} are realizations [math]a_{i,j}[/math] of iid RVs with some common probability distribution [math]\prob{a}[/math]. Different choices for the probability distribution [math]\prob{a}[/math] have been studied in the literature [14]. The Bernoulli distribution is used to obtain a compression matrix with binary entries. Another popular choice for [math]\prob{a}[/math] is the multivariate normal (Gaussian) distribution.
Consider data points whose raw feature vectors [math]\rawfeaturevec[/math] are located near a [math]\sparsity[/math]-dimensional subspace of [math]\mathbb{R}^{\featurelenraw}[/math]. The feature vectors [math]\featurevec[/math] obtained via \eqref{equ_feat_learning_matrix} using a random matrix \eqref{equ_def_iid_random_matrix} allows to reconstruct the raw feature vectors [math]\rawfeaturevec[/math] with high probability whenever
The constant [math]C[/math] depends on the maximum tolerated reconstruction error [math]\eta[/math] (such that
[math]\| \widehat{\rawfeaturevec} - \rawfeaturevec \|_{2}^{2} \leq \eta[/math] for any data point) and the probability that the features [math]\featurevec[/math] (see \eqref{equ_def_iid_random_matrix}) allow for a maximum reconstruction error [math]\eta[/math] [14](Theorem 9.27.).
Dimensionality Increase
The focus of this chapter is on dimensionality reduction methods that learn a feature map delivering new feature vectors which are (significantly) shorter than the raw feature vectors. However, it might sometimes be beneficial to learn a feature map that delivers new feature vectors which are longer than the raw feature vectors. We have already discussed two examples for such feature learning methods in Sections Polynomial Regression and Kernel Methods . Polynomial regression maps a single raw feature [math]\rawfeature[/math] to a feature vector containing the powers of the raw feature [math]z[/math]. This allows to use apply linear predictor maps to the new feature vectors to obtain predictions that depend non-linearly on the raw feature [math]\rawfeature[/math]. Kernel methods might even use a feature map that delivers feature vectors belonging to an infinite-dimensional Hilbert space [15].
Mapping raw feature vectors into higher-dimensional (or even infinite-dimensional) spaces might be useful if the intrinsic geometry of the data points is simpler when looked at in the higher-dimensional space. Consider a binary classification problem where data points are highly inter-winded in the original feature space (see Figure fig_kernelmethods). Loosely speaking, mapping into higher-dimensional_feature_space_might "flatten-out" a non-linear decision boundary between data points. We can then apply linear classifiers to the higher-dimensional features to achieve accurate predictions.
References
- Cite error: Invalid
<ref>tag; no text was provided for refs namedGoodfellow-et-al-2016 - Cite error: Invalid
<ref>tag; no text was provided for refs namedStrang2007 - 3.0 3.1 3.2 Cite error: Invalid
<ref>tag; no text was provided for refs namedhastie01statisticallearning - Cite error: Invalid
<ref>tag; no text was provided for refs namedRobustPCA - Cite error: Invalid
<ref>tag; no text was provided for refs namedRoweis98emalgorithms - 6.0 6.1 6.2 Cite error: Invalid
<ref>tag; no text was provided for refs namedprobabilistic-principal-component-analysis - Cite error: Invalid
<ref>tag; no text was provided for refs namedNewmannBook - 8.0 8.1 Cite error: Invalid
<ref>tag; no text was provided for refs namedLuxburg2007 - Cite error: Invalid
<ref>tag; no text was provided for refs namedWachter:2019wn - Cite error: Invalid
<ref>tag; no text was provided for refs namedMakhdoumiFunnel2014 - Cite error: Invalid
<ref>tag; no text was provided for refs namedShkel2021 - Cite error: Invalid
<ref>tag; no text was provided for refs namedgolub96 - Cite error: Invalid
<ref>tag; no text was provided for refs namedTippingProbPCA - 14.0 14.1 Cite error: Invalid
<ref>tag; no text was provided for refs namedRauhutFoucartCS - Cite error: Invalid
<ref>tag; no text was provided for refs namedLearningKernelsBook