[math] \newcommand{\NA}{{\rm NA}} \newcommand{\mat}[1]{{\bf#1}} \newcommand{\exref}[1]{\ref{##1}} \newcommand{\secstoprocess}{\all} \newcommand{\NA}{{\rm NA}} \newcommand{\mathds}{\mathbb}[/math]

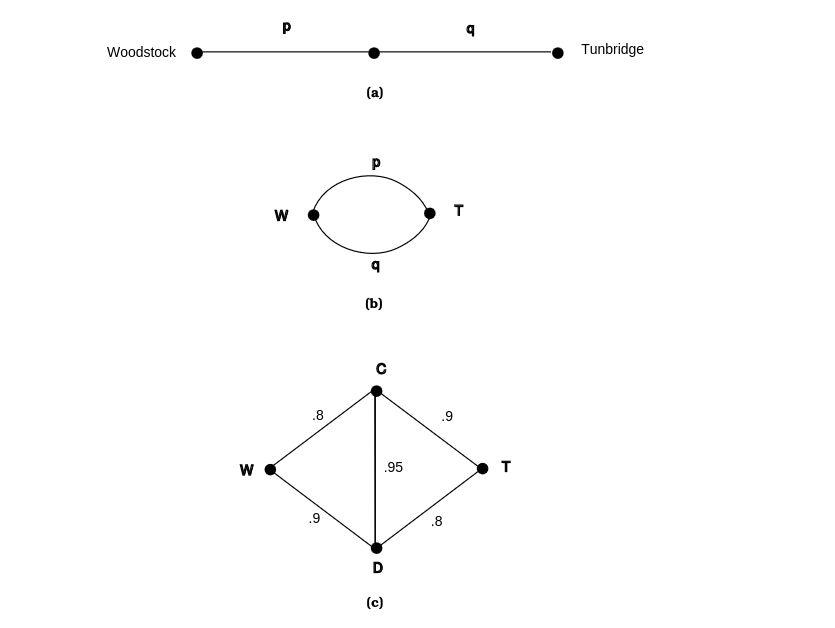
• There has been a blizzard and Helen is trying to drive from Woodstock to Tunbridge, which are connected like the top graph in Figure. Here [math]p[/math] and [math]q[/math] are the probabilities that the two roads are passable. What is the probability that Helen can get from Woodstock to Tunbridge?
• Now suppose that Woodstock and Tunbridge are connected like the middle graph in Figure. What now is the probability that she can get from [math]W[/math] to [math]T[/math]? Note that if we think of the roads as being components of a system, then in (a) and (b) we have computed the reliability of a system whose components are (a) in series and (b) in parallel.
• Now suppose [math]W[/math] and [math]T[/math] are connected like the bottom graph in Figure. Find the probability of Helen's getting from [math]W[/math] to [math]T[/math]. Hint: If the road from [math]C[/math] to [math]D[/math] is impassable, it might as well not be there at all; if it is passable, then figure out how to use part (b) twice.

From Woodstock to Tunbridge.