Dimension-free convex optimization

[math] \newcommand{\LS}{\mathtt{line\_search}} \newcommand{\mI}{\mathrm{I}} \newcommand{\mB}{\mathrm{B}} \newcommand{\conv}{\mathrm{conv}} \newcommand{\inte}{\mathrm{int}} \newcommand{\tg}{\tilde{g}} \newcommand{\tx}{\tilde{x}} \newcommand{\ty}{\tilde{y}} \newcommand{\tz}{\tilde{z}} \newcommand{\id}{\mathrm{id}} \newcommand{\K}{\mathrm{KL}} \newcommand{\kl}{\mathrm{kl}} \newcommand{\bp}{\boldsymbol{p}} \newcommand{\tr}{\mathrm{Tr}} \newcommand{\E}{\mathbb{E}} \newcommand{\N}{\mathbb{N}} \newcommand{\R}{\mathbb{R}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\KL}{\mathrm{KL}} \newcommand{\LG}{\overline{\log}(K)} \newcommand{\ocP}{\overline{\mathcal{P}}} \newcommand{\cZ}{\mathcal{Z}} \newcommand{\cA}{\mathcal{A}} \newcommand{\cR}{\mathcal{R}} \newcommand{\cB}{\mathcal{B}} \newcommand{\cN}{\mathcal{N}} \newcommand{\cM}{\mathcal{M}} \newcommand{\cF}{\mathcal{F}} \newcommand{\cL}{\mathcal{L}} \newcommand{\cX}{\mathcal{X}} \newcommand{\cI}{\mathcal{I}} \newcommand{\cJ}{\mathcal{J}} \newcommand{\cY}{\mathcal{Y}} \newcommand{\cH}{\mathcal{H}} \newcommand{\cP}{\mathcal{P}} \newcommand{\cT}{\mathcal{T}} \newcommand{\cC}{\mathcal{C}} \newcommand{\cS}{\mathcal{S}} \newcommand{\cE}{\mathcal{E}} \newcommand{\cK}{\mathcal{K}} \newcommand{\cD}{\mathcal{D}} \newcommand{\oD}{\overline{\mathcal{D}}} \newcommand{\oR}{\overline{R}} \newcommand{\wh}{\widehat} \newcommand{\argmax}{\mathop{\mathrm{argmax}}} \newcommand{\argmin}{\mathop{\mathrm{argmin}}} \newcommand{\todo}{{\bf TO DO } } \newcommand{\Ber}{\mathop{\mathrm{Ber}}} \newcommand{\beq}{\begin{equation}} \newcommand{\eeq}{\end{equation}} \newcommand{\beqa}{\begin{eqnarray}} \newcommand{\eeqa}{\end{eqnarray}} \newcommand{\beqan}{\begin{eqnarray*}} \newcommand{\eeqan}{\end{eqnarray*}} \newcommand{\qed}{\hfill\BlackBox} \newcommand{\charfct}{\ds1} % \newcommand{\Fcal}{\mathcal{F}} \newcommand{\Xcal}{\mathcal{X}} \newcommand{\Hcal}{\mathcal{H}} \newcommand{\Gcal}{\mathcal{G}} \newcommand{\Nat}{\mathbb{N}} \newcommand{\mathds}{\mathbb}[/math]

\label{dimfree} We investigate here variants of the {\em gradient descent} scheme. This iterative algorithm, which can be traced back to , is the simplest strategy to minimize a differentiable function [math]f[/math] on [math]\R^n[/math]. Starting at some initial point [math]x_1 \in \R^n[/math] it iterates the following equation:

[[math]] \begin{equation} \label{eq:Cau47} x_{t+1} = x_t - \eta \nabla f(x_t) , \end{equation} [[/math]]

where [math]\eta \gt 0[/math] is a fixed step-size parameter. The rationale behind \eqref{eq:Cau47} is to make a small step in the direction that minimizes the local first order Taylor approximation of [math]f[/math] (also known as the steepest descent direction). As we shall see, methods of the type \eqref{eq:Cau47} can obtain an oracle complexity {\em independent of the dimension}. This feature makes them particularly attractive for optimization in very high dimension. Apart from Section Conditional gradient descent, aka Frank-Wolfe, in this chapter [math]\|\cdot\|[/math] denotes the Euclidean norm. The set of constraints [math]\cX \subset \R^n[/math] is assumed to be compact and convex. We define the projection operator [math]\Pi_{\cX}[/math] on [math]\cX[/math] by

[[math]] \Pi_{\cX}(x) = \argmin_{y \in \mathcal{X}} \|x - y\| . [[/math]]

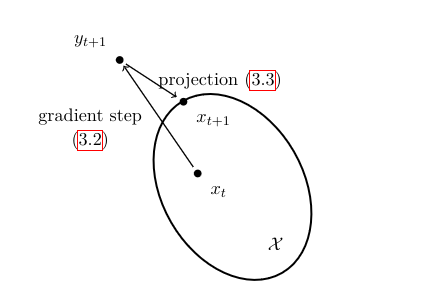
The following lemma will prove to be useful in our study. It is an easy corollary of Proposition, see also Figure.

Lemma

Let [math]x \in \cX[/math] and [math]y \in \R^n[/math], then

[[math]] (\Pi_{\cX}(y) - x)^{\top} (\Pi_{\cX}(y) - y) \leq 0 , [[/math]]

which also implies [math]\|\Pi_{\cX}(y) - x\|^2 + \|y - \Pi_{\cX}(y)\|^2 \leq \|y - x\|^2[/math].

Illustration of Lemma.

Unless specified otherwise all the proofs in this chapter are taken from (with slight simplification in some cases).

Projected subgradient descent for Lipschitz functions

In this section we assume that [math]\cX[/math] is contained in an Euclidean ball centered at [math]x_1 \in \cX[/math] and of radius [math]R[/math]. Furthermore we assume that [math]f[/math] is such that for any [math]x \in \cX[/math] and any [math]g \in \partial f(x)[/math] (we assume [math]\partial f(x) \neq \emptyset[/math]), one has [math]\|g\| \leq L[/math]. Note that by the subgradient inequality and Cauchy-Schwarz this implies that [math]f[/math] is [math]L[/math]-Lipschitz on [math]\cX[/math], that is [math]|f(x) - f(y)| \leq L \|x-y\|[/math]. In this context we make two modifications to the basic gradient descent \eqref{eq:Cau47}. First, obviously, we replace the gradient [math]\nabla f(x)[/math] (which may not exist) by a subgradient [math]g \in \partial f(x)[/math]. Secondly, and more importantly, we make sure that the updated point lies in [math]\cX[/math] by projecting back (if necessary) onto it. This gives the {\em projected subgradient descent} algorithm which iterates the following equations for [math]t \geq 1[/math]:

[[math]] \begin{align} & y_{t+1} = x_t - \eta g_t , \ \text{where} \ g_t \in \partial f(x_t) , \label{eq:PGD1}\\ & x_{t+1} = \Pi_{\cX}(y_{t+1}) . \label{eq:PGD2} \end{align} [[/math]]

This procedure is illustrated in Figure. We prove now a rate of convergence for this method under the above assumptions.

Illustration of the projected subgradient descent method.

Theorem

The projected subgradient descent method with [math]\eta = \frac{R}{L \sqrt{t}}[/math] satisfies

[[math]] f\left(\frac{1}{t} \sum_{s=1}^t x_s\right) - f(x^*) \leq \frac{R L}{\sqrt{t}} . [[/math]]

Show Proof

Using the definition of subgradients, the definition of the method, and the elementary identity [math]2 a^{\top} b = \|a\|^2 + \|b\|^2 - \|a-b\|^2[/math], one obtains

[[math]] \begin{eqnarray*} f(x_s) - f(x^*) & \leq & g_s^{\top} (x_s - x^*) \\ & = & \frac{1}{\eta} (x_s - y_{s+1})^{\top} (x_s - x^*) \\ & = & \frac{1}{2 \eta} \left(\|x_s - x^*\|^2 + \|x_s - y_{s+1}\|^2 - \|y_{s+1} - x^*\|^2\right) \\ & = & \frac{1}{2 \eta} \left(\|x_s - x^*\|^2 - \|y_{s+1} - x^*\|^2\right) + \frac{\eta}{2} \|g_s\|^2. \end{eqnarray*} [[/math]]

Now note that [math]\|g_s\| \leq L[/math], and furthermore by Lemma

[[math]] \|y_{s+1} - x^*\| \geq \|x_{s+1} - x^*\| . [[/math]]

Summing the resulting inequality over [math]s[/math], and using that [math]\|x_1 - x^*\| \leq R[/math] yield

[[math]] \sum_{s=1}^t \left( f(x_s) - f(x^*) \right) \leq \frac{R^2}{2 \eta} + \frac{\eta L^2 t}{2} . [[/math]]

Plugging in the value of [math]\eta[/math] directly gives the statement (recall that by convexity [math]f((1/t) \sum_{s=1}^t x_s) \leq \frac1{t} \sum_{s=1}^t f(x_s)[/math]).

■

We will show in Section Lower bounds that the rate given in Theorem is unimprovable from a black-box perspective. Thus to reach an [math]\epsilon[/math]-optimal point one needs [math]\Theta(1/\epsilon^2)[/math] calls to the oracle. In some sense this is an astonishing result as this complexity is independent of the ambient dimension [math]n[/math]. On the other hand this is also quite disappointing compared to the scaling in [math]\log(1/\epsilon)[/math] of the center of gravity and ellipsoid method of Chapter. To put it differently with gradient descent one could hope to reach a reasonable accuracy in very high dimension, while with the ellipsoid method one can reach very high accuracy in reasonably small dimension. A major task in the following sections will be to explore more restrictive assumptions on the function to be optimized in order to have the best of both worlds, that is an oracle complexity independent of the dimension and with a scaling in [math]\log(1/\epsilon)[/math]. The computational bottleneck of the projected subgradient descent is often the projection step \eqref{eq:PGD2} which is a convex optimization problem by itself. In some cases this problem may admit an analytical solution (think of [math]\cX[/math] being an Euclidean ball), or an easy and fast combinatorial algorithm to solve it (this is the case for [math]\cX[/math] being an [math]\ell_1[/math]-ball, see ). We will see in Section Conditional gradient descent, aka Frank-Wolfe a projection-free algorithm which operates under an extra assumption of smoothness on the function to be optimized. Finally we observe that the step-size recommended by Theorem depends on the number of iterations to be performed. In practice this may be an undesirable feature. However using a time-varying step size of the form [math]\eta_s = \frac{R}{L \sqrt{s}}[/math] one can prove the same rate up to a [math]\log t[/math] factor. In any case these step sizes are very small, which is the reason for the slow convergence. In the next section we will see that by assuming {\em smoothness} in the function [math]f[/math] one can afford to be much more aggressive. Indeed in this case, as one approaches the optimum the size of the gradients themselves will go to [math]0[/math], resulting in a sort of ``auto-tuning" of the step sizes which does not happen for an arbitrary convex function.

Gradient descent for smooth functions

We say that a continuously differentiable function [math]f[/math] is [math]\beta[/math]-smooth if the gradient [math]\nabla f[/math] is [math]\beta[/math]-Lipschitz, that is

[[math]] \|\nabla f(x) - \nabla f(y) \| \leq \beta \|x-y\| . [[/math]]

Note that if [math]f[/math] is twice differentiable then this is equivalent to the eigenvalues of the Hessians being smaller than [math]\beta[/math]. In this section we explore potential improvements in the rate of convergence under such a smoothness assumption. In order to avoid technicalities we consider first the unconstrained situation, where [math]f[/math] is a convex and [math]\beta[/math]-smooth function on [math]\R^n[/math]. The next theorem shows that {\em gradient descent}, which iterates [math]x_{t+1} = x_t - \eta \nabla f(x_t)[/math], attains a much faster rate in this situation than in the non-smooth case of the previous section.

Theorem

Let [math]f[/math] be convex and [math]\beta[/math]-smooth on [math]\R^n[/math]. Then gradient descent with [math]\eta = \frac{1}{\beta}[/math] satisfies

[[math]] f(x_t) - f(x^*) \leq \frac{2 \beta \|x_1 - x^*\|^2}{t-1} . [[/math]]

Before embarking on the proof we state a few properties of smooth convex functions.

Lemma

Let [math]f[/math] be a [math]\beta[/math]-smooth function on [math]\R^n[/math]. Then for any [math]x, y \in \R^n[/math], one has

[[math]] |f(x) - f(y) - \nabla f(y)^{\top} (x - y)| \leq \frac{\beta}{2} \|x - y\|^2 . [[/math]]

Show Proof

We represent [math]f(x) - f(y)[/math] as an integral, apply Cauchy-Schwarz and then [math]\beta[/math]-smoothness:

[[math]] \begin{align*} & |f(x) - f(y) - \nabla f(y)^{\top} (x - y)| \\ & = \left|\int_0^1 \nabla f(y + t(x-y))^{\top} (x-y) dt - \nabla f(y)^{\top} (x - y) \right| \\ & \leq \int_0^1 \|\nabla f(y + t(x-y)) - \nabla f(y)\| \cdot \|x - y\| dt \\ & \leq \int_0^1 \beta t \|x-y\|^2 dt \\ & = \frac{\beta}{2} \|x-y\|^2 . \end{align*} [[/math]]

■

In particular this lemma shows that if [math]f[/math] is convex and [math]\beta[/math]-smooth, then for any [math]x, y \in \R^n[/math], one has

[[math]] \begin{equation} \label{eq:defaltsmooth} 0 \leq f(x) - f(y) - \nabla f(y)^{\top} (x - y) \leq \frac{\beta}{2} \|x - y\|^2 . \end{equation} [[/math]]

This gives in particular the following important inequality to evaluate the improvement in one step of gradient descent:

[[math]] \begin{equation} \label{eq:onestepofgd} f\left(x - \frac{1}{\beta} \nabla f(x)\right) - f(x) \leq - \frac{1}{2 \beta} \|\nabla f(x)\|^2 . \end{equation} [[/math]]

The next lemma, which improves the basic inequality for subgradients under the smoothness assumption, shows that in fact [math]f[/math] is convex and [math]\beta[/math]-smooth if and only if \eqref{eq:defaltsmooth} holds true. In the literature \eqref{eq:defaltsmooth} is often used as a definition of smooth convex functions.

Lemma

Let [math]f[/math] be such that \eqref{eq:defaltsmooth} holds true. Then for any [math]x, y \in \R^n[/math], one has

[[math]] f(x) - f(y) \leq \nabla f(x)^{\top} (x - y) - \frac{1}{2 \beta} \|\nabla f(x) - \nabla f(y)\|^2 . [[/math]]

Show Proof

Let [math]z = y - \frac{1}{\beta} (\nabla f(y) - \nabla f(x))[/math]. Then one has

[[math]] \begin{align*} & f(x) - f(y) \\ & = f(x) - f(z) + f(z) - f(y) \\ & \leq \nabla f(x)^{\top} (x-z) + \nabla f(y)^{\top} (z-y) + \frac{\beta}{2} \|z - y\|^2 \\ & = \nabla f(x)^{\top}(x-y) + (\nabla f(x) - \nabla f(y))^{\top} (y-z) + \frac{1}{2 \beta} \|\nabla f(x) - \nabla f(y)\|^2 \\ & = \nabla f(x)^{\top} (x - y) - \frac{1}{2 \beta} \|\nabla f(x) - \nabla f(y)\|^2 . \end{align*} [[/math]]

■

We can now prove Theorem \begin{proof} Using \eqref{eq:onestepofgd} and the definition of the method one has

[[math]] f(x_{s+1}) - f(x_s) \leq - \frac{1}{2 \beta} \|\nabla f(x_s)\|^2. [[/math]]

In particular, denoting [math]\delta_s = f(x_s) - f(x^*)[/math], this shows:

[[math]] \delta_{s+1} \leq \delta_s - \frac{1}{2 \beta} \|\nabla f(x_s)\|^2. [[/math]]

One also has by convexity

[[math]] \delta_s \leq \nabla f(x_s)^{\top} (x_s - x^*) \leq \|x_s - x^*\| \cdot \|\nabla f(x_s)\| . [[/math]]

We will prove that [math]\|x_s - x^*\|[/math] is decreasing with [math]s[/math], which with the two above displays will imply

[[math]] \delta_{s+1} \leq \delta_s - \frac{1}{2 \beta \|x_1 - x^*\|^2} \delta_s^2. [[/math]]

Let us see how to use this last inequality to conclude the proof. Let [math]\omega = \frac{1}{2 \beta \|x_1 - x^*\|^2}[/math], then

[[math]] \omega \delta_s^2 + \delta_{s+1} \leq \delta_s \Leftrightarrow \omega \frac{\delta_s}{\delta_{s+1}} + \frac{1}{\delta_{s}} \leq \frac{1}{\delta_{s+1}} \Rightarrow \frac{1}{\delta_{s+1}} - \frac{1}{\delta_{s}} \geq \omega \Rightarrow \frac{1}{\delta_t} \geq \omega (t-1) . [[/math]]

Thus it only remains to show that [math]\|x_s - x^*\|[/math] is decreasing with [math]s[/math]. Using Lemma one immediately gets

[[math]] \begin{equation} \label{eq:coercive1} (\nabla f(x) - \nabla f(y))^{\top} (x - y) \geq \frac{1}{\beta} \|\nabla f(x) - \nabla f(y)\|^2 . \end{equation} [[/math]]

We use this as follows (together with [math]\nabla f(x^*) = 0[/math])

[[math]] \begin{eqnarray*} \|x_{s+1} - x^*\|^2& = & \|x_{s} - \frac{1}{\beta} \nabla f(x_s) - x^*\|^2 \\ & = & \|x_{s} - x^*\|^2 - \frac{2}{\beta} \nabla f(x_s)^{\top} (x_s - x^*) + \frac{1}{\beta^2} \|\nabla f(x_s)\|^2 \\ & \leq & \|x_{s} - x^*\|^2 - \frac{1}{\beta^2} \|\nabla f(x_s)\|^2 \\ & \leq & \|x_{s} - x^*\|^2 , \end{eqnarray*} [[/math]]

which concludes the proof. \end{proof} \subsection*{The constrained case} We now come back to the constrained problem

[[math]] \begin{align*} & \mathrm{min.} \; f(x) \\ & \text{s.t.} \; x \in \cX . \end{align*} [[/math]]

Similarly to what we did in Section Projected subgradient descent for Lipschitz functions we consider the projected gradient descent algorithm, which iterates [math]x_{t+1} = \Pi_{\cX}(x_t - \eta \nabla f(x_t))[/math]. The key point in the analysis of gradient descent for unconstrained smooth optimization is that a step of gradient descent started at [math]x[/math] will decrease the function value by at least [math]\frac{1}{2\beta} \|\nabla f(x)\|^2[/math], see \eqref{eq:onestepofgd}. In the constrained case we cannot expect that this would still hold true as a step may be cut short by the projection. The next lemma defines the ``right" quantity to measure progress in the constrained case.

Lemma

Let [math]x, y \in \cX[/math], [math]x^+ = \Pi_{\cX}\left(x - \frac{1}{\beta} \nabla f(x)\right)[/math], and [math]g_{\cX}(x) = \beta(x - x^+)[/math]. Then the following holds true:

[[math]] f(x^+) - f(y) \leq g_{\cX}(x)^{\top}(x-y) - \frac{1}{2 \beta} \|g_{\cX}(x)\|^2 . [[/math]]

Show Proof

We first observe that

[[math]] \begin{equation} \label{eq:chap3eq1} \nabla f(x)^{\top} (x^+ - y) \leq g_{\cX}(x)^{\top}(x^+ - y) . \end{equation} [[/math]]

Indeed the above inequality is equivalent to

[[math]] \left(x^+- \left(x - \frac{1}{\beta} \nabla f(x) \right)\right)^{\top} (x^+ - y) \leq 0, [[/math]]

which follows from Lemma. Now we use \eqref{eq:chap3eq1} as follows to prove the lemma (we also use \eqref{eq:defaltsmooth} which still holds true in the constrained case)

[[math]] \begin{align*} & f(x^+) - f(y) \\ & = f(x^+) - f(x) + f(x) - f(y) \\ & \leq \nabla f(x)^{\top} (x^+-x) + \frac{\beta}{2} \|x^+-x\|^2 + \nabla f(x)^{\top} (x-y) \\ & = \nabla f(x)^{\top} (x^+ - y) + \frac{1}{2 \beta} \|g_{\cX}(x)\|^2 \\ & \leq g_{\cX}(x)^{\top}(x^+ - y) + \frac{1}{2 \beta} \|g_{\cX}(x)\|^2 \\ & = g_{\cX}(x)^{\top}(x - y) - \frac{1}{2 \beta} \|g_{\cX}(x)\|^2 . \end{align*} [[/math]]

■

We can now prove the following result.

Theorem

Let [math]f[/math] be convex and [math]\beta[/math]-smooth on [math]\cX[/math]. Then projected gradient descent with [math]\eta = \frac{1}{\beta}[/math] satisfies

[[math]] f(x_t) - f(x^*) \leq \frac{3 \beta \|x_1 - x^*\|^2 + f(x_1) - f(x^*)}{t} . [[/math]]

|Lemma immediately gives

[[math]] f(x_{s+1}) - f(x_s) \leq - \frac{1}{2 \beta} \|g_{\cX}(x_s)\|^2 , [[/math]]

and

[[math]] f(x_{s+1}) - f(x^*) \leq \|g_{\cX}(x_s)\| \cdot \|x_s - x^*\| . [[/math]]

We will prove that [math]\|x_s - x^*\|[/math] is decreasing with [math]s[/math], which with the two above displays will imply

[[math]] \delta_{s+1} \leq \delta_s - \frac{1}{2 \beta \|x_1 - x^*\|^2} \delta_{s+1}^2. [[/math]]

An easy induction shows that

[[math]] \delta_s \leq \frac{3 \beta \|x_1 - x^*\|^2 + f(x_1) - f(x^*)}{s}. [[/math]]

Thus it only remains to show that [math]\|x_s - x^*\|[/math] is decreasing with [math]s[/math]. Using Lemma one can see that [math]g_{\cX}(x_s)^{\top} (x_s - x^*) \geq \frac{1}{2 \beta} \|g_{\cX}(x_s)\|^2[/math] which implies

[[math]] \begin{eqnarray*} \|x_{s+1} - x^*\|^2& = & \|x_{s} - \frac{1}{\beta} g_{\cX}(x_s) - x^*\|^2 \\ & = & \|x_{s} - x^*\|^2 - \frac{2}{\beta} g_{\cX}(x_s)^{\top} (x_s - x^*) + \frac{1}{\beta^2} \|g_{\cX}(x_s)\|^2 \\ & \leq & \|x_{s} - x^*\|^2 . \end{eqnarray*} [[/math]]

Show Proof

{{{4}}}

■

Conditional gradient descent, aka Frank-Wolfe

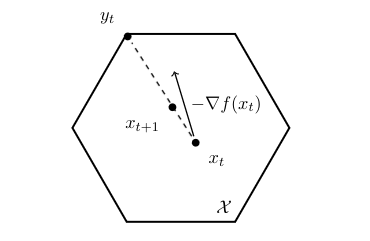
We describe now an alternative algorithm to minimize a smooth convex function [math]f[/math] over a compact convex set [math]\mathcal{X}[/math]. The {\em conditional gradient descent}, introduced in , performs the following update for [math]t \geq 1[/math], where [math](\gamma_s)_{s \geq 1}[/math] is a fixed sequence,

[[math]] \begin{align} &y_{t} \in \mathrm{argmin}_{y \in \mathcal{X}} \nabla f(x_t)^{\top} y \label{eq:FW1} \\ & x_{t+1} = (1 - \gamma_t) x_t + \gamma_t y_t . \label{eq:FW2} \end{align} [[/math]]

In words conditional gradient descent makes a step in the steepest descent direction {\em given the constraint set [math]\cX[/math]}, see Figure for an illustration. From a computational perspective, a key property of this scheme is that it replaces the projection step of projected gradient descent by a linear optimization over [math]\cX[/math], which in some cases can be a much simpler problem.

Illustration of conditional gradient descent.

We now turn to the analysis of this method. A major advantage of conditional gradient descent over projected gradient descent is that the former can adapt to smoothness in an arbitrary norm. Precisely let [math]f[/math] be [math]\beta[/math]-smooth in some norm [math]\|\cdot\|[/math], that is [math]\|\nabla f(x) - \nabla f(y) \|_* \leq \beta \|x-y\|[/math] where the dual norm [math]\|\cdot\|_*[/math] is defined as [math]\|g\|_* = \sup_{x \in \mathbb{R}^n : \|x\| \leq 1} g^{\top} x[/math]. The following result is extracted from (see also ).

Theorem

Let [math]f[/math] be a convex and [math]\beta[/math]-smooth function w.r.t. some norm [math]\|\cdot\|[/math], [math]R = \sup_{x, y \in \mathcal{X}} \|x - y\|[/math], and [math]\gamma_s = \frac{2}{s+1}[/math] for [math]s \geq 1[/math]. Then for any [math]t \geq 2[/math], one has

[[math]] f(x_t) - f(x^*) \leq \frac{2 \beta R^2}{t+1} . [[/math]]

Show Proof

The following inequalities hold true, using respectively [math]\beta[/math]-smoothness (it can easily be seen that \eqref{eq:defaltsmooth} holds true for smoothness in an arbitrary norm), the definition of [math]x_{s+1}[/math], the definition of [math]y_s[/math], and the convexity of [math]f[/math]:

[[math]] \begin{eqnarray*} f(x_{s+1}) - f(x_s) & \leq & \nabla f(x_s)^{\top} (x_{s+1} - x_s) + \frac{\beta}{2} \|x_{s+1} - x_s\|^2 \\ & \leq & \gamma_s \nabla f(x_s)^{\top} (y_{s} - x_s) + \frac{\beta}{2} \gamma_s^2 R^2 \\ & \leq & \gamma_s \nabla f(x_s)^{\top} (x^* - x_s) + \frac{\beta}{2} \gamma_s^2 R^2 \\ & \leq & \gamma_s (f(x^*) - f(x_s)) + \frac{\beta}{2} \gamma_s^2 R^2 . \end{eqnarray*} [[/math]]

Rewriting this inequality in terms of [math]\delta_s = f(x_s) - f(x^*)[/math] one obtains

[[math]] \delta_{s+1} \leq (1 - \gamma_s) \delta_s + \frac{\beta}{2} \gamma_s^2 R^2 . [[/math]]

A simple induction using that [math]\gamma_s = \frac{2}{s+1}[/math] finishes the proof (note that the initialization is done at step [math]2[/math] with the above inequality yielding [math]\delta_2 \leq \frac{\beta}{2} R^2[/math]).

■

In addition to being projection-free and ``norm-free", the conditional gradient descent satisfies a perhaps even more important property: it produces {\em sparse iterates}. More precisely consider the situation where [math]\cX \subset \R^n[/math] is a polytope, that is the convex hull of a finite set of points (these points are called the vertices of [math]\cX[/math]). Then Carath\’eodory's theorem states that any point [math]x \in \cX[/math] can be written as a convex combination of at most [math]n+1[/math] vertices of [math]\cX[/math]. On the other hand, by definition of the conditional gradient descent, one knows that the [math]t^{th}[/math] iterate [math]x_t[/math] can be written as a convex combination of [math]t[/math] vertices (assuming that [math]x_1[/math] is a vertex). Thanks to the dimension-free rate of convergence one is usually interested in the regime where [math]t \ll n[/math], and thus we see that the iterates of conditional gradient descent are very sparse in their vertex representation. We note an interesting corollary of the sparsity property together with the rate of convergence we proved: smooth functions on the simplex [math]\{x \in \mathbb{R}_+^n : \sum_{i=1}^n x_i = 1\}[/math] always admit sparse approximate minimizers. More precisely there must exist a point [math]x[/math] with only [math]t[/math] non-zero coordinates and such that [math]f(x) - f(x^*) = O(1/t)[/math]. Clearly this is the best one can hope for in general, as it can be seen with the function [math]f(x) = \|x\|^2_2[/math] since by Cauchy-Schwarz one has [math]\|x\|_1 \leq \sqrt{\|x\|_0} \|x\|_2[/math] which implies on the simplex [math]\|x\|_2^2 \geq 1 / \|x\|_0[/math]. Next we describe an application where the three properties of conditional gradient descent (projection-free, norm-free, and sparse iterates) are critical to develop a computationally efficient procedure. \subsection*{An application of conditional gradient descent: Least-squares regression with structured sparsity} This example is inspired by (see also ). Consider the problem of approximating a signal [math]Y \in \mathbb{R}^n[/math] by a ‘`small" combination of dictionary elements [math]d_1, \hdots, d_N \in \mathbb{R}^n[/math]. One way to do this is to consider a LASSO type problem in dimension [math]N[/math] of the following form (with [math]\lambda \in \R[/math] fixed)

[[math]] \min_{x \in \mathbb{R}^N} \big\| Y - \sum_{i=1}^N x(i) d_i \big\|_2^2 + \lambda \|x\|_1 . [[/math]]

Let [math]D \in \mathbb{R}^{n \times N}[/math] be the dictionary matrix with [math]i^{th}[/math] column given by [math]d_i[/math]. Instead of considering the penalized version of the problem one could look at the following constrained problem (with [math]s \in \R[/math] fixed) on which we will now focus, see e.g. ,

[[math]] \begin{eqnarray} \min_{x \in \mathbb{R}^N} \| Y - D x \|_2^2 & \qquad \Leftrightarrow \qquad & \min_{x \in \mathbb{R}^N} \| Y / s - D x \|_2^2 \label{eq:structuredsparsity} \\ \text{subject to} \; \|x\|_1 \leq s & & \text{subject to} \; \|x\|_1 \leq 1 . \notag \end{eqnarray} [[/math]]

We make some assumptions on the dictionary. We are interested in situations where the size of the dictionary [math]N[/math] can be very large, potentially exponential in the ambient dimension [math]n[/math]. Nonetheless we want to restrict our attention to algorithms that run in reasonable time with respect to the ambient dimension [math]n[/math], that is we want polynomial time algorithms in [math]n[/math]. Of course in general this is impossible, and we need to assume that the dictionary has some structure that can be exploited. Here we make the assumption that one can do {\em linear optimization} over the dictionary in polynomial time in [math]n[/math]. More precisely we assume that one can solve in time [math]p(n)[/math] (where [math]p[/math] is polynomial) the following problem for any [math]y \in \mathbb{R}^n[/math]:

[[math]] \min_{1 \leq i \leq N} y^{\top} d_i . [[/math]]

This assumption is met for many {\em combinatorial} dictionaries. For instance the dic­tio­nary ele­ments could be vec­tor of inci­dence of span­ning trees in some fixed graph, in which case the lin­ear opti­miza­tion prob­lem can be solved with a greedy algorithm. Finally, for normalization issues, we assume that the [math]\ell_2[/math]-norm of the dictionary elements are controlled by some [math]m \gt 0[/math], that is [math]\|d_i\|_2 \leq m, \forall i \in [N][/math]. Our problem of interest \eqref{eq:structuredsparsity} corresponds to minimizing the function [math]f(x) = \frac{1}{2} \| Y - D x \|^2_2[/math] on the [math]\ell_1[/math]-ball of [math]\mathbb{R}^N[/math] in polynomial time in [math]n[/math]. At first sight this task may seem completely impossible, indeed one is not even allowed to write down entirely a vector [math]x \in \mathbb{R}^N[/math] (since this would take time linear in [math]N[/math]). The key property that will save us is that this function admits {\em sparse minimizers} as we discussed in the previous section, and this will be exploited by the conditional gradient descent method. First let us study the computational complexity of the [math]t^{th}[/math] step of conditional gradient descent. Observe that

[[math]] \nabla f(x) = D^{\top} (D x - Y). [[/math]]

Now assume that [math]z_t = D x_t - Y \in \mathbb{R}^n[/math] is already computed, then to compute \eqref{eq:FW1} one needs to find the coordinate [math]i_t \in [N][/math] that maximizes [math]|[\nabla f(x_t)](i)|[/math] which can be done by maximizing [math]d_i^{\top} z_t[/math] and [math]- d_i^{\top} z_t[/math]. Thus \eqref{eq:FW1} takes time [math]O(p(n))[/math]. Computing [math]x_{t+1}[/math] from [math]x_t[/math] and [math]i_{t}[/math] takes time [math]O(t)[/math] since [math]\|x_t\|_0 \leq t[/math], and computing [math]z_{t+1}[/math] from [math]z_t[/math] and [math]i_t[/math] takes time [math]O(n)[/math]. Thus the overall time complexity of running [math]t[/math] steps is (we assume [math]p(n) = \Omega(n)[/math])

[[math]] \begin{equation} O(t p(n) + t^2). \label{eq:structuredsparsity2} \end{equation} [[/math]]

To derive a rate of convergence it remains to study the smoothness of [math]f[/math]. This can be done as follows:

[[math]] \begin{eqnarray*} \| \nabla f(x) - \nabla f(y) \|_{\infty} & = & \|D^{\top} D (x-y) \|_{\infty} \\ & = & \max_{1 \leq i \leq N} \bigg| d_i^{\top} \left(\sum_{j=1}^N d_j (x(j) - y(j))\right) \bigg| \\ & \leq & m^2 \|x-y\|_1 , \end{eqnarray*} [[/math]]

which means that [math]f[/math] is [math]m^2[/math]-smooth with respect to the [math]\ell_1[/math]-norm. Thus we get the following rate of convergence:

[[math]] \begin{equation} f(x_t) - f(x^*) \leq \frac{8 m^2}{t+1} . \label{eq:structuredsparsity3} \end{equation} [[/math]]

Putting together \eqref{eq:structuredsparsity2} and \eqref{eq:structuredsparsity3} we proved that one can get an [math]\epsilon[/math]-optimal solution to \eqref{eq:structuredsparsity} with a computational effort of [math]O(m^2 p(n)/\epsilon + m^4/\epsilon^2)[/math] using the conditional gradient descent.

Strong convexity

We will now discuss another property of convex functions that can significantly speed-up the convergence of first order methods: strong convexity. We say that [math]f: \cX \rightarrow \mathbb{R}[/math] is [math]\alpha[/math]-{\em strongly convex} if it satisfies the following improved subgradient inequality:

[[math]] \begin{equation} \label{eq:defstrongconv} f(x) - f(y) \leq \nabla f(x)^{\top} (x - y) - \frac{\alpha}{2} \|x - y \|^2 . \end{equation} [[/math]]

Of course this definition does not require differentiability of the function [math]f[/math], and one can replace [math]\nabla f(x)[/math] in the inequality above by [math]g \in \partial f(x)[/math]. It is immediate to verify that a function [math]f[/math] is [math]\alpha[/math]-strongly convex if and only if [math]x \mapsto f(x) - \frac{\alpha}{2} \|x\|^2[/math] is convex (in particular if [math]f[/math] is twice differentiable then the eigenvalues of the Hessians of [math]f[/math] have to be larger than [math]\alpha[/math]). The strong convexity parameter [math]\alpha[/math] is a measure of the {\em curvature} of [math]f[/math]. For instance a linear function has no curvature and hence [math]\alpha = 0[/math]. On the other hand one can clearly see why a large value of [math]\alpha[/math] would lead to a faster rate: in this case a point far from the optimum will have a large gradient, and thus gradient descent will make very big steps when far from the optimum. Of course if the function is non-smooth one still has to be careful and tune the step-sizes to be relatively small, but nonetheless we will be able to improve the oracle complexity from [math]O(1/\epsilon^2)[/math] to [math]O(1/(\alpha \epsilon))[/math]. On the other hand with the additional assumption of [math]\beta[/math]-smoothness we will prove that gradient descent with a constant step-size achieves a {\em linear rate of convergence}, precisely the oracle complexity will be [math]O(\frac{\beta}{\alpha} \log(1/\epsilon))[/math]. This achieves the objective we had set after Theorem: strongly-convex and smooth functions can be optimized in very large dimension and up to very high accuracy. Before going into the proofs let us discuss another interpretation of strong-convexity and its relation to smoothness. Equation \eqref{eq:defstrongconv} can be read as follows: at any point [math]x[/math] one can find a (convex) quadratic lower bound [math]q_x^-(y) = f(x) + \nabla f(x)^{\top} (y - x) + \frac{\alpha}{2} \|x - y \|^2[/math] to the function [math]f[/math], i.e. [math]q_x^-(y) \leq f(y), \forall y \in \cX[/math] (and [math]q_x^-(x) = f(x)[/math]). On the other hand for [math]\beta[/math]-smoothness \eqref{eq:defaltsmooth} implies that at any point [math]y[/math] one can find a (convex) quadratic upper bound [math]q_y^+(x) = f(y) + \nabla f(y)^{\top} (x - y) + \frac{\beta}{2} \|x - y \|^2[/math] to the function [math]f[/math], i.e. [math]q_y^+(x) \geq f(x), \forall x \in \cX[/math] (and [math]q_y^+(y) = f(y)[/math]). Thus in some sense strong convexity is a {\em dual} assumption to smoothness, and in fact this can be made precise within the framework of Fenchel duality. Also remark that clearly one always has [math]\beta \geq \alpha[/math].

Strongly convex and Lipschitz functions

We consider here the projected subgradient descent algorithm with time-varying step size [math](\eta_t)_{t \geq 1}[/math], that is

[[math]] \begin{align*} & y_{t+1} = x_t - \eta_t g_t , \ \text{where} \ g_t \in \partial f(x_t) \\ & x_{t+1} = \Pi_{\cX}(y_{t+1}) . \end{align*} [[/math]]

The following result is extracted from .

Theorem

Let [math]f[/math] be [math]\alpha[/math]-strongly convex and [math]L[/math]-Lipschitz on [math]\cX[/math]. Then projected subgradient descent with [math]\eta_s = \frac{2}{\alpha (s+1)}[/math] satisfies

[[math]] f \left(\sum_{s=1}^t \frac{2 s}{t(t+1)} x_s \right) - f(x^*) \leq \frac{2 L^2}{\alpha (t+1)} . [[/math]]

Show Proof

Coming back to our original analysis of projected subgradient descent in Section Projected subgradient descent for Lipschitz functions and using the strong convexity assumption one immediately obtains

[[math]] f(x_s) - f(x^*) \leq \frac{\eta_s}{2} L^2 + \left( \frac{1}{2 \eta_s} - \frac{\alpha}{2} \right) \|x_s - x^*\|^2 - \frac{1}{2 \eta_s} \|x_{s+1} - x^*\|^2 . [[/math]]

Multiplying this inequality by [math]s[/math] yields

[[math]] s( f(x_s) - f(x^*) ) \leq \frac{L^2}{\alpha} + \frac{\alpha}{4} \bigg( s(s-1) \|x_s - x^*\|^2 - s (s+1) \|x_{s+1} - x^*\|^2 \bigg), [[/math]]

Now sum the resulting inequality over [math]s=1[/math] to [math]s=t[/math], and apply Jensen’s inequality to obtain the claimed statement.

■

Strongly convex and smooth functions

As we will see now, having both strong convexity and smoothness allows for a drastic improvement in the convergence rate. We denote [math]\kappa= \frac{\beta}{\alpha}[/math] for the {\em condition number} of [math]f[/math]. The key observation is that Lemma can be improved to (with the notation of the lemma):

[[math]] \begin{equation} \label{eq:improvedstrongsmooth} f(x^+) - f(y) \leq g_{\cX}(x)^{\top}(x-y) - \frac{1}{2 \beta} \|g_{\cX}(x)\|^2 - \frac{\alpha}{2} \|x-y\|^2 . \end{equation} [[/math]]

Theorem

Let [math]f[/math] be [math]\alpha[/math]-strongly convex and [math]\beta[/math]-smooth on [math]\cX[/math]. Then projected gradient descent with [math]\eta = \frac{1}{\beta}[/math] satisfies for [math]t \geq 0[/math],

[[math]] \|x_{t+1} - x^*\|^2 \leq \exp\left( - \frac{t}{\kappa} \right) \|x_1 - x^*\|^2 . [[/math]]

Show Proof

Using \eqref{eq:improvedstrongsmooth} with [math]y=x^*[/math] one directly obtains

[[math]] \begin{eqnarray*} \|x_{t+1} - x^*\|^2& = & \|x_{t} - \frac{1}{\beta} g_{\cX}(x_t) - x^*\|^2 \\ & = & \|x_{t} - x^*\|^2 - \frac{2}{\beta} g_{\cX}(x_t)^{\top} (x_t - x^*) + \frac{1}{\beta^2} \|g_{\cX}(x_t)\|^2 \\ & \leq & \left(1 - \frac{\alpha}{\beta} \right) \|x_{t} - x^*\|^2 \\ & \leq & \left(1 - \frac{\alpha}{\beta} \right)^t \|x_{1} - x^*\|^2 \\ & \leq & \exp\left( - \frac{t}{\kappa} \right) \|x_1 - x^*\|^2 , \end{eqnarray*} [[/math]]

which concludes the proof.

■

We now show that in the unconstrained case one can improve the rate by a constant factor, precisely one can replace [math]\kappa[/math] by [math](\kappa+1) / 4[/math] in the oracle complexity bound by using a larger step size. This is not a spectacular gain but the reasoning is based on an improvement of \eqref{eq:coercive1} which can be of interest by itself. Note that \eqref{eq:coercive1} and the lemma to follow are sometimes referred to as {\em coercivity} of the gradient.

Lemma

Let [math]f[/math] be [math]\beta[/math]-smooth and [math]\alpha[/math]-strongly convex on [math]\R^n[/math]. Then for all [math]x, y \in \mathbb{R}^n[/math], one has

[[math]] (\nabla f(x) - \nabla f(y))^{\top} (x - y) \geq \frac{\alpha \beta}{\beta + \alpha} \|x-y\|^2 + \frac{1}{\beta + \alpha} \|\nabla f(x) - \nabla f(y)\|^2 . [[/math]]

Show Proof

Let [math]\phi(x) = f(x) - \frac{\alpha}{2} \|x\|^2[/math]. By definition of [math]\alpha[/math]-strong convexity one has that [math]\phi[/math] is convex. Furthermore one can show that [math]\phi[/math] is [math](\beta-\alpha)[/math]-smooth by proving \eqref{eq:defaltsmooth} (and using that it implies smoothness). Thus using \eqref{eq:coercive1} one gets

[[math]] (\nabla \phi(x) - \nabla \phi(y))^{\top} (x - y) \geq \frac{1}{\beta - \alpha} \|\nabla \phi(x) - \nabla \phi(y)\|^2 , [[/math]]

which gives the claimed result with straightforward computations. (Note that if [math]\alpha = \beta[/math] the smoothness of [math]\phi[/math] directly implies that [math]\nabla f(x) - \nabla f(y) = \alpha (x-y)[/math] which proves the lemma in this case.)

■

Theorem

Let [math]f[/math] be [math]\beta[/math]-smooth and [math]\alpha[/math]-strongly convex on [math]\R^n[/math]. Then gradient descent with [math]\eta = \frac{2}{\alpha + \beta}[/math] satisfies

[[math]] f(x_{t+1}) - f(x^*) \leq \frac{\beta}{2} \exp\left( - \frac{4 t}{\kappa+1} \right) \|x_1 - x^*\|^2 . [[/math]]

Show Proof

First note that by [math]\beta[/math]-smoothness (since [math]\nabla f(x^*) = 0[/math]) one has

[[math]] f(x_t) - f(x^*) \leq \frac{\beta}{2} \|x_t - x^*\|^2 . [[/math]]

Now using Lemma one obtains

[[math]] \begin{eqnarray*} \|x_{t+1} - x^*\|^2& = & \|x_{t} - \eta \nabla f(x_{t}) - x^*\|^2 \\ & = & \|x_{t} - x^*\|^2 - 2 \eta \nabla f(x_{t})^{\top} (x_{t} - x^*) + \eta^2 \|\nabla f(x_{t})\|^2 \\ & \leq & \left(1 - 2 \frac{\eta \alpha \beta}{\beta + \alpha}\right)\|x_{t} - x^*\|^2 + \left(\eta^2 - 2 \frac{\eta}{\beta + \alpha}\right) \|\nabla f(x_{t})\|^2 \\ & = & \left(\frac{\kappa - 1}{\kappa+1}\right)^2 \|x_{t} - x^*\|^2 \\ & \leq & \exp\left( - \frac{4 t}{\kappa+1} \right) \|x_1 - x^*\|^2 , \end{eqnarray*} [[/math]]

which concludes the proof.

■

Lower bounds

We prove here various oracle complexity lower bounds. These results first appeared in but we follow here the simplified presentation of . In general a black-box procedure is a mapping from ‘`history" to the next query point, that is it maps [math](x_1, g_1, \hdots, x_t, g_t)[/math] (with [math]g_s \in \partial f (x_s)[/math]) to [math]x_{t+1}[/math]. In order to simplify the notation and the argument, throughout the section we make the following assumption on the black-box procedure: [math]x_1=0[/math] and for any [math]t \geq 0[/math], [math]x_{t+1}[/math] is in the linear span of [math]g_1, \hdots, g_t[/math], that is

[[math]] \begin{equation} \label{eq:ass1} x_{t+1} \in \mathrm{Span}(g_1, \hdots, g_t) . \end{equation} [[/math]]

Let [math]e_1, \hdots, e_n[/math] be the canonical basis of [math]\mathbb{R}^n[/math], and [math]\mB_2(R) = \{x \in \R^n : \|x\| \leq R\}[/math]. We start with a theorem for the two non-smooth cases (convex and strongly convex).

Theorem

Let [math]t \leq n[/math], [math]L, R \gt 0[/math]. There exists a convex and [math]L[/math]-Lipschitz function [math]f[/math] such that for any black-box procedure satisfying \eqref{eq:ass1},

[[math]] \min_{1 \leq s \leq t} f(x_s) - \min_{x \in \mB_2(R)} f(x) \geq \frac{R L}{2 (1 + \sqrt{t})} . [[/math]]

There also exists an [math]\alpha[/math]-strongly convex and [math]L[/math]-lipschitz function [math]f[/math] such that for any black-box procedure satisfying \eqref{eq:ass1},

[[math]] \min_{1 \leq s \leq t} f(x_s) - \min_{x \in \mB_2\left(\frac{L}{2 \alpha}\right)} f(x) \geq \frac{L^2}{8 \alpha t} . [[/math]]

Note that the above result is restricted to a number of iterations smaller than the dimension, that is [math]t \leq n[/math]. This restriction is of course necessary to obtain lower bounds polynomial in [math]1/t[/math]: as we saw in Chapter one can always obtain an exponential rate of convergence when the number of calls to the oracle is larger than the dimension.

Show Proof

We consider the following [math]\alpha[/math]-strongly convex function:

[[math]] f(x) = \gamma \max_{1 \leq i \leq t} x(i) + \frac{\alpha}{2} \|x\|^2 . [[/math]]

It is easy to see that

[[math]] \partial f(x) = \alpha x + \gamma \conv\left(e_i , i : x(i) = \max_{1 \leq j \leq t} x(j) \right). [[/math]]

In particular if [math]\|x\| \leq R[/math] then for any [math]g \in \partial f(x)[/math] one has [math]\|g\| \leq \alpha R + \gamma[/math]. In other words [math]f[/math] is [math](\alpha R + \gamma)[/math]-Lipschitz on [math]\mB_2(R)[/math]. Next we describe the first order oracle for this function: when asked for a subgradient at [math]x[/math], it returns [math]\alpha x + \gamma e_{i}[/math] where [math]i[/math] is the {\em first} coordinate that satisfies [math]x(i) = \max_{1 \leq j \leq t} x(j)[/math]. In particular when asked for a subgradient at [math]x_1=0[/math] it returns [math]e_1[/math]. Thus [math]x_2[/math] must lie on the line generated by [math]e_1[/math]. It is easy to see by induction that in fact [math]x_s[/math] must lie in the linear span of [math]e_1, \hdots, e_{s-1}[/math]. In particular for [math]s \leq t[/math] we necessarily have [math]x_s(t) = 0[/math] and thus [math]f(x_s) \geq 0[/math]. It remains to compute the minimal value of [math]f[/math]. Let [math]y[/math] be such that [math]y(i) = - \frac{\gamma}{\alpha t}[/math] for [math]1 \leq i \leq t[/math] and [math]y(i) = 0[/math] for [math]t+1 \leq i \leq n[/math]. It is clear that [math]0 \in \partial f(y)[/math] and thus the minimal value of [math]f[/math] is

[[math]] f(y) = - \frac{\gamma^2}{\alpha t} + \frac{\alpha}{2} \frac{\gamma^2}{\alpha^2 t} = - \frac{\gamma^2}{2 \alpha t} . [[/math]]

Wrapping up, we proved that for any [math]s \leq t[/math] one must have

[[math]] f(x_s) - f(x^*) \geq \frac{\gamma^2}{2 \alpha t} . [[/math]]

Taking [math]\gamma = L/2[/math] and [math]R= \frac{L}{2 \alpha}[/math] we proved the lower bound for [math]\alpha[/math]-strongly convex functions (note in particular that [math]\|y\|^2 = \frac{\gamma^2}{\alpha^2 t} = \frac{L^2}{4 \alpha^2 t} \leq R^2[/math] with these parameters). On the other taking [math]\alpha = \frac{L}{R} \frac{1}{1 + \sqrt{t}}[/math] and [math]\gamma = L \frac{\sqrt{t}}{1 + \sqrt{t}}[/math] concludes the proof for convex functions (note in particular that [math]\|y\|^2 = \frac{\gamma^2}{\alpha^2 t} = R^2[/math] with these parameters).

■

We proceed now to the smooth case. As we will see in the following proofs we restrict our attention to quadratic functions, and it might be useful to recall that in this case one can attain the exact optimum in [math]n[/math] calls to the oracle (see Section Conjugate gradient). We also recall that for a twice differentiable function [math]f[/math], [math]\beta[/math]-smoothness is equivalent to the largest eigenvalue of the Hessians of [math]f[/math] being smaller than [math]\beta[/math] at any point, which we write

[[math]] \nabla^2 f(x) \preceq \beta \mI_n , \forall x . [[/math]]

Furthermore [math]\alpha[/math]-strong convexity is equivalent to

[[math]] \nabla^2 f(x) \succeq \alpha \mI_n , \forall x . [[/math]]

Theorem

Let [math]t \leq (n-1)/2[/math], [math]\beta \gt 0[/math]. There exists a [math]\beta[/math]-smooth convex function [math]f[/math] such that for any black-box procedure satisfying \eqref{eq:ass1},

[[math]] \min_{1 \leq s \leq t} f(x_s) - f(x^*) \geq \frac{3 \beta}{32} \frac{\|x_1 - x^*\|^2}{(t+1)^2} . [[/math]]

Show Proof

In this proof for [math]h: \R^n \rightarrow \R[/math] we denote [math]h^* = \inf_{x \in \R^n} h(x)[/math]. For [math]k \leq n[/math] let [math]A_k \in \R^{n \times n}[/math] be the symmetric and tridiagonal matrix defined by

[[math]] (A_k)_{i,j} = \left\{\begin{array}{ll} 2, & i = j, i \leq k \\ -1, & j \in \{i-1, i+1\}, i \leq k, j \neq k+1\\ 0, & \text{otherwise}. \end{array}\right. [[/math]]

It is easy to verify that [math]0 \preceq A_k \preceq 4 \mI_n[/math] since

[[math]] x^{\top} A_k x = 2 \sum_{i=1}^k x(i)^2 - 2 \sum_{i=1}^{k-1} x(i) x(i+1) = x(1)^2 + x(k)^2 + \sum_{i=1}^{k-1} (x(i) - x(i+1))^2 . [[/math]]

We consider now the following [math]\beta[/math]-smooth convex function:

[[math]] f(x) = \frac{\beta}{8} x^{\top} A_{2 t + 1} x - \frac{\beta}{4} x^{\top} e_1 . [[/math]]

Similarly to what happened in the proof Theorem, one can see here too that [math]x_s[/math] must lie in the linear span of [math]e_1, \hdots, e_{s-1}[/math] (because of our assumption on the black-box procedure). In particular for [math]s \leq t[/math] we necessarily have [math]x_s(i) = 0[/math] for [math]i=s, \hdots, n[/math], which implies [math]x_s^{\top} A_{2 t+1} x_s = x_s^{\top} A_{s} x_s[/math]. In other words, if we denote

[[math]] f_k(x) = \frac{\beta}{8} x^{\top} A_{k} x - \frac{\beta}{4} x^{\top} e_1 , [[/math]]

then we just proved that

[[math]] f(x_s) - f^* = f_s(x_s) - f_{2t+1}^* \geq f_{s}^* - f_{2 t + 1}^* \geq f_{t}^* - f_{2 t + 1}^* . [[/math]]

Thus it simply remains to compute the minimizer [math]x^*_k[/math] of [math]f_k[/math], its norm, and the corresponding function value [math]f_k^*[/math]. The point [math]x^*_k[/math] is the unique solution in the span of [math]e_1, \hdots, e_k[/math] of [math]A_k x = e_1[/math]. It is easy to verify that it is defined by [math]x^*_k(i) = 1 - \frac{i}{k+1}[/math] for [math]i=1, \hdots, k[/math]. Thus we immediately have:

[[math]] f^*_k = \frac{\beta}{8} (x^*_k)^{\top} A_{k} x^*_k - \frac{\beta}{4} (x^*_k)^{\top} e_1 = - \frac{\beta}{8} (x^*_k)^{\top} e_1 = - \frac{\beta}{8} \left(1 - \frac{1}{k+1}\right) . [[/math]]

Furthermore note that

[[math]] \|x^*_k\|^2 = \sum_{i=1}^k \left(1 - \frac{i}{k+1}\right)^2 = \sum_{i=1}^k \left( \frac{i}{k+1}\right)^2 \leq \frac{k+1}{3} . [[/math]]

Thus one obtains:

[[math]] f_{t}^* - f_{2 t+1}^* = \frac{\beta}{8} \left(\frac{1}{t+1} - \frac{1}{2 t + 2} \right) \geq \frac{3 \beta}{32} \frac{\|x^*_{2 t + 1}\|^2}{(t+1)^2}, [[/math]]

which concludes the proof.

■

To simplify the proof of the next theorem we will consider the limiting situation [math]n \to +\infty[/math]. More precisely we assume now that we are working in [math]\ell_2 = \{ x = (x(n))_{n \in \mathbb{N}} : \sum_{i=1}^{+\infty} x(i)^2 \lt + \infty\}[/math] rather than in [math]\mathbb{R}^n[/math]. Note that all the theorems we proved in this chapter are in fact valid in an arbitrary Hilbert space [math]\mathcal{H}[/math]. We chose to work in [math]\mathbb{R}^n[/math] only for clarity of the exposition.

Theorem

Let [math]\kappa \gt 1[/math]. There exists a [math]\beta[/math]-smooth and [math]\alpha[/math]-strongly convex function [math]f: \ell_2 \rightarrow \mathbb{R}[/math] with [math]\kappa = \beta / \alpha[/math] such that for any [math]t \geq 1[/math] and any black-box procedure satisfying \eqref{eq:ass1} one has

[[math]] f(x_t) - f(x^*) \geq \frac{\alpha}{2} \left(\frac{\sqrt{\kappa} - 1}{\sqrt{\kappa}+1}\right)^{2 (t-1)} \|x_1 - x^*\|^2 . [[/math]]

Note that for large values of the condition number [math]\kappa[/math] one has

[[math]] \left(\frac{\sqrt{\kappa} - 1}{\sqrt{\kappa}+1}\right)^{2 (t-1)} \approx \exp\left(- \frac{4 (t-1)}{\sqrt{\kappa}} \right) . [[/math]]

Show Proof

The overall argument is similar to the proof of Theorem. Let [math]A : \ell_2 \rightarrow \ell_2[/math] be the linear operator that corresponds to the infinite tridiagonal matrix with [math]2[/math] on the diagonal and [math]-1[/math] on the upper and lower diagonals. We consider now the following function:

[[math]] f(x) = \frac{\alpha (\kappa-1)}{8} \left(\langle Ax, x\rangle - 2 \langle e_1, x \rangle \right) + \frac{\alpha}{2} \|x\|^2 . [[/math]]

We already proved that [math]0 \preceq A \preceq 4 \mI[/math] which easily implies that [math]f[/math] is [math]\alpha[/math]-strongly convex and [math]\beta[/math]-smooth. Now as always the key observation is that for this function, thanks to our assumption on the black-box procedure, one necessarily has [math]x_t(i) = 0, \forall i \geq t[/math]. This implies in particular:

[[math]] \|x_t - x^*\|^2 \geq \sum_{i=t}^{+\infty} x^*(i)^2 . [[/math]]

Furthermore since [math]f[/math] is [math]\alpha[/math]-strongly convex, one has

[[math]] f(x_t) - f(x^*) \geq \frac{\alpha}{2} \|x_t - x^*\|^2 . [[/math]]

Thus it only remains to compute [math]x^*[/math]. This can be done by differentiating [math]f[/math] and setting the gradient to [math]0[/math], which gives the following infinite set of equations

[[math]] \begin{align*} & 1 - 2 \frac{\kappa+1}{\kappa-1} x^*(1) + x^*(2) = 0 , \\ & x^*(k-1) - 2 \frac{\kappa+1}{\kappa-1} x^*(k) + x^*(k+1) = 0, \forall k \geq 2 . \end{align*} [[/math]]

It is easy to verify that [math]x^*[/math] defined by [math]x^*(i) = \left(\frac{\sqrt{\kappa} - 1}{\sqrt{\kappa} + 1}\right)^i[/math] satisfy this infinite set of equations, and the conclusion of the theorem then follows by straightforward computations.

■

Geometric descent

So far our results leave a gap in the case of smooth optimization: gradient descent achieves an oracle complexity of [math]O(1/\epsilon)[/math] (respectively [math]O(\kappa \log(1/\epsilon))[/math] in the strongly convex case) while we proved a lower bound of [math]\Omega(1/\sqrt{\epsilon})[/math] (respectively [math]\Omega(\sqrt{\kappa} \log(1/\epsilon))[/math]). In this section we close these gaps with the geometric descent method which was recently introduced in . Historically the first method with optimal oracle complexity was proposed in . This method, inspired by the conjugate gradient (see Section Conjugate gradient), assumes an oracle to compute {\em plane searches}. In this assumption was relaxed to a line search oracle (the geometric descent method also requires a line search oracle). Finally in an optimal method requiring only a first order oracle was introduced. The latter algorithm, called Nesterov’s accelerated gradient descent, has been the most influential optimal method for smooth optimization up to this day. We describe and analyze this method in Section Nesterov's accelerated gradient descent. As we shall see the intuition behind Nesterov's accelerated gradient descent (both for the derivation of the algorithm and its analysis) is not quite transparent, which motivates the present section as geometric descent has a simple geometric interpretation loosely inspired from the ellipsoid method (see Section The ellipsoid method). We focus here on the unconstrained optimization of a smooth and strongly convex function, and we prove that geometric descent achieves the oracle complexity of [math]O(\sqrt{\kappa} \log(1/\epsilon))[/math], thus reducing the complexity of the basic gradient descent by a factor [math]\sqrt{\kappa}[/math]. We note that this improvement is quite relevant for machine learning applications. Consider for example the logistic regression problem described in Section Some convex optimization problems in machine learning: this is a smooth and strongly convex problem, with a smoothness of order of a numerical constant, but with strong convexity equal to the regularization parameter whose inverse can be as large as the sample size. Thus in this case [math]\kappa[/math] can be of order of the sample size, and a faster rate by a factor of [math]\sqrt{\kappa}[/math] is quite significant. We also observe that this improved rate for smooth and strongly convex objectives also implies an almost optimal rate of [math]O(\log(1/\epsilon) / \sqrt{\epsilon})[/math] for the smooth case, as one can simply run geometric descent on the function [math]x \mapsto f(x) + \epsilon \|x\|^2[/math]. In Section Warm-up: a geometric alternative to gradient descent we describe the basic idea of geometric descent, and we show how to obtain effortlessly a geometric method with an oracle complexity of [math]O(\kappa \log(1/\epsilon))[/math] (i.e., similar to gradient descent). Then we explain why one should expect to be able to accelerate this method in Section Acceleration. The geometric descent method is described precisely and analyzed in Section The geometric descent method.

Warm-up: a geometric alternative to gradient descent

One ball shrinks.

We start with some notation. Let [math]\mB(x,r^2) := \{y \in \R^n : \|y-x\|^2 \leq r^2 \}[/math] (note that the second argument is the radius squared), and

[[math]] x^+ = x - \frac{1}{\beta} \nabla f(x), \ \text{and} \ x^{++} = x - \frac{1}{\alpha} \nabla f(x) . [[/math]]

Rewriting the definition of strong convexity \eqref{eq:defstrongconv} as

[[math]] \begin{eqnarray*} & f(y) \geq f(x) + \nabla f(x)^{\top} (y-x) + \frac{\alpha}{2} \|y-x\|^2 \\ & \Leftrightarrow \ \frac{\alpha}{2} \|y - x + \frac{1}{\alpha} \nabla f(x) \|^2 \leq \frac{\|\nabla f(x)\|^2}{2 \alpha} - (f(x) - f(y)), \end{eqnarray*} [[/math]]

one obtains an enclosing ball for the minimizer of [math]f[/math] with the [math]0^{th}[/math] and [math]1^{st}[/math] order information at [math]x[/math]:

[[math]] x^* \in \mB\left(x^{++}, \frac{\|\nabla f(x)\|^2}{\alpha^2} - \frac{2}{\alpha} (f(x) - f(x^*)) \right) . [[/math]]

Furthermore recall that by smoothness (see \eqref{eq:onestepofgd}) one has [math]f(x^+) \leq f(x) - \frac{1}{2 \beta} \|\nabla f(x)\|^2[/math] which allows to shrink the above ball by a factor of [math]1-\frac{1}{\kappa}[/math] and obtain the following:

[[math]] \begin{equation} \label{eq:ball2} x^* \in \mB\left(x^{++}, \frac{\|\nabla f(x)\|^2}{\alpha^2} \left(1 - \frac{1}{\kappa}\right) - \frac{2}{\alpha} (f(x^+) - f(x^*)) \right) \end{equation} [[/math]]

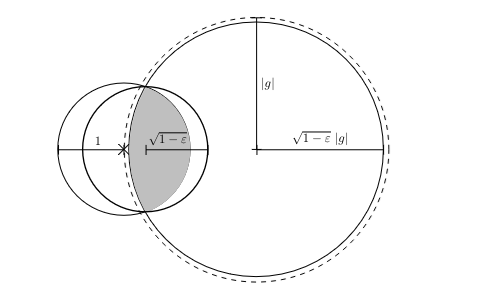
This suggests a natural strategy: assuming that one has an enclosing ball [math]A:=\mB(x,R^2)[/math] for [math]x^*[/math] (obtained from previous steps of the strategy), one can then enclose [math]x^*[/math] in a ball [math]B[/math] containing the intersection of [math]\mB(x,R^2)[/math] and the ball [math]\mB\left(x^{++}, \frac{\|\nabla f(x)\|^2}{\alpha^2} \left(1 - \frac{1}{\kappa}\right)\right)[/math] obtained by \eqref{eq:ball2}. Provided that the radius of [math]B[/math] is a fraction of the radius of [math]A[/math], one can then iterate the procedure by replacing [math]A[/math] by [math]B[/math], leading to a linear convergence rate. Evaluating the rate at which the radius shrinks is an elementary calculation: for any [math]g \in \R^n[/math], [math]\epsilon \in (0,1)[/math], there exists [math]x \in \R^n[/math] such that

[[math]] \mB(0,1) \cap \mB(g, \|g\|^2 (1- \epsilon)) \subset \mB(x, 1-\epsilon) . \quad \quad \text{([[#fig:one_ball|Figure]])} [[/math]]

Thus we see that in the strategy described above, the radius squared of the enclosing ball for [math]x^*[/math] shrinks by a factor [math]1 - \frac{1}{\kappa}[/math] at each iteration, thus matching the rate of convergence of gradient descent (see Theorem).

Acceleration

Two balls shrink.

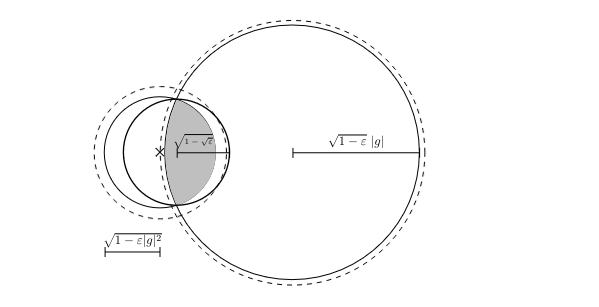
In the argument from the previous section we missed the following opportunity: observe that the ball [math]A=\mB(x,R^2)[/math] was obtained by intersections of previous balls of the form given by \eqref{eq:ball2}, and thus the new value [math]f(x)[/math] could be used to reduce the radius of those previous balls too (an important caveat is that the value [math]f(x)[/math] should be smaller than the values used to build those previous balls). Potentially this could show that the optimum is in fact contained in the ball [math]\mB\left(x, R^2 - \frac{1}{\kappa} \|\nabla f(x)\|^2\right)[/math]. By taking the intersection with the ball [math]\mB\left(x^{++}, \frac{\|\nabla f(x)\|^2}{\alpha^2} \left(1 - \frac{1}{\kappa}\right)\right)[/math] this would allow to obtain a new ball with radius shrunk by a factor [math]1- \frac{1}{\sqrt{\kappa}}[/math] (instead of [math]1 - \frac{1}{\kappa}[/math]): indeed for any [math]g \in \R^n[/math], [math]\epsilon \in (0,1)[/math], there exists [math]x \in \R^n[/math] such that

[[math]] \mB(0,1 - \epsilon \|g\|^2) \cap \mB(g, \|g\|^2 (1- \epsilon)) \subset \mB(x, 1-\sqrt{\epsilon}) . \quad \quad \text{([[#fig:two_ball|Figure]])} [[/math]]

Thus it only remains to deal with the caveat noted above, which we do via a line search. In turns this line search might shift the new ball \eqref{eq:ball2}, and to deal with this we shall need the following strengthening of the above set inclusion (we refer to for a simple proof of this result):

Lemma

Let [math]a \in \R^n[/math] and [math]\epsilon \in (0,1), g \in \R_+[/math]. Assume that [math]\|a\| \geq g[/math]. Then there exists [math]c \in \R^n[/math] such that for any [math]\delta \geq 0[/math],

[[math]] \mB(0,1 - \epsilon g^2 - \delta) \cap \mB(a, g^2(1-\epsilon) - \delta) \subset \mB\left(c, 1 - \sqrt{\epsilon} - \delta \right) . [[/math]]

The geometric descent method

Let [math]x_0 \in \R^n[/math], [math]c_0 = x_0^{++}[/math], and [math]R_0^2 = \left(1 - \frac{1}{\kappa}\right)\frac{\|\nabla f(x_0)\|^2}{\alpha^2}[/math]. For any [math]t \geq 0[/math] let

[[math]] x_{t+1} = \argmin_{x \in \left\{(1-\lambda) c_t + \lambda x_t^+, \ \lambda \in \R \right\}} f(x) , [[/math]]

and [math]c_{t+1}[/math] (respectively [math]R^2_{t+1}[/math]) be the center (respectively the squared radius) of the ball given by (the proof of) Lemma which contains

[[math]] \mB\left(c_t, R_t^2 - \frac{\|\nabla f(x_{t+1})\|^2}{\alpha^2 \kappa}\right) \cap \mB\left(x_{t+1}^{++}, \frac{\|\nabla f(x_{t+1})\|^2}{\alpha^2} \left(1 - \frac{1}{\kappa}\right) \right). [[/math]]

Formulas for [math]c_{t+1}[/math] and [math]R^2_{t+1}[/math] are given at the end of this section.

Theorem

For any [math]t \geq 0[/math], one has [math]x^* \in \mB(c_t, R_t^2)[/math], [math]R_{t+1}^2 \leq \left(1 - \frac{1}{\sqrt{\kappa}}\right) R_t^2[/math], and thus

[[math]] \|x^* - c_t\|^2 \leq \left(1 - \frac{1}{\sqrt{\kappa}}\right)^t R_0^2 . [[/math]]

Show Proof

We will prove a stronger claim by induction that for each [math]t\geq 0[/math], one has

[[math]] x^* \in \mB\left(c_t, R_t^2 - \frac{2}{\alpha} \left(f(x_t^+) - f(x^*)\right)\right) . [[/math]]

The case [math]t=0[/math] follows immediately by \eqref{eq:ball2}. Let us assume that the above display is true for some [math]t \geq 0[/math]. Then using [math]f(x_{t+1}^+) \leq f(x_{t+1}) - \frac{1}{2\beta} \|\nabla f(x_{t+1})\|^2 \leq f(x_t^+) - \frac{1}{2\beta} \|\nabla f(x_{t+1})\|^2 ,[/math] one gets

[[math]] x^* \in \mB\left(c_t, R_t^2 - \frac{\|\nabla f(x_{t+1})\|^2}{\alpha^2 \kappa} - \frac{2}{\alpha} \left(f(x_{t+1}^+) - f(x^*)\right) \right) . [[/math]]

Furthermore by \eqref{eq:ball2} one also has

[[math]] \mB\left(x_{t+1}^{++}, \frac{\|\nabla f(x_{t+1})\|^2}{\alpha^2} \left(1 - \frac{1}{\kappa}\right) - \frac{2}{\alpha} \left(f(x_{t+1}^+) - f(x^*)\right) \right). [[/math]]

Thus it only remains to observe that the squared radius of the ball given by Lemma which encloses the intersection of the two above balls is smaller than [math]\left(1 - \frac{1}{\sqrt{\kappa}}\right) R_t^2 - \frac{2}{\alpha} (f(x_{t+1}^+) - f(x^*))[/math]. We apply Lemma~ after moving [math]c_t[/math] to the origin and scaling distances by [math]R_t[/math]. We set [math]\epsilon =\frac{1}{\kappa}[/math], [math]g=\frac{\|\nabla f(x_{t+1})\|}{\alpha}[/math], [math]\delta=\frac{2}{\alpha}\left(f(x_{t+1}^+)-f(x^*)\right)[/math] and [math]a={x_{t+1}^{++}-c_t}[/math]. The line search step of the algorithm implies that [math]\nabla f(x_{t+1})^{\top} (x_{t+1} - c_t) = 0[/math] and therefore, [math]\|a\|=\|x_{t+1}^{++} - c_t\| \geq \|\nabla f(x_{t+1})\|/\alpha=g[/math] and Lemma~ applies to give the result.

■

One can use the following formulas for [math]c_{t+1}[/math] and [math]R^2_{t+1}[/math] (they are derived from the proof of Lemma). If [math]|\nabla f(x_{t+1})|^2 / \alpha^2 \lt R_t^2 / 2[/math] then one can tate [math]c_{t+1} = x_{t+1}^{++}[/math] and [math]R_{t+1}^2 = \frac{|\nabla f(x_{t+1})|^2}{\alpha^2} \left(1 - \frac{1}{\kappa}\right)[/math]. On the other hand if [math]|\nabla f(x_{t+1})|^2 / \alpha^2 \geq R_t^2 / 2[/math] then one can tate

[[math]] \begin{eqnarray*} c_{t+1} & = & c_t + \frac{R_t^2 + |x_{t+1} - c_t|^2}{2 |x_{t+1}^{++} - c_t|^2} (x_{t+1}^{++} - c_t) , \\ R_{t+1}^2 & = & R_t^2 - \frac{|\nabla f(x_{t+1})|^2}{\alpha^2 \kappa} - \left( \frac{R_t^2 + \|x_{t+1} - c_t\|^2}{2 \|x_{t+1}^{++} - c_t\|} \right)^2. \end{eqnarray*} [[/math]]

Nesterov's accelerated gradient descent

We describe here the original Nesterov's method which attains the optimal oracle complexity for smooth convex optimization. We give the details of the method both for the strongly convex and non-strongly convex case. We refer to for a recent interpretation of the method in terms of differential equations, and to for its relation to mirror descent (see Chapter).

The smooth and strongly convex case

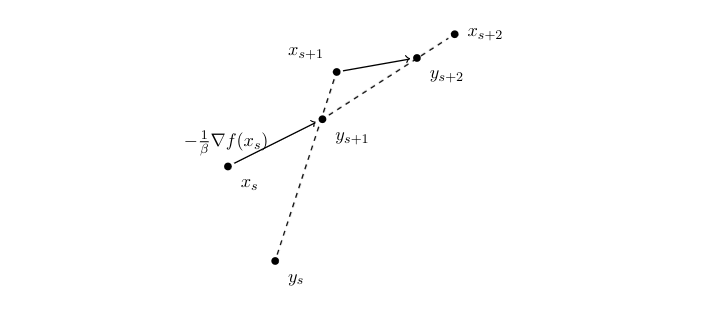
Nesterov's accelerated gradient descent, illustrated in Figure, can be described as follows: Start at an arbitrary initial point [math]x_1 = y_1[/math] and then iterate the following equations for [math]t \geq 1[/math],

[[math]] \begin{eqnarray*} y_{t+1} & = & x_t - \frac{1}{\beta} \nabla f(x_t) , \\ x_{t+1} & = & \left(1 + \frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1} \right) y_{t+1} - \frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1} y_t . \end{eqnarray*} [[/math]]

Illustration of Nesterov's accelerated gradient descent.

Theorem

Let [math]f[/math] be [math]\alpha[/math]-strongly convex and [math]\beta[/math]-smooth, then Nesterov's accelerated gradient descent satisfies

[[math]] f(y_t) - f(x^*) \leq \frac{\alpha + \beta}{2} \|x_1 - x^*\|^2 \exp\left(- \frac{t-1}{\sqrt{\kappa}} \right). [[/math]]

Show Proof

We define [math]\alpha[/math]-strongly convex quadratic functions [math]\Phi_s, s \geq 1[/math] by induction as follows:

[[math]] \begin{align} & \Phi_1(x) = f(x_1) + \frac{\alpha}{2} \|x-x_1\|^2 , \notag \\ & \Phi_{s+1}(x) = \left(1 - \frac{1}{\sqrt{\kappa}}\right) \Phi_s(x) \notag \\ & \qquad + \frac{1}{\sqrt{\kappa}} \left(f(x_s) + \nabla f(x_s)^{\top} (x-x_s) + \frac{\alpha}{2} \|x-x_s\|^2 \right). \label{eq:AGD0} \end{align} [[/math]]

Intuitively [math]\Phi_s[/math] becomes a finer and finer approximation (from below) to [math]f[/math] in the following sense:

[[math]] \begin{equation} \label{eq:AGD1} \Phi_{s+1}(x) \leq f(x) + \left(1 - \frac{1}{\sqrt{\kappa}}\right)^s (\Phi_1(x) - f(x)). \end{equation} [[/math]]

The above inequality can be proved immediately by induction, using the fact that by [math]\alpha[/math]-strong convexity one has

[[math]] f(x_s) + \nabla f(x_s)^{\top} (x-x_s) + \frac{\alpha}{2} \|x-x_s\|^2 \leq f(x) . [[/math]]

Equation \eqref{eq:AGD1} by itself does not say much, for it to be useful one needs to understand how ‘`far" below [math]f[/math] is [math]\Phi_s[/math]. The following inequality answers this question:

[[math]] \begin{equation} \label{eq:AGD2} f(y_s) \leq \min_{x \in \mathbb{R}^n} \Phi_s(x) . \end{equation} [[/math]]

The rest of the proof is devoted to showing that \eqref{eq:AGD2} holds true, but first let us see how to combine \eqref{eq:AGD1} and \eqref{eq:AGD2} to obtain the rate given by the theorem (we use that by [math]\beta[/math]-smoothness one has [math]f(x) - f(x^*) \leq \frac{\beta}{2} \|x-x^*\|^2[/math]):

[[math]] \begin{eqnarray*} f(y_t) - f(x^*) & \leq & \Phi_t(x^*) - f(x^*) \\ & \leq & \left(1 - \frac{1}{\sqrt{\kappa}}\right)^{t-1} (\Phi_1(x^*) - f(x^*)) \\ & \leq & \frac{\alpha + \beta}{2} \|x_1-x^*\|^2 \left(1 - \frac{1}{\sqrt{\kappa}}\right)^{t-1} . \end{eqnarray*} [[/math]]

We now prove \eqref{eq:AGD2} by induction (note that it is true at [math]s=1[/math] since [math]x_1=y_1[/math]). Let [math]\Phi_s^* = \min_{x \in \mathbb{R}^n} \Phi_s(x)[/math]. Using the definition of [math]y_{s+1}[/math] (and [math]\beta[/math]-smoothness), convexity, and the induction hypothesis, one gets

[[math]] \begin{eqnarray*} f(y_{s+1}) & \leq & f(x_s) - \frac{1}{2 \beta} \| \nabla f(x_s) \|^2 \\ & = & \left(1 - \frac{1}{\sqrt{\kappa}}\right) f(y_s) + \left(1 - \frac{1}{\sqrt{\kappa}}\right)(f(x_s) - f(y_s)) \\ & & + \frac{1}{\sqrt{\kappa}} f(x_s) - \frac{1}{2 \beta} \| \nabla f(x_s) \|^2 \\ & \leq & \left(1 - \frac{1}{\sqrt{\kappa}}\right) \Phi_s^* + \left(1 - \frac{1}{\sqrt{\kappa}}\right) \nabla f(x_s)^{\top} (x_s - y_s) \\ & & + \frac{1}{\sqrt{\kappa}} f(x_s) - \frac{1}{2 \beta} \| \nabla f(x_s) \|^2 . \end{eqnarray*} [[/math]]

Thus we now have to show that

[[math]] \begin{eqnarray} \Phi_{s+1}^* & \geq & \left(1 - \frac{1}{\sqrt{\kappa}}\right) \Phi_s^* + \left(1 - \frac{1}{\sqrt{\kappa}}\right) \nabla f(x_s)^{\top} (x_s - y_s) \notag \\ & & + \frac{1}{\sqrt{\kappa}} f(x_s) - \frac{1}{2 \beta} \| \nabla f(x_s) \|^2 . \label{eq:AGD3} \end{eqnarray} [[/math]]

To prove this inequality we have to understand better the functions [math]\Phi_s[/math]. First note that [math]\nabla^2 \Phi_s(x) = \alpha \mathrm{I}_n[/math] (immediate by induction) and thus [math]\Phi_s[/math] has to be of the following form:

[[math]] \Phi_s(x) = \Phi_s^* + \frac{\alpha}{2} \|x - v_s\|^2 , [[/math]]

for some [math]v_s \in \mathbb{R}^n[/math]. Now observe that by differentiating \eqref{eq:AGD0} and using the above form of [math]\Phi_s[/math] one obtains

[[math]] \nabla \Phi_{s+1}(x) = \alpha \left(1 - \frac{1}{\sqrt{\kappa}}\right) (x-v_s) + \frac{1}{\sqrt{\kappa}} \nabla f(x_s) + \frac{\alpha}{\sqrt{\kappa}} (x-x_s) . [[/math]]

In particular [math]\Phi_{s+1}[/math] is by definition minimized at [math]v_{s+1}[/math] which can now be defined by induction using the above identity, precisely:

[[math]] \begin{equation} \label{eq:AGD4} v_{s+1} = \left(1 - \frac{1}{\sqrt{\kappa}}\right) v_s + \frac{1}{\sqrt{\kappa}} x_s - \frac{1}{\alpha \sqrt{\kappa}} \nabla f(x_s) . \end{equation} [[/math]]

Using the form of [math]\Phi_s[/math] and [math]\Phi_{s+1}[/math], as well as the original definition \eqref{eq:AGD0} one gets the following identity by evaluating [math]\Phi_{s+1}[/math] at [math]x_s[/math]:

[[math]] \begin{align} & \Phi_{s+1}^* + \frac{\alpha}{2} \|x_s - v_{s+1}\|^2 \notag \\ & = \left(1 - \frac{1}{\sqrt{\kappa}}\right) \Phi_s^* + \frac{\alpha}{2} \left(1 - \frac{1}{\sqrt{\kappa}}\right) \|x_s - v_s\|^2 + \frac{1}{\sqrt{\kappa}} f(x_s) . \label{eq:AGD5} \end{align} [[/math]]

Note that thanks to \eqref{eq:AGD4} one has

[[math]] \begin{eqnarray*} \|x_s - v_{s+1}\|^2 & = & \left(1 - \frac{1}{\sqrt{\kappa}}\right)^2 \|x_s - v_s\|^2 + \frac{1}{\alpha^2 \kappa} \|\nabla f(x_s)\|^2 \\ & & - \frac{2}{\alpha \sqrt{\kappa}} \left(1 - \frac{1}{\sqrt{\kappa}}\right) \nabla f(x_s)^{\top}(v_s-x_s) , \end{eqnarray*} [[/math]]

which combined with \eqref{eq:AGD5} yields

[[math]] \begin{eqnarray*} \Phi_{s+1}^* & = & \left(1 - \frac{1}{\sqrt{\kappa}}\right) \Phi_s^* + \frac{1}{\sqrt{\kappa}} f(x_s) + \frac{\alpha}{2 \sqrt{\kappa}} \left(1 - \frac{1}{\sqrt{\kappa}}\right) \|x_s - v_s\|^2 \\ & & \qquad - \frac{1}{2 \beta} \| \nabla f(x_s) \|^2 + \frac{1}{\sqrt{\kappa}} \left(1 - \frac{1}{\sqrt{\kappa}}\right) \nabla f(x_s)^{\top}(v_s-x_s) . \end{eqnarray*} [[/math]]

Finally we show by induction that [math]v_s - x_s = \sqrt{\kappa}(x_s - y_s)[/math], which concludes the proof of \eqref{eq:AGD3} and thus also concludes the proof of the theorem:

[[math]] \begin{eqnarray*} v_{s+1} - x_{s+1} & = & \left(1 - \frac{1}{\sqrt{\kappa}}\right) v_s + \frac{1}{\sqrt{\kappa}} x_s - \frac{1}{\alpha \sqrt{\kappa}} \nabla f(x_s) - x_{s+1} \\ & = & \sqrt{\kappa} x_s - (\sqrt{\kappa}-1) y_s - \frac{\sqrt{\kappa}}{\beta} \nabla f(x_s) - x_{s+1} \\ & = & \sqrt{\kappa} y_{s+1} - (\sqrt{\kappa}-1) y_s - x_{s+1} \\ & = & \sqrt{\kappa} (x_{s+1} - y_{s+1}) , \end{eqnarray*} [[/math]]

where the first equality comes from \eqref{eq:AGD4}, the second from the induction hypothesis, the third from the definition of [math]y_{s+1}[/math] and the last one from the definition of [math]x_{s+1}[/math].

■

The smooth case

In this section we show how to adapt Nesterov’s accelerated gradient descent for the case [math]\alpha=0[/math], using a time-varying combination of the elements in the primary sequence [math](y_t)[/math]. First we define the following sequences:

[[math]] \lambda_0 = 0, \ \lambda_{t} = \frac{1 + \sqrt{1+ 4 \lambda_{t-1}^2}}{2}, \ \text{and} \ \gamma_t = \frac{1 - \lambda_t}{\lambda_{t+1}}. [[/math]]

(Note that [math]\gamma_t \leq 0[/math].) Now the algorithm is simply defined by the following equations, with [math]x_1 = y_1[/math] an arbitrary initial point,

[[math]] \begin{eqnarray*} y_{t+1} & = & x_t - \frac{1}{\beta} \nabla f(x_t) , \\ x_{t+1} & = & (1 - \gamma_s) y_{t+1} + \gamma_t y_t . \end{eqnarray*} [[/math]]

Theorem

Let [math]f[/math] be a convex and [math]\beta[/math]-smooth function, then Nesterov's accelerated gradient descent satisfies

[[math]] f(y_t) - f(x^*) \leq \frac{2 \beta \|x_1 - x^*\|^2}{t^2} . [[/math]]

We follow here the proof of . We also refer to for a proof with simpler step-sizes.

Show Proof

Using the unconstrained version of Lemma one obtains

[[math]] \begin{align} & f(y_{s+1}) - f(y_s) \notag \\ & \leq \nabla f(x_s)^{\top} (x_s-y_s) - \frac{1}{2 \beta} \| \nabla f(x_s) \|^2 \notag \\ & = \beta (x_s - y_{s+1})^{\top} (x_s-y_s) - \frac{\beta}{2} \| x_s - y_{s+1} \|^2 . \label{eq:1} \end{align} [[/math]]

Similarly we also get

[[math]] \begin{equation} \label{eq:2} f(y_{s+1}) - f(x^*) \leq \beta (x_s - y_{s+1})^{\top} (x_s-x^*) - \frac{\beta}{2} \| x_s - y_{s+1} \|^2 . \end{equation} [[/math]]

Now multiplying \eqref{eq:1} by [math](\lambda_{s}-1)[/math] and adding the result to \eqref{eq:2}, one obtains with [math]\delta_s = f(y_s) - f(x^*)[/math],

[[math]] \begin{align*} & \lambda_{s} \delta_{s+1} - (\lambda_{s} - 1) \delta_s \\ & \leq \beta (x_s - y_{s+1})^{\top} (\lambda_{s} x_{s} - (\lambda_{s} - 1) y_s-x^*) - \frac{\beta}{2} \lambda_{s} \| x_s - y_{s+1} \|^2. \end{align*} [[/math]]

Multiplying this inequality by [math]\lambda_{s}[/math] and using that by definition [math]\lambda_{s-1}^2 = \lambda_{s}^2 - \lambda_{s}[/math], as well as the elementary identity [math]2 a^{\top} b - \|a\|^2 = \|b\|^2 - \|b-a\|^2[/math], one obtains

[[math]] \begin{align} & \lambda_{s}^2 \delta_{s+1} - \lambda_{s-1}^2 \delta_s \notag \\ & \leq \frac{\beta}{2} \bigg( 2 \lambda_{s} (x_s - y_{s+1})^{\top} (\lambda_{s} x_{s} - (\lambda_{s} - 1) y_s-x^*) - \|\lambda_{s}( y_{s+1} - x_s )\|^2\bigg) \notag \\ & = \frac{\beta}{2} \bigg(\| \lambda_{s} x_{s} - (\lambda_{s} - 1) y_{s}-x^* \|^2 - \| \lambda_{s} y_{s+1} - (\lambda_{s} - 1) y_{s}-x^* \|^2 \bigg). \label{eq:3} \end{align} [[/math]]

Next remark that, by definition, one has

[[math]] \begin{align} & x_{s+1} = y_{s+1} + \gamma_s (y_s - y_{s+1}) \notag \\ & \Leftrightarrow \lambda_{s+1} x_{s+1} = \lambda_{s+1} y_{s+1} + (1-\lambda_{s})(y_s - y_{s+1}) \notag \\ & \Leftrightarrow \lambda_{s+1} x_{s+1} - (\lambda_{s+1} - 1) y_{s+1}= \lambda_{s} y_{s+1} - (\lambda_{s}-1) y_{s} . \label{eq:5} \end{align} [[/math]]

Putting together \eqref{eq:3} and \eqref{eq:5} one gets with [math]u_s = \lambda_{s} x_{s} - (\lambda_{s} - 1) y_{s} - x^*[/math],

[[math]] \lambda_{s}^2 \delta_{s+1} - \lambda_{s-1}^2 \delta_s^2 \leq \frac{\beta}{2} \bigg(\|u_s\|^2 - \|u_{s+1}\|^2 \bigg) . [[/math]]

Summing these inequalities from [math]s=1[/math] to [math]s=t-1[/math] one obtains:

[[math]] \delta_t \leq \frac{\beta}{2 \lambda_{t-1}^2} \|u_1\|^2. [[/math]]

By induction it is easy to see that [math]\lambda_{t-1} \geq \frac{t}{2}[/math] which concludes the proof.

■

General references

Bubeck, Sébastien (2015). "Convex Optimization: Algorithms and Complexity". arXiv:1405.4980 [math.OC].