1. Machine Learning: The Basics
  2. Transparent and Explainable ML
Revision as of 00:28, 11 June 2023 by Admin

Transparent and Explainable ML

[math] \( % Generic syms \newcommand\defeq{:=} \newcommand{\Tt}[0]{\boldsymbol{\theta}} \newcommand{\XX}[0]{{\cal X}} \newcommand{\ZZ}[0]{{\cal Z}} \newcommand{\vx}[0]{{\bf x}} \newcommand{\vv}[0]{{\bf v}} \newcommand{\vu}[0]{{\bf u}} \newcommand{\vs}[0]{{\bf s}} \newcommand{\vm}[0]{{\bf m}} \newcommand{\vq}[0]{{\bf q}} \newcommand{\mX}[0]{{\bf X}} \newcommand{\mC}[0]{{\bf C}} \newcommand{\mA}[0]{{\bf A}} \newcommand{\mL}[0]{{\bf L}} \newcommand{\fscore}[0]{F_{1}} \newcommand{\sparsity}{s} \newcommand{\mW}[0]{{\bf W}} \newcommand{\mD}[0]{{\bf D}} \newcommand{\mZ}[0]{{\bf Z}} \newcommand{\vw}[0]{{\bf w}} \newcommand{\D}[0]{{\mathcal{D}}} \newcommand{\mP}{\mathbf{P}} \newcommand{\mQ}{\mathbf{Q}} \newcommand{\E}[0]{{\mathbb{E}}} \newcommand{\vy}[0]{{\bf y}} \newcommand{\va}[0]{{\bf a}} \newcommand{\vn}[0]{{\bf n}} \newcommand{\vb}[0]{{\bf b}} \newcommand{\vr}[0]{{\bf r}} \newcommand{\vz}[0]{{\bf z}} \newcommand{\N}[0]{{\mathcal{N}}} \newcommand{\vc}[0]{{\bf c}} \newcommand{\bm}{\boldsymbol} % Statistics and Probability Theory \newcommand{\errprob}{p_{\rm err}} \newcommand{\prob}[1]{p({#1})} \newcommand{\pdf}[1]{p({#1})} \def \expect {\mathbb{E} } % Machine Learning Symbols \newcommand{\biasterm}{B} \newcommand{\varianceterm}{V} \newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} \newcommand{\nrfolds}{k} \newcommand{\mseesterr}{E_{\rm est}} \newcommand{\bootstrapidx}{b} %\newcommand{\modeldim}{r} \newcommand{\modelidx}{l} \newcommand{\nrbootstraps}{B} \newcommand{\sampleweight}[1]{q^{(#1)}} \newcommand{\nrcategories}{K} \newcommand{\splitratio}[0]{{\rho}} \newcommand{\norm}[1]{\Vert {#1} \Vert} \newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} \newcommand{\bmx}[0]{\begin{bmatrix}} \newcommand{\emx}[0]{\end{bmatrix}} \newcommand{\T}[0]{\text{T}} \DeclareMathOperator*{\rank}{rank} %\newcommand\defeq{:=} \newcommand\eigvecS{\hat{\mathbf{u}}} \newcommand\eigvecCov{\mathbf{u}} \newcommand\eigvecCoventry{u} \newcommand{\featuredim}{n} \newcommand{\featurelenraw}{\featuredim'} \newcommand{\featurelen}{\featuredim} \newcommand{\samplingset}{\mathcal{M}} \newcommand{\samplesize}{m} \newcommand{\sampleidx}{i} \newcommand{\nractions}{A} \newcommand{\datapoint}{\vz} \newcommand{\actionidx}{a} \newcommand{\clusteridx}{c} \newcommand{\sizehypospace}{D} \newcommand{\nrcluster}{k} \newcommand{\nrseeds}{s} \newcommand{\featureidx}{j} \newcommand{\clustermean}{{\bm \mu}} \newcommand{\clustercov}{{\bm \Sigma}} \newcommand{\target}{y} \newcommand{\error}{E} \newcommand{\augidx}{b} \newcommand{\task}{\mathcal{T}} \newcommand{\nrtasks}{T} \newcommand{\taskidx}{t} \newcommand\truelabel{y} \newcommand{\polydegree}{r} \newcommand\labelvec{\vy} \newcommand\featurevec{\vx} \newcommand\feature{x} \newcommand\predictedlabel{\hat{y}} \newcommand\dataset{\mathcal{D}} \newcommand\trainset{\dataset^{(\rm train)}} \newcommand\valset{\dataset^{(\rm val)}} \newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} \newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} \newcommand{\inspace}{\mathcal{X}} \newcommand{\sigmoid}{\sigma} \newcommand{\outspace}{\mathcal{Y}} \newcommand{\hypospace}{\mathcal{H}} \newcommand{\emperror}{\widehat{L}} \newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} \newcommand{\featurespace}{\mathcal{X}} \newcommand{\labelspace}{\mathcal{Y}} \newcommand{\rawfeaturevec}{\mathbf{z}} \newcommand{\rawfeature}{z} \newcommand{\condent}{H} \newcommand{\explanation}{e} \newcommand{\explainset}{\mathcal{E}} \newcommand{\user}{u} \newcommand{\actfun}{\sigma} \newcommand{\noisygrad}{g} \newcommand{\reconstrmap}{r} \newcommand{\predictor}{h} \newcommand{\eigval}[1]{\lambda_{#1}} \newcommand{\regparam}{\lambda} \newcommand{\lrate}{\alpha} \newcommand{\edges}{\mathcal{E}} \newcommand{\generror}{E} \DeclareMathOperator{\supp}{supp} %\newcommand{\loss}[3]{L({#1},{#2},{#3})} \newcommand{\loss}[2]{L\big({#1},{#2}\big)} \newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} \newcommand{\determinant}[1]{{\rm det}({#1})} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\itercntr}{r} \newcommand{\state}{s} \newcommand{\statespace}{\mathcal{S}} \newcommand{\timeidx}{t} \newcommand{\optpolicy}{\pi_{*}} \newcommand{\appoptpolicy}{\hat{\pi}} \newcommand{\dummyidx}{j} \newcommand{\gridsizex}{K} \newcommand{\gridsizey}{L} \newcommand{\localdataset}{\mathcal{X}} \newcommand{\reward}{r} \newcommand{\cumreward}{G} \newcommand{\return}{\cumreward} \newcommand{\action}{a} \newcommand\actionset{\mathcal{A}} \newcommand{\obstacles}{\mathcal{B}} \newcommand{\valuefunc}[1]{v_{#1}} \newcommand{\gridcell}[2]{\langle #1, #2 \rangle} \newcommand{\pair}[2]{\langle #1, #2 \rangle} \newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} \newcommand{\actionvalue}[1]{q_{#1}} \newcommand{\transition}{\mathcal{T}} \newcommand{\policy}{\pi} \newcommand{\charger}{c} \newcommand{\itervar}{k} \newcommand{\discount}{\gamma} \newcommand{\rumba}{Rumba} \newcommand{\actionnorth}{\rm N} \newcommand{\actionsouth}{\rm S} \newcommand{\actioneast}{\rm E} \newcommand{\actionwest}{\rm W} \newcommand{\chargingstations}{\mathcal{C}} \newcommand{\basisfunc}{\phi} \newcommand{\augparam}{B} \newcommand{\valerror}{E_{v}} \newcommand{\trainerror}{E_{t}} \newcommand{\foldidx}{b} \newcommand{\testset}{\dataset^{(\rm test)} } \newcommand{\testerror}{E^{(\rm test)}} \newcommand{\nrmodels}{M} \newcommand{\benchmarkerror}{E^{(\rm ref)}} \newcommand{\lossfun}{L} \newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} \newcommand{\cluster}{\mathcal{C}} \newcommand{\bayeshypothesis}{h^{*}} \newcommand{\featuremtx}{\mX} \newcommand{\weight}{w} \newcommand{\weights}{\vw} \newcommand{\regularizer}{\mathcal{R}} \newcommand{\decreg}[1]{\mathcal{R}_{#1}} \newcommand{\naturalnumbers}{\mathbb{N}} \newcommand{\featuremapvec}{{\bf \Phi}} \newcommand{\featuremap}{\phi} \newcommand{\batchsize}{B} \newcommand{\batch}{\mathcal{B}} \newcommand{\foldsize}{B} \newcommand{\nriter}{R} [/math]

The successful deployment of ML methods depends on their transparency or explainability.

We formalize the notion of an explanation and its effect using a simple probabilistic model in Section Personalized Explanations for ML Methods . Roughly speaking, an explanation is any artefact. such as a list of relevant features or a reference data point from a training set, that coneys information about a ML method and its predictions. Put differently, explaining a ML method should reduce the uncertainty (of a human end-user) about its predictions.

Explainable ML is umbrella term for techniques that make ML method transparent or explainable. Providing explanations for the predictions of a ML method is particularly important when these predictions inform decision making [1]. It is increasingly becoming a legal requirement to provide explanations for automated decision making systems [2].

Even for applications where predictions are not directly used to inform far-reaching decisions, providing explanations is important. The human end users have an intrinsic desire for explanations that resolve the uncertainty about the prediction. This is known as the “need for closure” in psychology [3][4]. Beside legal and psychological requirements, providing explanations for predictions might also be useful for validating and verifying ML methods. Indeed, the explanations of ML methods (and its predictions) can point the user (which might be a “domain expert”) to incorrect modelling assumptions used by the ML method [5].

Explainable ML is challenging since explanations must be tailored (personalized) to human end-users with varying backgrounds and in different contexts [6]. The user background includes the formal education as well as the individual digital literacy. Some users might have received university-level education in ML, while other users might have no relevant formal training (such as an undergraduate course in linear algebra). Linear regression with few features might be perfectly interpretable for the first group but be considered a “black box” for the latter. To enable tailored explanations we need to model the user background as relevant for understanding the ML predictions.

This chapter discusses explainable ML methods that have access to some user signal or feedback for some data points. Such a user signal might be obtained in various ways, including answers to surveys or bio-physical measurements collected via wearables or medical diagnostics. The user signal is used to determine (to some extent) the end-user background and, in turn, to tailor the delivered explanations for this end-user.

Existing explainable ML methods can be roughly divided into two categories. The first category is referred to as “model-agnostic” [1]). Model-agnostic methods do not require knowledge of the detailed work principles of a ML method. These methods do not require knowledge of the hypothesis space used by a ML method but learn how to explain its predictions by observing them on a training set [7].

A second category of explainable ML methods, sometimes referred to as “white-box” methods [1], uses ML methods that are considered as intrinsically explainable. The intrinsic explainability of a ML method depends crucially on its choice for the hypothesis space (see Section The Model ). This chapter discusses one recent method from each of the two explainable ML categories [8][9]. The common theme of both methods is the use of information-theoretic concepts to measure the usefulness of explanations [10].

Section Personalized Explanations for ML Methods discusses a recently proposed model-agnostic approach to explainable ML that constructs tailored explanations for the predictions of a given ML method [8]. This approach does not require any details about the internal mechanism of a ML method whose predictions are to be explained. Rather, this approach only requires a (sufficiently large) training set of data points for which the predictions of the ML method are known.

To tailor the explanations to a particular user, we use the values of a user (feedback) signal provided for the data points in the training set. Roughly speaking, the explanations are chosen such that they maximally reduce the “surprise” or uncertainty that the user has about the predictions of the ML method.

Section Explainable Empirical Risk Minimization discusses an example for a ML method that uses a hypothesis space that is intrinsically explainable [9]. We construct an explainable hypothesis space by appropriate pruning of a given hypothesis space such as linear maps (see Section Linear Regression ) or non-linear maps represented by either an artificial neural network (ANN) (see Section Deep Learning ) or decision trees (see Section Decision Trees ). This pruning is implemented via adding a regularization term to empirical risk minimization (ERM), resulting in an instance of structural risk minimization (SRM) which we refer to as explainable empirical risk minimization (EERM). The regularization term favours hypotheses that are explainable to a user. Similar to the method in Section Personalized Explanations for ML Methods , the explainability of a map is quantified by information theoretic quantities. For example, if the original hypothesis space is the set of linear maps using a large number of features, the regularization term might favour maps that depend only on few features that are interpretable. Hence, we can interpret EERM as a feature learning method that aims at learning relevant and interpretable features (see Chapter Feature Learning ).

Personalized Explanations for ML Methods

Consider a ML application involving data points with features [math]\featurevec = \big(\feature_{1},\ldots,\feature_{\featurelen}\big)^{T} \in \mathbb{R}^{\featurelen}[/math] and label [math]\truelabel \in \mathbb{R}[/math]. We use a ML method that reads in some labelled data points

[[math]] \begin{equation} \big(\featurevec^{(1)},\truelabel^{(1)}\big),\big(\featurevec^{(2)},\truelabel^{(2)}\big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big), \end{equation} [[/math]]

and learns a hypothesis

[[math]] \begin{equation} \label{equ_pred_map} h(\cdot): \mathbb{R}^{\featurelen} \rightarrow \mathbb{R}: \featurevec \mapsto \hat{\truelabel}=h(\featurevec). \end{equation} [[/math]]

The precise working principle of this ML method for how to learn this hypothesis [math]h[/math] is not relevant in what follows.

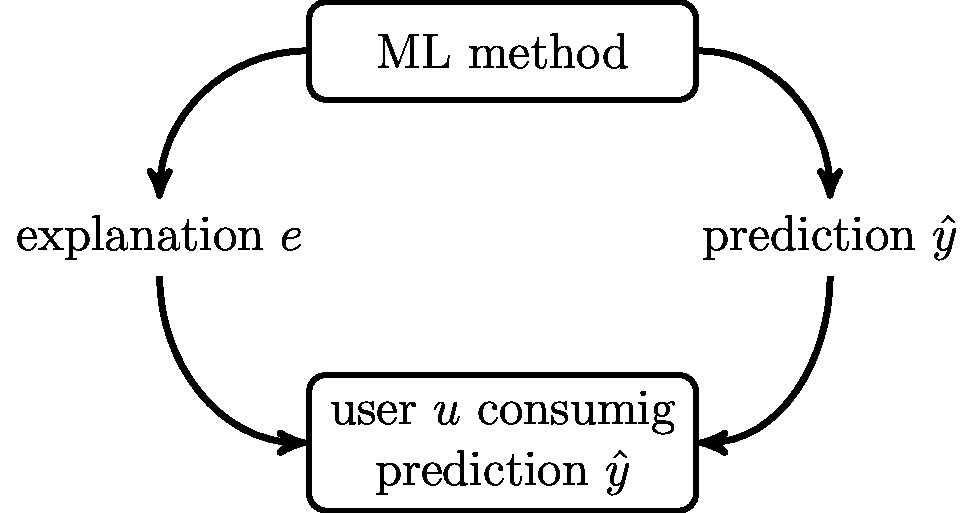
An explanation [math]\explanation[/math] provides additional information [math]I (\hat{\truelabel},\explanation|\user)[/math] to a user [math]\user[/math] about the prediction [math]\hat{\truelabel}[/math].

The learnt predictor [math]h(\featurevec)[/math] is applied to the features of a data point to obtain the predicted label [math]\hat{\truelabel}\!\defeq\!h(\featurevec)[/math]. The prediction [math]\hat{\truelabel}[/math] is then delivered to a human end-user (see Figure fig_explainable_ML). Depending on the ML application, this end-user might be a streaming service subscriber [11], a dermatologist [12] or a city planner [13].

Human users of ML methods often have some conception or model for the relation between features [math]\featurevec[/math] and label [math]\truelabel[/math] of a data point. This intrinsic model might vary significantly between users with different (social or educational) background. We will model the user understanding of a data point by a “user summary” [math]\user \in \mathbb{R}[/math]. The summary is obtained by a (possibly stochastic) map from the features [math]\featurevec[/math] of a data point. For ease of exposition, we focus on summaries obtained by a deterministic map

[[math]] \begin{equation} \label{eq_def_user_summary} \user(\cdot): \mathbb{R}^{\featurelen} \rightarrow \mathbb{R}: \featurevec \mapsto \user \defeq \user(\featurevec). \end{equation} [[/math]]

However, the resulting explainable ML method can be extended to user feedback [math]\user[/math] modelled as a stochastic maps. In this case, the user feedback [math]\user[/math] is characterized by a probability distribution [math]p(\user| \featurevec)[/math].

The user feedback [math]\user[/math] is determined by the features [math]\featurevec[/math] of a data point. We might think of the value [math]\user[/math] for a specific data point as a signal that reflects how the human end-user interprets (or perceives) the data point, given her knowledge (including formal education) and the context of the ML application. We do not assume any knowledge about the details for how the signal value [math]\user[/math] is formed for a specific data point. In particular, we do not know any properties of the map [math]\user(\cdot): \featurevec \mapsto \user[/math].

The above approach is quite flexible as it allows for very different forms of user summaries. The user summary could be the prediction obtained from a simplified model, such as linear regression using few features that the user anticipates as being relevant. Another example for a user summary [math]\user[/math] could be a higher-level feature, such as eye spacing in facial pictures, that the user considers relevant [14].

Note that, since we allow for an arbitrary map in \eqref{eq_def_user_summary}, the user summary [math]\user(\featurevec)[/math] obtained for a random data point with features [math]\featurevec[/math] might be correlated with the prediction [math]\hat{\truelabel}=h(\featurevec)[/math]. As an extreme case, consider a very knowledgable user that is able to predict the label of any data point from its features as well as the ML method itself. In this case, the maps \eqref{equ_pred_map} and \eqref{eq_def_user_summary} might be nearly identical. However, in general the predictions delivered by the learnt hypothesis \eqref{equ_pred_map} will be different from the user summary [math]\user(\featurevec)[/math].

We formalize the act of explaining a prediction [math]\hat{\truelabel} = h(\featurevec)[/math] as presenting some additional quantity [math]\explanation[/math] to the user (see Figure fig_explainable_ML). This explanation [math]\explanation[/math] can be any artefact that helps the user to understand the prediction [math]\hat{\truelabel}[/math], given her understanding [math]\user[/math] of the data point. Loosely speaking, the aim of providing explanation [math]\explanation[/math] is to reduce the uncertainty of the user [math]\user[/math] about the prediction [math]\hat{\truelabel}[/math] [4].

For the sake of exposition, we construct explanations [math]\explanation[/math] that are obtained via a deterministic map

[[math]] \begin{equation} \label{equ_def_explanation} \explanation(\cdot): \mathbb{R}^{\featurelen} \rightarrow \mathbb{R}: \featurevec \mapsto \explanation \defeq \explanation(\featurevec), \end{equation} [[/math]]

from the features [math]\featurevec[/math] of a data point. However, the explainable ML methods in this chapter can be generalized without difficulty to handle explanations obtained from a stochastic map. In the end, we only require the specification of the conditional probability distribution [math]p(\explanation|\featurevec)[/math].

The explanation [math]\explanation[/math] \eqref{equ_def_explanation} depends only on the features [math]\featurevec[/math] but not explicitly on the prediction [math]\hat{\truelabel}[/math]. However, our method for constructing the map \eqref{equ_def_explanation} takes into account the properties of the predictor map [math]h(\featurevec)[/math] \eqref{equ_pred_map}. In particular, Algorithm xml below requires as input the predicted labels [math]\hat{\truelabel}^{(\sampleidx)}[/math] for a set of data points (that serve as a training set for our method).

To obtain comprehensible explanations that can be computed efficiently, we must typically restrict the space of possible explanations to a small subset [math]\mathcal{F}[/math] of maps \eqref{equ_def_explanation}. This is conceptually similar to the restriction of the space of possible predictor functions in a ML method to a small subset of maps which is known as the hypothesis space.

Probabilistic Data Model for XML

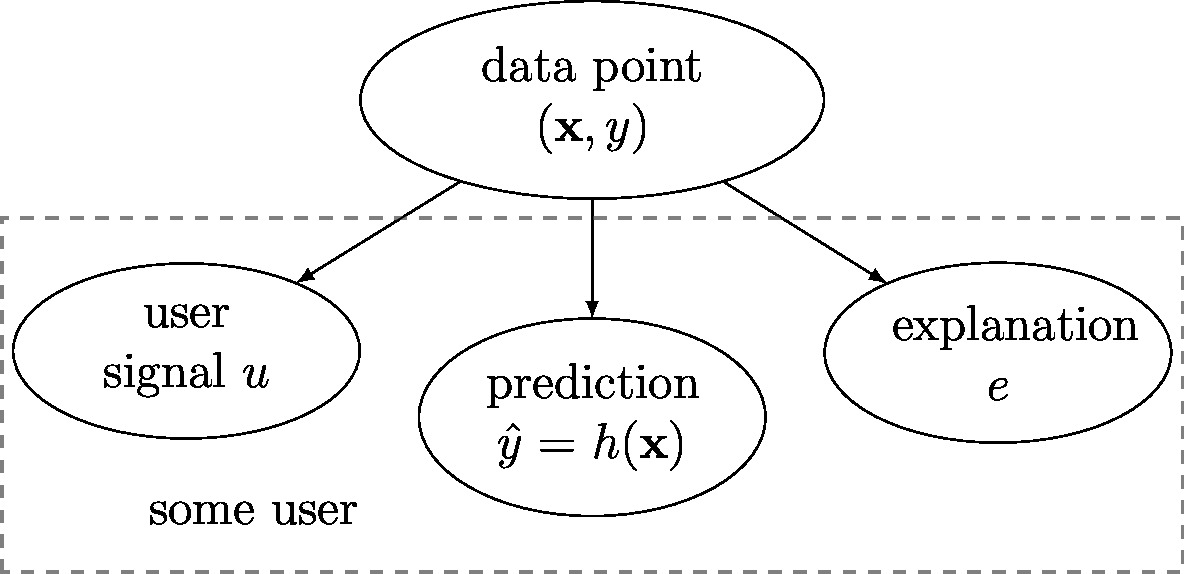
In what follows, we model data points as realizations of independent and identically distributed (iid) random variable (RV)s with common (joint) probability distribution [math]p(\featurevec,\truelabel)[/math] of features and label (see Section Probabilistic Models for Data ). Modelling the data points as realizations of RVs implies that the user summary [math]\user[/math], prediction [math]\hat{\truelabel}[/math] and explanation [math]\explanation[/math] are also realizations of RVs. The joint distribution [math]p(\user,\hat{\truelabel},\explanation,\featurevec,\truelabel)[/math] conforms with the Bayesian network [15] depicted in Figure fig_simple_prob_ML. Indeed,

[[math]] \begin{equation} \label{equ_joint_prob_factor} p(\user,\hat{\truelabel},\explanation,\featurevec,\truelabel) = p(\user|\featurevec) \cdot p(\explanation|\featurevec) \cdot p(\hat{\truelabel}|\featurevec) \cdot p(\featurevec,\truelabel). \end{equation} [[/math]]

We measure the amount of additional information provided by an explanation [math]\explanation[/math] for a prediction [math]\predictedlabel[/math] to some user [math]\user[/math] via the conditional mutual information (MI) [10](Ch. 2 and 8)

[[math]] \begin{equation} \label{eq_def_surprise} I(\explanation;\hat{\truelabel}|\user) \defeq \expect \bigg\{ \log \frac{p( \hat{\truelabel},\explanation|\user)}{p(\hat{\truelabel}|\user)p(\explanation|\user)} \bigg\}. \end{equation} [[/math]]

The conditional MI [math]I(\explanation;\predictedlabel|\user)[/math] can also be interpreted as a measure for the amount by which the explanation [math]\explanation[/math] reduces the uncertainty about the prediction [math]\hat{\truelabel}[/math] which is delivered to some user [math]\user[/math]. Providing the explanation [math]\explanation[/math] serves the apparent human need to understand observed phenomena, such as the predictions from a ML method [4].

A simple probabilistic graphical model (a Bayesian network [16][17]) for explainable ML. We interpret data points (with features [math]\featurevec[/math] and label [math]\truelabel[/math]) along with the user summary [math]\user[/math], [math]\explanation[/math] and predicted label [math]\hat{\truelabel}[/math] as realizations of RVs. These RVs satisfy conditional independence relations encoded by the directed links of the graph [17]. Given the data point, the predicted label [math]\hat{\truelabel}[/math], the explanation [math]\explanation[/math] and the user summary [math]\user[/math] are conditionally independent. This conditional independence is trivial if all these quantities are obtained from deterministic maps applied to the features [math]\featurevec[/math] of the data point.

Computing Optimal Explanations

Capturing the effect of an explanation using the probabilistic model \eqref{eq_def_surprise} offers a principled approach to computing an optimal explanation [math]\explanation[/math]. We require the optimal explanation [math]\explanation^{*}[/math] to maximize the conditional MI \eqref{eq_def_surprise} between the explanation [math]\explanation[/math] and the prediction [math]\hat{\truelabel}[/math] conditioned on the user summary [math]\user[/math] of the data point.

Formally, an optimal explanation [math]\explanation^{*}[/math] solves

[[math]] \begin{equation} \label{equ_opt_explanation} I(\explanation^{*};\predictedlabel|\user) = \sup_{\explanation \in \mathcal{F}} I(\explanation;\predictedlabel|\user). \end{equation} [[/math]]

The choice for the subset [math]\mathcal{F}[/math] of valid explanations offers a trade-off between comprehensibility, informativeness and computational cost incurred by an explanation [math]\explanation^{*}[/math] (solving \eqref{equ_opt_explanation}).

The maximization problem \eqref{equ_opt_explanation} for obtaining optimal explanations is similar to the approach in [7]. However, while [7] uses the unconditional MI between explanation and prediction, \eqref{equ_opt_explanation} uses the conditional MI given the user summary [math]\user[/math]. Therefore, \eqref{equ_opt_explanation} delivers personalized explanations that are tailored to the user who is characterized by the summary [math]\user[/math].


It is important to note that the construction \eqref{equ_opt_explanation} allows for many different forms of explanations. An explanation could be a subset of features of a data point (see [18] and Section Computing Optimal Explanations ). More generally, explanations could be obtained from simple local statistics (averages) of features that are considered related, such as nearby pixels in an image or consecutive amplitude values of an audio signal. Instead of individual features, carefully chosen data points from a training set can also serve as an explanation [19][20].

Let us illustrate the concept of optimal explanations \eqref{equ_opt_explanation} using linear regression. We model the features [math]\featurevec[/math] as a realization of a multivariate normal random vector with zero mean and covariance matrix [math]\mC_{\feature}[/math],

[[math]] \begin{equation} \label{equ_feature_vector_Gaussian} \featurevec \sim \mathcal{N}(\mathbf{0},\mC_{\feature}). \end{equation} [[/math]]

The predictor and the user summary are linear functions

[[math]] \begin{equation} \label{equ_pred_summary} \predictedlabel \defeq \weights^{T} \featurevec \mbox{, and } \user \defeq \mathbf{v}^{T} \featurevec. \end{equation} [[/math]]

We construct explanations via subsets of individual features [math]\feature_{\featureidx}[/math] that are considered most relevant for a user to understand the prediction [math]\predictedlabel[/math] (see [21](Definition 2) and [22]). Thus, we consider explanations of the form

[[math]] \begin{equation} \label{equ_def_explanation_subset} e \defeq \{ \feature_{\featureidx} \}_{\featureidx \in \explainset} \mbox{ with some subset } \explainset \subseteq \{1,\ldots,\featurelen\}. \end{equation} [[/math]]

The complexity of an explanation [math]e[/math] is measured by the number [math]|\explainset|[/math] of features that contribute to it. We limit the complexity of explanations by a fixed (small) sparsity level,

[[math]] \begin{equation} | \explainset | \leq \sparsity (\ll \featurelen). \end{equation} [[/math]]

Modelling the feature vector [math]\featurevec[/math] as Gaussian \eqref{equ_feature_vector_Gaussian} implies that the prediction [math]\hat{\truelabel}[/math] and user summary [math]u[/math] obtained from \eqref{equ_pred_summary} is jointly Gaussian for a given [math]\explainset[/math] \eqref{equ_def_explanation}. Basic properties of multivariate normal distributions [10](Ch. 8), allow to develop \eqref{equ_opt_explanation} as

[[math]] \begin{align} \max_{\substack{\explainset \subseteq \{1,\ldots,\featurelen\} \\ |\explainset| \leq s }} & I(\explanation;\hat{\truelabel}|\user) \nonumber \\  &= h(\hat{\truelabel}|\user) - h(\hat{\truelabel}|\user,\explainset) \nonumber \\[3mm] &= (1/2) \log \mC_{\hat{\truelabel}|\user} - (1/2) \log \det \mC_{\hat{\truelabel}|\user,\trainset} \nonumber \\[3mm] & = \label{equ_sup_mi_Gauss}(1/2) \log \sigma^2_{\hat{\truelabel}|\user} - (1/2) \log \sigma^{2}_{\hat{\truelabel}|\user,\trainset}. \end{align} [[/math]]

Here, [math]\sigma^2_{\hat{\truelabel}|\user}[/math] denotes the conditional variance of the prediction [math]\hat{\truelabel}[/math], conditioned on the user summary [math]\user[/math]. Similarly, [math]\sigma^{2}_{\hat{\truelabel}|\user,\explainset}[/math] denotes the conditional variance of [math]\hat{\truelabel}[/math], conditioned on the user summary [math]\user[/math] and the subset [math]\{\feature_{\featureidx}\}_{\featureidx\in \explainset}[/math] of features. The last step in \eqref{equ_sup_mi_Gauss} follows from the fact that [math]\hat{\truelabel}[/math] is a scalar random variable.

The first component of the final expression of \eqref{equ_sup_mi_Gauss} does not depend on the index set [math]\explainset[/math] used to construct the explanation [math]\explanation[/math] (see \eqref{equ_def_explanation_subset}). Therefore, the optimal choice for [math]\explainset[/math] solves

[[math]] \begin{equation} \label{equ_sup_m_sigma} \sup_{|\explainset| \leq \sparsity} - (1/2) \log \sigma^{2}_{\hat{\truelabel}|\user,\explainset}. \end{equation} [[/math]]

The maximization \eqref{equ_sup_m_sigma} is equivalent to

[[math]] \begin{equation} \label{equ_min_variance} \inf_{|\explainset| \leq \sparsity} \sigma^{2}_{\hat{\truelabel}|\user,\explainset}. \end{equation} [[/math]]

In order to solve \eqref{equ_min_variance}, we relate the conditional variance [math]\sigma^{2}_{\hat{\truelabel}|\user,\explainset}[/math] to a particular decomposition

[[math]] \begin{equation} \label{equ_def_linear_model} \hat{\truelabel} = \eta \user + \sum_{\featureidx \in \explainset} \beta_{\featureidx} \feature_{\featureidx} + \varepsilon. \end{equation} [[/math]]

For an optimal choice of the coefficients [math]\eta[/math] and [math]\beta_{\featureidx}[/math], the variance of the error term in \eqref{equ_def_linear_model} is given by [math]\sigma^{2}_{\hat{\truelabel}|\user,\explainset}[/math]. Indeed,

[[math]] \begin{equation} \label{equ_def_optimal_coef_linmodel} \min_{\eta,\beta_{\featureidx} \in \mathbb{R}} \expect\big\{ \big(\hat{\truelabel} - \eta \user - \sum_{\featureidx \in \explainset} \beta_{\featureidx} \feature_{\featureidx} \big)^{2}\big\} = \sigma^{2}_{\hat{\truelabel}|\user,\explanation}. \end{equation} [[/math]]

Inserting \eqref{equ_def_optimal_coef_linmodel} into \eqref{equ_min_variance}, an optimal choice [math]\explainset[/math] (of feature) for the explanation of prediction [math]\hat{\truelabel}[/math] to user [math]\user[/math] is obtained from

[[math]] \begin{align} & \inf_{|\explainset| \leq \sparsity} \min_{\eta,\beta_{\featureidx} \in \mathbb{R}} \expect\big\{ \big(\hat{\truelabel} - \eta \user - \sum_{\featureidx \in \explainset} \beta_{\featureidx} x_{\featureidx} \big)^{2}\big\} \label{equ_final_opt_E} \\ &= \min_{ \| {\bm \beta} \|_{0} \leq \sparsity } \expect\big\{ \big(\hat{\truelabel} - \eta \user - {\bm \beta}^{T} \featurevec \big)^{2}\big\} \label{equ_final_opt_beta}. \end{align} [[/math]]

An optimal subset [math]\explainset_{\rm opt}[/math] of features defining the explanation [math]\explanation[/math] \eqref{equ_def_explanation_subset} is obtained from any solution [math]{\bm \beta}_{\rm opt}[/math] of \eqref{equ_final_opt_beta} via

[[math]] \begin{equation} \label{equ_opt_expl_support} \explainset_{\rm opt} = \supp {\bm \beta}_{\rm opt}. \end{equation} [[/math]]

Section Computing Optimal Explanations uses the probabilistic model \eqref{equ_feature_vector_Gaussian} to construct optimal explanations via the (support of the) solutions [math]{\bm \beta}_{\rm opt}[/math] of the sparse linear regression problem \eqref{equ_final_opt_beta}. To obtain a practical algorithm for computing (approximately) optimal explanations \eqref{equ_opt_expl_support}, we approximate the expectation in \eqref{equ_final_opt_beta} using an average over the training set [math]\big(\featurevec^{(\sampleidx)},\predictedlabel^{(\sampleidx)},\user^{(\sampleidx)}\big)[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math]. This resulting method for computing personalized explanations is summarized in Algorithm xml.

XML Algorithm

Input: explanation complexity [math]\sparsity[/math], training set [math]\big(\featurevec^{(\sampleidx)},\predictedlabel^{(\sampleidx)},\user^{(\sampleidx)}\big)[/math] for [math]\sampleidx=1,\ldots,\samplesize[/math]

  1. compute [math]\widehat{\bm \beta}[/math] by solving

[[math]] \begin{equation} \label{equ_P0} \widehat{\bm \beta} \in \argmin_{\eta\!\in\!\mathbb{R},\| {\bm \beta} \|_{0} \leq \sparsity } (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big(\hat{\truelabel}^{(\sampleidx)} \!-\! \eta \user^{(\sampleidx)}\!-\!{\bm \beta}^{T} \featurevec^{(\sampleidx)} \big)^{2} \end{equation} [[/math]]

Output: feature set [math]\widehat{\explainset} \defeq {\rm supp} \widehat{\bm \beta}[/math]

Algorithm xml is interactive in the sense that the user has to provide a feedback signal [math]\user^{(\sampleidx)}[/math] for the data points with features [math]\featurevec^{(\sampleidx)}[/math]. Based on the user feedback [math]\user^{(\sampleidx)}[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math], Algorithm xml learns an optimal subset [math]\explainset[/math] of features \eqref{equ_def_explanation_subset} that are used for the explanation of predictions.

The sparse regression problem \eqref{equ_P0} becomes intractable for large feature length [math]\featurelen[/math]. However, if the features are weakly correlated with each other and the user summary [math]\user[/math], the solutions of \eqref{equ_P0} can be found by efficient convex optimization methods. One popular method to (approximately) solve sparse regression \eqref{equ_P0} is the least absolute shrinkage and selection operator (Lasso) (see Section The Lasso ),

[[math]] \begin{equation} \label{equ_Lasso} \widehat{\bm \beta} \!\in\!\argmin_{ \eta\!\in\!\mathbb{R},{\bm \beta} \in \mathbb{R}^{\featurelen}} (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big(\predictedlabel^{(\sampleidx)} \!-\! \eta \user^{(\sampleidx)}\!-\!{\bm \beta}^{T} \featurevec^{(\sampleidx)} \big)^{2}\!+\!\regparam \| {\bm \beta} \|_{1}. \end{equation} [[/math]]

There is large body of work that studies the choice of Lasso parameter [math]\regparam[/math] in \eqref{equ_Lasso} such that solutions \eqref{equ_Lasso} coincide with the solutions of \eqref{equ_P0} (see [23][24] and references therein). The proper choice for [math]\regparam[/math] typically requires knowledge of statistical properties of data. If such a probabilistic model is not available, the choice of [math]\regparam[/math] can be guided by simple validation techniques (see Section Validation ).

Explainable Empirical Risk Minimization

Section Structural Risk Minimization discussed SRM equ_ERM_fun_pruned as a method for pruning the hypothesis space [math]\hypospace[/math] used in ERM . This pruning is implemented either via a (hard) constraint as in equ_ERM_fun_pruned or by adding a regularization term to the training error as in equ_ERM_fun_regularized. The idea of SRM is to avoid (prune away) hypothesis maps that perform good on the training set but poorly outside, i.e., they do not generalize well. Here, we will use another criterion for steering the pruning and construction of regularization terms. In particular, we use the (intrinsic) explainability of a hypotheses map as a regularization term.

To make the notion of explainability precise we use again the probabilistic model of Section Probabilistic Data Model for XML . We interpret data points as realizations of iid RVs with common (joint) probability distribution [math]p(\featurevec,\truelabel)[/math] of features [math]\featurevec[/math] and label [math]\truelabel[/math]. A quantitative measure the intrinsic explainability of a hypothesis [math]h \in \hypospace[/math] is the conditional (differential) entropy [10](Ch. 2 and 8)

[[math]] \begin{equation} \label{eq_def_explainability} \condent(\predictedlabel|\user) \defeq - \expect\bigg\{ \log p(\predictedlabel|\user) \bigg\}. \end{equation} [[/math]]

The conditional entropy \eqref{eq_def_explainability} indicates the uncertainty about the prediction [math]\predictedlabel[/math], given the user summary [math]\hat{\user}=\user(\featurevec)[/math]. Smaller values [math]\condent(\predictedlabel;u)[/math] correspond to smaller levels of uncertainty in the predictions [math]\predictedlabel[/math] that is experienced by user [math]\user[/math].

We obtain EERM by requiring a sufficiently small conditional entropy \eqref{eq_def_explainability} of a hypothesis,

[[math]] \begin{equation} \label{equ_def_EERM} \hat{\predictor} \in \argmin_{\predictor \in \hypospace} \emperror \big( \predictor \big) \quad \mbox{s.t. } \quad \condent(\predictedlabel|\hat{u}) \leq \eta. \end{equation} [[/math]]

The random variable [math]\hat{\truelabel}=\predictor(\featurevec)[/math] in the constraint of \eqref{equ_def_EERM} is obtained by applying the predictor map [math]\predictor \in \hypospace[/math] to the features. The constraint [math]\condent(\predictedlabel|\hat{u}) \leq \eta[/math] in \eqref{equ_def_EERM} enforces the learnt hypothesis [math]\hat{\predictor}[/math] to be sufficiently explainable in the sense that the conditional entropy [math]\condent(\hat{\predictor}|\hat{u}) \leq \eta[/math] does not exceed a prescribed level [math]\eta[/math].

Let us now consider the special case of EERM \eqref{equ_def_EERM} for the linear hypothesis space

[[math]] \begin{equation} \label{equ_linear_predictor_map} \predictor^{(\weights)}(\featurevec) \defeq \weights^{T} \mathbf{x} \mbox{ with some parameter vector } \weights \in \mathbb{R}^{\featurelen}. \end{equation} [[/math]]

Moreover, we assume that the features [math]\featurevec[/math] of a data point and its user summary [math]u[/math] are jointly Gaussian with mean zero and covariance matrix [math]\mathbf{C}[/math],

[[math]] \begin{equation} \label{equ_Gaussian_feature_summary} \big(\featurevec^{T},\hat{\user}\big)^{T} \sim \mathcal{N}(\mathbf{0},\mathbf{C}). \end{equation} [[/math]]

Under the assumptions \eqref{equ_linear_predictor_map} and \eqref{equ_Gaussian_feature_summary} (see [10](Ch. 8)),

[[math]] \begin{align} \label{equ_codent_EERM} \condent(\hat{\user}|\predictedlabel) &= (1/2) \log \sigma^{2}_{\predictedlabel|\hat{\user}}. \end{align} [[/math]]

Here, we used the conditional variance [math]\sigma^{2}_{\predictedlabel|\hat{u}}[/math] of [math]\predictedlabel[/math] given the random user summary [math]\user=\user(\featurevec)[/math]. Inserting \eqref{equ_codent_EERM} into the generic form of EERM \eqref{equ_def_EERM},

[[math]] \begin{equation} \label{equ_def_EERM_Gaussian} \hat{\predictor} \in \argmin_{\predictor \in \hypospace} \emperror(h) \quad \mbox{s.t. } \quad \log \sigma^{2}_{\hat{\truelabel}|\hat{\user}} \leq \eta. \end{equation} [[/math]]

By the monotonicity of the logarithm, \eqref{equ_def_EERM_Gaussian} is equivalent to

[[math]] \begin{equation} \label{equ_def_EERM_Gaussian_1} \hat{\predictor} \in \argmin_{\predictor \in \mathcal{H}} \emperror(\predictor) \quad \mbox{s.t. } \quad \sigma^{2}_{\hat{y}|\hat{u}} \leq \explanation^{(\eta)}. \end{equation} [[/math]]

To further develop \eqref{equ_def_optimal_coef_linmodel}, we use the identity

[[math]] \begin{equation} \label{equ_def_optimal_coef_linmodel2} \min_{\eta \in \mathbb{R}} \expect\big\{ \big(\hat{\truelabel} - \eta \user \big)^{2}\big\} = \sigma^{2}_{\hat{\truelabel}|\hat{\user}}. \end{equation} [[/math]]

The identity \eqref{equ_def_optimal_coef_linmodel2} relates the conditional variance [math]\sigma^{2}_{\hat{\truelabel}|\hat{\user}}[/math] to the minimum mean squared error that can be achieved by estimating [math]\hat{\truelabel}[/math] using a linear estimator [math]\eta \hat{\user}[/math] with some [math]\eta \in \mathbb{R}[/math]. Inserting \eqref{equ_def_optimal_coef_linmodel} and \eqref{equ_linear_predictor_map} into \eqref{equ_def_EERM_Gaussian_1},

[[math]] \begin{equation} \label{equ_def_EERM_Gaussian_2} \hat{\predictor} \in \argmin_{\weights \in \mathbb{R}^{\featurelen},\eta \in \mathbb{R}} \emperror(\predictor^{(\weights)}) \quad \mbox{s.t. } \quad \expect\big\{ \underbrace{\big(\weights^{T}\featurevec}_{\stackrel{\eqref{equ_linear_predictor_map}}{=} \hat{\truelabel}} - \eta \hat{\user} \big)^{2}\big\} \leq \explanation^{(\eta)}. \end{equation} [[/math]]

The inequality constraint in \eqref{equ_def_EERM_Gaussian_2} is convex [25](Ch. 4.2.). For squared error loss, the objective function [math]\emperror(\predictor^{(\weights)})[/math] is also convex. Thus, for linear least squares regression, we can reformulate \eqref{equ_def_EERM_Gaussian_2} as an equivalent (dual) unconstrained problem [25](Ch. 5)

[[math]] \begin{equation} \label{equ_def_ELLRM_Gaussian_3} \hat{\predictor} \in \argmin_{\weights \in \mathbb{R}^{\featurelen},\eta \in \mathbb{R}} \explainset(\predictor^{(\weights)}) + \regparam \expect\big\{ \big(\weights^{T}\featurevec- \eta \hat{\user} \big)^{2}\big\}. \end{equation} [[/math]]

By convex duality, for a given threshold [math]\explanation^{(\eta)}[/math] in \eqref{equ_def_EERM_Gaussian_2}, we can find a value for [math]\regparam[/math] in \eqref{equ_def_ELLRM_Gaussian_3} such that \eqref{equ_def_EERM_Gaussian_2} and \eqref{equ_def_ELLRM_Gaussian_3} have the same solutions [25](Ch. 5). Algorithm eerm below is obtained from \eqref{equ_def_ELLRM_Gaussian_3} by approximating the expectation [math] \expect\big\{ \big(\weights^{T}\featurevec- \eta \hat{\user} \big)^{2}\big\}[/math] with an average over the data points [math]\big(\featurevec^{(\sampleidx)},\hat{\truelabel}^{(\sampleidx)},\hat{\user}^{(\sampleidx)}\big)[/math] for [math]\sampleidx=1,\ldots,\samplesize[/math].

Explainable Linear Least Squares Regression

Input: explainability parameter [math]\regparam[/math], training set [math]\big(\featurevec^{(\sampleidx)},\hat{\truelabel}^{(\sampleidx)},\hat{\user}^{\sampleidx)}\big)[/math] for [math]\sampleidx=1,\ldots,\samplesize[/math]

  1. solve
    [[math]] \begin{equation} \label{equ_P0_ellr} \widehat{\weights} \!\in\! \argmin_{\eta \in \mathbb{R},\weights \in \mathbb{R}^{\featurelen} } (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \underbrace{\big(\hat{\truelabel}^{(\sampleidx)} \!-\! \weights^{T} \featurevec^{(\sampleidx)} \big)^{2}}_{\mbox{empirical risk}} + \regparam \underbrace{( \weights^{T} \featurevec^{(\sampleidx)} - \eta \hat{\user}^{(i)})^{2}}_{\mbox{explainability}} \end{equation} [[/math]]

Output: weights [math]\widehat{\weights}[/math] of explainable linear hypothesis


References

  1. 1.0 1.1 1.2 Cite error: Invalid <ref> tag; no text was provided for refs named Cheng2019
  2. Cite error: Invalid <ref> tag; no text was provided for refs named Hacker:2020aa
  3. Cite error: Invalid <ref> tag; no text was provided for refs named DeBacker2006
  4. 4.0 4.1 4.2 Cite error: Invalid <ref> tag; no text was provided for refs named Kagan1972
  5. Cite error: Invalid <ref> tag; no text was provided for refs named WinklerMelanoma
  6. Cite error: Invalid <ref> tag; no text was provided for refs named LiaoXAI2021
  7. 7.0 7.1 7.2 Cite error: Invalid <ref> tag; no text was provided for refs named Chen2018
  8. 8.0 8.1 Cite error: Invalid <ref> tag; no text was provided for refs named JunXML2020
  9. 9.0 9.1 Cite error: Invalid <ref> tag; no text was provided for refs named JuEERM2020
  10. 10.0 10.1 10.2 10.3 10.4 Cite error: Invalid <ref> tag; no text was provided for refs named coverthomas
  11. Cite error: Invalid <ref> tag; no text was provided for refs named GomezUribe2016
  12. Cite error: Invalid <ref> tag; no text was provided for refs named Esteva2017
  13. Cite error: Invalid <ref> tag; no text was provided for refs named Yang2019
  14. Cite error: Invalid <ref> tag; no text was provided for refs named Jeong2015
  15. Cite error: Invalid <ref> tag; no text was provided for refs named Pearl1988
  16. Cite error: Invalid <ref> tag; no text was provided for refs named LauritzenGM
  17. 17.0 17.1 Cite error: Invalid <ref> tag; no text was provided for refs named koller2009probabilistic
  18. Cite error: Invalid <ref> tag; no text was provided for refs named Ribeiro2016
  19. Cite error: Invalid <ref> tag; no text was provided for refs named Mcinerney18
  20. Cite error: Invalid <ref> tag; no text was provided for refs named Ribeiro2018
  21. Cite error: Invalid <ref> tag; no text was provided for refs named Montavon2018
  22. Cite error: Invalid <ref> tag; no text was provided for refs named Molnar2019
  23. Cite error: Invalid <ref> tag; no text was provided for refs named HastieWainwrightBook
  24. Cite error: Invalid <ref> tag; no text was provided for refs named GeerBuhlConditions
  25. 25.0 25.1 25.2 Cite error: Invalid <ref> tag; no text was provided for refs named BoydConvexBook