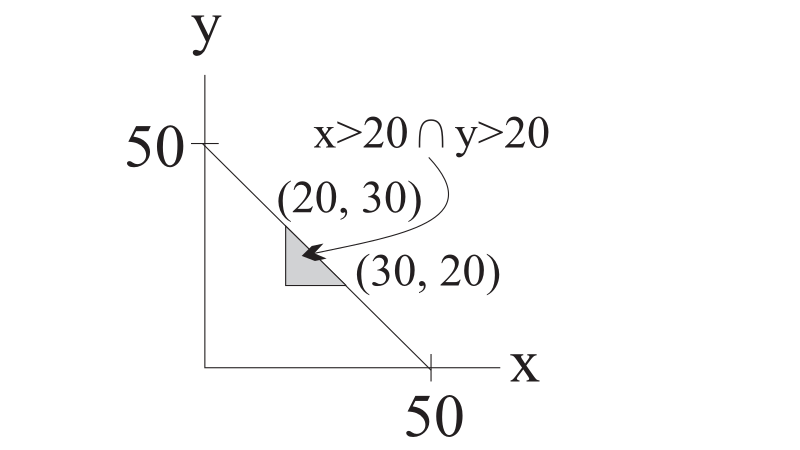The future lifetimes (in months) of two components of a machine have the following joint density function:
[[math]]
f(x,y) = \begin{cases}
\frac{6(50-x-y)}{125000}, \,\, 0 \lt x \lt 50-y \lt 50 \\
0, \, \textrm{Otherwise.}
\end{cases}
[[/math]]
Determine which of the following represents the probability that both components are still functioning 20 months from now.
- [math]\frac{6}{125000}\int_{0}^{20}\int_{0}^{20}(50-x-y)\,ds\,dt[/math]
- [math]\frac{6}{125000}\int_{20}^{30}\int_{20}^{50-x}(50-x-y)\,ds\,dt[/math]
- [math]\frac{6}{125000}\int_{20}^{30}\int_{20}^{50-x-y}(50-x-y)\,ds\,dt[/math]
- [math]\frac{6}{125000}\int_{20}^{50}\int_{20}^{50-x}(50-x-y)\,ds\,dt [/math]
- [math]\frac{6}{125000}\int_{20}^{50}\int_{20}^{50-x-y}(50-x-y)\,ds\,dt [/math]
Copyright 2023. The Society of Actuaries, Schaumburg, Illinois. Reproduced with permission.