A company is reviewing tornado damage claims under a farm insurance policy. Let [math]X[/math] be the portion of a claim representing damage to the house and let [math]Y[/math] be the portion of the same claim representing damage to the rest of the property. The joint density function of [math]X[/math] and [math]Y[/math] is

[[math]] f(x,y) = \begin{cases} 6 [1 − ( x + y ) ], \,\, x \gt 0, y \gt 0, x+y \lt 1 \\ 0, \, \textrm{Otherwise.} \end{cases} [[/math]]

Calculate the probability that the portion of a claim representing damage to the house is less than 0.2.

• 0.360
• 0.480
• 0.488
• 0.512
• 0.520

Copyright 2023. The Society of Actuaries, Schaumburg, Illinois. Reproduced with permission.

Solution: C

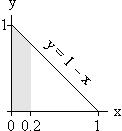
The domain of X and Y is pictured below. The shaded region is the portion of the domain over which X < 0.2 .

Now observe

[[math]] \begin{align*} \operatorname{P}[ X \lt 0.2 ] &= \int_0^{0.2} \int_0^{1-x} 6[1-(x+y)] dy dx \\ &= 6 \int_0^{0.2} [y - xy - \frac{1}{2} y^2]_0^{1-x} dx \\ &= 6 \int_0^{0.2} [1 - x - x(1-x) - \frac{1}{2}(1-x)^2 ]dx \\ &= 6 \int_0^{0.2} [(1-x)^2 - \frac{1}{2}(1-x)^2 ]dx \\ &= 6 \int_0^{0.2} \frac{1}{2}(1-x)^2 \, dx \\ &= -(1-x)^3 \Big |_0^{0.2} \\ &= -(0.8)^3 + 1\\ &=0.488. \end{align*} [[/math]]

Copyright 2023. The Society of Actuaries, Schaumburg, Illinois. Reproduced with permission.