Let [math]X[/math] be a random variable which is Poisson distributed with parameter [math]\lambda[/math]. Show that [math]E(X) = \lambda[/math]. Hint: Recall that

Recall that in Exercise, we considered a town with two hospitals. In the large hospital about 45 babies are born each day, and in the smaller hospital about 15 babies are born each day. We were interested in guessing which hospital would have on the average the largest number of days with the property that more than 60 percent of the children born on that day are boys. For each hospital find the expected number of days in a year that have the property that more than 60 percent of the children born on that day were boys.

An insurance company has 1,00 policies on men of age 50. The company estimates that the probability that a man of age 50 dies within a year is .01. Estimate the number of claims that the company can expect from beneficiaries of these men within a year.

Using the life table for 1981 in Appendix C, write a program to compute the expected lifetime for males and females of each possible age from 1 to 85. Compare the results for males and females. Comment on whether life insurance should be priced differently for males and females.

A deck of ESP cards consists of 20 cards each of two types: say ten stars, ten circles (normally there are five types). The deck is shuffled and the cards turned up one at a time. You, the alleged percipient, are to name the symbol on each card before it is turned up.

Suppose that you are really just guessing at the cards. If you do not get to see each card after you have made your guess, then it is easy to calculate the expected number of correct guesses, namely ten.

If, on the other hand, you are guessing with information, that is, if you see each card after your guess, then, of course, you might expect to get a higher score. This is indeed the case, but calculating the correct expectation is no longer easy.

But it is easy to do a computer simulation of this guessing with information, so we can get a good idea of the expectation by simulation. (This is similar to the way that skilled blackjack players make blackjack into a favorable game by observing the cards that have already been played. See Exercise)

• First, do a simulation of guessing without information, repeating the experiment at least 1000 times. Estimate the expected number of correct answers and compare your result with the theoretical expectation.
• What is the best strategy for guessing with information?
• Do a simulation of guessing with information, using the strategy in (b). Repeat the experiment at least 1000 times, and estimate the expectation in this case.
• Let [math]S[/math] be the number of stars and [math]C[/math] the number of circles in the deck. Let [math]h(S,C)[/math] be the expected winnings using the optimal guessing strategy in (b). Show that [math]h(S,C)[/math] satisfies the recursion relation
  [[math]] h(S,C) = \frac S{S + C} h(S - 1,C) + \frac C{S + C} h(S,C - 1) + \frac {\max(S,C)}{S + C}\ , [[/math]]
  and [math]h(0,0) = h(-1,0) = h(0,-1) = 0[/math]. Using this relation, write a program to compute [math]h(S,C)[/math] and find [math]h(10,10)[/math]. Compare the computed value of [math]h(10,10)[/math] with the result of your simulation in (c). For more about this exercise and Exercise see Diaconis and Graham.^{[Notes 1]}

Notes

Consider the ESP problem as described in Exercise. You are again guessing with information, and you are using the optimal guessing strategy of guessing star if the remaining deck has more stars, circle if more circles, and tossing a coin if the number of stars and circles are equal. Assume that [math]S \geq C[/math], where [math]S[/math] is the number of stars and [math]C[/math] the number of circles.

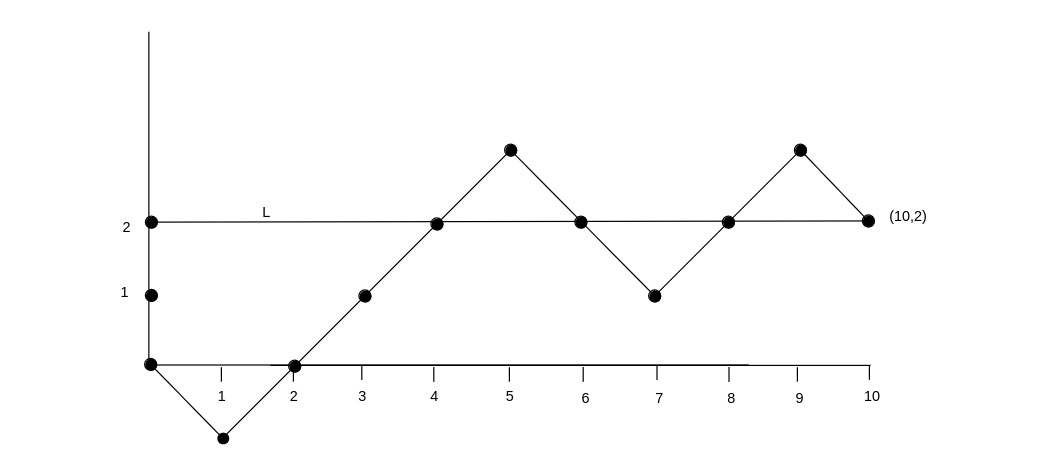
We can plot the results of a typical game on a graph, where the horizontal axis represents the number of steps and the vertical axis represents the difference between the number of stars and the number of circles that have been turned up. A typical game is shown in Figure. In this particular game, the order in which the cards were turned up is [math](C,S,S,S,S,C,C,S,S,C)[/math]. Thus, in this particular game, there were six stars and four circles in the deck. This means, in particular, that every game played with this deck would have a graph which ends at the point [math](10, 2)[/math]. We define the line [math]L[/math] to be the horizontal line which goes through the ending point on the graph (so its vertical coordinate is just the difference between the number of stars and circles in the deck).

• Show that, when the random walk is below the line [math]L[/math], the player guesses right when the graph goes up (star is turned up) and, when the walk is above the line, the player guesses right when the walk goes down (circle turned up). Show from this property that the subject is sure to have at least [math]S[/math] correct guesses.
• When the walk is at a point [math](x,x)[/math] on the line [math]L[/math] the number of stars and circles remaining is the same, and so the subject tosses a coin. Show that the probability that the walk reaches [math](x,x)[/math] is
  [[math]] \frac{{S \choose x}{C \choose x}}{{{S + C} \choose {2x}}}\ . [[/math]]
  Hint: The outcomes of [math]2x[/math] cards is a hypergeometric distribution (see Important Distributions).
• Using the results of (a) and (b) show that the expected number of correct guesses under intelligent guessing is
  [[math]] S + \sum_{x = 1}^C \frac12 \frac{{S \choose x}{C \choose x}}{{{S + C} \choose {2x}}}\ . [[/math]]

It has been said^{[Notes 1]} that a Dr. B. Muriel Bristol declined a cup of tea stating that she preferred a cup into which milk had been poured first. The famous statistician R. A. Fisher carried out a test to see if she could tell whether milk was put in before or after the tea. Assume that for the test Dr. Bristol was given eight cups of tea---four in which the milk was put in before the tea and four in which the milk was put in after the tea.

• What is the expected number of correct guesses the lady would make if she had no information after each test and was just guessing?
• Using the result of Exercise Exercise find the expected number of correct guesses if she was told the result of each guess and used an optimal guessing strategy.

Notes

In a popular computer game the computer picks an integerfrom 1 to [math]n[/math] at random. The player is given [math]k[/math] chances to guess the number. After each guess the computer responds “correct,” “too small,” or “too big.”

• Show that if [math]n \leq 2^k - 1[/math], then there is a strategy that guarantees you will correctly guess the number in [math]k[/math] tries.
• Show that if [math]n \geq 2^k - 1[/math], there is a strategy that assures you of identifying one of [math]2^k - 1[/math] numbers and hence gives a probability of [math](2^k - 1)/n[/math] of winning. Why is this an optimal strategy? Illustrate your result in terms of the case [math]n = 9[/math] and [math]k = 3[/math].

In the casino game of blackjack the dealer is dealt two cards, one face up and one face down, and each player is dealt two cards, both face down. If the dealer is showing an ace the player can look at his down cards and then make a bet called an insurance bet. (Expert players will recognize why it is called insurance.) If you make this bet you will win the bet if the dealer's second card is a ten card: namely, a ten, jack, queen, or king. If you win, you are paid twice your insurance bet; otherwise you lose this bet. Show that, if the only cards you can see are the dealer's ace and your two cards and if your cards are not ten cards, then the insurance bet is an unfavorable bet. Show, however, that if you are playing two hands simultaneously, and you have no ten cards, then it is a favorable bet. (Thorp^{[Notes 1]} has shown that the game of blackjack is favorable to the player if he or she can keep good enough track of the cards that have been played.)

Notes

Assume that, every time you buy a box of Wheaties, you receive a picture of one of the [math]n[/math] players for the New York Yankees (see Exercise). Let [math]X_k[/math] be the number of additional boxes you have to buy, after you have obtained [math]k - 1[/math] different pictures, in order to obtain the next new picture. Thus [math]X_1 = 1[/math], [math]X_2[/math] is the number of boxes bought after this to obtain a picture different from the first pictured obtained, and so forth.

• Show that [math]X_k[/math] has a geometric distribution with [math]p = (n - k + 1)/n[/math].
• Simulate the experiment for a team with 26 players (25 would be more accurate but we want an even number). Carry out a number of simulations and estimate the expected time required to get the first 13 players and the expected time to get the second 13. How do these expectations compare?
• Show that, if there are [math]2n[/math] players, the expected time to get the first half of the players is
  [[math]] 2n \left( \frac 1{2n} + \frac 1{2n - 1} +\cdots+ \frac 1{n + 1} \right)\ , [[/math]]
  and the expected time to get the second half is
  [[math]] 2n \left( \frac 1n + \frac 1{n - 1} +\cdots+ 1 \right)\ . [[/math]]
• In Example we stated that
  [[math]] 1 + \frac 12 + \frac 13 +\cdots+ \frac 1n \sim \log n + .5772 + \frac 1{2n}\ . [[/math]]
  Use this to estimate the expression in (c). Compare these estimates with the exact values and also with your estimates obtained by simulation for the case [math]n = 26[/math].