Replicate the results of Figure. More precisely, sample 100 points each of two Gaussians in [math]\mathbb{R}^{1000}[/math], one centered at zero and the other at [math](1,1,\dots)[/math]. Then compute the pairwise distances within the whole sample and plot their distribution.
Implement the naive separation algorithm, that picks one data point at random and then labels that half of the data set which is closest to the first point as [math]0[/math] and the rest as [math]1[/math]. Test the algorithm on the data set from Problem. When generating the data, mark the data points with [math]0[/math] and [math]1[/math] and after running the separation algorithm, let your code count how many data points got classified correctly.
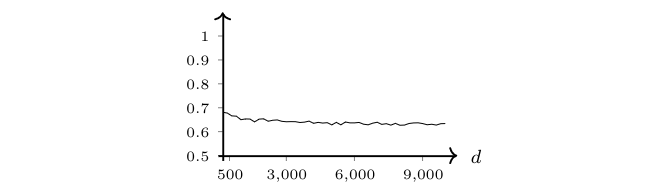
Replicate the results of Figure. More precisely, run the code from Problem for different dimensions [math]d[/math] and different distance functions [math]\Delta=\Delta(d)[/math], e.g., [math]\Delta\equiv c \gt 0[/math], [math]\Delta=2\sqrt{d}[/math], [math]\Delta=d^{0.3}[/math] or [math]\Delta=d^{1/4}[/math]. Plot the rate of correctly classified data points as a function of the dimension. Simulate also the case [math]\Delta=2d^{0.2}[/math] and confirm that this leads to a low correct classification rate which decreases for large dimensions.
A weak spot of our method above is that the point that we start with could lie somewhere far away from both of the two annuli. Think of ways to improve on this.
The table below contains actual heights sampled from adults aged 40-49 years in the U.S. The numbers represent the percentage that has height less than the value in the top row of the same column and larger than the value in the row left of it [Notes 1].
| 147.32 | 149.86 | 152.40 | 154.94 | 157.48 | 160.02 | 162.56 | 165.10 | 167.64 | 170.18 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Women | 1.6 | 3.4 | 5.8 | 9.0 | 11.0 | 15.2 | 12.0 | 14.2 | 10.8 | 8.2 |
| Men | 0 | 0 | 0 | 0 | 1.9 | 1.9 | 1.8 | 4.2 | 9.6 | 10.9 |
| 172.72 | 175.26 | 177.80 | 180.34 | 182.88 | 185.42 | 187.96 | 190.50 | 193.04 | 195.58 | |
| Women | 3.5 | 3.1 | 1.6 | 0.1 | 0 | 0 | 0 | 0 | 0.5 | 0 |
| Men | 10.1 | 14.0 | 15.2 | 9.5 | 8.3 | 5.1 | 5.2 | 1.3 | 0.4 | 0.5 |
Try with our algorithm (of which we know that it works in high dimensions) to separate the 1-dimensional data set.
Notes