Discrete Probability Distributions
In this book we shall study many different experiments from a probabilistic point of view. What is involved in this study will become evident as the theory is developed and examples are analyzed. However, the overall idea can be described and illustrated as follows: to each experiment that we consider there will be associated a random variable, which represents the outcome of any particular experiment. The set of possible outcomes is called the sample space. In the first part of this section, we will consider the case where the experiment has only finitely many possible outcomes, i.e., the sample space is finite. We will then generalize to the case that the sample space is either finite or countably infinite. This leads us to the following definition.
Random Variables and Sample Spaces
Suppose we have an experiment whose outcome depends on chance. We represent the outcome of the experiment by a capital Roman letter, such as [math]X[/math], called a random variable. The sample space of the experiment is the set of all possible outcomes. If the sample space is either finite or countably infinite, the random variable is said to be discrete.
We generally denote a sample space by the capital Greek letter [math]\Omega[/math]. As stated above, in the correspondence between an experiment and the mathematical theory by which it is studied, the sample space [math]\Omega[/math] corresponds to the set of possible outcomes of the experiment.
We now make two additional definitions. These are subsidiary to the
definition of sample space and serve to make precise some of the common terminology used
in conjunction with sample spaces. First of all, we define the elements of a sample space
to be outcomes. Second, each subset of a sample space is defined to be
an event. Normally, we shall denote outcomes by lower case letters and
events by capital letters.
Example A die is rolled once. We let [math]X[/math] denote the outcome of this experiment. Then the sample space for this experiment is the 6-element set
where each outcome [math]i[/math], for [math]i = 1, \ldots, 6,[/math] corresponds to the number of dots on the face which turns up. The event
corresponds to the statement that the result of the roll is an even number. The event [math]E[/math] can also be described by saying that [math]X[/math] is even. Unless there is reason to believe the die is loaded, the natural assumption is that every outcome is equally likely. Adopting this convention means that we assign a probability of 1/6 to each of the six outcomes, i.e., [math]m(i) = 1/6[/math], for [math]1 \le i \le 6[/math].
Distribution Functions
We next describe the assignment of probabilities. The definitions are motivated by the example above, in which we assigned to each outcome of the sample space a nonnegative number such that the sum of the numbers assigned is equal to 1.
Let [math]X[/math] be a random variable which denotes the value of the outcome of a certain experiment, and assume that this experiment has only finitely many possible outcomes. Let [math]\Omega[/math] be the sample space of the experiment (i.e., the set of all possible values of [math]X[/math], or equivalently, the set of all possible outcomes of the experiment.) A distribution function for [math]X[/math] is a real-valued function [math]m[/math] whose domain is [math]\Omega[/math] and which satisfies:
- [math]m(\omega) \geq 0\ , \qquad[/math]for all [math]\,\,\omega\in\Omega\ [/math], and
- [math]\sum\limits_{\omega \in \Omega} m(\omega) = 1\ [/math].
For any subset [math]E[/math] of [math]\Omega[/math], we define the probability of [math]E[/math] to be the number [math]P(E)[/math] given by
Example Consider an experiment in which a coin is tossed twice. Let [math]X[/math] be the random variable which corresponds to this experiment. We note that there are several ways to record the outcomes of this experiment. We could, for example, record the two tosses, in the order in which they occurred. In this case, we have [math]\Omega = \{HH,HT,TH,TT\}[/math]. We could also record the outcomes by simply noting the number of heads that appeared. In this case, we have [math]\Omega = \{0,1,2\}[/math]. Finally, we could record the two outcomes, without regard to the order in which they occurred. In this case, we have [math]\Omega = \{HH,HT,TT\}[/math].
We will use, for the moment, the first of the sample spaces given above. We will assume that
all four outcomes are equally likely, and define the distribution function [math]m(\omega)[/math] by
Let [math]E = \{HH,HT,TH\}[/math] be the event that at least one head comes up. Then, the probability
of [math]E[/math] can be calculated as follows:
Similarly, if [math]F = \{HH,HT\}[/math] is the event that heads comes up on the first toss, then we have
Example The sample space for the experiment in which the die is rolled is the 6-element set [math]\Omega = \{1,2,3,4,5,6\}[/math]. We assumed that the die was fair, and we chose the distribution function defined by
If [math]E[/math] is the event that the result of the roll is an even number, then [math]E =\{2,4,6\}[/math] and
Notice that it is an immediate consequence of the above definitions that, for every [math]\omega \in \Omega[/math],
That is, the probability of the elementary event [math]\{\omega\}[/math], consisting of a single outcome [math]\omega[/math], is equal to the value [math]m(\omega)[/math] assigned to the outcome [math]\omega[/math] by the distribution function.
Example Three people, A, B, and C, are running for the same office, and we assume that one and only one of them wins. The sample space may be taken as the 3-element set [math]\Omega = \{A,B,C\}[/math] where each element corresponds to the outcome of that candidate's winning. Suppose that A and B have the same chance of winning, but that C has only 1/2 the chance of A or B. Then we assign
Since
we see that
which implies that [math]5m(\mbox{C}) = 1[/math]. Hence,
Let [math]E[/math] be the event that either A or C wins. Then [math]E = \{A,C\}[/math], and
In many cases, events can be described in terms of other events through the use of the standard constructions of set theory. We will briefly review the definitions of these constructions. The reader is referred to Figure for Venn diagrams which illustrate these constructions.
Let [math]A[/math] and [math]B[/math] be two sets. Then the union of [math]A[/math] and [math]B[/math] is the set
The intersection of [math]A[/math] and [math]B[/math] is the set
The difference of [math]A[/math] and [math]B[/math] is the set
The set [math]A[/math] is a subset of [math]B[/math], written [math]A \subset B[/math], if every element of [math]A[/math] is also an element of [math]B[/math]. Finally, the complement of [math]A[/math] is the set
The reason that these constructions are important is that it is typically the
case that
complicated events described in English can be broken down into simpler
events using
these constructions. For example, if [math]A[/math] is the event that “it will snow
tomorrow and it
will rain the next day,” [math]B[/math] is the event that “it will snow tomorrow,” and
[math]C[/math] is
the event that “it will rain two days from now,” then [math]A[/math] is the intersection
of the events
[math]B[/math] and [math]C[/math]. Similarly, if [math]D[/math] is the event that “it will snow tomorrow or
it will rain the next day,” then [math]D = B \cup C[/math]. (Note that care must be
taken here,
because sometimes the word “or” in English means that exactly one of the two
alternatives
will occur. The meaning is usually clear from context. In this book, we
will always use
the word “or” in the inclusive sense, i.e., [math]A[/math] or [math]B[/math] means that at least
one of the two
events [math]A[/math], [math]B[/math] is true.) The event [math]\tilde B[/math] is the event that “it will
not snow
tomorrow.” Finally, if [math]E[/math] is the event that “it will snow tomorrow but it
will not rain
the next day,” then [math]E = B - C[/math].
Properties
The probabilities assigned to events by a distribution function on a sample space [math]\Omega[/math] satisfy the following properties:
- [math]P(E) \geq 0[/math] for every [math]E \subset \Omega\ [/math].
- [math]P(\Omega) = 1\ [/math].
- If [math]E \subset F \subset \Omega[/math], then [math]P(E) \leq P(F)\ [/math].
- If [math]A[/math] and [math]B[/math] are disjoint subsets of [math]\Omega[/math], then [math]P(A \cup B) = P(A) + P(B)\ [/math].
- [math]P(\tilde A) = 1 - P(A)[/math] for every [math]A \subset \Omega\ [/math].
For any event [math]E[/math] the probability [math]P(E)[/math] is determined from the distribution [math]m[/math] by
Property 2 is proved by the equations
Suppose that [math]E \subset F \subset \Omega[/math]. Then every element [math]\omega[/math] that
belongs to [math]E[/math] also belongs to [math]F[/math]. Therefore,
Suppose next that [math]A[/math] and [math]B[/math] are disjoint subsets of
[math]\Omega[/math]. Then every element [math]\omega[/math] of [math]A \cup B[/math] lies either in [math]A[/math] and
not
in [math]B[/math] or in [math]B[/math] and not in [math]A[/math]. It follows that
Finally, to prove Property 5, consider the disjoint union
It is important to realize that Property 4 in Theorem
can be extended to more than two sets. The general finite additivity
property is given by the following theorem.
If [math]A_1, \ldots, A_n[/math] are pairwise disjoint subsets of [math]\Omega[/math] (i.e., no two of the [math]A_i[/math]'s have an element in common), then
Let [math]\omega[/math] be any element in the union
We shall often use the following consequence of the above theorem.
Let [math]A_1, \ldots,A_n[/math] be pairwise disjoint events with [math]\Omega = A_1 \cup \cdots \cup A_n[/math], and let [math]E[/math] be any event. Then
The sets [math]E \cap A_1, \ldots,E \cap A_n[/math] are pairwise disjoint, and their union is the set [math]E[/math]. The result now follows from Theorem.
For any two events [math]A[/math] and [math]B[/math],
Property 4 can be generalized in another way. Suppose that [math]A[/math] and [math]B[/math] are
subsets of [math]\Omega[/math] which are not necessarily disjoint. Then:\hfil\break
If [math]A[/math] and [math]B[/math] are subsets of [math]\Omega[/math], then
The left side of Equation \ref{eq 1.1} is the sum of [math]m(\omega)[/math] for [math]\omega[/math] in either [math]A[/math] or [math]B[/math]. We must show that the right side of Equation \ref{eq 1.1} also adds [math]m(\omega)[/math] for [math]\omega[/math] in [math]A[/math] or [math]B[/math]. If [math]\omega[/math] is in exactly one of the two sets, then it is counted in only one of the three terms on the right side of Equation \ref{eq 1.1}. If it is in both [math]A[/math] and [math]B[/math], it is added twice from the calculations of [math]P(A)[/math] and [math]P(B)[/math] and subtracted once for [math]P(A \cap B)[/math]. Thus it is counted exactly once by the right side. Of course, if [math]A \cap B = \emptyset[/math], then Equation \ref{eq 1.1} reduces to Property 4. (Equation can also be generalized; see Theorem.)
Tree Diagrams
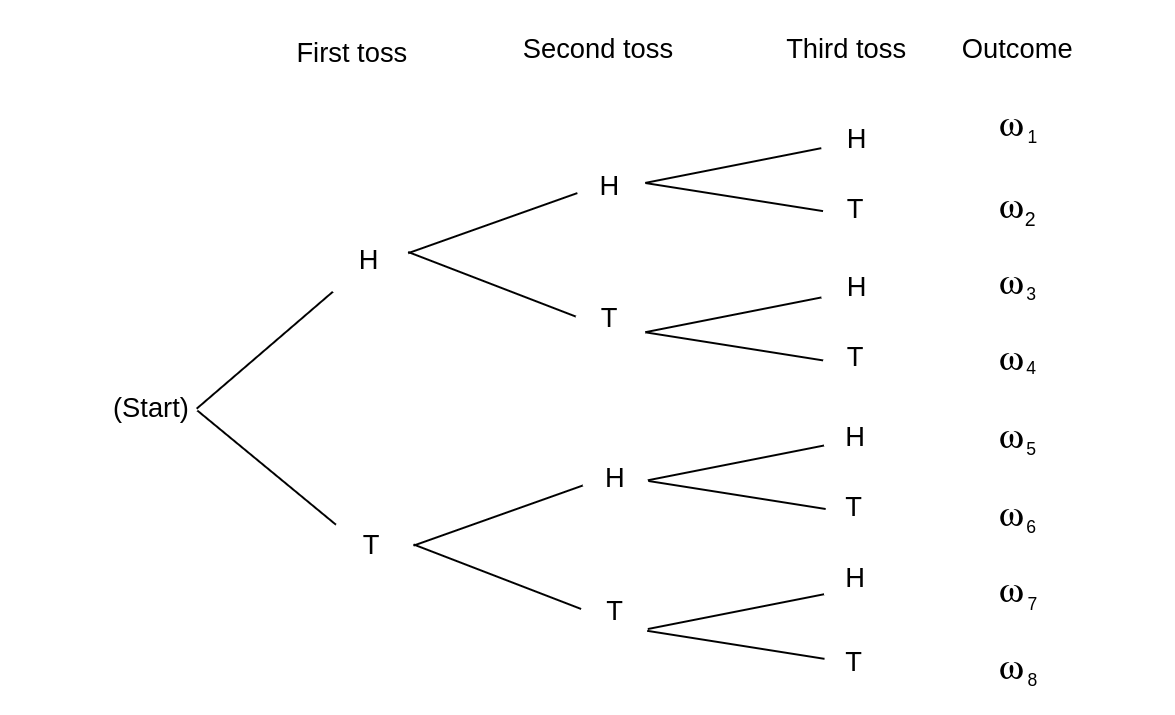
Example Let us illustrate the properties of probabilities of events in terms of three tosses of a coin. When we have an experiment which takes place in stages such as this, we often find it convenient to represent the outcomes by a tree diagram as shown in Figure.
A path through the tree corresponds to a possible outcome of the experiment. For the case of three tosses of a coin, we have eight paths [math]\omega_1, \omega_2, \ldots, \omega_8[/math] and, assuming each outcome to be equally likely, we assign equal weight, 1/8, to each path. Let [math]E[/math] be the event “at least one head turns up.” Then [math]\tilde E[/math] is the event “no heads turn up.” This event occurs for only one outcome, namely, [math]\omega_8 = \mbox{TTT}[/math]. Thus, [math]\tilde E = \{\mbox{TTT}\}[/math] and we have
By Property 5 of Theorem,
Note that we shall often find it is easier to compute the probability that an event does not happen rather than the probability that it does. We then use Property 5 to obtain the desired probability. Let [math]A[/math] be the event “the first outcome is a head,” and [math]B[/math] the event “the second outcome is a tail.” By looking at the paths in Figure we see that
Moreover, [math]A \cap B = \{\omega_3,\omega_4\}[/math], and so [math]P(A \cap B) = 1/4.[/math] Using Theorem, we obtain
Since [math]A \cup B[/math] is the 6-element set,
we see that we obtain the same result by direct enumeration.
In our coin tossing examples and in the die rolling example, we have assigned
an equal probability to each possible outcome of the experiment.
Corresponding
to this method of assigning probabilities, we have the following definitions.
Uniform Distribution
The uniform distribution on a sample space [math]\Omega[/math] containing [math]n[/math] elements is the function [math]m[/math] defined by
It is important to realize that when an experiment is analyzed to describe its possible outcomes, there is no single correct choice of sample space. For the experiment of tossing a coin twice in Example, we selected the 4-element set [math]\Omega = \{HH,HT,TH,TT\}[/math] as a sample space and assigned the uniform distribution function. These choices are certainly intuitively natural. On the other hand, for some purposes it may be more useful to consider the 3-element sample space [math]\bar\Omega = \{0,1,2\}[/math] in which 0 is the outcome “no heads turn up,” 1 is the outcome “exactly one head turns up,” and 2 is the outcome “two heads turn up.” The distribution function [math]\bar m[/math] on [math]\bar\Omega[/math] defined by the equations
is the one corresponding to the uniform probability density on the original sample space [math]\Omega[/math]. Notice that it is perfectly possible to choose a different distribution function. For example, we may consider the uniform distribution function on [math]\bar\Omega[/math], which is the function [math]\bar q[/math] defined by
Although [math]\bar q[/math] is a perfectly good distribution function, it is not consistent with observed data on coin tossing.
Example Consider the experiment that consists of rolling a pair of dice. We take as the sample space [math]\Omega[/math] the set of all ordered pairs [math](i,j)[/math] of integers with [math]1\leq i\leq 6[/math] and [math]1\leq j\leq 6[/math]. Thus,What is the probability of getting neither snakeeyes (double ones) nor boxcars (double sixes)? The event of getting either one of these two outcomes is the set
In the above coin tossing and the dice rolling experiments, we have assigned an equal probability to each outcome. That is, in each example, we have chosen the uniform distribution function. These are the natural choices provided the coin is a fair one and the dice are not loaded. However, the decision as to which distribution function to select to describe an experiment is not a part of the basic mathematical theory of probability. The latter begins only when the sample space and the distribution function have already been defined.
Determination of Probabilities
It is important to consider ways in which probability distributions are determined in practice. One way is by symmetry. For the case of the toss of a coin, we do not see any physical difference between the two sides of a coin that should affect the chance of one side or the other turning up. Similarly, with an ordinary die there is no essential difference between any two sides of the die, and so by symmetry we assign the same probability for any possible outcome. In general, considerations of symmetry often suggest the uniform distribution function. Care must be used here. We should not always assume that, just because we do not know any reason to suggest that one outcome is more likely than another, it is appropriate to assign equal probabilities. For example, consider the experiment of guessing the sex of a newborn child. It has been observed that the proportion of newborn children who are boys is about .513. Thus, it is more appropriate to assign a distribution function which assigns probability .513 to the outcome boy and probability .487 to the outcome girl than to assign probability 1/2 to each outcome. This is an example where we use statistical observations to determine probabilities. Note that these probabilities may change with new studies and may vary from country to country. Genetic engineering might even allow an individual to influence this probability for a particular case.
Odds
Statistical estimates for probabilities are fine if the experiment under consideration can be repeated a number of times under similar circumstances. However, assume that, at the beginning of a football season, you want to assign a probability to the event that Dartmouth will beat Harvard. You really do not have data that relates to this year's football team. However, you can determine your own personal probability by seeing what kind of a bet you would be willing to make. For example, suppose that you are willing to make a 1 dollar bet giving 2 to 1 odds that Dartmouth will win. Then you are willing to pay 2 dollars if Dartmouth loses in return for receiving 1 dollar if Dartmouth wins. This means that you think the appropriate probability for Dartmouth winning is 2/3. Let us look more carefully at the relation between odds and probabilities. Suppose that we make a bet at [math]r[/math] to [math]1[/math] odds that an event [math]E[/math] occurs. This means that we think that it is [math]r[/math] times as likely that [math]E[/math] will occur as that [math]E[/math] will not occur. In general, [math]r[/math] to [math]s[/math] odds will be taken to mean the same thing as [math]r/s[/math] to 1, i.e., the ratio between the two numbers is the only quantity of importance when stating odds.
Now if it is [math]r[/math] times as likely that [math]E[/math] will occur as that [math]E[/math] will
not occur, then the probability that [math]E[/math] occurs must be [math]r/(r+1)[/math], since we
have
If [math]P(E) = p[/math], the odds in favor of the event [math]E[/math] occurring are [math]r : s[/math] ([math]r[/math] to [math]s[/math]) where [math]r/s = p/(1-p)[/math]. If [math]r[/math] and [math]s[/math] are given, then [math]p[/math] can be found by using the equation [math]p = r/(r+s)[/math].
Example In Example we assigned probability 1/5 to the event that candidate C wins the race. Thus the odds in favor of C winning are [math]1/5 : 4/5[/math]. These odds could equally well have been written as [math]1 : 4[/math], [math]2 : 8[/math], and so forth. A bet that C wins is fair if we receive 4 dollars if C wins and pay 1 dollar if C loses.
Infinite Sample Spaces
If a sample space has an infinite number of points, then the way that a distribution function is defined depends upon whether or not the sample space is countable. A sample space is countably infinite if the elements can be counted, i.e., can be put in one-to-one correspondence with the positive integers, and uncountably infinite otherwise. Infinite sample spaces require new concepts in general (see Chapter Simulation of Continuous Probabilities), but countably infinite spaces do not. If
Example A coin is tossed until the first time that a head turns up. Let the outcome of the experiment, [math]\omega[/math], be the first time that a head turns up. Then the possible outcomes of our experiment are
for [math]-1 \lt r \lt 1[/math].
Putting [math]r = 1/2[/math], we see that we have a probability of 1 that the coin
eventually turns up heads. The possible outcome of tails every time has to
be
assigned probability 0, so we omit it from our sample space of possible
outcomes.
Let [math]E[/math] be the event that the first time a head turns up is after an even
number of tosses. Then
Historical Remarks
An interesting question in the history of science is: Why was probability not developed until the sixteenth century? We know that in the sixteenth century problems in gambling and games of chance made people start to think about probability. But gambling and games of chance are almost as old as civilization itself. In ancient Egypt (at the time of the First Dynasty, ca. 3500 B.C.) a game now called “Hounds and Jackals” was played. In this game the movement of the hounds and jackals was based on the outcome of the roll of four-sided dice made out of animal bones called astragali. Six-sided dice made of a variety of materials date back to the sixteenth century B.C. Gambling was widespread in ancient Greece and Rome. Indeed, in the Roman Empire it was sometimes found necessary to invoke laws against gambling. Why, then, were probabilities not calculated until the sixteenth century? Several explanations have been advanced for this late development. One is that the relevant mathematics was not developed and was not easy to develop. The ancient mathematical notation made numerical calculation complicated, and our familiar algebraic notation was not developed until the sixteenth century. However, as we shall see, many of the combinatorial ideas needed to calculate probabilities were discussed long before the sixteenth century. Since many of the chance events of those times had to do with lotteries relating to religious affairs, it has been suggested that there may have been religious barriers to the study of chance and gambling. Another suggestion is that a stronger incentive, such as the development of commerce, was necessary. However, none of these explanations seems completely satisfactory, and people still wonder why it took so long for probability to be studied seriously. An interesting discussion of this problem can be found in Hacking.[Notes 1]
The first person to calculate probabilities systematically was Gerolamo
Cardano
(1501--1576) in his book Liber de Ludo Aleae. This was translated from
the Latin by Gould and appears in the book Cardano: The Gambling
Scholar
by Ore.[Notes 2] Ore provides a fascinating discussion of
the life of this colorful scholar with accounts of his interests in many
different fields, including medicine, astrology, and mathematics. You will
also find there a detailed account of Cardano's famous battle with Tartaglia
over the solution to the cubic equation.
In his book on probability Cardano dealt only with the special case that we
have called the uniform distribution function. This restriction to equiprobable outcomes
was
to continue for a long time. In this case Cardano realized that the
probability that an event occurs is the ratio of the number of favorable
outcomes to the total number of outcomes.
Many of Cardano's examples dealt with rolling dice. Here he realized that
the
outcomes for two rolls should be taken to be the 36 ordered pairs [math](i,j)[/math]
rather than the 21 unordered pairs. This is a subtle point that was still
causing problems much later for other writers on probability. For example,
in
the eighteenth century the famous French mathematician d'Alembert, author of
several works on probability, claimed that when a coin is tossed twice
the number of heads that turn up would be 0, 1, or 2, and hence we should
assign equal probabilities for these three possible
outcomes.[Notes 3] Cardano chose the correct sample space
for
his dice problems and calculated the correct probabilities for a variety of
events.
Cardano's mathematical work is interspersed with a lot of advice to the
potential gambler in short paragraphs, entitled, for example: “Who Should
Play
and When,” “Why Gambling Was Condemned by Aristotle,” “Do Those Who Teach
Also Play Well?” and so forth. In a paragraph entitled “The Fundamental
Principle of Gambling,” Cardano writes:
The most fundamental principle of all in gambling is simply equal conditions, e.g., of opponents, of bystanders, of money, of situation, of the dice box, and of the die itself. To the extent to which you depart from that equality, if it is in your opponent's favor, you are a fool, and if in your own, you are unjust.[Notes 4]
Cardano did make mistakes, and if he realized it later he did not go back and change his error. For example, for an event that is favorable in three out of four cases, Cardano assigned the correct odds [math]3 : 1[/math] that the event will occur. But then he assigned odds by squaring these numbers (i.e., [math]9 : 1[/math]) for the event to happen twice in a row. Later, by considering the case where the odds are [math]1 : 1[/math], he realized that this cannot be correct and was led to the correct result that when [math]f[/math] out of [math]n[/math] outcomes are favorable, the odds for a favorable outcome twice in a row are [math]f^2 : n^2 - f^2[/math]. Ore points out that this is equivalent to the realization that if the probability that an event happens in one experiment is [math]p[/math], the probability that it happens twice is [math]p^2[/math]. Cardano proceeded to establish that for three successes the formula should be [math]p^3[/math] and for four successes [math]p^4[/math], making it clear that he understood that the probability is [math]p^n[/math] for [math]n[/math] successes in [math]n[/math] independent repetitions of such an experiment. This will follow from the concept of independence that we introduce in Section.
Cardano's work was a remarkable first attempt at writing down the laws of probability, but it was not the spark that started a systematic study of the subject. This came from a famous series of letters between Pascal and Fermat. This correspondence was initiated by Pascal to consult Fermat about problems he had been given by Chevalier de Méré, a well-known writer, a prominent figure at the court of Louis XIV, and an ardent gambler.
The first problem de Méré posed was a dice problem. The story goes that he
had been betting that at least one six would turn up in four rolls of a die and
winning too often, so he then bet that a pair of sixes would turn up in 24
rolls of a pair of dice. The probability of a six with one die is 1/6 and, by
the product law for independent experiments, the probability of two sixes when
a pair of dice is thrown is [math](1/6)(1/6) = 1/36[/math]. Ore[Notes 5] claims that a gambling rule of the
time suggested that, since four repetitions was favorable for the occurrence of
an event with probability 1/6, for an event six times as unlikely, [math]6 \cdot 4 =
24[/math] repetitions would be sufficient for a favorable bet. Pascal showed, by
exact calculation, that 25 rolls are required for a favorable bet for a pair of
sixes.
The second problem was a much harder one: it was an old problem and concerned
the determination of a fair division of the stakes in a tournament when the
series, for some reason, is interrupted before it is completed. This problem
is now referred to as the problem of points. The problem
had been a standard problem in mathematical texts; it appeared in Fra Luca
Paccioli's book summa de Arithmetica, Geometria, Proportioni et
Proportionalità, printed in Venice in 1494,[Notes 6] in the
form:
A team plays ball such that a total of 60 points are required to win the game, and each inning counts 10 points. The stakes are 10 ducats. By some incident they cannot finish the game and one side has 50 points and the other 20. One wants to know what share of the prize money belongs to each side. In this case I have found that opinions differ from one to another but all seem to me insufficient in their arguments, but I shall state the truth and give the correct way.
Reasonable solutions, such as dividing the stakes according to the ratio of
games won by each player, had been proposed, but no correct solution had been
found at the time of the Pascal-Fermat correspondence.
The letters deal mainly with the attempts of Pascal and Fermat to solve this problem. Blaise
Pascal (1623--1662) was a child prodigy, having published his
treatise on conic sections at age sixteen, and having invented a calculating
machine at age eighteen. At the time of the letters, his demonstration of the weight of the
atmosphere had already established his position at the forefront of
contemporary physicists. Pierre de Fermat (1601--1665) was a learned jurist in
Toulouse, who studied mathematics in his spare time. He has been called by some the prince of
amateurs and one of the greatest pure mathematicians of all times.
The letters, translated by Maxine Merrington, appear in Florence David's
fascinating historical account of probability, Games, Gods and Gambling.[Notes 7] In a letter dated Wednesday, 29th July, 1654, Pascal writes to
Fermat:
Sir,
Like you, I am equally impatient, and although I am again ill in bed, I cannot help telling you that yesterday evening I received from M. de Carcavi your letter on the problem of points, which I admire more than I can possibly say. I have not the leisure to write at length, but, in a word, you have solved the two problems of points, one with dice and the other with sets of games with perfect justness; I am entirely satisfied with it for I do not doubt that I was in the wrong, seeing the admirable agreement in which I find myself with you now...
Your method is very sound and is the one which first came to my mind in this research; but because the labour of the combination is excessive, I have found a short cut and indeed another method which is much quicker and neater, which I would like to tell you here in a few words: for henceforth I would like to open my heart to you, if I may, as I am so overjoyed with our agreement. I see that truth is the same in Toulouse as in Paris.
Here, more or less, is what I do to show the fair value of each game, when two opponents play, for example, in three games and each person has staked 32 pistoles.
Let us say that the first man had won twice and the other once; now they play another game, in which the conditions are that, if the first wins, he takes all the stakes; that is 64 pistoles; if the other wins it, then they have each won two games, and therefore, if they wish to stop playing, they must each take back their own stake, that is, 32 pistoles each.
Then consider, Sir, if the first man wins, he gets 64 pistoles; if he loses he gets 32. Thus if they do not wish to risk this last game but wish to separate without playing it, the first man must say: ‘I am certain to get 32 pistoles, even if I lost I still get them; but as for the other 32, perhaps I will get them, perhaps you will get them, the chances are equal. Let us then divide these 32 pistoles in half and give one half to me as well as my 32 which are mine for sure.’ He will then have 48 pistoles and the other 16...
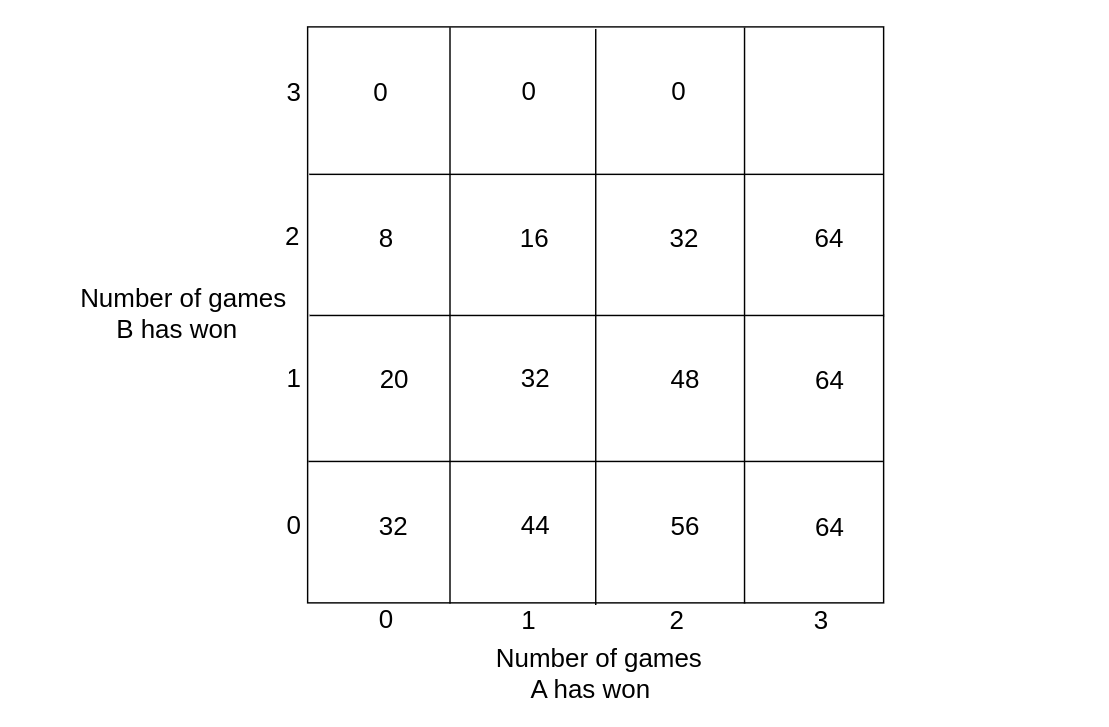
Pascal's argument produces the table illustrated in Figure for the amount due player A at any quitting point.
Each entry in the table is the average of the numbers just above and to the right of the number. This fact, together with the known values when the tournament is completed, determines all the values in this table. If player A wins the first game, then he needs two games to win and B needs three games to win; and so, if the tounament is called off, A should receive 44 pistoles.
The letter in which Fermat presented his solution has been lost; but
fortunately, Pascal describes Fermat's method in a letter dated Monday, 24th
August, 1654. From Pascal's letter:[Notes 8]
This is your procedure when there are two players: If two players, playing several games, find themselves in that position when the first man needs two games and second needs three, then to find the fair division of stakes, you say that one must know in how many games the play will be absolutely decided.
It is easy to calculate that this will be in four games, from which you can conclude that it is necessary to see in how many ways four games can be arranged between two players, and one must see how many combinations would make the first man win and how many the second and to share out the stakes in this proportion. I would have found it difficult to understand this if I had not known it myself already; in fact you had explained it with this idea in mind.
Fermat realized that the number of ways that the game might be finished may not be equally likely. For example, if A needs two more games and B needs three to win, two possible ways that the tournament might go for A to win are WLW and LWLW. These two sequences do not have the same chance of occurring. To avoid this difficulty, Fermat extended the play, adding fictitious plays, so that all the ways that the games might go have the same length, namely four. He was shrewd enough to realize that this extension would not change the winner and that he now could simply count the number of sequences favorable to each player since he had made them all equally likely. If we list all possible ways that the extended game of four plays might go, we obtain the following 16 possible outcomes of the play:
| [math]\underline{WWWW}[/math] | [math]\underline{WLWW}[/math] | [math]\underline{LWWW}[/math] | [math]\underline{LLWW}[/math] |
| [math]\underline{WWWL}[/math] | [math]\underline{WLWL}[/math] | [math]\underline{LWWL}[/math] | [math]LLWL[/math] |
| [math]\underline{WWLW}[/math] | [math]\underline{WLLW}[/math] | [math]\underline{LWLW}[/math] | [math]LLLW[/math] |
| [math]\underline{WWLL}[/math] | [math]WLLL[/math] | [math]LWLL[/math] | [math]LLLL[/math] |
Player A wins in the cases where there are at least two wins (the 11 underlined cases), and B wins in the cases where there are at least three losses (the other 5 cases). Since A wins in 11 of the 16 possible cases Fermat argued that the probability that A wins is 11/16. If the stakes are 64 pistoles, A should receive 44 pistoles in agreement with Pascal's result. Pascal and Fermat developed more systematic methods for counting the number of favorable outcomes for problems like this, and this will be one of our central problems. Such counting methods fall under the subject of combinatorics, which is the topic of Chapter Combinatorics.
We see that these two mathematicians arrived at two very different ways to solve the problem of points. Pascal's method was to develop an algorithm and use it to calculate the fair division. This method is easy to implement on a computer and easy to generalize. Fermat's method, on the other hand, was to change the problem into an equivalent problem for which he could use counting or combinatorial methods. We will see in Chapter Combinatorics that, in fact, Fermat used what has become known as Pascal's triangle! In our study of probability today we shall find that both the algorithmic approach and the combinatorial approach share equal billing, just as they did 300 years ago when probability got its start.
General references
Doyle, Peter G. (2006). "Grinstead and Snell's Introduction to Probability" (PDF). Retrieved June 6, 2024.
Notes
- I. Hacking, The Emergence of Probability (Cambridge: Cambridge University Press, 1975).
- O. Ore, Cardano: The Gambling Scholar (Princeton: Princeton University Press, 1953).
- J. d'Alembert, “Croix ou Pile,” in L'Encyclopédie, ed. Diderot, vol. 4 (Paris, 1754).
- O. Ore, op. cit., p. 189.
- O. Ore, “Pascal and the Invention of Probability Theory, American Mathematics Monthly, vol. 67 (1960), pp. 409--419.
- ibid., p. 414.
- F. N. David, Games, Gods and Gambling (London: G. Griffin, 1962), p. 230 ff.
- ibid., p. 239ff.