Exercise
May 07'23
Answer
Solution: D
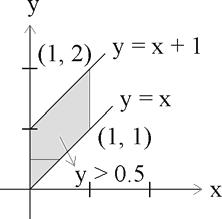
The diagram below illustrates the domain of the joint density [math]f ( x, y )[/math] of [math]X[/math] and [math]Y[/math] .
We are told that the marginal density function of [math]X[/math] is [math]f_X( x ) = 1 , 0 \lt x \lt 1 [/math] while [math]f_{y|x} ( y | x) = 1, \, x \lt y \lt x + 1. [/math] It follows that
[[math]]
f(x,y) = f_X(x) f_{y | x}(y | x) = \begin{cases} 1, \, 0 \lt x \lt 1, \, x \lt y \lt x+ 1 \\ 0, \, \textrm{otherwise} \end{cases}
[[/math]]
Therefore
[[math]]
\begin{align*}
\operatorname{P}[ Y \gt 0.5 ] = 1- \operatorname{P}[Y \leq 0.5] &= 1- \int_0^{1/2} \int_x^{1/2} dydx \\
&= 1- \int_0^{1/2} y \Big |_x^{1/2} dx \\
&= 1- \int_0^{1/2} (\frac{1}{2} - x) dx \\
&= 1- [\frac{1}{2}x - \frac{1}{2}x^2] \Big |_0^{1/2} \\
&= 1- \frac{1}{4} + \frac{1}{8} = \frac{7}{8}.
\end{align*}
[[/math]]
Note since the density is constant over the shaded parallelogram in the figure the solution is also obtained as the ratio of the area of the portion of the parallelogram above y equals 0.5 to the entire shaded area.